House Price Prediction with Optimistic Machine Learning Methods

Using Bayesian Optimization

Haolan Jiang

Faculty of Engineering and Information Technology, University of Melbourne, Melbourne, 3010, Australia

Keywords: XGboost, Optimization, House Price, Machine Learning, Random Forest

Abstract: Recently, housing has been a fundamental necessity for human survival. However, the challenge lies in the

often-inflated housing prices, particularly in high-GDP cities. House price prediction is crucial for citizens as

it aids in effective financial planning and contributes to social stability. This study delves into the factors

influencing house prices, employing and evaluating four regression models: multiple linear regression,

regression decision tree, Random Forest, and XGBoost. The focus is on optimizing the performance of the

two most promising models. The study finds that there is no substantial positive or negative association

between the prediction label, which is the average house price of a region, and any individual attribute in the

dataset. Through model comparisons, it is observed that the decision tree model outperforms the regression

model significantly, with the integrated models, specifically Random Forest and XGBoost, outshining the

regular regression tree model. In 5-fold cross-validation, the Bayesian optimized XGBoost model yields the

best results in this study. The post-optimization R2 value of XGBoost is 0.846, showcasing an improvement

of 0.024 compared to the pre-optimization phase. The hybrid model introduced in this study holds significant

research potential in the realm of house price prediction. Additionally, it provides valuable insights for

individuals, enabling them to make well-informed financial plans, particularly in terms of home purchase

decisions. This, in turn, contributes to addressing potential social issues and fostering greater social harmony

and stability.

1 INTRODUCTION

With the rapid expansion of urban areas and a rising

population, the real estate market experiences

frequent and unpredictable fluctuations. Given that

housing is a fundamental requirement for societal

well-being, variations in housing demand directly

influence social security and economic well-being.

Changes in housing prices can impact a nation's

economy, political framework, urban safety, and

various other aspects (Malang et al. 2017). This

phenomenon has garnered recognition from

numerous international organizations and research

institutes (Ebekozien et al. 2019). The significant rise

in housing prices in certain countries has led to a lack

of purchasing power for many citizens. This, in turn,

has directly impacted the country's economy and the

quality of life for its citizens (Cheng 2018, Tian et al.

2020, Allen et al. 2009). In the realm of predictive

modeling, machine learning stands out as a potent

tool, capable of delivering precise and comprehensive

predictions.

With its widespread application in recent years,

machine learning proves effective in tasks ranging

from regression target prediction to classification

target prediction (Hansen 2020, Ho et al. 2021).

Leveraging extensive datasets and features, machine

learning excels in uncovering intricate relationships

concealed within the data. Consequently, there is a

need to explore and identify which machine learning

models, among the myriad options available, yield

superior results in the prediction of house prices

(Truong et al. 2020). Researchers typically focused

on testing either the effectiveness of integrated

models for house price prediction, or solely

regression models, or conducting tests without

optimization attempts (Gupta et al. 2022, Debanjan&

Dutta 2017, Mu et al. 2014, Abigail et al. 2022).

However, comprehensively evaluates regression

models, supervised learning models, and integrated

models. Additionally, Bayesian optimization is

applied as a mixed optimization technique on the

better-performing models.

488

Jiang, H.

House Price Prediction with Optimistic Machine Learning Methods Using Bayesian Optimization.

DOI: 10.5220/0012825400004547

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 488-496

ISBN: 978-989-758-690-3

This paper aims to compare and analyze various

machine learning models for house price prediction.

The study evaluates four different machine learning

models, including multiple linear regression,

regression decision tree, Random Forest, and

XGBoost. This study approaches the prediction of

housing prices as a regression problem, utilizing a

publicly available housing-themed dataset from

Kaggle for research. The objective is to assess various

models' learning capabilities on feature values,

identify the most effective model, and subsequently

optimize it. This paper uses the R2 coefficient of

determination as its primary evaluation metric. A

five-fold cross-validation procedure is used to

examine the research findings. The experimental

findings indicate that, among the four models

assessed in this study, the XGBoost model

consistently outperforms the others. Through

Bayesian optimization applied to the XGBoost

model, there is a notable enhancement in the R2

score, underscoring the positive impact of Bayesian

optimization within the scope of this research. The

hybridization of XGBoost and Bayesian optimization

not only demonstrates promising results but also

holds enduring exploratory research significance,

particularly in the domain of house price prediction.

2 METHODOLOGY

2.1 Dataset Description and

Preprocessing

Data preprocessing is an essential stage in machine

learning to guarantee the accuracy and quality of the

data. In order to ensure that the input data to the model

is both dependable and applicable, this research does

extensive preprocessing. In this investigation, the

20433 × 10 "California Housing Prices" dataset from

Kaggle is used (Kaggle 2023). The features include

longitude, latitude, housing median age, total

bedrooms, population, housing holds, median

income, median house value, and ocean proximity.

Median house value is considered a predictive label,

while ocean proximity is a categorical feature

classified into five categories: NEAR BAY, <1H

OCEAN, INLAND, NEAR OCEAN, and ISLAND.

The remaining eight features are random numeric

variables.

As the dataset is relatively complete, with only

207 missing values in total bedrooms, constituting a

small portion of the overall dataset, this paper chooses

to remove these items directly. Further research

reveals that the ISLAND feature in ocean proximity

appears only 5 times, and the corresponding house

prices are significantly higher than the average.

Therefore, ISLAND is removed to improve the

accuracy of the model prediction. According to the

average house price distribution graph, house prices

above $500,000 stand out as outliers, significantly

higher than the average house price and exhibiting a

sudden rise in the distribution graph. Hence, this

study also deletes them as noise points. For the

classification type data ocean proximity, Label

Encoder is used in this paper to process it and convert

it into numerical form for model training. In the

meantime, the dataset is split into test and training

sets in a 7:3 ratio for cross-validation purposes in

order to evaluate the model's capacity for

generalization. Table 1 contains detailed information

on the feature values.

Table 1: The description of the dataset

Features Data Type Description

Longitude float64 Longitude of the

area

Latitude float64 Latitude of the

area

Housing

median age

float64 Housing median

age of the area

Total rooms float64 Total rooms of

the area

Total bedrooms float64 Total bedrooms

of the area

Population float64 Population of

the area

Households float64 Number

households of

the area

Median income float64 Median income

of the area

Median house

value

float64 Median house

value of the area

Ocean

proximity

object The proximity

pf a location to

ocean

2.2 Proposed Approach

In this research, the focus is on conducting a thorough

exploration and analysis of the correlation between

feature values and labels within the dataset. This

analysis is approached through three dimensions: box

plots, Correlation heat map, and distribution plots.

Subsequently, the feature values are utilized for

training in machine learning models. The resulting

outcomes from these models are then subjected to

evaluation, with a comprehensive analysis of four

models. Ultimately, the model demonstrating

superior performance undergoes further optimization.

House Price Prediction with Optimistic Machine Learning Methods Using Bayesian Optimization

489

The entirety of this process is elucidated in the

accompanying Figure 1.

Figure 1: Flow chart of Methodology (Photo/Picture credit:

Original)

2.2.1 Data Analysis

Prior to the assessment of machine learning models,

this study delves into a comprehensive exploration of

the correlations among feature values within the

dataset. A nuanced understanding of the relationship

between feature values and the predicted labels is

deemed imperative for enhancing the efficacy of

subsequent model development.

First, distribution plot analysis is conducted as

part of data exploration. Distribution plots provide an

intuitive understanding of data distribution, aiding in

observing the overall shape, central tendency, and

dispersion of the data. They also facilitate the

identification of outliers, making it easy to detect any

anomalies or outliers. Through distribution plots, it

becomes apparent whether there are outliers or

abnormal points, enabling straightforward data

cleaning or outlier handling. In distribution plots, the

incorporation of Gaussian distribution aids in

analyzing the charts. The presence of Gaussian

distribution in the dataset distribution contributes to a

better understanding of the data's characteristics,

laying the foundation for subsequent statistical

analysis and modeling. The formula for Gaussian

distribution is:

()

fx e

πσ

−

=⋅

(1)

Where,

:Mean of the distribution

:Standard

deviation

:Natural logarithm

The graphical characteristics of a Gaussian

distribution include symmetry, with the mean as the

central point, resulting in a symmetrical distribution

on both sides. The distribution graph exhibits a

typical bell-shaped curve, gradually decreasing on

either side and approaching the horizontal axis.

Second, this study conducted an analysis of the

dataset using a correlation heatmap. During the data

exploration phase, a correlation heatmap proves

valuable in identifying features that may significantly

influence the target variable. This information guides

subsequent feature engineering or modeling

processes. By examining the correlation heatmap, one

can discern the degree of correlation between

features. Highly correlated features may contain

similar information, prompting consideration for

removing one feature during model training to reduce

redundancy and enhance model simplicity.

Third, this study conducted a box plot analysis on

the dataset. Box plots provide a concise way to

represent the distribution of a dataset, including the

median, quartiles, and potential outliers. They are

highly effective for a quick comparison of central

tendency and spread across multiple datasets. This is

particularly useful in exploratory data analysis for

comparing different groups or categories. Important

elements of a box plot: The median (Q2) is the

midpoint number obtained by sorting the data in

ascending order. Q1, or lower quartile: The 25th

percentile of the data, representing the value at the

25% location. Upper Quartile (Q3): The value at the

75% position, or the 75th percentile of the data.

Interquartile Range (IQR): IQR indicates the spread

of the data and is calculated as IQR = Q3 - Q1. Lower

Whisker: Calculated as Q1 - 1.5 × IQR, the starting

point of the whisker. Upper Whisker: Calculated as

Q3 + 1.5 × IQR, the end point of the whisker.

Outliers: Data points beyond the upper and lower

whiskers are considered outliers and are typically

marked with individual points on the box plot.

2.2.2 Multiple Linear Regression

Multiple linear regression is a commonly used

regression analysis method in the fields of statistics

and machine learning. It aims to study the linear

relationship between multiple independent variables

and a dependent variable. This method attempts to

establish a linear model to explain or predict the

variability of a dependent variable, taking into

account the combined effects of multiple influencing

factors:

01122 pp

Yxx x

ββ β β ε

=+ + ++ +

(2)

where Y represents the dependent variable (predicted

label values), x represents the independent. variable

(features involved in model training),

is the

coefficient specific to the independent variable,

representing the intercept,

is the error term,

representing the unexplained portion of the model. In

this study, the parameters for multiple linear

regression were configured with the following

settings: In the model fitting process, the 'fit intercept'

parameter is configured as True, enabling the

calculation of the intercept. Similarly, the 'normalize'

ICDSE 2024 - International Conference on Data Science and Engineering

490

parameter is set to True, ensuring normalization of the

regression variables before fitting. Additionally,

'copy X' is adjusted to True, leading to the creation of

a data copy. Lastly, the 'n job' parameter is set to -1,

allowing the utilization of all available CPUs for

efficient computation."

2.2.3 Decision Tree Regression

Decision tree regression is a machine learning

algorithm used to address regression problems. In this

study, decision tree regression is employed to predict

house prices. The generation process involves

recursively partitioning the feature space by selecting

the optimal features to divide the dataset into subsets

until reaching a stopping condition. Each leaf node

stores a numerical value, representing the continuous

output prediction. This study employed an exhaustive

grid search to optimize decision tree regression. The

purpose was to identify the optimal parameter

configurations. Exhaustive grid search is a technique

that explores all possible combinations within

specified parameter ranges. Widely used in machine

learning, especially in hyperparameter tuning, the

main advantage of exhaustive grid search lies in its

ability to try all possible parameter combinations,

ensuring the discovery of the globally optimal

hyperparameter configuration. Through exhaustive

grid search, the final optimal parameter ranges for

decision tree regression were determined as follows:

The 'max depth' parameter is defined within the range

of 10 to 17, while 'min samples split' is fine-tuned

with values [35, 40, 45, 50]. Simultaneously, 'min

impurity decrease' undergoes adjustments with the

values [0, 0.0005, 0.001, 0.002, 0.003, 0.005, 0.006,

0.007]. The 'max depth' setting governs the maximum

depth of the decision tree, striking a balance between

model complexity and generalization. Regarding 'min

samples split,' it denotes the minimum number of

samples a node must have before splitting,

influencing tree growth and mitigating overfitting

risks for larger values. Similarly, 'min impurity

decrease,' representing the Minimum Impurity

Decrease, establishes a threshold for evaluating the

worthiness of a split, thereby controlling tree growth

and minimizing overfitting. The remaining

parameters adhere to the default settings for decision

tree regression in scikit-learn.

2.2.4 XGboost

XGBoost is a powerful gradient boosting algorithm

that employs decision trees as base learners. It

iteratively trains weak learners, focusing on samples

that the previous model failed to classify correctly,

gradually improving the overall model accuracy.

XGBoost uses CART trees, defines an objective

function incorporating regularization terms to

measure model performance, and fits new tree models

through gradient boosting. Regularization is

employed to prevent overfitting. Ultimately, by

summing the predictions of all trees, the final

prediction of the XGBoost model is obtained.

XGBoost is renowned for its efficiency, fast training

speed, robust performance, and handling of missing

values. In this study, the XGBoost model is

configured with the following parameters: The 'n

estimators' parameter is configured at 300, signifying

the number of base learners employed.

Simultaneously, 'learning rate' is fine-tuned to 0.1,

governing the weight contraction of each base

learner. Additionally, 'max depth' is established at 7,

delineating the maximum depth of each base learner.

All remaining parameters in the XGBoost regressor

retain their default values.

2.2.5 Random Forest

Several decision trees are used in Random Forest, a

potent ensemble learning method, to make

predictions. A randomly chosen sample of the data

and features is used to train each decision tree.

Random Forest delivers great accuracy, robustness,

and successfully reduces overfitting by mixing

predictions from numerous trees. In this study, the

Random Forest model is configured with the

following parameters: The 'n estimators' parameter is

established at 300, designating the number of base

learners (decision trees) within the ensemble. The

'criterion' is configured to 'mse,' specifying the

criterion for tree splitting using mean squared error.

'Max depth' is set to 6, indicating the maximum depth

of each base learner. 'Min samples split' is defined as

0.1, determining the minimum number of samples

required for internal node splitting. Additionally, 'min

impurity decrease' is set to 0.01, specifying the

minimum impurity reduction necessary for a split. All

remaining parameters adhere to the default values in

the scikit-learn Random Forest implementation.

2.2.6 Optimization

This study utilized Bayesian optimization to fine-tune

hyperparameters for XGBoost and Random Forest

models. Bayesian optimization is an iterative method

for global optimization, aiming to find the global

optimum with minimal iterations. It combines prior

knowledge and observed results to estimate the

posterior distribution of the objective function. In

each step, it selects the next sampling point to

House Price Prediction with Optimistic Machine Learning Methods Using Bayesian Optimization

491

maximize expected improvement in the objective

function, making it effective for complex, nonlinear

optimization problems with significant noise

interference.

The steps of Bayesian optimization include:

Select Prior Distribution: Choose an initial prior

distribution for the objective function. Sampling: Use

the prior distribution to select the next sampling point,

minimizing uncertainty in the objective function.

Evaluation: Calculate the objective function value at

the new sampling point. Update Posterior: Update the

posterior distribution with new observed results,

adjusting mean and variance parameters. Select Next

Sampling Point: Choose the next sampling point

based on the posterior distribution, maximizing

expected improvement. Iteration: Repeat these steps

until reaching the predetermined number of iterations

or other stopping criteria.

In this study, the model optimization is based on

the "bayes opt" library. For Random forests, the

Bayesian optimization process involves defining the

hyperparameter search range and executing the

optimization function. The grid search includes 'n

estimators' within the range of 100 to 1000, 'max

depth' adjusted from 2 to 20, and 'min samples leaf'

ranging from 1 to 10. Following this, optimal

parameters and scores are generated and evaluated on

the validation set. Subsequently, a Random Forest

regression model is constructed using these optimal

parameters, and predictions are made on the test set.

In the case of XGBoost, Bayesian optimization

commences by establishing the search range for

hyperparameters, including 'max depth' ranging from

1 to 5, 'n estimators' from 100 to 500, and 'learning

rate' adjusted between 0.01 and 0.2. The optimization

function is then invoked to yield optimal parameters

and scores. After evaluating the validation set, the

optimal parameters are utilized to construct the

XGBoost regression model, and predictions are made

on the test set for a comprehensive analysis.

3 RESULT AND DISCUSSION

This section presents an analysis and visual

representation of the dataset and model testing

results.

3.1 Analysis of Distribution Plots

Results

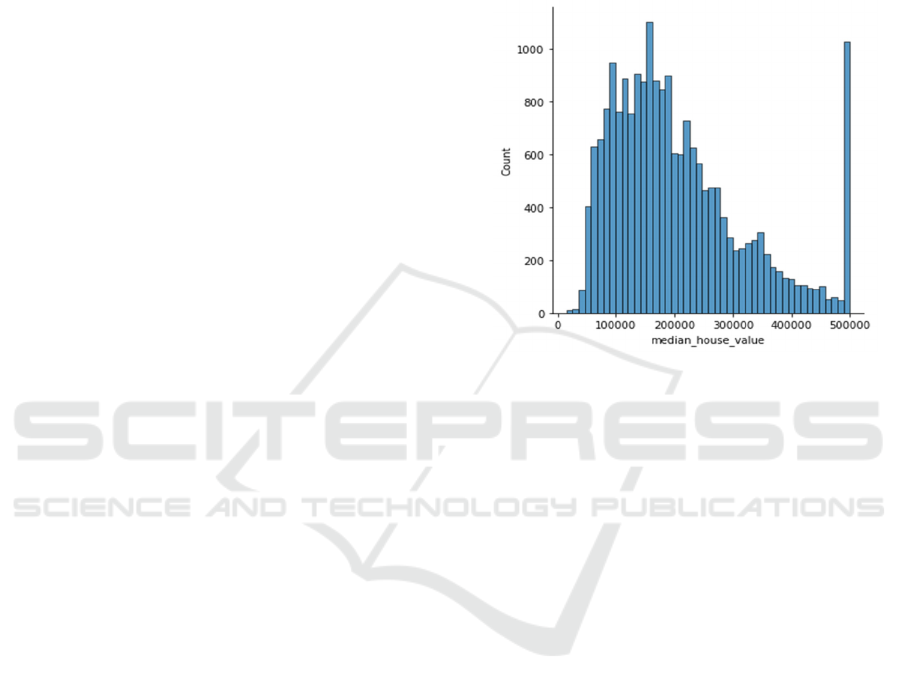
First, Figure 2 displays the distribution of median

house value, revealing that it does not follow a

Gaussian distribution trend. This distribution

characteristic, where the graph is not symmetric about

the center, and there is a difference between the

median and mean values, suggests a high dispersion

and non-linear correlation in housing prices. This

non-linear trend could be attributed to various factors

such as market sentiment, government policies,

indicating outcomes beyond a simple linear

relationship.

Figure 2: Median house value distribution (Photo/Picture

credit: Original).

Second, Figure 3 presents a clustering correlation

heatmap, revealing that the predicted label, housing

price, does not exhibit strong positive or negative

correlations with other features. This observation may

be attributed to the influence of outliers and non-

linear correlations, as an abundance of outliers can

lead to data skewness, resulting in overall weak

correlations. Additionally, it's important to note that

correlation heatmaps primarily reflect linear

relationships, suggesting the potential need for non-

linear models when dealing with non-linear

correlated data.

This finding sets the stage for subsequent model

testing, suggesting that models designed to handle

non-linear correlations may yield better results. The

observation of clustering complexity in this dataset

indicates diverse clustering patterns. The intricate

nature of clustering may signify the presence of

multiple correlation patterns or complex data

structures. This complexity could be attributed to

interactions or dependencies between different

features, denoted as "feature interactions."

Understanding these nuances contributes to a better

comprehension of the data's underlying structure,

providing valuable insights for further analysis and

modeling.

ICDSE 2024 - International Conference on Data Science and Engineering

492

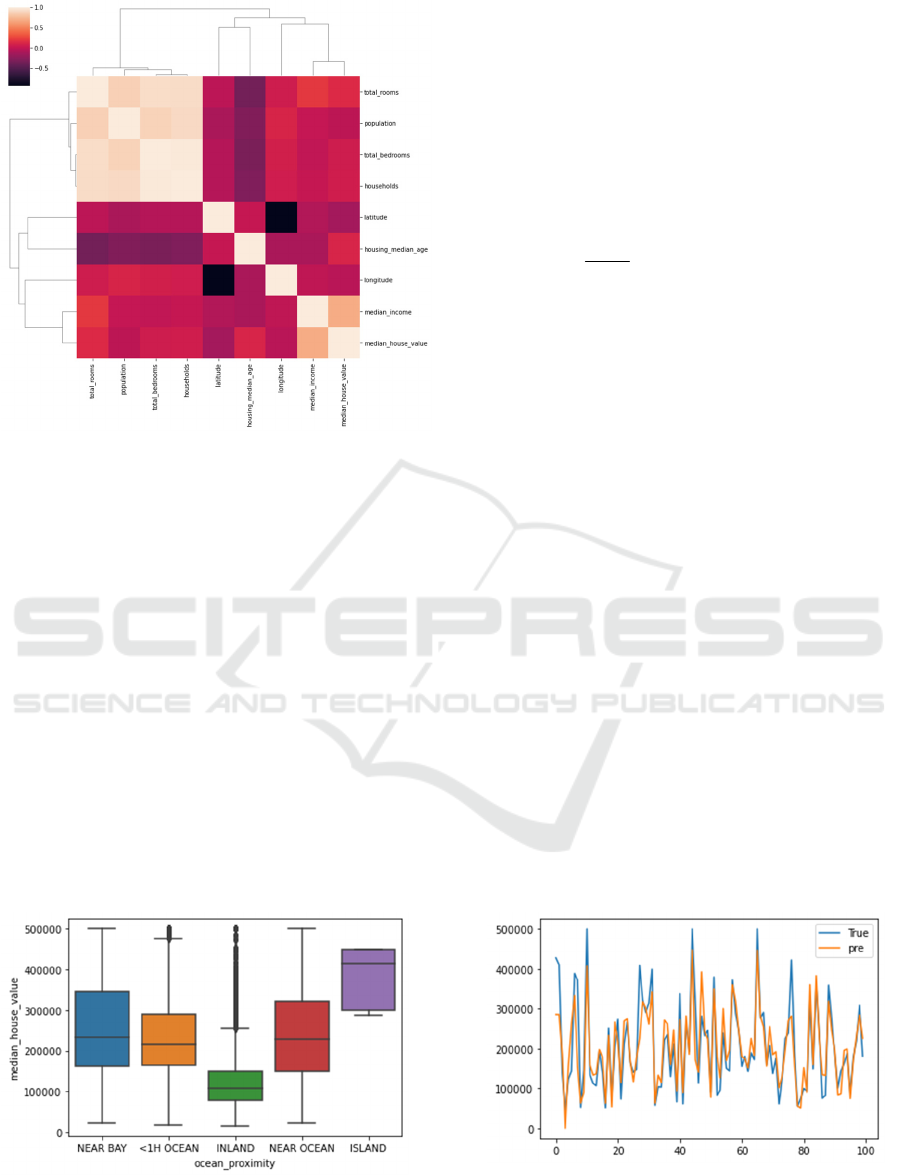
Figure 3: Correlation heat map (Picture credit: Original).

Third, In Figure 4, it is observed that the INLAND

feature has a significant number of outliers, indicating

that inland areas may possess market characteristics

different from coastal regions. The presence of

outliers may reflect larger fluctuations in housing

prices in this region or the influence of unique factors.

For the ISLAND feature, it is noted that the median is

considerably higher than other features, and there is

no upper whisker. Further examination reveals that

this feature consists of only 5 rows of samples, with

an average house price of $380,440, significantly

higher than the average house prices of other features

($206,821). Considering that ISLAND does not align

with mainstream housing preferences and exhibits an

unusually high average house price, this study opts to

remove it to ensure the generality and robustness of

the model. This decision is grounded in a thorough

analysis of the data, aiming to ensure that the model

Figure 4: Box plot between ocean proximity and median

house value (Picture credit: Original).

reflects general market trends more effectively during

data processing, without being unduly influenced by

individual outlier samples.

This study employs the scikit-learn learning

library for Python coding, implemented within the

Spyder source code editor. The primary metric for

evaluating model performance is the coefficient of

determination (R2). The calculation formula is as

follows:

SSR

SST

=−

(3)

where SSR represents the portion of variability in the

target variable that the model fails to explain. In

contrast, SST encompasses the overall variability of

the target variable.

The capacity of a regression model to explain

variance in the target variable, or the percentage of

the target variable's variability that the model can

account for, is measured by the regression model's

goodness of fit, or R2. It accepts values in the range

of 0 to 1, with a value closer to 1 denoting a higher

explanatory power of the model—that is, a closer

match between the expected and actual values.

3.2 Model Performance Analysis

First, in this study the multiple linear regression

model achieved an R2 score of 0.442 on the test set,

which is the lowest among all tested models. First,

observing Figure 5 reveals that the fitting effect

between predicted values and actual values is

unsatisfactory, indicating significant prediction

errors. This could be related to the linear regression

model's assumption of linearity in the connection

between independent and dependent variables, which

may be insufficient to fully represent the complexities

of non-linear interactions.

Figure 5: Multiple linear regression visualization line graph

(Picture credit: Original).

House Price Prediction with Optimistic Machine Learning Methods Using Bayesian Optimization

493

Second, decision tree regression achieves an R2

of 0.735 on the test set. Observing Figure 6, compared

to the multiple linear regression model, the residuals

between true and predicted values decrease,

indicating an overall better fit to the true values. This

suggests that grid search optimization has a positive

impact on enhancing the performance of decision tree

regression on this dataset. Furthermore, Fig 6 reveals

that while predictions align well with true values in

certain intervals, there are areas where the fit is not as

accurate. This phenomenon may be attributed to

specific circumstances or trends affecting certain

regions, potentially manifesting as anomalies or

larger errors in the model. The contribution of feature

values to the model cannot be ignored, as nonlinear

relationships between certain features and the target

variable may result in increased errors in specific

segments.

Figure 6: Decision tree regression visualization line chart

(Picture credit: Original)

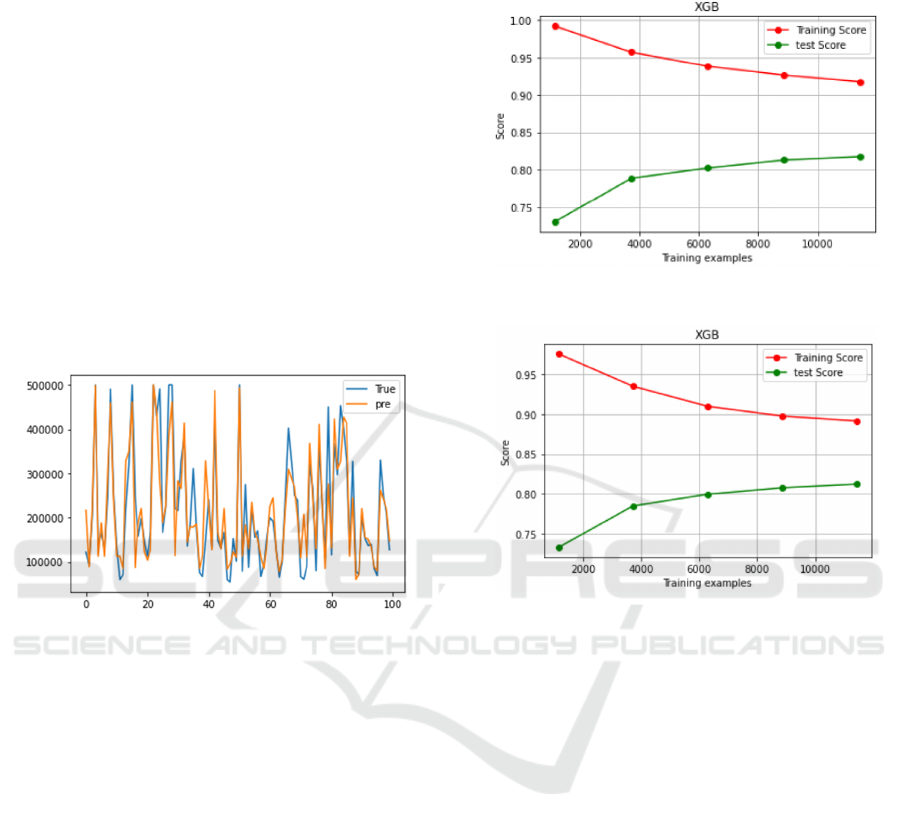
Third, XGBoost model achieves an R2 score of

0.822 on the test set, and after 5-fold cross-validation,

the R2 improves to 0.828. The model exhibits strong

performance in cross-validation, demonstrating its

ability to generalize well to unseen data. This

suggests that the model effectively captures the

overall patterns in the data, including variations in

both the training and test sets, without overfitting to

the training data. This is a positive indication,

indicating the model's robust performance when

faced with new data. In Figure 7 and Figure 8,

learning curves show that further adjusting

XGBoost's 'n estimators' can help reduce overfitting.

Four, the Random Forest model achieves an R2

score of 0.805 on the test set, and after 5-fold cross-

validation, the R2 improves to 0.809. It is evident that

the performance of the Random Forest model in the

5-fold cross-validation is superior to that on the

original test set. The results indicate that ensemble

models outperform individual decision tree and linear

regression models in addressing the house price

regression problem for this dataset. Among them,

XGBoost attains the highest R2 score.

Figure 7: XGboost learning curve (Picture credit: Original).

Figure 8: XGboost learning curve (Picture credit: Original).

3.3 Bayesian Optimization of XGboost

and Random Forest

After Bayesian optimization, the R2 scores on the test

set for XGBoost and Random Forest improved to

0.846 and 0.825, respectively. The findings show that

maximizing the home price regression problem in this

dataset benefits from the application of Bayesian

optimization. The fitting effect of the predicted values

to the actual values is better than Decision Tree

Regression and Multivariate Linear Regression, as

shown in Figure 9 and Figure 10. Among the two

ensemble models discussed in this paper, XGBoost

consistently exhibits higher R2 values than Random

Forest, both before and after optimization. The

underlying reason may lie in the fact that XGBoost,

as a gradient boosting algorithm, iteratively trains

multiple weak learners and combines them,

progressively enhancing model performance. In

contrast, while Random Forest is also an ensemble

learning algorithm, it may be constrained by the

complexity of individual decision trees. XGBoost

incorporates regularization terms, aiding in

ICDSE 2024 - International Conference on Data Science and Engineering

494

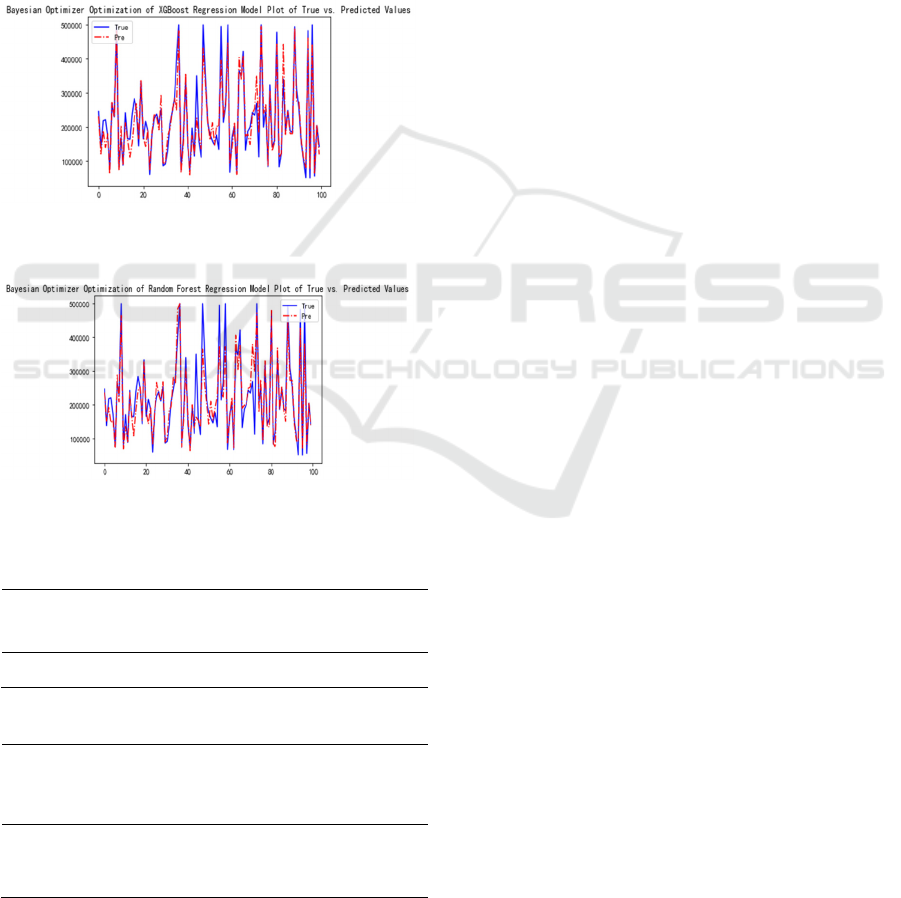
preventing overfitting, which could contribute to its

better generalization on unseen data compared to

Random Forest, making it more robust.

Visualizations of the four models discussed in this

paper reveal that in certain specific intervals, none of

the models can fit the actual values well. This might

be attributed to significant nonlinear relationships

between feature values and prediction labels in those

specific intervals, influenced by special

circumstances or trends in that area. For instance, a

particular geographical region may be affected by

seasonal or short-term events. Table 2 and Table 3 are

detailed comparative tables of all the machine

learning models tested in this study.

Figure 9: XGboost bayesian optimization visualization

chart (Picture credit: Original).

Figure 10: Random forest Bayesian optimization

visualization chart (Picture credit: Original).

Table 2: Summary of results.

Multiple

Linear

ression

Decision

Tree

ression

XGBoost

Random

Forest

R2 0.442 0.735 0.822 0.805

Table 2: Summary of results.

After

Bayesian

optimization

Mean

Squared

Error (MSE)

Explained

Variance

(EV)

Mean

Absolute

Error

(MAE)

XGBoost

0.846 2162782139.6 0.83 30852.9

Random

Forest

0.825 2377672267.9 0.82 31415.89

4 CONCLUSION

This study aims to predict housing prices using

multiple linear regression, decision tree regression,

XGBoost, and Random Forest. The goal is to identify

the model that performs best in predicting housing

prices on the dataset. The conclusion is that XGBoost

exhibits the best performance in predicting housing

prices on this dataset. Building on XGBoost, the

study proposes a novel hybrid model incorporating

Bayesian optimization. Bayesian optimization

positively influences the performance of the

XGBoost model in this study. Therefore, the hybrid

model proposed in this research holds further research

significance for housing price prediction. One

limitation is the low correlation between the features

and the predicted labels (housing prices), as revealed

in the data analysis section. This may impact the

predictive performance of the model, making it

challenging to learn useful patterns from the features

due to weak correlation. The model might struggle to

capture the true data generation process, resulting in

inaccurate predictions and potential overfitting to the

training data. Future research could involve using

datasets with higher feature-label correlation to train

and test the proposed hybrid model, addressing this

limitation. Additionally, a more detailed

hyperparameter tuning of XGBoost and Bayesian

optimization can be explored. Researchers may also

consider employing neural network models for

housing price prediction due to their ability to handle

nonlinear relationships effectively, leveraging

network structures and activation functions.

REFERENCES

A. Abigail, A. Oluwatobi, A. Funmilola, et al,

Procedia Computer Science, pp. 806-813 (2022).

A. Ebekozien, A. R. Abdul-Aziz, and M. Jaafar,

Habitat International, pp. 27–35 (2019).

Banerjee, Debanjan, and S. Dutta, "Predicting the

housing price direction using machine learning

techniques." In 2017 IEEE International

Conference on Power, Control, Signals and

Instrumentation Engineering (ICPCSI) (2017).

C. S. Malang, E. Java, and R. E. Febrita, International

Journal of Advanced Computer Science and

Applications, pp. 323–326 (2017).

C. W. Cheng, Universiti Tunku Abdul Rahman

(2018).

D. Allen, G. Yap, R. Shareef, Math. Comput. Simulat,

pp. 2733–2740 (2009).

House Price Prediction with Optimistic Machine Learning Methods Using Bayesian Optimization

495

J. Mu, F. Wu, A. Zhang, Abstract and Applied

Analysis, pp. 1–7 (2014).

K. B. Hansen, Big Data Soc, p. 2053951720926558

(2020).

Kaggle - california-housing-prices, 2023, available at

https://www.kaggle.com/datasets/camnugent/cali

fornia-housing-prices.

L. Tian, Y. Yan, G. Lin, Y. Wu, L. Shao, Cities, p.

102878 (2020).

Q. Truong, M. Nguyen, H. Dang, et al, Procedia

Computer Science, pp. 433-442 (2020).

R. Gupta, H. A. Marfatia, C. Pierdzioch, et al, The

Journal of Real Estate Finance and Economics,

pp. 1-23 (2022).

W. K. Ho, B. S. Tang, S. W. Wong, J. Property Res,

pp. 48–70 (2021).

ICDSE 2024 - International Conference on Data Science and Engineering

496