Exploring LSTM Networks for Stock Price Prediction in the Chinese

Baijiu Industry

Yixiang Kong

Mathematics with Financial Mathematics, Natural Sciences Department, M13 9PL University of Manchester, U.K.

Keywords: Stock Prediction, LSTM, Machine Learning, Deep Learning, Baijiu.

Abstract: This comprehensive essay explores the use of Long Short-Term Memory (LSTM) networks for stock price

prediction, focusing on China's Baijiu industry. It addresses the challenges in stock market prediction and the

emergence of LSTM as a solution. The study elaborates on LSTM's architecture, its core components, and its

application in predicting stock prices. It details parameterization strategies for LSTM models, including time

step, batch size, epochs, optimizer, loss function, and feature incorporation. The essay examines model

performance through various metrics such as Root Mean Square Error (RMSE), Mean Absolute Error (MAE),

and Mean Absolute Percentage Error (MAPE), and provides insights into the model's efficiency in handling

time-series data for stock prediction. The research aims to demonstrate the practicality and reliability of LSTM

models in financial market analysis, underlining the potential of machine learning in revolutionizing stock

market predictions. The essay also discusses the real-world implications of LSTM-based models in the finance

sector, emphasizing their role in informed decision-making and investment strategies.

1 INTRODUCTION

In the rapidly advancing field of financial technology,

accurately predicting stock prices is a significant

challenge that captures the interest of investors and

analysts. This paper explores the use of Long Short-

Term Memory (LSTM) networks, a type of machine

learning, to forecast next-day stock prices in China’s

Baijiu industry, blending cutting-edge tech with

practical financial strategies to potentially

revolutionize stock market analysis (Yu et al, 2019).

The importance of accurate stock prediction

cannot be overstated in the realm of economics

(Pahwa et al, 2017). It is pivotal for efficient resource

allocation, informed investment strategies, and

maintaining market stability. However, the inherent

complexity and unpredictability of the stock market,

influenced by a multitude of variables including

economic indicators, political events, and company

performance, make this task exceedingly challenging.

The emergence of machine learning technologies,

particularly LSTM networks, has brought a new

dimension to stock prediction. These advanced

techniques can process and analyze large volumes of

data, uncovering patterns and trends that are

imperceptible to traditional analytical methods.

Consequently, this leads to more accurate and reliable

predictions, which are crucial for effective risk

management and decision-making in investments.

Moreover, the burgeoning field of stock

prediction is attracting extensive research efforts,

focusing on integrating machine learning and

artificial intelligence to refine prediction models. This

not only aids investors in identifying profitable

opportunities but also plays a significant role in

strategizing risk management.

The motivation for this study arises from the

complexity of stock markets and the limitations of

traditional analysis methods. By applying machine

learning to the Baijiu sector, this research aims to

decode market data and reveal patterns beyond

human analyst detection using comprehensive

datasets. The main goal is to build and optimize an

LSTM model to accurately predict stock prices,

testing its robustness and reliability. Additionally, the

study addresses skepticism about machine learning in

stock predictions by focusing on real-world financial

implications and decision-making.

The backbone of this study is a carefully curated

dataset from Choice Finance Terminal, encompassing

five years of trading data from the Chinese Baijiu

industry’s publicly traded companies (Yihan). This

dataset is rich with key financial metrics: daily

110

Kong, Y.

Exploring LSTM Networks for Stock Price Prediction in the Chinese Baijiu Industry.

DOI: 10.5220/0012827500004547

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st Inter national Conference on Data Science and Engineering (ICDSE 2024), pages 110-115

ISBN: 978-989-758-690-3

opening and closing prices, the highs and lows of the

trading day, and the volume of shares traded. These

indicators are invaluable for analyzing the market’s

pulse and forecasting future price movements using

LSTM networks. The selection of a half-decade span

ensures a comprehensive analysis of market trends,

seasonality, and the impact of economic cycles on

these stocks.

2 LSTM: AN OVERVIEW

2.1 The Emergence of LSTM in

Machine Learning

In the realm of machine learning, the development of

Recurrent Neural Networks (RNNs) marked a

significant advance in the ability to process sequences

of data (Sherstinsky, 2020). However, traditional

RNNs are plagued by challenges such as vanishing

and exploding gradient problems, which impede their

ability to learn long-range dependencies within a data

sequence. This limitation is particularly problematic

in complex and volatile domains like stock market

prediction, where past information can have a

prolonged influence on future outcomes. It is in this

context that LSTM networks emerge as a

breakthrough.

2.2 LSTM: A Specialized Form of RNN

LSTM networks, a specialized form of RNN, were

introduced to specifically address the shortcomings of

traditional RNNs. Developed by Sepp Hochreiter and

Ju¨rgen Schmidhuber in 1997, LSTMs are designed

to remember information for long periods, making

them exceptionally suited for applications where

understanding the context from long data sequences

is crucial (Hochreiter & Schmidhuber, 1997). Unlike

standard RNNs that use a single layer for processing,

LSTMs have a complex structure with four

interacting layers, each playing a distinct role in

managing and retaining information.

2.3 Core Components of LSTM

Architecture

The core components of an LSTM unit include the

cell state, the input gate, the output gate, and the

forget gate (Yu et al, 2019). The cell state acts as the

central highway of information, carrying relevant

data through the sequence of the network. The input

gate controls the extent to which new information is

added to the cell state, while the output gate regulates

the information that is output from the cell state. The

most critical addition in LSTM, the forget gate,

allows the unit to discard irrelevant information,

which is pivotal in learning long-term dependencies.

This intricate interplay of gates and states enables

LSTMs to effectively capture time-based

dependencies, a capability that is essential in

predicting stock prices where past trends and patterns

can significantly influence future movements.

2.4 LSTM’s Application in Stock Price

Prediction

In the domain of stock price prediction, LSTMs

leverage their ability to process time-series data

effectively (Hamilton, 2020). By learning from

historical price data and other relevant financial

indicators, LSTM models can uncover complex

patterns and relationships that are not immediately

apparent. These models can provide a more nuanced

understanding of market dynamics, aiding in the

prediction of future stock prices. The LSTM’s

proficiency in handling time-series data makes it

particularly well-suited for financial markets, where

the sequence and timing of events can be as critical as

the events themselves.

In the following sections, this paper will delve

deeper into the technical aspects of LSTMs, their

parameterization, and how they are specifically

tailored for predicting the stock prices of companies

within the Chinese Baijiu industry (Yadav et al, 2020).

3 PARAMETERIZATION OF THE

LSTM MODEL FOR STOCK

PRICE PREDICTION

LSTM models’ success in stock price prediction

relies on parameter tuning. These parameters dictate

the model’s data processing, learning, and forecasting

accuracy (Reimers, 2017).

3.1 Time Step: Capturing the Relevant

Time Frame

The time step is a vital parameter in LSTM that

dictates the amount of historical data the model uses

for prediction. A 30-day time step was chosen to

provide a comprehensive view of the market without

overloading the model.

Exploring LSTM Networks for Stock Price Prediction in the Chinese Baijiu Industry

111

3.2 Batch Size and Epochs: Balancing

Learning Efficiency and Accuracy

Batch size and epochs are key parameters influencing

LSTM learning. We’ve selected a batch size of 5 and

60 epochs, striking a balance between efficient

learning and model stability.

3.3 Optimizer and Loss Function:

Steering the Learning Process

The optimizer and loss function are critical for the

LSTM’s learning trajectory. The Adam optimizer,

known for handling sparse data efficiently, and the

MSE loss function, aligning with our goal of

minimizing prediction errors, are utilized.

3.4 Role of ’Dense’ in Model

Architecture

The ‘Dense’ layer is instrumental after LSTM layers

have processed the data. It consolidates the features

and helps in making accurate predictions. The

arrangement of ‘Dense’ layers affects the model’s

ability to generalize without overfitting.

3.5 Incorporation of Features:

Enhancing Model Accuracy

‘Features’ in LSTM models refer to the input

variables that the model uses to make predictions. The

choice and processing of these features are crucial,

and in this project, they were selected to provide a

comprehensive view of the Baijiu industry’s stock

price movements.

3.6 Balancing Dense Layers and

Feature Selection

The interplay between ’Dense’ layers and feature

selection is crucial for model accuracy. The specific

arrangement of ’Dense’ layers and features was

iteratively optimized to enhance the model’s

predictive accuracy for the Baijiu industry.

4 MONITORING MODEL

PERFORMANCE: TRAINING

LOSS INSIGHTS

4.1 Analyzing the Training Loss Graph

A paramount step in the development of a machine

learning model, particularly an LSTM for stock price

prediction, is the ongoing monitoring of its

performance. This is typically achieved through the

analysis of the training loss over each epoch during

the model’s training phase. In the case of analyzing

stocks, mean squared error (MSE) is used as a metric

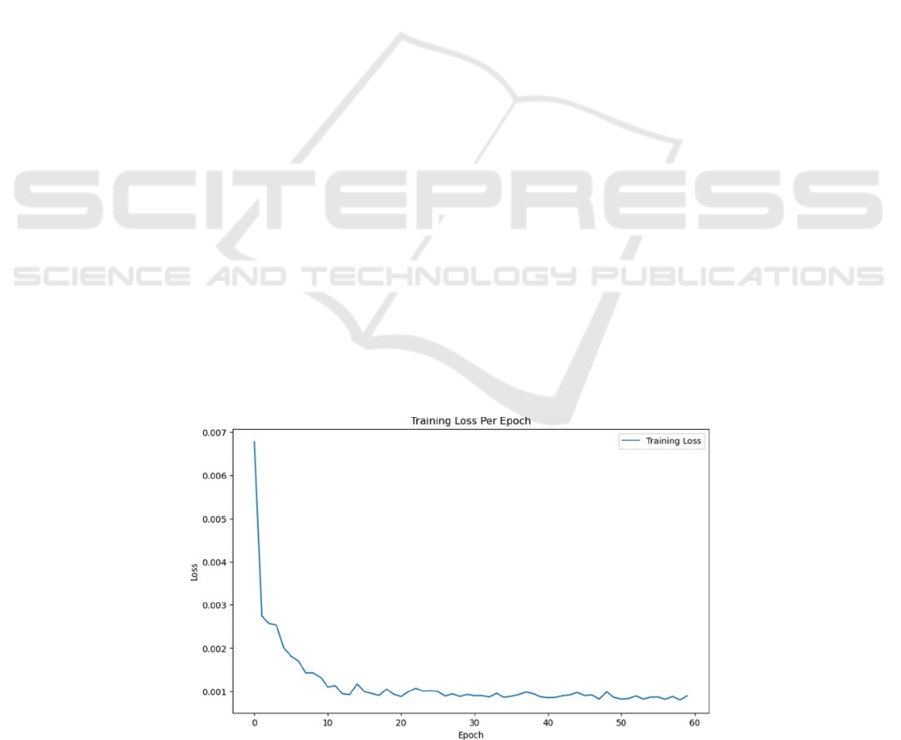
for the loss (Chai & Draxler, 2014). Figure 1 offers a

visual representation of this process, plotting the loss

for each epoch.

Figure 1 shows that after this initial phase, the rate

of decrease in loss slows down, indicating that the

model starts to converge to a more stable state. This

trend is typical in the training of neural networks,

where significant improvements are often seen

initially, followed by more gradual enhancements.

Figure 1: Training loss per epoch (Picture credit: Original).

ICDSE 2024 - International Conference on Data Science and Engineering

112

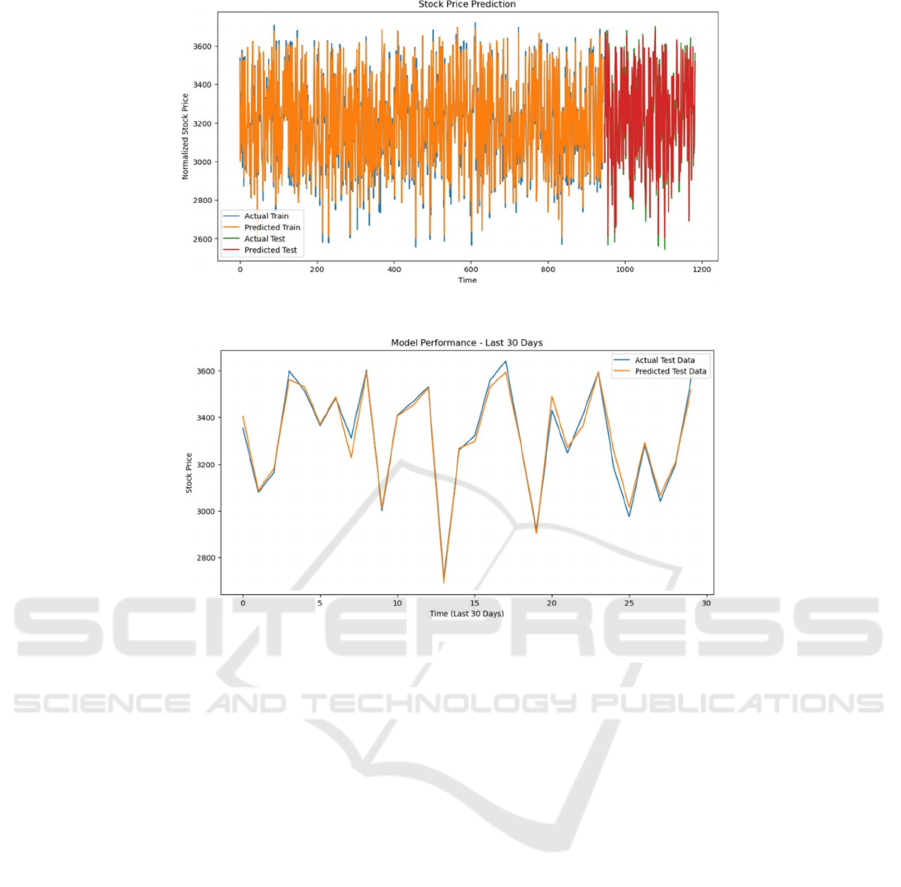
Figure 2: Comprehensive prediction performance (Photo/Picture credit: Original).

Figure 3: Model Performance Over the Last 30 Days (Photo/Picture credit: Original).

4.2 Ensuring Proper Model Training

The smooth decline of the loss to a plateau without

drastic fluctuations or increases is a positive sign. It

indicates that the model is not experiencing issues

like overfitting, where the loss might decrease for the

training set but increase for a validation set.

Moreover, Figure 1 suggests that the chosen batch

size and learning rate are appropriate, as they lead to

a consistent decrease in loss, rather than causing

instability in the learning process.

5 EVALUATING FINAL

PERFORMANCE

5.1 Comprehensive Stock Price

Prediction Performance

Figure 2 offers an extensive view of the LSTM

model’s performance across the entire dataset. It

showcases the predicted and actual stock prices

during both the training and testing phases. The blue

line for the actual training prices and the orange line

for the predicted training prices illustrate the model’s

ability to learn the patterns in the historical data. The

close correspondence between these lines suggests

the model is effectively capturing the underlying

trends during the training phase.

In the testing phase, represented by the green

(actual) and red (predicted) lines, the model’s

predictions are put to the test with new, unseen data.

The degree to which these lines coincide is crucial as

it indicates the model’s capability to generalize

beyond the training data. A successful model will

show a high degree of overlap in the testing phase,

which would be a strong indicator of its practical

application for forecasting future stock prices.

5.2 Model Performance over the Last

30 Days

Moving to Figure 3 this visualization narrows the

focus to the last 30 days of the test data. This short-

term view is particularly important for assessing the

model’s predictive accuracy in a timeframe that is

highly relevant for traders and investors who make

daily decisions. The close tracking of the predicted

test data (in orange) against the actual test data (in

Exploring LSTM Networks for Stock Price Prediction in the Chinese Baijiu Industry

113

blue) demonstrates the model’s precision in making

short-term predictions. The performance over these

30 days is a testament to the model’s utility in a

practical trading context.

5.3 Synthesizing Insights from the

Graphs

When viewed together, Figure 2 and Figure 3 tell a

comprehensive story about the LSTM model’s

performance. Figure 2 confirms the model’s ability to

learn from historical data and make accurate

predictions during the training phase, while Figure 3

demonstrates that the model maintains this accuracy

when applied to the critical short-term prediction

window of the last 30 days.

The consistency across both the training and

testing phases, as seen in Figure 2, alongside the

precision in the short-term as seen in the 30-day

Figure 3, provides a compelling case for the model’s

efficacy. The detailed evaluation of the model’s

predictions against actual stock prices offers a

convincing argument for its application in the

financial industry, especially within the volatile

Chinese Baijiu market.

In the ensuing sections, we will delve deeper into

the statistical validation of the model’s performance

and explore its potential impacts on investment

strategies within the Chinese Baijiu industry.

5.4 Root Mean Square Error (RMSE)

RMSE measures the square root of the average

squared differences between the predicted and actual

values. This metric is particularly sensitive to large

errors, meaning that higher values of RMSE indicate

larger errors being made by the model. A lower

RMSE value is preferable as it indicates that the

model’s predictions are closer to the actual stock

prices. In the context of your LSTM model, a

comparatively low RMSE would suggest that the

model is capable of making predictions with a high

degree of precision (Willmott & Matsuura, 2005).

5.5 Mean Absolute Error (MAE)

MAE, on the other hand, calculates the average of the

absolute differences between the predicted and actual

values. Unlike RMSE, MAE treats all errors equally,

providing a straightforward measure of prediction

accuracy without excessively penalizing larger errors.

A smaller MAE value would indicate that on average,

the model’s predictions deviate less from the actual

values, which is desirable in a stock price prediction

model (Chai & Draxler, 2014).

5.6 Mean Absolute Percentage Error

(MAPE)

MAPE expresses the average absolute error as a

percentage of the actual values. This metric is

particularly useful in contexts where you need to

understand the size of the prediction errors about the

actual stock prices. MAPE is beneficial for

comparative analysis and for communicating the

model’s performance in percentage terms, which can

be intuitively understood by a wide range of

stakeholders. A lower MAPE indicates that the

model’s predictions are highly accurate in relative

terms.

When these statistical measures are considered

together, they offer a comprehensive picture of the

LSTM model’s predictive performance. For instance,

if the model boasts a low RMSE, it suggests that there

are no large individual prediction errors, which is

complemented by a low MAE indicating consistent

accuracy across all predictions. A low MAPE would

further confirm the model’s precision in relative

terms, giving confidence that the predictions are

generally close to the actual stock prices.

In conclusion, the statistical analysis using RMSE,

MAE, and MAPE provides a robust framework for

evaluating the LSTM model’s accuracy. For investors

and analysts in the Chinese Baijiu industry, these

metrics are crucial for determining the reliability and

practical utility of the model’s predictions in real-world

financial decision-making scenarios. If the LSTM

model achieves favorable scores across these metrics,

it underscores its potential as a valuable tool for

forecasting and potentially for guiding profitable

investment strategies.

5.7 How Different Parameters Affect

the Metric Performance

Table 1 presents the model performance metrics

under two different sets of training parameters: one

with a time-step of 30, batch size of 5, and epochs of

60, and another with a time-step of 60, batch size of

1, and a single epoch. The former parameter set yields

lower RMSE, MAE, and MAPE values for both

training and testing datasets, indicating more accurate

predictions. Conversely, the latter set results in higher

error metrics, suggesting suboptimal performance.

This contrast underscores the critical role of

parameter optimization in enhancing the LSTM

model’s predictive accuracy (Hamilton, 2020).

ICDSE 2024 - International Conference on Data Science and Engineering

114

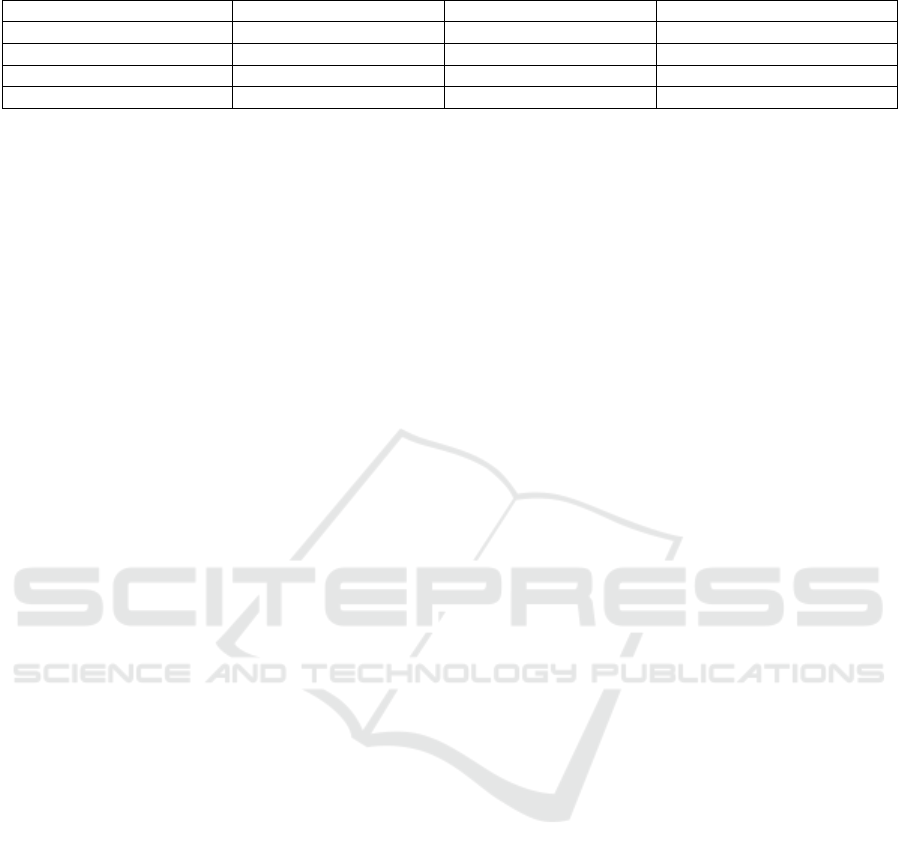
Table 1: Model performance metrics.

DATA RMSE MAE MAPE

Training (30, 5, 60) 35.35835718307 26.3225935671897 0.8341834817291175%

Testing (30, 5, 60) 33.9687217759959 25.39854838896207 0.8004823100669486%

Training (60, 1, 1) 66.7942895566151 49.77742150749857 1.580022362048114%

Testin

(

60, 1, 1

)

65.44305245140346 50.79953193065587 1.5895670307381864%

6 CONCLUSION

In conclusion, this essay has presented an in-depth

exploration of the use of LSTM networks for

predicting stock prices within the Chinese Baijiu

industry, a sector that plays a pivotal role in China’s

economy. From the initial motivation, driven by the

intricate dance of market forces and the allure of

predictive analytics, to the detailed elaboration of the

LSTM model’s parameters and architecture, this

research has traversed the landscape of financial

technology with a focus on machine learning’s

potential to revolutionize stock market predictions.

The essay has delved into the parameters that are

instrumental in shaping the LSTM model’s learning

process—time steps, batch size, epochs, optimizer,

loss function, ’Dense’ layers, and feature selection—

and their meticulously calibrated values. The

subsequent discussion on the model’s performance,

illustrated through the analysis of training loss graphs

and the close tracking of predicted versus actual stock

prices, has highlighted the model’s proficiency in

capturing market trends and translating them into

accurate predictions.

Statistical measures like RMSE, MAE, and

MAPE have provided quantitative testament to the

model’s precision, reinforcing the visual insights

gleaned from the performance graphs. A low RMSE

indicates the absence of large prediction errors, while

a small MAE confirms the model’s consistent

accuracy across predictions, and a minimal MAPE

assures that the model’s forecasts are closely aligned

with the actual values in relative terms.

The culmination of these investigations points to

a promising horizon for the application of LSTM

models in stock price prediction. The evidence

suggests that machine learning can indeed serve as a

powerful ally to investors and analysts, providing

them with nuanced insights and a competitive edge in

the marketplace. However, it is crucial to remember

that no model can guarantee absolute precision,

especially in the ever-volatile realm of stock trading,

where unpredictability is the only certainty.

As the financial world continues to evolve with

technological advancements, the integration of

machine learning models like LSTM into stock price

prediction is likely to become more prevalent. While

challenges and skepticism remain, the potential for

these models to inform and enhance investment

strategies is undeniable. This essay stands as a

testament to the strides made in financial technology,

showcasing the LSTM model’s journey from

conceptualization to application, and set- ting the

stage for its continued evolution and adoption in the

complex world of stock market analysis.

REFERENCES

Y. Yu, X. Si, C. Hu, J. Zhang, Neural Comput. 31(7), 1235-

1270 (2019).

N. Pahwa, N. Khalfay, V. Soni, D. Vora, Int. J. Comput.

Appl. 163(5), 36-43 (2017).

M. Yihan, Choice Finance Terminal.

https://www.statista.com/topics/7815/baijiu-industry-

in-china/

A. Sherstinsky, Physica D. 404, 132306 (2020).

S. Hochreiter, J. Schmidhuber, Neural Comput. 9(8), 1735-

1780 (1997).

J. D. Hamilton, PUP. (2020).

A. Yadav, C. K. Jha, A. Sharan, Procedia Comput. Sci. 167,

2091-2100 (2020).

N. Reimers, I. arXiv. 1707.06799 (2017).

T. Chai, R. R. Draxler, Geosci. Model Dev. Discuss. 7(1),

1525-1534 (2014).

C. Willmott, K. Matsuura, Clim. Res. 30(1), 79-82 (2005).

Exploring LSTM Networks for Stock Price Prediction in the Chinese Baijiu Industry

115