Possibilities of Simulation of the Socio-Political Conflicts Based on the

Mathematical Technique of the Langmuir Monolayers Theory

A. Y. Petukhov

1,2 a

, A. N. Morozov

, Yu. M. Selivantyev

, I. V. Vorotyntsev

, O. A. Raitman

and N. S. Morozov

Lomonosov Moscow State University, Leninskie Gory, 1, 119991, Moscow, Russia Federation

ANO «Neymark» Lobachevsky State University, Nizhniy Novgorod, Alexeevskaya 6/16, 603000, Russia Federation

Mendeleev University of Chemical Technology, Miusskaya sq., 9, Moscow, 125047, Russia Federation

Lobachevsky State University, Nizhniy Novgorod, Gagarina Ave., 23, 603022, Russia Federation

Keywords: Monolayer, Mathematical Simulation, Socio-Political Processes, Socio-Political Conflicts.

Abstract: The possibility of creating the model of social and political processes (in particular, that of conflicts) with use

of the chemical theory of monolayers is studied. The main theoretical approaches to simulation of the social

processes are analyzed. A formalized dynamic parameters of protest pro-cesses in the crowd are defined. The

mathematical model based on the chemical theory of mono-molecular layers and the coupling field parameter

(h) are proposed. In addition, the basic equations are derived, interpreted and applied to social processes. The

main effects in the studied pro-cesses are described.

1 INTRODUCTION

The question on forecasting the social and political

conflicts, including that by means of mathematical

simulation, is of the most actuality, especially in the

conditions of increasing geopolitical confrontation.

In terms of classical approaches developed earlier,

a social conflict is defined in general as a terminal

phase in increased confrontation of interests between

single individuals, groups of people or in society at

whole. This phase is featured by incongruity of

separate interests, goals and positions of the

interacted subjects. Conflicts can be hidden or

explicit, but they are always based on the

unwillingness to compromise or even on the complete

absence of dialogue between the opposing sides

(Dahrendorf, 1965; Gurr and Harff, 1994).

As to mathematical models derived from physical

and chemical analogies, they are still relatively rare in

sociological researches. Nevertheless, there are a

number of works concerning a question on simulation

of social and political processes, which a certain

success has been achieved in - (Mason, 2013; Traud

et al., 2011).

https://orcid.org/0000-0002-7412-5397

The models presented up to date can be divided

into three types:

The 1st type are the conceptual models based on

identification and analysis of general historical

regularities shaped as cognitive schemes and

described the logical links between various factors

which affect historical processes. Such models are

featured by high degree of generalization, but they are

still not mathematical ones, being rather logical and

conceptual in their nature.

The 2nd type are the particular mathematical

models of simulation type which are focused on the

certain historical event or phenomenon. In such

models, the main attention is paid to analysis and

detailed description of factors and processes that

effect the phenomena under research. The models of

that type work, as a rule, only if the event under

consideration is highly localized and limited by

duration. These models are "tied" to a specific

historical event and are not applicable for a long

period of time.

The 3rd type are the mixed models combining the

former two ones. These models simulate a certain

class of social processes, without claiming to describe

392

Petukhov, A., Morozov, A., Selivantyev, Y., Vorotyntsev, I., Raitman, O. and Morozov, N.

Possibilities of Simulation of the Socio-Political Conﬂicts Based on the Mathematical Technique of the Langmuir Monolayers Theory.

DOI: 10.5220/0012828500003758

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2024), pages 392-398

ISBN: 978-989-758-708-5; ISSN: 2184-2841

in detail the features for each specific historical case

(Malkov, 2004).

As a rule, the classical theoretical model of

dynamic processes in nonlinear systems (an example

of which can be social movements too) operates with

multidimensional differential equations,

mathematical technique of cellular automata,

approaches of theory of catastrophes, and that of the

theory of self-organized criticality. Stochastic

differential equations by Langevin and Ito-

Stratonovich are used too, as well as analysis of

chaotic systems with reconstruction of stable states

(attractors) by time series (Malkov, 2004; Weber et

al., 2015).

A number of studies were devoted to ethnical

diversity and its impact on economic, social, cultural

development and related processes (Weber et al.,

2015). These are cross-cutting studies on mutual

influence of ethnic and social problems and the

economy. They take into account ethnic and cultural

factors and their combined impact on possible and

running conflicts.

Forecasting and description of social and political

processes uses of variety of methods (Mikhailov and

Gorbatikov, 2012).

Since social conflicts have a significant impact on

society and processes in it, the development of

methods and approaches to describe such phenomena,

as well as to predict them, is of great im-portance.

The use of the mathematical techniques of

Langmuir Monolayers Theory (LMT) for simulations

of social conflicts and their acute phase, which the

mass protests are, was attempted in this study.

2 THEORETICAL BASES OF

SIMULATION

It is easy to see that the parametrization of

mathematical tools used in physics and chemistry

needs to be adjusted in relation to the social process

and should be adapted to the phenomenon that is

currently being considered. Processes in physics and

chemistry and processes in society and politics are not

the same thing. However, we will hypothetically

proceed from the fact that common patterns and

phenomena (threshold effects, self-organization,

fractals, etc.) are spread in nature almost everywhere,

and, consequently, almost the same processes (i.e. the

similar ones) can be observed in society, since people

are also part of nature and must obey the laws of it

too. However, the question on whether the model

does function properly or does not (at least in

particular cases) can be answered only after a

numerical experiment is over and its results (which

are a short- or medium-term forecast) are compared

with what actually happened.

From a mathematical point of view, social and

political processes are not what can be detailed and

completely characterized by a set of parameters, since

the latter undergo constant changes and deformations.

Here, the analogy with Brownian motion seems to be

close enough: it seems that a single particle moves by

well-defined trajectory, but only before it is examined

more closely (Hołyst et al., 2000; Petukhov et al.,

2020; Petukhov and Kaminchenko, 2021; Petukhovm

2021): the real shapes of the tracks turn out to be

tortuous and nonlinear. These smaller changes in

motion (trajectory fluctuations) are influenced by

closer and smaller particles (molecules), which,

randomly moving nearby a large particle, correct the

trajectory of its movement. In social processes, such

fluctuations are caused by manifestations of the free

will of its participants, as well as by other accidental

environmental influences. The next step in

developing such a model should be to consider

external influences that are not accidental, but

external interference.

The proposed model is based on the assumption

that individuals interact in society through a

conditional "communication field" – h. This concept

was introduced earlier (Hołyst et al., 2000), but had a

different type of parametrization and other initial

equations.

The necessity of introducing that concept is

caused by a number of factors:

i) Any live cognitive system (which is both a

society and a person) acts through exchange of in-

formation carried out through nerve impulses in the

brain or in the opioid system of the cerebellum, or in

the form of Internet information flows, or in any other

suitable form.

ii) As follows from the above, the model of

individuals’ behaviour in society is directly related to

the model of information exchange.

iii) That is why it is desirable to use the function

of information exchange as the basis for the model.

For this purpose, the h-function has been

introduced into model. Actually, this is a function of

information exchange occurring in individuals’

medium. But from a mathematical point of view, this

function is to be considered as an informational field

created by any person in society, which modulates the

information interaction itself.

Possibilities of Simulation of the Socio-Political Conﬂicts Based on the Mathematical Technique of the Langmuir Monolayers Theory

393

Also, from the point of view of the physical and

mathematical description, it should be borne in mind

that here we are talking about a society that cannot be

attributed to a separate object in spatial topology, as

it happens in classical physics. Indeed, from the point

of view of information exchange between individuals,

social space should combine both classical spatial

coordinates and additional specific parameters and

features. This is due to the fact that in the modern

information environment there is no need to be

physically closer to the object of influence in order to

transmit information to it.

Thus, society is a multidimensional socio-

physical space that models the ability of one

individual to cover another with a personal

communicative field, i.e. to exert an informational

influence on him, change his parameters and the

ability to move in this space. And, thus, the mutual

position of those who act in this space also models the

level of relationship between them and involvement

in the exchange of information.

From the point of view of modelling, the conflict

control by means of external influence or any other

way of mediating it (Dahrendorf, 1965) may be

represented as an additional function that depends at

least on the spatial coordinate and that affects overall

stability of the social system and structure of the last

one. There are a number of analogies acting in

physical systems, for example, the dissipative

function, which can appear and work by a number of

ways depending on physical conditions (Hołyst et al.,

2000).

2.1 Monolayer Theory

The Langmuir Monolayer Theory (LMT) is one of the

most successful theories describing the behaviour of

separate molecules on the plane (or at the interface),

as well as their influence on each other upon

concentration increasing. It describes well the

physical and chemical properties of 2D systems,

taking into account the cooperative interaction of

molecules in them. However, before using the LMT

mathematical tools to describe the processes under

study, it is necessary to briefly explain its physical

meaning and draw an analogy with the phenomena

under study.

Monolayers on the aqueous subphase, which are

the films at the air/water interface constructed of

amphiphilic compounds with a thickness of just one

molecule, have a special structure and exhibit unusual

physical and chemical properties (Arslanov et al.,

2022). Depending on number of molecules the

monolayer is formed from, it can be sparse or tightly

packed. The thermodynamic properties of the film are

usually studied using a Langmuir device. It consists

of the following elements: a "trough", which is a

container filled with aqueous subphase; movable

barriers designed to change the surface water area;

and a Langmuir film balance with a Wilhelmy plate

for surface tension measurement (Moehwald and

Brezesinski, 2016). In order to determine the

thermodynamic parameters of a monolayers, Irving

Langmuir has introduced the concept of surface

pressure which is the mathematical difference

between the values of surface tension of pure water

and that with the surfactant present. In addition,

surface pressure is a two-dimensional analogue of

common thermodynamic pressure; that is the force

acting on the unit length of the measuring plate.

Knowing exactly the amount of substance placed on

the surface and, consequently, the number of

"floating" molecules, it is possible to build the so-

called monolayer compression isotherm by smoother

changing the water surface area (using movable

barriers). The isotherm represents the dependence of

the monolayer surface pressure (π, mN/m) on the

water surface area available to each molecule (A, Å

Analyzing this function (insert in Fig. 1), it is possible

to make conclusions about the processes occurring in

the monolayer, such as interaction of molecules, their

reorientation and conformational rearrangement, as

well as about phase transitions in the film.

If the area provided to one molecule is large

enough, the molecules do not interact with each other,

and the system as a whole can be represented as a

two-dimensional ideal gas (see Figure 1a), which

conforms the equation:

𝜋𝐴 = 𝑘𝑇 (1)

This equation is a two-dimensional analogue of

the Mendeleev and Clapeyron equations for two

degrees of freedom for translational motion of

molecules.

When the surface area becomes too small and,

consequently, the pressure increases, equation (1)

stops working properly, and behaviour of monolayer

can be described with a certain accuracy by two-

dimensional analogue of Van-der-Waals equation:



𝜋+











𝐴−𝑏



= 𝑘𝑇 (2)

Here the coefficient a is introduced for correcting

the pressure reduced due to interaction of amphiphilic

molecules with each other. This interaction consists

in dispersed attraction of hydrocarbon chains,

accompanied by Coulomb repulsion of charged

carboxyl groups. The coefficient b corresponds to

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

394

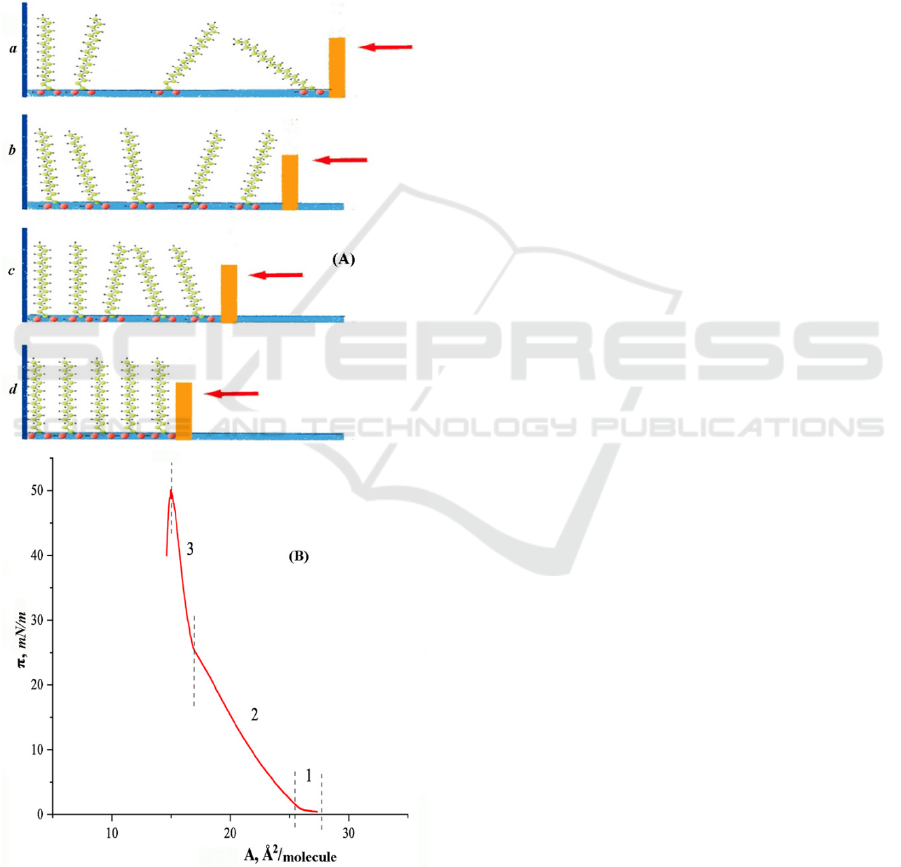
minimum value of area per molecule in a tightly

packed monolayer.

An increase in pressure transforms the monolayer

into a two-dimensional liquid state, in which the

molecules come close enough to interact with each

other, but there is still no definite order in the film

structure (Fig. 1, b).

By reducing the surface area available per

molecule, the monolayer is first converted into a

liquid crystal phase, and then into a two-dimensional

solid state (Fig. 1, c and d, respectively). Hydrocarbon

Figure 1: (A): States of phase in monolayer of stearic acid

at various surface pressure: 2D gas (a), 2D liquid (b), liquid

crystal (c), 2D solid state (d). (B): An isotherm of stearic

acid compression at a temperature of 20°C.

chains become less flexible and line up almost

perpendicular to the surface. Such transformations are

phase transitions of the first kind. Further limitation

of the subphase surface and, consequently, reduction

of the monolayer area is accompanied by a rapid

increase in pressure. As a result, the system,

previously structured in two dimensions, breaks

down, being unable to withstand such a load (Figure

1). So called collapse of the monolayer occur. The

structure loses its integrity: one part of the molecules

moves into the water, while the second begins to

crawl on top of each other, forming both regular

multi-layered ensembles and disordered aggregates

(Oliveira et al., 2022).

Until now, the physical aspects of phase

transitions in monolayers, placed on the surface of

water, have not been well studied, and there is still no

numerical theory explaining the multilevel

supramolecular interactions of amphiphilic molecules

with each other, as well as with subphase molecules.

From a chemical point of view, in order to

combine all the influencing factors into a single

system, this is necessary to take into account the

following phenomena: steric repulsion and dispersion

attraction of hydrocarbon chains; Coulomb and

dipole-dipole interaction between polar fragments of

molecules; formation of two-dimensional hydrates

and hydrogen bonds between surfactants and water;

changes in the structure of the aqueous layer surface

affected by monolayer; and so on. Moreover, the

introduction of ions (regardless on the charge sign)

into the subphase should drastically change the

potential of the double electric layer at the air/water

interface, affecting the thermodynamic properties of

two-dimensional phase transitions and phase states.

In this regard, approximate calculation methods are

currently mainly used, such as the mean field method,

the scaling method and other approaches, including

the Monte-Carlo method, grid models and other

microscopic approaches (Lösche M. et al. 1985).

It is important to note here that a number of

interesting phenomena are observed in such systems,

including threshold effects associated with the

processes of collapsing, self-organization of

molecules (clustering), etc. These effects are of

interest as they are the analogues of processes

occurring in a crowd, for example, during mass riots,

protests, etc., i.e. when previously unorganized crowd

begins to organize itself to give separate groups and

leaders appearance, or when a relatively peaceful

protest goes far and destructive actions occur

(threshold effect, collapse). Of course, these are the

cases when protest has no serious preliminary

preparation, being just spontaneous one.

Possibilities of Simulation of the Socio-Political Conﬂicts Based on the Mathematical Technique of the Langmuir Monolayers Theory

395

3 MATHEMATICAL

REPRESENTATION OF THE

SYSTEM

Within the framework of this study, a type of

mathematical simulation based on concept of

monolayers’ behaviour in liquid and liquid-crystal

state is used. Here, the hydrophobic parts of

amphiphilic molecules can be considered as elements

of the individual's communication field. The phase

transition from the 2D-gas state to that of 2D-liquid

corresponds to process of information exchange

between separate individuals or groups of them. The

absence of interactions itself is out of interest for this

study since the complete individuals' isolation is an

analogue of monolayer’s two-dimensional gas state.

Thus, the transition from communication to the

unification of individuals into groups (the liquid

crystal state of a monolayer) is the first phase

transition that is the subject of further research. Also

here, the general alignment of molecules in similar

spatial positions (Fig.1. b-d) can be interpreted as

mutual coordination of communication fields, that is,

a certain alignment of the general information in the

crowd (coordination of requirements, alignment of

position, self-organization).

Of most interest is the simulation of the second

phase transition., i.e. from liquid crystal state to that

of crystal lattice. Exploration of this process may help

to predict the maximum social stress, after which the

system goes to self-organization. Of the greatest

interest are also cases when self-organization (crystal

formation) is localized in defined areas or even

points, but has not yet spread over the surface in

whole. At the same time, it is worth noting once again

that to solve this problem a lot of resources are

required and, as to numerical methods, at present

there are only partial solutions based on them, and a

complete analytical solution is still not available.

At the first stage, we will limit ourselves by

developing a model with a single-phase transition

(from a liquid state to a liquid-crystal state) and

consider it in context of conditions for consolidation

of a part of society (or a protest crowd) into well-

structured groups.

To perform the simulation procedure, it is

necessary to set the parameter h, which corresponds

to radius of the communication field, and b, which

represents the radius of a person's personal space. If p

is taken as a measure of social tension, then equation

(2) can be transformed as follows:

𝑝 =











()

(3)

where T parameter (acting as the temperature factor

(kT) in initial model) is a measure of social activity of

individuals, i.e. the ability of individual to undertake

a socially significant action.

When individuals (or any related elements) come

each other at a distance less than h, they unite and

form an "island" with an area equal to bn, where n is

a number of individuals in group. Using a chemical

analogy, the situation can be represented as a tightly

packed layer. In the future, it is planned to explore

various structures of such systems, which can be

oligomeric, dendritic and insular. From the point of

view of social sciences, this means the emergence of

various types of associating the individuals into

groups.

With this approach, the pressure will gradually

increase with decreasing area, the trend will be

similar to 1 /x (when moving along the x axis), but

there are sharp changes caused by formation of the

groups, followed by releasing spaces for residual

actors.

It is important to add that in this model the process

of reducing the monolayer area (leading to pressure

increase potentially explainable by use of appropriate

thermodynamic function analogue) is interpreted as

two factors:

i) The indoor influence which is the growth of

social tension due to internal processes in crowd

(so called "massing" effects in classic researches

by Lebon and Moscovici).

ii) The outdoor influence, i.e. provocation,

incitement, etc. (or at least part of such external

influence, which can be interpreted as

temperature factor).

These factors may work together or separately and are

to be the subject for further investigation.

Bearing in mind the above, expression (3) should

be corrected. The parameter of surface area A works

as a function of the two-factor parameter u, which is

a measure of social tension, and, as a first

approximation, a circular distribution equation can be

used:

𝐴

(

𝑢

)

= 𝜋

(

𝑅



−𝑢

)



(4)

where R

is the initial value.

The number of individuals, N (or the number of

particles in the chemical model), is randomly

distributed over this surface. Each individual

occupies an area that is part of the whole surface and

under normal conditions, i.e. when the local tension

is lower than its threshold value, corresponds to

parameter h, which is the relative comfortable social

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

396

distance. When the strain exceeds, this parameter

changes drastically. As mentioned above, at the first

stage we will consider the transition to a tightly

stacked layer. This means that area occupied by a

single person will change to b, which is the minimum

area occupied by compact structure:

𝑆



(

𝑢



)

= 

𝜋ℎ



, 𝑢



< 𝑢



𝑏, 𝑢



≥ 𝑢



(5)

The local intensity of u

local

depends on

concentration of actors on the mutual surface area:

𝑢



(

𝑟

)

= 𝑃

∑

𝑓



(𝑅



, 𝑟



, 𝑟)





(6)

where P is the proportionality coefficient,

interact

(T) is the distance from selected point r(x,

y), which characterizes the maximum radius of

interaction (the average path length during Brown

motion of the particle) and depends on measure of

social mobility T, r

(x, y) are the coordinates of the

actor i, and the f

inc

is function which can be written

like this:

𝑓



(

𝑅



, 𝑟



, 𝑟

)

= 

𝑟−𝑟



≤𝑅



𝑟−𝑟



> 𝑅



(7)

And finally, the model itself may be represented

as the following:

𝑝 (𝑢)=













(



)

(8)

When appropriate parameters for this simulation

are well set, the model can be used to assess and

analyze critical phenomena in order to maintain the

stability of social pressure under random initial

distribution of individuals. It still requires further

refinement since it does not consider the structure of

compact connections between actors. Such structures

can be simulated with use of well-designed methods

of fractal theory, and the processes occurring inside

them can be described in terms of theory of

percolation (Koposov and Iudin, 2008). When local

intensity parameter u

loc

changes, these structures can

undergo the transformations from sparse state to tight

one. Here, the compact monolayer formation is

concerned as the terminate phase, after which the

destruction of the particles themselves (representing

individuals in given model) begins. This can be

interpreted as terminal level of protest followed by

acute conflict, leading to collisions and human

casualties

4 CONCLUSIONS

The social hyper-clasterization of society, the sharp

separation in the informational and social

environment of individuals, as well as cultural and

interethnic disunity, creates conditions for social

conflicts and subsequent protests, riots, etc.

Prevention of social conflicts, determination of their

threshold conditions and search for the most effective

scenarios for their suppression is an important task of

modern social sciences.

In this article, the main approaches to modeling

social processes were briefly considered, and a

formalized definition of parameters describing the

dynamics of mass protest processes was given.

A mathematical model based on the chemical

theory of Langmuir monolayers and the coupling

field parameter h is proposed. In addition, the basic

equations are given, the interpretation and adaptation

of the obtained formulas for social phenomena are

proposed, and the main effects in the processes under

study are described.

The next step planned for refinement of the model

will include its approbation based on a numerical

experiment in order to compare its results with data

on real protest processes.

ACKNOWLEDGEMENTS

The research was carried out with the support of the

Expert Institute for Social Research (research projects

in the form of a state assignment, in the field of socio-

political sciences, competition 2024).

REFERENCES

Dahrendorf R. (1965) Elemente eines Theorie des sozialen

Konflikts. Dahrendorf R. Gesellschaft und Freiheit.

Munchen.

Gurr Т., Harff B. (1994) Ethnic Conflict in World Politics.

Boulder, San Francisco, Oxford.

Mason J.W. D. (2013) Consciousness and the Structuring

Property of Typical Data. Complexity, Volume 18,

Issue 3, pages 28–37, January/February. DOI:

10.1002/cplx.21431

Traud, A. L., Kelsic, E. D., Mucha, P. J. & Porter, M. A.

(2011) Comparing Community Structure to

Characteristics in Online Collegiate Social Networks.

SIAM Review, 53, 526–543.

Malkov S. Yu. (2004) Mathematical Modeling of Historical

Dynamics. Approaches and processes. Ed. M. G.

Dmitriev, RSSU.

Possibilities of Simulation of the Socio-Political Conﬂicts Based on the Mathematical Technique of the Langmuir Monolayers Theory

397

Weber Sh., Davydov D.V., Dover P.A. Transfers and

Conflict Prevention: pros and cons. Economics and

Mathematical Methods. 2015, 51(2), 60-69.

Mikhailov, A. P. Gorbatikov E. A. (2012). The Basic Model

of the Muumvirate in the System "Power-Society"”,

Mathem. modeling, 24:1, 33-45

Hołyst J. A., Kacperski K., Schweitzer F. (2000). Phase

transitions in social impact models of opinion

formation. Physica A: Statistical Mechanics and its

Applications. 285 (1–2)199–210.

Petukhov A. Y., Malkhanov A.O., Sandalov V.M.,

Petukhov Y.V. (2020) Mathematical modeling ethno-

social conflicts with the introduction of the control

function. Simulation. 96(3) 337–346, DOI:

10.1177/0037549719884629

Petukhov A. Y., Kaminchenko D.I. (2021) Forecasting the

dynamics of socio-political protests in the Republic of

Belarus in 2020. Bulletin of the Tomsk State University,

64, 214-223 DOI: 10.17223/1998863Х/64/20

Petukhov A.Y. (2021) Development of the Russian state in

the 20th and 21st centuries: mathematical modeling

based on the socio-energy approach. Izvestiya Vysshikh

Uchebnykh Zavedeniy. Prikladnaya Nelineynaya

Dinamika, 2021, 29(3), 365–375. DOI:

10.18500/0869-6632-2021-29-3-365-375

Arslanov V. V. et al. (2022) Planar Supramolecular

Systems: Assembly and Functional Potential. Colloid

Journal.. Vol. 84, № 5. P. 581–610.

Moehwald H., Brezesinski G. (2016). From Langmuir

Monolayers to Multilayer Films. Langmuir. 32(41).

10445–10458.

Oliveira O.N., Caseli L., Ariga K. (2022) The Past and the

Future of Langmuir and Langmuir–Blodgett Films.

Chem Rev.. 122(6). 6459–6513.

Lösche M. et al. (1985). Formation of Langmuir-Blodgett

films via electrostatic control of the lipid/water

interface. Thin Solid Films. 133 (1–4), 51–64.

Koposov E.V., Iudin D.I. (2008). Percolation mechanism of

gravitational instability of dispersed systems. Volga

Scientific Journal. 1, 102–109.

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

398