An Index Bucketing Framework to Support Data Manipulation and

Extraction of Nested Data Structures

Jeffrey Myers II and Yaser Mowafi

School of Engineering and Applied Sciences, Western Kentucky University, Bowling Green, Kentucky, U.S.A.

Keywords: Nested Data Structures, Irregular Schema, Skewed Distribution, Information Loss, Duplication Explosion.

Abstract: Handling nested data collections in large-scale distributed data structures poses considerable challenges in

query processing, often resulting in substantial costs and error susceptibility. These challenges are exacerbated

in scenarios involving skewed, nested data with irregular inner data collections. Processing such data demands

costly operations, leading to extensive data duplication and imposing challenges in ensuring balanced

distribution across partitions—consequently impeding performance and scalability. This work introduces an

index bucketing framework that amalgamates upfront computations with data manipulation techniques,

specifically focusing on flattening procedures. The framework resembles principles from the bucket spreading

strategy, a parallel hash join method that aims to mitigate adverse implications of data duplication and

information loss, while effectively addressing both skewed and irregularly nested structures. The efficacy of

the proposed framework is assessed through evaluations conducted on prominent question-answering datasets

such as QuAC and NewsQA, comparing its performance against the Pandas Python API and recursive,

iterative flattening implementations.

1 INTRODUCTION

The widespread rise in big data analytics has spurred

interest in query processing systems that allow for

performing complex analytical tasks over distributed

data structures of arbitrary data types—including

nested data collections. Implementations of

languages integrated with query systems are

evidenced in large-scale distributed data processing

platforms (Apache Flink. http://flink.apache.org/;

Apache Spark, http://spark.apache.org/; Pandas

Python, https://pandas.pydata.org/). Despite their

vaunted support of nested data, these systems provide

no direct processing for nested data manipulation

over different distributed collections, whose values

may themselves be collections.

To stave off this penalty, declarative querying

APIs have been employed for integrating data query

languages with host programming languages’ data

processing features using higher-order operations—

i.e., Google’s F1 query (Samwel et al., 2018).

Apart from their intricate and computational

challenges, unnesting and manipulating data

collections inherently entail the generation of large

amounts of duplicated data and redundant

computations that significantly degrade the run-time

performance of these techniques. These challenges are

exacerbated for skewed nested data with irregular inner

data collections – where loading unnecessarily large

amounts of data to enforce balancing across partitions

can lead to performance deficiency and error

susceptibility (Diestelkämper et al., 2021; Smith,

2021).

To illustrate these challenges, consider the

reading comprehension question-answering dataset.

The dataset consists of questions where the answer to

every question is a segment of text, or span, from the

corresponding reading passage, or the question might

be unanswerable with an indeterminant plausible

answer (Fig. 1).

The dataset articulates a schema that can be

structured within the following relational database

tables: Sources (src), Questions (qst), Answers (ans),

and Plausible Answers (pls). For the sake of clarity

and brevity, the number of records within a table is

denoted as n. Table 1 comprises source records

featuring id and context fields. The id field

encompasses incremental integers (INC), i = 1, …, n,

while context (ctx) stores textual excerpts (STR),

extracted from source document paragraphs. Table 2

incorporates id, text (txt), and i fields. The id field

embodies incremental integers (INC), j = 1, …, n,

Myers II, J. and Mowaﬁ, Y.

An Index Bucketing Framework to Support Data Manipulation and Extraction of Nested Data Structures.

DOI: 10.5220/0012828800003838

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 191-199

ISBN: 978-989-758-716-0; ISSN: 2184-3228

191

Figure 1: Question-answering dataset structure of

answerable and unanswerable plausible answers.

housing textual representations (STR) of questions.

The i field functions as a foreign key (FK) referencing

records in Table 1. Table 3 encompasses the id,

answer start (srt), answer end, and j fields. The id

field spans incremental integers (INC), k = 1, …, n,

while start (srt) and end signify the index positions of

answers within the context of the related resource

dataset. The j field acts as a foreign key (FK) referring

to records in Table 2. Table 4 accommodates

plausible yet indeterminate answers to questions,

acknowledging instances, where a definitive answer

might be unattainable. Table 4 augments the dataset

by mirroring fields akin to those in Table 3, with

incremental integers (INC), l = 1, …, n, representing

its incremental id. The j field acts as a foreign key

(FK) referring to records in Table 2.

Table 1: Sources (src). Table 2:

Questions (qst).

(

)

Context

(

ctx

)

INC STR

(j)

text

(

txt

)

INC STR F

Table 3: Answers (ans). Table 4: Plausible Answers

(pls).

id (k) start (srt) end j id (l)

Start (srt) end j

INC INT INT FK INC

INT INT FK

These interconnected tables establish a nested

relationship structure, delineating diverse data

distribution patterns, while exemplifying irregular

schema through the inclusion of Table 4. To further

visualize the nested data structure portrayed by the

relational Tables 1, 2, 3, and 4, consider the tree

representations in Fig. 2 of an irregular nested

structure with a given source (src), i of a context (ctx),

and j questions (qst). A given question (qst), j of a text

(txt) may have k answers (ans) or l plausible answers

(pls) or both, where each answer (ans), k or plausible

answer (pls), l has a start (srt) and end.

Figure 2: Irregular question answering nested structure.

With the tree-based representations, it becomes

evident that sources might lack associated questions,

and questions might encompass answers, plausible

answers, both, or neither. This variability extends to

the varying counts of answers and plausible answers

within each question, along with fluctuations in the

number of questions within each source. Such

variability typifies an irregular nested structure

marked by skewed data distribution. Next, we present

the challenges associated with manipulating and

information extraction of these nested data structures.

2 CHALLENGES

2.1 Duplication Explosion

Duplication explosion is a phenomenon characterized

by an overwhelming proliferation of duplicated data

during the flattening process. As the term implies, this

explosion also known as a data avalanche or data

storm results in an excessive replication of data, aka

N + 1 query problems or avalanches (Grust et al.,

2010). This often leads to severe memory utilization

issues and potential system failures, especially when

handling extensive datasets. Current flattening

solutions, primarily relying on recursion, fail to

mitigate the adverse effects of this rampant data

duplication.

2.2 Skewed Distribution

Another hurdle to overcome in nested data collections

is unbalanced distributions of information. When

flattening such data, ensuring that each flattened

Context: {" The Normans (Norman: Nourmands; French:

Normands; Latin: Normanni) were the people who in

the 10th and 11th centuries gave their name to

Normandy, a region in France. They were descended

from Norse ("Norman" comes from "Norseman")

raiders and pirates from Denmark, Iceland and

Norway who, under their leader Rollo, agreed to

swear fealty to King Charles III of West Francia."

}

Answerable question: {"question": "In what country is

Normandy located?", "id":

"56ddde6b9a695914005b9628", "answers": [ {"text":

"France", "answer_start": 159 } ],

"is_impossible": false

}

Unanswerable question: {"plausible_answers": [ { "text":

"Normans", "answer_start": 4 }c ], "question":

"Who gave their name to Normandy in the 1000's and

1100's", "id": "5ad39d53604f3c001a3fe8d1",

"answers": [], "is_impossible": true

}

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

192

instance contains all requisite keys introduces a

problem akin to duplication explosion. However, in

this case, missing keys necessitate filling with null

values, requiring comprehensive parsing of the

dataset to gather all keys. The challenge lies in

distributing these missing keys throughout the

flattened data. Strategies may involve parsing before

flattening, allowing simultaneous filling, or

conducting a secondary traversal after flattening,

although the former, while superior, present

implementation complexities (Smith et al., 2020).

2.3 Irregular Schema

Here, disparate data collections within the dataset

may contain entirely different keys at the same

nesting level, significantly complicating parsing and

filling algorithms. Akin to skewed distribution,

solving irregular schema involves filling in missing

keys throughout the dataset. However, it presents an

even more intricate challenge, where the endeavor to

enforce balance across partitions escalates runtime

inefficiencies and scalability limitations,

exacerbating disk spillage and load imbalance issues

(Smith et al., 2021).

2.4 Information Loss

The final challenge, information loss, poses some

concern, describing the repercussions of processing

nested data structures. The flattened data loses crucial

information required for reconstructing the original

nested form. Without incorporating metadata into the

flattened dataset, reconstructing the initial

hierarchical structure becomes unfeasible

(Diestelkämper, 2021). Reverting to the original data

necessitates reloading the data file or maintaining a

copy of the original data, which could be time-

consuming and can proliferate memory utilization

problems, especially with large datasets.

To address these challenges, we propose a novel

framework, which we refer to as index bucketing. The

basis of our framework resembles principles from the

bucket spreading strategy, a parallel hash join method

that allows for handling irregular data distribution for

relational database systems by utilizing bucketing

mechanisms. The strategy aims to evenly distribute

the load among processes, always fully exploiting

(Kitsuregawa & Ogawa, 1990). Index bucketing

draws on applying these principles to a tree-based

nesting by mapping the data indexes corresponding to

their respective hierarchical structure within the

original data.

3 FRAMEWORK

This section delineates a concise implementation of

the index bucketing framework provided by the

following algorithmic classes (Algorithms 1, 2, 3, 4,

5, 6). The framework is designed to address the

aforementioned challenges, accentuating the

framework's prowess in surmounting the diverse

challenges encountered in nested data structure

manipulation.

3.1 Base Node – Algorithm 1

As a foundational base class, the N

ODE

class serves as

the common blueprint inherited by the L

EAF

RANCH

, and R

OOT

classes within the index

bucketing framework. The N

ODE

class lays out the

essential structural elements shared across all

inheriting classes:

•

ODE

– This is the shared base constructor for all

inheriting node classes and is responsible for

setting the shared node attributes – kdx, value,

level, and parent. The kdx attribute is a key or

index value used for gathering index and key

paths. The value attribute contains a collection of

child N

ODE

types or serves as a B

ASE

value type

for leaves. The level attribute is used to determine

the depth of the node within the tree. The parent

attribute is used to establish a link to the node’s

parent node.

•

IBUCKET

– By collecting a set of index paths, each

aligning with the maximum depth of the nested

data tree, this method is responsible for gathering

the index bucket.

Algorithm 1: Node Class.

This standardized class structure established by

the N

ODE

class ensures coherence and consistency in

defining and organizing nodes across the index

bucketing framework.

3.2 Leaf Node – Algorithm 2

Within the framework, the L

EAF

class, along with its

inheriting classes – I

NDEXED

EAF

and K

EYED

EAF

–

An Index Bucketing Framework to Support Data Manipulation and Extraction of Nested Data Structures

193

fulfill the role of nodes encapsulating the terminus of

nested data structures. These classes define essential

functionalities pivotal to handling leaf nodes within

the index bucketing framework:

•

EAF

– Rather than directly receiving the level

parameter argument, the LEAF constructor derives

its level value from the parent node, ensuring

hierarchical consistency within the tree structure.

•

IBUCKET

– This method accepts the maximum

depth value of the tree as a parameter argument. It

validates whether the depth value matches its

level, subsequently returning its index path

enclosed in an index bucket set object if true;

otherwise, an empty index bucket set object is

returned. Employing a bottom-to-top algorithm,

this method is invoked by non-leaf nodes to

update and collate their child leaf node value

fields into a set collection.

•

FLATTEN

– Disregarding the index path parameter

argument, ipath, when invoked by the leaf nodes

corresponding parent, this method returns a new

mapping of the leaf node’s key path and value,

adhering to a top-to-bottom calling sequence and

resulting in a bottom-to-top return sequence.

•

IPATH

KPATH

– Defined in the I

NDEXED

EAF

and K

EYED

EAF

classes which serve to

differentiate leaves based on their indexing

nature: indexed with integers or keyed with

strings during tree initialization, these class

methods manage bottom-to-top index paths or key

paths by integrating the leaf node’s kdx field along

with its parent’s index or key path, respectively.

In cases where index paths are gathered, the leaf

node converts arrays of index values into tuples of

the same size.

Algorithm 2: Leaf Classes.

By segregating leaves between indexed and keyed

types during tree initialization, the classes circumvent

the need for conditional evaluations. This strategic

segregation bolsters performance and scalability,

especially in managing larger datasets.

3.3 Branch Node – Algorithm 3

The B

RANCH

class integrates into various specialized

nodes, including I2B, KIB, IKB, and K2B which are

defined by inheriting combinations of I

NDEXED

and

EYED

classes with I

NDEXING

RANCH

and

EYING

RANCH

classes.

•

NDEXED

– The I

NDEXED

class encapsulates nodes

indexed with integers, defining the

IPATH

method

to append the current node’s index value to the

parent’s index path.

•

EYED

– The K

EYED

class represents nodes keyed

with strings, providing the

KPATH

method to

append the node’s key value to the parent’s key

path.

•

NDEXING

RANCH

– The I

NDEXING

RANCH

class

inherits from B

RANCH

, designed for indexed

branches. Its constructor sets attributes based on

the provided values and parent node, and the

FLATTEN

method retrieves the corresponding child

node based on the index path.

•

EYING

RANCH

– The K

EYING

RANCH

class,

also extending B

RANCH

, targets keyed branches.

Its constructor initializes attributes, and the

FLATTEN

method iterates through child nodes,

updating a map with their flattened results.

•

I2B – The I2B class combines I

NDEXED

and

NDEXING

RANCH

functionalities.

•

KIB – The KIB class combines K

EYED

and

NDEXING

RANCH

functionalities.

•

IKB – The IKB class combines I

NDEXED

and

EYING

RANCH

functionalities.

•

K2B – The K2B class combines K

EYED

and

EYING

RANCH

functionalities.

Algorithm 3: Branch Classes.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

194

These specialized branch classes cater to different

scenarios, providing distinct methods for handling

various types of nested data collections. Each class

offers unique functionalities for efficient execution,

minimizing conditional evaluations during execution.

3.4 Root Node – Algorithm 4

The Root class, and its inheriting classes, mark the

starting point of top-to-bottom processes and the

conclusion of bottom-to-top processes within the

index bucketing framework.

•

OOT

– Inheriting from the Node class, the base

Root class undergoes constructor modification,

accepting solely value and level parameters. Root

nodes lack kdx or parent attributes. Consequently,

both the

IPATH

and

KPATH

methods return new

empty arrays. Notably, the

FLATTEN

method’s

signature undergoes modification, now accepting

the index bucket, ibucket, and flat template as

parameters, and returning an array of flat

mappings rather than a single mapping as seen in

prior class definitions.

•

NDEXING

OOT

– This class inherits the base

OOT

class, but its constructor configures the root

node’s level to 0 during instantiation, aligning its

child node call

ing behavior with that of

NDEXING

RANCH

nodes. Its

FLATTEN

method

iterates over the index bucket,

IBUCKET

dispatching each index path to the appropriate

child nodes for further processing. An array of flat

mappings, each of which is applied to a copy of

the flat template, is gathered from the child nodes

and is returned.

•

EYING

OOT

– Also inheriting from the base

OOT

class, the K

EYING

OOT

class sets its level

to -1 within the constructor since its child-calling

behavior does not utilize the indexes from the

index bucket. Its

FLATTEN

method operates by

passing index paths,

IPATH

, from the index bucket,

IBUCKET

, to its child nodes for further processing.

Likewise, an array of flat mappings, each of which

is applied to a copy of the flat template, is

gathered from the child nodes and is returned.

By distinguishing between K

EYING

OOT

and

NDEXING

OOT

nodes, the tree’s root node ensures

that subsequent level attributes are set appropriately

during initialization and the index bucket is

distributed accordingly during execution.

Algorithm 4: Root Classes.

3.5 Tree Structure – Algorithm 5

The Tree class serves as the foundational structure to

organize the nested dataset for the execution of the

index bucketing algorithm. In the constructor, the

initialization commences by setting the depth field to

0 and creating an empty set object for the key bucket,

kbucket. These fields are then used to analyze the data

parameter’s nested structure while the tree itself is

constructed and stored within the tree field which acts

as a reference to the root node. Next, the algorithm

gathers the index bucket, ibucket. Additionally, it

constructs the template by iterating through the key

bucket, compiling all key paths into a mapping with

initial null values for each key path. This flat template

formation streamlines the subsequent data

organization process.

•

FLATTEN

– To facilitate the flattening process, the

Tree class defines its own

FLATTEN

method. This

method initiates the root node’s

FLATTEN

method,

passing along the index bucket and flat template.

•

LEAF

– The

LEAF

method initializes and returns the

relevant L

EAF

class node. Additionally, the

LEAF

method identifies the maximum depth of the tree

and aggregates key paths into the key bucket.

•

BRANCH

– The

BRANCH

method initializes and

returns the relevant B

RANCH

class node. If the

collection passed as data is empty, then the

BRANCH

method delegates the parameter

arguments to the

LEAF

method with null passed for

the data parameter’s argument. Otherwise,

respective to the nested data types, the

BRANCH

method directs nested information to either another

BRANCH

method call or a

LEAF

method call.

An Index Bucketing Framework to Support Data Manipulation and Extraction of Nested Data Structures

195

•

ROOT

– The

ROOT

method initializes and returns

the relevant R

OOT

class node. The

ROOT

method

returns null when the data parameter is an empty

collection, indicating that no data is present.

Otherwise, respective to the nested data types, the

ROOT

method directs nested information to either

BRANCH

method call or a

LEAF

method call.

Algorithm 5: Tree Class.

3.6 Generator Alternative – Algorithm

To allow for the implementation flexibility of the

index bucketing algorithm, R

OOT

and T

REE

class

definitions are modified to transform the framework

into a generator capable of delivering flattened data

incrementally rather than in a single instance.

Instead of the R

OOT

node managing the index

bucket within its

FLATTEN

method, this responsibility

is shifted to the T

REE

class’s

FLATTEN

method.

Introducing a count field, initialized at 0, enables the

Algorithm 6: Generator Implementation.

tracking of index bucket progress. When the count

reaches the end of the index bucket, it is reset to 0,

and null is returned to signal completion. This

generator-style implementation offers a controllable

method to alleviate the adverse effects of duplication

explosion which can otherwise overload memory

usage. The adaptability of index bucketing as an

algorithm allows for diverse implementations,

offering various advantages to address challenges that

stem from other recursion-intensive approaches.

4 EVALUATION

To assess the efficacy of the index bucketing

algorithm, we evaluate the performance

measurements across two prominent question-

answering datasets: QuAC (QuAC, Question

Answering in Context. https://quac.ai/) and NewsQA

(NewsQA: A Machine Comprehension Dataset.

https://www.microsoft.com/en-us/research/publicati

on/newsqa-machine-comprehension-dataset/). These

datasets vary in file size: 74 MB and 151 MB

respectively. Both datasets come with a myriad of

restructuring challenges described below.

•

QuAC dataset requires that the background

attribute be prepended to each paragraph’s

context attribute, and data with

“CANNOTANSWER”

questions

and questions

without answers need to be filtered

out (Fig. 3).

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

196

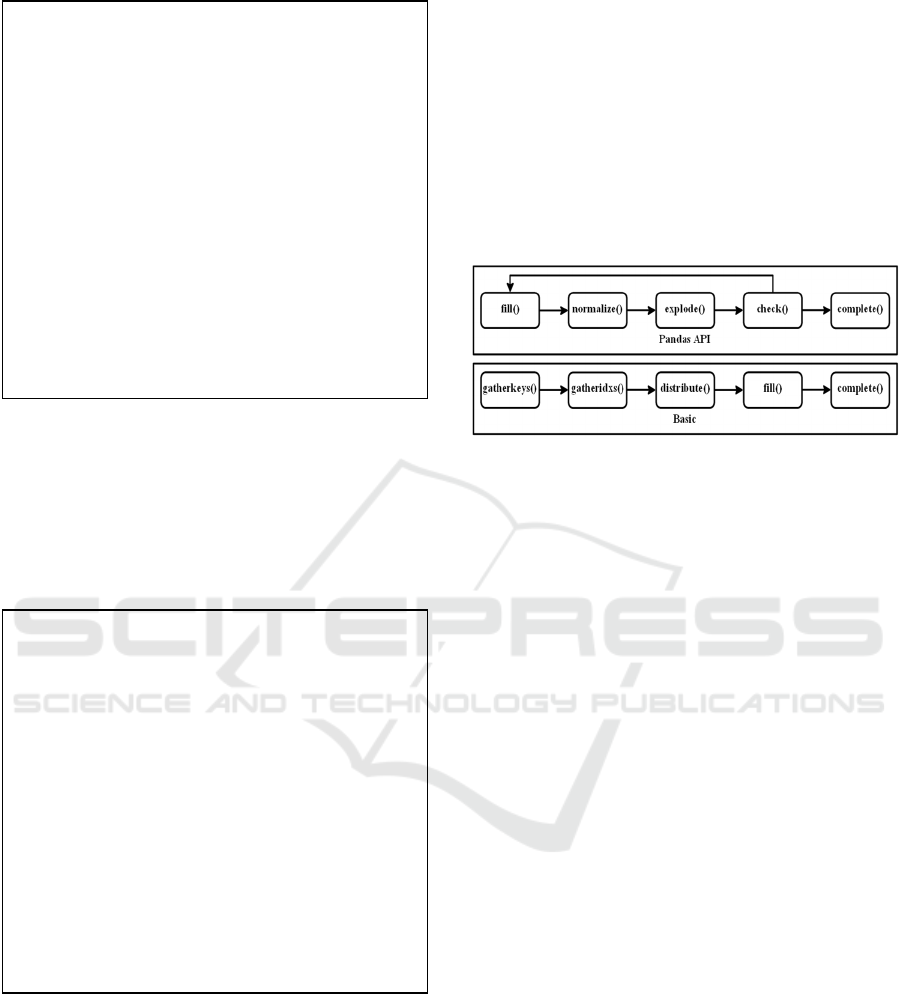
Figure 3: QuAC question answering dataset structure.

•

NewsQA dataset requires data extraction from

start and end attributes, into a new answer

attribute containing the indicated substring found

in the text context, and data with

“isQuestionBad”

questions ne ed to be filtered

out (Fig. 4).

Figure 4: NewsQA question answering dataset structure.

The index bucketing algorithm was juxtaposed

against two alternative flattening implementations:

one leveraging the Pandas Python API and another

employing a basic solution that combines recursive

and iterative techniques. Summarized in 0, Pandas

Python is used as a benchmark for comparison, as it

offers a competitive set of methods to flatten nested

data collections, such as filling missing values,

normalizing dictionaries into new columns, and

exploding lists into new records. The basic

implementation, on the other hand, serves to

demonstrate the worst-case effects of each challenge

Evaluations span various subsets of each dataset

incrementally from a Fibonacci-based sequence in the

range of 0.1% to 100% to gauge scalability. Each

subset underwent evaluations of the observed total

time of initialization and execution runtimes. The

average runtimes across the evaluations were

recorded to ensure more robust assessments.

Figure 5: Pandas Python implementation & basic execution

pipelines.

The ensuing graphs are organized by

implementation and dataset, plotting subset size,

measured in bytes, against runtime, measured in

seconds. These evaluations were conducted on an

Intel Core i7-8750H CPU, 32 GB RAM PC, clocking

in at a base frequency of 2.20 GHz, and capable of

reaching a maximum turbo frequency of 4.10 GHz. A

stringent maximum time limit of thirty minutes was

set to avoid prolonged executions, triggering a

timeout exception if exceeded. Notably, the basic

algorithm showcases an exponential growth pattern in

total runtimes, vividly illustrating the cost escalations

attributed to challenges that the index bucketing

algorithm aims to address. Compared to Pandas

Python implementation, our index bucketing

framework shows a 24.7% faster total runtime with

the QuAC dataset evaluations (0). With the NewsQA

larger dataset, the Pandas Python encounters failures,

which we suspect are attributed to duplicated data

instances within the original dataset. While Pandas

Python offers potential solutions to address these

errors, implementing such remedies remains

nontrivial to the best of our knowledge.

By preserving the original dataset structure, index

bucketing eliminates the need for dataset

reacquisition during subsequent executions. For

instance, considering a scenario where the flattening

process is repeated 100 times for each

implementation, the index bucketing showcases

substantial performance superiority. Although

multiple iterations of flattening might not align with

typical real-world scenarios, this comparison

{"text": "Miami ... contributed to this report.",

"type": "train",

"questions": [{

"isQuestionBad": 0.0,

"consensus": {

"s": 15,

"e": 32

"validatedAnswers": [{

"count": 2,

"s": 15,

"e": 32

}],

"answers": [{

"sourcerAnswers": [{

"s": 15,

"e": 32

}]

}],

"q": "Who reportedly suffers a seizure?",

"isAnswerAbsent": 0.0

}],

"storyId":

"./cnn/stories/6ebb8ab29b94430fa68f0e256c7703d9a41

f8bff.story"}…

{"text": "Miami ... contributed to this report.",

"type": "train",

"questions": [{

"isQuestionBad": 0.0,

"consensus": {

"s": 15,

"e": 32

"validatedAnswers": [{

"count": 2,

"s": 15,

"e": 32

}],

"answers": [{

"sourcerAnswers": [{

"s": 15,

"e": 32

}]

}],

"q": "Who reportedly suffers a seizure?",

"isAnswerAbsent": 0.0

}],

"storyId":

"./cnn/stories/6ebb8ab29b94430fa68f0e256c7703d9a41

f8bff.story"

}

…

An Index Bucketing Framework to Support Data Manipulation and Extraction of Nested Data Structures

197

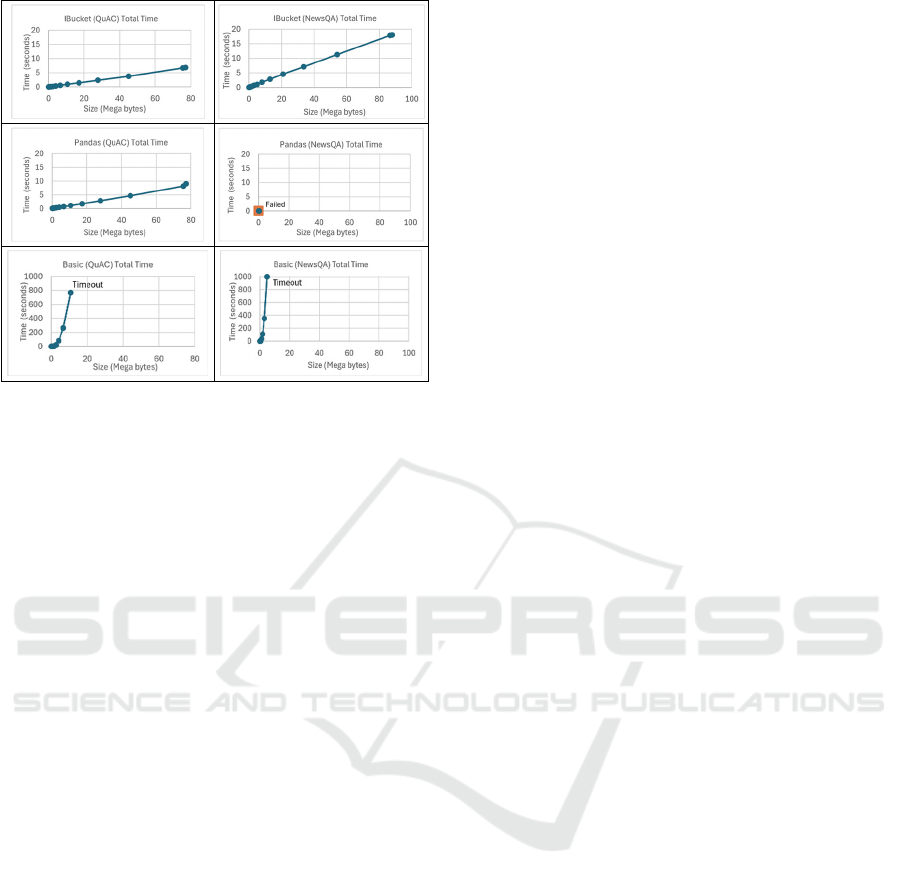
Figure 6: Total runtime evaluation.

demonstrates the index bucketing’s efficiency in

executing additional feature implementations beyond

flattening. Tasks like conditional filtering or attribute

selection can be executed notably more efficiently

with index bucketing compared to other

implementations. The performance results exemplify

the enduring advantages of the index bucketing

approach in handling repetitive operations and

processing complex tasks.

5 RELATED WORK

We have discussed nearly related work on employing

declarative querying APIs for integrating data query

languages with host programming languages’ data

processing. Transforming nested queries into

efficient forms using set-oriented operators has been

investigated for decades in different contexts

(Agrawal, 1988; Suciu, 1996). Work presented by

(Ulrich, 2019) offers a review of query flattening and

descriptions of query flattening in database theory.

Obtaining flat outputs in the presence of collection

queries was extended to multiset collections via

normalization and conservative algorithms (Fegaras

& Maier, 2000; Van den Bussche, 2001). Several

applications of nested data models build on this

calculus (Fegaras & Noor, 2018; Ricciotti & Cheney,

2021).

Another closely related work proposes a

framework that translates nested collection queries

into a semantically equivalent sequence of queries,

where outputs may then be nested and efficiently

evaluated (Smith et al., 2021). The framework

flattens nested queries by utilizing a series of

preprocessing and post-processing algorithms

referred to as query shredding and query stitching.

This has exhibited effectiveness in addressing

information loss, duplication explosion, and irregular

schema within the confines of traditional relational

database environments.

For resiliency against skewed distribution in

query processing, (Rödiger et al., 2016)introduce a

distributed join algorithm that detects skewness for

relational data by using small approximate

histograms and adapting the redistribution scheme to

resolve load imbalances. Nonetheless, alleviating

performance inefficiencies of flattening nested

collections with skew problems remains an open

question in the context of query processing (Smith et

al., 2020). Our framework addresses the

aforementioned challenges which also arise when

manipulating these large nested data structures, and

has shown the potential to extend its scope to the

realm of query processing.

6 CONCLUSIONS

We introduce a novel framework, index bucketing,

that aims to address the irregular schema, skewed

distribution, information loss, and duplication

explosion challenges in the manipulation of nested

data structures. Our contributions can be summarized

as the following. Employing proactive processes,

computational overheads that impede performance

are effectively offloaded during initialization, hence

enabling a controllable solution for data duplication

(Challenge A). Addressing skewed data distribution

(Challenge B) before manipulating the nested

structure. This is achieved by aggregating index paths

into an index bucket, a mechanism facilitating

efficient indexed-hashing access for nested data and

ultimately producing flattened records. Addressing

irregular schema (Challenge C) in the initialization

process that includes constructing a flat template—a

critical step ensuring every flattened record

encompasses all absent keys filled with null values.

The architecture of index bucketing, rooted in a

platform-independent, tree-based algorithmic

structure, aligns seamlessly with the original nested

data, preserving its inherent structure and

circumventing potential information loss (Challenge

D). The work explores an intuitive framework for

mitigating these challenges assessed on prominent

question-answering datasets such as NewsQA and

QuAC. Performance is compared against a

competitive Pandas Python API implementation and

a basic recursive, iterative implementation. Index

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

198

bucketing compares favorably against these

alternatives, exemplifying the enduring advantages of

the ability of the framework algorithm to handle

repetitive operations and process complex nested data

structures. Comparing the performance of index

bucketing against larger datasets is a limitation of this

study. More insights can be gleaned from further

evaluations expanding to other datasets and

implementations. Future work will, in part, explore

the implications of index bucketing to handle

repetitive operations and process complex nested data

structures.

REFERENCES

Agrawal, R. (1988). Alpha: an extension of relational

algebra to express a class of recursive queries. IEEE

Transactions on Software Engineering, 14(7), 879-885.

https://doi.org/10.1109/32.42731

Apache Flink. http://flink.apache.org/.

Apache Spark, http://spark.apache.org/.

Diestelkämper, R. (2021). Explaining existing and missing

results over nested data in big data analytics systems

http://dx.doi.org/10.18419/opus-12052.

Diestelkämper, R., Lee, S., Herschel, M., & Glavic, B.

(2021). To Not Miss the Forest for the Trees - A Holistic

Approach for Explaining Missing Answers over Nested

Data Proceedings of the 2021 International Conference

on Management of Data, Virtual Event, China.

https://doi.org/10.1145/ 3448016.3457249.

Fegaras, L., & Maier, D. (2000). Optimizing object queries

using an effective calculus. ACM Trans. Database

Syst., 25(4), 457–516. https://doi.org/10.1145/3776

74.3 77676.

Fegaras, L., & Noor, M. H. (2018, 2-7 July 2018). Compile-

Time Code Generation for Embedded Data-Intensive

Query Languages. 2018 IEEE International Congress

on Big Data (BigData Congress), doi: 10.1109/

BigDataCongress.2018.00008.

Grust, T., Rittinger, J., & Schreiber, T. (2010). Avalanche-

safe LINQ compilation. Proc. VLDB Endow., 3(1–2),

162–172. https://doi.org/10.14778/ 1920841.1920866.

Kitsuregawa, M., & Ogawa, Y. (1990). Bucket Spreading

Parallel Hash: A New, Robust, Parallel Hash Join

Method for Data Skew in the Super Database Computer

(SDC). Vldb '90, 210–221.

NewsQA: A Machine Comprehension Dataset. https://

www.microsoft.com/en-us/research/publication/news q

a-machine-comprehension-dataset/.

Pandas Python, https://pandas.pydata.org/.

QuAC, Question Answering in Context. https://quac.ai/.

https://quac.ai/.

Ricciotti, W., & Cheney, J. (2021). Query Lifting.

Programming Languages and Systems, 12648, 579 -

606.

Rödiger, W., Idicula, S., Kemper, A., & Neumann, T.

(2016, 16-20 May 2016). Flow-Join: Adaptive skew

handling for distributed joins over high-speed

networks. 2016 IEEE 32nd International Conference on

Data Engineering (ICDE), https://doi.org/10.1109/

ICDE.2016.7498324.

Samwel, B., Cieslewicz, J., Handy, B., Govig, J., Venetis,

P., Yang, C., Peters, K., Shute, J., Tenedorio, D., Apte,

H., Weigel, F., Wilhite, D., Yang, J., Xu, J., Li, J.,

Yuan, Z., Chasseur, C., Zeng, Q., Rae, I., Biyani, A.,

Harn, A., Xia, Y., Gubichev, A., El-Helw, A., Erling,

O., Yan, Z., Yang, M., Wei, Y., Do, T., Zheng, C.,

Graefe, G., Sardashti, S., Aly, A. M., Agrawal, D.,

Gupta, A., & Venkataraman, S. (2018). F1 query:

declarative querying at scale. Proc. VLDB Endow.,

11(12), 1835–1848. https://doi.org/10.14778/32298

63.3229871.

Smith, J. (2021). Declarative nested data transformations

at scale and biomedical applications, University of

Oxford.

Smith, J., Benedikt, M., Moore, B., & Nikolic, M. (2021).

TraNCE: transforming nested collections efficiently.

Proc. VLDB Endow., 14(12), 2727–2730.

https://doi.org/10.14778/3476311.3476330.

Smith, J., Benedikt, M., Nikolic, M., & Shaikhha, A.

(2020). Scalable querying of nested data. arXiv preprint

arXiv:2011.06381.

Suciu, D. (1996). Parallel programming languages for

collections, University of Pennsylvania.

Ulrich, A. (2019). Query Flattening and the Nested Data

Parallelism Paradigm Universität Tübingen].

Van den Bussche, J. (2001). Simulation of the nested

relational algebra by the flat relational algebra, with an

application to the complexity of evaluating powerset

algebra expressions. Theoretical Computer Science,

254(1-2), 363-377.

An Index Bucketing Framework to Support Data Manipulation and Extraction of Nested Data Structures

199