Research on Solutions to Non-IID and Weight Dispersion

Haosen Jiang

, Yuting Lan

and Yihan Wang

School of Continuing Education Zhejiang University, Zhejiang University, Hangzhou, Zhejiang, 310063, China

Glasgow College Hainan, University of Electronic Science and Technology of China, Lingshui, Hainan, 572423, China

Department of Engineering, Shenzhen MSU-BIT University, Shenzhen, Guangdong, 518172, China

Keywords: Federated Learning, Non-IID, SCAFFOLD, Weight Dispersion, MOON

Abstract: Federated learning is an emerging basic technology of artificial intelligence. The design goal is to carry out

high-efficiency machine learning among multi-participants or multi-computing nodes under the premise of

ensuring information security during big data exchange, protecting terminal data and personal data privacy,

and ensuring legal compliance. At the same time, federated learning also faces many challenges, such as the

heterogeneity of data, that is, the problem of the non-independent and identically distributed (Non-IID), and

the problem of weight dispersion. After a comprehensive review of the literature and experiments, the

following conclusions are reached: For Non-IID, the SCAFFOLD algorithm uses a control variable c to

correct the training direction, which is also updated when the client and server are updated. For the weight

dispersion problem, this paper takes the Model-contrastive Federated Learning (MOON) algorithm as an

example to analyze that the reason for the problem is that only the weight distribution of the output layer is

considered, while the similarity measurement of model parameters on other layers is ignored. Based on this

conclusion, this study gives suggestions for improvement and prospects for the future: Non-IID caused by

distributed databases needs to reconsider the federated learning model and algorithm, and selective sampling

according to the data distribution type of clients may improve the performance and stability of the federated

learning system. Federated learning algorithms such as MOON, which have weight dispersion problems, can

reduce the impact by removing negative sample pairs, or increase the loss of weight similarity.

1 INTRODUCTION

In 2016, the Google team published Federated

Learning: Strategies for Improving Communication

Efficiency, which introduced the concept of federated

learning. From the initial Horizontal Federated

Learning, to solve the problem of model training on

the user terminal device at the C end, to the later

Vertical Federated Learning, with the increasing

attention to data privacy and security issues, Vertical

Federated Learning began to receive attention and

application at the B end, and then it was further

extended to Federated Transfer Learning. Through

the combination of Transfer Learning and Federated

Learning, Model migration and knowledge sharing

can be achieved. Federated Learning is a method of

machine learning that trains high-quality centralized

models on the premise that the training data is

distributed across a large number of customer agents.

Traditional centralized learning methods often

require raw data to be uploaded to a central server for

model training, which can lead to the risk of privacy

disclosure. On the one hand, an attacker may steal the

data stored on the server, thereby revealing the

sensitive information of the user; On the other hand,

even if the data is encrypted, the server may infer the

user's private information by analyzing the data

pattern. By contrast, Federated Learning avoids

uploading raw data to a central server by training the

model on a local device, thereby reducing the risk of

privacy breaches. In Federated Learning, the parties

only upload model updates to the server, not the raw

data itself, which allows for better data privacy

protection. In addition, the Federation Learned to

adopt technical means such as encryption and security

protocols to further enhance the security of data.

However, several challenges in Federated Learning

can degrade the performance of the model, including

data heterogeneity, that is, non-independent and

identically distributed (Non-IID), and Weight

Dispersion Problems.

By studying the Non-IID data problem and

Weight Dispersion Problem, this paper introduces the

148

Jiang, H., Lan, Y. and Wang, Y.

Research on Solutions to Non-IID and Weight Dispersion.

DOI: 10.5220/0012832600004547

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 148-153

ISBN: 978-989-758-690-3

Software-Configured Application Framework for

Object-oriented Layered Design (SCAFFOLD) and

Model-contrastive Federated Learning (MOON)

under the background of Federated Learning and

proposes the algorithm of adjusting model parameters

and Feature-Contrastive Graph Federated Learning

(FcgFed) for weight dispersion problem. This paper

aims to optimize model performance and weight

distribution to improve the effectiveness of Federated

Learning systems.

2 RELATED WORKS

2.1 Data Silos

Non-IID data have different characteristics,

distributions, or data types. The key challenge of

federated learning is the heterogeneity of data among

clients, i.e. Non-IID (Kairouz et al, 2019). Non-IID

will reduce the effectiveness of machine learning

models (Li et al, 2018).

"Federated Learning (FL) with Non-IID Data"

published by YueZhao et al. studied the difference in

model performance between IID data and Non-IID

data and found that the performance dropped

significantly (Yue et al, 2018). "Federated Learning

on Non-IID Data Silos: An Experimental Study"

published by Li Qinbin et al. used a comprehensive

Non-IID data case to conduct experiments to evaluate

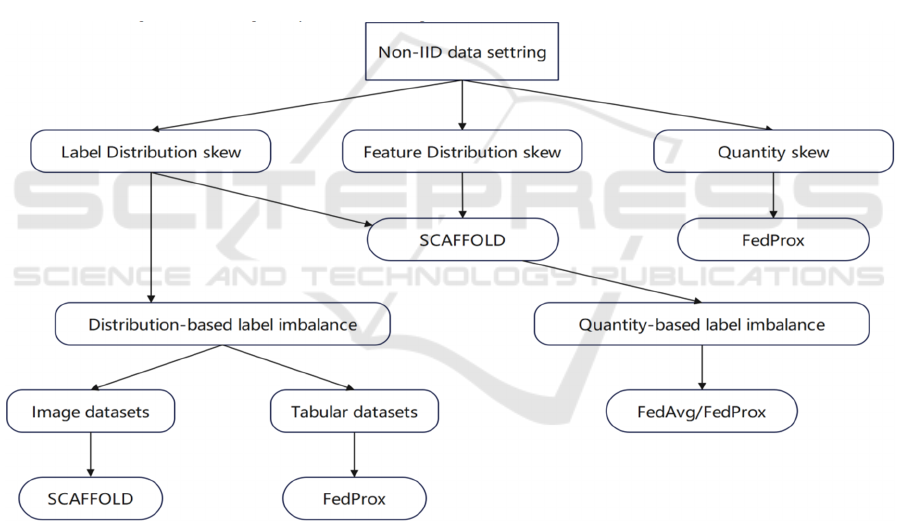
the most advanced FL algorithm. This study defines

Non-IID types: label distribution deviation, feature

distribution deviation, same labels but different

features, same features but different labels, and data

volume deviation. This experimental study has a

more comprehensive data setting, and the best FL

algorithm can be selected through a Non-IID type

setting (Qinbin et al, 2021). as shown in Figure 1.

Figure 1. The optimal decision tree for the FL algorithm is given the Non IID setting (Qinbin et al, 2021).

2.2 Development of FcgFed

Framework

Feiyue Wang and his team wherein they conducted

research and developed a new framework called the

FcgFed algorithm (Xingjie et al, 2023). This

algorithm successfully addressed the issue of weight

divergence present in the MOON algorithm (Xingjie

et al, 2023). The final experimental results of the

study demonstrate its implementation and provide the

pseudocode for the FcgFed algorithm. The code

reveals that the FcgFed algorithm initially transfers

data from the central model to the local models

multiple times (Xingjie et al, 2023). Subsequently, it

adjusts the initial weight distribution of the central

model through communication during training in the

local models (Xingjie et al, 2023). Finally, accuracy

is improved by increasing the number of learning

rounds (Xingjie et al, 2023).

Research on Solutions to Non-IID and Weight Dispersion

149

3 RESEARCH

3.1 Algorithm for Non-IID

Controlled variable for federated learning:

Karimireddy et al. proposed the Stochastic Controlled

Averaging for Federated Learning (SCAFFOLD)

algorithm. SCAFFOLD uses a "controlled variable" c

to correct the direction of system training. When the

client and server update the model, the variable will

also be updated (Sai et al, 2021).

Karimireddy et al. conducted experiments using

the EMNIST dataset. The SCAFFOLD algorithm

performs best compared to the FedAvg algorithm and

the FedProx algorithm. The latter two will suffer from

client drift, so the convergence effect and speed will

become worse. The SCAFFOLD algorithm is not

affected by data heterogeneity or client sampling data

and has a faster convergence speed. Such as Table 1

(Sai et al, 2021).

Table 1. The optimal testing accuracy of SGD, FedAvg,

and SCAFFOLD (Sai et al, 2021).

0% similarity 10% similarity

SGD 0.766 0.764

FedAvg 0.787 0.828

SCAFFOLD 0.801 0.842

Model-Contrastive Federated Learning: Model-

Contrastive Federated Learning (MOON) proposed

by Li Qinbin et al. uses the similarity between model

representations to correct local learning. Traditional

contrastive learning is data-level, such as SimCLR.

Its essential idea is that similar ones gather together

and heterogeneous ones separate. MOON is model-

level. It takes the same idea and improves it based on

the local model training phase of FedAvg. It aims to

reduce the distance of learned representations

between local models and increase the distance of

learned representations between local models and

global models (Qinbin et al, 2021).

Based on this optimization goal, MOON uses the

Model-Contrastive Loss function as



((,



)/

((,



)/((,



)/

(1)

Experimental results by Li Qinbin et al. show that

MOON has higher accuracy in different tasks than

other methods shown in Table 2 (Qinbin et al, 2021).

Table 2: The test accuracy of FL algorithm with different tasks (Qinbin et al, 2021).

Method CIFAR-10 CIFAR-100 Tiny-Imagenet

MOON 69.1% ± 0.4% 67.5% ± 0.4% 25.1% ± 0.1%

FedAv

66.3% ± 0.5% 64.5% ± 0.4% 23.0% ± 0.1%

FedProx 66.9% ± 0.2% 64.6% ± 0.2% 23.2% ± 0.2%

SCAFFOLD 66.6% ± 0.2% 52.5% ± 0.3% 16.0% ± 0.2%

SOLO 46.3% ± 5.1% 22.3% ± 1.0% 8.6% ± 0.4%

In terms of heterogeneity, MOON can always

achieve the best accuracy among the three imbalance

levels β set by Li Qinbin et al shown in Table 3

(Qinbin et al, 2021).

Table 3: The test accuracy of FL algorithm with different unbalanced level (Qinbin et al, 2021).

Method β= 0.1 β= 0.5 β= 5

MOON 64.0% 67.5% 68.0%

FedAv

62.5% 64.5% 65.7%

FedProx 62.9% 64.6% 64.9%

SCAFFOLD 47.3% 52.5% 55.0%

SOLO 15.9% ± 1.5% 22.3% ± 1.0% 26.6% ± 1.4%

ICDSE 2024 - International Conference on Data Science and Engineering

150

3.2 Definition of the Weight Divergence

Problem

The weight divergence problem refers to the situation

where the weights assigned by the central node to

client nodes exhibit excessive similarity or

concentration (Xingjie et al, 2023, Mostafa, 2019,

Fuxun et al, 2021). This can lead to the model

becoming trapped in a specific pattern during the

early stages of training, causing slow learning or

convergence to local minimum values (Xingjie et

al, 2023, Mostafa, 2019, Fuxun et al, 2021).

Consequently, this may result in suboptimal model

performance, making it challenging to effectively

learn the complex features of the data (Xingjie et al,

2023, Mostafa, 2019, Fuxun et al, 2021).

Case: Weight Divergence Problem in the MOON

Algorithm:

In the MOON algorithm, the weight divergence

problem is characterized by its exclusive

consideration of the weight distribution in the output

layer, neglecting the measurement of similarity in

model parameters across other layers (Xingjie et al,

2023). This introduces a heightened risk of weight

divergence in layers other than the output layer

(Xingjie et al, 2023). This risk is particularly

pronounced in the analysis of image information

(Xingjie et al, 2023). When the central node allocates

weights to client nodes, some crucial client nodes

may receive smaller weights or be overlooked,

leading to the omission of important labels (Xingjie

et al, 2023).

Two Suggestions for Addressing the Weight

Divergence Problem:

Suggestion 1: Reduce Weight Divergence by

Adjusting Model Parameters

(1) Mostafa proposed representation matching to

reduce the divergence of local models through

activation alignment (Fuxun et al, 2021).

(2) A research team from George Mason

University introduced a federated learning

framework with feature alignment to address the issue

of structural feature inconsistency (Fuxun et al,

2021).

Limitations of (1) and (2): However, both of these

approaches require consideration of client-side model

parameters for weight allocation (Xingjie et al, 2023).

Even if the weights of local models have been

appropriately adjusted, the weight distribution of the

central model does not update as the model training

progresses (Xingjie et al, 2023).

Suggestion 2: To achieve convergence with

different types of datasets and overcome the risk of

weight divergence in all model parameter weights,

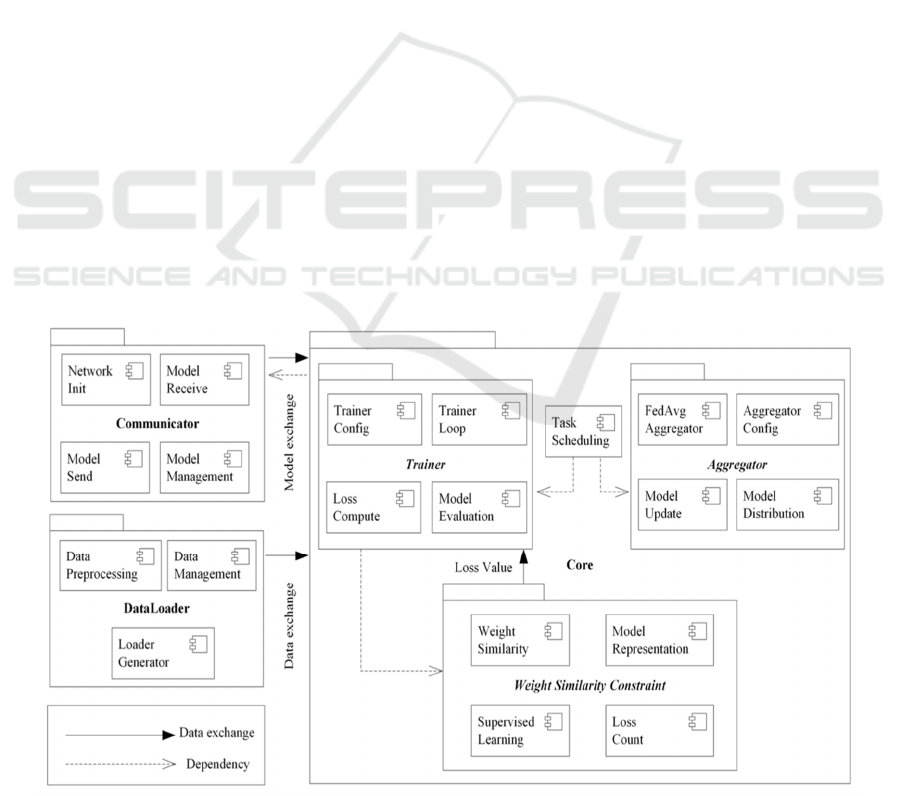
the team led by Feiyue Wang proposed the FcgFed

learning method. The specific process involves two

steps: firstly, designing an architecture for the FcgFed

learning system to analyze image information, and

collect features, and labels, as shown in Figure 2

(Xingjie et al, 2023). Secondly, introduces a

contrastive learning-based federated learning method

for images that can autonomously update data and

alleviate weight divergence in federated learning, as

illustrated in Figure 3 (Xingjie et al, 2023).

Figure 2: The image analysis framework in the FcgFed algorithm (Mostafa, 2019).

Research on Solutions to Non-IID and Weight Dispersion

151

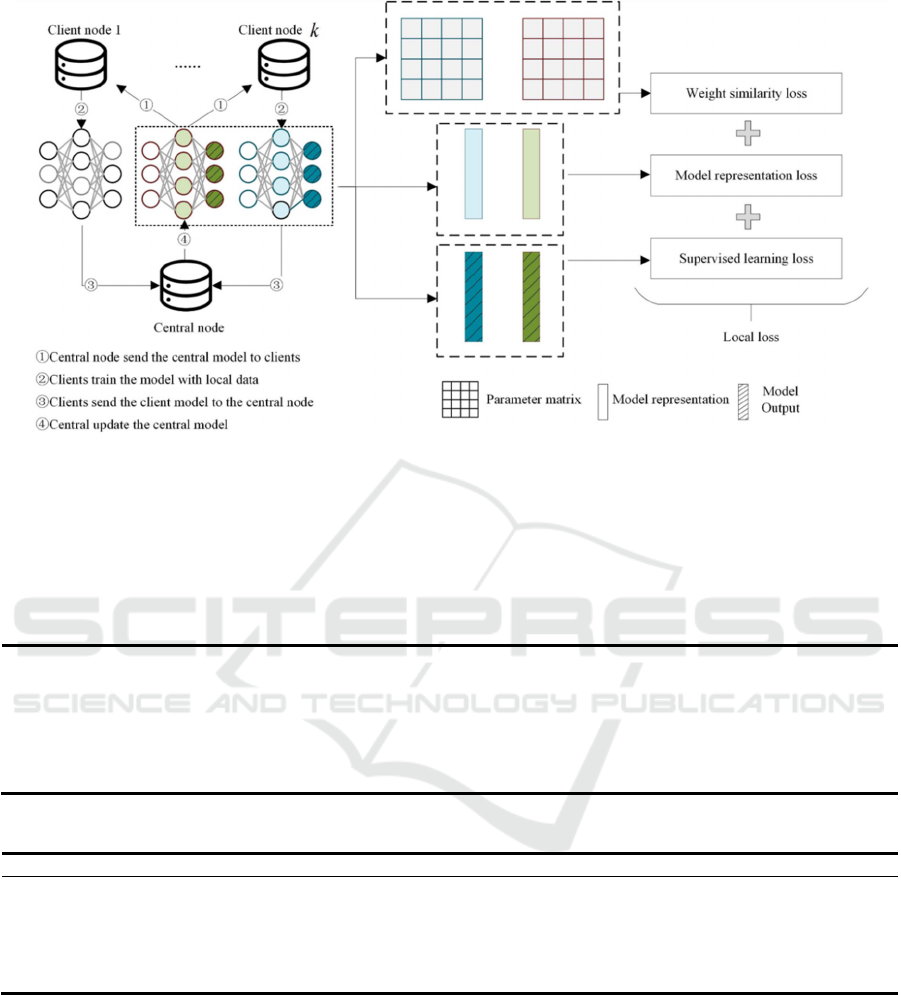
Figure 3: The learning process of FcgFed (Xingjie et al, 2023).

Specific Implementation of Suggestion 2: The

team led by Feiyue Wang designed a model

representation assessment and weight similarity

constraint method based on contrastive learning. This

implementation achieved optimization for the weight

divergence problem in the MOON algorithm. The

optimization results are presented in Table 4 and

Table 5.

Table 4. Accuracy of Different Methods in Node Classification (Mostafa, 2019).

Dataset Model Cora

GAT

Cora

GCN

CiteSeer

GAT

CiteSeer

GCN

PubMed

GAT

PubMed

GCN

FedAv

0.858 0.854 0.657 0.666 0.842 0.854

MOON 0.842 0.845 0.686 0.686 0.850 0.851

Fed.C 0.850 0.845 0.607 0.683 0.859 0.850

FcgFed.S 0.842 0.848 0.692 0.698 0.858 0.856

0.840 0.855 0.713 0.716 0.861 0.857

Table 5. Accuracy of Different Methods in Graph Classification (Mostafa, 2019).

Method GIN GAT GCN

FedAv

0.354 0.305 0.423

MOON 0.369 0.277 0.368

FcdFed.C 0.383 0.308 0.303

Fed.S 0.379 0.376 0.388

0.374 0.356 0.425

4 ANALYSIS

The non-IID problem caused by distributed databases

requires rethinking federated learning models and

algorithms. Selective sampling based on the client's

data distribution type may improve the performance

and stability of federated learning systems. For

algorithms, researchers start from the following

perspectives: 1) develop algorithms that add

additional parameters (defined according to global

and local differences) to reduce client drift or correct

training directions; 2) develop algorithms with fewer

training rounds to Reduce communication volume

and speed up fitting (Qinbin et al, 2021).

Some federated learning algorithms, such as

MOON, exhibit the issue of weight divergence. To

ICDSE 2024 - International Conference on Data Science and Engineering

152

address this problem, researchers can consider the

following approaches:

1) Reducing Negative Sample Pairs: By

eliminating negative sample pairs, the impact can be

reduced. Negative sample pairs refer to data that is

unnecessary or unexpected for certain experiments

(Xingjie et al, 2023, Lu et al, 2024).

2) Introducing Additional Loss Components: For

example, increasing the loss associated with weight

similarity can be effective (Xingjie et al, 2023).

5 CONCLUSION

For the Non-IID problem, this study analyzes the

advantages of the Controlled variable for federated

learning and MOON to solve this problem and gives

the following suggestions.

For Federated Learning, the Stochastic Controlled

Averaging for Federated Learning (SCAFFOLD)

algorithm uses a "control variable" c to correct the

training direction of the system. When the model is

updated by the client and server, the variable is also

updated.

MOON uses similarities between Model

representations to correct local learning.

Future research directions include designing

innovative algorithms that add additional parameters

to reduce client drift, correct training direction, and

developing algorithms with fewer training rounds to

reduce traffic and improve fitting speed, thus

effectively mitigating the impact of non-independent

co-distribution problems. In addition, the influence of

weight dispersion can be reduced more effectively by

optimizing the strategies for dealing with negative

samples, such as introducing weight similarity loss.

AUTHORS CONTRIBUTION

Yuting Lan: Relevant work on the weight dispersion

issue, the research content, and the future prospects

of the weight dispersion problem are specifically

presented in sections 2.2, 3.2, and 4.2 of the report.

Haosen Jiang: Regarding non-independent and

non-identically distributed work, research, and

recommendations, the specific content is covered in

sections 2.1, 3.1, and 4.1.

Yihan Wang: The research abstract, the

Introduction section, the Conclusion section, and the

organization of references.

All the authors contributed equally and their

names were listed in alphabetical order.

REFERENCES

P. Kairouz, H. B. McMahan, B. Avent, et al. arXiv preprint

arXiv:1912.04977, (2019).

T. Li, A. K. Sahu, M. Zaheer, et al. arXiv preprint

arXiv:1812.06127, (2018).

Z. Yue, M. Li, L. Liangzhen, et al. arXiv preprint

arXiv:1806.00582, (2018).

L. Qinbin, D. Yiqun, C. Quan, et al. arXiv preprint

arXiv:2102.02079, (2021).

Z.Xingjie, Z. Tao, B. Zhicheng, et al. "Feature-Contrastive

Graph Federated Learning: Responsible AI in Graph

Information Analysis," in IEEE Transactions on

Computational Social Systems, 10(6), (2023), pp.

2938-2948.

K. Sai P, S. Kale, M. Mohri, et al. arXiv preprint

arXiv:1910.06378, (2021).

L. Qinbin, H. Bingsheng, S. Dawn, et al. arXiv preprint

arXiv:2103.16257, (2021).

H. Mostafa. arXiv:1912.13075, (2019).

Y. Fuxun, Z. Weishan, Q. Zhuwei, et al. "Fed2: Feature-

aligned federated learning," In Proceedings of the 27th

ACM SIGKDD Conference on Knowledge Discovery

& Data Mining, (2021), pp. 2066-2074.

W. Lu, D. Chao, L. Chuan, et al. arXiv preprint

arXiv:2401.08690, (2024).

Research on Solutions to Non-IID and Weight Dispersion

153