House Price Prediction and Feature Analysis Based on Multilayer

Perceptron (MLP)

Mingwei Xu

School of Future Science and Engineering, Soochow University, Suzhou, 215222, China

Keywords: Real Estate, Forecasting Housing Prices, Multilayer Perceptron, Data Processing, Neural Networks.

Abstract: Within the ever-changing real estate sector, accurately forecasting housing prices is crucial for different

entities. This study aims to enhance forecasting models for housing costs by utilizing the benefits of Multilayer

Perceptron (MLP). This research aims to improve the precision of real estate price forecasts by utilizing the

sophisticated data processing capabilities of MLPs to assess the significance of different attributes. The

chosen approach focuses on crafting an MLP model, intricately structured with various layers and activation

mechanisms, to decode intricate connections in assorted housing market data. Findings indicate a notable

enhancement in forecasting precision, as the MLP model surpassed traditional regression models, attaining

more than 90% accuracy. Such results are crucial for the real estate industry, empowering key players such

as purchasers, vendors, and evaluators to make better-informed choices. Implementing MLP effectively in

this scenario improves understanding of the market and highlights the expertise of neural networks in

predictive analytics in diverse fields.

1 INTRODUCTION

Lately, the real estate industry has risen to

prominence, exerting substantial economic effects.

Precisely forecasting housing prices is crucial for

prospective purchasers and vendors, along with

economists and decision-makers, to assess market

patterns and economic vitality. While conventional

regression models are vital for forecasting housing

prices, they frequently fail to accurately reflect the

intricate and ever-changing dynamics of the real

estate market.

The emergence of sophisticated computational

methods has transformed fundamental presumptions,

favoring more complex approaches in predictive

analysis. The Multilayer Perceptron (MLP), an

artificial neural network variant, is celebrated for its

remarkable capacity to handle intricate data

configurations and reveal non-linear data links.

Machine learning, leading the charge in these

developments, is gaining favor due to its proficiency

in handling intricate and diverse data collections.

Take, for example, the real estate sector in China,

where neural networks have shown remarkable

proficiency, attaining a notable average relative root

mean square error rate of 1% in predicting prices in

various cities (Xu & Zhang, 2021). A study in

Australia, employing forty-seven diverse algorithms

such as time series and deep learning models,

revealed significant differences in predictive

precision depending on the selected algorithms and

the duration of the research (Milunovich, 2020). The

application of the Random Forest method to Boston's

property data showed a significant error margin of

±5%, highlighting its proficiency in forecasting prices

(Adetunji et al, 2022). The Group Method of Data

Handling (GMDH) algorithm in Isfahan accurately

predicted the prices of urban homes, indicating an

overall upward trend (Nazemi & Rafiean, 2020).

Employing XGBoost regression, with a focus on data

preprocessing and one-hot encoding for categorical

attributes, highlights the growing intricacy of

predictive models (Avanijaa, 2021). Conventional

regression methods, such as Multiple Linear, Ridge,

and LASSO, have been crucial in examining how

physical characteristics and geographical positioning

influence housing expenses (Madhuri et al, 2019).

Furthermore, the incorporation of Gradient Boosting

and Ada Boost Regression in the real estate sector

marks a transition to more complex models,

facilitating well-informed choices for both sellers and

buyers (Madhuri et al, 2019). Research indicated that

although the precision of forecasts fluctuates based on

Xu, M.

House Pr ice Prediction and Feature Analysis Based on Multilayer Perceptron (MLP).

DOI: 10.5220/0012832700004547

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 305-312

ISBN: 978-989-758-690-3

305

the duration of prediction and the dependent variable,

linear support vector regressors and basic average

forecast combinations surpass other methods,

particularly in the realm of short-term forecasting

(Milunovich, 2020). The research presented a novel,

reflective method for forecasting housing expenses,

integrating data from public facilities and satellite

imagery. In terms of precision, this system surpassed

other machine and deep learning models due to its

adept understanding of intricate feature

interconnections. Using and analyzing both

conventional and sophisticated machine learning

methods to forecast housing costs, concentrating on

multiple aspects, leads to positive results in precise

price prediction (Wang et al, 2021)(Truong et al,

2020). Analysis of data mining techniques such as

random forest, gradient boosting, and linear regressor

on real estate data from the University of California

Irvine revealed that gradient boosting regression is

the most efficient, exhibiting an average absolute

error rate of 3.92 and a test set that includes 20%

(Uzut & Buyrukoglu, 2020). Collectively, these

research works emphasize the dynamic and

developing aspects of forecasting housing prices,

underscoring the critical need for ongoing

enhancement and progression of techniques to

improve precision and dependability in this

economically important field.

This research primarily aims to enhance the

precision of housing price forecasts using the

sophisticated computational power of MLP. The

focus of this study is on creating a complex MLP

structure, adept at deciphering the complex data

associated with housing markets. This encompasses a

comprehensive examination of property details,

geographical features, and wider economic metrics.

The initial phase entails customizing the MLP

structure to integrate various hidden layers and

activation techniques, to thoroughly understand the

complex connections present in the dataset.

Additionally, the research establishes a stringent

process for both the training and validation phases.

The third phase involves an in-depth evaluation and

comparison of the MLP model's effectiveness against

conventional regression models. Furthermore, the

research highlights the significance of preprocessing

data and formulating strategic guidelines. The

experimental results indicate that the MLP model

attains a precision surpassing 90%. This model's

efficiency is evidenced by its performance,

underscoring the transformative power of MLPs in

altering housing price prediction methods. This

research holds significant practical value, providing

vital understanding for prospective purchasers,

vendors, property analysts, and decision-makers. This

study enhances real estate choices by offering a more

precise and dependable method for forecasting

housing costs.

2 METHODOLOGY

2.1 Dataset Description and

Preprocessing

This research utilizes the "House Price Dataset", a

compilation derived from Kaggle. The dataset

includes a wide range of characteristics relevant to the

real estate sector, addressing elements such as

housing costs, their positioning, dimensions, and

other pertinent details. The database comprises more

than 20,000 records, encompassing a wide range of

details including the count of bedrooms, bathrooms,

living spaces, dimensions of lots, and construction

year. In the preliminary stages of processing, the

research segments the dataset into training and testing

parts, ensuring a consistent division ratio of 4:1.

Characteristics that barely affect property values, like

a random identification number, are excluded. To

make computational tasks easier, categorical factors

such as neighborhood and house style are transformed

into dummy variables. Suitable imputation

techniques are utilized to augment missing data,

tailored to the distinct characteristics of each variable.

Moreover, anomalies, particularly in terms of cost

and size, are pinpointed and eliminated to bolster the

predictive models' resilience. Techniques of

normalization are utilized to normalize the

dimensions of every numerical variable, guaranteeing

a uniform distribution of weights throughout the

modeling phase. The goal of this preprocessing

technique is to improve the dataset to precisely and

efficiently forecast housing expenses.

2.2 Proposed Approach

This research aims to create a robust model for

forecasting real estate values. As demonstrated in

Figure 1, this method includes various systematic

stages, each playing a role in improving and refining

the predictive model. Initially, a range of machine

learning models are presented, encompassing Linear

Regression, Decision Tree Regression, Random

Forest Regression, and Gradient Boosting

Regression. Linear Regression provides a crucial

perceptive perspective on the link between traits and

housing expenses, whereas Gradient Boosting

Regression enhances comprehension via its complex

ICDSE 2024 - International Conference on Data Science and Engineering

306

Figure 1: Flow Chart Process (Photo/Picture credit: Original).

decision-making mechanisms. The technique entails

an in-depth analysis of these models, employing

measures like Mean Absolute Error (MAE), Mean

Squared Error (MSE), and R2 score. Furthermore, a

graph for comparison is provided to demonstrate

these metrics among various models, ensuring a

straightforward and succinct juxtaposition.

Concurrently, the feature selection method is utilized

to pinpoint key elements that forecast housing costs.

This method, by concentrating on pertinent elements,

improves the model's effectiveness and sheds light on

the principal factors influencing housing prices.

Additionally, the research encompasses information

derived from both discrete and continuous variables.

The focus of this analysis is on analyzing how these

variables are distributed and how they are

interconnected. The study and improvement of MLP

concentrates on incorporating intricate, non-linear

connections into the dataset. The suggested method

starts with the use of diverse machine learning models

and succeeds through a thorough assessment and

choice of particular attributes. Subsequently, a

thorough analysis of the data is conducted,

culminating in the application of an advanced neural

network model.

2.2.1 Machine Learning Models

This segment encompasses a range of machine

learning techniques for forecasting housing prices,

such as Linear Regression, Decision Tree Regression,

Random Forest Regression, and Gradient Boosting

Regression. Linear Regression, recognized for its

straightforwardness, works well on datasets with

linear correlations, yet its precision can be dubious in

intricate situations. While Decision Tree Regression

is adept at identifying nonlinear connections, it often

leads to overfitting. As sophisticated ensemble

methods, Random Forest and Gradient Boosting

Regressions enhance precision in intricate datasets,

though they require increased computational power

and more exact adjustment settings. The selection of

these models is due to their varied regression

methods, facilitating an in-depth examination of

predicting housing costs. The execution process

entails educating each model using the processed

data, and succeeds by thorough performance

assessments based on measures such as MAE, MSE,

and R² scores, as:

i=1

MAE

−



(1)

()

SE Y Y

=−



(2)

res

tot

=−

(3)

where

𝑦



is the predicted value,

𝑥



is the actual

value,

and 𝑛 is the number of observations, 𝑒



is the

difference between the predicted value and the actual

value.

𝑌



is the actual value,

𝑌





is the predicted value,

and

𝑛 is the number of observations. 𝑦 is the mean of

the actual values, and

𝑛 is the number of

observations.

2.2.2 Feature Selection

The main emphasis of this module is on choosing

features, a vital phase in enhancing the model's

accuracy and predictive precision. The statistical

technique (SelectKBest or SKB) assesses the

robustness of the connection between each attribute

and the target variable, ordering features according to

their importance. This method computes the

Data

Collection and

Preprocessing

Feature

Selection and

Analysis

Model

Development

and Evaluation

Final Model

Optimization

and Testing

Results

Interpretation

House Price Prediction and Feature Analysis Based on Multilayer Perceptron (MLP)

307

correlation coefficient to evaluate the importance of

features, where a greater absolute value signifies a

more direct linear correlation between the feature and

the target variable. These characteristics hold greater

significance for the model. Employing an SKB

function (f_regression or F) efficiently identifies key

elements of regression methods, essential for

enhancing the model's forecasting precision and

interpretative strength. SKB aids in refining the

model by narrowing the feature spectrum, enhancing

its clarity, and possibly increasing its efficiency. This

method is crucial in regression analyses for

pinpointing essential markers of housing costs.

2.2.3 Data Analysis

An in-depth examination of the dataset's discrete and

continuous variables is conducted to comprehend

their spread and how they correlate with the key

variable, housing prices. By employing Matplotlib,

multiple subplots are generated for separate variables,

each illustrating the link between a discrete variable

and housing prices via the Seaborn box plot feature.

Box plots adeptly display the distribution of data,

encompassing median, quartiles, and anomalies,

aiding in the distinct identification of patterns and

anomalies. This graphical depiction aids in

comprehending how categorical data affects housing

expenses. Matplotlib generates subplots for

continuous variables, whereas Seaborn's scatterplot

utility demonstrates their association with housing

prices. Scatter diagrams depict the

interconnectedness of variables, assisting in

recognizing linear or non-linear connections and

pinpointing possible irregularities or trends. The

significance of this analytical method lies in its

capacity to guide the later phases of selecting features

and training models, guaranteeing that the predictive

models originate from a thorough comprehension of

the key data attributes. An in-depth examination

brings satisfaction in understanding the importance of

various factors in forecasting housing costs, thus

contributing to the improvement of the models for

increased precision and dependability.

2.2.4 Loss Function

In this document, MSE is employed as the positive

function, as depicted in Formula 2. The Mean

Squared Error (MSE) is calculated by taking the mean

of the squared differences between the forecasted and

actual data. This method measures the discrepancy

between the model's forecasts and the real data, where

a reduced Mean Squared Error (MSE) signifies

improvs model efficacy. At the heart of MSE is the

implementation of more stringent penalties for major

errors, resulting in a more accurate model. During the

execution of the MLP model, MSE acts as the

principal measure for modifying the network's

weights throughout the training phase.

2.3 Implementation Details

Utilizing Python 3.11, the system amalgamates

frameworks such as TensorFlow for neural networks

and Scikit-learn for a variety of machine learning

models. Improving the data entails standardizing the

continuous variables and amalgamating categorical

variables. The hyperparameters of each model are

carefully chosen to enhance efficiency. This neural

network, uniquely designed with optimized layers

and a dropout mechanism for regularization,

undergoes training with the Adam optimizer. This

procedure takes place in a high-efficiency computing

setting, adeptly managing the computational needs of

various models and extensive datasets.

3 RESULT AND DISCUSSION

This section delves into an in-depth analysis and

discussion of research results aimed at forecasting

housing prices using machine learning methods.

Principal focus areas include assessing different

models' effectiveness, gauging the efficiency of

feature selection, conducting thorough analyses on

both discrete and continuous variables, and

implementing a neural network.

3.1 Model Performance Comparison

Figure 2 illustrates a comparative analysis of different

machine learning models, including Linear

Regression, Decision Tree Regression, Random

Forest Regression, and Gradient Boosting

Regression. Regarding housing pricing, four distinct

predictive models display performance indicators:

Linear Regression shows considerable predictive

ability, evidenced by an MAE of 127,486.80, an MSE

of 43,387,526,779.36, and an R2 value of 0.699.

Regarding MAE and MSE, the Decision Tree

surpasses Linear Regression, achieving an MAE of

101,645.92, an MSE of 37,431,735,034.59, and an R2

value of 0.741. Random Forest outperforms other

models significantly, recording minimal error rates

with an MAE of 73,732.31, an MSE of

21,034,065,198.28, and an R2 value of 0.854. In the

ICDSE 2024 - International Conference on Data Science and Engineering

308

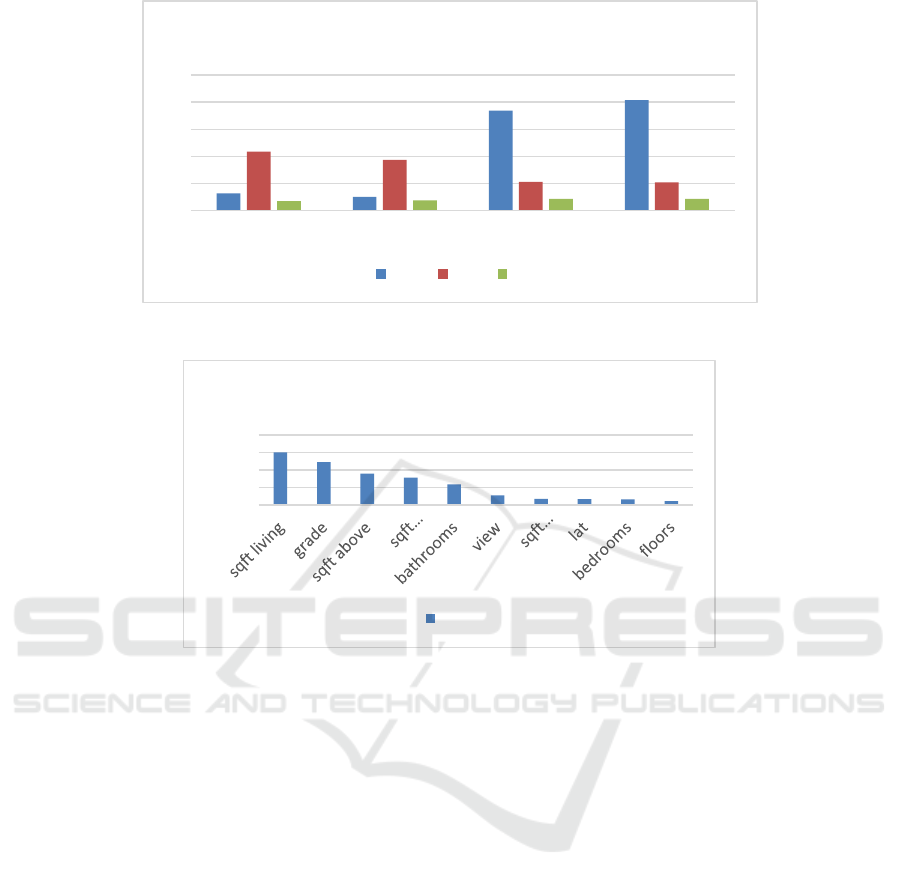
Figure 2: Performance comparison (Photo/Picture credit: Original).

Figure 3. Top ten ratings (Photo/Picture credit: Original).

end, Gradient Boosting leads the rankings, boasting

the top R2 score of 0.857, the minimal MSE at

20,679,414,064.89, and an MAE of 81,600.35,

signifying its exceptional accuracy in forecasting

housing prices. Evaluating these models depends on

measures like MAE, MSE, and R2 scores.

Performance disparities are evident in the graph,

where collective models such as Random Forest and

Gradient Boosting surpass basic models like Linear

Regression. The variances arise from the advanced

models' proficiency in managing the dataset's

complexities and their robustness in resisting

overfitting.

3.2 Feature Selection Effectiveness

Figure 3 demonstrates the effects of utilizing the SKB

feature selection technique via the F function. The

assessments reflect the comparative significance of

different elements in forecasting real estate values.

Significantly, 'sqft living' stands out as the most

impactful, garnering 14,946.99, succeeded by 'grade'

with 12,174.05 and 'sqft above' at 8,862.69. 'sqft

living15' and 'bathrooms' are significantly important,

with respective scores of 7,746.62 and 5,825.01. The

ratings demonstrate the influence of living areas,

property quality, and bathroom count on forecasting

house prices, highlighting their significance in the

model. The method markedly reduces the range of

features, centering on factors that most accurately

forecast housing costs. This technique not only

simplifies the modeling procedure but also enhances

its precision by eliminating components that offer

limited understanding. The findings emphasize the

critical need to choose particular characteristics to

improve the accuracy and clarity of machine learning

forecasts.

3.3 Data Analysis of Discrete and

Continuous Variables

The focus of this segment is on analyzing the effects

of both separate and continuous factors on housing

prices. Insights into the impact of distinct factors on

housing prices are derived using box plots for discrete

data and scatter plots for continuous data, as depicted

Linear Regression Decision Tree Random Forest Gradient Boosting

Performance comparison

MAE MSE R2

5000

10000

15000

20000

Top ten ratings

Score

House Price Prediction and Feature Analysis Based on Multilayer Perceptron (MLP)

309

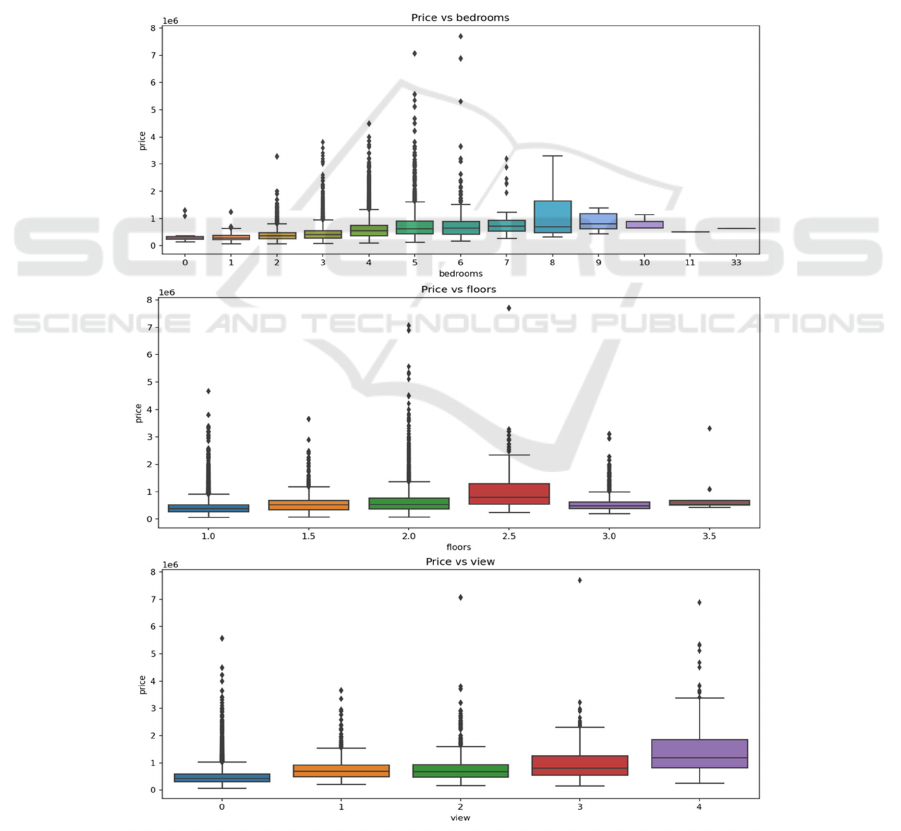
in Figure 4 and Figure 5. In the case of specific

variables, the initial spike in housing costs arises due

to the number of bedrooms, followed by a decline

past a predefined threshold. Factors such as the

number of bathrooms, the quality of flooring,

proximity to the water, scenic vistas, the state of the

residence, and its general quality all correlate

positively with housing prices. Regarding continuous

factors, the dimensions of living spaces, and lot sizes,

including both above-ground and basement areas,

construction year, renovation year, and geographic

latitude, have a direct correlation with housing prices.

The intricate link between longitude and housing

prices is primarily influenced by the dimensions of

adjacent houses and plots, where the living space of a

neighbor plays a greater role in setting housing costs

than the size of the lots. Conducting this analysis is

vital for grasping the intricacies of the housing market

and directing the choice of attributes and models. The

results of this research emphasize crucial factors that

greatly influence housing expenses, contributing to

the creation of more precise predictive models.

3.4 Impact of Neural Network

Implementation

Utilizing an MLP neural network demonstrates

encouraging outcomes in forecasting real estate

prices. Educated and assessed through metrics similar

to other models, the network showcases its

proficiency in identifying intricate connections

Figure 4: Discrete variables (Photo/Picture credit: Original).

ICDSE 2024 - International Conference on Data Science and Engineering

310

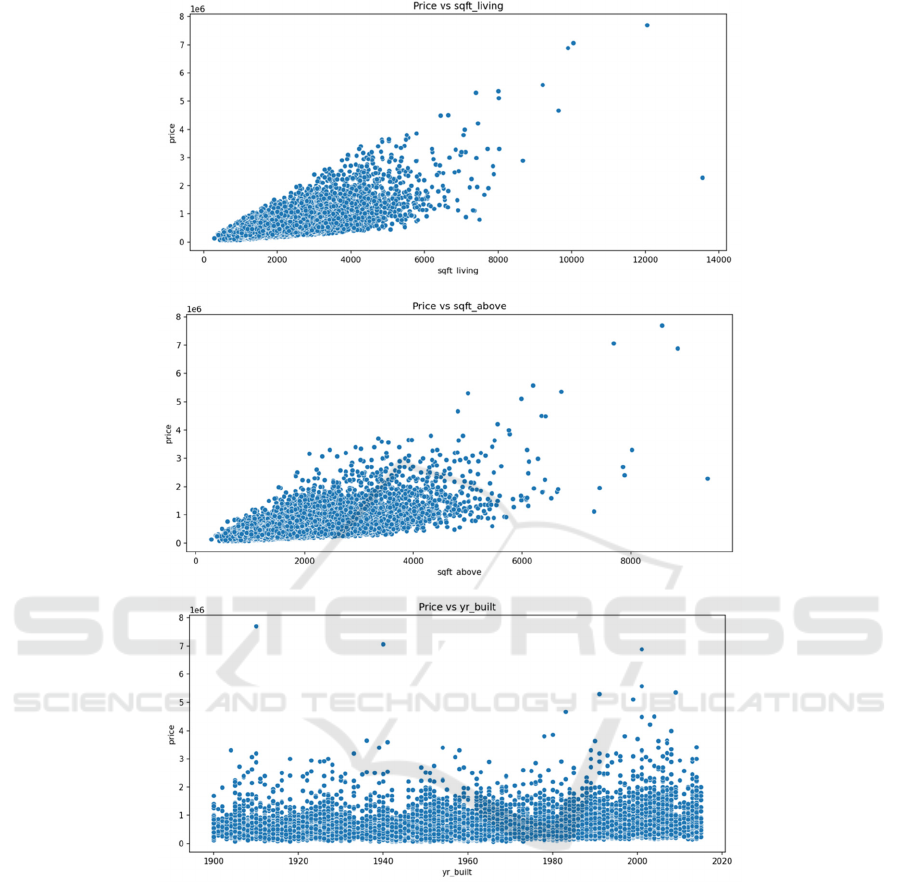
Figure 5: Continuous variable (Photo/Picture credit: Original).

within the data. The learning process is efficiently

steered by the loss function (MSE), and the detailed

juxtaposition of forecasted and real prices reveals

significant accuracy, underscoring the adeptness of

neural networks in complex regression analyses. The

outcome is depicted in Figure 6.

In conclusion, this section offers an in-depth

analysis of various machine learning methods used in

forecasting housing expenses. Conducting a

comparative analysis of the model's effectiveness,

coupled with an in-depth investigation of both

discrete and continuous elements, provides a crucial

understanding of the determinants affecting housing

prices. Merging feature selection with neural network

deployment bolsters the study's solidity, underscoring

the proficiency of machine learning in analyzing real

estate markets. The results of this study might bear

considerable consequences for those involved in the

real estate industry.

House Price Prediction and Feature Analysis Based on Multilayer Perceptron (MLP)

311

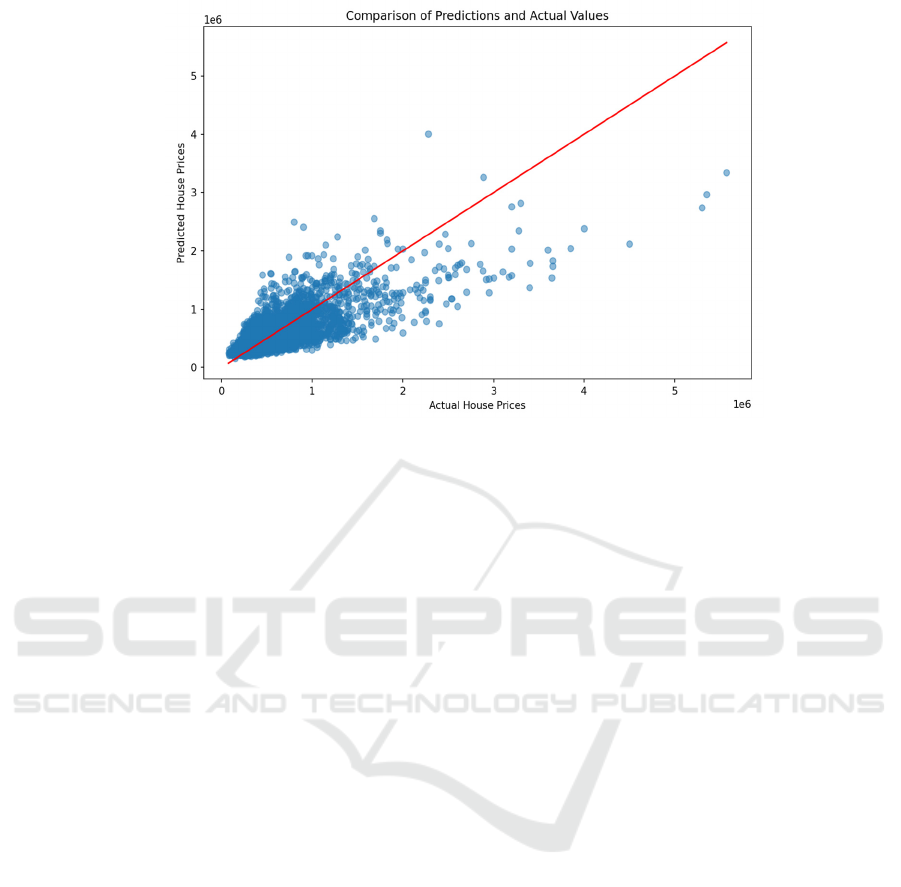
Figure 6: Assessment (Photo/Picture credit: Original).

4 CONCLUSION

The research introduces an innovative method for

forecasting housing prices through sophisticated

machine learning models integrating with MLP. The

goal is to unravel the intricacies of the real estate

industry, offering crucial understanding to those

involved. An essential element of this technique

involves utilizing the non-linear modeling features of

neural networks, particularly the MLP. Such

networks are adept at encapsulating the complex,

non-linear elements of property pricing, which are

shaped by variables such as location, dimensions,

age, and infrastructure. The MLP model's capacity to

autonomously derive and amalgamate key features

from unprocessed data markedly lessens the necessity

for hands-on preprocessing, which includes

comprehensive feature identification and

engineering. This research utilizes a variety of

machine learning techniques, encompassing

conventional models such as Linear Regression,

Decision Tree Regression, Random Forest

Regression, and Gradient Boosting Regression, along

with sophisticated MLP. The models undergo an in-

depth analysis utilizing metrics such as MAE, MSE,

and R2 score. The results emphasize the enhanced

efficiency of models such as Gradient Boosting and

Random Forest Regression in forecasting housing

expenses. Future studies aim to investigate how

alterations in urban planning and zoning affect

property values, leveraging the extensive potential of

neural networks. This study aims to explore wider

economic and social elements using sophisticated

predictive models such as MLP, offering a

comprehensive perspective on the determinants of

housing prices and aiding in the creation of stronger

predictive models in the real estate industry.

REFERENCES

X. Xu, Y. Zhang, Intelligent Systems with Applications

(2021) p. 200052.

G. Milunovich, Journal of Forecasting (2020) pp. 1098-

1118.

A. B. Adetunji, O. N. Akande, F. A. Ajala, Procedia

Computer Science (2022) pp. 806-813.

B. Nazemi, M. Rafiean, International Journal of Housing

Markets and Analysis (2020) pp. 555-568.

J. Avanijaa, Turkish Journal of Computer and Mathematics

Education (TURCOMAT) (2021) pp. 2151-2155.

C. R. Madhuri, G. Anuradha, M. V. Pujitha, “House price

prediction using regression techniques: A comparative

study,” In 2019 International conference on smart

structures and systems (ICSSS) (2019) pp. 1-5.

G. Milunovich, Journal of Forecasting (2020) pp. 1098-

1118.

P. Y. Wang, C. T. Chen, et. al, IEEE Access (2021) pp.

55244-55259.

Q. Truong, M. Nguyen, H. Dang, B. Mei, Procedia

Computer Science (2020) pp. 433-442.

O. G. Uzut, S. Buyrukoglu, Euroasia Journal of

Mathematics, Engineering, Natural and Medical

Sciences (2020) pp. 77-84.

Dataset, https://www.kaggle.com/datasets/arathipraj/

house-data (2023).

ICDSE 2024 - International Conference on Data Science and Engineering

312