
QPTA: Quantum-Safe Privacy-Preserving Multi-Factor Authentication
Scheme for Lightweight Devices
Basker Palaniswamy
a
and Arijit Karati
b
Cryptology and Network Security Lab, Department of Computer Science and Engineering,
National Sun Yat-sen University, Kaohsiung, Taiwan
Keywords:
Authenticated Key Agreement, Privacy, Multi-Factor Authentication, Smart Healthcare, Quantum-Safe
Authentication, Post-Quantum Authentication, Attack Detection Logic.
Abstract:
Smart healthcare is ubiquitous to lift the convenience of managing patients’ medical records. Accessibility
of patients’ sensitive data stored in medical servers needs source authenticity. To ensure this, (Karati et al.,
2023) proposed a three-factor authentication scheme using physical uncolonable functions. However, the
scheme is vulnerable to a quantum adversary. To this end, we design a multi-factor authentication scheme
called QPTA resistant to quantum adversaries for a healthcare scenario involving a user and a medical server.
QPTA enables choice within the same factor in multi-factor authentication. The security of QPTA is formally
analyzed using the “Attack Detection Logic.” QPTA is safe from known attacks, including unknown key share
and man-in-the-middle attacks. We perform an informal security analysis of QPTA to ensure various security
goals and privacy properties, namely anonymity, unlinkability, and conditional traceability. QPTA satisfies
comprehensive security features and is suitable for the post-quantum era.
1 INTRODUCTION
Smart healthcare enables physicians to manage pa-
tients’ data in a way that is quickly accessible, and
they can access the medical records of patients by
storing the records in a medical server and retrieving
those data using hand-held equipment, such as smart-
phones, tablets, etc. Smart healthcare improves pa-
tients’ convenience as they do not need to save every
record produced in the hospitals. Because they are
managed systematically within the hospitals. Though
data management is most efficiently handled in Smart
healthcare for patients and physicians, the stored and
retrieved data on the server require security and pri-
vacy against attackers. Fig. 1 shows the conceptual
overview of the major phases in the proposed pro-
tocol wherein a physician (Alice) securely accesses
the data of patients from a medical server (Bob). The
security and privacy of the medical records are pre-
served by ensuring the confidentiality, authenticity,
integrity, anonymity, and unlinkability of the records.
To preserve these goals, physicians should be authen-
ticated to access the medical records in the presence
of an adversary who can potentially manipulate med-
a
https://orcid.org/0000-0002-3661-6048
b
https://orcid.org/0000-0001-5605-7354
Trusted Authority
Server (Bob)
User (Alice)
IV. Dynamic user addition
II. User registration
III. Authentication
V. Password and PIN change
System
Administrator
PIN
PWD
Attacker
VI. Revocation
Figure 1: Conceptual overview.
ical records. So, an authenticated key agreement pro-
tocol is inevitable for Smart healthcare. Even if an ad-
versary is passive, the curious adversary can monitor
patients’ health conditions. In the future, adversaries
can have quantum computers to bypass the security
imposed by classical cryptosystems. Considering the
evolving threat to medical records, several authenti-
cations have been proposed for the smart healthcare
scenario (Karati et al., 2023; Qiu et al., 2020; Baner-
jee et al., 2020; Kwon et al., 2021). Nevertheless, they
do not satisfy at least five security goals (ref. Table 1).
In particular, the work (Banerjee et al., 2020) lacks
resistance towards known attacks. Inheriting the same
weakness, the research (Qiu et al., 2020) does not
allow adding dynamic users. Moreover, the scheme
suggests honey lists for handling online password-
804
Palaniswamy, B. and Karati, A.
QPTA: Quantum-Safe Privacy-Preserving Multi-Factor Authentication Scheme for Lightweight Devices.
DOI: 10.5220/0012835100003767
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 804-811
ISBN: 978-989-758-709-2; ISSN: 2184-7711
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

guessing attacks. Whenever the honey lists exceed the
threshold value, authorized servers block users. This
introduces denial of service (DoS) for the users. For
instance, an adversary can target all users at random
for the attack. The work (Kwon et al., 2021) does
not support user revocation. Consequently, if trusted
users misbehave in the network, such users cannot
be controlled. The security lapse of the work (Kwon
et al., 2021) applies to this work. The research (Karati
et al., 2023) has suggested a trifactor authentication
scheme for Smart healthcare. However, this scheme
has at least two disadvantages: lacking multifactor se-
curity and vulnerability to a quantum adversary. Gen-
erally, while considering the resistance to a quantum
adversary and multifactor security, all these schemes
do not meet the requirements. Table 1 presents ex-
haustive security requirements. Thus, we present our
contributions in two-fold.
• We design a quantum-safe, multi-factor authenti-
cation scheme, QPTA, for a two-party scenario in-
volving a server. It has online password and per-
sonal identification number (PIN) changes, user
revocation, and dynamic user addition phases.
• We apply the “Attack Detection Logic (ADC)”
(Jurcut et al., 2017) to formally analyse QPTA.
QPTA is safe from known attacks. Further, infor-
mal analysis for various security goals and privacy
traits, namely anonymity, unlinkability and condi-
tional traceability confirms the security of QPTA.
The paper is organized as follows. Sections 2 and
3 elaborate on the preliminaries and construction of
QPTA. Formal and informal analysis of QPTA is put
forth in Section 4. Section 5 presents the efficiency
analysis. Section 6 concludes our work.
2 PRELIMINARIES
We describe notations, adversarial models, security
goals, and cryptographic primitives at a high level.
2.1 Notations
Let q be a large prime, and let F
q
= Z/qZ be the fi-
nite field defined by integers bounded by q; it ranges
in the limit [0, q − 1]. Let R
q
be the quotient ring
formed by
Z
q
[X]
f (x)
, where f (x) = X
n
+ 1 denotes the
irreducible cyclotomic polynomial in which n is the
power of 2. We use small bold-face to represent
polynomials in the text. A polynomial d ∈ R
q
is
mentioned as d = d
0
+d
1
x
1
+d
2
x
2
+,...,d
n−1
x
n−1
, where
each coefficient of d is a vector [d]
i ∈ [0,n]
. We use
a ←−
$
S/a ∈
R
Z
q
to mention an element (a) is drawn
uniformly at random from the set (S/Z
q
). The dis-
tribution of the secret polynomial and error polyno-
mial is in R
q[C]
, where the elements of R
q[C]
∈ [-C,
C]. ⌈x⌋
l
=
x−[x]
2
l
2
l
denotes l-bit modular rounding of x,
where [x]
2
l
ranges in (−2
l−1
,2
l−1
]. ⌈x⌋
l
is congruent
to x mod 2
l
. ⌊ x ⌋ mentions that x is made to its nearest
value. ∥ is the concatenation operator and ⊕ is bitwise
exclusive-OR. E and E
−1
are symmetric encryption
and symmetric decryption, respectively. H(.) denotes
the hash function. Let n be the security parameter.
2.2 Adversarial Model
We consider extensions to the Dolev-Yao adversar-
ial model (Dolev and Yao, 1983). The adversary can
intercept, replay, masquerade, block, and inject new
messages. Further, we consider the adversary to be
able to obtain past session keys and passwords. The
adversary can acquire users’ private keys, but it can-
not acquire the remaining credentials, such as biomet-
rics and passwords. Also, the adversary is honest-but-
curious (HBC) but passive in the HBC role.
2.3 Security Goals
We provide security and privacy goals based on the
authenticated key exchange system.
2.3.1 Security Goals
Entity Authentication (SG1): Using a pre-shared
long-term secret, the user and server should identify
each other to agree on a short-term secret.
Session Key Security (SG2): The user and server
should derive a matching session key. And the ad-
versary should not know it.
Implicit Key Authentication (SG3): The user should
ensure that it generates the key material.
Explicit Key Confirmation (SG4): The user must
know that the server has accurately derived the ses-
sion key.
Known Key Secrecy (SG5): The adversary can not de-
rive remaining session keys by knowing a session key.
Forward Secrecy (SG6): The leakage of the long-term
secret should not expose any past session keys.
Resilience to Ephemeral Secret Key Leakage (SG7):
The leakage of the short-term session-specific secrets
should not expose session keys.
Future Quantum Attack Resilience (SG8): The adver-
sary with quantum computers cannot get session keys.
Denial of Service Resilience (SG9): Deploying honey
lists against online password-guessing attacks should
not block the user from accessing data in the server.
QPTA: Quantum-Safe Privacy-Preserving Multi-Factor Authentication Scheme for Lightweight Devices
805

Multifactor Security (SG10): QPTA requires pass-
words, PINs, fingerprints, iris data, and smart cards
for authentication. User can pick among passwords,
PINs, fingerprints, and iris data (SG15).
2.3.2 Privacy Goals
Unlinkability (SG12): Any two messages the user
sends should not be linked by the adversary.
Conditional Traceability (SG13): In case of dispute,
the trusted authority (TTP) should know the sender
identity of every scrambled message.
QPTA offers anonymity (SG11) (Karati et al., 2023)
and resistance towards known attacks, namely replay,
masquerading, main-in-the-middle, password guess-
ing, PIN guessing, stolen smart card verifier and
stolen verifier table (SG14). SG20 resists HBC.
2.4 Cryptographic Primitives
QPTA relies on a key derivation function (KDF)
(Krawczyk, 2010), physical unclonable function
(PUF) (Sahoo et al., 2017), fuzzy extractor (Fan et al.,
2023), dynamic accumulator (Benaloh and De Mare,
1993) and a singcrtyption with key encapsulation
mechanism (KEM) SETLA-KEM (G
´
erard and Mer-
ckx, 2018). The security of SETLA-KEM depends
on the ring learning with error problem (RLWEP)
(Lyubashevsky et al., 2010). RLWEP is computation-
ally infeasible to solve using quantum computers.
We use only these algorithms explicitly in QPTA.
KDF has two algorithms, namely HKDF.Extract(.)
and HKDF.Expand(.). PUF is instantiated as cM-
PUF(.). In the fuzzy extractor, FE.Gen(.) is used for
generating biometric template creation. The dynamic
accumulator has ACC.KeyGen(.), ACC.Acc.Gen(.),
ACC.Acc.verify(.), ACC.Acc.Update(.),
ACC.WitGen(.) and ACC.Wit.Update(.).
3 CONSTRUCTION
QPTA has six phases: initialization, registration, au-
thentication, authentication credential change, and
user revocation. We assume that users and the server
have a tamper-proof module that stores long-term se-
crets securely. Further, the server enforces RBAC to
authorize users to access the sensitive data.
3.1 Initialization Phase
We set q = 2
25
− 2
12
+ 1, n = 512 ({0,1}
256
), C = 1,
k = 4, pwlist
i ∈ {ID}
=
/
0, pinlist
i ∈ {ID}
=
/
0 and
hlist
i ∈ {ID}
=
/
0. This work recommends correspond-
ing AES − 256 and SHAKE − 256 as the symmetric
encryption and hashing algorithms.
3.2 Registration Phase
The registration phase has user registration, smart
card registration, and revocation-credential registra-
tion sub-phases. We denote the user by U/Alice and
Bob does the server by S/Bob interchangeably, and
this phase is for registering Alice by Bob.
3.2.1 User Registration
U submits her certificate to S to validate her public
key (PK
U
). S verifies the public key of U by using the
verification key of TTP. S verifies U sufficiently, i.e.,
verifying the identity proof. U chooses her authenti-
cation credentials, namely password (pwd) and PIN
(pin) such that the password is an eight-digit data and
PIN ∈ N. S picks a salt salt ∈ {0, 1}
256
and computes
AC
1
= H(ID∥pwd∥salt) and AC
2
= H(ID∥pin∥salt).
S gets biometrics of U, namely iris (ir) and fingerprint
( f p). S gets R
ir
and R
f p
using FE.Gen(.). S computes
AC
3
= H(ID∥R
ir
∥salt) and AC
4
= H(ID∥R
f p
∥salt). S
issues a four-digit code word (CW ) to U for choosing
the preference of authentication credentials. Briefly,
CW = “1111” indicates the use of authentication cre-
dentials AC
1
, AC
2
, AC
3
and AC
4
. The condition is
that out of AC
1
and AC
2
, at least one must be cho-
sen by U . Similarly, out of AC
3
and AC
4
, at least
one must be chosen by U. Public keys and private
keys are generated as per the SETLA algorithm. The
version for Bob is a
1
,a
2
←−
$
R
q
(public parameter),
t
b,1
, t
b,2
∈ R
2
q
(public key) and s, e
b,1
, e
b,2
∈ R
3
q[1]
(secret key). Similarly, for Alice, TTP generates cre-
dentials. The subscript a is carried for Alice. S
stores ⟨H(ID),hlist,AC
1
,AC
2
,AC
3
,AC
4
,pwlist,pinlist⟩
in its database. Further, S stores ⟨AC
1
,AC
2
,AC
3
,AC
4
⟩
in the hand-held device of the user.
3.2.2 Smart Card Registration
U submits a request for a smart card by choosing a
random number (rnd
1
∈
R
Z
q
)to S. While submit-
ting, the user gives her identity (ID). After getting
rnd
1
and ID from U, the server (S) chooses a secret
(sec
1
∈
R
Z
q
). Using H(.), S computes the smart card
credentials SC = H(rnd
1
∥ID∥sec
1
). S ensures that
⟨SC⟩ is stored in the smart card.
3.2.3 Revocation-Credential Registration
For U , S uses ACC.KeyGen(.) for generating a
symmetric key (hk). Initially, S make revoca-
SECRYPT 2024 - 21st International Conference on Security and Cryptography
806
User:
1) Insert smart card, Enter ID;
2) Compute H(ID);
3) Compute V
1
= H(H(ID)||SC);
4) Choose code w ord (CW);
5) Compute V
2
= (AC
1
ÅAC
2
)Å(AC
3
ÅAC
4
);
6) Compute V
3
= V
2
ÅV
1
;
Device:
7) Retriv e SC, AC
1
,
AC
2
, AC
3
,AC
4
;
8) Compute V'
1
, V'
2
, V'
3
;
9) Check V
3
== V
3
';
10) Authenticate User;
11) Compute ACC.AccVerify(A,W
U
,U);
12) Generate R Î
R
Z
p
;
13) Compute V
4
= H(R,V
1
,V
2
);
14) Compute V
5
= cMPUF(V
4
);
15) Compute V
6
= H(sec
1
||V
2
)ÅV
5
;
16) Compute V
7
= HKDF.Extract(V
5,
R);
17) sk = HKDF.Expand(V
7,
256);
18) Choose K Î
R
{0,1}
256
;
19) Compute V
8
= V
6
ÅK;
20) Compute m = R||H(ID)||CW||V
6
;
21) Choose y Î
R
R
q[C]
;
22) Compute c = H(ëa
1
.y ù
l
,ëa
2
.y ù
l
,m,V
8
,pk
a
,pk
b
);
23) Compute z = s
a
×
c + y ;
24) Compute w
1
= a
1
.y - e
a,1
.c;
25) Compute w
2
= a
2
.y - e
a,2
.c;
26) Choose y " Î
R
R
q[C]
;
27) Compute x = t
b1
.y + y " + Encode(V
8
);
28) E = E(m||V
8
); M
1
= z,c,x ,E;
Add your text here
29) Compute w
1
= a
1
.z - t
a,1
.c;
30) Compute w
2
= a
2
.z - t
a,2
.c;
31) V
8
= Decode(x - w
1
.s
b
);
32) m = E
-1
(E);
33) Check c = H(v, m,V
8
,pk
a
,pk
b
);
34) Check z;
35) Check L;
36) Compute V
2
" = (AC
1
ÅAC
2
)Å(AC
3
ÅAC
4
);
37) Compute H(sec
1
||V
2
"
);
38) Recov er V
5
" = V
6
ÅH(sec
1
||V
2
");
39) Compute V
7
" = HKDF.Ex tract(V
5
",R);
40) sk = HKDF.Expand(V
7
",256);
41) Compute V
9
= H(V
6
||R||pk
b
||pk
a
||sk);
M
2
= V
9
;
42) Compute V
9
" = H(V
6
||R||pk
b
||pk
a
||sk);
43) Verify V
9
" = V
9
;
Establish session under sk
SU
Send M
1
Send M
2
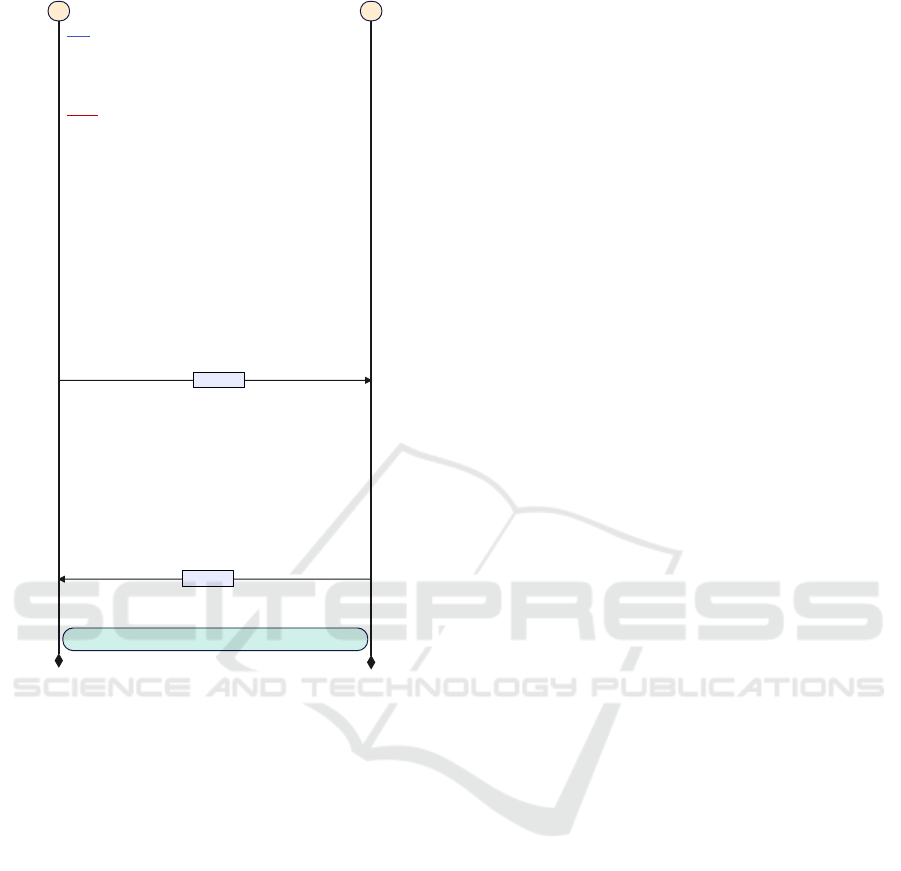
Figure 2: MSC of QPTA.
tion list (L ) as null. It generates an accumula-
tor for L as A using ACC.Acc.Gen(.). The server
generates non-membership witness for U as W
U
,
W
U
using ACC.WitGen(.). The server makes A
and W
U
available on the public ledger. S assigns
two variables T
tol
and T
exp
for tracking the smart
card’s tolerance limit and expiry time. S stores
⟨H(ID),AC
1
,AC
2
,AC
3
,AC
4
,T
tol
,T
exp
⟩ in its database.
When the registration procedure is complete with
the user, S stores ⟨H(ID),sec
1
,salt,hk,sk
U
,SC⟩
in its tamper-proof module. Moreover,
⟨H(ID),AC
1
,AC
2
,AC
3
,AC
4
,hk,SC,salt⟩ is stored
in the tamper-proof module of the user device.
3.3 Authentication Phase
Fig. 2 shows the authenticated key exchange steps be-
tween U and S in the message sequence chart (MSC).
User Authentication : The user authenticates with
her device, initially. The user inserts her smart card
and enters her ID (Step 1). The user computes H(ID)
and V
1
= H(H(ID)||SC). According to the prefer-
ences, U selects the code word (CW), and computes
V
2
= (AC
1
⊕ AC
2
) ⊕ (AC
3
⊕ AC
4
) and V
3
= V
2
⊕V
1
.
Recall that out of AC
1
and AC
2
, U has to choose at
least one choice; out of AC
3
and AC
4
, U has to se-
lect at least one choice. Based on the choice, the code
word (CW ) is assigned. For example, for all choices,
the code word is CW = 1111. Seeing CW , S retrieves
⟨SC,AC
1
,AC
2
,AC
3
,AC
4
⟩ from its memory. Using SC,
the user’s device computes V
′
1
. Using authentication
credentials, the device calculates V
′
2
. Then, it com-
putes V
′
3
. The device authenticates the user if V
3
= V
′
3
.
U −→ S : Upon successful authentication, U exe-
cutes ACC.AccVeri f y(A,W
U
,U) to check she is not
revoked. Once the device authenticates the user,
the user performs the following steps by access-
ing the stored credentials from the device. Here-
after, the device and user are the same. U selects a
random number R (nonce) (Step 12) and computes
V
4
= H(R,V
1
,V
2
). Using PUF, the user computes
V
5
= cMPU F(V
4
). U computes V
6
= H(sec
1
||V
2
) ⊕
V
5
. U computes V
7
= HKDF.Extract(V
5
,R) to de-
rive the session key. U computes the session key
sk = HKDF.Expand(V
7
,256).At Step 18, U gener-
ates K (nonce). To make K sender and receiver
bound, Step 19 is done by U as V
8
= V
6
⊕ K.
Now, the message m is assembled by U as m =
R||H(D)||CW||V
6
. U draws y uniformly at random
from the error distribution. Then, U computes the
hash c = H(⌊a
1
.y⌉
l
,⌊a
2
.y⌉
l
,m,V
8
, pk
a
, pk
b
). z is en-
crypted as s
a
.c + y. U computes w
1
= a
1
.y − e
a,1
.c
and w
2
= a
2
.y − e
a,2
.c. Choosing y
”
, V
8
is encrypted,
where Encode(V
8
). Then, m is encrypted under V
8
us-
ing symmetric encryption algorithm as E = E(m||V
8
).
Message (M
1
= z,c,x,E) is transmitted from U to S.
S −→ U : Upon receiving M
1
from U, S computes
w
1
= a
1
.z − t
a,1
.c and w
2
= a
2
.z − t
a,2
.c. S de-
codes V
8
, where V
8
∈ {0, 1}. S gets the message
(m) by decrypting E. S checks c; it checks whether
z is within the limit of the error distribution. See-
ing H(ID), S checks the revocation list (L) to know
whether H(ID) is revoked. Observing CW, S com-
putes V
”
2
= (AC
1
⊕ AC
2
) ⊕ (AC
3
⊕ AC
4
). Retriev-
ing (sec
1
), S computes H(sec
1
||V
”
2
). S recovers the
key material V
”
5
. To derive the session key (sk),
S computes V
”
7
. To make sk uniform, S executes
HKDF.Expand(V
”
7
,256). As the key confirmation
step, S computes V
9
= H(V
6
||R||pk
b
||pk
a
||sk) and
makes it M
2
. Then it forwards M
2
to U. U checks
V
9
. If the confirmation is successful, U and S form a
secure channel under the session key sk.
QPTA: Quantum-Safe Privacy-Preserving Multi-Factor Authentication Scheme for Lightweight Devices
807

3.4 Dynamic User Addition Phase
Whenever a new or existing user approaches S, it ex-
ecutes the following procedure. S checks whether the
user is revoked. If the user is revoked, S aborts fur-
ther process. If not, then it checks the expiry time of
the smart card (T
exp
). Suppose T
exp
= True; then
it reissues a new smart card to the user by following
the steps in Sections 3.2.1, 3.2.2, and 3.2.3. When
the expiry time is False, S checks T
tol
of the user and
initiates the procedure in Section 3.5 for changing the
password and PIN. This phase contributes to SG17.
3.5 Password and PIN Change Phase
U picks ⟨cw, pwd/pin or pwd, pin⟩ and forwards
E(cw||sk) to S. S retrieves cw as E
−1
(E(cw||sk)). S
checks hlist and T
tol
for U . When T
tol
exceeds its up-
per limit, S facilitates U the password and PIN via
email. S records all passwords and PINs of U in
pwlist and pinlist, respectively. Whenever any user
is targeted for an online password-guessing attack by
the attackers, S stores the passwords tried by the at-
tackers in hlist for the user. Moreover, the index of
hlist is held in T
tol
. When T
tol
is filled, say 100, then
S puts the targeted user in a blocklist and informs U
that she is temporarily blocked. U can check L and
execute ACC.Acc.Veri f y(.) to know whether or not
she is not blocked permanently. In this way, due to
the online password-guessing attack, DoS is handled.
For changing biometric credentials (AC
3
and AC
4
), U
has to contact S in person as it is sensitive informa-
tion. This phase contributes to SG18.
3.6 Revocation Phase
Whenever the user misbehavior is beyond
the threshold value or dies, the server uses
ACC.Acc.U pdate(.) algorithm for updating A as
A
∗
and ACC.WitU pdate(.) for updating W
U
as W
∗
U
. S
updates L s.t. U ∈ L . With this information, the user
can check whether or not she is revoked (Step 11 of
Fig. 2). This phase contributes to SG19.
4 SECURITY ANALYSIS
This section uses “Attack Detection Logic (ADC)” to
formally analyze QPTA (SG16) (Jurcut et al., 2017).
4.1 Formal Analysis
ADC has a rich set of twenty-two rules in first-order
logic under four categories: message freshness, mes-
sage symmetries, challenge-response handshake con-
struction and signed messages. These rules are built
based on twenty-one axioms that have sub-axioms
(Jurcut et al., 2017). We discuss only the applica-
ble rules. Further, we use the same rule number as
specified in the work (Jurcut et al., 2017) to have a
one-to-one correspondence.
4.1.1 Applying ADC
We examine only the applicable rules. Freshness
rules R1.1, R1.2 and R1.3 are not activated. Sym-
metry rules R2.1 is not activated. In signed statement
rules, rules R3.1∼3 are not activated. Under the hand-
shake rule, R4.5.1∼2, and R4.7 are not activated. It is
proved that freshness attacks and interleaving session
attacks are infeasible in QPTA, so it is safe from the
known attacks. Precisely, QPTA is secured against the
insider threat. Attacks, such as replay, masquerading
and man-in-the-middle are infeasible in QPTA.
4.2 Informal Analysis
Proposition 1: QPTA satisfies known key secrecy.
Adversaries knowing previous session keys cannot
compute the current session key because of the re-
quirement of PUF. In addition, every session key is
derived as the function of authentication credentials
f (AC
1
,AC
2
,AC
3
,AC
4
), so without knowing these au-
thentication credentials the adversaries cannot com-
pute the current session key. Further, at S, to derive
the current session key, V
5
” is required, but, this needs
the knowledge of sec
1
, so by knowing previous ses-
sion keys, an adversary cannot derive sk.
Proposition 2: QPTA ensures forward secrecy. Ev-
ery session key material V
6
is obfuscated under
H(sec
1
||V
2
) while sending to S, where V
2
is the cho-
sen authentication credentials and sec
1
is stored in the
tamper-proof module. Even if the long-term secret
of Bob is compromised, the security of the session
key is preserved for the current session because of
the hiding of the key material under the authentica-
tion credentials. Note that the compromise of long-
term secrets corresponds to either the secret key of
Alice or Bob, but not all secrets, such as authenti-
cation credentials. Compromise of all secrets in the
tamper-proof module of Bob not only leads to a to-
tal break but also paves the way for the exposure
of sensitive information (biometric details) of users.
Proposition 3: QPTA assures resilience to DoS at-
tack. QPTA tracks password-guessing attacks using
hlist. hlist makes an entry for every wrong password.
Whenever the index of hlist exceeds T
tol
, the targeted
user is blocked for a temporary time using RBAC.
The user can confirm this by checking L and execut-
SECRYPT 2024 - 21st International Conference on Security and Cryptography
808

ing ACC.Acc.Veri f y(A,WU,U). When the verifica-
tion result is true, U know the fact that she has been
blocked for some time, and she can try later or reach
the server. QPTA assures resilience to DoS.
Proposition 4: QPTA assures resilience to leakage of
ephemeral secret keys. Every x in M
1
is encrypted un-
der the public key of Bob, so the leakage of K of every
session does not risk the security of QPTA since the
adversary is restricted by the requirement of the long-
term secret key (sk
b
) for decrypting x of M
1
.
Proposition 5: QPTA prevents stolen smartcard-
verifier attack. An adversary with the smart card can-
not pass the authentication steps. Despite knowing
SC and computing V
1
= H(H(ID)||SC), the adversary
cannot find V
2
= (AC
1
⊕ AC
2
) ⊕ (AC
3
⊕ AC
4
) as they
are authentication credentials stored in the devise of
U. Thus, it resits stolen smart card verifier attacks.
Proposition 6: QPTA prevents stolen verifier table
attack. An adversary who knows the database of S
may use the credentials to violate the authentication
of U, however, this attempt is futile for the adversary.
To compute sk, the adversary needs sk
b
so that it can
recover K. Further, to recover V
”
5
, it requires sec
1
for
computing H(sec
1
||V
”
2
). Consequently, the adversary
is unsuccessful in the stolen verifier table attack.
Proposition 7: QPTA prevents password and PIN
guessing attacks with overwhelming probability. The
adversary may acquire the password and PIN of U
via offline guessing attack, nonetheless, due to the
requirement of at least one choice out of Ac
3
⊕ AC
4
(biometrics) in Step 5, it cannot succeed in the user
authentication with probability more than
1
2
n
.
Proposition 8: QPTA assures anonymity with non-
negligible probability. Let WIN be an event in which
the adversary successfully violates the anonymity.
Since every M
1
is encrypted under the public key of
Bob pk
a
and it is randomized by nonce R, the proba-
bility of W IN is bounded by Pr(W IN) ≤
1
2
n
.
Proposition 9: QPTA ensures unlinkability with non-
negligible probability. The adversary has to link at
least any two M
1
and M
2
to violate unlinkability.
Because R is a nonce, every time m changes by at
least the probability of 1 −
1
2
n
, the resulting signcryp-
text changes with probability 1 −
1
2
n
. The adversarial
probability of linking any two M
1
and M
2
is
1
2
n
.
Proposition 10: QPTA ensures conditional trace-
ability. At Bob, after successful decryption of
x, if the verification of c = H(v,m,V
8
, pk
a
, pk
b
)
is false, Bob can report M
1
to the trusted third
party. The trusted third party can confirm this by
computing w
1
= a
1
.z − t
a,1
.c, w
2
= a
2
.z − t
a,2
.c,
V
8
= Decode(x − w
1
.s
b
) and m = E
−1
(E) and ver-
ifying c = H(v,m,V
8
, pk
a
, pk
b
) from M
1
. Note that
to do this, T T P needs the server’s secret key.
5 EFFICIENCY ANALYSIS
We compare computation, transmission, and storage
costs and safety traits of QPTA with related schemes
W1 (Banerjee et al., 2020), W2 (Qiu et al., 2020), W3
(Kwon et al., 2021) and W4 (Karati et al., 2023).
5.1 Security Features
The work (Qiu et al., 2020) does not hold resilience
to stolen data and password attacks, stolen smartcard
and password attacks and stolen verifier table attacks.
Further, (Banerjee et al., 2020) the work fails to re-
sist stolen data and password attacks (Karati et al.,
2023). Notably, Table 1 shows that QPTA satisfies
at least five security features more than the existing
schemes. QPTA ensures the comprehensive satisfac-
tion of twenty security goals.
5.2 Computation Cost
In Table 2, exclusive-OR operations, and encoding
and decoding operations are left because their cost is
negligible. Based on Table 2, compared to the most
recent work (Karati et al., 2023), QPTA has a higher
computation cost, but it attains enhanced security fea-
tures at the cost of increased computation.
5.3 Communication and Storage Costs
We assume the following: a salt, random num-
ber and ID of 16 bytes, biometric data, sym-
metric key and a hash of 32 bytes, and pub-
lic and secret key of 256 bytes. In QPTA,
S stores ⟨H(ID),AC
1
,AC
2
,AC
3
,AC
4
⟩ = 160
bytes in its database. ⟨SC⟩ is stored
in the smart card, which is 32 bytes.
⟨H(ID), AC
1
,AC
2
,AC
3
,AC
4
,hk,SC, salt⟩ = 240 bytes
is stored in U. ⟨H(ID),sec
1
,salt,hk,sk
U
,SC⟩ = 400
bytes. In total, QPTA consumes 800 bytes for storage.
regarding communication cost, M
1
consumes 576
bytes, and M
2
consumes 32 bytes. QPTA consumes
608 bytes as the communication cost. Figure 3 shows
the storage and communication costs of all schemes.
QPTA is quantum-safe, whereas the remaining
schemes are vulnerable to quantum adversaries.
6 CONCLUSION
This paper presented a quantum-safe privacy-
preserving multi-factor authentication scheme called
QPTA for lightweight devices. QPTA ensured multi-
factor security. QPTA facilitated users to choose more
QPTA: Quantum-Safe Privacy-Preserving Multi-Factor Authentication Scheme for Lightweight Devices
809
Table 1: Security features comparison.
Schemes
Security features
SG1 SG2 SG3 SG4 SG5 SG6 SG7 SG8 SG9 SG10 SG11 SG12 SG13 SG14 SG15 SG16 SG17 SG18 SG19 SG20
W1
(Banerjee et al., 2020)
♣
W2
(Qiu et al., 2020)
♣
W3
(Kwon et al., 2021)
♣
W4
(Karati et al., 2023)
♣
QPTA
: Satisfied; : Not satisfied; ♣: Not applicable; SG1: Entity authentication; SG2:Session key security; SG3:Implicit key authentication; SG4:Explicit key confirmation; SG5:Known key secrecy; SG6:Forward
secrecy; SG7:Resilience to ephemeral secret key leakage; SG8:Future quantum attack resilience; SG9:Denial of service resilience; SG10:Multifactor security; SG11:Anonymity SG12:Unlinkability; SG13:Conditional
traceability; SG14:Resistance to known attacks; SG15:Choice within same factor; SG16:Formal analysis; G17:Dynamic user addition; G18:Online password and PIN change; G19:User revocation; G20:Resilience to HBC.
Table 2: Computation cost comparison.
Schemes Registeration
overhead
Authentication
overahead
Total
overhead
W1
(Banerjee et al., 2020)
T
FE
+4T
H
T
FE
+25T
H
2T
FE
+29T
H
W2
(Qiu et al., 2020)
T
FE
+T
ECM
+4T
H
T
FE
+6T
ECM
+19T
H
2T
FE
+7T
ECM
+23T
H
W3
(Kwon et al., 2021)
T
FE
+5T
H
2T
FE
+T
PUF
+32T
H
3T
FE
+T
PUF
+37T
H
W4
(Karati et al., 2023)
T
FE
+T
PUF
+T
ECM
+T
SE
+2T
H
T
FE
+T
PUF
+2T
ECM
+2T
SE
+3T
SD
+7T
H
2T
FE
+2T
PUF
+3T
ECM
+3T
SE
+3T
SD
+9T
H
QPTA 2T
FE
+4T
PM
+
4T
PA
+4T
H
T
PUF
+9T
PM
+7T
PAS
+
T
SE
+T
SD
+15T
H
2T
FE
+T
PUF
+13T
PM
+
11T
PAS
+T
SE
+T
SD
+19T
H
T
PUF
: Time to execute one PUF; T
FE
: Time to run either FE.Gen(.) or FE.Rec(.); T
ECM
: Time
to execute one extended chaotic map; T
SE
/T
SD
:Time for one symmetric encryption/one symmetric
decryption; T
H
: Time for one hash operation; T
PM
: Time for one polynomial multiplication;
T
PAS
: Time for one polynomial addition/polynomial subtraction.
Figure 3: Storage and communication costs.
than one choice within a factor. The security of QPTA
relied on the security of the underlying signcryption
scheme, physical unclonable functions, key deriva-
tion function, dynamic accumulator, and fuzzy extrac-
tor. QPTA was formally analyzed using the “Attack
Detection Logic.” The formal analysis revealed that
QPTA is free from freshness attacks and interleaving
session attacks. It is free from known attacks, such as
replay, masquerading, and man-in-the-middle attacks.
QPTA was informally analyzed for various security
goals and privacy properties. QPTA assured compre-
hensive twenty security goals. QPTA is suitable for
adoption as it satisfies the pos-quantum security trait.
QPTA offers a security solution for a two-party
case (physicians and medical server), neglecting pa-
tients’ involvement. In the future, we will extend
QPTA to a tri-party scenario, where patients’ authen-
tic data are stored in the medical server. Further, it
will be implemented on a practical testbed mimicking
the real-world scenario.
ACKNOWLEDGEMENTS
This work was supported in part by the National Sci-
ence and Technology Council (NSTC) under grants
NSTC 12-2811-E-110-019 and 112-2221-E-110-027.
REFERENCES
Banerjee, S., Odelu, V., Das, A. K., Chattopadhyay, S., and
Park, Y. (2020). An efficient, anonymous and robust
authentication scheme for smart home environments.
Sensors, 20(4).
Benaloh, J. and De Mare, M. (1993). One-way accumula-
tors: A decentralized alternative to digital signatures.
In Workshop on the Theory and Application of of
Cryptographic Techniques, pages 274–285. Springer.
Dolev, D. and Yao, A. (1983). On the security of public key
protocols. IEEE Trans. Inf. Theory, 29(2):198–208.
Fan, C.-I., Karati, A., and Wu, S.-L. (2023). A privacy-
aware provably secure smart card authentication pro-
tocol based on physically unclonable functions. IEEE
Trans. Dependable Secure Comput., pages 1–13.
G
´
erard, F. and Merckx, K. (2018). Setla: Signature and
encryption from lattices. In International Conference
on Cryptology and Network Security, pages 299–320.
Springer.
Jurcut, A., Coffey, T., and Dojen, R. (2017). A novel secu-
rity protocol attack detection logic with unique fault
discovery capability for freshness attacks and inter-
leaving session attacks. IEEE Trans. Dependable Se-
cure Comput., 16(6):969–983.
Karati, A., Chang, Y.-S., and Chen., T.-Y. (2023). Robust
three-factor lightweight authentication based on ex-
tended chaotic maps for portable resource-constrained
devices. In Proc. of the 20th International Confer-
ence on Security and Cryptography - SECRYPT, pages
673–682. INSTICC, SciTePress.
Krawczyk, H. (2010). Cryptographic extraction and key
derivation: The hkdf scheme. In Annual Cryptology
Conference, pages 631–648. Springer.
Kwon, D., Park, Y., and Park, Y. (2021). Provably secure
three-factor-based mutual authentication scheme with
puf for wireless medical sensor networks. Sensors,
21(18).
SECRYPT 2024 - 21st International Conference on Security and Cryptography
810

Lyubashevsky, V., Peikert, C., and Regev, O. (2010). On
ideal lattices and learning with errors over rings. In
Advances in Cryptology–EUROCRYPT 2010: 29th
Annual International Conference on the Theory and
Applications of Cryptographic Techniques, French
Riviera, May 30–June 3, 2010, pages 1–23. Springer.
Qiu, S., Wang, D., Xu, G., and Kumari, S. (2020). Prac-
tical and provably secure three-factor authentication
protocol based on extended chaotic-maps for mobile
lightweight devices. IEEE Trans. Dependable Secure
Comput., 19(2):1338–1351.
Sahoo, D. P., Mukhopadhyay, D., Chakraborty, R. S., and
Nguyen, P. H. (2017). A multiplexer-based arbiter
puf composition with enhanced reliability and secu-
rity. IEEE Trans. on Computers, 67(3):403–417.
QPTA: Quantum-Safe Privacy-Preserving Multi-Factor Authentication Scheme for Lightweight Devices
811
