Graph-Based Modelling of Maximum Period Property

for Nonlinear Feedback Shift Registers

Eric Filiol

1,3

and Pierre Filiol

Thales Digital Factory, Thales Group, Paris, France

Lab-STICC, ENSTA Bretagne, Brest, France

ENSIBS, Vannes, France

Keywords:

NLFSR, Stream Cipher, Binary Sequence, Maximum Period, Graph Representation, Incidence Matrix.

Abstract:

NonLinear Feedback Shift Registers (NLFSRs) are key primitives to design pseudorandom generators in mod-

ern stream ciphers, especially when the feedback function is of low degree. Contrary to their linear counter-

parts (LFSRs) for which a general and comprehensive theory has been established, many fundamental prob-

lems related to NLFSRs remain open. In particular ﬁnding a systematic procedure of acceptable complexity

for constructing NLFSRs with a guaranteed long period is still a general open problem and only a few results

have been obtained so far. In this paper, we present the results of a exhaustive exploratory search and anal-

ysis of NLFSRs of low degree. We ﬁrst model NLFSRs as graphs using their incidence matrix and express

the maximum period property as graph properties. This enables to reduce the number of possible candidates

greatly that can be tested ﬁnally for the maximum period property by HPC on GPGPUs and Massively Parallel

Processor Array (MPPA).

1 INTRODUCTION

Binary sequences produced by feedback shift regis-

ters (FSRs) are widely used in stream ciphers and ran-

dom generators. These registers are the key primitive

used in these cryptographic systems.

A binary n-stage feedback shift register is deﬁned

as a mapping from F

to F

n−1

,...,x

) 7→ ( f (x

n−1

,...,x

),x

n−1

,...,x

) (1)

where f is a Boolean function, called feedback func-

tion, F

denotes the binary ﬁeld and F

the n-

dimensional vector space over F

consisting of the n-

tuples of elements of F

. Whenever f is a linear trans-

formation, we deal with a Linear Feedback Shift Reg-

ister (LFSR) otherwise ( f is nonlinear) with a Nonlin-

ear Feedback Shift Register (NLFSR). In this paper,

we focus on NLFSRs deﬁned by a bijective mapping

(nonsingular mapping).

Consider a binary sequence σ = (σ

)

∞

i=0

. From the

n ﬁrst ﬁxed terms σ

,σ

,..., σ

n−1

(called the initial

state vector), we derived the register output sequence

uniquely deﬁned by the recurrence relation for all i >

n+i

= f (σ

,σ

i+1

,...,σ

i+n−1

) (2)

If there exists an integer p > 0 such that σ

i+p

= σ

for all i ∈ F

\ {(0, 0, . . . , 0)} , the sequence is called

periodic of period p. The most desirable property for

NLFSRs (as well as for LFSRs) is to have a maximal

possible period length of 2

− 1. If we iterate f over

, we then have two cycles (see Figure 1): one of

length 1 (the loop over the single point (0, 0, . . . , 0)

and a cycle of length 2

− 1. In this case, NLFSRs

generate maximal length sequences or m-sequences

(Golomb, 1981).

From the cryptographic or random number gener-

ation perspective, it is strongly desirable that NLF-

SRs’ feedback function fulﬁls the following condi-

tions (Augustynowicz, 2018):

• The number of feedback function’s linear and

nonlinear terms should remain as small as possi-

ble. It is especially a desirable property for hard-

ware implementation (number of logic gates).

• The algebraic degree of the feedback function

should be the lowest possible (at least 2 however).

The goal is somehow that NLFSRs are as close as pos-

sible to all the main advantages of LFSRs such as low

power consumption, easy implementation and high

efﬁciency while providing a better resistance against

known attacks (Kuznetsov et al., 2022, page 5).

832

Filiol, E. and Filiol, P.

Graph-Based Modelling of Maximum Period Property for Nonlinear Feedback Shift Registers.

DOI: 10.5220/0012839300003767

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 832-837

ISBN: 978-989-758-709-2; ISSN: 2184-7711

The paper hence focus on nonlinear feedback

functions whose Algebraic Normal Form (ANF) is

given by:

f (x

n−1

,...,x

) =

n−1

∑

i=0

+ x

(3)

for all possible pair j, k such that 0 < j, k < n and

where c

are binary coefﬁcients describing whether

the register cell is considered (c

= 1) or not (c

= 0).

We have conducted an exhaustive exploratory anal-

ysis to ﬁnd all feedback functions up to the degree

n = 28. To reduce the computing time it has been nec-

essary to ﬁnd a new way of NLFSR modelling. For

that purpose, we represent NLFSR as directed graphs

whose incidence matrix exhibits speciﬁc properties to

express the maximal period property. It is worth men-

tioning that the present study can be easily applied to

any other forms of feedback polynomials (for instance

more quadratic terms).

It is the ﬁrst exhaustive search to date whereas pre-

vious works only published a very few number of re-

sults due to the search complexity. From the results

obtained, we have identiﬁed a number of news re-

sults that can be of high interest to explore further for

n > 28.

In the rest of this article we will consider all oper-

ations in the ﬁnite ﬁeld (F

,+,.).

The paper is organized as follows. Section 2 anal-

yses the overall complexity of searching of NLF-

SRs producing m-sequence and presents the related

works. Section 3 introduces our combinatorial model

for NLFSRs and formalizes the maximal period prop-

erty in terms of algebraic equations. Then Section 4

details the particular implementation aspects that have

been used to perform an effective computation. Fi-

nally Section 5 presents the detailed results of our

exhaustive search and identify a few new interesting

properties before concluding in Section 6.

2 PRELIMINARIES

2.1 Complexity Analysis of NLFSR

To date, there are no theoretical results that allow to

easily ﬁnd maximum period NLFSRs as is the case

for LFSRs (Golomb, 1981). In this section we look at

the approach currently being favoured in recent years.

Let us rewrite (3) in a more simple way:

f (x

n−1

,...,x

) = l(x

n−1

,...,x

) + x

(4)

where l(x) = l(x

n−1

,...,x

) =

∑

n−1

i=0

+ x

is the

linear part of f .

The search for such NLFSRs of length n can be

formalized according the two following steps:

1. Among the 2

possible candidates corresponding

l(x), for a given pair i, j ﬁxing the degree-2 mono-

mial, we retain those which validate a certain

number of algebraic or combinatorial properties

,...,I

. If these properties are independent,

with respective probabilities of being realized by

a good candidate P(I

) = p

, then at the end of this

stage we retain N = 2

∏

i=1

. This step has an

incompressible complexity of 2

n−1

(a symmetry

property presented in Section 2.3 enables to cut

search work in half).

2. For each valid candidate for l(x), we check

whether it is in the maximum period by calcu-

lating the cycle. Complexity is in 2

in the

worst case. The average complexity is 2

n−1

from

(Golomb, 1981, Corollary 11, p. 183). No result

is known for this step that would allow us to re-

duce this complexity (except in certain very spe-

ciﬁc cases, see (Golomb, 1981, Chapter VII)).

The overall worst-case complexity is therefore 2

2n−1

and the average-case complexity is 2

2n−2

. To reduce

this complexity, the focus must be on the ﬁrst stage

to reduce the number of candidates to be tested in the

second stage. Some of these properties are already

known (see Section 2.3). In this paper we are going

to add many others thanks to results from graph the-

ory and matrix calculus on the associated incidence

matrix. This signiﬁcantly reduces the overall com-

plexity of the exhaustive search. This has enabled us

to perform an exploratory analysis up to n = 28.

2.2 Related and Previous Work

Since the Jansen’s seminal thesis in 1989 (Jansen,

1989), the main approach for searching for NLFSRs

of the simplest form considers more or less sophisti-

cated exhaustive search. In (Dabrowski et al., 2014),

this approach has been initiated with parallel comput-

ing.

Later on in (Poluyanenko, 2017), the author stud-

ies NLFSRs implementation on FPGAs and discusses

issues of their optimization. Search method of NLF-

SRs generating M-sequence was given. It was based

on a practical synthesis and explores the possibility of

NLFSR implementation of FPGA.

In (Augustynowicz, 2018), the authors consider

a multi-stages hybrid algorithm which uses Graph-

ics Processor Units (GPU) and developed for process-

ing data-parallel throughput computation. They focus

and give results for feedback polynomials of the form

l(x) + x

+ x

(two quadratic monomials). Later

Graph-Based Modelling of Maximum Period Property for Nonlinear Feedback Shift Registers

833

the same authors (Augustynowicz and Kanciak, 2020)

optimize their search methods by applying particular

vector processor instructions. Their aim was to max-

imize the advantage of Single Instruction Multiple

Data (SIMD) and Single Instruction Multiple Threads

(SIMT) execution patterns. Their results are only par-

tial and contains errors (especially regarding the num-

ber of sparse feedback polynomials, see Section 5).

Finally in 2022, the authors of (Poluyanenko,

2017) have extended their results given in (Kuznetsov

et al., 2022), giving a bit more feedback polynomials.

Unfortunately only a very few number of results are

obtained due to the high computing complexity.

As a result, no exhaustive enumeration of max-

imum period NLFSR polynomials is yet available.

Such a result would perhaps allow to identify unsus-

pected properties which could help to ﬁnd a general

theory of construction of these NLFSRs as is the case

for their linear counterparts (LFSRs). This is the aim

of the present article.

Studies considering exhaustive search all try to re-

duce the ﬁrst step of search described in Section 2 by

using a very few number of algebraic properties sat-

isﬁed by the feedback coefﬁcients a

. We recall them

in Section 2.3.

2.3 Known Algebraic Properties

Golomb (Golomb, 1981) in 1982 identiﬁes a very im-

portant property that deﬁnes the condition for a shift

feedback function is bijective: each x has a unique

successor f (x) and any f (x) has a unique predecessor

(see Fig. 2).

Theorem 1. (Golomb, 1981) The cycles generated by

a feedback shift register have no branch points if and

only if its feedback function can be decomposed as

f (x

,...,x

n−l

) = x

+ g(x

,...,x

n−1

) (5)

It implies that any integer encoding the linear part

l(x) must be an odd value (monomial x

is always

present). Later on Chan, Game and Rushanan (Chan

et al., 1993) identiﬁed three more generic algebraic

properties.

• The Hamming weight of the integer encoding l(x)

is even (we add the bit corresponding to monomial

so c

= 1).

• The Hamming weight of the integer encoding l(x)

must be at least equal to 2.

• If x

+ g(x

,...,x

n−1

) generates a quadratic m-

sequence, then x

+ g(x

n−1

,...,x

) generates a

quadratic m-sequence as well. Then we can di-

vide the search over half the pairs {i, j} deﬁning

the degree 2 monomial in Equation 4. Each time

we have a solution, we generate the conjugate so-

lution for replacing all indices i by n − i in Equa-

tion 4.

In the next section, we present how to have more sta-

tistically independent such equations for a larger re-

duction.

3 NLFSR AND GRAPH

INCIDENCE MATRIX

Modelling NLFSRs using graph incidence matrices

was ﬁrst mentioned by Gonzalo, Ferrero and Sori-

ano (Gonzalo et al., 2002) in a rather imprecise and

succinct manner. No results were given. No analysis

of the independence of potential equations was pre-

sented. The computational and algorithmic aspects

were not discussed, even though they are fundamental

as soon as n > 10. Indeed, the size of the matrix grows

exponentially with n, which limits their approach to

small values of n. Our work is based on their ap-

proach, which we have effectively implemented and

optimised.

3.1 Combinatorial Model for NLFSR

Let us consider a NLFSR of size n whose feed-

back polynomial has the general form f (x) = x

∑

n−1

i=0

+ x

for 0 < j, k < n. For each possible

pair { j, k} we search for all n-uples (c

,...,c

n−1

) for

which the NLFSR fulﬁls the maximum period prop-

erty. We can model any NLFSR by a directed graph

of 2

points. Any maximal period NLFSR more pre-

cisely is a (2

)-graph with two cycles: one cycle

of length 1 (loop on the null point) and one cycle of

length 2

n−1

To illustrate our approach, let us consider the feed-

back function x

+ x

denoted for

short as 0, 1, 2, (1, 2). Fig. 1 describes the two cor-

responding cycles.

Figure 1: Graph for 0, 1, 2,(1,2).

To simplify notations for i = (i

n−1

,...,i

) ∈

SECRYPT 2024 - 21st International Conference on Security and Cryptography

834

let us note

= (0,i

n−1

, . . . , i

) and

(1,i

n−1

,...,i

) the right-shifted versions i whose

most signiﬁcant bit is updated respectively with 0 and

1. This notation describes the state of an NLFSR,

which changes from state i to state

depending

on the feedback value f (i) of the NLFSR calculated

on state i.

Let us consider its incidence matrix whose entries

are expressed as linear polynomials in the unknown c

as follows: ∀i = (i

n−1

n−2

,...,i

) ∈ F

then f (i)

equals 0 or 1 and hence produce either

de-

pending on the values of coefﬁcients c

. We can then

deﬁne the formal incidence matrix A = [a

i, j

] where i

and j are in F

∀i ∈ F

\ {(0,0,...,0)}



= 1 + f (i)

= f (i)

(6)

For instance let us consider the formal feedback poly-

nomials f (x) = x

+c3.x

and i = (0,1,1,1). We have a

= c

+ c

and a

1 + c

+ c

. If we consider the formal feedback poly-

nomial f

(x) = x

, the cor-

responding formal incidence matrix of order 2

−1 =

7 is given in (7).

It is important to note that for i = (0,0,1) and

= (1, 1, 1) have only one possible successor if we

want the cycle to have maximal period (respectively

and

. Recall also from Theorem 1 that c

= 1. We

can observe that the sum of matrix entries linewise

is always equal to 1 as well as columnwise (in fact

= 1).

3.2 Formalisation of Max-Period

Property

The Max-Period property can be expressed in differ-

ent ways (see Figure 1).

It is a well known result that each entry a

i, j

a power matrix A

describes the number of paths of

length k between i and j (Brouwer and Haemers,

2012). If we want a NLFSR be in maximal period

then there must be no loop (a

i,i

= 0) and there must

exist a unique path between between i and j (refer to

Fig. 2) for any value of k ≥ 1.

Exploiting this formalisation efﬁciently requires

to manage two issues:

• A complexity issue. If almost all matrix computa-

tion have polynomial complexity, the actual com-

plexity is exponential since the size of the matrix

is in O(2

). We then need to ﬁnd ways of manag-

ing this explosion in complexity.

• The different equations have to be statistically

independent in order to minimize their number.

Optimally n statistically independent equations

should drastically reduce the number of suitable

candidates at the end of the ﬁrst step of the ex-

haustive search.

To obtain several independent algebraic equations

while limiting the computing effort, we calculated

the successive powers A

...,A

of the inci-

dence matrix A. The results conﬁrm that this approach

does indeed yield statistically independent equations.

The probability for a candidate to satisfy all of diag-

onal equations is indeed

. By restricting ourselves

to k ≤

, the computational effort remains moderate

while guaranteeing a very signiﬁcant reduction in the

ﬁrst stage of the exhaustive search described in Sec-

tion 2. It is worth noting that the statistical indepen-

dence of the diagonal equations obtained is compliant

with the fact that the cycle-length distribution is ﬂat

(Golomb, 1981, Section 2.2). We have evaluated the

statistical independence of these additional equations

and we have observed that they are always satisﬁed

if the diagonal equation is. So they do not bring any

new bit of information. It means that each squaring

iteration provides only one signiﬁcant equation.

4 COMPUTATIONAL APPROACH

Modelling the maximum-period NLFSR search prob-

lem using graphs means that their incidence matrices

are square matrices of size N = 2

−1. As far as naive

matrix multiplication is concerned, the computation

of the diagonal equations is of cubic complexity but

the size of the data is of exponential complexity in

n−1

. It is therefore not possible to compute the ma-

trix products directly (naive product of matrices) as

soon as n > 18.

However these matrices are extremely sparse. The

initial matrix deﬁned in Equation 7 has 2

n+1

− 4 en-

tries out of 2

− 2

n+1

+ 1 possible entries. The ma-

trix sparsity is asymptotically deﬁned by S (A) =

n−1

when n → ∞.

We used a speciﬁc compact matrix representation.

There are several possible forms of representation and

we have opted for the form described in Table 1. The

matrix entries are not integer or real values, but for-

mal polynomials whose maximum number of mono-

mials is 2

. This maximum number is never reached

in practice (for small values of k), which means that

effective calculations can be carried out with limited

memory requirements. This form consists of storing

the (i, j) coordinates of the only non-zero inputs, to-

gether with their polynomials. We give this represen-

tation for the matrix (7) and in its general expression

in Table 1.

Graph-Based Modelling of Maximum Period Property for Nonlinear Feedback Shift Registers

835

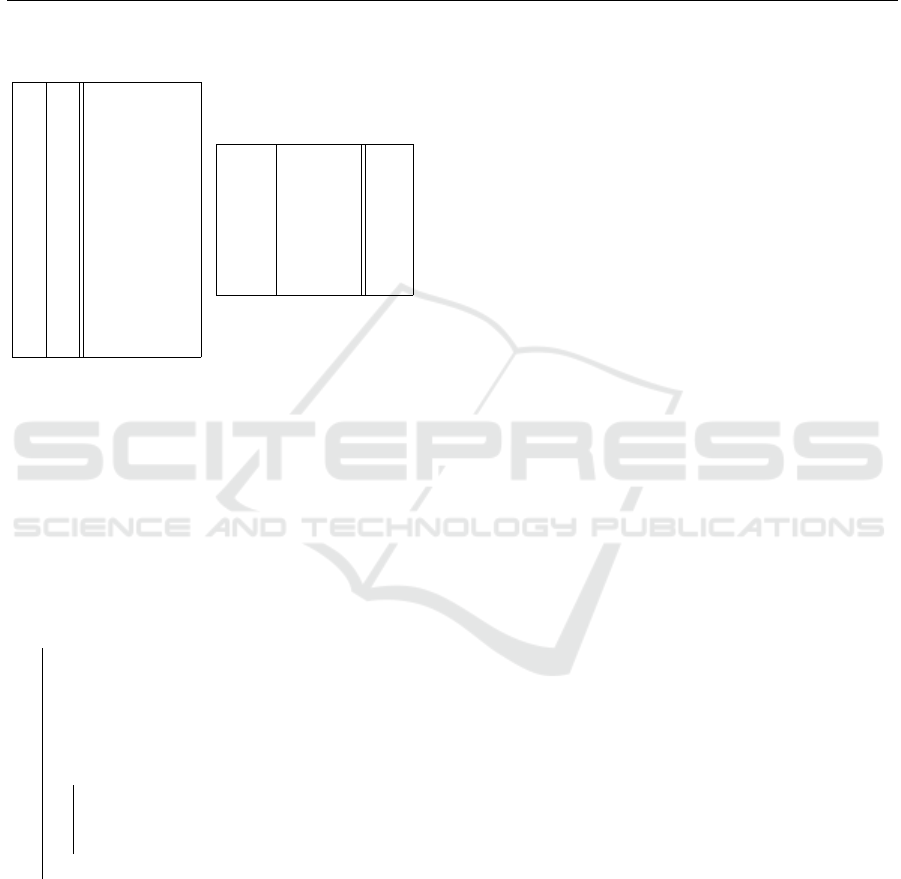
A =







0 0 0 c

0 0 0

1 + c

0 0 0 c

0 0

1 + c

+ c

0 0 0 c

+ c

0 0

0 1 + c

0 0 0 c

0 c

+ c

+ 1 0 0 0 c

+ c

0 0 c

+ c

0 0 0 1 + c

+ c

0 0 c

+ c

0 0 0 0







(7)

Table 1: Compact Representation of (7) (left) - General

Case (right).

1 4 c

2 1 1 + c

2 5 c

3 1 1 + c

+ c

3 5 c

+ c

4 2 1 + c

4 6 c

5 2 c

+ c

+ 1

5 6 c

+ c

6 3 c

+ c

6 7 1 + c

+ c

7 3 c

+ c

. . . . . . . . .

. . .

i + 1

(i + 1)

. . .

i + 1

(i + 1)

. . .

. . . . . . . . .

This form of matrix product computation is fast,

efﬁcient and optimizes memory resources. The algo-

rithm is described in Table 1. Note that for clarity of

presentation, the form described in Table 1 has been

implemented a bit differently so as to allow direct ac-

cess to the various items without having to use local

search in the table (thus eliminating tests).

Data: Matrix A of size N

Result: Compute A

Allocate result table MatRes of size 2.N;

for x from 1 to N do

/* For nonzero entries of A */;

/* Coord. (i, j) & polynomial */;

i = A[x][1]

j = A[x][2]

= A[i][3]

for all y such that A[y][1] == j do

/* Nonzero entries ( j, k) */

= A[ j][y];

MatRes[i][A[y][2]]+ = p

∗ p

;

end

Return MatRes;

Algorithm 1: Fast Large Sparse Matrix Square Algo-

rithm.

It is worth noting a few important points:

• Since the number of entries for the second For

loop is constant, the overall complexity is that of

main loop. Hence the overall complexity is in

O(N). However, for the initial matrix we have

N = 2

− 1. The number of non zero matrix en-

tries roughly doubles with each squaring. So after

k squaring, the number of non zero entries is 2

.N.

• At the end of the squaring procedure, the result

matrix MatRes is already ordered according to

matrix line indices i. There is consequently no

need of an additional sorting step.

5 RESULTS AND DISCUSSION

5.1 Results

We have applied our method to search exhaustively

all NLFSRs with feedback polynomials of the form

given by (3). Until now we have completed this

search up to n = 27 (for n = 28 search is in progress).

For small value of n (n ≤ 20), we also performed a

naive exhaustive search in order to validate our alge-

braic approach by comparing both results obtained.

Our approach has been fully conﬁrmed.

This research work required four months of com-

puting on an AMD Ryzen 32/64-core Linux machine

with 256 Mb of RAM and equipped with a Kalray

256-core Massively Parallel Processor Array (MPPA)

and a Nvidia RTX 2080 Ti GPGPU. We did not par-

allelize Algorithm 1, preferring to run threads on the

different pairs (i, j) for the monomial x

Table 2 presents the deﬁnitive results for 15 ≤

n ≤ 26. The (i, j) rate describes the proportion of

pairs {i, j} for which at least one solution has been

found. The minimal weight of l(x) is of high im-

portance since they provide the most simple form

for hardware implementation while maintaining ex-

cellent non-linearity for cryptographic designs.

5.2 Analysis of Results

This exhaustive research enabled us ﬁrst to compare

our results with the few published ones. While the

solutions we found systematically included and con-

ﬁrmed the few solutions already published, we were

SECRYPT 2024 - 21st International Conference on Security and Cryptography

836

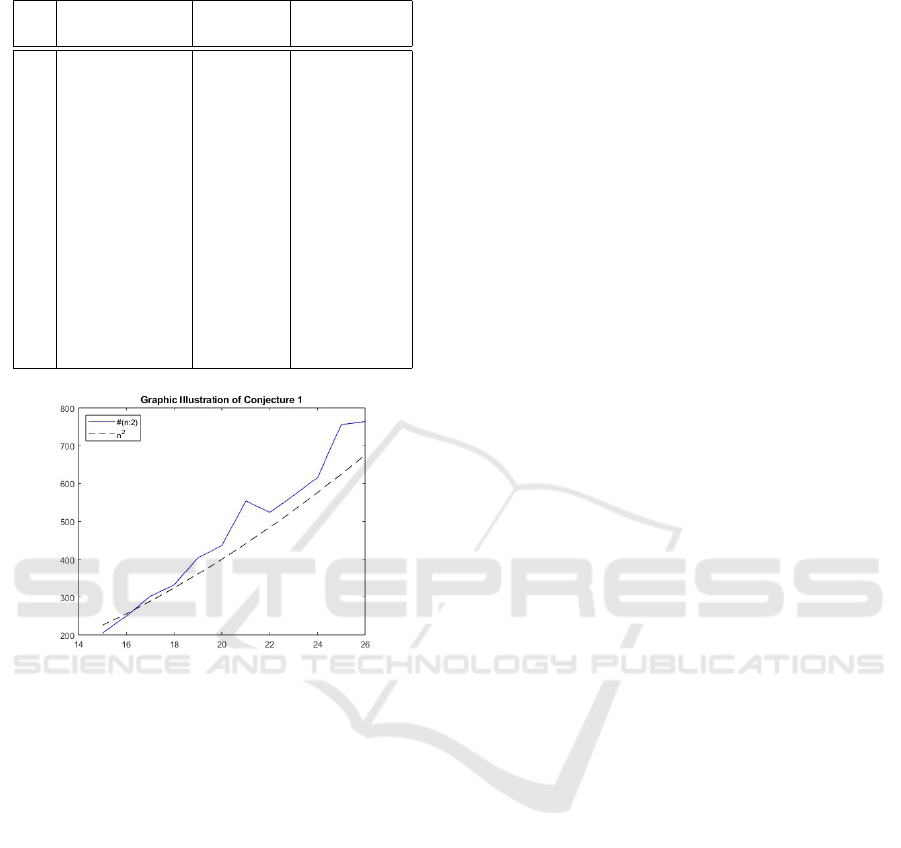
Table 2: Results of Exhaustive Search.

n # polynomials (i, j) rate Min. weight

of l(x)

15 204 0.7821 3

16 250 0.9428 3

17 302 0.9083 5

18 332 0.8235 5

19 404 0.8627 3

20 436 0.8596 5

21 554 0.8947 5

22 524 0.8666 5

23 568 0.8268 5

24 616 0.8650 5

25 756 0.8731 7

26 764 0.8933 7

27 737 0.8615 7

28 > 120 > 0.3418 ≤ 7

Figure 2: Graphic Illustration of Conjecture 1.

able to disprove certain results. For instance Au-

gustynowicz and K. Kanciak (Augustynowicz and

Kanciak, 2020, p. 21, Table VII) claim that no feed-

back polynomials of weight 7 does exist for n = 26

and n = 27 while we have found several ones. For

instance n = 27 x

+ x

. A number of other of their results are also in-

complete or wrong.

We have also initiated an in-depth analysis of the

results to identify some interesting properties. For ex-

ample, the number of solutions varies signiﬁcantly ac-

cording to the respective parities of the indices i and

j of the monomial x

Finally we can formulate the following conjecture

concerning the number of polynomials as a function

of n.

Conjecture 1. The number of feedback polynomials

of the form (3), denoted #(n : 2), is in O(n

This Conjecture is illustrated in Figure 2.

6 CONCLUSION

In this paper we have presented how combinatorial

modelling of an NLFSR via the incidence matrix of

the state graph can help to signiﬁcantly reduce the

computational effort in the exhaustive search for feed-

back polynomials. This enabled us to carry out this

search up to n ≤ 28 for a minimal form that is very

important in the design of encryption algorithms.

This exhaustive search will be carried out for

n > 28. However, memory requirements quite

soon exceeds current capacities (n = 31 requires a

machine with 1Tb RAM). We are therefore con-

sidering emulating RAM with disk space and use

MapReduce-type functions on Distributed File Sys-

tems (DFS) (Leskovec et al., 2014, Chap. 2). The

computation time will be longer, but this is of relative

importance for an exhaustive one-time search (once

and for all search).

REFERENCES

Augustynowicz, P. (2018). Scalable method of searching

for full-period nonlinear feedback shift registers with

gpgpu. new list of maximum period nlfsrs. Inter-

national Journal of Electronics and Telecommunica-

tions, 64.

Augustynowicz, P. and Kanciak, K. (2020). The search

of square m-sequences with maximum period via gpu

and cpu. Infocommunications Journal, XI:17.

Brouwer, A. E. and Haemers, W. H. (2012). Spectra of

Graphs. New York, NY

Chan, A. H., Games, R. A., and Rushanan, J. J. (1993). On

quadratic m-sequences. In Fast Software Encryption,

Cambridge Security Workshop, page 166–173, Berlin,

Heidelberg. Springer-Verlag.

Dabrowski, P., Labuzek, G., Rachwalik, T., and Szmidt, J.

(2014). Searching for nonlinear feedback shift reg-

isters with parallel computing. Inf. Process. Lett.,

114(5):268–272.

Golomb, S. W. (1981). Shift Register Sequences. Aegean

Park Press, USA.

Gonzalo, R. P., Ferrero, D., and Soriano, M. (2002). Non-

linear feedback shift registers with maximum period.

Jansen, C. (1989). Investigations on Nonlinear Streamci-

pher Systems: Construction and Evaluation Methods.

PhD thesis, TU Delft.

Kuznetsov, A., Potii, O., Poluyanenko, N., Gorbenko, Y.,

and Kryvinska, N. (2022). Stream Ciphers in Modern

Real-time IT Systems: Analysis, Design and Compar-

ative Studies.

Leskovec, J., Rajaraman, A., and Ullman, J. D. (2014). Min-

ing of Massive Datasets. Cambridge University Press,

USA, 2nd edition.

Poluyanenko, N. (2017). Development of the search method

for nonlinear shift registers using hardware, imple-

mented on ﬁeld programmable gate arrays. EUREKA:

Physics and Engineering, 1:53–60.

Graph-Based Modelling of Maximum Period Property for Nonlinear Feedback Shift Registers

837