
Efficiently Computing Maximum Clique of Sparse Graphs with
Many-Core Graphical Processing Units
Lorenzo Cardone
a
, Salvatore Di Martino
b
and Stefano Quer
c
Department of Control and Computer Engineering (DAUIN), Politecnico di Torino, Turin, Italy
Keywords:
High-Performace Computing, Graphs, Maximum Clique, GPU, Heuristics, Software, Algorithms.
Abstract:
The Maximum Clique is a fundamental problem in graph theory and has numerous applications in various
domains. The problem is known to be NP-hard, and even the most efficient algorithm requires significant
computational resources when applied to medium or large graphs. To obtain substantial acceleration and
improve scalability, we enable highly parallel computations by proposing a many-core graphical processing
unit implementation targeting large and sparse real-world graphs. We developed our algorithm from CPU-
based solvers, redesigned the graph preprocessing step, introduced an alternative parallelization scheme, and
implemented block-level and warp-level parallelism. We show that the latter performs better when the amount
of threads included in a block cannot be fully exploited. We analyze the advantages and disadvantages of the
proposed strategy and its behavior on different graph topologies. Our approach, applied to sparse real-world
graph instances, shows a geomean speed-up of 9x, an average speed-up of over 19x, and a peak speed-up of
over 70x, compared to a parallel implementation of the BBMCSP algorithm. It also obtains a geometric mean
speed-up of 1.21x and an average speed-up of over 2.0x on the same graph instances compared to the parallel
implementation of the LMC algorithm.
1 INTRODUCTION
A Maximum Clique (MC) of an undirected graph
G = (V, E) is a subset of the vertices V such that ev-
ery pair of vertices (v
i
, v
j
) in the subset is connected
by an edge e ∈ E and is impossible to add more ver-
tices to the subset maintaining this property. Intu-
itively, an MC is the most significant fully connected
subgraph within the original graph. This problem
has been proved to be NP-Hard (Karp, 1972), and it
is often solved with approximated strategies (Zuck-
erman, 1996). Nonetheless, it has multiple appli-
cations in many fields where evaluating groups of
related elements is essential. Significant examples
are the analysis of social network (Gschwind et al.,
2015), bioinformatics (Malod-Dognin et al., 2009),
coding theory (Etzion and Ostergard, 1998), and eco-
nomics (Boginski et al., 2006).
Many researchers have worked to find computa-
tionally efficient algorithms. Exact solutions are of-
ten based on branch and bound procedures derived by
a
https://orcid.org/0009-0008-7553-4839
b
https://orcid.org/0009-0007-6761-7143
c
https://orcid.org/0000-0001-6835-8277
subsequent optimizations of the Bron-Kerbosch algo-
rithm (Bron and Kerbosch, 1973). Several approaches
prune a significant section of the search space by com-
puting an upper bound of the MC size. Many compute
the bound by solving the graph coloring problem on
the same graph. Indeed, node colors already include
information on neighboring as a graph colored with
n different colors cannot have a clique larger than n.
Unfortunately, the coloring problem is also NP-hard.
Consequently, a few approaches try to overcome this
limitation by adding further analysis steps on top of
the coloring procedure. For example, encoding the
puzzle into a SATisfiability (SAT) (Ans
´
otegui and
Many
`
a, 2004) problem using an SAT-related problem
called MaxSAT (Tompkins and Hoos, 2005) is partic-
ularly effective.
Graphical Processing Units (GPUs) are designed
to perform parallel computations efficiently. They
have numerous cores that can execute computations
simultaneously, making them well-suited for tackling
computationally intensive tasks (Quer et al., 2020;
Cardone and Quer, 2023). Nonetheless, develop-
ing algorithms that efficiently exploit GPUs on graph
problems is not trivial because of hardware con-
straints.
Cardone, L., Di Martino, S. and Quer, S.
Efficiently Computing Maximum Clique of Sparse Graphs with Many-Core Graphical Processing Units.
DOI: 10.5220/0012852700003753
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 19th International Conference on Software Technologies (ICSOFT 2024), pages 539-546
ISBN: 978-989-758-706-1; ISSN: 2184-2833
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
539

This work focuses on an exact parallel branch and
bound maximum clique algorithm that explicitly tar-
gets the manipulation of large graphs on GPUs. It is
particularly efficient on sparse graphs. To the best of
our knowledge, such a direction has never been thor-
oughly investigated in the literature in the past. We
started by noticing that very few attempts have been
made to bring MC algorithms to GPU; the Maximum
Clique Solver Using Bitsets on GPUs (VanComper-
nolle et al., 2016) is somehow one of the exceptions.
However, its source code is not publicly available.
Therefore, we start our work from a parallel GPU
implementation of the Maximal Clique Enumeration
(MCE) (Almasri et al., 2023). The MCE finds all
maximal cliques and can be adapted to report only the
desired result. Then, we modified it by reimplement-
ing many optimizations found in other algorithms,
such as the BitBoard Maximum Clique SParse (Pablo
et al., 2017) and the Large Maximum Clique (Jiang
et al., 2016), applicable only to the MC problem. In
particular, starting from the latter work, we redesign
the vertex sorting and the graph reduction techniques.
Our final preprocessing phase is more efficient and
scalable, and the core algorithm uses the high paral-
lelism of GPUs more efficiently, showing a reduced
divergence among threads.
We compare our approach with three efficient al-
gorithms for computing the Maximum Clique: The
BitBoard Maximum Clique SParse (BBMCSP), the
Large Maximum Clique (LMC), and the Maximum
Clique Branch Reduce and Bound (MC-BRB). The
results show that our approach achieves, on sparse
real-world graphs, a geometric mean speed-up of 9x
and an average speed-up of 19x over the parallel
BBMCSP algorithm. It also obtained a geometric
mean speed-up of 1.21x and an average speedup of
over 2.0x compared to the parallel LMC algorithm.
Our software and all experimental results are
made available on GitHub
1
.
2 BACKGROUND
2.1 Graph Notation
A graph G = (V, E) is a set of vertices V and a set of
nodes (or links) E. Edges indicate relationships be-
tween vertices and can represent different interactions
between them. Given two nodes u, v ∈ V , we identify
an edge between them as E(u, v). We only consider
undirected graphs since the maximum clique problem
1
https://github.com/stefanoquer/Maximum-Clique-on-
GPU
is defined only for them.
The neighborhood of a vertex u, Γ(u) is the ver-
tices adjacent to u. Given a set of vertices P ⊆ V , we
define G[P] as the subgraph of G induced by the P
vertices.
A clique is a complete graph, i.e., a graph in which
each node is adjacent to all nodes. A clique is said to
be maximal if it cannot grow by adding any other ad-
jacent vertices. The largest maximal clique in a graph
is the maximum clique ω(G).
A k-core of a graph G is a subgraph of G where
all vertices have a degree at least equal to k. Given
a graph G, we call degeneracy of G the size of its
maximum core. The core number of a vertex u is the
lowest k of all k-cores, including u. The core number
of a graph G, referred to as k(G), is the highest core
number among all its vertices. The k-core of the graph
represents an upper bound of the size of the maximum
clique, i.e., ω(G) ≤ k(G) + 1.
Furthermore, we define the ego network of a ver-
tex v, the vertex itself, and its neighborhood. The
ego-network G[N
+
(v
i
)] is the subgraph of, given an
ordering, the highest-ranked neighbors of v
i
.
We compute the density of a given undirected
graph G as d(G) =
2|E|
|V|(|V |−1)
.
2.2 Graph Coloring
Graph coloring finds the minimum number of colors
to assign to the vertices of a given graph such that
every two adjacent vertices (u, v) ∈ E have a differ-
ent color, i.e., the color of u (C(u)) differs from the
color of v (C(v)). Coloring can be used to compute
an upper bound of the maximum clique since every
node in the clique must have a different color. This
property can be used to prune the search space during
MC computations. The minimum number of colors
needed to color a graph is called the chromatic num-
ber of the graph. We refer to it as χ(G). As every node
in a clique must have a different color, χ(G) is an up-
per bound of the maximum clique, i.e., ω(G) ≤ χ(G).
Since graph coloring is NP-Hard, many recent works
present algorithms to find approximate solutions to
the problem (Chen et al., 2023; Borione et al., 2023).
Approximate methods find a coloring χ
greedy
(G) that
is an upper bound of the chromatic number ω(G) ≤
χ(G) ≤ χ
greedy
(G).
2.3 State-of-the-Art MC Algorithms
The Bron-Kerbosh algorithm (Bron and Kerbosch,
1973) selects a vertex of the graph G and separates
the remaining ones into two groups: The adjacent
nodes and the non-adjacent ones. Since the maxi-
ICSOFT 2024 - 19th International Conference on Software Technologies
540

mum clique is a set of fully connected vertices, the
algorithm only needs to explore the adjacent nodes
fully. Then, the procedure recurs on the adjoining
set, which is considered a new instance of the MC
problem. During the recursion, it searches for the MC
between the neighboring nodes of the ones selected
in the previous steps. Over the years, several opti-
mizations have been proposed to speed up the pro-
cedure, such as reducing the vertices that need to be
visited and pruning unsatisfactory branches. Further-
more, MC solvers optimized for large sparse graphs
often perform a pre-processing of the input graph, or-
der the vertices, compute an initial clique, and prune
the search based on the size of the initial clique.
The BitBoard Maximum Clique SParse (Pablo
et al., 2017) (BBMCSP) adopts an internal data rep-
resentation based on bitsets. Bitsets encode sets to re-
duce the memory requirement. Moreover, they allow
bit parallel sets operations, enabling efficient search
and coloring.
The Large Maximum Clique (Jiang et al., 2016)
(LMC) uses a k-core computation to compute an ini-
tial degeneracy-based clique. Moreover, it introduces
a new pruning strategy based on incremental MaxSAT
reasoning. Furthermore, it exploits the Re-NUMBER
procedure (Tomita et al., 2010) to reduce the number
of colors and branching vertices.
The Maximum Clique, Branch Reduce, and
Bound (Chang, 2020) (MC-BRB) solves the MC
problem differently. First, it adopts a greedy proce-
dure named the Maximum Clique Degeneracy De-
gree (MC-DD) to compute two initial cliques, i.e., a
degeneracy-based and a degree-based clique. After
that, it uses a procedure called MC-EGO (which ex-
ploits information from the ego networks) to improve
the maximum clique found by MC-DD and the up-
per bound. To compute the maximum clique, each
instance of the MC problem is transformed into an
equivalent task in which it is necessary to find cliques
of size k on dense subgraphs. Thanks to the MC-ECO
algorithm’s efficiency in computing “almost” maxi-
mum cliques and the performance of the procedure to
reduce the graph, the overall execution time is signif-
icantly improved.
The most noteworthy efforts to implement the MC
algorithm on GPUs are the Maximum Clique Solver
Using Bitsets on GPUs (VanCompernolle et al., 2016)
(BBMCG) and the Parallel Maximal Clique Enumer-
ation on GPUs (Almasri et al., 2023). BBMCG is a
GPU implementation of BBMC that uses bitsets to
improve its efficiency. It is suitable only for small
and dense graph instances and runs out of memory
for large graphs. For that reason, we do not consider
it in our experimental section. The Parallel Maximal
Clique Enumeration on GPUs implements a branch
and bound Bron-Kerbosh approach and solves the
Maximal Clique Enumeration (MCE) problem. This
is a slightly different and more complex version of the
MC problem. Thus, we do not consider it in our ex-
perimental section as the comparison would weigh in
our favor.
3 OUR IMPLEMENTATION
3.1 Block-Wise Parallelism
To implement a fast and scalable algorithm able to
manipulate large graphs even with constrained mem-
ory resources, we leverage several well-known con-
cepts and propose a new GPU algorithm exploiting
the best aspects of BBMCSP and LMC described in
Section 2.3. Algorithm 1 shows our pseudo-code for
computing the MC. To parallelize the process, the
procedure iterates on the first level of the recursion
tree (often called “the first level independent subtree”)
in parallel as, thanks to vertex ordering, each iteration
is made independent from the following ones.
Algorithm 1: Pseudo-code for our parallel GPU-based MC
algorithm.
Input: Graph G = (V,E)
Output: Maximum clique C
max
1 begin
2 (G
′
= (V
′
, E
′
),C
′
) ← Pre process (G);
3 C
max
← C
′
;
4 for v
i
∈ |V
′
| in parallel per GPU block do
5 P = Γ(v
i
) ∩ {v
i+1
, v
i+2
, ..., v
|V
′
|
};
6 Compute adjacency matrix of (G
′
[P]);
7 Compute greedy coloring χ
greedy
(G
′
[P]);
8 core() ← k-core analysis of G
′
[P];
9 P
′
= {u ∈ P|core(u) + 1 ≥ |C
max
|};
10 Compute adjacency matrix of (G
′
[P
′
]);
11 C
max
← SearchMaxClique(G
′
[P
′
], P
′
,
{v
i
}, C
max
);
The algorithm initially preprocesses the input
graph G (line 2), performing the following three steps.
First, it exploits the parallel implementation of the
MCE algorithm on GPUs to sort the vertices V of
G by descending core number. Then, following the
LMC algorithm (Section 2.3), it finds an initial clique
representing our lower bound. Finally, it simplifies
the graph G, removing all vertices with a core number
smaller than the initial clique. Function Pre-process
returns the reduced graph G
′
(not including vertices
that cannot belong to the final MC) and the initial
clique C
′
(representing our lower bound).
Efficiently Computing Maximum Clique of Sparse Graphs with Many-Core Graphical Processing Units
541

After that pre-processing step, we find the desired
MC working on the reduced graph G
′
. Line 4 shows
the primary iteration construct of the algorithm. This
cycle takes care of the first level of the recursion
tree, which is usually called a “first-level indepen-
dent subtree”. The iteration runs over all vertices of
G
′
and can be easily parallelized by running an in-
dependent thread for each vertex. Unfortunately, in
this approach, the P sets and the adjacency matrix
must be stored for each thread. Consequently, the
method requires an amount of memory proportional
to the number of threads, making it unsuitable for
GPUs that usually have minimal memory to store data
efficiently. To solve this problem, we adopt the ap-
proach proposed by BBMCG, which is to assign each
task to blocks instead of assigning tasks to threads.
This strategy reduces the memory used and, simulta-
neously, the divergence among threads.
In line 5, the algorithm computes the intersection
between the neighborhood of the selected node (v
i
) of
the current block and the following vertices v
i
adopt-
ing the pre-computed order. Note that it is possible to
precompute all the sets P before the parallel for loop
and slightly optimize the process but, for clarity, we
moved the computation where each task computes its
own set.
In line 6, we create G
′
[P], and in line 7, we color
it using an greedy approach. This technique was ini-
tially proposed in BBMCSP. Since each GPU block
consists of multiple threads, we exploit these threads
to parallelize the inter-set operations typical of the
coloring procedure. To speed up this process, the
graph is represented as an array of bits on which
accessing the neighborhood information of a node
merely involves accessing the right row. The number
of colors the procedure finds is used to compute the
upper bound for the clique size. As a further optimiza-
tion, it is possible to stop coloring when the number of
colors exceeds the bound |C
max
|−|C| as no additional
useful information is gained by further coloring the
remaining vertices of P. The search should continue
as long as the current bound can improve the best so-
lution.
Line 8 repeats the first step performed by function
Pre process but works on the graph G
′
and runs only
the threads in the block. After this step, it is possible
to recompute a clique as in the preprocessing phase,
but this procedure has been proven to be too time-
consuming to achieve any benefit. Thus, in line 9, we
repeat the node reduction, i.e., we remove from P any
node u whose core number does not allow it to par-
ticipate in a clique larger than the maximum already
found.
In line 10, we create G
′
[P
′
], and finally, in line 11,
we call the function SearchMaxClique to find the
maximum clique on the subgraph including only the
vertices in P
′
.
Algorithm 2: Our parallel function SearchMaxClique
(called by Algorithm 1) to compute the final MC.
Input: Graph G = (V,E), Set P, Set C, Set C
max
Output: Maximum clique C
max
1 begin
2 if P =
/
0 then
3 if |C| > |C
max
| then
4 C
max
← C;
5 return C
max
;
6 B ← GetBranchingNodes(P, |C
max
| − |C|);
7 if B =
/
0 then
8 return C
max
;
9 A ← P \ (B = {b
1
, b
2
, ..., b
|B|
});
10 for b
i
∈ B do
11 if first level subtree explored then
12 Donate tasks to idle blocks;
13 break;
14 P
′
← A ∪ (Γ(b
i
) ∩ {b
i+1
, b
i+2
, ..., b
|B|
});
15 C
max
← SearchMaxClique(G, P
′
,
C ∪ {b
i
}, C
max
);
16 return C
max
;
Function SearchMaxClique is described by Algo-
rithm 2.
In lines 2-5, we try to expand the current clique if
the set P is empty.
Line 6 computes B, i.e., a subset of P, using the
greedy coloring procedure previously presented. The
nodes included in B are the ones that received a color
greater than |C
max
| − |C|. The presence of nodes with
a color greater than this bound implies the possibility
of expanding the current clique. If this set turns out to
be empty, we can terminate the execution (line 7-8).
In lines 11-13, we check whether the remaining
work can be shared between the idle blocks, and then
we donate to each block a (|C| + 1)-level task. A task
consists of selecting a vertex and recurring on the sub-
problem created by this choice. This operation dy-
namically rebalances the workload between threads.
In line 14, we compute a new vertex set P
′
(includ-
ing all nodes that can be used to expand the current
solution) . In line 15, we recur on the MC subprob-
lem . Since the algorithm is executed on a GPU, the
recursion is performed by adopting an explicit stack
recording the current state.
3.2 Warp-Wise Parallelism
As already shown in the previous section, at each
recursive call of line 15, the size of the MC sub-
ICSOFT 2024 - 19th International Conference on Software Technologies
542

problem is reduced, and, at a certain point, there are
not enough nodes to distribute the work between all
threads inside a block. Thus, block-wise parallelism
is effective only until the subgraph G
′′
= G
′
[P
′
] has a
vertex set size |V (G
′′
)| larger or equal to 32 times the
number of threads in a block. To minimize this ef-
fect, we propose the following solution. Since we can
virtually guarantee enough nodes to make the block-
wise parallelization worthwhile at the first recursion
level, we left this level untouched, as already shown
in Algorithm 1. On the contrary, Algorithm 2, from
the second level subtree, receives a subproblem to be
solved for each GPU warp (i.e., 32 GPU threads).
Since GPU warps are the lowest hierarchical level on
a GPU to possess an independent program counter,
we reduce the number of nodes we can process in
parallel and increase the number of instances we can
solve in parallel by the same amount. This feature
allows increased flexibility since we waste less com-
putational resources when the subproblem decreases
in size. Unfortunately, each instantiated subproblem
requires a certain amount of memory to be allocated,
increasing the memory requirements. Moreover, each
warp shares the adjacency matrix of G
′
[P
′
]. Dynamic
work balancing is performed at the warp instead of
the block level. It is performed internally inside the
block before the first level subtree has been explored
and globally among warps of different blocks after the
first level subtree has been explored.
4 EXPERIMENTAL RESULTS
4.1 Experimental Setup
We ran our tests on a workstation equipped with a
CPU Intel Core i9-10900KF, 64 GBytes of DDR4
RAM, and a GPU NVIDIA RTX 3070 with 8GB of
onboard memory. The CPU runs with 10 physical
cores and 20 threads (with hyperthreading).
All our algorithms are written in C++ and com-
piled with g++. The GPU implementation is written
in C++/CUDA, adopting the Toolkit version 12.2.
The dataset mainly includes online graphs avail-
able at the Network Repository (Rossi and Ahmed,
2015)
2
. However, we randomly generated graphs
with specific densities to compare the performances
of the different algorithms in particular conditions.
Since not all parallel versions of state-of-the-art
algorithms are available online, we proceed as fol-
lows to perform a significant comparison. The BBM-
2
https://networkrepository.com/
CSP algorithm
3
has been implemented following the
guidelines of the authors (Pablo et al., 2017), and
we reproduced BBMCPara using the OpenMP library.
LMC is available from its repository
4
in its single-
threaded version. We did not modify the preprocess-
ing strategy but parallelized the first level using the
POSIX threads library. MC-BRB is only available in
its single-thread version
5
. We parallelized it by fol-
lowing the guidelines of the original work (Chang,
2020). Both MC-EGO and MC-BRB have been par-
allelized using the OpenMP library. The other pre-
processing procedure (like MC-DD) remains single-
threaded.
4.2 Result on Random Graphs
In this section, we collect our algorithms’ results on
randomly generated graphs. We generated graphs
of medium-large size with low-medium density to
have meaningful results. This feature highlights that
the pruning strategy of LMC and MC-BRB becomes
more effective with higher densities. All tests have
been performed using the block version of our algo-
rithm (not the warp one). To obtain reliable data, we
generated ten different graph sets sharing each value
of size and density, and we presented the average run-
times for each group.
Figure 1 shows the running times of each algo-
rithm as a function of the density with graphs of dif-
ferent sizes. The plots show that our approach outper-
forms every other algorithm in practically all graph
instances. In particular, our data shows that on these
graph topologies, the most critical factor in reducing
the execution time is the level of parallelism achiev-
able, which significantly benefits the GPU implemen-
tation. Our data illustrates that we achieve increasing
speed-ups over BBMCPara as the density decreases,
going from 3x to over 10x. We also achieve a speed-
up of around 2x-3x on low-density instances com-
pared to MC-BRB. Finally, we obtained a speed-up of
over 2x over LMC, often the second fastest approach
for sparse graphs.
As a final remark, notice that many experiments
reach the timeout while still showing a diverging be-
havior. This leads us to the conjecture that extend-
ing the timeout further will increase the speed-ups ob-
tained with our tool.
3
https://github.com/psanse/CliqueEnum
4
https://home.mis.u-picardie.fr/∼cli/EnglishPage.html
5
https://github.com/LijunChang/MC-BRB
Efficiently Computing Maximum Clique of Sparse Graphs with Many-Core Graphical Processing Units
543
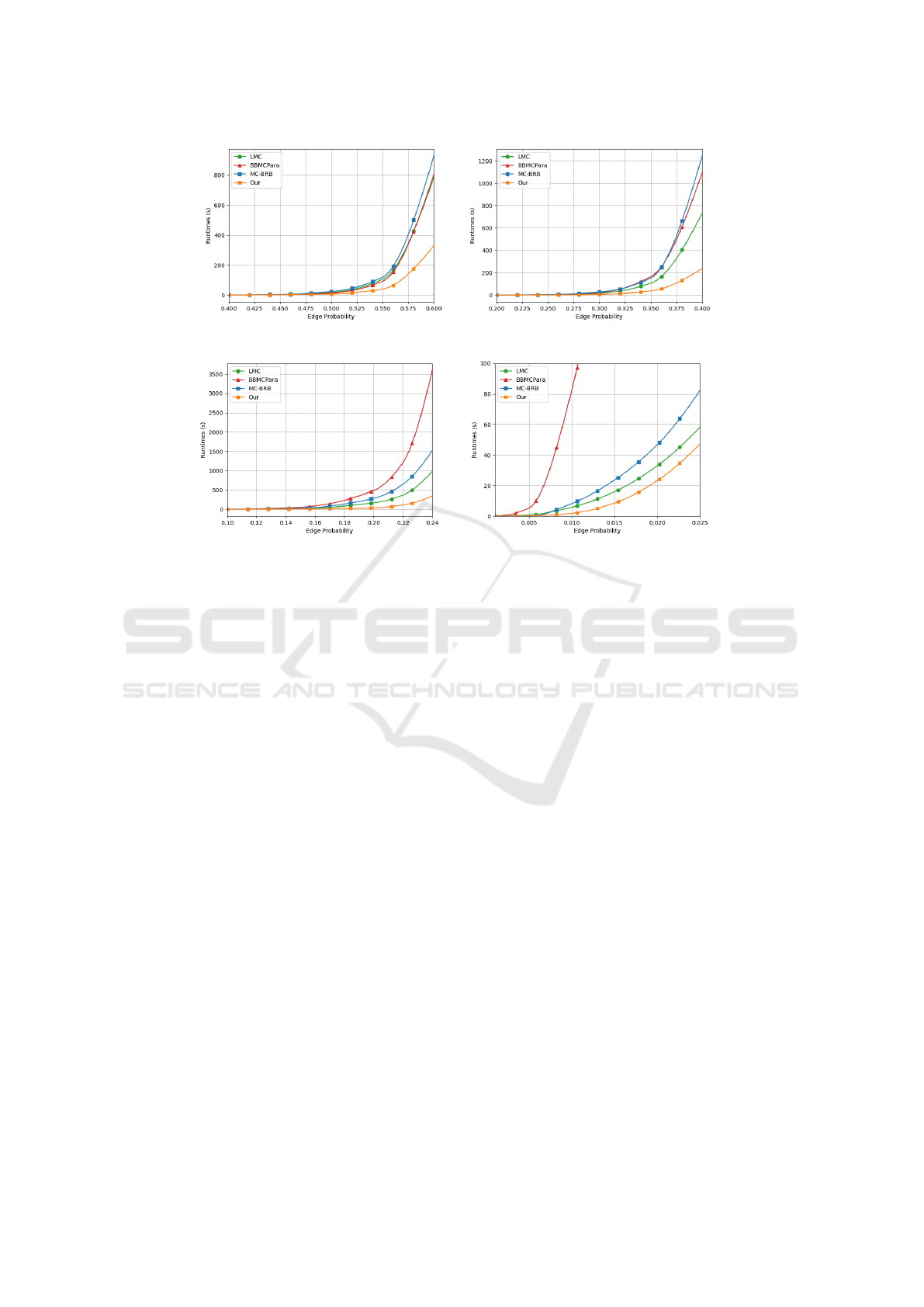
(a) Graphs with 1,000 vertices. (b) Graphs with 3,000 vertices.
(c) Graphs with 10,000 vertices. (d) Graphs with 100,000 vertices.
Figure 1: Runtimes of our algorithms (on the y-axis) on random graphs as a function of the graph density (reported on the
x-axis). All times are reported in seconds.
4.3 Results on Dataset Graphs
This section compares the execution time of the same
algorithms analyzed in the previous section on pub-
licly available graphs.
Table 1 collects the characteristics of our graph
set. The graphs are sorted according to their average
density after the reduction at the first level. We se-
lected graphs with significantly different features to
evaluate the efficiency of all algorithms with many
graph topologies.
Table 2 reports all algorithms’ initialization (I) and
search (S) runtimes. It also reports the total (T) run-
ning times for all algorithms. Furthermore, to indi-
cate the accuracy of the preprocessing step, it shows
the value |ω
0
|, which represents the size of the initial
clique found during the preprocessing step. OOM in-
dicates an out-of-memory error, and TO a time-out,
i.e., a running time larger than one hour. A symbol -
suggests that the problem has been solved during the
previous phase or has run out of memory.
As Table 2 shows, MC-BRB is the fastest algo-
rithm on average. Even if its preprocessing time is
often the highest among the approaches, its ability to
find a larger initial clique and its more efficient al-
gorithm to solve the most challenging instances pro-
duce a lower computation time. The MaxSAT ap-
proach implemented by LMC also shows excellent
results in a few cases where the speed-ups are signifi-
cant. Our implementation shows promising results in
almost all cases when compared to BBMCSP. It also
produces competitive runtimes on the lower-density
graphs compared to all other approaches, making it
a valid alternative with graphs locally sparse. Notice
that these results are coherent with the ones presented
in the previous section on random graphs. However,
we can see that our algorithm pays a penalty on graphs
whose density increases on lower recursion levels due
to lower thread utilization and less effective pruning
strategies. If we compare our solution on all graphs
on which all algorithms performed a search (the first
four graphs are solved during preprocessing), we are
two to four times faster than the other implementa-
tions. Compared to the most dense graphs, MC-BRB
manages to solve many of the graphs during the pre-
computation step, which results in tremendous speed-
up when the other algorithms must perform a time-
consuming search. Moreover, the warp-parallel ver-
sion has runtimes similar to the block version in those
instances where the optimization couldn’t be applied;
even in the worst case, the slowdown is usually mini-
mal. The effect of the optimization is more evident in
instances that take a longer execution time. In those
cases, we can significantly speed up the previous ver-
sion. As discussed in the last section, the warp-base
ICSOFT 2024 - 19th International Conference on Software Technologies
544

Table 1: The table shows the statistics about our dataset, i.e., number of vertices, number of edges, density, maximum and
average degree of the nodes, and the size of the maximum clique.
Id Instance |V| |E| Density Max. degree Avg. degree |ω(G)|
g
01
co-papers-dblp 540,486 15,245,730 0.000104 3,299 56 337
g
02
web-uk-2002-all 18,520,486 298,113,763 2e-06 194,956 32 944
g
03
c-62ghs 41,731 300,538 0.000345 5,061 14 2
g
04
web-it-2004 509,338 7,178,414 5.5e-05 469 28 432
g
05
aff-orkut-user2groups 8,730,857 327,037,488 9e-06 318,268 75 6
g
06
rec-yahoo-songs 136,737 49,770,696 0.005324 31,431 728 19
g
07
soc-livejournal-user-groups 7,489,073 112,307,386 4e-06 1,053,749 30 9
g
08
socfb-konect 59,216,214 92,522,018 0 4,960 3 6
g
09
aff-digg 872,622 22,624,728 5.9e-05 75,715 52 32
g
10
soc-orkut 2,997,166 106,349,210 2.4e-05 27,466 71 47
g
11
soc-sinaweibo 58,655,849 261,321,072 0 278,491 9 44
g
12
wiki-talk 2,394,385 5,021,411 2e-06 100,032 4 26
g
13
bn-human-Jung2015 M87113878 1,772,034 76,500,873 4.9e-05 6,899 86 227
g
14
bn-human-BNU 1 0025864 session 2-bg 1,827,241 133,727,517 8e-05 8,444 146 271
g
15
soc-flickr 513,969 3,190,453 2.4e-05 4,369 12 58
g
16
tech-p2p 5,792,297 147,830,699 9e-06 675,080 51 178
g
17
bn-human-BNU 1 0025864 session 1-bg 1,827,218 143,158,340 8.6e-05 15,114 157 294
g
18
soc-flickr-und 1,715,255 15,555,043 1.1e-05 27,236 18 98
g
19
socfb-A-anon 3,097,165 23,667,395 5e-06 4,915 15 25
g
20
bn-human-Jung2015 M87126525 1,827,241 146,109,301 8.8e-05 8,009 160 220
g
21
bio-human-gene1 22,283 12,345,964 0.049731 7,940 1,108 1,335
g
22
bio-human-gene2 14,340 9,041,365 0.087942 7,230 1,261 1,300
g
23
soc-LiveJournal1 4,847,571 68,475,392 6e-06 22,887 28 321
g
24
web-wikipedia link it 2,936,413 104,673,034 2.4e-05 840,650 71 870
g
25
web-indochina-2004-all 7,414,866 194,109,312 7e-06 256,425 52 6,848
Table 2: Runtime statistics: The table reports all algorithms’ preprocessing solution size found (|ω
0
|), preprocessing (I),
search (S), and total time (T). The time-out (TO) is set to 3,600 seconds, i.e., one hour. The quantity of memory available is
8 GBytes of GPU RAM for our approach and 64 GBytes of system RAM for all the others. Beyond those limits, we have an
out-of-memory error (OOM). A symbol - indicates that the problem has been solved during the previous phase or has run out
of memory. For our algorithm, we report data for both the block-based and warp-based versions.
Id
Our BBMCPara LMC MC-BRB
|ω
0
| I S T S T |ω
0
| I S T |ω
0
| I S T |ω
0
| I S T
(Block) (Block) (Warp) (Warp)
g
01
337 0.07 - 0.07 - 0.07 337 0.24 - 0.24 337 0.11 - 0.11 337 0.01 - 0.01
g
02
944 0.65 - 0.65 - 0.65 944 7.40 - 7.40 944 5.59 - 5.59 944 1.13 - 1.13
g
03
2 0.06 0.00 0.06 0.00 0.06 2 0.08 0.00 0.09 2 0.01 0.01 0.02 2 0.00 - 0.00
g
04
432 0.04 - 0.04 - 0.04 432 0.07 - 0.07 432 0.03 - 0.03 432 0.00 - 0.00
g
05
2 16.29 1.78 18.07 1.66 17.95 5 - OOM - 2 25.09 21.25 46.34 6 95.41 0.74 96.15
g
06
16 1.65 3.21 4.86 2.91 4.55 11 42.85 77.95 120.80 16 2.61 6.44 9.05 18 12.08 6.56 18.64
g
07
5 11.88 0.26 12.13 0.25 12.13 8 378.73 117.45 496.17 4 7.46 2.37 9.83 9 14.31 0.59 14.90
g
08
5 1.26 0.01 1.28 0.01 1.27 6 56.65 0.09 56.75 6 7.33 0.12 7.45 6 4.89 - 4.89
g
09
28 0.78 12.36 13.13 5.92 6.70 25 15.65 55.59 71.25 29 0.85 13.71 14.56 30 4.02 42.15 46.17
g
10
18 3.40 0.24 3.64 0.23 3.62 46 71.99 3.49 75.48 17 9.33 1.68 11.01 47 9.12 - 9.12
g
11
7 6.94 0.25 7.19 0.24 7.17 41 530.51 10.37 540.88 8 20.44 2.5 22.94 44 21.54 1.42 22.96
g
12
23 0.23 0.01 0.24 0.01 0.24 16 4.4 0.03 4.43 25 0.13 0.02 0.15 26 0.18 0.01 0.19
g
13
138 1.46 65.59 67.05 69.04 70.50 221 48.82 2.47 51.30 133 3.50 16.89 20.39 227 7.34 0.02 7.35
g
14
200 2.71 11.43 14.14 14.18 16.89 271 95.62 37.23 132.85 199 6.08 24.36 30.44 271 19.44 0.17 19.61
g
15
54 0.18 0.05 0.23 0.05 0.23 40 1.54 0.23 1.77 52 0.1 0.09 0.19 57 0.20 0.12 0.32
g
16
173 2.14 742.51 744.64 379.19 381.32 153 207.42 TO TO 172 12.46 12.8 25.26 175 17.24 9.53 26.77
g
17
223 2.49 65.91 68.41 34.70 37.19 276 103.41 TO TO 222 6.44 31.52 37.96 283 23.83 2.71 26.54
g
18
75 0.48 1.13 1.62 0.72 1.20 68 9.05 9.62 18.68 74 0.63 1.3 1.93 96 1.52 1.39 2.90
g
19
23 0.50 0.03 0.53 0.03 0.53 24 14.73 0.57 15.30 23 1.36 0.24 1.6 25 1.29 - 1.29
g
20
195 2.18 4.88 7.05 4.57 6.74 206 71.90 128.52 200.42 196 5.44 12.87 18.31 219 6.83 0.08 6.91
g
21
1,329 0.48 468.93 469.41 219.45 219.93 1,268 4.86 TO TO 1,328 0.27 169.23 169.50 1,335 4.33 1.46 5.78
g
22
1,293 0.44 43.27 43.71 58.62 59.06 1,229 2.71 288.54 291.24 1,290 0.19 27.21 27.40 1,300 2.82 0.79 3.61
g
23
320 0.33 0.10 0.43 0.1 0.44 316 20.79 0.01 20.80 320 2.35 0.01 2.36 321 1.08 - 1.08
g
24
869 1.25 0.98 2.23 0.97 2.20 869 29.51 0.02 29.53 869 2.52 0.02 2.54 870 3.22 - 3.22
g
25
6,848 1.10 2.02 3.12 OOM - 6,848 25.01 0.01 25.03 6,848 1.92 4.57 6.49 6,848 0.53 - 0.53
version achieves the best performances where the ex-
ecution slows down because of the wasted computa-
tional resources. Thanks to this, we have speed-ups
of over 2x over our block-based version.
5 CONCLUSIONS
In this paper, we focus on solving the Maximum
Clique problem. Although GPU-based implementa-
tions seem an excellent path to follow to improve
the scalability of the existing algorithms, very few
Efficiently Computing Maximum Clique of Sparse Graphs with Many-Core Graphical Processing Units
545

works can be found on the topic, and, as far as we
know, no implementation is available online. Conse-
quently, starting from works on parallelizing the max-
imal clique enumeration on GPUs and merging con-
tributions and ideas coming from other approaches
into this methodology, we propose a GPU implemen-
tation for the Maximum Clique problem.
Our experimental analysis compares our version
with the main state-of-the-art algorithms. We show
that we can reach speed-ups up to 70x on graph in-
stances that, once reduced, are dense or have a high
maximum degree vs an implementation of BBMC-
Para.
In future works, we still have to run our algo-
rithm with proper implementation of the incremental
MaxSAT reasoning and the incremental upped-bound
approach. These contributions can further improve
scalability and reduce our running times.
REFERENCES
Almasri, M., Chang, Y.-H., Hajj, I. E., Nagi, R., Xiong,
J., and mei Hwu, W. (2023). Parallelizing Maximal
Clique Enumeration on GPUs.
Ans
´
otegui, C. and Many
`
a, F. (2004). Mapping Prob-
lems with Finite-Domain Variables to Problems with
Boolean Variables. In SAT (Selected Papers), pages
1–15.
Boginski, V., Butenko, S., and Pardalos, P. M. (2006). Min-
ing market data: A network approach. Computers &
Operations Research, 33(11):3171–3184.
Borione, A., Cardone, L., Calabrese, A., and Quer, S.
(2023). An experimental evaluation of graph color-
ing heuristics on multi- and many-core architectures.
IEEE Access, 11:125226–125243.
Bron, C. and Kerbosch, J. (1973). Algorithm 457: finding
all cliques of an undirected graph. Commun. ACM,
16(9):575–577.
Cardone, L. and Quer, S. (2023). The Multi-Maximum and
Quasi-Maximum Common Subgraph Problem. Com-
putation, 11(4).
Chang, L. (2020). Efficient maximum clique computation
and enumeration over large sparse graphs. The VLDB
Journal, pages 999–1022.
Chen, Y., Brock, B., Porumbescu, S., Buluc, A., Yelick,
K., and Owens, J. (2023). Atos: A task-parallel gpu
scheduler for graph analytics. In Proceedings of the
51st International Conference on Parallel Processing,
ICPP ’22, New York, NY, USA. Association for Com-
puting Machinery.
Etzion, T. and Ostergard, P. R. (1998). Greedy and heuristic
algorithms for codes and colorings. IEEE Transac-
tions on Information Theory, 44(1):382–388.
Gschwind, T., Irnich, S., Furini, F., Calvo, R. W., et al.
(2015). Social Network Analysis and Community
Detection by Decomposing a Graph into Relaxed
Cliques. Technical report, Gutenberg School of
Management and Economics, Johannes Gutenberg-
Universit
¨
at Mainz.
Jiang, H., Li, C.-M., and Many
`
a, F. (2016). Combining Ef-
ficient Preprocessing and Incremental MaxSAT Rea-
soning for MaxClique in Large Graphs. In Proceed-
ings of the Twenty-Second European Conference on
Artificial Intelligence, ECAI’16, page 939–947, NLD.
IOS Press.
Karp, R. M. (1972). Reducibility among combinatorial
problems. Complexity of Computer Computations:
Proceedings of a symposium on the Complexity of
Computer Computations, pages 85–103.
Malod-Dognin, N., Andonov, R., and Yanev, N. (2009).
Maximum cliques in protein structure comparison.
Pablo, S. S., Alvaro, L., Artieda, J., and Pardalos, P. M.
(2017). A Parallel Maximum Clique Algorithm for
Large and Massive Sparse Graphs. Optimization Let-
ters, 11:343–358.
Quer, S., Marcelli, A., and Squillero, G. (2020). The
maximum common subgraph problem: A parallel and
multi-engine approach. Computation, 8(2).
Rossi, R. A. and Ahmed, N. K. (2015). The network data
repository with interactive graph analytics and visual-
ization. In AAAI.
Tomita, E., Sutani, Y., Higashi, T., Takahashi, S., and
Wakatsuki, M. (2010). A simple and faster branch-
and-bound algorithm for finding a maximum clique.
In Rahman, M. S. and Fujita, S., editors, WALCOM:
Algorithms and Computation, pages 191–203, Berlin,
Heidelberg. Springer Berlin Heidelberg.
Tompkins, D. A. and Hoos, H. H. (2005). UBCSAT: An
implementation and experimentation environment for
SLS algorithms for SAT and MAX-SAT. In The-
ory and Applications of Satisfiability Testing: 7th In-
ternational Conference, SAT 2004, Vancouver, BC,
Canada, May 10-13, 2004, Revised Selected Papers
7, pages 306–320. Springer.
VanCompernolle, M., Barford, L., and Harris, F. (2016).
Maximum Clique Solver Using Bitsets on GPUs. In
Latifi, S., editor, Information Technology: New Gen-
erations, pages 327–337, Cham. Springer Interna-
tional Publishing.
Zuckerman, D. (1996). On unapproximable versions
of np-complete problems. SIAM J. Comput.,
25(6):1293–1304.
ICSOFT 2024 - 19th International Conference on Software Technologies
546
