Balancing Act: Navigating the Privacy-Utility Spectrum in Principal

Component Analysis

Saloni Kwatra

1 a

, Anna Monreale

2 b

and Francesca Naretto

2 c

Department of Computing Science, Ume

a University, Sweden

Department of Computer Science, University of Pisa, Italy

Keywords:

k-anonymity, Data Reconstruction Attack, Membership Inference Attack, Generative Networks, Principal

Component Analysis, Federated Learning.

Abstract:

A lot of research in federated learning is ongoing ever since it was proposed. Federated learning allows col-

laborative learning among distributed clients without sharing their raw data to a central aggregator (if it is

present) or to other clients in a peer to peer architecture. However, each client participating in the federation

shares their model information learned from their data with other clients participating in the FL process, or

with the central aggregator. This sharing of information, however, makes this approach vulnerable to vari-

ous attacks, including data reconstruction attacks. Our research speciﬁcally focuses on Principal Component

Analysis (PCA), as it is a widely used dimensionality technique. For performing PCA in a federated setting,

distributed clients share local eigenvectors computed from their respective data with the aggregator, which

then combines and returns global eigenvectors. Previous studies on attacks against PCA have demonstrated

that revealing eigenvectors can lead to membership inference and, when coupled with knowledge of data dis-

tribution, result in data reconstruction attacks. Consequently, our objective in this work is to augment privacy

in eigenvectors while sustaining their utility. To obtain protected eigenvectors, we use k-anonymity, and gen-

erative networks. Through our experimentation, we did a complete privacy, and utility analysis of original

and protected eigenvectors. For utility analysis, we apply HIERARCHICAL CLUSTERING, RANDOM FOREST

regressor, and RANDOM FOREST classiﬁer on the protected, and original eigenvectors. We got interesting

results, when we applied HIERARCHICAL CLUSTERING on the original, and protected datasets, and eigenvec-

tors. The height at which the clusters are merged declined from 250 to 150 for original, and synthetic version

of CALIFORNIA-HOUSING data, respectively. For the k-anonymous version of CALIFORNIA-HOUSING data,

the height lies between 150, and 250. To evaluate the privacy risks of the federated PCA system, we act as an

attacker, and conduct a data reconstruction attack.

1 INTRODUCTION

The demand for Artiﬁcial Intelligence (AI) tools that

align with legal regulations such as GDPR (Voigt

and Von dem Bussche, 2017) and individual privacy

preferences has become crucial. Federated Learn-

ing (FL), introduced by McMahan et al. (McMahan

et al., 2017), addresses this need by enabling col-

laborative model learning among distributed clients

without transmitting raw data. Despite its initial por-

trayal as a privacy-preserving solution, it is now ac-

knowledged that FL is susceptible to various attacks

on data, models, and communication links (Zhu et al.,

https://orcid.org/0000-0002-4896-7849

https://orcid.org/0000-0001-8541-0284

https://orcid.org/0000-0003-1301-7787

2019). Therefore, developing FL frameworks, which

also preserves privacy is our main goal. FL was ini-

tially proposed for deep learning models. But, now it

has been applied to many classical machine learning

algorithms as well. Our study focuses on FL algo-

rithms (Hartebrodt and R

ottger, 2022) that perform

PCA (Principal Component Analysis). To perform

data analysis of high dimensional data, we need di-

mensionality reduction techniques, and PCA is one

of the most popular dimensionality reduction tech-

niques. Through our research, we want to show

that FL-PCA algorithms, particularly those that share

information like local eigenvectors computed from

each distributed client’s data, lack privacy, as shar-

ing eigenvectors can reveal the members of train-

ing data, as shown in the paper (Zari et al., 2022),

850

Kwatra, S., Monreale, A. and Naretto, F.

Balancing Act: Navigating the Privacy-Utility Spectrum in Principal Component Analysis.

DOI: 10.5220/0012855000003767

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 850-857

ISBN: 978-989-758-709-2; ISSN: 2184-7711

which showed a Membership Inference attack (MIA)

against PCA. When this knowledge is combined with

the knowledge of data distribution, the attacker can

estimate the original data of clients participating in

the FL process, as shown in the paper (Kwatra and

Torra, 2023), which showed a data reconstruction at-

tack against PCA. Hence, our objective is to introduce

protection in the eigenvectors and evaluate the util-

ity and privacy of protected eigenvectors compared

to the original eigenvectors. Our proposed privacy-

preserving approach can also be applied to real-life

scenarios. For example, consider there are hospi-

tals located at different locations, which have high-

dimensional data of RNA sequences, and their aim

is to identify genes associated with certain conditions

or diseases. Hence, hospitals can apply privacy pro-

tected FL-PCA algorithms to facilitate the collabora-

tion while preserving privacy, and also saving the

computation resources by removing the overhead of

collecting all the data at one location. Finally, we list

the contributions of this paper as follows.

• Introduction of privacy measures in the the com-

putation of eigenvectors by computing them on

private data. For creating private data, we use k-

anonymity, and synthetic data generated by Con-

ditional Tabular Generative Adversarial Network

(CTGAN).

• Evaluation of the privacy of the system by act-

ing as an intruder/attacker, who has some back-

ground knowledge, such as knowledge of some

top eigenvectors, and the knowledge of data dis-

tribution, and then conduct a data reconstruction

attack. We compare the case when the attacker

is aware of some top private (k-anonymous, and

synthetic) eigenvectors with the case when the at-

tacker is aware of some top original eigenvectors.

• Evaluation of utility through RANDOM FOREST,

and dendrogram analysis on both original and pro-

tected (k-anonymous, and synthetic) eigenvectors.

The subsequent sections of this paper are orga-

nized as follows: Section 2 reviews essential con-

cepts, including PCA, FL-PCA algorithms, member-

ship inference attack, and data reconstruction at-

tack. Section 3 elaborates on our contributions, where

we provide a comprehensive analysis of utility and

privacy using a RANDOM FOREST, HIERARCHICAL

CLUSTERING, and data reconstruction attack. This

analysis is relevant and adaptable to centralized and

Federated Learning (FL) scenarios. Section 4 outlines

the datasets and attack settings. Section 5 presents

and discusses the results, and Section 6 concludes the

paper with insights into future directions.

2 BACKGROUND AND RELATED

WORK

In this section, we explain all the relevant background

theories needed to understand our proposed analysis.

2.1 Principal Component Analysis

Given a set D = {x

∈ R

: n = 1 : N }, where N is

the number of samples, and x

is a sample in R

, PCA

aims to determine a p dimensional subspace that ap-

proximates each sample x

(Abdi and Williams, 2010)

in a way that the maximum variance of the data is re-

tained. The formulation of PCA is as follows:

min

E =

∑

n=1

∑

n=1

||x

− π

(1)

In the above expression, π

represents the projection

matrix onto the p-dimensional subspace. E is the

reconstruction error or the mean squared error, rep-

resenting the average squared distance between the

original sample x

and its projection π

. The solu-

tion to this optimization problem (1) can be obtained

through the Singular Value Decomposition (SVD)

of a sample covariance matrix Σ

cov

of the standard-

ized data matrix D . The SVD of Σ

cov

is given by

∑

i=1

, where λ

≥ λ

. . . λ

are the eigenval-

ues, and v

, v

. . . v

are the corresponding eigenvec-

tors of Σ

cov

, respectively. Let V

denote the matrix

whose columns are the top p eigenvectors. The op-

timal projection matrix is then deﬁned as π

and it provides the solution to the PCA optimization

problem in (1). This projection matrix π

allows for

the representation of the data in a lower-dimensional

subspace while minimizing the reconstruction error.

2.2 Federated PCA Algorithms

There are many existing algorithms to perform PCA

in a federated setting. In FL-PCA algorithms, the

clients compute the reduced subspace from its data,

and sends it to the aggregator. The aggregator does

it job by aggregating those reduced subspaces, and

sends the aggregated subspace back to the clients. In

this section, we discuss some of the FL-PCA algo-

rithms in detail, with the aim of analysing their pri-

vacy breaches, and further improving their privacy

protection while maintaining their utility. PCA is an

unsupervised machine learning method. There is also

a supervised version of FL-PCA in this recent work

(Briguglio et al., 2023). Nevertheless, in this pa-

per, our focus is on unsupervised FL-PCA algorithms.

In (Hartebrodt and R

ottger, 2022) Hartebrodt et al.

present a plethora of state-of-the-art approaches for

Balancing Act: Navigating the Privacy-Utility Spectrum in Principal Component Analysis

851

FL-PCA. They analyze both iterative and single-shot

approaches for horizontally partitioned data.

Regarding the ﬁrst approach, Federated Subspace

Iteration (FSI) (Pathak and Raj, 2011) is one of

the state-of-the-art methods. FSI uses an exact ap-

proach for privacy-preserving computation of eigen-

vector matrices. Clients and aggregator exchange and

compute local and global matrices iteratively. With

a large number of iterations, the complete covariance

matrices can be recovered, which is a privacy breach,

as discussed in Section 2.3.

In terms of single-shot approaches, they require

the computation of local subspaces at the client side,

and the server aggregates the local subspaces received

from the distributed clients, and sends the global sub-

space back to the clients, such as P-COV, AP-COV,

AP-STACK (Liang et al., 2014). In AP-COV and

AP-STACK, the clients perform SVD on its data and

sends the local eigenvectors to the aggregator. In AP-

COV, the aggregator aggregates the local eigenvectors

by doing element wise addition, while in AP-STACK,

the aggregator aggregates the local eigenvectors by

stacking the local eigenvectors vertically. In the study

by Hartebrodt et al., it was empirically proven that

both methodologies exhibit comparable performance.

For this reason, for our investigation, we will concen-

trate on AP-COV. This choice is also inﬂuenced by

the presence of the parameter k, which constrains the

sharing of local eigenvectors. In a broader context,

sharing eigenvectors poses risks of revealing member-

ship information and data, as discussed in Section 2.3.

2.3 Privacy Attacks Against PCA

This Section brieﬂy present two of the most popular

state-of-the-art privacy attacks against PCA-based ap-

proaches.

Membership Inference Attack(MIA) was ﬁrst

published in 2017 (Shokri et al., 2017). It is a pri-

vacy attack against Machine Learning models, with

the objective of determining the membership of a

record to the original training dataset. In the case

of MIA for PCA-based approaches, Zari et al.(Zari

et al., 2022) deﬁned a variant of MIA in which it is

assumed that the adversary intercepts certain princi-

pal components (eigenvectors) from PCA-transformed

data, which may contain sensitive information. The

adversary employs these intercepted eigenvectors to

calculate the reconstruction error for a given target

sample, representing the disparity between the orig-

inal and projected samples. The main insight is that

samples from the training set will show a lower re-

construction error compared to those outside the train-

ing set. This highlights the importance of protecting

eigenvectors in privacy-preserving scenarios to miti-

gate such membership inference risks.

Data Reconstruction Attack Recently, Kwatra et

al. (Kwatra and Torra, 2023) empirically proved that

in the context of PCA-based approaches, also a data

reconstruction attack is possible. The reconstruction

attack tries to approximate as closely as possible the

original data and to perform it requires the knowledge

of leaked eigenvectors. This attack generates syn-

thetic data, exploiting a Conditional Tabular Genera-

tive Adversarial Networks (CTGAN) (Xu et al., 2019)

and obtaining:

X = X

anonymized or synthesized

. At

this point, the efﬁcacy of the attack is assessed by

computing the reconstruction accuracy, which quanti-

ﬁes the proximity between the estimated data and the

original data. Kwatra et al. showed the reconstruc-

tion attack, and did not mention about the utility of

protected eigenvectors. Hence, in this work we also

do the utility analysis of the protected eigenvectors,

and aim to provide a complete picture for the util-

ity and privacy. In this work, we experiment with k-

anonymous (Samarati, 2001; Samarati and Sweeney,

1998; Sweeney, 2002) eigenvectors, where we com-

pute eigenvectors from k-anonymous data using Mon-

drian.

3 PRIVACY-PRESERVING

COMPUTATION OF PCA

In this paper we consider the FL setting similar to the

one outlined in AP-COV algorithm, where each client

participating to the federation, sends to the aggregator

the local eigenvectors and the server will aggregate

the local contribution to compute an approximation

of the hypothetical global covariance matrix. Given

the privacy issues discussed above, we propose a pre-

liminary study which analyzes the effect of applying a

mitigation strategy on the client data before the eigen-

vector computation. Our methodology, illustrated in

Figure 1, involves the use of Mondrian k-anonymity

transformation (LeFevre et al., 2006) and a synthetic

data generation by CTGAN at the client level.

3.1 Threat Model and Attack

Methodology

In our attack setting, the client generates anonymous

or synthetic data, one at a time. We denote the k-

anonymous data as D

anonymized

, and the synthetic data

as D

syn

. D

anonymized

can be created by choosing the

value of parameter k according to the privacy require-

ments of client, and the synthetic data can be created

SECRYPT 2024 - 21st International Conference on Security and Cryptography

852

using different percentages (10%, 30%, 50%, 70%,

100%) of samples from the original data D, using

CTGAN. The client then computes the eigenvectors

of the synthetic data or the anonymized data, and

sends these to a trusted party, which is an aggrega-

tor in FL. We assume that the attacker A intercepts

some or all of the eigenvectors computed by eaves-

dropping on the communication channel. To do a suc-

cessful data reconstruction attack, the attacker needs

two things, eigenvectors, and the knowledge about the

distribution of the data. For the distribution of the

data, we assume that the attacker has access either to

the synthetic data, which is created using some per-

centage of samples from the original data or to the

k-anonymous data, which is a noisy version of the

original data. Both, k-anonymous, and synthetic data

have reduced re-identiﬁcation risks, as compared to

the original data, which means they are not personal

data anymore. So, GDPR does not applies. Hence,

the attacker can utilize them to conduct the attack.

In Table 1, we list the possible combinations of the

assumptions for the attacker to conduct a data recon-

struction attack. E.g., the attacker may have access to

the original eigenvectors, and the synthetic data cre-

ated using 10% of the samples from the original data,

where those 10% samples can be selected either using

random sampling or stratiﬁed sampling.

After conducting the attack, it is needed to mea-

sure the efﬁcacy of the attack to quantify the privacy

breach. We evaluate the success of our attack as fol-

lows.

Deﬁnition 1. Suppose R is the reconstructed data,

which is the estimator for the original data O. Let δ

be a parameter for reconstruction error, which quan-

tiﬁes the acceptable deviation. The reconstruction ac-

curacy, R.A. is deﬁned as follows:

R.A. =

i, j

: |O

i, j

− R

i, j

|, i = 1, ...n, j = 1, ..., d ≤ δ

n × d

(2)

where # means count, and n is the number of

records. Hence, R.A. expresses the percentage of re-

constructed entries for which the relative errors are

within δ.

4 DATA AND EXPERIMENTAL

SETTINGS

We conducted experiments on CALIFORNIA-

HOUSING, and COD-RNA datasets. The

CALIFORNIA-HOUSING dataset has 20,640 records,

and the COD-RNA dataset has 59,535 records. Both

Table 1: Cases for the privacy evaluation concerning data

reconstruction attack. Here, O.D. stands for Original Distri-

bution. S.S. stands for Stratiﬁed Sampling, and R.S. stands

for Random Sampling.

Eigenvectors (EVs) Data Distribution Infor-

mation

Original EVs Synthetic data from com-

plete O.D.

Synthetic data from 10%

O.D. via R.S.

Synthetic data from 10%

O.D. via S.S.

Synthetic EVs Synthetic data from the

complete O.D.

Synthetic from 10% O.D.

via R.S.

Synthetic from 10% of

O.D. via S.S.

k-anonymous EVs Used all the k-anonymous

data

Synthetic data from com-

plete k-anonymous data

Synthetic data from 10%

k-anonymous data (via

R.S. and S.S.)

datasets have 9 features. The CALIFORNIA-HOUSING

dataset is for a regression task, where the goal is to

estimate the housing prices, based on features such

as income, housing occupancy, and geographical lo-

cation attributes across various districts in California.

These features contain sensitive information. Hence,

privacy incorporation is important for data analysing.

The COD-RNA dataset is for a classiﬁcation task.

For the utility analysis of CALIFORNIA-HOUSING

dataset, we use R

, also known as Coefﬁcient of

Determination. R

determines the proportion of

variability in the dependent variable that can be

explained by the independent variable(s) included

in the model. Mathematically, R

is expressed as

follows.

= 1 −

∑

i=1

− ˆy

)

∑

i=1

− ¯y

)

(3)

Both, CALIFORNIA-HOUSING and COD-RNA are nu-

merical datasets. Therefore, as part of the pre-

processing, we implement standardization using the

scikit-learn library in Python. In our evaluation,

we utilize a 10-fold cross validation, and report mean

± standard deviation for R

in Table 2.

5 RESULTS AND DISCUSSION

We explain our main experimental ﬁndings as fol-

lows.

Balancing Act: Navigating the Privacy-Utility Spectrum in Principal Component Analysis

853

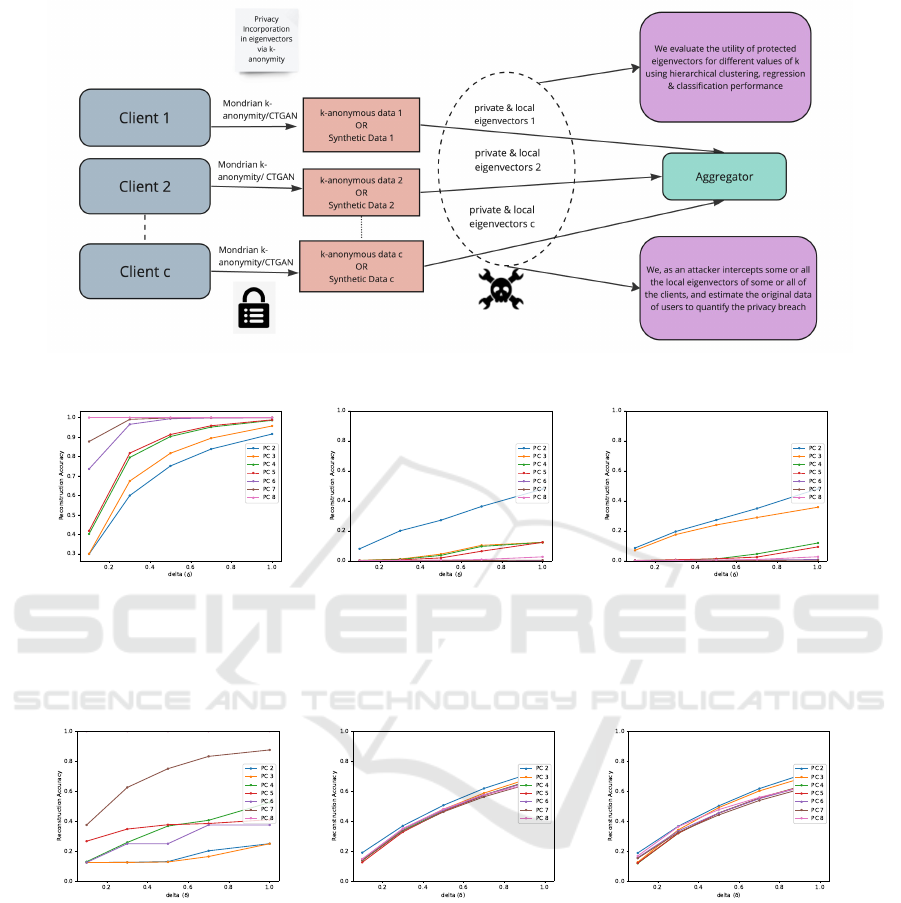
Figure 1: Our Methodology.

(a) R.A. in general PCA

where we reach close to the

original data on increasing

no. of PCs.

(b) R.A. b/w original and

reconstructed data when

20-anonymous eigenvectors

and 20-anonymous data is

known.

reconstructed data when

10-anonymous eigenvectors

and 10% data is randomly

drawn from 10-anonymous

data is known.

(d) R.A. b/w anonymous

and reconstructed data when

eigenvectors computed from

the original data, and syn-

thetic data generated using

10% samples from the orig-

inal data via random sam-

pling.

(e) R.A. b/w original and

reconstructed data when

eigenvectors computed

from the original data, and

synthetic data generated

using 10% samples from the

original data via stratiﬁed

sampling.

(f) R.A. b/w original and

reconstructed data when

eigenvectors computed

from the original data, and

synthetic data generated

using 10% samples from

the original data via random

sampling.

Figure 2: Reconstruction Accuracy (R.A.) for California housing dataset with varied assumptions by the attacker.

• From the results in Table 2, we found out that

as we increase the number of principal compo-

nents, utility improves, and as the value of k in-

creases upto 20, the utility is almost constant,

which shows that the utility of data can be pre-

served while enhancing data privacy. This is be-

cause the machine learning models aim to avoid

overﬁtting.

• We show reconstruction attack results in the

Figure 2, which shows that the reconstructed

SECRYPT 2024 - 21st International Conference on Security and Cryptography

854

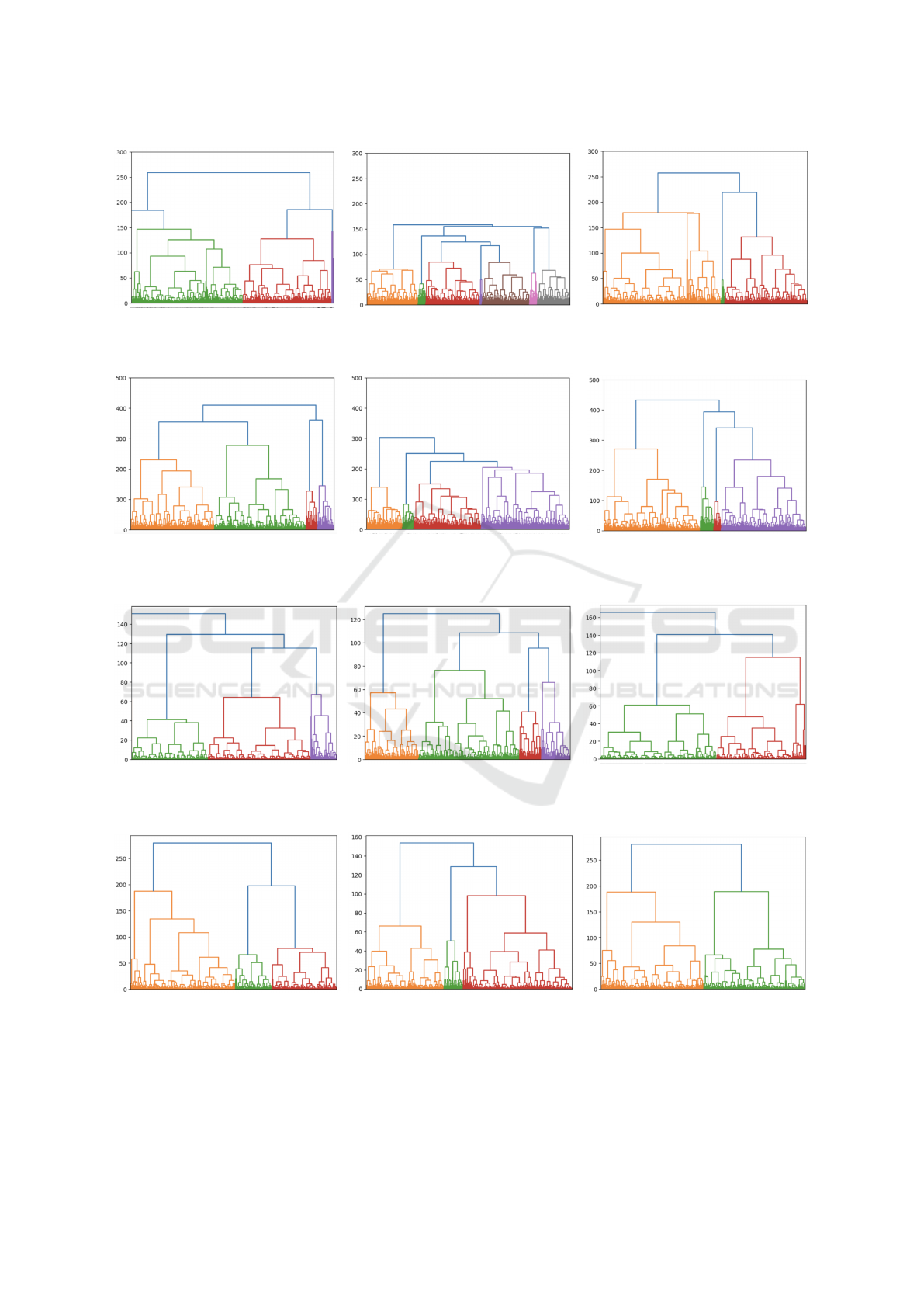
(a) Original data. (b) Synthetic data created using CTGAN. (c) 30-anonymous data.

Figure 3: Dendrograms showing the HIERARCHICAL CLUSTERING for the CALIFORNIA-HOUSING data.

(a) Original data. (b) Synthetic data. (c) 30-anonymous data.

Figure 4: Dendrograms showing the HIERARCHICAL CLUSTERING for the cod-rna data.

(a) Original Top 3 projection scores. (b) Synthetic Top 3 projection scores. (c) 10-anonymous Top 3 projection scores.

Figure 5: HIERARCHICAL CLUSTERING for California-housing’s Top 3 projection scores.

(a) Original Top-3 projection scores. (b) Synthetic Top-3 projection scores. (c) 10-anonymous Top-3 projection scores.

Figure 6: Dendrograms showing results of HIERARCHICAL CLUSTERING for cod-rna’s Top 3 projection scores.

Balancing Act: Navigating the Privacy-Utility Spectrum in Principal Component Analysis

855

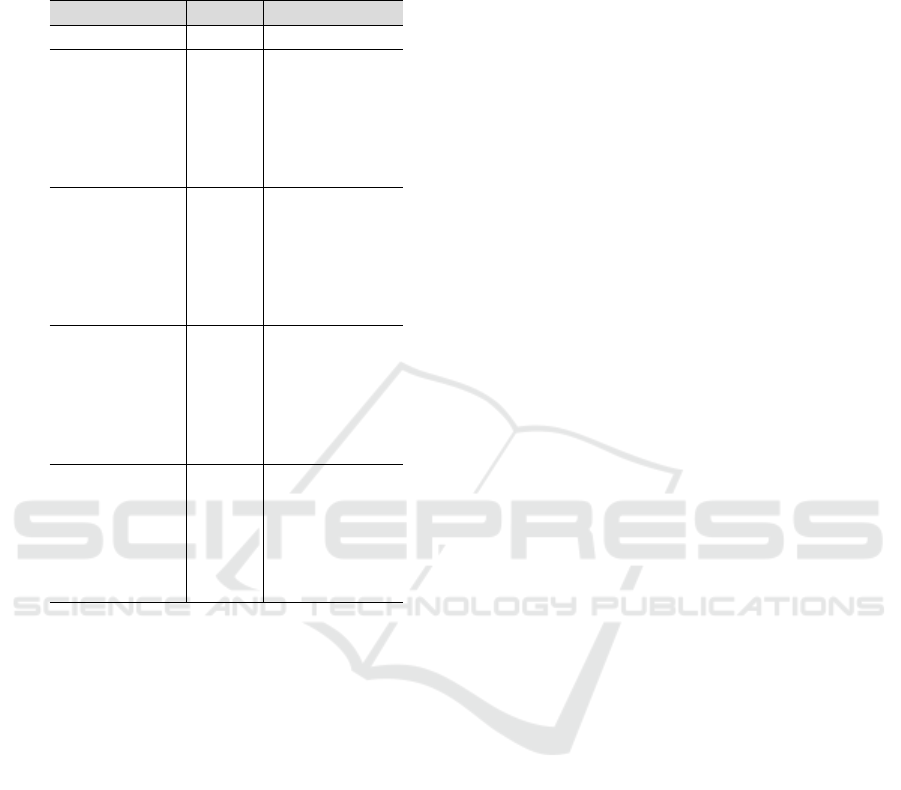
Table 2: Utility analysis via regression task on

CALIFORNIA-HOUSING dataset. O-PCA refers to Original

PCA, S-PCA is Synthetic PCA and A-PCA is Anonymized PCA

with different values for k.

PCA # PCs R

Baseline all 0.781 ± 0.019

O-PCA 3 0.148 ± 0.034

S-PCA 3 0.134 ± 0.030

A-PCA (k=5) 3 0.135 ± 0.030

A-PCA (k=10) 3 0.147 ± 0.035

A-PCA (k=15) 3 0.134 ± 0.030

A-PCA (k=20) 3 0.134 ± 0.030

O-PCA 4 0.455 ± 0.038

S-PCA 4 0.445 ± 0.034

A-PCA (k=5) 4 0.444 ± 0.034

A-PCA (k=10) 4 0.454 ± 0.038

A-PCA (k=15) 4 0.445 ± 0.034

A-PCA (k=20) 4 0.445 ± 0.035

O-PCA 5 0.631 ± 0.034

S-PCA 5 0.624 ± 0.029

A-PCA (k=5) 5 0.624 ± 0.029

A-PCA (k=10) 5 0.629 ± 0.035

A-PCA (k=15) 5 0.624 ± 0.029

A-PCA (k=20) 5 0.623 ± 0.029

O-PCA 6 0.697 ± 0.029

S-PCA 6 0.689 ± 0.003

A-PCA (k=5) 6 0.690 ± 0.032

A-PCA (k=10) 6 0.696 ± 0.030

A-PCA (k=15) 6 0.689 ± 0.032

A-PCA (k=20) 6 0.689 ± 0.032

dataset is farthest from the original dataset in

the case when eigenvectors are computed on the

k-anonymous data in comparison with the case

when eigenvectors are computed on the synthetic

dataset. Using the anonymous eigenvectors, we

can reach closer to the anonymous data, but not

to the original data, which means that anonymous

eigenvectors provide protection concerning the re-

construction attack. Hence, we observe that the

efﬁcacy of attacker in inferring the data of users

in CALIFORNIA-HOUSING dataset declines, if we

incorporate privacy protection mechanism in our

data before the data analysis.

• We show the dendrograms obtained after em-

ploying HIERARCHICAL CLUSTERING on the

CALIFORNIA-HOUSING, and COD-RNA datasets

in Figure 3. The dendrograms of the original data,

and the anonymous data are quite similar for both

the datasets. For the synthetic data, the dendro-

grams look quite different, in the sense that the Y-

axis in ﬁgures, which shows the height at which

the clusters are merged is declined in synthetic

data, which shows that the clustering information

is somewhat lost in the synthetic datasets. In k-

anonymous datasets, as the value of k increases,

the clusters become compact.

• We show the dendrograms for the original and

protected projection scores in Figures 5, and 6.

We got the similar trends as we got when we ap-

plied HIERARCHICAL CLUSTERING on the origi-

nal, anonymous, and the synthetic datasets. The

reason for the different clustering results for the

synthetic datasets/eigenvectors from the original

datasets/eigenvectors is that the synthetic data

generation algorithm, which is CTGAN in our case

reproduce data points within a ﬁxed range, which

leads to loss of information concerning the actual

number of clusters.

• We found out that datasets, and eigenvectors pro-

tected using k-anonymity produces more accu-

rate clustering results in comparison with the syn-

thetic datasets created using CTGAN. For syn-

thetic datasets, the size of clusters becomes com-

pact in comparison with the original, and the

k-anonymized dataset. Hence, generative algo-

rithms can be utilised, if we intend to protect the

outliers in the data. But, it should be avoided if we

want better clustering results, especially for criti-

cal applications.

• In conclusion, eigenvectors computed from k-

anonymous data provide better privacy-utility

tradeoff in comparison with the eigenvectors com-

puted from synthetic data, and eigenvectors with

no privacy, in our attack, and utility analysis setup.

6 CONCLUSION AND FUTURE

DIRECTIONS

This paper focuses on FL-PCA algorithms, in which

each client participating in the FL framework shares

the information of eigenvectors with the central ag-

gregator, which can leak the data of clients. Hence,

we explore Privacy Preserving Principal Component

Analysis (PP-PCA). We propose that each client

creates a protected database using k-anonymity, and

generative networks, one at a time. This protected

database is basically k-anonymous, and synthetic

database, respectively. On the protected database,

each client computes private eigenvectors. We eval-

uate the utility and privacy of private eigenvectors

against their original counterparts. We employed re-

gression, classiﬁcation and HIERARCHICAL CLUS-

TERING for utility assessment, demonstrating strong

performance of anonymized data and eigenvectors.

Privacy evaluation involves a data reconstruction at-

SECRYPT 2024 - 21st International Conference on Security and Cryptography

856

tack on PCA, showcasing the attacker’s success in re-

constructing the original databases. Our results reveal

that anonymized eigenvectors maintain good utility

compared to the original ones. Differential Privacy

(DP) is also utilised in FL-PCA (Grammenos et al.,

2020). In future, we will also consider DP to pro-

tect eigenvectors. As, in this work, we quantify in-

dividual privacy leakage arising from sharing of local

eigenvectors, which were derived from the data of in-

dividual clients. So, our future investigation will ex-

tend to privacy leakage post-aggregation. In the case,

when global eigenvectors are compromised, there is

a potential risk of the attacker to deduce the records

of speciﬁc individuals, particularly those who are in-

ﬂuencing the aggregation step predominantly. Hence,

our future research aims to focus on the performance

of PP-PCA when aggregated or global eigenvectors are

compromised in a FL scenario.

ACKNOWLEDGEMENT

This study was partially funded by the Wallenberg AI;

Autonomous Systems and Software Program (WASP)

funded by the Knut and Alice Wallenberg Foun-

dation; the computations were enabled by the su-

percomputing resource Berzelius provided by Na-

tional Supercomputer Centre at Link

oping University

and the Knut and Alice Wallenberg foundation; the

EU NextGenerationEU programme under the funding

schemes PNRR-PE-AI FAIR (Future Artiﬁcial Intel-

ligence Research); PNRR-“SoBigData.it - Strength-

ening the Italian RI for Social Mining and Big Data

Analytics” - Prot. IR0000013; the EU – Horizon 2020

Program under the scheme “INFRAIA-01-2018-2019

– Integrating Activities for Advanced Communities”

(G.A. n.871042) “SoBigData++: European Integrated

Infrastructure for Social Mining and Big Data Analyt-

ics” (http://www.sobigdata.eu).

REFERENCES

Abdi, H. and Williams, L. J. (2010). Principal component

analysis. Wiley interdisciplinary reviews: computa-

tional statistics, 2(4):433–459.

Briguglio, W., Yousef, W. A., Traor

e, I., and Mamun, M.

(2023). Federated supervised principal component

analysis. IEEE Transactions on Information Forensics

and Security.

Grammenos, A., Mendoza Smith, R., Crowcroft, J., and

Mascolo, C. (2020). Federated principal component

analysis. Advances in neural information processing

systems, 33:6453–6464.

Hartebrodt, A. and R

ottger, R. (2022). Federated hori-

zontally partitioned principal component analysis for

biomedical applications. Bioinformatics Advances,

2(1):vbac026.

Kwatra, S. and Torra, V. (2023). Data reconstruction at-

tack against principal component analysis. In Interna-

tional Symposium on Security and Privacy in Social

Networks and Big Data, pages 79–92. Springer.

LeFevre, K., DeWitt, D. J., and Ramakrishnan, R.

(2006). Mondrian multidimensional k-anonymity. In

22nd International conference on data engineering

(ICDE’06), pages 25–25. IEEE.

Liang, Y., Balcan, M.-F. F., Kanchanapally, V., and

Woodruff, D. (2014). Improved distributed principal

component analysis. Advances in neural information

processing systems, 27.

McMahan, B., Moore, E., Ramage, D., Hampson, S., and

y Arcas, B. A. (2017). Communication-efﬁcient learn-

ing of deep networks from decentralized data. In Ar-

tiﬁcial intelligence and statistics, pages 1273–1282.

PMLR.

Pathak, M. A. and Raj, B. (2011). Efﬁcient protocols for

principal eigenvector computation over private data.

Trans. Data Priv., 4(3):129–146.

Samarati, P. (2001). Protecting respondents identities in mi-

crodata release. IEEE transactions on Knowledge and

Data Engineering, 13(6):1010–1027.

Samarati, P. and Sweeney, L. (1998). Protecting privacy

when disclosing information: k-anonymity and its en-

forcement through generalization and suppression.

Shokri, R., Stronati, M., Song, C., and Shmatikov, V.

(2017). Membership inference attacks against ma-

chine learning models. In 2017 IEEE symposium on

security and privacy (SP), pages 3–18. IEEE.

Sweeney, L. (2002). k-anonymity: A model for protecting

privacy. International journal of uncertainty, fuzziness

and knowledge-based systems, 10(05):557–570.

Voigt, P. and Von dem Bussche, A. (2017). The eu gen-

eral data protection regulation (gdpr). A Practical

Guide, 1st Ed., Cham: Springer International Pub-

lishing, 10(3152676):10–5555.

Xu, L., Skoularidou, M., Cuesta-Infante, A., and Veera-

machaneni, K. (2019). Modeling tabular data using

conditional gan. Advances in Neural Information Pro-

cessing Systems, 32.

Zari, O., Parra-Arnau, J.,

Unsal, A., Strufe, T., and

Onen,

M. (2022). Membership inference attack against prin-

cipal component analysis. In Privacy in Statisti-

cal Databases: International Conference, PSD 2022,

Paris, France, September 21–23, 2022, Proceedings,

pages 269–282. Springer.

Zhu, L., Liu, Z., and Han, S. (2019). Deep leakage from

gradients. Advances in neural information processing

systems, 32.

Balancing Act: Navigating the Privacy-Utility Spectrum in Principal Component Analysis

857