Virtually Free Randomisations of NTT in RLWE Cryptosystem to

Counteract Side Channel Attack Based on Belief Propagation

Christophe Negre

and Mbaye Ngom

1,2

DALI-LIRMM, Perpignan, France

eShard, Pessac, France

Keywords:

Side Channel Attack, Belief Propagation, Number Theoretic Transform, Randomisation, Post-Quantum

Cryptosystems.

Abstract:

At CHES 2017, Primas, Pessl and Mangard presented an attack on RLWE cryptosystem based on Belief Prop-

agation. The attack applies on the Number Theoretic Transform (NTT) used to decipher a message. It gathers

power consumption leakage of the multiplication by roots of unity in the NTT and then applies Belief Propa-

gation to circulate the information of all leakage nodes, until the combined leakage reveal most of the output

coefﬁcients of the NTT. In this paper we present some randomisations which either induce in NTT some ran-

dom mask on values or randomly rearrange the sequence of operations. We evaluate the level of randomisation

provided by the proposed counter-measures and also the effect on the processed values in the NTT. We apply

Belief Propagation on the proposed randomised NTT and we study how these randomisations affect the attack.

Finally we point out that a set of three combined strategies provide a high level of randomisation and a good

protection against Belief Propagation attack of Primas et al.

1 INTRODUCTION

The progress of quantum computers combined with

Shor’s algorithm (Shor, 1999) is threatening cryp-

tosystems like RSA, ECC. NIST launched a compe-

tition in 2017

for selecting a set of post-quantum

cryptosystems. The competition is now ﬁnished, an-

other round of competition was launch for additional

digital signature scheme. There were many candi-

dates based on Ring/Module Learning With Error

(RLWE/MLWE) problem for key establishment and

digital signature and some were selected. The theo-

retical security of these post-quantum cryptosystems

were intensively analysed during these past years. Se-

curity and protection against side channel analysis

might be pursued.

One component in RLWE computation is the

Number Theoretic Transform (NTT) which evaluates

a polynomial at the roots of unity. This is used for

efﬁcient multiplication in the ring Z

[X]/(X

+ 1) of

RLWE cryptosystems. In 2017 Primas, Pessl and

Mangard (Primas et al., 2017) proposed an attack on

NTT based on Belief Propagation (Pearl, 1982). Their

https://csrc.nist.gov/projects/post-quantum-

cryptography

attack used leakage in power consumption or electro-

magnetic emanation in the computation of the NTT.

They used Belief Propagation to gather scattered in-

formation due to leakage in the multiplication by the

roots of unity, in order to recover most of the output

coefﬁcients of the NTT. This attack only requires a

single trace and is an important threat on RLWE cryp-

tosystem on embedded devices. The purpose of this

paper is to propose and study counter-measures pre-

venting this attack.

Contributions. We study a set of randomisations of

NTT computation to counteract Primas et al.’s at-

tack. We focus on virtually free randomisation, which

means that the studied randomisation does not imply

additional operations in the ring Z

[X]/(X

+ 1). We

study the following approaches: shufﬂing of opera-

tions at each stage of the NTT, randomisation of the

roots of unity, randomisation by random multiplica-

tive masks, randomisation of the reduction modulo q,

and random choice of the butterﬂy formula in NTT.

For all these considered randomisations we study the

effect on the data processed in NTT and provide the

level of randomisation. We also simulate the Belief

Propagation attack on randomised NTT to evaluate

the effect of the randomisation on this attack.

866

Negre, C. and Ngom, M.

Virtually Free Randomisations of NTT in RLWE Cryptosystem to Counteract Side Channel Attack Based on Belief Propagation.

DOI: 10.5220/0012857500003767

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 866-875

ISBN: 978-989-758-709-2; ISSN: 2184-7711

Organisation of the Paper. In Section 2 we review

some background on RLWE cryptosystem and algo-

rithms used for NTT. In Section 3 we review Belief

Propagation and the attack of Primas et al. (Primas

et al., 2017). In Section 4 we present a set of ran-

domisation of NTT to counteract Primas et al.’s at-

tack, we analyse the impact of the randomisation on

the processed value in NTT. In Section 5 we provide

some simulation results of Belief Propagation attack

applied on our proposed randomised NTT. Finally, in

Section 6, we give some concluding remarks.

2 RLWE CRYPTOSYSTEM AND

NUMBER THEORETIC

TRANSFORM (NTT)

In this section we review a cryptosystem presented

in (Lyubashevsky et al., 2010) based on the Ring

Learning with Error (RLWE) problem. This cryp-

tosystem will be our reference encryption scheme to

analyse the proposed counter-measure on this type of

cryptosystem. We also review the algorithm used for

the NTT computation involved in the ring multiplica-

tion of the ciphering/deciphering operations.

2.1 RLWE Cryptosystem

In (Lyubashevsky et al., 2010) Lyubashevsky et al.

present a public-key encryption scheme based on

RLWE. Let us ﬁrst recall the RLWE problem. We

consider a ring R

= Z

[X]/(X

+ 1) with q a prime

integer, the coefﬁcients of an element in R

are taken

in {−⌊q/2⌋,... ,⌊q/2⌋}. We also consider two ran-

dom distributions on R

• a

←− R

the uniform distribution.

• e

←− R

a distribution centered at 0 with small

coefﬁcients, e.g., a discrete Gaussian distribution

with a small standard deviation.

Then, the RLWE can be formulated as follows.

Deﬁnition 1 (RLWE problem.). We randomly set

←− R

and s, e

←− R

. The RLWE problem consists

in computing s from:

a and b = a ×s + e

It was shown in (Regev, 2009) that the LWE prob-

lem is as hard as ﬁnding short vector/basis in a lattice

(the RLWE is also assumed to be difﬁcult but to the

best of our knowledge its hardness is unknown).

The public-key encryption scheme of (Lyuba-

shevsky et al., 2010) based on RLWE problem works

as follows: the plaintext is a bit string m of n bits

,. .. , m

n−1

, and it is transformed into a polynomial

m ∈ R

with coefﬁcients m

= (−1)

×⌊q/4⌋.

• Key Generation:

– Private : r

←− R

– Public : a

←− R

and b = r

−a ·r

• Encryption: Plaintext m ∈ {0,1}

is ﬁrst en-

coded as m ∈ R

, and then encrypted as

) = (a ·e

+ e

,b ·e

+ e

+ m)

with e

←− R

• Decryption:

m = Decode(c

·r

+ c

)

where Decode rounds each coefﬁcient towards

±⌊q/4⌋ and then deduces the bits m

In the recent NIST competition

for Post Quantum

Cryptography standards a number of the candidates

were variants of the above cryptosystem based on

RLWE. So the discussion in the remaining of the pa-

per could be applied with only a few changes to these

cryptosystems. Speciﬁcally, the chosen standard Ky-

ber (Bos et al., 2018) for key-encapsulation can bene-

ﬁt from the proposed counter-measure against BP at-

tack.

2.2 Number Theoretic Transform

(NTT)

The main operation in RLWE encryption and decryp-

tion is the multiplication in R

. The prime q is gen-

erally chosen in order to have a primitive 2n-th root

ω of unity in R

. In this case, X

+ 1 splits entirely

and the multiplication in R

can be transformed into

a point-wise multiplication through the Chinese re-

mainder theorem (CRT) isomorphism

[X]/(X

+ 1)

∼

∏

n−1

i=0

[X]/(X −ω

2i+1

)

f 7→ (f(ω

2i+1

))

i=0,...,n−1

where we used the following on the right side:

f(X) mod (X −ω

2i+1

) = f(ω

2i+1

). Then, applying,

the above isomorphism to f(X) =

∑

n−1

i=0

consists

in computing for i = 0, .. .,n −1:

f(ω

2i+1

) =

n−1

∑

j=0

(2i+1) j

n−1

∑

j=0

( f

)(ω

)

. (1)

https://csrc.nist.gov/projects/post-quantum-

cryptography

Virtually Free Randomisations of NTT in RLWE Cryptosystem to Counteract Side Channel Attack Based on Belief Propagation

867

The NTT

is the multi-evaluation of a polynomial at

the n-th roots of unity. This means that the right side

of equation (1) is the NTT of f

′

(X) =

∑

n−1

j=0

( f

in the n-th root of unity ω

for i = 0, .. .,n −1. The

NTT

of a degree n −1 polynomial can be computed

recursively with O(nlog(n)) operations modulo q, as

shown in the following subsections.

2.2.1 NTT with Odd-Even Splitting

We brieﬂy recall the approach of Cooley-Tukey (Coo-

ley and Tukey, 1965) for the computation of NTT.

This approach uses an even-odd splitting of the poly-

nomial f(X):

f(X) =

n/2−1

∑

k=0

| {z }

)

+X ×

n/2−1

∑

i=0

2i+1

| {z }

)

If we evaluate the above equation in ω

for j =

0,. .. , n −1 we will get the following equations. This

shows that NT T

of f is deduced from NT T

n/2

) and

NT T

n/2

) by the following butterﬂy operations:

f(ω

) = f

(ω

2 j

) + ω

(ω

2 j

)

f(ω

n/2+ j

) = f

(ω

2 j

) −ω

(ω

2 j

)

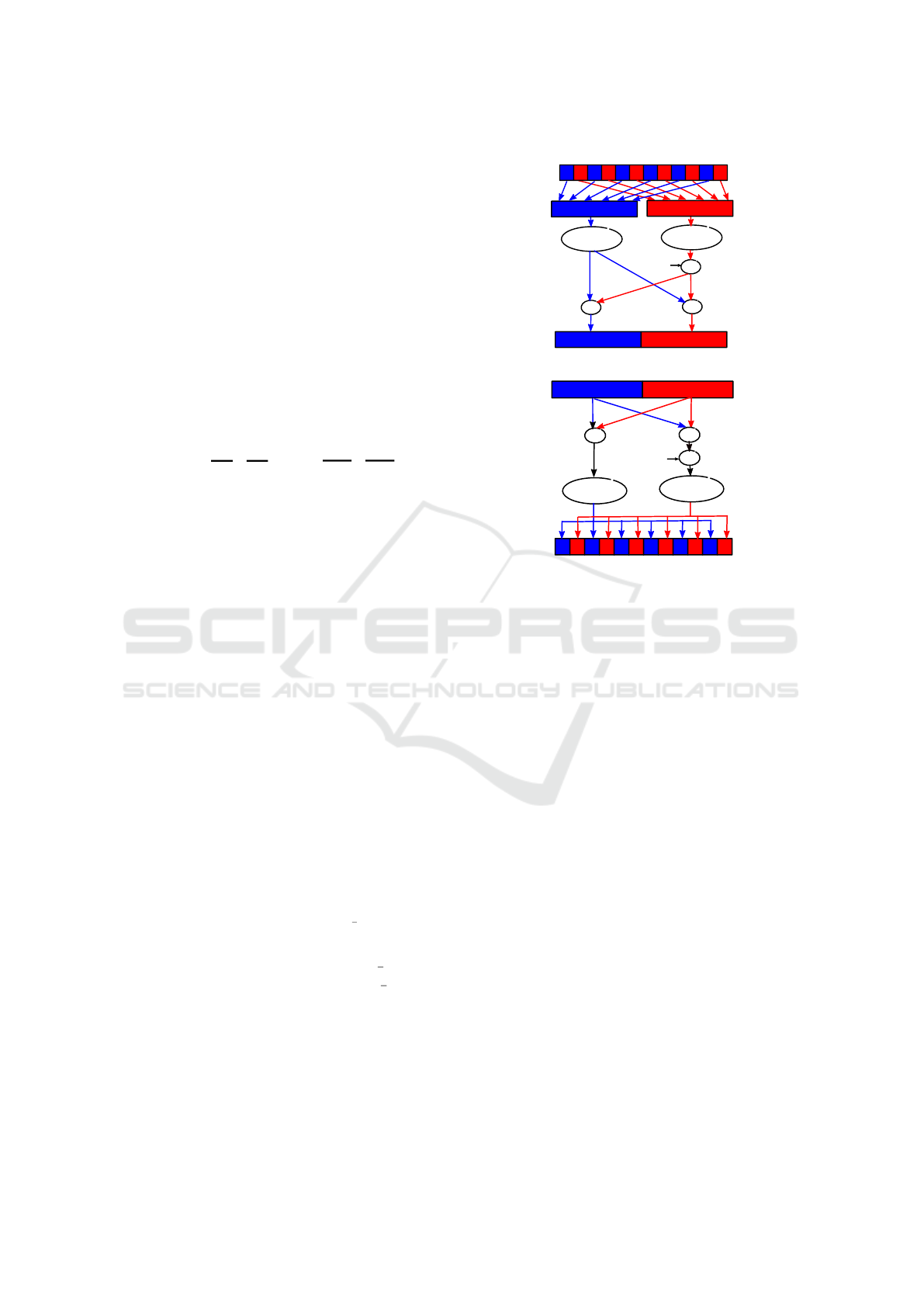
Figure 1a shows the sequence of operations (reorder-

ing, recursion, multiplication and addition) involved

in the Cooley-Tukey NTT computation. We can no-

tice that in this case the multiplication is always done

ahead of an addition and a subtraction.

2.2.2 NTT with High-Low Splitting

We recall Gentleman-Sande’s approach for the NTT

computation. Let us consider the two following poly-

nomials

′

(X) =

∑

n/2−1

i=0

( f

+ f

n/2+i

′′

(X) =

∑

n/2−1

i=0

( f

− f

n/2+i

)ω

We obtain the NTT

coefﬁcients of f for even powers

(resp. odd powers) of ω from the NTT

of f

′

(resp. of

′′

) as follows:

f(ω

2 j

) = f

′

(ω

2 j

) for j = 0,. ..,

−1

f(ω

2 j+1

) = f

′′

(ω

2 j

) for j = 0,. ..,

−1

The diagram shown in Fig. 1b provides the sequence

of operations (High-Low splitting, multiplication, ad-

dition/subtraction, recursion and reordering) with the

High-Low splitting approach for NTT.

Organisation of the NTT Operations. In the sequel we

will randomise the computations done in the NTT, so

add

NTT n/2

sub

NTT n/2

Recursion

mult

Odd-even splitting

ω,...,ω

n/2-1

(a) Odd-Even splitting

add

NTT n/2

sub

Recursion

mult

NTT n/2

Recursion

ω,...,ω

n/2-1

High Low splitting

(b) High-Low splitting

Figure 1: NTT recursions.

to clearly explain how these randomisations are done

we need to clearly established the sequence of opera-

tions done in an NTT. The operations at each level are

as follows:

• In level 0. We have one group of butterﬂy opera-

tions on the n input coefﬁcients f

• In level 1. We have two groups of butterﬂy op-

erations: one on the coefﬁcients 0,. .., n/2 and a

second on the coefﬁcients 0,. .., n/2.

• In level 2. we have four groups of butterﬂy opera-

tions, each of size n/4.

• etc.

We provide in Fig. 2 an NTT with 2 recursion levels

of the High-Low splitting approach.

3 BELIEF PROPAGATION ON

NTT

In (Primas et al., 2017) Primas, Pessl and Mangard

proposed an attack on NTT which uses side chan-

nel leakage of multiplication by the root of unity

and apply belief propagation (Pearl, 1982) to de-

duce most of the coefﬁcients of the output polynomial

NT T (f). This attack is an extension of the SASCA

attack (Veyrat-Charvillon et al., 2014) on AES to the

SECRYPT 2024 - 21st International Conference on Security and Cryptography

868

Add

Sub

Mul

Add

Sub

Mul

level 0

level 1

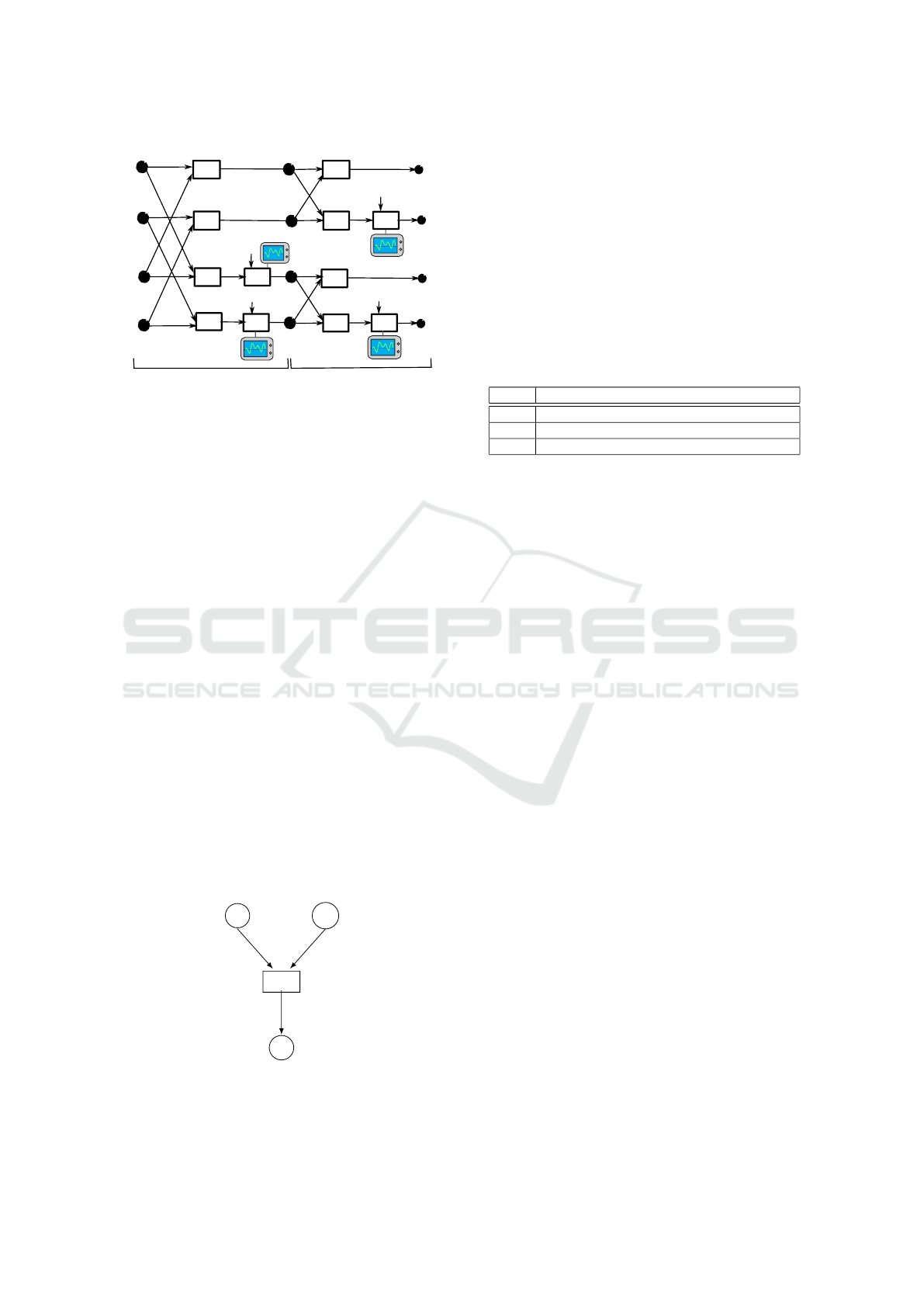
Figure 2: Leakage in NTT

computation.

NTT computation. We brieﬂy review the principle of

this attack and give some background on belief prop-

agation.

The authors in (Primas et al., 2017) use a leakage

in the multiplication by ω

in the NTT in order to get

a likelihood estimation of the value x ∈ Z

processed

in this multiplication. Figure 2 shows an example of

leakage in NTT

. This likelihood estimation can be

obtained by constructing a template of the leakage of

a multiplication by a prescribed root of unity ω

The information provided by all the likelihood es-

timation at each multiplication of the NTT does not

give likelihood estimation for all other values pro-

cessed in the NTT. Indeed, some temporary values in

the NTT are not directly involved in a multiplication

with ω

, so such values remain unknown. The authors

in (Primas et al., 2017) propose to use the belief prop-

agation algorithm (BP) (Pearl, 1982) to propagate the

scattered information throughout the NTT computa-

tions, in order to deduce the missing unknown values.

Let us sketch the idea of belief propagation on a

simple example. We consider the addition z = x + y

mod q of two values x, y ∈ Z

. Let us denote P(x)

(resp. P(y)) as the probability (i.e. likelihood estima-

tion) of the value x (resp. y) input to an adder (Fig. 3).

Add

P(x) P(y)

P(z)

Figure 3: Probability propagation on an addition.

We can propagate these probabilities, to get the

probability P(z) of the output z = x + y as

P(z) =

∑

x+y mod q=z

P(x)P(y) (2)

Let us illustrate this fact with a small example: we

assume that q = 3 and that the probabilities of x and

y are the ones shown in the table below. With these

probabilities we know with a high probability that x =

−1 and y = 0. Then propagating the probability to z

with the above formula leads to the probability of z

shown in the table. And then we know that with high

probability z = −1.

Variable Probabilities

x P(−1) = 0.9, P(0) = 0.05, P(1) = 0.05

y P(−1) = 0.03, P(0) = 0.91, P(1) = 0.06

z P(−1)

∼

0.82, P(0)

∼

0.101, P(1)

∼

0.075

Note that, in belief propagation, the probabilities are

also propagated as follows: from P(z) and P(y) to get

P(x) and from P(z) and P(x) to get P(y).

Belief Propagation on NTT. Due to lack of space we

just sketch the main process of the Belief Propagation

on the NTT of (Primas et al., 2017). For further de-

tails the reader may refer to (Primas et al., 2017). For

all intermediate variables of the NTT we set a proba-

bility for each variable: for variable resulting from a

multiplication with ω

this probability comes from a

template of the power consumption leakage, for other

variables the probality it set to the uniform distribu-

tion. The propagation is then done by applying prop-

agation formula similar to the one in (2) for each Add

and Sub operation of the NTT. We repeat this process

a number of times, and this effectively propagates the

information of the templates to unkown variables (the

one with uniform distribution). At the end, we suc-

ceed if in the output variables of the NTT the values

with the highest propbabilities a the correct correct

values.

4 RANDOMISATION OF NTT

In this section we ﬁrst review the randomisation pro-

posed in the literature. We then present a set of ran-

domisations and evaluate their effect to prevent Belief

Propagation attack on NTT.

State of the Art: Randomisation at the Input of

the NTT. In the literature we can ﬁnd the three fol-

lowing strategies for the randomisation of the input of

the NTT:

Virtually Free Randomisations of NTT in RLWE Cryptosystem to Counteract Side Channel Attack Based on Belief Propagation

869

Multiplicative

mask

′

= α ×f with a random α ∈ Z

′

= NT T (f

′

)

f = α

−1

′

Additive mask

random split f = f

′

+ f

′′

′

= NT T (f

′

)

′′

= NT T (f

′′

)

f =

′

′′

Shifting

′

= X

×f mod (X

−1)

′

= NT T (f

′

)

f = (ω

−ir

′

)

i=0,...,n−1

These three randomisations do not protect NTT

from the attack of Primas et al. based on Belief Prop-

agation. Indeed, the attack can be conducted on the

computation of NT T (f

′

) (and NT T (f

′′

) for the addi-

tive mask). Then to recover f we just have to add f

′

and f

′′

for the additive mask, or guess the random pa-

rameter (α or r) for the two other strategies and then

proceed to the computation of the secret key as in Pri-

mas et al. attack (Primas et al., 2017).

State of the Art: Randomisation of the Whole

NTT.

Ravi et al. in (Ravi et al., 2020) proposed the fol-

lowing shufﬂing and masking randomisation to pro-

tect the NTT from Primas et al.’s attack..

Shufﬂing. This approach is detailed in (Ravi et al.,

2020) but it is classical approach known for some

time. At each level butterﬂy operations are performed

in a random order, using a pseudo random generator

which randomly produces the pairs of (m,i) of each

butterﬂy iteration of level j: m gives the group of but-

terﬂies of level j and i the index of this butterﬂy in

this group.

This randomisation renders difﬁcult to associate

each portion of power trace of multiplication by a

root ω

of unity. But if the processed values are not

masked, it could then be easier for attacker to ﬁnd

the root ω

involved in the trace and/or link input and

output value from two NTT recursion levels. So this

randomisation might be associated with another one

to be effective.

Let us eavaluation the level of randomisation: in

the general case, at each level of NTT the are

! pos-

sible reordering of the pairs (m,i). This gives a level

of randomization of (

log

(n)

Multiplicative Mask. This approach masks each in-

termediate variable a with a multiplicative mask a

′

a ×ω

, with r

random, which is refreshed at each

butterﬂy operation. In (Ravi et al., 2020) the authors

propose several variants of this approach to reduce the

cost. But all these strategies have, at least, an increase

in cost of

log

(n) multiplications in the NTT.

4.1 Proposed Randomisations

We present in this section a set of virtually free

randomisation techniques of the NTT. Virtually free

means that they do not induce additionnal operations

in Z

. Shufﬂing approach is an example of such ap-

proach, and we will consider it in the sequel as a com-

plement of the proposed approaches.

4.1.1 Random Primitive Root of Unity

• Description of the randomisation. This approach

only applies to NTT with High-Low splitting. In

this approach, at any recursive level of the NTT,

and before each group of butterﬂy operations, we

randomly pick the primitive root of unity. Since

n = 2

the primitive roots are w

with e an odd

integer smaller than n. This results in the follow-

ing pseudo-code for the splitting part of the NTT

recursion.

←− {1,3, . .. ,n −3,n −1}

′

= ω

// High-Low splitting and butterﬂy operations

′

←

∑

n/2−1

i=0

( f

+ f

n/2+i

′′

←

∑

n/2−1

i=0

( f

− f

n/2+i

)ω

′i

This randomisation does not involve any addi-

tional cost in Z

, when all ω

are precomputed.

• Quality of the Randomisation. As we can see in

the pseudo code

– At each recursion level, only half of the coefﬁ-

cients are masked by the random root: n/2 in

level 1, 2 ×n/4 = n/2 in level 2, 4×n/8 = n/2

in level 3, and so on.

– The number of coefﬁcients masked at least

once during the whole NTT computation is

n/2 after the level 1, n/2 + n/4 after level 2,

n/2 + n/4 + n/8 after level 3 and so on. So at

the end we get n −2 masked coefﬁcients (the

last level does not involve multiplication).

• Level of Randomisation At the i-th level of the

NTT recursion, there are 2

group of butterﬂy op-

eration and for each group we pick ω

′

among

n/2

i+1

primitive roots of unity. Taking the prod-

uct for i = 0, ... ,t −2, we obtain the following

level of randomisation:

∏

t−2

i=0

t−1−i

)

∑

t−2

i=0

(t−1−i)2

n−1

SECRYPT 2024 - 21st International Conference on Security and Cryptography

870

4.1.2 Random Multiplicative Mask in Each

Multiplication with a Root of Unity

This randomisation applies only on NTT formula with

High-Low splitting.

• Description of the Randomisation. In this ap-

proach, before the High-Low butterﬂy operation

of a recursion level we pick a random r, and we

replace in the multiplication ω

by ω

×ω

= ω

i+r

The resulting randomised butterﬂy operations are

shown below :

←− {0,. . ., n −1}

// HL splitting and butterﬂy operation

′

←

∑

n/2−1

i=0

( f

+ f

n/2+i

′′

←

∑

n/2−1

i=0

( f

− f

n/2+i

)ω

i+r

Since all power of ω are all precomputed this does

not require any additional computation, the result-

ing coefﬁcients of NT T (f

′′

) are masked by ω

This approach is somehow a variation of the mul-

tiplicative mask randomisation of (Ravi et al.,

2020): we apply it on High-Low splitting formula

and with a and b sharing the same mask.

• Quality of Randomisation. The analysis is exactly

the same as in the randomisation of the primitive

root of unity. This means that at each NTT level

n/2 values are masked, and at the end of the NTT

n −2 coefﬁcients are masked at least once during

the computation.

This version of the randomisation with multiplica-

tive mask, is weaker than the one of Ravi et

al. (Ravi et al., 2020). Indeed in (Ravi et al.,

2020) all variables are masked during the whole

NTT computation. But, in counter part, the pro-

posed approach is more efﬁcient since it does not

involved any additional cost.

• Level of Randomisation. The analysis of the ran-

domisation shows that: at recursive level 1 we

pick one random r among n integers, at level 2

we pick two random r among n integers, at level

3 we pick four random r among n integers and so

on until level t −2. This results in the following

level of randomisation:

∏

t−2

i=0

(n)

−1

4.1.3 Random High-Low/Odd-Even Butterﬂy

Operations

We randomise the sequence of butterﬂy operations of

the NTT by randomly choosing the type of splitting

used (i.e. High/Low or Odd/Even) at each group of

each level.

• Description of the randomisation. In Section 2

we reviewed the two approaches for the recursive

computation of NTT: High-Low and Odd-Even

splitting. We also showed that the sequence of

operations (addition, subtraction, multiplication

and recursion) in these two approaches are differ-

ent. We propose to randomly choose High-Low

or Odd-Even splitting recursion for each group of

butterﬂy operations.

A sketch of the pseudo code of this approach is

shown below:

←− {0,1}

if r = 0 then

// Apply High-Low splitting butterﬂy and re-

cursion

...

else

// Apply Odd-Even splitting butterﬂy and re-

cursion

...

• Quality of Randomisation. Since the sequence of

operations is random, the intermediate values in

the NTT computation are also random and then

less predictable. But the sequence of operations

could leak out the type of splitting approach used

(i.e. the values of the random bits r): addi-

tion/subtraction followed by a multiplication cor-

responds to a High-Low splitting butterﬂy, while

multiplication followed by addition/subtraction

corresponds to an Odd-Even splitting butterﬂy.

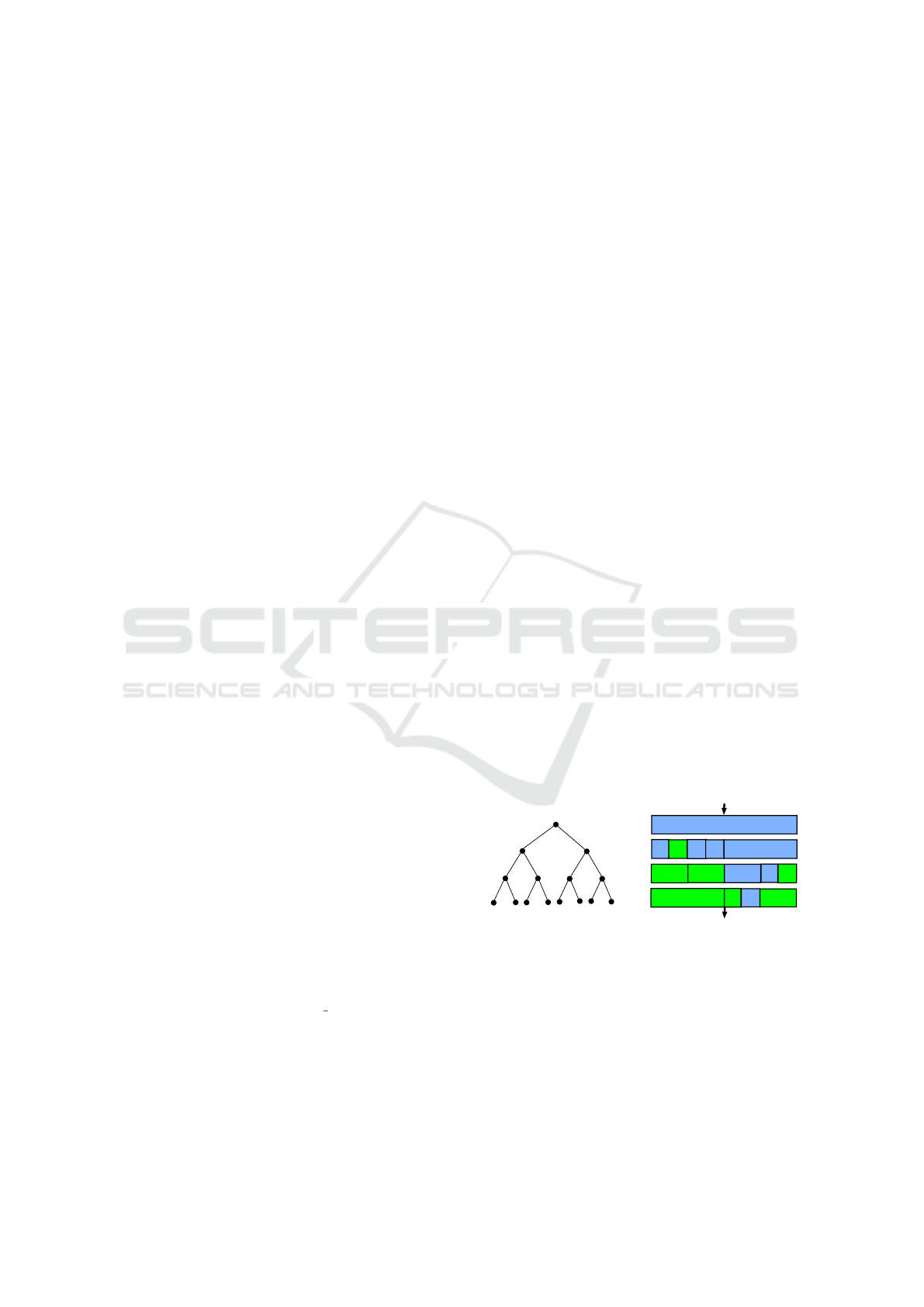
• Example. We set n = 16 and we pick the values of

r shown in Subﬁg 4a for each recursive level.

(a) Random bits

level 0

level 1

level 2

level 3

(b) Butterﬂy operations

Figure 4: Leakage in HLOE randomisation.

The diagram in Subﬁg 4b shows the organisation

of the operation for the above random bits r. We

can see that the block with OE butterﬂy operations

in level 1 is leaked out, as is the block with HL

butterﬂy operations in the level 3.

In order to prevent the leakage due to the sequence

of operations, we can restrict the bit r to be half of

Virtually Free Randomisations of NTT in RLWE Cryptosystem to Counteract Side Channel Attack Based on Belief Propagation

871

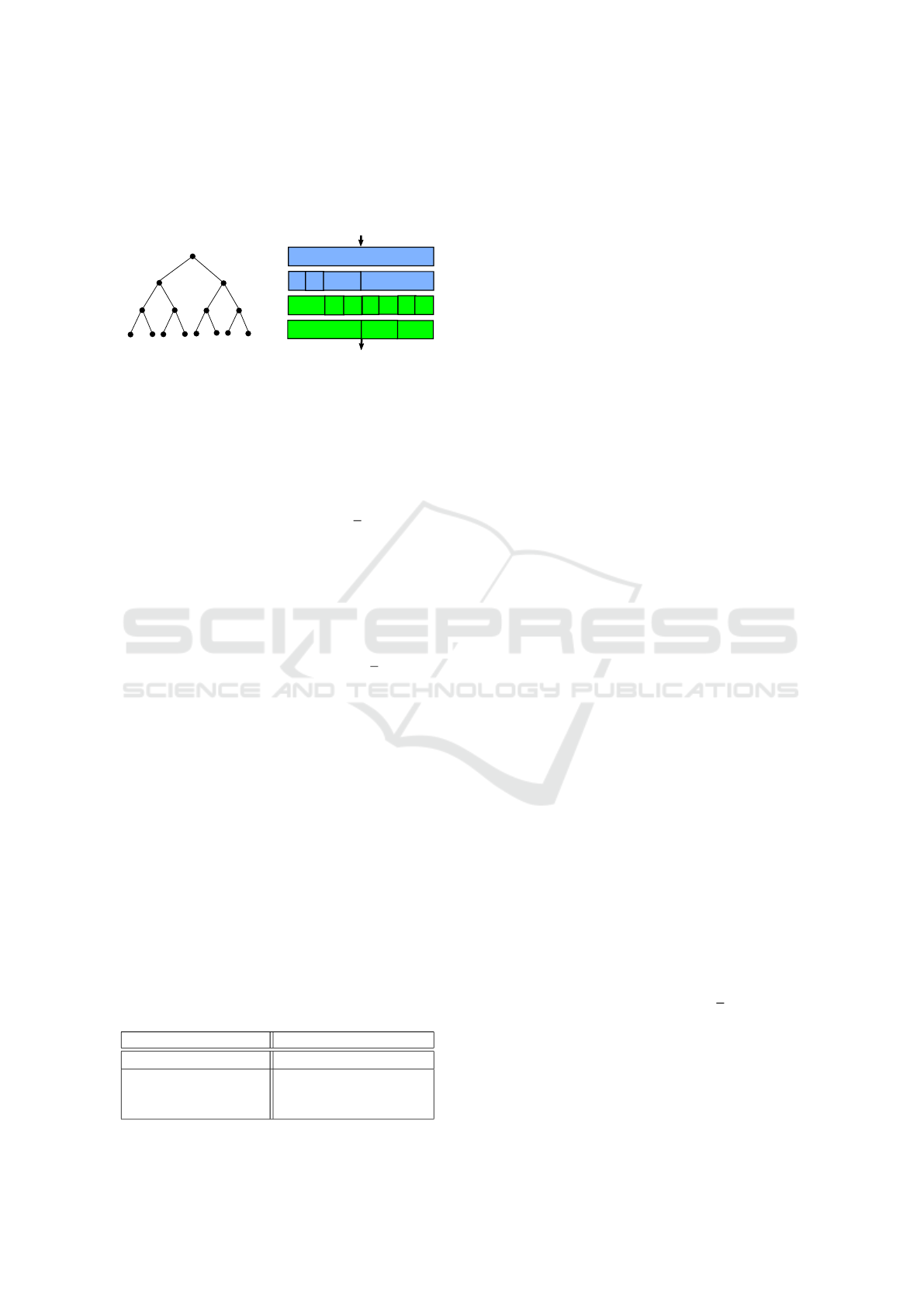
the time 0 and half of the time 1 in each path from

root to leaves in the recursion tree. In Figure 5

we show an example on such restricted random-

ization.

(a) Balanced random

bits

level 0

level 1

level 2

level 3

(b) Non-leaking butterﬂy oper-

ations

Figure 5: Non leaking HLOE randomisation.

• Level of Randomisation. If we can pick freely the

bit r for each group of butterﬂy operations, we

would get the following level of randomisation :

1 + 2 + 2

+ . .. + 2

t−2

−1

But, to prevent leakage, if we restrict the randomi-

sation in order to get half of the levels with High-

Low butterﬂy operations and the other half with

Odd-Even butterﬂy operations, then only for the

ﬁrst t/2 level the bit r can be chosen freely. This

means that the level of randomisation is at least :

1 + 2 + 2

+ . .. + 2

t/2

∼

√

4.1.4 Randomise Modular Reduction

We propose to randomly select the algorithm for mul-

tiplication modulo q for each group of butterﬂy oper-

ations.

• Description of the Randomisation. There are sev-

eral ways to perform a multiplication of two el-

ements x and y modulo q, the two most popular

are the Montgomery multiplication and the Bar-

rett multiplication. Let us assume that q is an

ℓ-bit prime integer. In Barrett algorithm reduces

the product x ×y by clearing the ℓ most signif-

icant bits, while Montgomery algorithm reduces

the product x ×y by clearing the ℓ least signiﬁcant

bif of x ×y, producing a factor 2

−ℓ

in the result.

then these two algorithm are shown in Table 1.

Table 1: Barrett and Montgomery modular multiplication.

Barrett modular mult Montgomery modular mult

Precomp. q

′

= ⌊2

2ℓ

/q⌋ Precomp. q

′

= q

−1

mod 2

ℓ

z ←x ×y

s ←⌊⌊z/2

ℓ−1

⌋q

′

ℓ+1

⌋

r ← z −s ×q

z ←x ×y

s ←q

′

×z (mod 2

ℓ

)

r ← (z −s ×q)/2

ℓ

Then we modify the High-Low splitting approach

of NTT as follows: before each step of butter-

ﬂy operation we ﬂip a coin b and we apply Bar-

rett multiplication (BM) if b = 0 and Montgomery

multiplication if b = 1. A sketch of the pseudo-

code for randomised butterﬂy operations is shown

below :

←− {0,1}

if b = 0 then

// High-Low butterﬂy with BM and recursion

...

else

// High-Low butterﬂy with MM and recur-

sion

...

• Quality of the Randomisation. We notice the fol-

lowing:

– Only the values involved in a multiplication

with ω

are randomised. This means that n/2

value are randomised at each level of recursion

and at the end, n −2 values are randomised at

least once during the NTT.

– A Montgomery multiplication produces a mul-

tiplicative mask 2

−ℓ

. A ﬁnal coefﬁcient

′

involved between 0 and t −2 multiplications in

the whole randomised NTT computation. This

means that

′

has a random multiplicative mask

as follows

′

×(2

−ℓ

)

for some k ∈{0,... ,t −2}.

– Even if Barrett multiplication and Montgomery

multiplication are very similar in terms of the

sequence of operations (multiplications and

shiftings), there are some slight differences (the

type of shift done). These slight differences

could be visible in the power consumption leak-

age and this could leak out which algorithm was

used, revealing the randomisation used.

• Level of Randomisation. For n = 2

, at the ﬁrst

level of recursion we ﬂip one coin, at level 2 we

ﬂip two coins, at third level we ﬂip 4 coins and so

on. In the last level there is no multiplication, so

randomisation stop at level t −1. We then obtain

the following level of randomisation:

1 + 2 + 2

+ . .. + 2

t−2

−1.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

872

5 SECURITY EVALUATION OF

THE PROPOSED

RANDOMISATIONS OF NTT

In this section we present simulation results of Belief

Propagation. We ﬁrst show how the Belief Propaga-

tion behaves when no randomisation is applied in the

NTT. Afterwards for each proposed randomisation we

will show how the Belief Propagation is affected and

ﬁnally we will study some combination of randomi-

sation to see if it reinforces the security of the imple-

mentation.

Leakage of Multiplication. To simulate the power

consumption we used the Hamming distance between

the considered value v and the processed value v

without any noise. So the attacker has a good infor-

mation on the value processed in a multiplication. We

derive the probability that a value v is involved in the

multiplication v

×ω

mod q with a centered Gaus-

sian likelihood estimator with deviation σ = 0.25:

P(v) = e

−

HamDist(v,v

)

Note that this assumption gives more power to the at-

tacker than the model used in (Primas et al., 2017).

Indeed, in (Primas et al., 2017) the leakage model the

hamming weight of the processed value which leaks

out less information that the hamming distance.

5.1 Simulation Results for Non-Mixed

Randomisations

Now we present simulation results of Belief Propaga-

tion on NTT for different randomisation approaches

and for n = 256 and q = 3329, which are the ones

used in Kyber (Bos et al., 2018).

We consider in this section randomisation of NTT

with only one approach among (RandRoot, MulMask,

RandRed and RandHLOE) and the Shufﬂing ran-

domisation of Ravi (Ravi et al., 2020). For compar-

ison purpose, we also provide the result for a non-

randomised NTT.

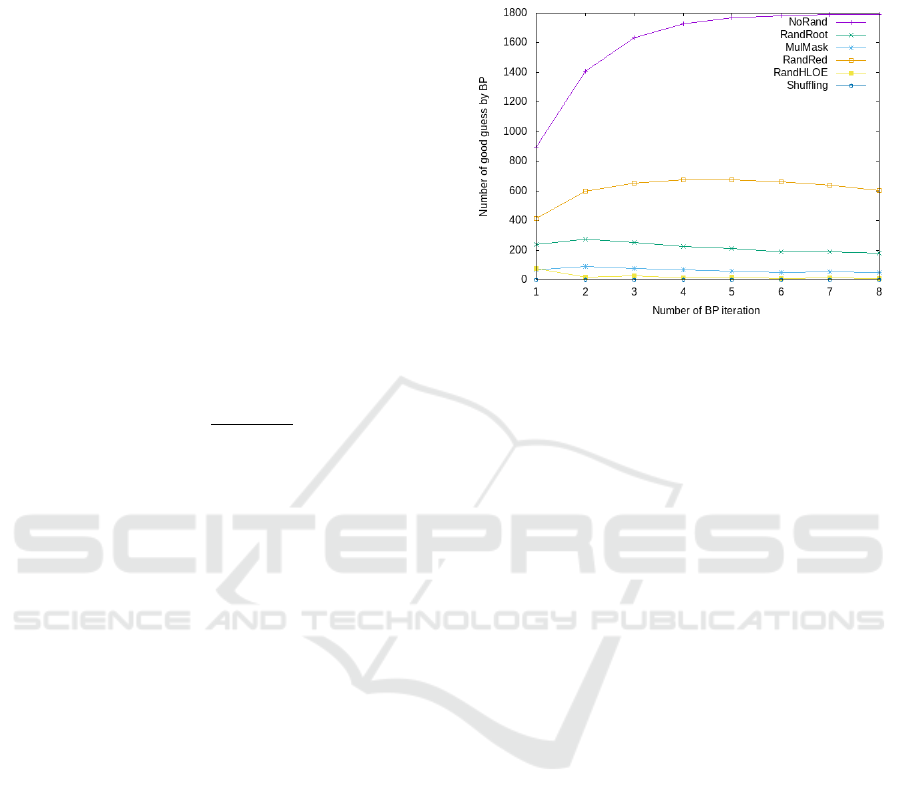
5.1.1 Correct Guess in the Whole NTT

Fig. 6 shows the number of values with highest prob-

ability which are correct among all variable nodes of

Belief Propagation graph. For n = 2

the total number

of variable nodes are (t + 1) ×n, so for n = 256 we

have 2356 variable nodes.

For the non-randomised NTT, the curve shows

that we need around t iterations to reach a maxi-

mum of 1800 variables with correctly guessed val-

ues (among 2356 variables). The other variables are

hidden by the remaining uniform probability sources,

and we believe that this cannot be changed by more

BP iterations. So we cannot recover more variables.

Figure 6: Number of correct coefﬁcient on the whole NTT.

For the randomised NTTs, we can notice that the

number of correct guess is signiﬁcantly higher for

randomisation which does not affect the sequence of

operations in NTT (i.e. RandRoot, RandMultMask,

RandRed). We can also notice that RandRed is the

least effective randomisation.

The HLOE randomisation, disorganises the oper-

ations done in NTT, so the graph used in Belief propa-

gation does not match the sequence of operations pro-

cessed for the NTT and this produces the low number

of correct guess. The same is true for the Shufﬂing

approach of (Ravi et al., 2020).

5.1.2 Correct Guess in the Last Level of NTT

Looking at the correct guess in the last level tells us

if the Belief Propagation is inefﬁcient or not. Indeed,

if the number of correct guess is really small, then

almost no information leaks out and the secret cannot

be recovered. In Fig. 7 we show the number of correct

guess for non-randomised NTT and for all considered

randomisation during the execution of Belief Propa-

gation.

We ﬁrst notice that, in the case of non-randomised

NTT, the number of correct guess increases during

the ﬁrst iterations, to reach the maximal value of

254 = n −2. For the randomised NTT most of the

curves are ﬂat or decrease. The only curve which

increases is the one for RandRed, which means that

belief propagation is able to combine distant informa-

tion to recover some unknown values. This means

that the leakage in RandRed approach remains impor-

tant.

But we can notice that all the considered randomi-

sations prevent the Belief Propagation to be success-

Virtually Free Randomisations of NTT in RLWE Cryptosystem to Counteract Side Channel Attack Based on Belief Propagation

873

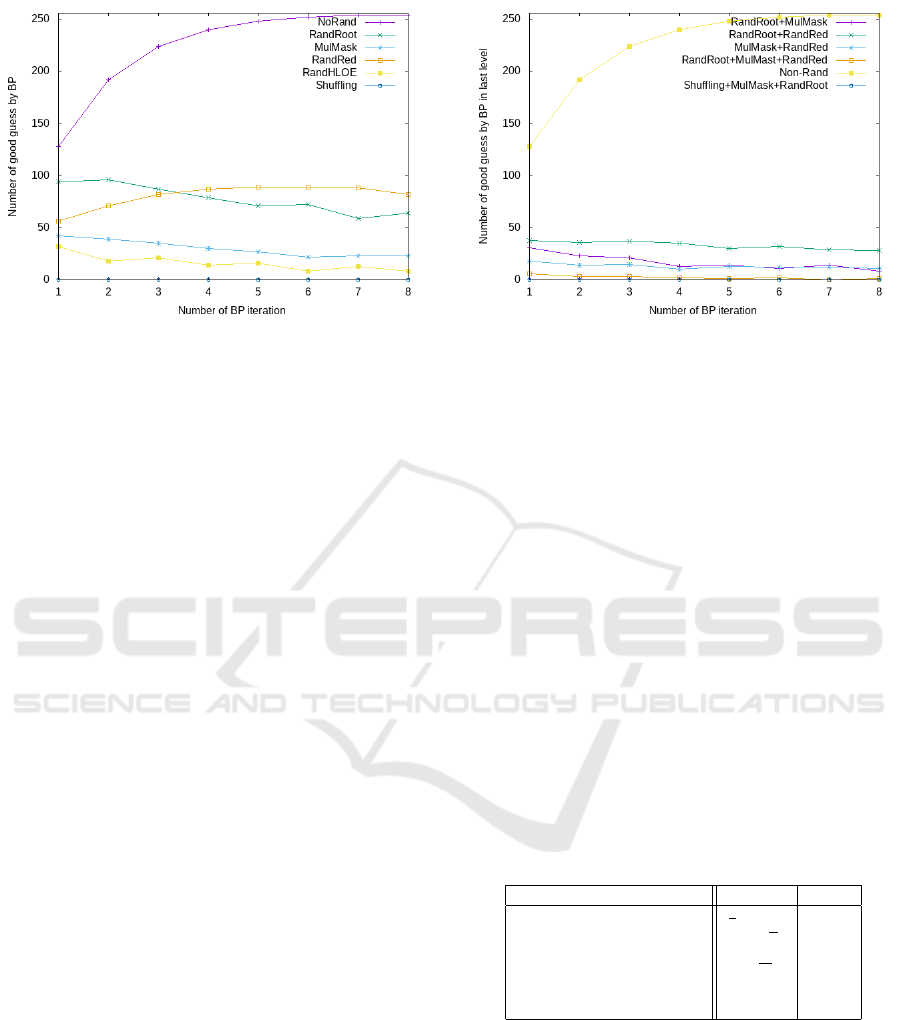
Figure 7: Correct guessed value in last NTT level.

ful: the number of correctly guess coefﬁcients is too

small to recover the whole secret output.

5.2 Simulation Results for Mixed

Randomisation

Some randomisations can be combined: RandOrder,

RandRed, RandRoot and RandMulMask. Indeed they

are all applied to NTT with High-Low splitting strat-

egy and the randomisations can be applied indepen-

dently from each other.

The RandHLOE approach partly uses Odd-Even

splitting formula, which requires to have data with

the same multiplicative mask. This prevents the use

of RandHLOE combined with RandRed, RandRoot

and/or RandMulMask since they produces masked

data with possibly different masks.

The shufﬂing randomisation of (Ravi et al., 2020)

can be combined to all the other approaches. But

since shufﬂing already provide curve really close to

zero, we only provide the simulation result for Shuf-

ﬂing+RandRoot+RandMulMask.

The numbers show that, as expected, the com-

bination of two or three randomisations lower the

number of correct guess. The combination Rand-

Root+MulMask+RandRed give a curve really close to

zero, this means that it does not leak any information.

The combination of Rand-

Root+RandMulMask+Shufﬂing seems to be the

most effective one. Indeed, even if the attacker is able

to know the root of unity used in each multiplication,

the use of the RandRoot prevent him to know the

node of graph of the NTT it should be associated

with: it could be anyone in the same group. And in

this case, the graph cannot be correctly constructed

and Belief Propagation would then fails.

Figure 8: Total number of correct guess per BP iteration for

combined randomisations.

6 CONCLUSION

In this paper we considered the security of Ring

LWE cryptosystems relatively to Primas et al.’s attack

based on Belief Propagation (Primas et al., 2017).

The attack in (Primas et al., 2017) focuses on the

Number Theoretic Transform and exploits scattered

leakage information to recover the output of NTT. We

proposed a set of virtually free randomisations which

reorganise/modify the sequence of operations of the

NTT and/or induce a random mask in the processed

values.

The level of randomisation of each approach is

shown in Table 2. These results show that the level

of randomisation for RandHLOE and RandRed is re-

ally low and could be attacked by exhaustive search of

the random bits used. The other randomisations have

a quite large level of randomisation.

Table 2: Level of randomisation.

Formula n = 256

Shufﬂing (Ravi et al., 2020) (

log

(n)

5729

RandHLOE ∼

√

n 2

RandRoot ∼

247

RandMulMask ∼ n

n/2

1024

RandRed n/2 2

We applied Belief Propagation on all randomisa-

tions of NTT and also on some combination of these

randomisations. These simulation results told us that

Shufﬂing, RandHLOE are the most efﬁcient to pre-

vent Belief Propagation, since the number of correctly

guessed values with BP remains low.

Finally, when considering combination of ran-

domisations, we noticed that RandHLOE cannot

be combined with RandRoot, RandMulMask and/or

RandRed. The best approach combines Shufﬂing,

SECRYPT 2024 - 21st International Conference on Security and Cryptography

874

RandRoot and RandMulMask which has a high level

of randomisation, and even if the roots of unity can

be guessed from leakage they cannot be used to ap-

ply the attack since it is not possible to construct the

Belief Propagation graph of NTT.

REFERENCES

Bos, J. W., Ducas, L., Kiltz, E., Lepoint, T., Lyubashevsky,

V., Schanck, J. M., Schwabe, P., Seiler, G., and Stehl

D. (2018). CRYSTALS - kyber: A cca-secure module-

lattice-based KEM. In 2018 IEEE European Sympo-

sium on Security and Privacy (EuroS&P), pages 353–

367. IEEE.

Cooley, J. and Tukey, J. (1965). An algorithm for the ma-

chine calculation of complex Fourier series. Mathe-

matics of Computation, 19:297–301.

Lyubashevsky, V., Peikert, C., and Regev, O. (2010). On

Ideal Lattices and Learning with Errors over Rings.

In EUROCRYPT 2010, volume 6110 of LNCS, pages

1–23. Springer.

Pearl, J. (1982). Reverend bayes on inference engines: A

distributed hierarchical approach. Probabilistic and

Causal Inference.

Primas, R., Pessl, P., and Mangard, S. (2017). Single-Trace

Side-Channel Attacks on Masked Lattice-Based En-

cryption. In CHES 2017, volume 10529 of LNCS,

pages 513–533. Springer.

Ravi, P., Poussier, R., Bhasin, S., and Chattopadhyay,

A. (2020). On conﬁgurable SCA countermeasures

against single trace attacks for the NTT - A perfor-

mance evaluation study over kyber and dilithium on

the ARM cortex-m4. In SPACE 2020, volume 12586

of LNCS, pages 123–146. Springer.

Regev, O. (2009). On lattices, learning with errors, random

linear codes, and cryptography. J. ACM, 56(6):34:1–

34:40.

Shor, P. (1999). Polynomial-Time Algorithms for Prime

Factorization and Discrete Logarithms on a Quantum

Computer. SIAM Rev., 41(2):303–332.

Veyrat-Charvillon, N., G

erard, B., and Standaert, F.

(2014). Soft analytical side-channel attacks. In ASI-

ACRYPT 2014, volume 8873 of LNCS, pages 282–

296. Springer.

Virtually Free Randomisations of NTT in RLWE Cryptosystem to Counteract Side Channel Attack Based on Belief Propagation

875