Smart Widening for the Polyhedral Analysis

Yassamine Seladji

Abou Bekr Belkaid university, Tlemcen, Algeria

Keywords:

Abstract Interpretation, Static Analysis, Polyhedra Abstract Domain.

Abstract:

The polyhedron abstract domain is a cornerstone of static program analysis, providing a powerful mathematical

framework for reasoning about numerical properties of programs. It can express a large number of properties.

This makes it complex and time-consuming. In the polyhedral analysis, the widening operator with threshold

proposes a good compromise between precision and time execution. However, ensuring both termination

and precision in the analysis process remains a challenge, particularly when dealing with complex programs

and high-dimensional state spaces. This paper proposes a novel approach to improve polyhedral analysis by

dynamically computing relevant widening thresholds, thereby improving both the termination and precision of

the analysis. We demonstrate the effectiveness of our approach through experimental evaluation on a variety of

benchmark programs. Our results show signiﬁcant improvements in both analysis termination and precision.

1 INTRODUCTION

Static analysis by abstract interpretation aims to au-

tomatically proving properties of computer programs,

by computing invariants that over-approximate the set

of program behaviours (Cousot and Cousot, 1977;

Cousot and Cousot, 1992). Static analysis uses the

(concrete) program semantic function F to deﬁne a

program invariant X, such that F(X) = X. This rep-

resents the set of reachable program states, but is

however not computable. To deal with that, an over-

approximation is introduced using abstract interpre-

tation (Cousot and Cousot, 1977). The main idea is

to deﬁne a new (abstract) semantic function F

♯

which

computes an abstract program invariant including the

concrete program invariant. This inclusion guarantees

the safety of the result but not its accuracy: the larger

the over-approximation is, the higher the probability

to add false alarms. This over-approximation is due

to the type of elements manipulated by F

♯

; the most

common and expressive abstraction is to represent

the reachable states of numerical programs as con-

vex polyhedra (Cousot and Halbwachs, 1978). The

polyhedron abstract domain (Cousot and Halbwachs,

1978) returns invariants that express a large set of

properties. However, this expressiveness makes the

analysis more complex and expensive: it has expo-

nential space and time complexity in the worst case.

The polyhedra abstract domain also faces signiﬁ-

cant challenges and limitations. These include scala-

bility concerns in handling large programs with high-

dimensional state spaces, imprecision in handling

non-linear expressions and non-convex constraints,

and the trade-off between precision and efﬁciency in

analysis algorithms. Various techniques have been

proposed to alleviate this complexity burden, aiming

to strike a balance between analysis efﬁciency and

accuracy. However, many of these approaches in-

evitably sacriﬁce accuracy in order to achieve compu-

tational tractability. In (Castagna and Gordon, 2017),

a new version of the polyhedra abstract domain is de-

ﬁned, to decrease the complexity of the analysis. For

that, a decomposed version of the polyhedron is used.

In (Yu and Monniaux, 2019), authors propose a new

polyhedral projection operator based on parametric

linear programming using ﬂoating-point arithmetic.

This operator is more efﬁcient than the classical

Fourier-Motzkin elimination method. A new opera-

tor is proposed in (Arceri et al., 2023) to model the

splitting of control ﬂow paths. This operator is used

to allow more efﬁcient analysis when using abstract

domains that are expensive to compute. Note that

the proposed split operator has no impact on preci-

sion. To ﬁnd a good trade-off between expressive-

ness and efﬁciency, new domains have been devel-

oped. These domains provide coarse-grained repre-

sentations of numerical properties, sacriﬁcing preci-

sion for computational efﬁciency. While suitable for

certain types of analysis, these approximations may

fail to capture intricate dependencies or non-linear re-

Seladji, Y.

Smart Widening for the Polyhedral Analysis.

DOI: 10.5220/0012860500003753

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Conference on Software Technologies (ICSOFT 2024), pages 79-87

ISBN: 978-989-758-706-1; ISSN: 2184-2833

lationships present in the program, leading to impre-

cise results. They are known as weakly relational ab-

stract domains (Min

e, 2006; Sankaranarayanan et al.,

2005; Goubault et al., 2012; Seladji and Bouissou,

2013; Seladji, 2017).

The other tool to reduce the computation time

of the analysis is to modify the Kleene algorithm

to make it faster. By using operators like widen-

ing (Cousot and Cousot, 1992) and narrowing that

accelerate convergence in iterative analysis algo-

rithms by approximating ﬁxpoints or reﬁning abstrac-

tions. Widening introduces imprecision by over-

approximating program states to ensure termination,

while narrowing aims to restore precision by reﬁning

abstractions iteratively. However, striking the right

balance between widening and narrowing parameters

is crucial to avoid excessive imprecision or divergence

in the analysis. The widening operator in the poly-

hedra domain is used to ensure termination in iter-

ative analysis algorithms, particularly when dealing

with loops or recursive structures. By removing con-

straints that are not stable from one iteration to the

next. However, it is essential to recognize that widen-

ing introduces a large over-approximation, leading to

imprecise analysis results.

Techniques have been developed to minimise this

loss of accuracy. Threshold widening (Lakhdar-

Chaouch et al., 2011) predeﬁnes a set of thresholds,

the elements of which are used as candidate bounds

at each iteration. However, the choice of widen-

ing thresholds signiﬁcantly impacts the analysis qual-

ity, balancing termination and precision. Finding

the optimal widening threshold is non-trivial and of-

ten requires manual tuning, limiting the scalability

and effectiveness of the analysis. In our previous

work (Bouissou et al., 2012), we presented a method

that dynamically computes a relevant set of thresholds

using relevant set of thresholds using numerical anal-

ysis tools. This technique was applied to the interval

and octagon abstract domains. It should be noted that

the solutions proposed to improve the computational

time of a polyhedral analysis can be categorized into

two main strategies:

• restricted data representation : One approach to

improving computational time in polyhedral anal-

ysis involves simplifying the representation of

program data to facilitate manipulation.

• improvement of ﬁxed-point computation tech-

niques : it focuses on enhancing the efﬁciency

of ﬁxed-point computation algorithms, typically

by employing better widening operators or con-

vergence strategies.

In this paper, we combines the advantages of

both data representation simpliﬁcation and ﬁxed-

point computation improvement techniques to im-

prove the polyhedral analysis. By exploiting the com-

pactness of support function-based representations,

our method facilitates faster convergence in ﬁxed-

point computation algorithms while maintaining anal-

ysis precision. In addition, the use of support func-

tions allows efﬁcient manipulation of program con-

straints, further improving computational efﬁciency.

The paper is organized as follows: in Section 2, we

explain the proposed method using a simple example.

In Section 3, we introduce some useful deﬁnitions. In

Section 4, we present our main contribution. Some

benchmarks are given in Section 5. Finally, we con-

clude with a conclusion and some perspectives.

2 AN ILLUSTRATED EXAMPLE

To illustrate the intuition behind our approach, let’s

consider a simple example involving a linear ﬁlter

program. Figure 1 depicts the structure of the pro-

gram. Analyzing the given program using the poly-

hedral abstract domain presents challenges due to its

inherent complexity. The analysis couldn’t terminate

within a reasonable time (e.g., more than 10 minutes),

it indicates the complexity of the program and the lim-

itations of the polyhedral analysis approach for this

particular case. In such scenarios, it’s essential to con-

sider alternative analysis techniques such as the use

of the widening operator. Note that, the analysis re-

sult for the given program, using widening, is an un-

bounded polyhedron. Indeed, widening with thresh-

olds (Lakhdar-Chaouch et al., 2011), offers an inter-

esting alternative approach. By using a predeﬁned

set of thresholds as ﬁxed-point candidates, this tech-

nique aims to control the trade-off between analysis

precision and computational complexity. However,

the static nature of threshold selection can be a bot-

tleneck, as it does not take into account the dynamics

of the analysed program. In this paper, we propose an

approach to compute dynamically relevant thresholds

for polyhedral analysis. This approach aims to adap-

tively adjust widening thresholds based on the evolv-

ing program state.

For that, we perform a pre-analysis using a sub-

polyhedra abstract domain (Seladji and Bouissou,

2013). This domain is based on a given set of tem-

plates. In this example, we deﬁne these templates

as a set of vectors uniformly distributed on a unit

sphere. First, a pre-analysis is performed using an

sub-polyhedron abstract domain (Seladji and Bouis-

sou, 2013) based on a given set of templates, such as

vectors uniformly distributed on a unit sphere. In Fig-

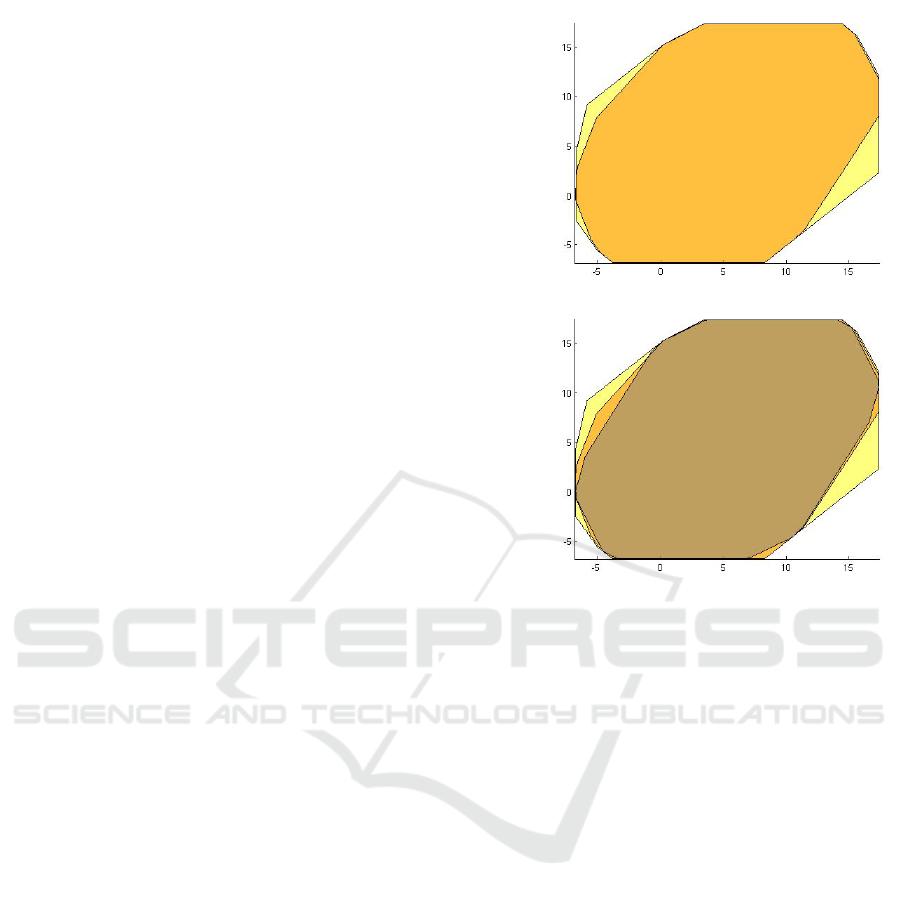
ure 2, the yellow polyhedron represents the result of

ICSOFT 2024 - 19th International Conference on Software Technologies

double input() {

double u = 10.0, l = 0.0;

return ( rand()/(double)RAND_MAX ) * (u-l) + l;

}

int main() {

double xn, yn, ynm1,ynm2 ;

xn=xnm1=xnm2=yn=ynm1=ynm2=0;

int i=0;

while (i<4000) {

yn = xn + 0.5*ynm1 - 0.45*ynm2;

printf("%f %f\n",ynm1,yn);

ynm2=ynm1;

ynm1=yn;

xn = input();

}

return 0;

}

Figure 1: The body of the illustrated program called

filter2.

the pre-analysis, denoted as P. The obtained result

corresponds to a template representation of the ﬁxed

point obtained using the polyhedra abstract domain.

Note that this pre-analysis has polynomial complex-

ity in the number of iterations and linear complexity

in the number of template vectors, which contributes

to the scalability and efﬁciency of the analysis pro-

cess.

The main idea is to use P to improve the polyhedral

analysis. To do this, we consider P as a ﬁxed point

candidate and use it as a relevant threshold for the

widening operator to accelerate the analysis.

In Figure 2, the accuracy and efﬁciency of the pro-

posed approach is demonstrated by comparing the or-

ange polyhedron obtained by using P as a relevant

threshold with the brown polyhedron obtained from

the 200th Kleene iteration using polyhedral analysis

Note that, this analysis is done in less than 7 seconds,

which we consider very fast.

3 BACKGROUND

This section outlines some of the important notions

used in this article. In the rest, we note by R the set

of real numbers and ∀x, y ∈ R,< x, y > represents the

scalar product of x by y.

3.1 The Polyhedral Analysis

A convex polyhedron is a subset of R

deﬁned as the

intersection of ﬁnitely many half-spaces, each half-

space is given as a constraint of the form

∑

i=1

< α

>≤ c

where ∀i ∈ [1, n], α

∈ R and c ∈ R. We here adopt

the constraint representation of polyhedron, which is

Figure 2: The yellow polyhedron represents the one ob-

tained using the sub-polyhedra abstract domain and the or-

ange polyhedron is the one obtained using our method. The

polyhedron in brown represents the one obtained in the

200

kleene iteration using the polyhedra abstract domain.

best suited for static analysis. The set of all convex

polyhedra has a lattice structure with an exact inter-

section operator and the convex hull as union (Cousot

and Halbwachs, 1978). Obviously, for implementa-

tion issues, the coefﬁcients of the constraints are usu-

ally chosen as rational numbers and the set of con-

straints is encoded using a matrix representation.

Deﬁnition 1 The abstract domain of convex polyhe-

dra, noted C

, is the set of all pairs (A, b) where

A ∈ R

n×k

is a real matrix and b ∈ R

is a real vector.

A polyhedron P given by the pair (A, b) represents the

set of all points (x

,. .., x

) ∈ R

such that

∀ j ∈ [1,k],

∑

i=1



j,i



≤ b

Given a polyhedron P = (A,b), the j

constraint

of P is





≤ b

where X is the vector of variables

and A

is the j

row of A.

The static analysis of a program with the poly-

hedra domain consists in computing the least ﬁx-

point P

∞

of a monotone map F : C

→ C

given by

the program semantics. To do so, the most used

method is Kleene algorithm that uses the equation

Smart Widening for the Polyhedral Analysis

Algorithm 1: Kleene iteration algorithm for the polyhedra

abstract domain.

1: P

:= ⊥

2: repeat

3: P

:= P

i−1

⊔ F(P

i−1

)

4: until P

⊑ P

i−1

∞

k∈I

(⊥), where ⊥ is the least element of

. Kleene iteration Algorithm for the polyhedra ab-

stract domain is given in Algorithm 1. So analysing

programs using the abstract interpretation based static

analysis of a program consists of computing the least

ﬁxed point of the equation P = P ⊔ F(P). As Kleene

algorithm may not terminate and may not compute

the least ﬁxed point P

∞

, a widening operator is used

to compute an over-approximation P

⊒ P

∞

3.2 The Sub-Polyhedral Analysis

The sub-polyhedra abstract domain presented in (Se-

ladji and Bouissou, 2013) is based on support func-

tions (Hiriart-Urrut and Lemarechal, 2004). This do-

main is an abstraction of convex polyhedra over R

where n is the number of variables of the program

being analyzed. We denote this abstract domain by

∆

, parametrized by a template ∆. It represents a ﬁ-

nite set of directions ∆ = {

⃗

,. ..,

⃗

}. Note that, the

set ∆ can be computed randomly as vectors uniformly

distributed on the unit sphere. A novel approach to

compute a relevant ∆ is presented in (Seladji, 2017),

which is based on statistical analysis. The deﬁnition

of P

∆

is given in Deﬁnition 2.

Deﬁnition 2 Let ∆ ⊆ R

be the set of vectors and

∞

= R ∪ {−∞,+∞} . We deﬁne P

∆

as the set

of all functions from ∆ to R

∞

, i.e P

∆

= ∆ → R

∞

We denote ⊥

∆

(resp. ⊤

∆

) the function such that

∀

⃗

d ∈ ∆, ⊥

∆

(

⃗

d) = −∞ (resp. ⊤

∆

(

⃗

d) = +∞).

For each Ω ∈ P

∆

, Ω(

⃗

d) is the value of Ω in direction

⃗

d ∈ ∆. Intuitively, Ω is a support function with ﬁnite

domain.

The abstraction and concretization functions of P

∆

are

deﬁned in Deﬁnition 3.

Deﬁnition 3 Let ∆ ⊆ R

be the set of vectors.

We deﬁne the concretization function γ

∆

: P

∆

→ C

by:

∀Ω ∈ P

∆

, γ

∆

(Ω) =

⃗

d∈∆

{x ∈ R

⃗

d, x >≤ Ω(

⃗

d)} .

The abstraction function α

∆

: C

→ P

∆

is deﬁned by:

∀P ∈ C

,α

∆

(P) =







⊥ if P =

⊤ if P = R

⃗

d. δ

(

⃗

d) otherwise

where, δ

(

⃗

d) is the support function (Hiriart-Urrut

and Lemarechal, 2004) of the polyhedron P using the

vector

⃗

Note that, the concretization of an abstract element of

∆

is a polyhedron deﬁned by the intersection of half-

spaces, where each one is characterized by its normal

vector

⃗

d ∈ ∆ and the coefﬁcient Ω(

⃗

d). The abstrac-

tion function on the other side is the restriction of the

support function of the polyhedron on the set of di-

rections ∆. The order structure of P

∆

is deﬁned using

properties of support functions.

We combine Kleene iteration algorithm and the P

∆

abstract domain to perform the analysis. Let take in

consideration loops of the form:

while(C)

X=AX+b;

We suppose that A is a real matrix, b may be a set

of real values, given as a polyhedra P

, and C is a

guard. Such loops include for example linear ﬁlters

in which P

represents the possible values of the

new input at each loop iteration. We assume that the

program variables belong initially to the polyhedron

. Using properties of support function in the case

of loops without guard, we can deﬁne the abstract

element obtained in the i

Kleene iteration as follows:

∀

⃗

d ∈ ∆, Ω

(

⃗

d) =

max



(

⃗

d), max

j∈[1,i]



T j

⃗

d) +

∑

k=1

T (k−1)

⃗





(1)

Equation 1 is used to deﬁne a special version of

Kleene algorithm. The obtained analysis has a poly-

nomial time complexity in the number of iterations

and linear in the number of directions in ∆. In ad-

dition, its result is as accurate as possible: at each

Kleene iteration, we have that Ω

= α

∆

), such that

Ω

(resp. P

) is the result of the ith Kleene iteration

using the P

∆

domain (respectively the polyhedra ab-

stract domain). So Ω

∞

= α

∆

∞

), with Ω

∞

is the ﬁxed

point obtained in the P

∆

analysis and P

∞

is the one

obtained using polyhedra domain.

4 THE SMART WIDENING

The Kleene algorithm plays a crucial role in static

analysis by abstract interpretation, particularly in

computing the least ﬁxed point for various abstract

domains, including the polyhedral abstract domain.

In polyhedral analysis, it is performed to com-

pute the least ﬁxed point of a set of constraints.

Widening is used to accelerate convergence by over-

ICSOFT 2024 - 19th International Conference on Software Technologies

approximating the solution space, it is applied itera-

tively until a stable ﬁxed point is reached, thus ensur-

ing the termination of the analysis.

One of the main drawbacks of Widening is the po-

tential for overly coarse results that quickly diverge

towards inﬁnity. To deal with the loss of precision,

we deﬁne the so-called Smart widening operator. It

adds an intermediate step to extrapolate the potential

ﬁxed point using a relevant threshold.

In polyhedron analysis, ﬁnding a relevant threshold

consists of automatically computing a polyhedron

that serves as a candidate ﬁxed point in the Kleene

iteration. The polyhedron threshold is obtained us-

ing sub-polyhedral analysis, which means that the dy-

namics of the analysed program are taken into account

in the threshold computation process.

For the rest, we adopt the constraint representation of

the polyhedron. In this section, we present our main

contribution: the dynamic computation of a relevant

threshold to improve the widening operator in poly-

hedral analysis, thereby accelerating the analysis pro-

cess. Our approach consists of two main steps: ﬁrst,

we describe the technique for dynamically comput-

ing a relevant threshold, and then we show how this

threshold improves the widening operator and speeds

up polyhedral analysis.

4.1 The Threshold Computation

In this section, We present a technique to dynamically

compute a relevant threshold during the analysis pro-

cess. This technique is based on sub-polyhedral anal-

ysis as described by (Seladji and Bouissou, 2013) .

A relevant threshold is deﬁned as a polyhedron that

allows the polyhedral ﬁxed point computation to be

accelerated without losing accuracy.

For that we use the P

∆

abstract domain given in Sec-

tion 3.2. Let us consider the case of programs with

afﬁne loops. Such loops are very common in embed-

ded systems, especially in the case of linear ﬁlters.

Let the program with the afﬁne loop be given as fol-

lows:

while(C)

X=AX+b;

With A ∈ R

n×n

and b ∈ R

. Let C be a boolean ex-

pression. We assume that the program variables are

initially inside the polyhedron P

. For the rest, we

put C = true.

Using the polyhedra abstract domain C

, the loop in-

variant, P ∈ C

, is deﬁned as the least ﬁxed point of

the equation P = P ⊔



AP + P



. Usually, the ﬁxed

point is deﬁned as the limit of the kleene iterates given

by P

= P

i−1

⊔ (AP

i−1

+ P

). Using the P

∆

analysis,

we have that, the i

kleene iterate computes the sup-

port function of P

, noted δ

, as follows :

∀

⃗

d ∈ ∆, δ

(

⃗

d) =

max



(

⃗

d), max

j∈[1,i]



T j

⃗

d) +

∑

k=1

T (k−1)





(2)

Let denote by P

♯

the ﬁxed point of the equation P =

P ⊔



AP + P



. The P

∆

analysis computes the support

function of P

♯

in a given vector

⃗

d ∈ R

, noted δ

♯

(

⃗

d).

As shown in Equation 2, the computation of δ

♯

(

⃗

used only P

, P

and A, which represent the input of

the program to be analysed. Let Θ be the function that

computes δ

♯

(

⃗

d) using the P

∆

analysis, it is given in

Deﬁnition 4.

Deﬁnition 4 Let P

♯

be the ﬁxed point of the equation

P = P ⊔



AP + P



Let Θ : R

×C

× R

n×n

−→ R be a function de-

ﬁned as follows :

(∀

⃗

d ∈ R

∈ C

,A ∈ R

n×n

Θ(

⃗

d, P

,A) = δ

♯

(

⃗

d) (3)

Where δ

♯

(

⃗

d) is the support function of P

♯

for the vec-

tor

⃗

d, obtained using the P

∆

analysis.

As presented in (Seladji and Bouissou, 2013), the

computation of δ

♯

(

⃗

d) has a polynomial complexity

in the number of iterations and linear in the number

⃗

d in ∆. So, this computation is efﬁciency.

We know that for a given convex polyhedron P, the

support function allows us to deﬁne P in the follow-

ing way :

∀

⃗

d ∈ R

,P =

⃗

d∈R



x ∈ R

|⟨x,

⃗

d⟩ ≤ δ

(

⃗



. (4)

Note that computing δ

(

⃗

d) for all

⃗

d ∈ R

is a dif-

ﬁcult task. We can only compute it for a subset ∆ of

, which allows us to get an over-approximation of

∀∆ ⊆ R

,P ⊆

⃗

d∈∆



x ∈ R

|⟨x,

⃗

d⟩ ≤ δ

(

⃗



. (5)

So, we can compute an over-approximation of P

♯

using the Equation 3 of Deﬁnition 4. This computa-

tion is given in Deﬁnition 5.

Deﬁnition 5 Let the function

Λ : (R

× R

) × C

× C

× R

n×n

7−→ C

de-

ﬁned as follows : (∀∆ ⊆ R

∈ C

,A ∈

n×n

),Λ(∆, P

,A) =

⃗

d∈∆



x ∈ R

|⟨x,

⃗

d⟩ ≤ Θ(

⃗

d, P

,A)



. (6)

So, from Deﬁnition 5, we can deduce that

♯

⊆ Λ(∆, P

,A).

Smart Widening for the Polyhedral Analysis

In the context of polyhedral analysis, P

∆

analysis

refers to an abstract domain that captures properties

of convex polyhedra based on a set ∆ of templates.

The function Λ is used to deﬁne the best template

abstraction of P

♯

using the set ∆. The polyhedron

given in deﬁnition 5 is considered as a relevant thresh-

old. By dynamically computing this relevant thresh-

old, the analysis can adapt to the speciﬁc character-

istics and dynamics of the program being analysed.

Once the threshold polyhedron is computed, it is inte-

grated into the polyhedral analysis framework as a rel-

evant threshold to improve the analysis process. This

threshold guides the widening and reﬁnement opera-

tions, ensuring that the analysis efﬁciently converges

to a stable ﬁxed point solution.

The P

∆

analysis can be applied to a wider range of

programs than just those with afﬁne loops. While

afﬁne loops are a common scenario, especially in em-

bedded systems and signal processing applications.

The P

∆

analysis provides a powerful framework that

can consider programs with complex loop structures

involving non-linear loops and afﬁne transformations.

4.2 The Widening Computation

In this section, we integrate the threshold polyhedron

obtained from Deﬁnition 5 into the widening opera-

tor used in the Kleene iteration. For that, new oper-

ator are deﬁned called the smart widening operator,

denoted ∇

. This operator considers the polyhedron

given in Deﬁnition 6 as a Kleene ﬁxed point candi-

date and uses it as a threshold in the Kleene iteration

algorithm. Use the modiﬁed widening operator within

the Kleene iteration algorithm to iteratively reﬁne the

analysis results towards a ﬁxed point solution. At

each iteration, the polyhedron is used as a threshold to

guide the widening process, ensuring that the analysis

converges efﬁciently and accurately. The deﬁnition of

∇

is given in Deﬁnition 6.

Deﬁnition 6 For a given P, P

∈ C

, A ∈ R

n×n

and ∆ ⊆ R

, the smart widening operator ∇

is de-

ﬁned as follows :

P∇

(AP + P

) = P ∪ Λ(∆,P

,A).

In Deﬁnition 6, the smart widening operator substi-

tutes the expression (AP + P

) with the threshold re-

turned by the function Λ(∆,P

,A) . Afterwards,

the union operator is performed between P and the

polyhedron resulting from Λ(∆,P

,A).

So, we have that the function Λ(∆, P

,A) com-

putes a threshold polyhedron based on the input pa-

rameters : the set of templates ∆, the initial polyhe-

dron represented by P

and P

, and the afﬁne trans-

formation matrix A. This threshold polyhedron rep-

resents a relevant approximation of the program state

space. The smart widening operator replaces the ex-

pression (AP + P

) by the obtained threshold. This

ensures that the widening operation is guided by the

threshold polyhedron, focusing the analysis on rele-

vant ranges of the program state space where signiﬁ-

cant changes are occurring. After substituting the ex-

pression with the threshold polyhedron, the union op-

erator is performed between the current polyhedron

P and the threshold one. This union operation com-

bines the information collected by p with the reﬁned

approximation provided by the threshold polyhedron,

improving the accuracy and convergence of the analy-

sis. In Algorithm 2 we consider the adapted version of

the Kleene iteration algorithm using the smart widen-

ing operator. This adapted algorithm incorporates the

smart widening operator to guide the iterative reﬁne-

ment process towards a stable ﬁxed-point solution.

Algorithm 2: Kleene iteration algorithm based on smart

widening operator.

Require: ∆, A, P

1: i := 0

2: repeat

3: if i ≥ 10 then

4: ∆Generation();

5: P

:= P

i−1

∇

(AP

i−1

+ P

)

6: i := 0

7: else

8: P

:= P

i−1

∪ (AP

i−1

+ P

)

9: i := i + 1

10: end if

11: until P

⊑ P

i−1

The smart widening operator is used to extrapolate

the sequence of polyhedra obtained by Kleene itera-

tion up to the polyhedron computed by the Λ function.

In the algorithm 2 we introduce a deliberate delay in

the application of the smart widening operator, choos-

ing to apply it after every 10 Kleene iterations. This

delay is designed to allow the Kleene algorithm to sta-

bilise and attempt to converge to the ﬁxed point be-

fore introducing the reﬁnement provided by the smart

widening operator. Note that practical experiments

show that only one application of smart widening is

needed to speed up ﬁxed-point computation.

In fact, the quality of the polyhedron calculated with

the function Λ is closely related to the quality of the

chosen set ∆. The set ∆ serves as the basis for con-

structing templates that approximate the behaviour of

the program, and the effectiveness of these templates

directly affects the accuracy and precision of the anal-

ysis results. One intuitive method for selecting tem-

plates is to take vectors that are uniformly distributed

on the unit sphere. Another method is to consider

the current kleene iteration polyhedron to compute the

ICSOFT 2024 - 19th International Conference on Software Technologies

set ∆. The polyhedron P

i−1

obtained at the (i

− 1)

Kleene iteration contains constraints that deﬁne the

boundaries of the program’s state space at that itera-

tion. The normal vectors of the constraints of P

i−1

represent directions in the program’s state space that

are relevant to the analysis. These normal vectors cap-

ture the local geometry and behavior of the program

at the previous iteration. They can be used as tem-

plates for constructing the set ∆ for the current itera-

tion. By basing the selection of templates on the pre-

vious iteration’s polyhedron, this method adapts dy-

namically to the program’s behavior and changes in

the state space. It allows the analysis to focus on di-

rections that are relevant to the current state of the

program, enhancing the accuracy and effectiveness of

the analysis process. This method is represented in

the Algorithm by the function ∆Generation(). To en-

sure efﬁciency and effectiveness, it’s advantageous to

apply this method after computing a sufﬁcient num-

ber of Kleene iterations to obtain a polyhedron P

i−1

with a substantial number of constraints. Construct-

ing ∆ based on a polyhedron with a large number of

constraints enables the selection of a diverse and rep-

resentative set of vectors, enhancing the quality and

coverage of the template set.

Utilizing Principal Components Analysis (PCA), as

presented in (Seladji, 2017), to compute an interesting

set ∆ offers another alternative for constructing tem-

plates in polyhedral analysis. PCA is a statistical tech-

nique that can be leveraged to identify the most sig-

niﬁcant directions or principal components in a high-

dimensional dataset.

5 EXPERIMENTATIONS

The smart widening operator proposed a good trade

off between expressiveness and efﬁciency. For the ex-

perimentation, we apply Algorithm 2 with the poly-

hedra abstract domain to analyze several programs,

this analysis is called the smart polyhedral analysis.

The programs used contain a number of stable lin-

ear systems and digital ﬁlters, which are well-known

to be difﬁcult to analyse using polyhedral analysis.

To show the efﬁciency and the scalability of the the

smart polyhedral analysis, it is tested on programs

with many variables. The smart polyhedral analysis

is implemented using PPL (Bag, ). PPL (the Parma

Polyhedra Library) is a library that provides an ef-

ﬁcient implementation of the polyhedra abstract do-

main. Note that its implementation is based on ra-

tional numbers. We use also the MPFR Library

https://www.mpfr.org/

handle the ﬂoating point arithmetics. The experimen-

tations are done on a 2.4GH

Intel Core2 Duo laptop,

with 8Gb of RAM.

First of all, the efﬁciency aspect of the smart

polyhedral analysis strongly depends on its execution

time. So, we evaluate the efﬁciency of this analy-

sis by computing its execution time. Table 1 shows

the execution time obtained using the smart polyhe-

dral analysis. In this experimentations, the function

∆Generation() in the Algorithm 2 deﬁned ∆ as a set

of vectors uniformly distributed on a surface of the

n-dimensional sphere plus the orthogonal vectors, its

cardinality is noted |∆|. We have also that the col-

umn labeled t is the execution time (in seconds). The

column labeled by |V | represents the number of pro-

grams variables. Note that, |V | also represents the

dimension of the computed polyhedron. In general,

when a program uses a large number of variables, it

means that the corresponding analysis is calculating

high-dimensional polyhedra. High-dimensional poly-

hedra present several challenges in terms of compu-

tation and analysis. The polyhedra generated depend

on the analysis tool and the program under analysis.

Their dimensions can range from a few variables in C

programs to a thousand in Lustre programs. In gen-

eral, the analysis tools try to limit their use of polyhe-

dral analysis to a small number of variables and con-

straints. In the case where those limits are exceeded,

the analysis switches to less expressive abstract do-

main, as for example the interval domain. So, the pa-

rameter |V | is used in our experimentation to show the

scalability of our method.

We emphasize that for most of these programs the

polyhedral analysis don’t terminate before the time-

out (more than 10 minutes). If we use the widening

operator the results go to top, which represents a bad

accuracy. In Table 1 thus shows the efﬁciency of our

method with several programs.

To further illustrate the expressiveness aspect of the

smart widening operator, we display on Figure 3 and

Figure 4 the results of the smart polyhedral analysis,

given by the red and orange polyhedra, respectively,

the used threshold obtained using the P

∆

analysis is

given by the blue and yellow polyhedra, respectively.

Note that, on Figure 3 the blue polyhedra are con-

tained within the red polyhedra , this shows the qual-

ity of the invariant we compute.

6 CONCLUSION

In this article we have deﬁned a new method to im-

prove polyhedral analysis. Introducing a new ver-

sion of the Kleene iteration algorithm that utilizes a

Smart Widening for the Polyhedral Analysis

Table 1: Table of results obtained using our analysis and the polyhedral one.

Program Polyhedral analysis with ∇

Polyhedral analysis

Name |V | |∆| t(s) t(s)

prog 2 308 2.202 TO

filter1 4 332 2.202 TO

filter2 4 332 6.264 TO

filter3 4 332 59.764 TO

filter4 5 350 2m10.953 TO

lead leg controller 5 350 5m58.748 TO

Dampened oscillator 6 332 15.291 TO

Harmonic oscillator 6 332 4.882 TO

lp iir 9600 2 6 372 1m13.537 TO

double input1() {

double u = 10.0;

double l = -10.0;

return ( rand()/(double)RAND_MAX )

* (u-l) + l;

}

double input2() {

double u = 3.0;

double l = 0.0;

return ( rand()/(double)RAND_MAX )

* (u-l) + l;

}

int main() {

double x, xn, y,yn;

srand(time(NULL));

x=input1();

y=input2();

xn=yn=0;

int i=0;

while (i<10000){

xn = 0.5 *x - y - 2.5;

yn = 0.9 *y + 10;

x = xn;

y = yn;

}

return 0;

}

Figure 3: (Left) The body of the program called prog. (Right) The red polyhedron is the post ﬁxed point obtained using the

smart widening operator. The blue polyhedron is the threshold obtained using P

∆

analysis.

novel widening operator, the ”smart widening opera-

tor,” represents a signiﬁcant advancement in polyhe-

dral analysis techniques. The smart widening opera-

tor applies the P

∆

analysis on the program under anal-

ysis. P

∆

The result of the P

∆

analysis serves as the

ﬁxed-point candidate for the polyhedral analysis. The

result obtained from the P

∆

represents a template rep-

resentation of the ﬁxed point achieved through poly-

hedral analysis. These templates capture important

directions or patterns in the program’s state space,

providing a compact and informative representation

of the ﬁxed point. The smart widening operator is in-

tegrated into the Kleene iteration algorithm to guide

the iterative reﬁnement process. Instead of apply-

ing traditional widening techniques, the algorithm ap-

plies the P

∆

analysis to obtain the ﬁxed-point can-

didate, which serves as the threshold for widening.

By using the template representation obtained from

∆

analysis, the smart widening operator aims to im-

prove both the efﬁciency and precision of the polyhe-

dral analysis. The experimental results show that the

smart widening operator allows to speed up the poly-

ICSOFT 2024 - 19th International Conference on Software Technologies

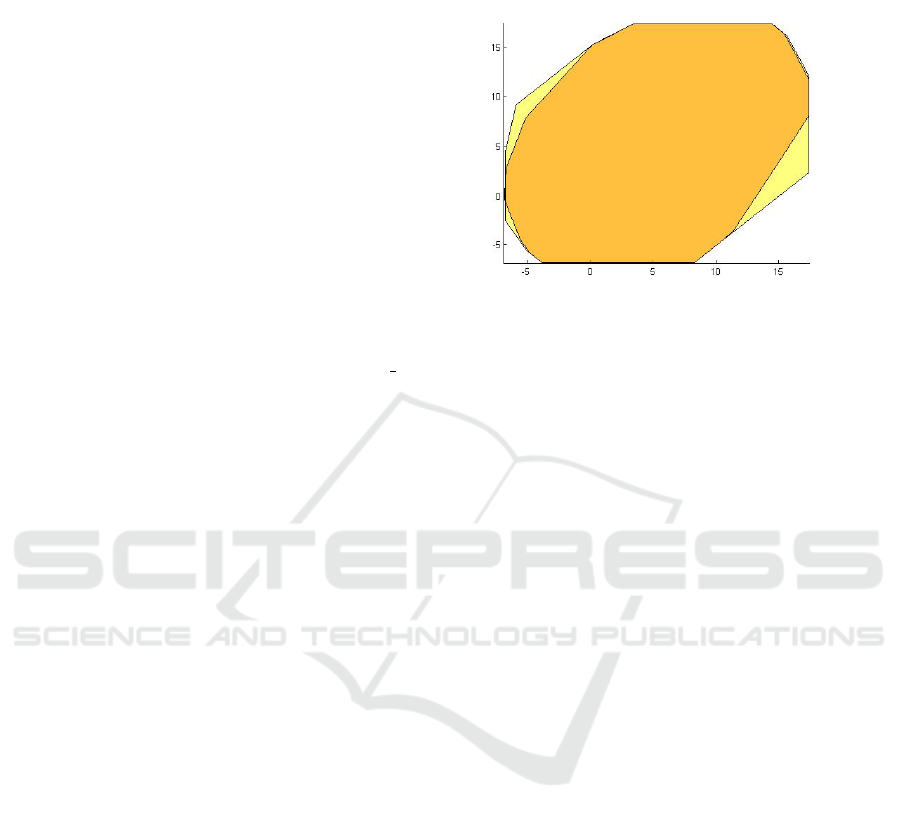
double input() {

double u = 10.0, l = 0.0;

return ( rand()/(double)RAND_MAX )

* (u-l) + l;

}

int main() {

double xn, yn, ynm1,ynm2 ;

xn=xnm1=xnm2=yn=ynm1=ynm2=0;

int i=0;

while (i<4000) {

yn = xn + 0.5*ynm1 - 0.45*ynm2;

printf("%f %f\n",ynm1,yn);

ynm2=ynm1;

ynm1=yn;

xn = input();

}

return 0;

}

Figure 4: (Left)The body of the program called Filter 2.(right) The orange polyhedron is the post ﬁxed point obtained using

the smart widening operator. The yellow polyhedron is the threshold obtained using P

∆

analysis.

hedral analysis when the standard polyhedral analy-

sis fails. The smart widening operator can easily be

adapted to other abstract domains, for which the set

∆ should be adapted to the shape of the correspond-

ing domain. The choice of this set plays an important

role in the accuracy and relevance of the result of the

smart widening operator. In our future work, we will

develop a method to dynamically deﬁne a relevant set

∆ using the work presented in (Seladji, 2017).

REFERENCES

Arceri, V., Dolcetti, G., and Zaffanella, E. (2023). Speed-

ing up static analysis with the split operator. In Fer-

rara, P. and Hadarean, L., editors, Proceedings of the

12th International Workshop on the State Of the Art in

Program Analysis,Orlando, FL, USA.

Bouissou, O., Seladji, Y., and Chapoutot, A. (2012). Accel-

eration of the abstract ﬁxpoint computation in numeri-

cal program analysis. J. Symb. Comput., 47(12):1479–

1511.

Castagna, G. and Gordon, A. D. (2017). Fast polyhedra ab-

stract domain. In Proceedings of the 44th ACM SIG-

PLAN Symposium on Principles of Programming Lan-

guages, Paris, France.

Cousot, P. and Cousot, R. (1977). Abstract interpretation: a

uniﬁed lattice model for static analysis of programs by

construction or approximation of ﬁxpoints. In POPL,

pages 238–252.

Cousot, P. and Cousot, R. (1992). Comparing the Galois

connection and widening/narrowing approaches to ab-

stract interpretation, invited paper. In PLILP, volume

631 of LNCS, pages 269–295. Springer-Verlag.

Cousot, P. and Halbwachs, N. (1978). Automatic discovery

of linear restraints among variables of a program. In

POPL.

Goubault, E., Putot, S., and V

edrine, F. (2012). Modular

static analysis with zonotopes. In Static Analysis-19th

International Symposium, 2012, Deauville, France.

Proceedings.

Hiriart-Urrut, J.-B. and Lemarechal, C. (2004). Fundamen-

tals of Convex Analysis. Springer.

Lakhdar-Chaouch, L., Jeannet, B., and Girault, A. (2011).

Widening with thresholds for programs with complex

control graphs. In ATVA, pages 492–502.

Min

e, A. (2006). The octagon abstract domain. Higher-

Order and Symbolic Computation, 19(1):31–100.

Sankaranarayanan, S., Sipma, H. B., and Manna, Z. (2005).

Scalable analysis of linear systems using mathemati-

cal programming. In VMCAI, volume 3385 of LNCS,

pages 25–41.

Seladji, Y. (2017). Finding relevant templates via the princi-

pal component analysis. In Veriﬁcation, Model Check-

ing, and Abstract Interpretation - 18th International

Conference, VMCAI 2017, Paris, France, January 15-

17, 2017, Proceedings.

Seladji, Y. and Bouissou, O. (2013). Numerical abstract do-

main using support functions. In NASA Formal Meth-

ods, 5th International Symposium, NFM 2013, Moffett

Field, CA, USA. Proceedings.

Yu, H. and Monniaux, D. (2019). An efﬁcient parametric

linear programming solver and application to polyhe-

dral projection. In Chang, B.-Y. E., editor, Static Anal-

ysis.

Smart Widening for the Polyhedral Analysis