A Model of the Control System of a Carbon Dioxide Gas Turbine in

Supercritical Condition

Marcin Zawadzki, Jarosław Milewski

and Arkadiusz Szczęśniak

Institute of Heat Engineering, Faculty of Power and Aeronautical Engineering, Warsaw University of Technology,

21/25 Nowowiejska Street, 00-665 Warsaw, Poland

Keywords: Gas Turbine, Closed Cycle, Power Control, Carbon Dioxide, Supercritical State, Model, GateCycle.

Abstract: The primary goal of the paper was to develop a model for a supercritical carbon dioxide gas turbine. The

model was built using the GateCycle program It is designed for potential implementation in emerging

Concentrating Solar Plants, with a focus on simple yet efficient construction in the recuperation model.

Analyses were conducted on three types of power control systems: bypass, inventory, and turbine inlet

temperature-based, using the Lee-Kesler real gas model for calculations. Key mathematical formulas used by

the program are cited, and results are thoroughly analyzed and presented in charts. In conclusion, a

combination of bypass and inventory control systems is recommended.

1 INTRODUCTION

The global energy industry is currently moving

toward renewable energy sources. The main obstacle

standing in its way is the heavy dependence of energy

production on non-anthropogenic factors. Various

strategies could be applied, such as the integration of

Renewable Energy Sources (RES) with electrolysers

for synthetic fuel generation (Milewski et al., 2024)

or combining RES with traditional technologies. An

interesting idea is the use of gas turbines operating in

closed circuits. These systems show good

controllability, which can help solve the outlined

problem. The closed-cycle Gas Turbine (GT) could

serve as a power conversion system for non-CO2

emission energy sources (Olumayegun, Wang and

Kelsall, 2016) such as nuclear reactors, concentrated

solar power, biomass, geothermal, and fuel cells

(Kim, Kim and Favrat, 2012).

Contrary to appearances, this is not a new,

innovative technology, as the first concepts for the

construction of closed-cycle gas turbine systems

appeared as early as the 1930s (Miller, 1984). The

most likely reason for the stagnation in the

development of this area was the rapid growth of

open-system gas turbine systems. Open-circuit

systems dominated the gas turbine market after the

https://orcid.org/0000-0003-1215-1802

use of blade cooling technology, which enabled

turbine inlet temperatures of 1,700°C, allowing them

to achieve significantly higher efficiency than closed-

circuit systems. Thanks to the development of high-

temperature-resistant materials and the emergence of

new potential applications, closed-cycle gas turbine

systems are once again becoming the focus of

research centers and are poised to enter the industrial

market. Due to their nature, the opportunity for

commercial implementation of closed-loop gas

turbine systems is in Concentrating Solar Plants

(CSP) in Solar Tower (ST) systems (Stein and Buck,

2017; Merchán et al., 2021) . This technology is

recognized as a renewable and carbon-neutral source

of energy (Wu et al., 2021) . For this reason, the main

parameters of the system have been selected so that it

can be implemented in newly built power plants of

this type. The world's largest Solar Tower

Concentrated Solar Plant has a net capacity of 377

MW (Boretti, Castelletto and Al-Zubaidy, 2019).

State-of-the-art technologies using molten salts allow

working medium temperatures of 550°C and energy

storage for several hours.

The optimization of the system with

recompression was performed by Sarkar et al.

(Sarkar and Bhattacharyya, 2009) . The authors

indicated that the maximum efficiency improvement

using reheating is determined to be 3.5% under

Zawadzki, M., Milewski, J. and Szcze¸

sniak, A.

A Model of the Control System of a Carbon Dioxide Gas Turbine in Supercritical Condition.

DOI: 10.5220/0012866200003758

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2024), pages 443-455

ISBN: 978-989-758-708-5; ISSN: 2184-2841

443

optimum conditions. An in-depth analysis of the topic

was reported by Dostal et al. (Dostal, Driscoll and

Hejzar, 2004)

, who concluded that the recompression

cycle offers the best efficiency and retains its

simplicity. Intercooling, however, is less appealing

for this cycle type because it only provides a slight

boost in efficiency. Reheating holds more promise,

though it is suitable solely for indirect cycles.

Ma et al. (Ma et al., 2024)

developed a model of

a 5 MW S-CO2 recompression cycle oriented toward

operational control. The model includes validated

dynamic models of the following components:

printed circuit heat exchangers, compressors, and gas

turbines. The validated control strategies for the

system involve using a cooling water controller to

keep the compressor inlet temperature above CO2's

critical temperature (304.13 K). They also adjust the

circulating mass flow rate to change output power and

control the exhaust gas flow rate to maintain safe

turbine inlet temperatures. Performance comparisons

between PI (Proportional-Integral) controllers (tuned

via SIMC rule) and ADRC (Active Disturbance

Rejection Control) controllers (tuned via bandwidth

method) show that both effectively manage operating

conditions and suppress exhaust fluctuations.

However, ADRC controllers outperform by reducing

settling time by 55% in load-tracking scenarios.

Dario et al. (Alfani et al., 2021)

optimized various

sCO2 cycles for waste heat recovery. The simple

recuperative cycle with bypass was selected as the

optimal configuration. The authors revealed that the

implementation of an external CO2 storage tank,

which enables varying the CO2 inventory in the

system, beneficially influences the system's

efficiency during part-load operation. Specifically,

when dealing with low flue gas mass flows—at 30%

of the nominal rate—a 20% enhancement in power

generation is achievable compared to strategies where

the CO2 inventory remains unchanged.

The purpose of this paper is the theoretical

analysis of various methods of power control of a

fabricated gas turbine model with CO2 with

supercritical parameters as the working medium,

together with a review of current research on the

systems considered. Three basic control methods will

be compared with each other: bypass, by

displacement, and by temperature. Despite numerous

studies related to the subject under discussion, the

problem under consideration has not yet been

sufficiently addressed.

The paper presents a novel model of a

supercritical carbon dioxide gas turbine designed for

potential implementation in emerging Concentrating

Solar Plants. The key contributions of this paper

include the development of a comprehensive model

using the GateCycle program, focusing on simplicity

and efficiency in the recuperation model. The model

integrates existing power control methods, namely

bypass, inventory, and turbine inlet temperature-

based controls, and evaluates their effectiveness using

the Lee-Kesler real gas model for calculations. One

significant contribution is the recommendation of a

combined approach of bypass and inventory control

systems, which balances the need for quick

responsiveness and maintaining high efficiency. The

paper thoroughly analyzes these control systems,

providing detailed mathematical formulas and results

presented in various charts. Additionally, the model's

adaptability to high-pressure and high-temperature

conditions using the Lee-Kesler equations marks an

advancement in accurately simulating supercritical

carbon dioxide gas turbine systems. This work paves

the way for integrating such advanced models into

next-generation renewable energy power plants,

specifically those utilizing solar energy, thus

contributing to the global shift towards sustainable

energy solutions.

The application of closed-cycle gas turbine

systems, especially those utilizing supercritical

carbon dioxide as the working medium, presents a

promising solution for integration into Concentrating

Solar Plants (CSP). These systems are particularly

suited for Solar Tower (ST) configurations, where

high operational temperatures and efficiency are

paramount. By leveraging the unique properties of

supercritical CO

, these turbines can achieve higher

efficiencies and better performance in CSP

applications compared to traditional working fluids.

This makes them an ideal choice for enhancing the

viability and sustainability of solar energy power

generation. Consequently, the implementation of

these advanced gas turbine systems in CSP not only

supports the drive towards renewable energy but also

addresses the need for efficient and reliable power

conversion technologies in solar energy applications.

The advancements in control strategies and system

optimization outlined in this paper further underscore

the potential of these technologies to play a critical

role in the future of renewable energy infrastructure.

2 THEORETICAL

BACKGROUND

One of the advantages of gas turbines in closed

systems is the ability to regulate power over a large

range with almost no drop in efficiency. The power

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

444

of the system depends on the mass flow, the turbine

inlet temperature (TIT), the gas temperature before

the compressor, the compression ratio, and the

efficiency. Control possibilities include the use of a

storage tank, bypass, or temperature control.

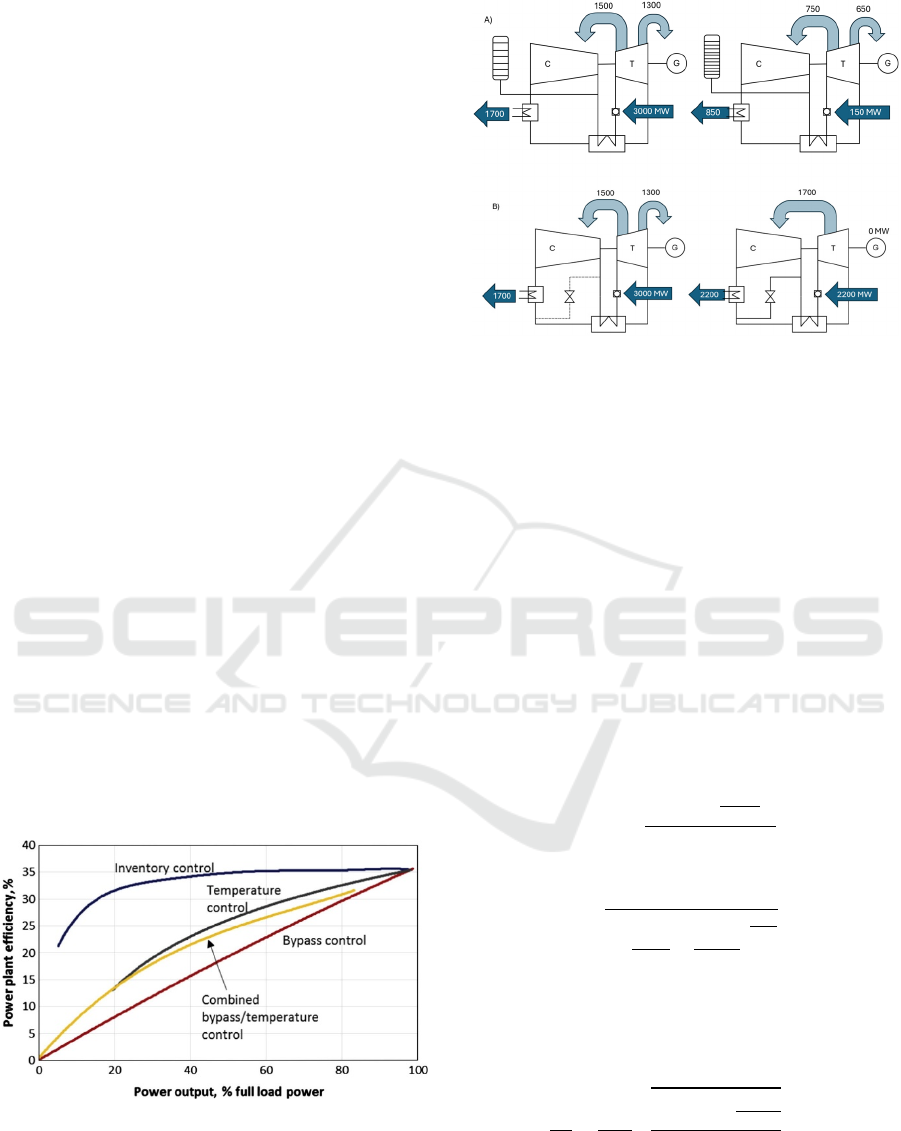
The most advantageous method is to change the

discharge by using a storage tank. This is called

discharge control or pressure control. When

decreasing from the current load, some of the gas is

diverted to the storage tank. This causes a decrease in

mass flow and pressure at the compressor inlet. As

power increases, gas is released from the tank into the

system. Within a large power range, this method

allows smooth control with a relatively small

decrease in efficiency—see Figure 1 , line "inventory

control." The downsides of this method are the

relatively slow response time and the need for large

storage tanks. For this reason, this method of

regulation should be abandoned in favor of the others

for larger power units. A schematic of the system with

applied mass flow control is shown in Figure 2 (a).

Another method is bypass control. It involves the

use of a bypass of the expander and the heat

exchanger with the upper heat source, reducing the

flow of gas through these components while leaving

the compressor unchanged. A schematic of the

system with bypass control is shown in Figure 2 (b).

The advantage of this solution is the ability to respond

almost immediately to rapid changes in power. The

major disadvantage, on the other hand, is the

significant drop in system efficiency during power

reduction.

The third method is upper source temperature

control. This is the slowest method presented but

provides higher efficiency at lower loads than bypass

control.

Figure 1: Effect of power regulation on efficiency

(Olumayegun, Wang and Kelsall, 2016).

Figure 2: Schematic of the power control system: (a)

method using a storage tank (b) bypass method.

2.1 Closed System of Gas Turbine

Figure 1 shows the dependence of system efficiency

as a function of load for the methods described. The

best solution is to use a combination of bypass

regulation, which would operate when

responsiveness is crucial, with regulation using a

regulating tank—slower, but allowing the system to

maintain a high level of efficiency.

When analyzing the operation of the system under

changed conditions, it is important to note the most

significant relationships describing it. When

controlling the system, the discharge pressure from

the compressor changes due to the forcing caused by

the turbine inlet. This forcing is determined by the

following relation:

𝐶𝑜𝑛𝑠𝑡𝑎𝑛𝑡=

𝑚









𝜅⋅

𝐴



⋅𝑃



(1)

Where:

𝜅=



𝑔⋅

𝛾

𝑅



⋅

𝛾1







(2)

The speed of the compressor also changes, which

can be determined by an algorithm using the flow

equation:

𝑛



𝐶𝑆





𝑇



⋅𝑍⋅

𝑀𝑊



𝑀𝑊

𝑇



⋅𝑍



(3)

Where the subscript D stands for design

parameters (design mode).

A Model of the Control System of a Carbon Dioxide Gas Turbine in Supercritical Condition

445

In situations where access to the compressor map

is impossible, its isentropic efficiency can be

calculated based on the equation:



⬚

1−SEC⋅

CS−CS

⬚



⬚

⋅PF⋅



1−α⋅VEC



(4)

The above relationships are applicable to

GateCycle software and will be used to make the

model.

3 MODEL DEVELOPMENT

Research is based on the mathematical model of a

supercritical carbon dioxide gas turbine. The model

has been constructed in the GateCycle program,

which capabilities in reliability of simulations of are

confirmed by many papers such as e.g. (Malinowski,

Lewandowska and Giannetti, 2017; Ary Bachtiar and

Maryono, 2019; Hasananto, Darmadi and Yuliati,

2021). It provides accurate thermodynamic analysis,

integrates detailed component models, and allows for

precise performance predictions under various

operating conditions.

The model's parameters have been set so that it

could be implemented in emerging Concentrating

Solar Plants. The recuperation model has been

created for simplicity of construction while providing

high efficiency. Analyses have been performed on

three types of power control systems: bypass,

inventory, and turbine inlet temperature-based. Real

gas equations were used in the model. For

calculations in areas of very high pressures or

temperatures and around the critical point, these

equations may not provide sufficient quality results.

According to GE Energy, the Lee-Kesler equations

give the closest results for CO2 and air to VDI

Warmeatlas table data over a large range of pressures

and temperatures. For this reason, it was decided to

use this real gas model.

The disadvantage of the model is the inability to

simulate the molten salt compounds forming the

upper heat source. For this reason, it was described

as a water flow with the most relevant parameters the

same as the actual medium.

The main assumptions for the simulation have

been listed in Table 1.

Table 1: Main assumptions for model development.

Parameter Value

Temp. at inlet to compressor, °C 31

Pressure at inlet to compressor, MPa

7.4

Temp. at turbine inlet, °C 550

Pressure at turbine inlet, MPa 24

Mass flow rate of the medium, kg/s 500

Max. upper heat source temp,

°C

565

Ambient temp., °C 20

Real gas model

Lee-Kesler

model

A system with heat regeneration was chosen for

the simulations because of its relatively high

efficiency while keeping the system simple and

compact. The layout of the model implemented in

GateCycle is shown in Figure 3 and the main

operating parameters are shown in Table 2.

Table 2: Parameters of the examined cycle.

T p M H

K kPa Kg/s kJ/kg

1 347.82 24487.3 500 155.53

2 347.82 24487.3 500 155.53

3 569.95 24242.4 500 216.48

4 823.15 24000.0 500 535.28

5 686.25 7550.3 500 384.84

6 362.82 7474.7 500 9.11

7 362.82 7474.7 500 9.11

8 304.15 7400.0 500 187.35

9 293.15 101.3 500 4.25

10 351.82 100.31 500 63.81

11 838.14 4000.0 500 3592.77

12 669.94 3960.0 500 3208.89

The model consists of a compressor (C1 in Figure

4), which was simulated with the following settings

listed in Table 2.

Table 3: C1 compressor settings.

Parameter Value

Desired Isentropic Efficiency 0.82

Desired Outlet Pressure

24,487.297 kPa

Design Compressor RPM 3,000

Mechanical Efficiency 0.98

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

446

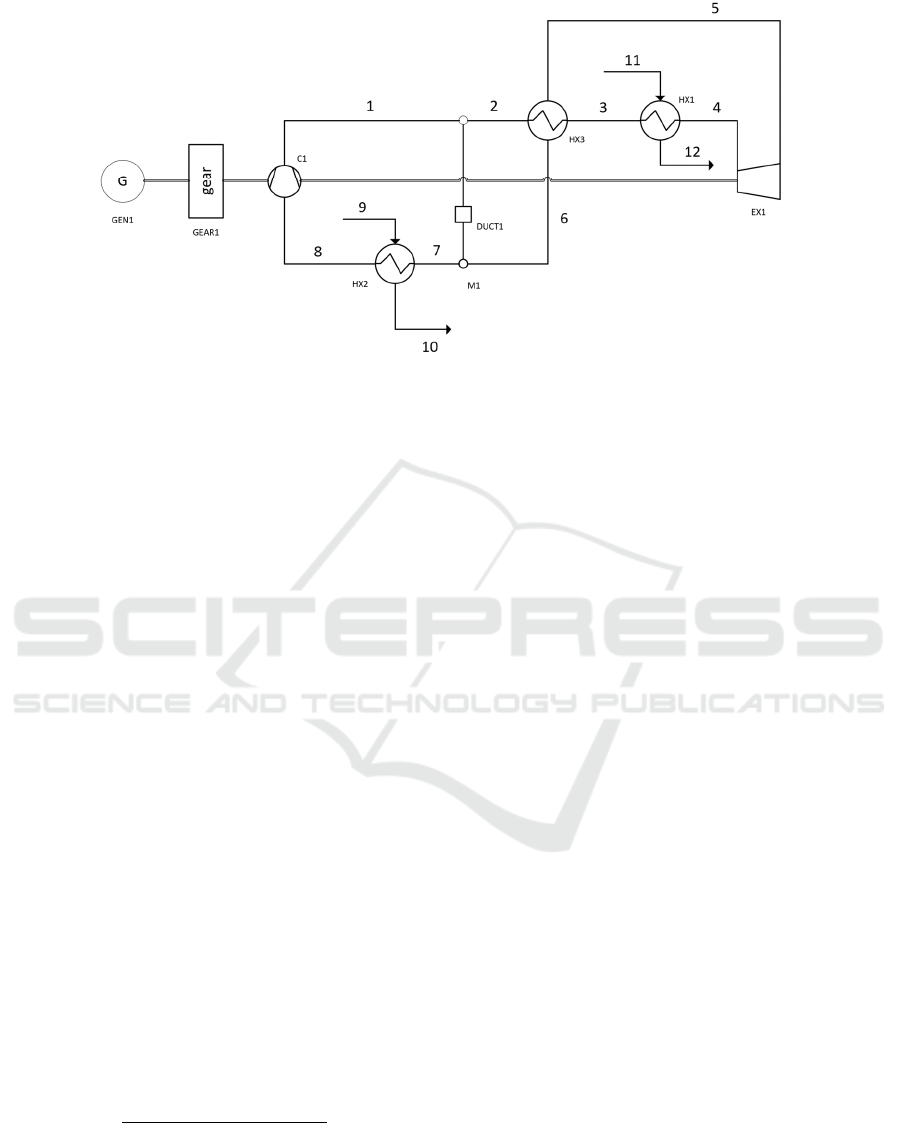
Figure 3: Scheme of the examined cycle.

The upper heat source was simulated by heat

exchanger HX1. The set parameters of the added

elements are given below:

• Design Method: Cold Side Outlet

Temperature

• Desired Cold Side Outlet Temperature:

823.15K

• Second Design Method: Pinch (Hot Out -

Cold In)

• Desired Pinch (Hot Out - Cold In): 100 K

• Demand Flow Method: Generate Hot Side

Demand Flow

• Cold Side Pressure Loss: 0.01

• Hot Side Pressure Loss: 0.01

• Limits:

• Minimum Overall Heat Transfer

Coefficient: 0.01

The EX1 turbine was attached to the system,

connected by a shaft to the compressor. The

parameters of the gas turbine were:

• Outlet Pressure: 7,550.25 kPa

• Desired Isentropic Efficiency: 0.9

The default setting is left: Calculate Flow Area

Using Inlet Pressure, Temperature, and Flow, which

will determine the area of the inlet channel, allowing

further off-design calculations. The definition of

isentropic efficiency is:



𝑊



𝑚ℎ









𝑚ℎ









𝑚ℎ





−



𝑚ℎ





(5)

where the subscripts denote: 0-inlet, 1-outlet, 2-

nozzle cooling, 4-rotor cooling, s-isentropic

conditions.

The lower source heat exchanger was simulated by

HX2 heat exchanger with the following settings:

• Design Method: Hot Side Outlet Temperature

• Desired Cold Side Outlet Temperature:

304.15 K

• Second Design Method: Pinch (Hot In - Cold

Out)

• Desired Pinch (Hot In - Cold Out): 11 K

• Demand Flow Method: Generate Cold Side

Demand Flow

• Hot Side Pressure Loss: 0.01

• Cold Side Pressure Loss: 0.01

• Number of HTX Passes: 40

• Limits:

• Minimum Overall Heat Transfer

Coefficient: 0.01

A bypass control system was attached to the model,

consisting of the DUCT1 flow valve, SP1 flow

distributor, and M1 mixer. Duct is an element that

allows modeling of pressure and temperature drops in

gas streams. A similar effect can be achieved with the

Flow Pressure-Temperature Modifier, which

additionally allows changing the flow rate.

SP1:

• Primary Port (S12) Control Method: Specify

Flow Fraction

• Primary Port Desired Fraction: 1

• Secondary Port (S13) Control Method:

Remainder Port

M1:

• Equalize Inlet Pressures Method: Equalize to

Pressure of Specified Port

A Model of the Control System of a Carbon Dioxide Gas Turbine in Supercritical Condition

447

• Controlled Inlet Port for Pressure: Primary

(S9)

DUCT1:

• Pressure Method Flag: Outlet Pressure

• Desired Exit Pressure: 7,474.74 kPa

As GateCycle does not allow the insertion of an

accumulation tank into the system, a Flow-Pressure-

Temperature Modifier was included to simulate it

behind the compressor. By forcing a specific flow

value, a change in tank filling is simulated.

During off-design operation, the speed of the

system changes under the influence of changes in the

parameters of the working medium, so a gearbox is

required to keep the generator synchronized with the

grid. It has been added to the model under the name

GEAR1. In the method used, power losses are

calculated using equations implemented in the

program. In the off-design mode, calculations of

gearbox efficiency are identical to those in the design

mode, so there is no need to change the settings of this

element for further calculations.

To carry out off-design simulations, new model

cases were created in which the following elements

were set for off-design calculations: EX1, HX1, HX2,

HX3, C1, GEN1. In addition, the following settings

were made.

HX2:

• Second Design Method: Hot Side Outlet

Temperature

• Desired Hot Side Outlet Temperature: 304.15

• Demand Flow Method: Generate Cold Side

Demand Flow

• Minimum Pinch Limit: 10 K

C1:

• Off Design Pressure Method: Flow Equation

with Flow, RPM (Revolutions Per Minute) or

CS and Pressure Input

• Desired Outlet Pressure: 24,487.972 kPa

• Off Design Flow/RPM Method: Accept

• Incoming Flow

• Minimum Compressor %CS: 40

• Off-Design Efficiency Method: Use Equation

to Calculate Isentropic Efficiency

HX1:

• Second Design Method: Cold Side Outlet

Temperature

• Desired Cold Side Outlet Temperature: 823.15

• Demand Flow Method: Generate Hot Side

Demand Flow

Off-design calculations were carried out to simulate

the three basic methods of power control: flow

change, bypass, and temperature change. Flow

change was induced using the FPT1 element by

changing the Desired Outlet Flow value in 5%

increments of the nominal flow. This method also

allowed the turbine to be topped off with a flow

higher than nominal. Bypass control was achieved by

changing the Primary Port Desired Fraction value at

the splitter, also in 5-percentage point steps. The

change in inlet temperature to the turbine was

achieved by changing the Desired Cold Side Outlet

Temperature in HX1, decreasing it, as in the previous

cases, also in 5-percentage point increments. The

results with analysis are presented in the following

sections.

4 RESULTS

After three series of calculations, the results from all

cases were collected and presented in graphs.

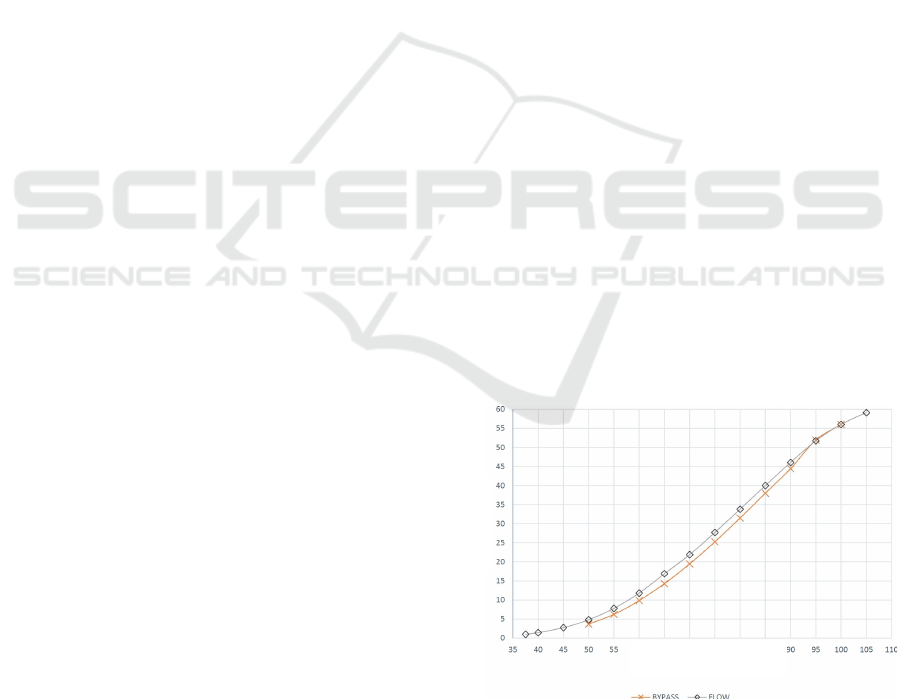
Figure 4

and Figure 5 how the change in system power as a

function of the change in flow through the turbine

(with bypass and discharge regulation, labelled

BYPASS and FLOW, respectively, on the graph) and

the change in inlet temperature to the turbine (with

temperature regulation labelled TEMP). As can be

seen, the methodology used for flow or temperature

changes allowed for a uniform distribution of post-

measurement points with a thickening in the direction

of decreasing power, which is a desirable

phenomenon.

Figure 4: Power as a function of factor output through the

turbine.

Flow through the turbine [%]

Power [MW]

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

448

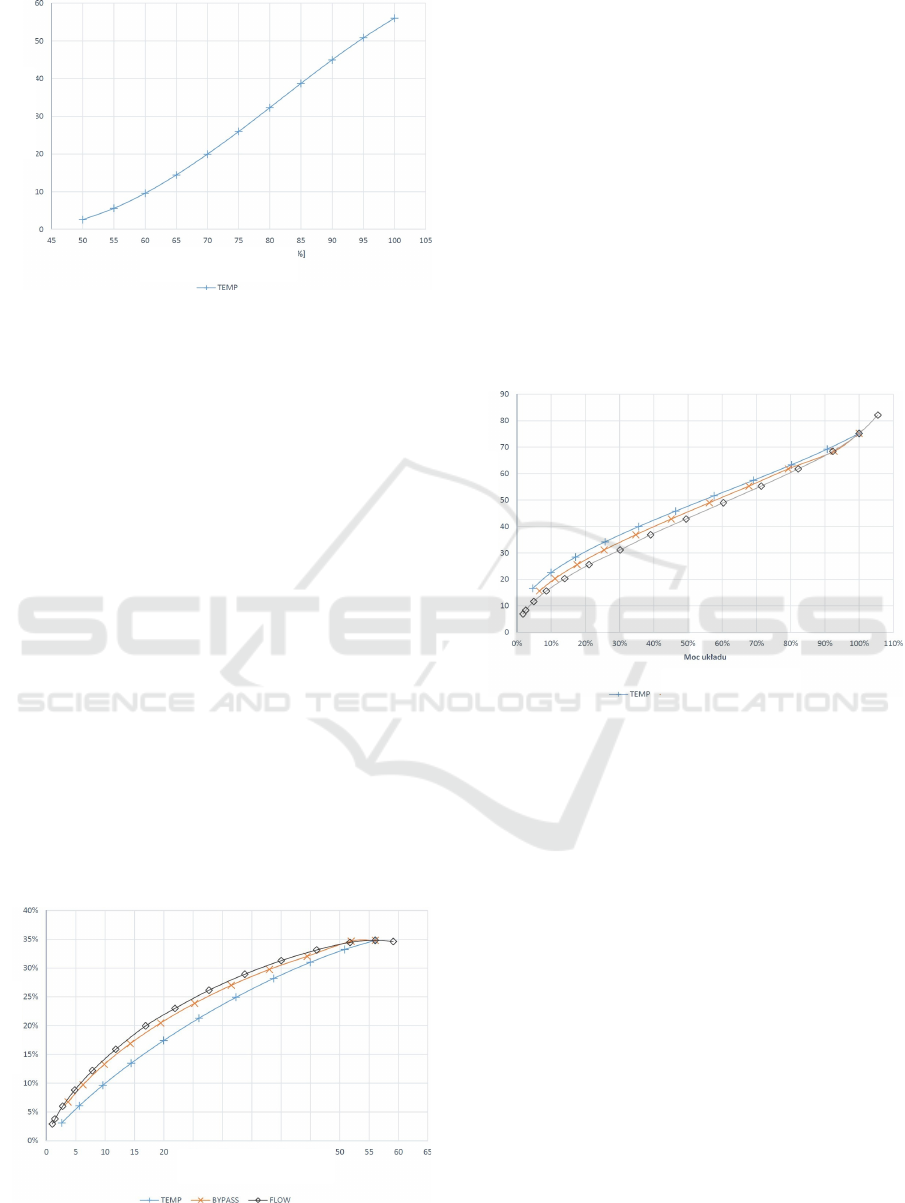
Figure 5: System power as a function of inlet temperature

change per turbine.

The main factors in choosing a power control

system are efficiency, response time, and cost. The

stability of the system's operation under changed

conditions is also an important aspect. Analyzing the

graph of the efficiency of the system as a function of

its power (see Figure 6), it can be concluded that the

best in this respect is the flow rate control system.

Slightly lower values are achieved by the bypass

control system, and significantly lower by the

temperature control system.

After three series of calculations, the results from

all cases were collected and presented in graphs.

Figure 5 and Figure 6 show the change in system

power as a function of the change in flow through the

turbine (with bypass and discharge regulation,

labelled BYPASS and FLOW, respectively, on the

graph) and the change in inlet temperature to the

turbine (with temperature regulation labelled TEMP).

As can be seen, the methodology used for flow or

temperature changes allowed for a uniform

distribution of post-measurement points with a

thickening in the direction of decreasing power,

which is a desirable phenomenon.

Figure 6: System efficiency as a function of generator

power.

The main factors in choosing a power control

system are efficiency, response time, and cost. The

stability of the system's operation under changed

conditions is also an important aspect. Analyzing the

graph of the efficiency of the system as a function of

its power (see Figure 6), it can be concluded that the

best in this respect is the flow rate control system.

Slightly lower values are achieved by the bypass

control system, and significantly lower by the

temperature control system.

The graph from the theoretical part was made for

a system for which the working medium was not

specified in the source, but it was most likely air or a

perfect gas. For this reason, the efficiency curves

obtained in the simulation have a distinctly different

shape.

Figure 7: Power generated by the expander as a function of

system power.

To further explain this phenomenon, it is

worthwhile to analyze the operation of rotating

machines under the changed conditions. The expander

was analyzed first. Figure 7 shows a graph of the

power generated on the turbine as a function of the

power of the whole system. As can be seen, the

expander generates the highest power with

temperature control and the lowest with output

control, which is quite the opposite of what would

seem consistent with the efficiency graph (Figure 6).

Thus, the factor determining the efficiency of the

system is the power consumed by the compressor.

Turbine inlet temperature [%]

Power [MW]

Efficiency

Power

Turbine power [MW]

A Model of the Control System of a Carbon Dioxide Gas Turbine in Supercritical Condition

449

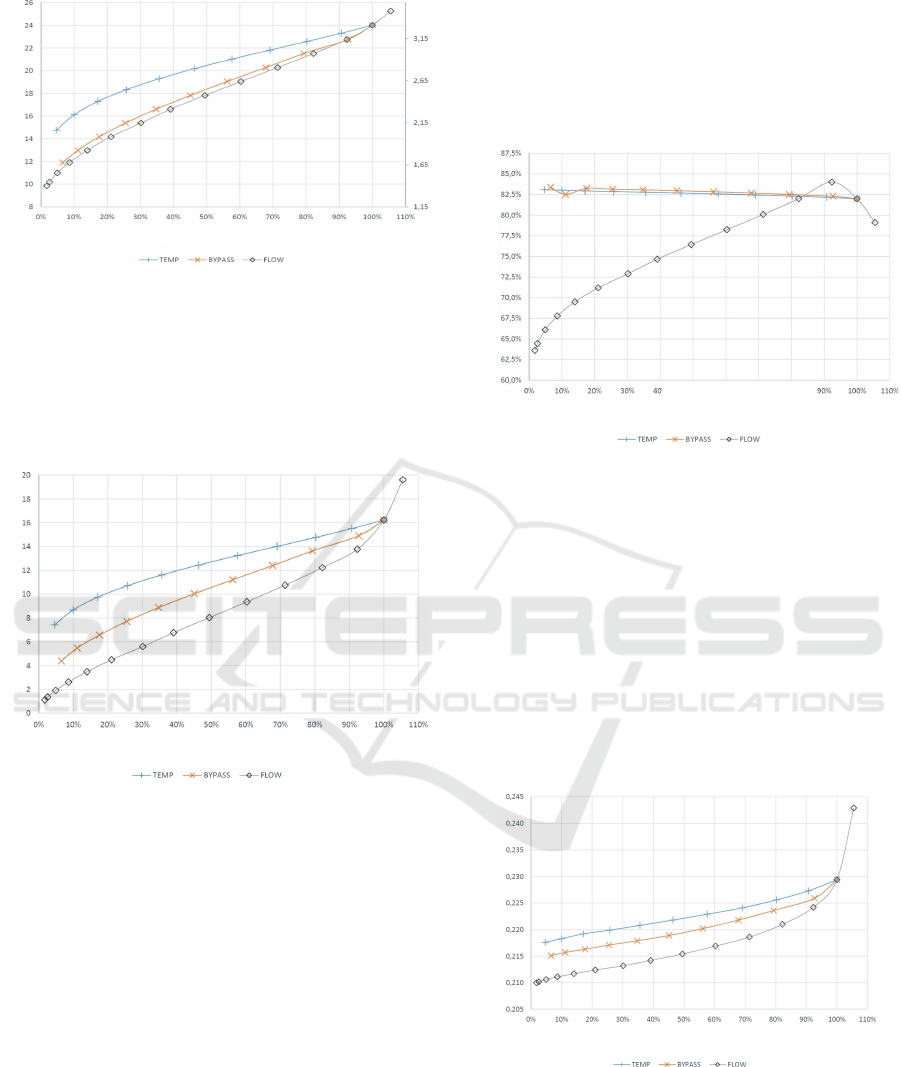
Figure 8: Power generated by the expander as a function of

system power.

Considering that the inlet pressure on the

compressor, which is the lowest pressure in the

system, almost does not change, Figure 8 plots the

values of the system compression on the auxiliary

axis (on the right side of the graph).

Figure 9: Compressor power as a function of system power.

A more in-depth analysis of individual results

reveals significant insights. For instance, Figure 8

shows the power generated by the expander as a

function of system power. The expander generates the

highest power with temperature control, despite this

method resulting in the lowest overall system

efficiency (Figure 6). This discrepancy indicates that

the power consumption by the compressor is a crucial

factor. Figure 9 supports this observation, illustrating

that the compressor consumes the least power under

discharge control, which correlates with the highest

system efficiency.

With all other parameters unchanged, an increase

in system compression implies an increase in the

power consumed by the compressor. Such a

relationship can be seen by comparing the TEMP and

BYPASS curves on the graph of compressor power

as a function of system power (see Figure 9). It can

also be seen that the least power is consumed by the

compressor when controlling the discharge. This is

due to the reduced flow rate. The graph in Figure 9

also shows that a 5 percentage point increase in flow

causes a greater increase in power than a decrease in

power with a corresponding decrease in flow.

Figure 10: Compressor isentropic efficiency as a function

of system power.

Additionally, Figure 10 depicts the isentropic

efficiency of the compressor as a function of system

power. It is evident that the efficiency is significantly

influenced by the discharge method, which minimizes

power consumption more effectively than other

methods. This is further corroborated by Figure 11

and Figure 12, showing the compressibility factor (Z-

factor) at the compressor inlet and outlet. The Z-

factor remains relatively stable at the inlet but

fluctuates at the outlet, especially under temperature

control, indicating complex interactions between the

working fluid's properties and system performance.

Figure 11: Compressor inlet refrigerant compressor

compressibility factor as a function of system power.

A decrease in the power consumed by the

compressor does not directly translate into an increase

in its isentropic efficiency, as can be seen in Figure

10. The graph of the compressor's isentropic

Power

Z IN

Turbine inlet pressure [MPa]

Compressor isentropic efficiency

Compressor power [MW]

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

450

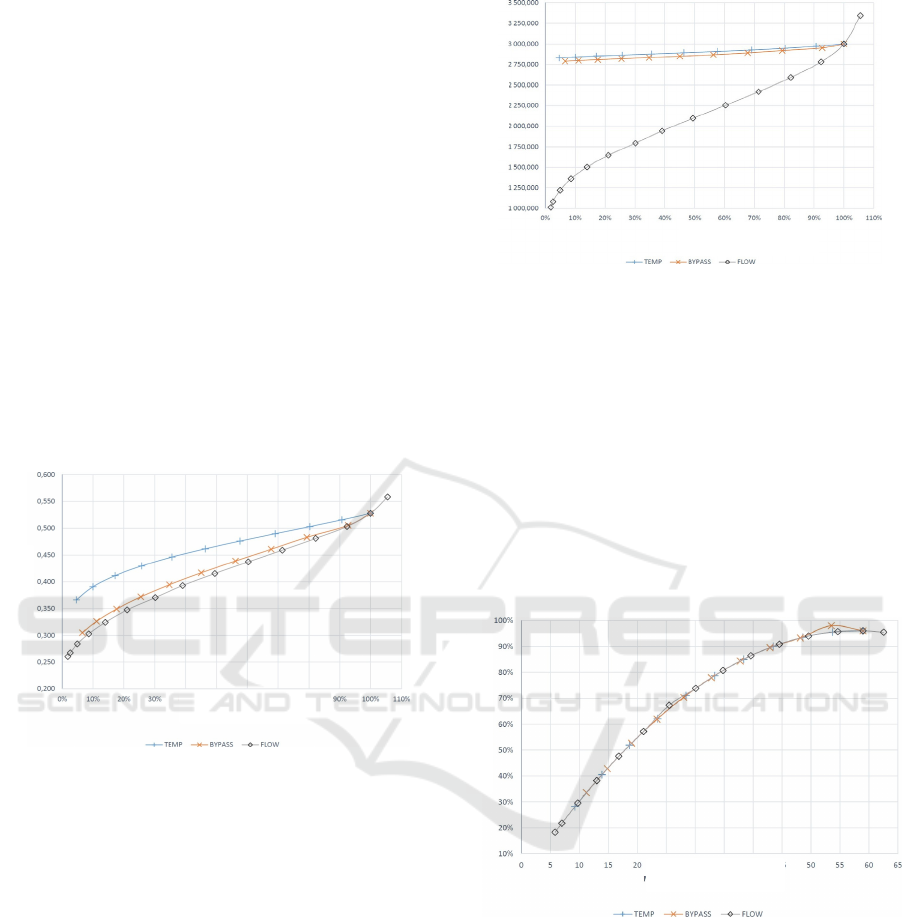
efficiency as a function of system power clearly

shows that the decisive influence on this efficiency is

due to the change in working refrigerant discharge.

The slight increase in compressor efficiency

occurring with a decrease in system power is due to

the change in compression and average

compressibility of the working medium. The

GateCycle program does not allow you to read the

average value of this factor in a given component, but

it does allow you to read its value at the inlet and

outlet of the compressor. Based on Figure 11, which

shows the Z-factor (Compressibility Factor) at the

compressor inlet, it can be concluded that its value

hardly changes in this area. Thus, assuming, in

accordance with engineering knowledge, the absence

of local maxima and minima of this coefficient inside

the compressor, it can be concluded that an increase

in the value of the Z coefficient at the compressor

outlet implies an increase in the average value of this

coefficient throughout the component.

Figure 12: Compressibility factor of the working fluid at the

compressor outlet as a function of system power.

Based on Figure 12, it can be concluded that

higher values of the Z-factor occur with temperature

control. The main effect of the compressibility

coefficient on system operation is expressed

differently. As already stated, GateCycle determines

the off-design compressor speed. In the equation,

only the compressibility factor Z changes, which

helps explain the shape of the curves on the graph of

compressor speed as a function of system power (see

Figure 13).

Figure 13: Rotating machine speed as a function of system

power.

Figure 14 and Figure 15 highlight the importance of

maintaining synchronization with the grid via a

gearbox. The gearbox efficiency sharply declines

with decreasing system power, emphasizing the need

for efficient gearbox design and operation. Moreover,

Figure 18 through Figure 20 demonstrate significant

variability in heat exchanger performance under

different control strategies. Notably, the efficiency of

HX2 drops drastically under bypass control,

suggesting that operational strategies or design

modifications are necessary for optimizing heat

exchanger performance.

Figure 14: Gearbox efficiency as a function of power

delivered at the driving shaft.

As can be seen, especially in the case of output

control, the speed changes. To maintain

synchronization with the grid, a gearbox is necessary

in the system. Its efficiency significantly affects the

efficiency of the entire system, as it significantly

decreases with a decrease in the power of the system,

as shown in Figure 14. Interestingly, the power of the

system is the decisive factor affecting the efficiency

of the gearbox, and the change in speed does not play

a major role. In Figure 14, one point deviation from

Power

Z OUT

RPM

Effectivity of gearbox

Power at gearbox [MW]

A Model of the Control System of a Carbon Dioxide Gas Turbine in Supercritical Condition

451

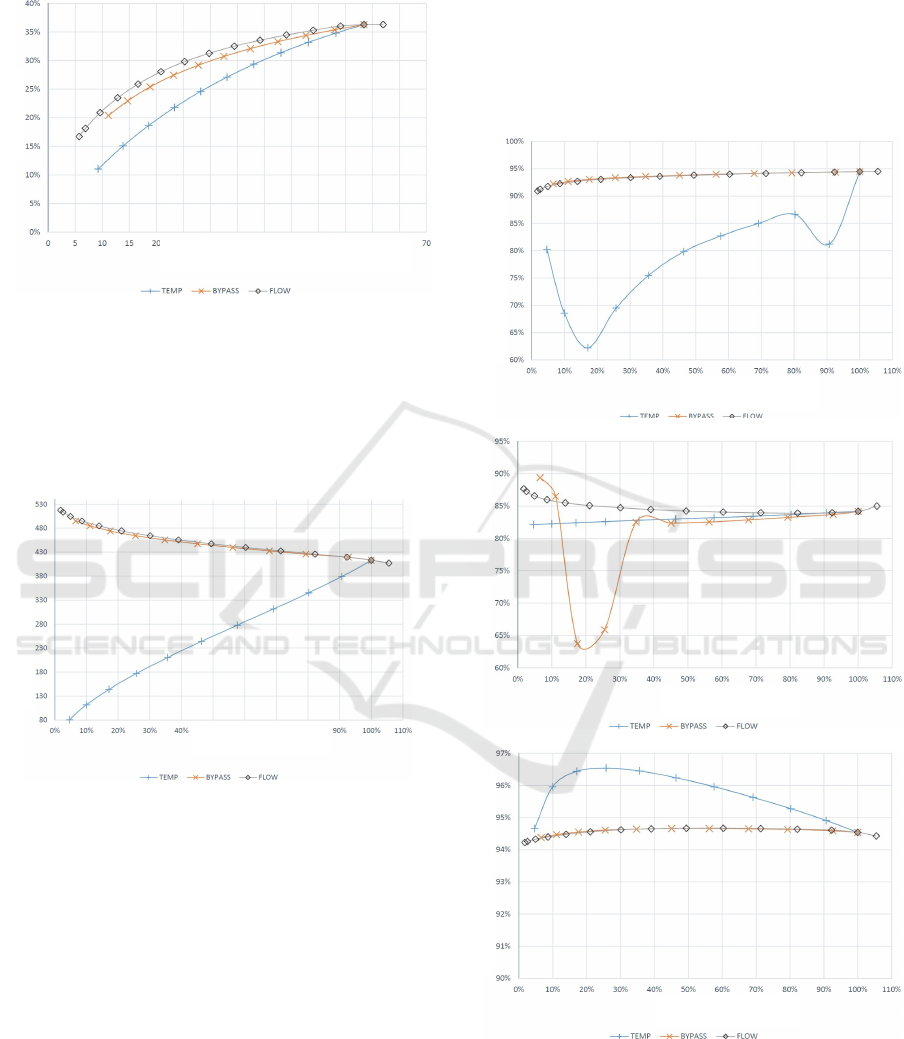
the plotted curves can be observed, which is probably

an iteration error.

Figure 15: System efficiency as a function of system power

at 100% gear efficiency.

It is also possible that the system would operate in

island mode and synchronization with the grid would

not be necessary. In such a case, after eliminating the

gearbox from the system, its efficiency as a function

of power would look like in Figure 15.

Figure 16: Turbine medium outlet temperature as a function

of system power.

As stated earlier, the efficiency of the system is

not the only factor in choosing the optimal power

control system. The stability of operation is also very

important. Figure 17 shows a graph of turbine outlet

temperature as a function of system power. As can be

seen from it, with bypass control and factor output, as

the system power decreases, the outlet temperature

increases, while in the case of temperature control,

the opposite phenomenon occurs—temperature

decreases at three times the speed. Such temperature

changes cause changes in the efficiency of heat

exchangers, as can be seen in Figure 18, Figure 19,

Figure 20, which show graphs of the efficiency of

heat exchangers (HX1, HX2, and HX3, respectively)

as a function of system power. In the case of output

control, the changes are smooth. The same happens

with bypass control in exchangers HX1 and HX3 and

with temperature control in exchanger HX2.

Particularly noteworthy is the sharp drop in the

efficiency of the HX2 exchanger with bypass

regulation.

Figure 17: HX1, HX2 and HX3 heat exchanger efficiency

as a function of system power, respectively a), b) and c).

Power

HX1 effectivity

HX2 effectivity

HX3 effectivity

Power (no including gearbox) [MW]

Turbine outlet temperature [C]

)

Efficiency

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

452

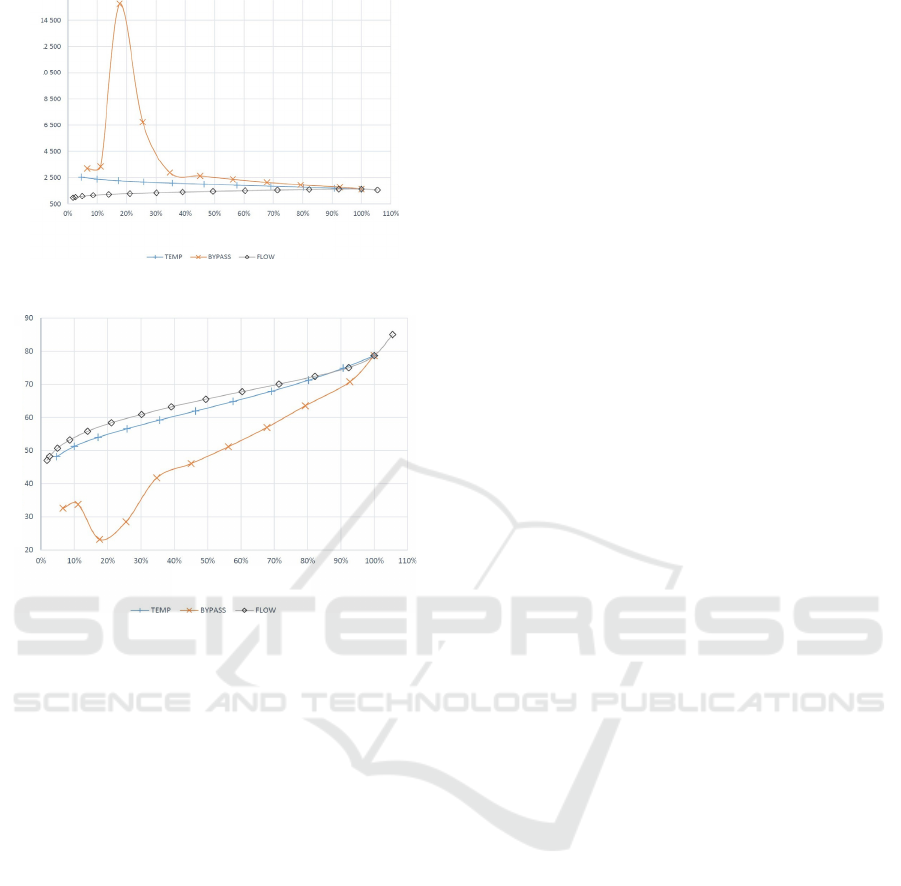
Figure 18: Cooling air flow as a function of system power.

Figure 19: Graph of cooling air outlet temperature as a

function of system power.

This large drop in efficiency entails either

increasing the cooling airflow or using an additional

cooling system, such as water.

Figure 18

shows a clear

jump in the 10-30% area. On the other hand, the

advantage of controlling the output is that the

required cooling airflow decreases with a drop in

system power. Additionally, Figure 19shows a graph

of the cooling air outlet temperature. It can be

deduced from it that the scavenging heat is difficult

to use due to the low temperature, not exceeding

80°C.

The intricate dynamics and performance of

control systems in a supercritical carbon dioxide gas

turbine circuit, as delineated in the results of this

study, provide a profound understanding of the

efficiency and operational stability under various

control strategies. The discussion herein elaborates on

the salient findings from the experimental data,

interprets their practical implications, and delineates

potential avenues for future investigations to enhance

system design and efficiency.

The experimental results vividly demonstrate that

flow rate control systems consistently maintain

higher efficiency compared to other control

mechanisms under variable operational conditions.

This observation is substantiated by the data

presented in Figure 6, where flow rate control systems

showed superior performance in terms of system

efficiency. In contrast, temperature control systems

exhibited a significant decline in efficiency,

suggesting their limited applicability in conditions

where maintaining efficiency is critical. These

findings challenge some of the conventional theories

that advocate the versatility of temperature control

systems across different operational parameters,

suggesting a need for a more nuanced understanding

of these systems in practical applications.

One of the more compelling insights from the

study is the relationship between compressor power

consumption and the overall efficiency of the system.

Detailed in Figure 10, the results indicate an inverse

relationship between flow rate reduction and power

consumption by the compressor. Interestingly, this

reduction in power does not correlate with an increase

in the isentropic efficiency of the compressor,

contrary to typical thermodynamic expectations. This

anomaly points to a complex interaction between the

flow rate and the thermodynamic properties of the

supercritical CO2, which may not be adequately

captured by existing theoretical models. This suggests

that current models may need to be revised or

expanded to incorporate these nuanced interactions

more accurately.

The study also highlighted the critical role of the

compressibility factor (Z-factor) in system

performance, particularly its minimal changes at the

compressor inlet and more pronounced fluctuations at

the outlet, as depicted in Figure 11 and Figure 12.

These findings emphasize the delicate balance

required in managing the working fluid's

thermodynamic properties to optimize system

performance. It also underscores the potential for

significant performance enhancements through

focused modifications in the handling and treatment

of the working fluid under different operating

conditions.

Another key area of focus is the efficiency of the

gearbox, which exhibits a substantial decline with

decreasing system power (Figure 14). This decline in

efficiency does not strongly correlate with changes in

the system's speed, indicating potential areas for

improvement in gearbox design or operation. This

could include exploring new materials, design

modifications, or even entirely new gearbox

technologies that could reduce mechanical losses and

enhance overall system efficiency.

The performance of heat exchangers under

different control strategies revealed significant

Power

Air outlet temperature [C]

Cooling air flow [kg/s]

A Model of the Control System of a Carbon Dioxide Gas Turbine in Supercritical Condition

453

variability, as shown in Figure 17. Particularly

notable is the drastic drop in efficiency of HX2 under

bypass control, necessitating a reconsideration of

either the operational strategy or the design of the heat

exchanger itself. Optimizing heat exchanger

performance could involve detailed analysis of fluid

dynamics within the exchangers or even the

introduction of new materials or technologies that

could withstand the operational demands of different

control strategies more effectively.

Overall, these detailed analyses underscore the

intricate dynamics within the supercritical CO2 gas

turbine system and the necessity for carefully

selecting and optimizing power control strategies to

achieve the best performance outcomes.

5 DISCUSSION

Based on the findings of this study, several areas for

future research emerge. First, there is a clear need for

more refined theoretical models that incorporate the

real gas effects observed under extreme conditions

more accurately. This could involve computational

fluid dynamics (CFD) simulations or experimental

studies to better understand the interactions at play.

Additionally, the exploration of alternative materials

for compressors and heat exchangers could lead to

improvements in system efficiency and durability.

Finally, the integration of advanced predictive

maintenance technologies could significantly

enhance operational stability and extend the lifespan

of system components.

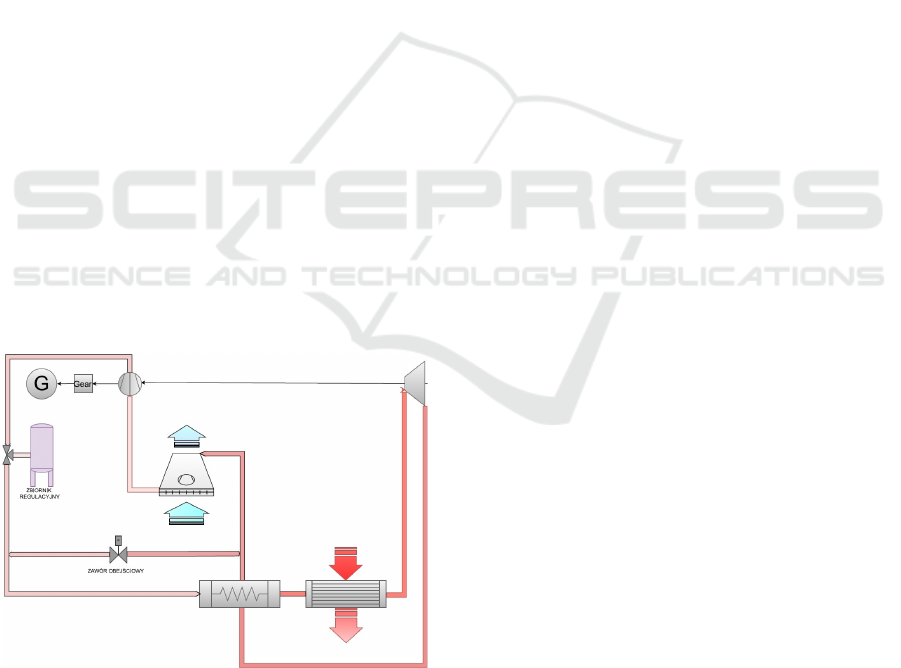
Figure 20: Schematic of the recommended layout.

The proposed hybrid approach in Figure 20 integrates

both discharge and bypass controls, allowing adaptive

management of power control. This dual system

compensates for the limitations of each method under

varying operational conditions, offering a balanced

solution that enhances system responsiveness while

maintaining high efficiency. The schematic in Figure

23 represents this hybrid system, which is poised to

address the trade-offs observed in single-method

control systems, offering an optimal path forward for

supercritical CO2 gas turbine applications in

Concentrating Solar Plants.

The insights from this study provide a robust

framework for understanding the operational

dynamics of supercritical CO2 gas turbines under

different control strategies. While the current control

mechanisms offer substantial benefits, there is

considerable scope for improvement in system design

and operational protocols. The research conducted

herein sets the stage for further innovations and

enhancements in this critical field of energy

technology.

6 CONCLUSIONS

This investigation developed a model of a

supercritical carbon dioxide gas turbine system,

focusing on power modulation within the system. The

model parameters were meticulously selected for

application in next-generation power facilities,

particularly those employing Concentrating Solar

Plants technology. The model was designed for

simplicity and high efficiency, incorporating a heat

regeneration system.

Three distinct power control strategies were

evaluated: bypass, flow rate, and turbine inlet

temperature control. Extensive calculations and

analyses determined that turbine inlet temperature

control yielded the least favorable outcomes, with

significantly lower efficiency and longer response

times.

The discharge control system demonstrated

marginally higher efficiencies but required

significant changes in machinery speed and the

addition of an accumulation tank, increasing cost and

complexity. The bypass control system offered the

fastest response times and ease of implementation but

required increased cooling airflow at lower power

outputs.

The optimal solution is a hybrid approach integrating

both discharge and bypass controls. This dual system

allows adaptive power management, with each

method compensating for the other's limitations under

varying conditions. This proposed solution is

diagrammatically represented in Figure 20.

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

454

ACKNOWLEDGEMENTS

The research results presented in the paper were

achieved within the project entitled “Waste heat

technology management for improvement of energy

efficiency on natural gas IC engines” (no.

POIR.01.01.01-00-0597/19-00), co-financed by the

Polish National Centre of Research and

Development.

REFERENCES

Alfani, D. et al. (2021) ‘sCO2 power plants for waste heat

recovery: design optimization and part-load operation

strategies’, Applied Thermal Engineering, 195, p.

117013. doi:

10.1016/J.APPLTHERMALENG.2021.117013.

Ary Bachtiar, K. P. and Maryono, A. (2019)

‘Thermodynamic analysis of extraction pressure

variation effect on high pressure turbine against the

performance of steam power plant Suralaya 410 MW

by gate cycle modeling’, in AIP Conference

Proceedings. American Institute of Physics Inc. doi:

10.1063/1.5095283.

Boretti, A., Castelletto, S. and Al-Zubaidy, S. (2019)

‘Concentrating solar power tower technology: Present

status and outlook’, Nonlinear Engineering, 8(1), pp.

10–31. doi: 10.1515/nleng-2017-0171.

Dostal, V., Driscoll, M. J. and Hejzar, P. (2004) ‘A

Supercritical Carbon Dioxide Cycle for Next

Generation Nuclear Reactors’, Advanced Nuclear

Power Technology Program.

Hasananto, N., Darmadi, D. B. and Yuliati, L. (2021)

‘Modelling of load variation effect on the steam power

plant heat rate and performance using Gatecycle’, IOP

Conference Series: Materials Science and Engineering,

1034(1), p. 012048. doi: 10.1088/1757-

899x/1034/1/012048.

Kim, Y. M., Kim, C. G. and Favrat, D. (2012) ‘Transcritical

or supercritical {CO2} cycles using both low- and high-

temperature heat sources’, Energy, 43(1), pp. 402–415.

doi: http://dx.doi.org/10.1016/j.energy.2012.03.076.

Ma, B. et al. (2024) ‘Dynamic Modeling and Control of

Supercritical Carbon Dioxide Power Cycle for Gas

Turbine Waste Heat Recovery’, Energies, 17(6), p.

1343. doi: 10.3390/en17061343.

Malinowski, L., Lewandowska, M. and Giannetti, F. (2017)

‘Analysis of the secondary circuit of the DEMO fusion

power plant using GateCycle’, Fusion Engineering and

Design, 124, pp. 1237–1240. doi:

10.1016/j.fusengdes.2017.03.026.

Merchán, R. P. et al. (2021) ‘High temperature central

tower plants for concentrated solar power: 2021

overview’. doi: 10.1016/j.rser.2021.111828.

Milewski, J. et al. (2024) ‘Pilot-scale SOE-MCFC hybrid

system for Co2/H2 mixture production – First

experiences in the “Tennessee” project’, International

Journal of Hydrogen Energy, 52, pp. 1369–1380. doi:

10.1016/j.ijhydene.2023.10.054.

Miller, A. (1984) Gas Turbines and Gas Turbines

Combined Cycles [Turbiny gazowe i układy parowo-

gazowe] (in Polish). Edited by A. Miller.

Wydawnictwa Politechniki Warszawskiej.

Olumayegun, O., Wang, M. and Kelsall, G. (2016) ‘Closed-

cycle gas turbine for power generation: A state-of-the-

art review’, Fuel. Elsevier Ltd, pp. 694–717. doi:

10.1016/j.fuel.2016.04.074.

Sarkar, J. and Bhattacharyya, S. (2009) ‘Optimization of

recompression S-CO2 power cycle with reheating’,

Energy Conversion and Management, 50(8), pp. 1939–

1945. doi:

http://dx.doi.org/10.1016/j.enconman.2009.04.015.

Stein, W. H. and Buck, R. (2017) ‘Advanced power cycles

for concentrated solar power’, Solar Energy, 152, pp.

91–105. doi: 10.1016/j.solener.2017.04.054.

Wu, X. et al. (2021) ‘Is solar power renewable and carbon-

neutral: Evidence from a pilot solar tower plant in

China under a systems view’, Renewable and

Sustainable Energy Reviews, 138, p. 110655. doi:

10.1016/j.rser.2020.110655.

A Model of the Control System of a Carbon Dioxide Gas Turbine in Supercritical Condition

455