
Comparative Analysis of Predictive Models for Estimating Body Fat
Percentage Using Three Models
Yuxuan Qiu
Case School of Engineering, Case Western Reserve University, Cleveland, Ohio, 44106, United State
Keywords: Artificial Intelligence, Body Fat Rate, Comparison of Models.
Abstract: Obesity is a common health problem and body fat is an important indicator to measure obesity. However,
most methods of measuring body fat require specialized equipment and come at a high cost. Therefore, it is a
portable, non-invasive, and cost-effective approach to use a machine learning model to predict body fat.
Because existing techniques for measuring body fat have certain challenges and limitations, it is necessary to
develop and improve simpler, more economical, and easier methods for measuring body fat. This study will
use a body fat prediction dataset from Kaggle to train three different supervised machine learning models:
linear regression, decision trees, and support vector machines. Then, the research will compare the
performance of three different models through Mean Absolute Error (MAE), Mean Squared Error (MSE), and
R square. The evaluation results show that both the linear regression model and the decision tree model have
good performance in predicting body fat, while the support vector machine has poor performance in predicting
body fat.
1 INTRODUCTION
Obesity in medicine refers to the accumulation of
excess fat in the body to the extent that it is harmful
to health. This disease is linked to a range of health
consequences, including metabolic syndrome,
infertility, ischemic heart disease, cardiovascular
issues, type 2 diabetes, and different forms of cancer
(Patel et al. 2023). Obesity is a widespread health
problem in society. The overweight and obesity rates
of Chinese adults are 34.3% and 16.4%, respectively,
which means that more than half of the population is
overweight or obese (National Health Commission
2020). The body mass index (BMI) is a common way
to assess obesity, which is computed by dividing a
person's weight in kilograms by the square of their
height in meters. However, BMI may not be a reliable
indicator of a person's body composition because it
does not measure body fat directly. Body fat
percentage is a more accurate indicator of obesity as
it specifically measures the proportion of one's weight
that comes from fat. Therefore, it is meaningful to
measure a person’s body fat.
Underwater weighing and dual-energy X-ray
absorptiometry are techniques to assess an
individual's body fat (Jensky-Squires et al. 2008).
While these approaches are accurate, they require
specialized equipment and come at a high cost,
making them less commonly employed for clinical
applications. Anthropometry is a straightforward,
quick, and cost-effective technique for assessing body
mass. It relies on measurements such as height,
weight, diameter, or circumference of body parts to
gauge obesity. However, because these indicators do
not directly measure body fat, they are not sufficient
to predict health risks (Huxley et al. 2010).
Integrating anthropometry with machine learning
models offers a portable, non-invasive, and cost-
effective approach to predicting body fat. This
method accurately predicts body fat by combining
precise measurements of body size with advanced
computational techniques. This method combines
traditional measurement methods with innovative
technologies, which not only ensures the convenience
and accessibility of body fat prediction but also
improves the efficiency and affordability of
prediction. Lai et al. conducted research introducing a
hybrid approach to feature selection (Lai et al. 2022).
To accurately estimate body fat percentage, they used
an improved simplified group optimization (iSSO)
with a multi-filter ensemble method (VMFET) based
on VlseKriterijumska Optimizacija I Kompromisno
Resenje (VIKOR) (Lai et al. 2022). The study used
594
Qiu, Y.
Comparative Analysis of Predictive Models for Estimating Body Fat Percentage Using Three Models.
DOI: 10.5220/0012866600004547
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 594-598
ISBN: 978-989-758-690-3
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

nine datasets to objectively verify the effectiveness of
the proposed strategies (Lai et al. 2022). When
compared to other algorithms, iSSO performs the best
(Lai et al. 2022). Chiong et al. have enhanced the
Support Vector Machine (SVM) method for
predicting body fat by improving its relative error
performance (Chiong et al. 2021). Through the
improvement, they have achieved a higher accuracy
in predicting body fat compared with the original
method (Chiong et al. 2021).
Because obesity is associated with a variety of
health problems, the use of machine learning models
to accurately assess body fat has important
implications in the prevention and management of
related diseases. Although there are already some
methods available for measuring body fat, there are
still challenges and limitations. Therefore, research
on simpler, more economical, and easily
implementable methods to measure body fat remains
a noteworthy area of focus.
To fill this research gap, this study is going to
develop three distinct predictive models for
estimating body fat percentage, which are linear
regression, decision tree, and support vector machine.
Each of these models offers unique strengths and
capabilities. After the three models are established,
their predictive performance will be compared. The
goal is to ascertain which model exhibits superior
predictive capabilities in estimating body fat
percentage under the given dataset and conditions.
The results of this study not only contribute to the
development of the field of body fat prediction, but
also provide valuable insights into the effectiveness
of linear regression, decision trees, and support vector
machine models in this particular context. These
insights could aid future research and applications in
the health and fitness field, providing practitioners
with more informed methods for estimating body fat
based on the strengths of each predictive model.
2 METHOD
2.1 Dataset
This study utilizes a dataset for predicting body fat,
sourced from Kaggle and supplied by Dr. A. Garth
Fisher, who has granted permission for its free
distribution and non-commercial use. The dataset
comprises fifteen columns, encompassing estimates
of body fat percentage, and the features are used to
predict body fat. This comprehensive dataset captures
information from 252 men, providing a robust
foundation for the analysis and exploration of factors
influencing body fat estimation. Table 1 shows the
description of the table, every serial number in the
first column corresponds to a man. Table 2 presents
the dataset's profile information, encompassing the
minimum, maximum, mean, and standard deviation
values for each feature.
Table 1: Five men’s body-related measurements are presented.
Density
BodyFat
Age
Weight
Height
Neck
Chest
0
1.0708
12.3
23
154.25
67.75
36.2
93.1
1
1.0853
6.1
22
173.25
72.25
38.5
93.6
2
1.0414
25.3
22
154
66.25
34
95.8
3
1.0751
10.4
26
184.75
72.25
37.4
101.8
4
1.034
28.7
24
184.25
71.25
34.4
97.3
Abdomen
Hip
Thigh
Knee
Ankle
Biceps
Forearm
Wrist
85.2
94.5
59
37.3
21.9
32
27.4
17.1
83
98.7
58.7
37.3
23.4
30.5
28.9
18.2
87.9
99.2
59.6
38.9
24
28.8
25.2
16.6
86.4
101.2
60.1
37.3
22.8
32.4
29.4
18.2
100
101.9
63.2
42.2
24
32.2
27.7
17.7
Table 2: The mean, standard deviation, minimum value, and maximum value for each feature are presented.
Density
BodyFat
Age
Weight
Height
Neck
Chest
Abdomen
mean
1.055574
19.15079
44.88492
178.9244
70.14881
37.99206
100.8242
92.55595
std
0.019031
8.36874
12.60204
29.38916
3.662856
2.430913
8.430476
10.78308
min
0.995
0
22
118.5
29.5
31.1
79.3
69.4
max
1.1089
47.5
81
363.15
77.75
51.2
136.2
148.1
Hip
Thigh
Knee
Ankle
Biceps
Forearm
Wrist
mean
99.90476
59.40595
38.59048
23.10238
32.27341
28.66389
18.22976
Comparative Analysis of Predictive Models for Estimating Body Fat Percentage Using Three Models
595

std
7.164058
5.249952
2.411805
1.694893
3.021274
2.020691
0.933585
min
85
47.2
33
19.1
24.8
21
15.8
max
147.7
87.3
49.1
33.9
45
34.9
21.4
2.2 Supervised Machine Learning
Algorithm
In this study, supervised machine learning is used to
predict body fat. In supervised machine learning, the
algorithm is trained on a labeled dataset, which
consists of input data that has been paired with
appropriate output labels (Nasteski 2017).
A statistical technique called linear regression is
used to model the connection between a dependent
variable and one or more independent variables.
(Montgomery et al. 2021). This supervised learning
algorithm is commonly used in machine learning and
statistics (Montgomery et al. 2021). The fundamental
idea behind linear regression is to find the best-fitting
straight line (the regression line) that represents the
relationship between the variables (Montgomery et al.
2021). This line is defined by a linear equation of the
form: 𝑦 = 𝑚𝑥 + 𝑏 (Montgomery et al. 2021).
The decision tree methodology is a popular
technique for building predicting algorithms for a
target variable or classification systems based on
several variables (Song & Ying 2015). Using this
method, a population is divided into segments that
resemble branches, creating an inverted tree structure
with a root node, internal nodes, and leaf nodes (Song
& Ying 2015). It is a non-parametric algorithm that
efficiently handles large, complex datasets without
requiring intricate parametric structures (Song & Ying
2015). When the sample size is large enough, the
research data can be divided into training and
validation datasets. A decision tree model is built using
the training dataset, and the validation dataset assists in
determining the ideal tree size required to produce the
best possible final model (Song & Ying 2015).
For problems involving regression and
classification, supervised machine learning
algorithms like SVM are employed (Vojislav 2005).
It works especially well in high-dimensional spaces
and is widely used for tasks such as image
classification, text categorization, and handwriting
recognition (Vojislav 2005). The primary goal of an
SVM is to find a hyperplane in the feature space that
best separates the data points of one class from
another (Vojislav 2005). A decision boundary that
optimizes the margin between the two classes is called
a hyperplane (Vojislav 2005). The distance between
the hyperplane and the closest data point from each
class is known as the margin (Vojislav 2005). The
SVM algorithm is also robust against overfitting, as it
focuses on maximizing the margin and is less
influenced by individual data points (Vojislav 2005).
Additionally, SVMs have been extended for
multiclass classification and regression tasks
(Vojislav 2005).
2.3 Correlation Coefficient Analysis
A technique used to evaluate the degree of correlation
between two sets of dataset features—which may
include dependent or independent variables—is
correlation coefficient analysis (Bruce 2009). The
correlation coefficient r is a numerical value ranging
from a negative one to a positive one, indicating the
strength of the relationship between the sets (Bruce
2009). A positive value signifies a positive
relationship, while a negative value indicates a
negative relationship (Bruce 2009). For values
between 0 and 0.3 (or 0 and -0.3), the correlation
suggests a weak positive (negative) linear
relationship, characterized by a somewhat unstable
linear pattern (Bruce 2009). In the range of 0.3 to 0.7
(or -0.3 to -0.7), the correlation implies a moderate
positive (negative) linear relationship, displaying a
somewhat stable but not extremely strong linear
pattern (Bruce 2009). Values from 0.7 to 1.0 (or -0.7
to -1.0) indicate a strong positive (negative) linear
relationship, reflecting a robust and well-defined
linear pattern (Bruce 2009).
In this study, the correlation coefficient analysis is
utilized to ascertain the association between the
independent variable, body fat, and the dependent
variables, rest features. Figure 1 shows that body fat
has a strong relationship with abdomen circumference
and density, a moderate relationship with weight,
neck circumference, chest circumference, hip
circumference, thigh circumference, knee
circumference, bicep circumference, wrist
circumference, and forearm circumference, and weak
relationship with age, height and ankle
circumference.
ICDSE 2024 - International Conference on Data Science and Engineering
596
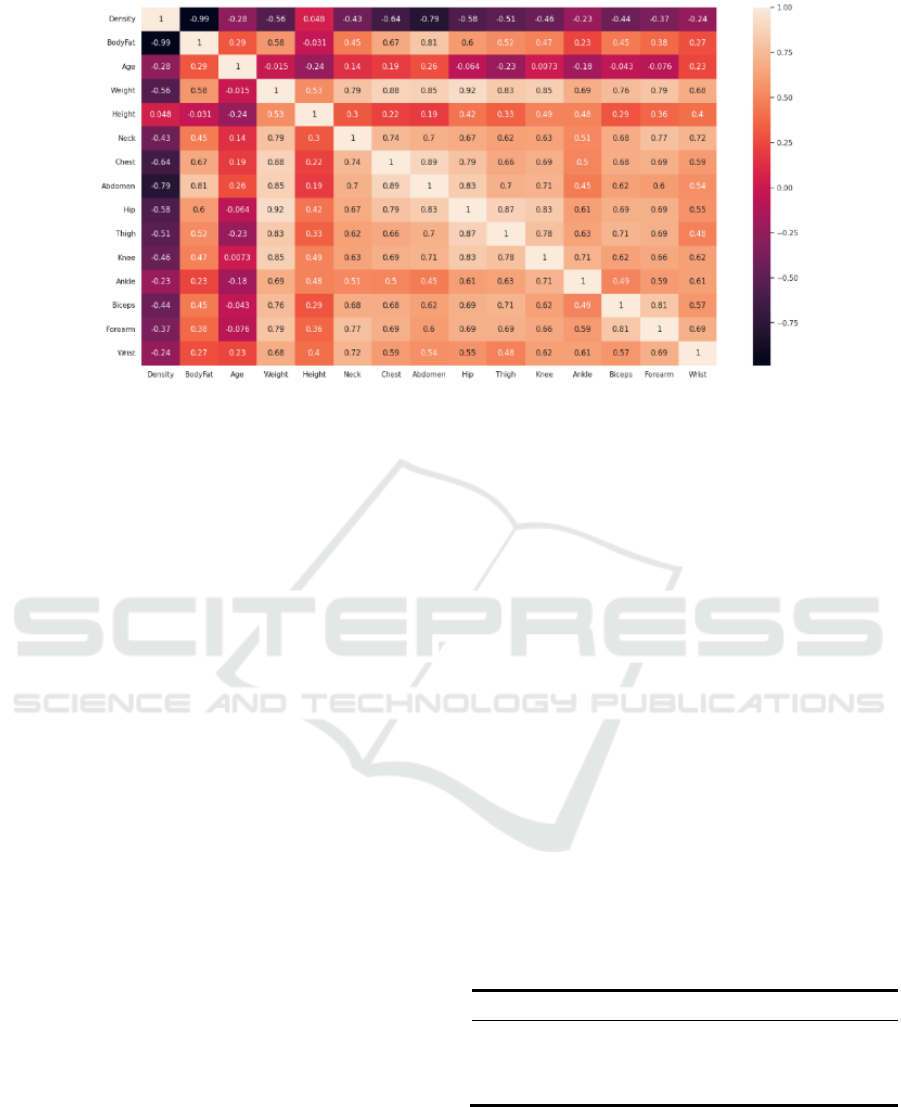
Figure 1: The heat map shows the relationship between each feature (Picture credit: Original).
2.4 Experimental Setup
Python is used to implement supervised machine
learning algorithms. All necessary libraries for
correlation analysis and model training are installed.
2.5 Predictive Models for Body Fat
In this study, a body fat prediction dataset from
Kaggle is used to build three different models to
predict body fat. Support vector machines, decision
trees, and linear regression are examples of
supervised machine learning models. Before training
the model, correlation coefficient analysis is utilized
with the dataset, to find the relationship between each
feature and body fat. After the correlation coefficient
analysis, age, height, and ankle circumference are
dropped from the dataset because they have a weak
relationship with body fat. Then, all the data are
standardized through sklearn.preprocessing.standard
scaler standard scaler. This method will normalize
features by subtracting the mean and dividing by the
standard deviation to achieve a standard score
(Sklearn 2007).
There were training and testing sets of the data.
80% of the data will be used to train the model, and
20% will be used for testing. Three different
algorithms which are linear regression, decision tree,
and support vector machine are used to predict a
person’s body fat with eleven features.
MAE, MSE, and R square are used to evaluate and
compare the performance of the models.
MAE is a measurement of the mean absolute
disparities between the values that were anticipated
and actual values. It is computed by averaging the
absolute deviations between the values that were
anticipated and those that were observed.
MSE is a measure of the average squared
differences between the anticipated and actual values.
It penalizes more on greater faults than on lesser ones.
R squared is a statistical metric that shows the
percentage of the dependent variable's volatility that
can be predicted based on the independent variables.
It ranges from 0 to 1, with higher values indicating a
better fit.
3 RESULT AND DISCUSSION
Predicting body fat can provide people with a better
view of their health condition. In this research, linear
regression, decision tree, and support vector machine
are developed by training with body fat prediction
dataset from Kaggle. The performance of the models
is evaluated with MAE, MSE, and R squared. The
performance of the models is shown in Table 3.
Table 3: The performances of each model are presented.
MAE
MSE
R2
LR
0.4056
0.283
0.9939
DTR
0.3549
0.5715
0.9877
SVM
4.653
31.2
0.3274
Among the three models developed, the decision
tree model exhibits the most favorable performance
with the lowest MAE of 0.3549. In comparison, the
linear regression model follows closely with an MAE
of 0.4056, while the support vector machine lags
Comparative Analysis of Predictive Models for Estimating Body Fat Percentage Using Three Models
597

significantly behind with a much higher MAE of
4.653. When considering MSE, the linear regression
model outperforms the others, boasting the smallest
value of 0.283. In contrast, the decision tree model
and support vector machine yield MSE values of
0.5715 and 31.2, respectively. Examining the
coefficient of determination (R square), the linear
regression model stands out with the highest value of
0.9939. The decision tree model also demonstrates
strong predictive capability with an R square of
0.9877, while the support vector machine lags far
behind at 0.3274.
Both the linear regression and decision tree
models showcase commendable performance in
predicting body fat, as evidenced by their low MAE
and MSE values and high R square. However, the
support vector machine exhibits suboptimal
predictive accuracy in this context.
4 CONCLUSION
In conclusion, this study aimed to develop and
compare three distinct predictive models for
estimating body fat percentage: linear regression,
decision tree, and support vector machine. The
research utilized a comprehensive dataset from
Kaggle, containing various features related to body
fat estimation. The dataset was analyzed using
correlation coefficient analysis to understand the
relationships between different features and body fat.
After dropping features with weak relationships,
the data was standardized, and the models were
trained using supervised machine learning algorithms
in Python. The evaluation metrics, including MAE,
MSE, and R squared, were employed to assess the
predictive performance of each model. Among the
three models, decision tree and linear regression
models showcased commendable performance in
predicting body fat, displaying low MAE and MSE
values and high R squared. However, the support
vector machine exhibited suboptimal predictive
accuracy in this specific context.
Body fat prediction models offer personalized
insights for informed decisions in health and fitness.
They enhance accuracy in assessing body fat levels
for healthcare and fitness planning. These models
empower individuals and practitioners to promote
healthier lifestyles and preventive healthcare
measures.
These findings contribute valuable insights into
the relative effectiveness of these models for body fat
estimation, providing practitioners with informed
approaches to health and fitness assessments. Further
research in this area could explore additional models
or refine existing ones to enhance predictive accuracy
and broaden applications in health management.
REFERENCES
A. V. Patel, K. S. Patel, L. R. Teras, Surgery for Obesity and
Related Diseases, 9(7): 742-745, (2023).
C. M. Lai, C. C. Chiu, Y. C. Shih, H. P. Huang, Computer
Methods and Programs in Biomedicine, 226, 107183,
(2022).
D. C. Montgomery, A. P. Elizabeth, and G. G.
Vining, Introduction to linear regression analysis, pp.
12-17. 2021.
K. Vojislav, "Support vector machines–an introduction." in
Support vector machines: theory and applications,
(Berlin, Heidelberg: Springer Berlin Heidelberg, 2005),
pp.1-47.
N. E. Jensky-Squires, C. M. Dieli-Conwright, A. Rossuello,
D. N. Erceg, S. McCauley, E. T. Schroeder, British
Journal of Nutrition, 100(4), 859-865, (2008).
National Health Commission, Journal of Nutrition, 42(6):
521, (2020).
R. Bruce, Journal of Targeting, Measurement and Analysis
for Marketing, 17, 139-142, (2009).
R. Chiong, Z. Fan, Z. Hu, F. Chiong, Computer Methods
and Programs in Biomedicine, 98: 105749, (2021).
R. Huxley, S. Mendis, E. Zheleznyakov, S. Reddy, J. Chan,
European Journal of Clinical Nutrition, 64(1), 16-22,
(2010).
Sklearn. preprocessing. StandardScaler. scikit. (n.d.). 2007
available at https://scikit-
learn.org/stable/modules/generated/sklearn.preprocessi
ng
V. Nasteski, Horizons. b, 4: 51-62, (2017).
Y. Y. Song, L. U. Ying, Shanghai archives of psychiatry,
27(2): 130-135, (2015).
ICDSE 2024 - International Conference on Data Science and Engineering
598
