Traffic Flow Prediction Model Based on BDBO-TCN

Zhang Xijun and Chen Xuan

School of Computer and Communication, Lanzhou University of Technology, Lanzhou 730050, China

Keywords: Traffic Flow Prediction, TCN, DBO.

Abstract: In order to improve the accuracy of short-term traffic flow prediction and overcome the shortcomings of

single prediction model and the limitations of traditional depth learning based on experience to set

hyperparameters, a time convolution network (TCN) model based on improved dung beetle algorithm

(DBO) is proposed. In order to solve the problem of slow convergence of traditional TCN model, the dung

beetle algorithm is introduced, and the Bernoulli chaotic mapping algorithm is used to improve the initial

value, considering the randomness and diversity of the initialization of dung beetle algorithm, the traffic

flow prediction model based on BDBO-TCN is constructed. To verify the predictive effect of the

experiment, experiments were conducted on two different real data sets, the multi-step prediction is

compared with the TCN model optimized by DBO based on various chaotic mapping algorithms to further

verify the prediction performance of the model. This model is superior to other models.

1 INTRODUCTION

Traffic flow prediction is the basis of traffic control

and traffic guidance. At present, the common short-

term traffic flow prediction models are LSTM(Ma et

al., 2015), GRU (Wu et al., 2018), TCN(Lea et al.)

etc., in the field of traffic flow prediction, the

common optimization algorithms such as particle

swarm optimization (Kennedy and Eberhart) ,

genetic algorithm (Goldberg, 1989)etc., in this

paper, dung beetle Optimizer algorithm(Xue and

Shen, 2023) is used to solve the hyperparameters of

TCN model, and chaos mapping algorithm(Yu et al.,

2018)is introduced into intelligent optimization

algorithm to increase population diversity. Chaotic

mapping algorithms include Tent mapping(Zhao,

2012), Logistic mapping(Zhang and Liang, 2012)

Bernoulli mapping(Saito and Yamaguchi, 2016)and

so on. The hyperparameters of TCN are optimized

by DBO algorithm of dung beetle, and the traffic

flow prediction of TCN is made by the optimal

hyperparameters. The main contributions are as

follows:

(1) Aiming at the problem that the

hyperparameters of TCN are difficult to determine in

the traffic flow prediction, in this paper, TCN traffic

flow prediction model based on improved dung

beetle algorithm is designed by combining TCN

with improved dung beetle algorithm. The

simulation results show that the proposed model is

superior to other optimized TCN prediction models.

(2) Using the method of randomly generating the

initial population in traditional dung beetle

algorithm, the distribution of the initial population is

not uniform, which leads to the decrease of the

population diversity and the low quality of the

population, the problem of unbalanced global

exploration and local development capability affects

the convergence speed of the algorithm. In this

paper, chaotic maps are introduced to improve the

quality of initial population distribution in the search

space, thus strengthening the global search

capability.

2 MODEL

2.1 Dung Beetle Optimizer

Dung Beetle Optimizer (DBO) is a new heuristic

swarm intelligence optimization algorithm inspired

by the behavior of Dung beetles in nature. The dung

beetle algorithm selects the optimal solution by

modelling dung beetle, survival behavior ， ball

rolling and dancing behavior, foraging behavior,

breeding behavior and stealing behavior.

The rolling behavior of dung beetles can be

divided into barrier mode and barrier-free mode. The

Xijun, Z. and Chen, X.

Trafﬁc Flow Prediction Model Based on BDBO-TCN.

DOI: 10.5220/0012876100004536

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Mining, E-Lear ning, and Information Systems (DMEIS 2024), pages 31-36

ISBN: 978-989-758-715-3

rolling behavior of dung beetles is influenced by

celestial cue navigation, and the rolling position path

of dung beetles is changed by the change of light

intensity. The location update formula is shown

()

ttt

iii

XSgxX xX

′′ ′ ′′

=+××−+−

(1)

Where t is the number of current iterations,

which

is the position information of the first

dung beetle during the t iteration, k is the deflection

coefficient and b is the natural coefficient,

x−

indicates the change of light intensity,

is the worst position in the current population.

The natural coefficient

of -1,1, when

= 1

means the natural environment does not affect the

original direction, when

= -1 means the natural

environment deviates from the original direction.

The

value is determined by the probability

value.

When a dung beetle encounters an obstacle and

is unable to move forward, it changes the direction

and position of its ball by dancing. Update such as

type:

tan

tt tt

ii ii

xxx

+−

=+ −

(2)

The position of the dung beetle does not change

when the angle of deflection of

= 0,

Reproductive behavior dung beetles hide their

dung balls by rolling them to a safe area, providing a

boundary selection strategy to simulate the female

dung beetles spawning and brood areas. Female

dung beetles lay their eggs and raise their young.



𝑈𝑏

′

= 𝑚𝑖𝑛( 𝑋

′

×(1+𝑅), 𝑈𝑏

𝐿𝑏

′

= 𝑚𝑎𝑥( 𝑋

′

×(1−𝑅), 𝐿𝑏)

𝑅=1−







(3)

Among them,

′

is the upper and lower

bounds of the spawning region,

is the upper

and lower bounds of the search space, respectively,

′

is the optimal positions of the current population,

R is the dynamic selection factor, and

max

T is the

optimal iteration order.

Once the female has identified the area where

she will lay her eggs, she will incubate the ball and

only produce one egg per iteration, thus, the position

of the oocyte changes dynamically with the iteration

of the spawning area, it is defined as follows:

()

BXbBLbb

′′

=+× − +

(4)

Where,

is the position of the i oosphere at

the t iteration,

b ,

b are the independent random

variable of D for the optimization problem.

Foraging behavior after hatching, young dung

beetles need to be guided to a limited optimal

foraging area. The boundary of the optimal foraging

area is defined as follows:

min( (1 ), )

max( (1 ), )

Ub X R Ub

Lb X R Lb

′′ ′′

=×+





′′ ′′

=×−



(5)

For

′′

is the global optimal position,

′′

is the upper and lower limits of the optimal

foraging, the position of the small dung beetle can

be defined after the location update as shown:

()()

tt t t

ii i i

xC xLb C xUb

′′ ′′

=+× − +× − (6)

Where,

is the position information of the i

little dung beetle in the iteration of the t generation,

C is a random number following normal

distribution, and

C is a random vector of (0,1).

Some dung beetles don't want to play their own

game, they want to play for free, the best place in the

world, the best place to eat. Assuming that the

thieving dung beetles are competing for food nearby,

during the iteration, the thieving dung beetle

position updates as follows:

()

ttt

iii

XSgxX xX

′′ ′ ′′

=+××−+−

(7)

Where

is the position information of the i

thief dung beetle in the t generation iteration, g is a

random variable of size 1*D with a normal

distribution and S represents a constant.

2.2 Chaotic Algorithm

In order to improve the diversity of population

initialization, chaotic maps are used to generate the

diversity of initial population in the initialization

stage of DBO, the probability of the middle value of

the Logistic map is uniform, but the probability of

the two ends is very high, so it is disadvantageous to

find the global optimal point when it is not at the

two ends of the design variable space Secondly, Tent

map has good ergodicity, but there are small periods

and unstable period points in its iterative sequence,

so if the sequence falls into it, the sequence tends to

be stable and the algorithm is invalid Because

Bernoulli mapping can affect the whole process of

algorithm and obtain better optimization results, it

has the characteristics of ergodic uniformity and

moderate convergence speed, and is widely used in

algorithm initialization. Therefore, Bernoulli map is

used to initialize the population of DBO in order to

improve the distribution quality of the initial

population in the search space and enhance its global

search ability. Bernoulli was used to map the initial

position of dung beetle, the resulting values were

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

projected into the chaotic variable space, and then

the resulting chaotic values were mapped into the

algorithm initial space by linear transformation, the

specific formula for the Bernoulli mapping is shown:

𝑍



= 







,0≤𝑍



≤1 −𝛽





()



,1−𝛽≤𝑍



≤1

(8)

Where

is the mapping parameter.

2.3 BDBO-TCN

BDBO-TCN algorithm based on time convolution

network can extract the temporal characteristics of

traffic flow across time steps. TCN model is chosen

as traffic flow prediction model, which has simple

structure and can accurately capture and predict the

inherent patterns and trends of sequence data. In this

paper, the DBO algorithm based on Bernoulli map is

used to optimize the TCN parameters, taking the

time series of traffic flow as input and the prediction

error as the fitness, the next stage of traffic flow

forecast is the output matrix. An improved DBO-

TCN prediction model is convolutional neural

network as follows:

(1) firstly, the structure of TCN model is

determined, the model structure diagram for this

article is shown in Figure 2.2. 3, and then randomly

initialize the parameters of the TCN model.

(2) The initial population of DBO (suppose

rolling ball dung beetle: foraging dung beetle:

breeding dung beetle: larceny dung beetle: 20% :

20%: 25%: 35%) , and the initial value is determined

by chaos mapping method.

(3) in this paper, the prediction error of TCN

model is taken as the fitness function of dung beetle

algorithm, so that the dung beetle algorithm is

related to TCN model.

(4) using the strategy of dung beetle algorithm

introduced in Section 4.2, we get the updated value

of super-parameter, and train the TCN model on the

training set, and get the prediction error of the

model. (5) if the current prediction error meets the

set requirements or reaches the upper limit of the

cycle, the optimal TCN superparameter is obtained.

(6) if the end condition of step (5) is not

satisfied, return to step (4) to continue until the loop

end condition of step (5) is satisfied.

A summary of the above steps results in an

improved DBO-TCN traffic flow prediction

flowchart as shown in Figure 1.

3 EXPERIMENTAL ANALYSIS

3.1 Data Description

In order to verify the superiority of the proposed

model. Experiments were performed using two real-

time California highway datasets PEMSD4 and

PEMSD8 collected every 30 seconds by the Caltrans

Performance Measurement System. This paper

chooses the traffic flow data as the research object.

Traffic flow data are collected every 5 minutes. The

specific dataset statistics are shown in Table 1

Table 1: Description of experience dataset.

Datasets Number of

sensors

Edges

Time

ste

Time

ran

PEMSD4 307 340 16992 1/1/2018-

2/28/2018

PEMSD8 170 277 17856 7/1/2016-

8/31/2016

The data sets are divided into training set,

verification set and test set according to the ratio of

6:2:2. And early stop method is used to prevent

over-fitting. In order to eliminate the influence of

different variables on the data set, the maximum-

minimum normalization method is used to process

the data in [0, 1] interval. The normalization

operation is as follows:

min

max min

−

′

−

(9)

where

′

is the normalized data,

is the original

data,

min

is the minimum value in the data sample,

and

max

is the maximum value in the data sample.

3.2 Experimental Environment and

Parameter Settings

This experiment is compiled and run on Windows

Server (CPU: Intel (R) Core (TM) i5-8300H CPU @

2.30 GHz, GPU: NVIDIA GeForce GTX 1050 Ti)

using PyTorch depth framework to complete in

Pycharm development environment. The specific

parameters are set as follows: Historical traffic flow

window size is 6,num_channels= [128,64,32,16,4,1]

in TCN, The loss function is MSELoss, Adam

Optimizer, Batch size=64, epoch = 100, learned

number =0.001, deflection coefficient k is 0.1, the

natural coefficient b is 0.5,number of iterations is

100 and use the early stop method with patience =

10.

Trafﬁc Flow Prediction Model Based on BDBO-TCN

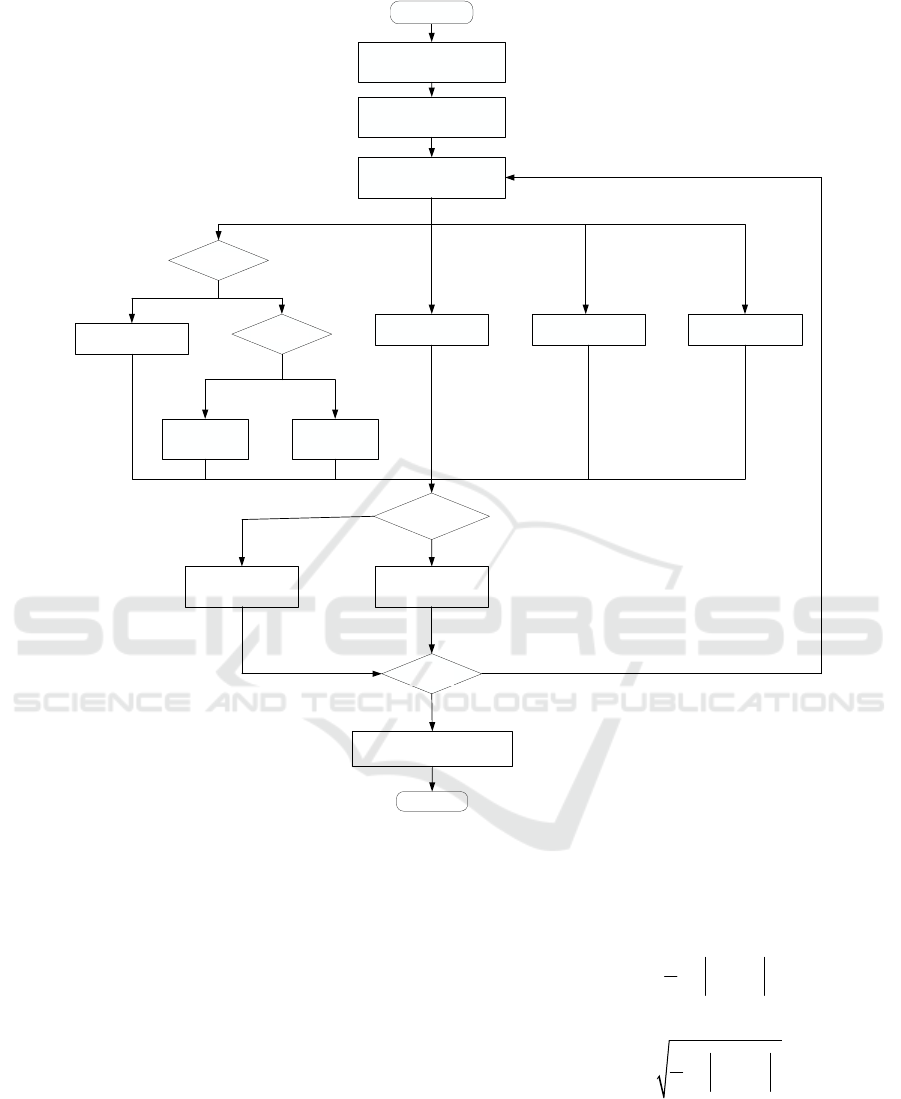
Chaos mapping initializes dung

beetle location

Calculate the fitness value for

each dung beetle

Determine the α and

update t he location

The location is not

updated

Dancing behavior,

updating the

position

Breeding behavior,

updating the position

Foraging behavior,

updating location

Stealing, updating the

location

Start

0.9

0, / 2,

θππ

Enter the target function and

related parameters

The new location is better

than the original location

The original position

remains the same

The new location

replaces the original

location

The optimal position and optimal

fitness values are output

End

max

tT<

Figure 1: Traffic flow prediction flow chart of BDBO-TCN.

•Baseline Methods

(1) TCN: Time convolutional network

(2) DBO-TCN: Dung Beetle algorithm optimizes

TCN

(3) TDBO-TCN: The dung Beetle algorithm under

Tent mapping optimizes TCN

(4) LDBO-TCN: The dung Beetle algorithm under

Logistic mapping optimizes TCN

(5) BDBO-TCN: The dung Beetle algorithm

under Bernoulli mapping optimizes TCN

3.2 Evaluation Index

In order to quantitatively analyze the effectiveness

of the model for data repair, this paper uses the

complete traffic volume to verify it, and adopts the

following evaluation indexes to measure the

prediction and repair ability of the model.

(1)

Mean Absolute Error (MAE):

AE y y

′

−



＝ (10)

(2)

Root Mean Square Error (RMSE):

RMSE y y

′

−



＝

(11)

Where n is the number of true data,

y is the true

value of the i-th true data, and

′

is the predicted

value of the ith data. The smaller the above

evaluation index, the better the prediction and repair

ability of the model.

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

4 RESULTS

Table 2: Short-term traffic flow forecast with 5-minute

interval.

model

datasets PEMSD4 PEMSD8

Metrics MAE RMSE MAE RMSE

TCN

17.94 28.68 13.87 21.43

DBO-TCN

15.88 26.36 12.25 19.57

TDBO-TCN

15.36 25.88 11.94 19.23

LDBO-TCN

15.48 25.62 11.83 19.32

BDBO-TCN

15.21 25.23 11.73 18.72

Table 3: Short-term traffic flow forecast with 10-minute

interval.

model

datasets PEMSD4 PEMSD8

Metrics MAE RMSE MAE RMSE

TCN

18.96 30.32 14.97 23.26

DBO-TCN

17.62 28.29 13.69 21.62

TDBO-TCN

17.35 27.63 13.45 20.98

LDBO-TCN

17.22 27.52 13.48 21.06

BDBO-TCN

17.02 27.31 13.22 20.85

Table 4: Short-term traffic flow forecast with 15-minute

interval.

model

datasets PEMSD4 PEMSD8

Metrics MAE RMSE MAE RMSE

TCN

20.25 32.21

16.23 25.42

DBO-TCN

18.87 30.14

14.95 23.61

TDBO-TCN

18.68 29.56

14.85 23.32

LDBO-TCN

18.54

29.75 14.77 23.18

BDBO-TCN

18.33

29.26 14.51 22.88

As can be found in the table, the accuracy of the

model increases with the increase of the forecast

time interval, because there are many factors

affecting the traffic flow, when the number of

forecast steps increases, the correlation between the

data decreases, the performance of traffic flow

prediction is reduced, and it can be found that the

optimization algorithm can improve the accuracy of

the model, but the chaos mapping algorithm has

little influence on the optimization algorithm.

5 CONCLUSIONS

In this paper, a traffic flow prediction model of

BDBO-TCN is proposed. The parameters of TCN

(Temporal Convolutional Network) model were

optimized by using the improved dung beetle

algorithm, and the fitness objective was to minimize

the predicted RMSE (root mean square error) value,

thus, the model parameter configuration with the

highest precision and efficiency can be found. In

order to verify the performance of the model,

experiments were carried out on PEMSD4 and

PEMSD8 data sets, and the results were compared

with the TCN model under other optimization

algorithms. The experimental results show that

BDBO-TCN model performs well in traffic flow

prediction and is superior to other parameter

optimization models. With the increase of time

interval, the model can still maintain a high

prediction accuracy. In addition, we also study the

effect of different chaotic algorithms and different

synchronization lengths on the prediction accuracy,

and find that the selection of hyperparameters has an

important effect on the model performance,

moreover, it is a challenging task to determine the

optimal hyperparameters. By combining the

improved dung beetle algorithm with TCN model,

the parameters are optimized with high precision and

high efficiency. The model shows good adaptability

in dealing with time interval variation.

ACKNOWLEDGEMENTS

This work was supported by National Natural

Science Foundation of China (Grant No 62162040);

Key Program of the Natural Science Foundation of

Gansu Province, China (Grant No.22JR5RA226);

Gansu Province Higher Education Innovation Fund-

funded Project(Grant No.2021A-028)

REFERENCES

Goldberg, D. E. 1989. Genetic Algorithm in Search,

Optimization, and Machine Learning, Genetic

Algorithms in Search Optimization and Machine

Learning. https://xueshu.baidu.com/usercenter/paper

/show?paperid=f8fbd5f000b3e0591fdb69866df614a&

site=xueshu_se&hitarticle=1

Kennedy, J. & Eberhart, R.1995. Particle Swarm

Optimization. Icnn95-international Conference on

Neural Networks. DOI:10.1109/ICNN.1995.488968.

Trafﬁc Flow Prediction Model Based on BDBO-TCN

Lea, C., Flynn, M. D., Vidal, R., Reiter, A. & Hager, G.

D.2016. Temporal convolutional networks for action

segmentation and detection. Proceedings of the IEEE

Conference on Computer Vision and Pattern

Recognition. 156-165. DOI:10.1109/CVPR.2017.113.

Ma, X. L., Tao, Z. M., Wang, Y. H., Yu, H. Y. & Wang,

Y. P. 2015. Long short-term memory neural network

for traffic speed prediction using remote microwave

sensor data. Transportation Research Part C-Emerging

Technologies, 54, 187-197. DOI:10.1016/j.trc.

2015.03.014

Saito, A. & Yamaguchi, A. 2016. Pseudorandom number

generation using chaotic true orbits of the Bernoulli

map. Chaos, 26. DOI:10.1063/1.4954023

Wu, Y., Tan, H., Qin, L., Ran, B. & Jiang, Z. 2018. A

hybrid deep learning based traffic flow prediction

method and its understanding. Transportation

Research Part C: Emerging Technologies, 90, 166-

180. DOI:https://doi.org/10.1016/j.trc.2018.03.001

Xue, J. K. & Shen, B. 2023. Dung beetle optimizer: a new

meta-heuristic algorithm for global optimization.

Journal of Supercomputing, 79, 7305-7336.

DOI:10.1007/s11227-022-04959-6

Yu, Y., Gao, S., Cheng, S., Wang, Y. R., Song, S. Y. &

Yuan, F. 2018. CBSO: a memetic brain storm

optimization with chaotic local search. Memetic

Computing, 10. DOI:10.1007/s12293-017-0247-0

Zhang, K. & Liang, L. 2012. Chaotic System

Identification Based on BP Neural Network of Two

Order Particle Swarm Optimization. Computer

Systems & Applications. https://kns.cnki.net/kcms2

/article/abstract?v=0Q9DRdE4I9fZuncGRxPpCpozzL

y2qVIvjjfIjlS52HGwxr6HAsrCuSM27Z_Tnxqgl6g9pI

txFdL1g-OHf99HNoagiyvfYPO8LduczZrltUEFDHEt

aAEEXcThQBDktU6C74CTGfCZiOg=&uniplatform

=NZKPT&language=CHS

Zhao, X. 2012. Research on optimization performance

comparison of different one-dimensional chaotic

maps. Application Research of Computers, 29, 913-

915. DOI:10.3969/j.issn.1001-3695.2012.03.031

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems