Fault Diagnosis of Process Systems based on Graph Neural Network

Wentao Ouyang

and Yang Jin

Civil Aviation of China University, Tianjin, China

Keywords: GNNs, Process System, Fault Diagnosis, Correlation of Unit.

Abstract: The fault diagnosis methods for process systems are generally based on rules and experience, which

struggle with complex and uncertain issues. Therefore, In this study, a fault diagnosis method for process

systems using adaptive Graph Neural Networks (GNNs) is proposed. This method effectively utilizes the

correlations and dynamic changing among sensors, constructing a graph structure that reflects the complex

relationships between sensors. By employing the graph convolutional neural network as the model

foundation, it effectively extracts the primary changing features of faults, thereby addressing the problem of

multi-class fault diagnosis. Comparative experiments were conducted using the fault diagnosis task of a

three-phase flow system. The proposed method outperforms traditional models in terms of accuracy,

precision, recall, and F1 score, demonstrating its effectiveness in fault diagnosis of process industrial

systems.

1 INTRODUCTION

Process systems are complex systems that include

various devices and subsystems. These devices are

interconnected during operation, and a failure in any

one device can affect the performance of the entire

system. Therefore, fault diagnosis of process

systems is of utmost importance. Traditional fault

diagnosis methods often only consider the

performance of individual devices, neglecting the

correlations between devices, which limits the

accuracy and efficiency of fault diagnosis. In

traditional control systems, all analysis and control

strategy designs are based on the premise that the

characteristics of the process system remain

unchanged, and all sensors, actuators, and signal

transmission channels are functioning normally. A

fault in any unit of the system can affect the normal

operation and safe production of the system. Faults

or failures in any part of the process control system

can pose threats to property and personnel safety,

causing immeasurable losses and even potentially

leading to major accidents (Ma et al., 2019).With the

development of modern process systems towards

greater complexity, the likelihood of system failures

increases, along with the economic losses and

potential harms caused by system failures, such as

casualties, property damage, and environmental

pollution. Therefore, timely understanding of the

operating state of process systems, effective

anomaly monitoring, and fault diagnosis to take

appropriate control strategies in response to

anomalies or faults are crucial for ensuring the

quality and safe operation of process systems,

reducing operating costs, and are of great

significance for the production efficiency of process

systems. Real-time monitoring of the operational

state of process systems, especially for the detection,

diagnosis, and elimination of faults, is necessary to

ensure the reliability and safety of actual systems.

This requires the establishment of a process

monitoring system to monitor the operational state

of the entire control system in real-time, detect

changes in the system, and read fault information

promptly to take effective preventive measures,

ensuring the safety of process systems and

preventing catastrophic accidents. Constructing a

reliable and stable equipment process supervision

system has become a priority in mechanical

equipment manufacturing, effectively reducing

maintenance costs while ensuring the safety of

industrial machinery equipment. Currently, most

industrial equipment detection systems rely on

multiple sensor data for monitoring, such as aircraft

engines, rotating machinery rolling bearings,

multiphase flow separators, etc., while these

Ouyang, W. and Jin, Y.

Fault Diagnosis of Process Systems Based on Graph Neural Network.

DOI: 10.5220/0012876300004536

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Mining, E-Learning, and Information Systems (DMEIS 2024), pages 37-45

ISBN: 978-989-758-715-3

monitoring systems usually store historical data for

training. For complex industrial mechanical systems,

multi-sensor data often have high-dimensional and

complex interaction characteristics (Jiang and Yin,

2018), posing many challenges to traditional fault

diagnosis and health monitoring systems, making

supervised machine learning methods feasible.

Traditional fault diagnosis methods often focus

on Statistical Process Control (Yu and Wang, 2005)

(SPC) and model-based approaches (Wang and

Wang, 2006, 2009). Nowadays, fault diagnosis in

complex industrial systems is categorized into two

main types: model-based and data-driven methods.

Due to the complexity and high cost of modeling in

industrial systems, model-based methods are severely

limited in practical applications. In contrast, data-

driven methods, aiming to extract relevant data

features and identify fault types through statistical

analysis or feature discrimination learning, have been

widely applied and rapidly developed. Common fault

diagnosis techniques include Support Vector

Machines(Mahadevan and Shah, 2009), (SVM),

Multilayer Perceptrons (MLP), Convolutional Neural

Networks, and Graph Neural Networks. Gu (Gu et

al., 2014) employed a method combining Principal

Component Analysis (PCA) and Support Vector

Machine (SVM) to extract and analyze the fault

features of rolling bearings. However, real-world

data often contain noise and may be excessively large,

which can affect the effectiveness of this diagnostic

method. Wang(Wang et al., 2005) and others

conducted fault diagnosis on mixed circuits using

Multilayer Perceptrons (MLPs) to solve complex

classification problems. MLPs address the issue of

non-linearity between features, but when facing

process fault diagnosis, the prevalence of clear fault

data scarcity can lead to overfitting or obtaining local

optimum solutions. Additionally, there is a lack of

model interpretability. Convolutional Neural

Networks (CNNs) have also gradually become

widely applied. Chen (Chen and Yu, 2020) used

CNNs for feature learning and fault diagnosis in

multivariable processes. However, small datasets

cannot support the training of deep networks, and for

signals transmitted by mechanical or semiconductor

components, which are mostly converted into image

signals for convolutional training, this approach fails

to capture the correlations between multiple

components.

To address these challenges, this article proposes

a fault diagnosis method for process systems based

on adaptive Graph Neural Networks (GNNs).

Recently, GNNs have been widely applied in the

field of deep learning with significant success. Gori

(Gori et al., 2005) first introduced GNNs, designed

to directly process graph structures, including

directed/undirected graphs, cyclic graphs, and

labeled graphs. Due to their ability to accurately

represent real-world systems, GNN-based fault

diagnosis methods have potential advantages in

processing complex mechanical industrial data,

especially in mining the topological structures and

interactions between sensor data. Wu (Wu et al.,

2020) proposed a scalable graph convolution that

enables semi-supervised learning with graph-

structured data through the combined action of

GNNs and Convolutional Neural Networks.

The application of fault diagnosis of process

system to graph neural network has gradually

become a trend. It handles complex relationships,

automatically learns fault features and works for

large industrial systems; and performs end-to-end

training; handles dynamic graphs and multimodal

fusion, etc. for instance Li

(Li et al., 2020) by

comparing the disadvantages of other deep learning

networks to show the relationship between mining

signals, we propose a multiple receptive field graph

convolutional network (MRF-GCN) based on the

original model to effectively carry out data

relationship mining. Yang(Yang et al., 2021) this

paper proposes a method based on the space-time

graph, SuperGraph, which can transform the graph

classification task into classifying the nodes in

SuperGraph. Zhang (Yu et al., 2021) A fast graph

convolution network is proposed, using the method

of wavelet decomposition to preprocess the original

vibration signal of wind power gearbox to show the

time-frequency characteristics in the form of graph,

using the fast graph convolution kernel and specific

pooling improvement to reduce the number of nodes

and realize fast classification. Stewart E

(Ding et al.,

2020) The deep graph convolution network (DGCN)

based on graph theory is applied to the fault

diagnosis of roller bearings. This method uses the

graph structure constructed to detect the failure of

roller bearings of different types and severity of the

same type. Kenning (Kenning et al., 2022) The

directed graph convolutional neural network

(DGCNN) is proposed, and a simple method to

alleviate the inherent class imbalance in the graph is

described. Zhang (Tong et al., 2021) This paper

proposes a transmission line fault detection and

classification method based on graph convolution

neural network, and establishes a transient fault

detection and classification framework based on the

idea of prior knowledge. It is not difficult to see that

the fusion of data information is crucial for

industrial process fault diagnosis (Tang et al., 2021).

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

For the identification and classification of faults, we

need to extend them to the graph level classification

level. When constructing the graph level

classification model, the corresponding graph

topology for each fault to form graph level

differentiation. At the same time, in order to retain

the graph structure characteristics, it is necessary to

effectively fuse the multi-sensor data information to

ensure the accuracy and comprehensiveness of fault

identification.

This paper aims to elaborate an innovative

method for process system in mechanical industry.

This method is based on the graph neural network,

and its core advantage is that it can deeply mine the

topology structure and mutual influence information

in the multi-sensor data, so as to improve the

detection and diagnosis accuracy of system faults.

First, this paper transforms the one-dimensional time-

domain sensor data into graph structure data, where

the nodes represent the measurements of each sensor

and the edges represent the intercorrelation between

the sensors. After the adaptive node importance

screening, a graph neural network model was

constructed. Through the model, hidden information

about the fault features and topology in multi-scale

sensor data.

2 MODELING

2.1 Relevance and Centrality Filtering

Fault diagnosis in process systems is a complex

issue involving many variables and potential

problems. It often overlooks the linear or nonlinear

relationships between devices. Graph Neural

Networks (GNNs) address this by modeling the

interactions between devices (variables) in the

system, thereby offering a better solution.

There is graph G (V, E), V is a collection of

nodes and E is used to represent the connection

between nodes. In statistics, Pearson cross-relations

(Dominic. Edelmann et al., 2021) (Pearson

Correlation Coefficient) It can be used to reflect the

degree of linear correlation between two random

temporal variables. With this point, this paper tries

to measure the correlation relationship between

nodes and construct graph data. The Pearson's

correlation coefficient is as follows:

𝑟 =

∑

(𝑋



−𝑋



)(𝑌



−𝑌



)







∑

(𝑋



−𝑋



)









∑

(𝑌



−𝑌



)







(1)

The larger the value is, the stronger the

correlation between the two nodes is, which solves

the linear relationship between the device variables.

The Pearson correlation coefficient is used to

calculate the linear relationship between nodes, and

then the threshold Q is set to restrict, thus further

obtaining a streamlined graph data structure,

reducing the redundancy of data calculation, and

enhancing the efficiency of data feature extraction.

𝑟



= 

0 ⋯⋯𝑟< 𝑄

1 ⋯⋯𝑟≥

𝑄

(2)

When the Pearson correlation coefficient

between any nodes in the graph structure is greater

than or equal to the threshold value, it is concluded

that the two nodes are mutually first-order

neighbors, and otherwise, the connection

relationship cannot be constructed.

For each node feature vector v

The eigenvector

centrality of node i is obtained, and the eigenvector

centrality score for all nodes is finally calculated and

normalized. Through the variant sigmoid function,

the final node importance vector is multiplied as the

node weight value by the graph adjacency matrix

from the initial calculation, to obtain the final graph

structure matrix, thus forming M fault sample maps.

Eigenvector centrality involves finding the

principal eigenvector of the adjacency matrix (i. e.,

the eigenvector associated with the maximum

eigenvalue). Suppose that λ is the maximum

eigenvalue of the adjacency matrix A, and x is the

corresponding eigenvector. Then, x satisfies the

following characteristic equation:

xAx

(3)

Each element x in the feature vector x

Denotes

the eigenvector centrality score of the corresponding

nodes. Usually, we standardize x:

)))((

)(((

βxnormalizesigmoid

βxnormalizesigmoidAA

iji,ji,

),,min×=

′

(4)

2.2 Dataset of Graph

The graph dataset consists of n small graphs, denoted

as G = {G1, G2, G3, G4, …, Gn}, where each graph

Gi = (Xi, Vi, Ei, Yi). Here,𝑋



∈(𝑛



× 𝑚) denote the

input feature matrix of the nodes, with n

being the

number of nodes in the i-th graph (in this paper, aside

from the normal state graph data and the sixth fault

graph data which have 24 nodes, all other graph data

consist of 23 nodes), and m being the number of

features per node. V

is the set of nodes, E

represents

the connections between nodes (including the

adjacency matrix𝐴





∈ℜ







×





), and Y

denotes the

Fault Diagnosis of Process Systems Based on Graph Neural Network

one-hot encoded value of the i-th graph. In the graph

convolutional layer, the input matrix for the k-th

layer is denoted

𝐻





∈ℝ







×



, where (𝑛





, 𝑑



)

represents the number and dimension of node

embeddings in the k-th hidden layer, with the

adjacency matrix being denoted

. accordingly.

Following each graph convolutional layer is a graph

average pooling layer, which calculates the feature

vector for each node to obtain a global

representation, with the value on each dimension

being the average of the features of all nodes on that

dimension. After passing through k-layers of

convolutional and pooling layers, the output enters a

fully connected layer and an Activation Function

ReLU to produce the final output. The scores for

each category are calculated using a Softmax

function to obtain the model's predicted labels, which

are then compared with the true labels. At the same

time, a loss function (such as the CrossEntropy Loss

function) is used to measure the performance of this

graph-level classification model, and gradient

Backward is performed. This process iteratively

trains the model for effectiveness and stability.

2.3 Graph Neural Network Based on

the Weighted Graph under the

Correlation

This section is mainly carried out on the

improvement of graph data operation, so that the

graph convolutional neural network model is easier

to extract the feature structure and make more

accurate prediction.

In the face of non-European data, according to the

graph node information and the data model of the

original connection correlation calculation to get the

new graph adjacent matrix, the method, while

retaining the key connection information of the

original model missing connection due to noise or

other reasons, and solve the interference of the

artificial design figure structure, reduce manpower

and reduce labor cost.

Table 1 for the graph convolutional neural

network model input and output parameter

dimensions, after the original data calculation

correlation can get the graph connection under

different fault mode, and for each sensor data change

adaptive central screening to realize multiple

weighted graph data set, improve the accuracy and

stability of GCN (Graph Convolution Networks) in

data-driven fault diagnosis.

Table 1: Input-output dimensions of each layer.

Layer Name

Input Data

Dimension

Output Data

Dimensions

Convolutional Layer M

﹡

F M

﹡

F’

Pooling Layer M

﹡

F’ M

﹡

N’

﹡

F’’

Full Connect Layer M

﹡

N’

﹡

F’’ M*(categories)

3 EXPERIMENTS

This section presents the performance evaluation of

fault diagnosis in mechanical industrial processes

based on Graph Convolutional Neural Networks

(GCN). The model structure of the method proposed

in this paper is shown in Figure 1. Experiments are

conducted using a three-phase separator dataset to

demonstrate the following points: Compared to

traditional fault diagnosis methods, the graph

convolutional neural network approach is effective

and stable in fault diagnosis of process industrial

systems.

Figure 1: Model structure graph.

3.1 Introduction to the Dataset

The data set presented in this paper uses the Three-

phase Flow Facility (TFF) data set of the University

of Cranfield (Ruiz-Cárcel et al., 2015). The

simulation encompasses the Three-phase flow

process commonly encountered in sectors such as the

oil and gas industry, involving three types of mixed

inputs/outputs: gas, liquid, and solid particles, as

illustrated in Figure 2. Within the TFF dataset, it is

possible to introduce various types of faults into the

system through specific manipulations, simulating

issues that might occur in a real plant, such as

blockages, operational errors, or unconventional

operating conditions. In experiments, the dataset is

collected under various operating conditions to

ensure that fault detection is not limited to steady-

state situations. The datasets can be used to evaluate

and compare the performance of multivariate process

monitoring techniques based on real experimental

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

data. The dataset includes normal states under

steady-state working conditions and 6 types of

simulated faults (all typical faults in actual

operation), with each fault data transitioning from a

normal state to a weak fault, to a severe fault, and

back to a normal state, sampled at a frequency of

1Hz.

Figure 2: Architecture of the three-phase flow

facility(Ruiz-Cárcel et al., 2015).

In this paper, normal data value in the fault data

are removed, focusing only on the fault states, and

normalization is applied to each sensor's data.

Data normalization involves scaling input data to

a common range, thereby eliminating the impact

on model recognition caused by disparate ranges

of feature parameters. The normalization process

is represented as follows, constraining the input

parameter values within the range [0,1].

minmax

min

−

(5)

During the process of creating sample graphs,

every 20 data points are used to form a feature

segment to construct the sample graph.

Subsequently, the fault dataset and the normal

dataset are randomly merged, with 70% of the

combined dataset randomly selected as the

training dataset and 30% as the test dataset. Table

2 displays the fault classification and the label

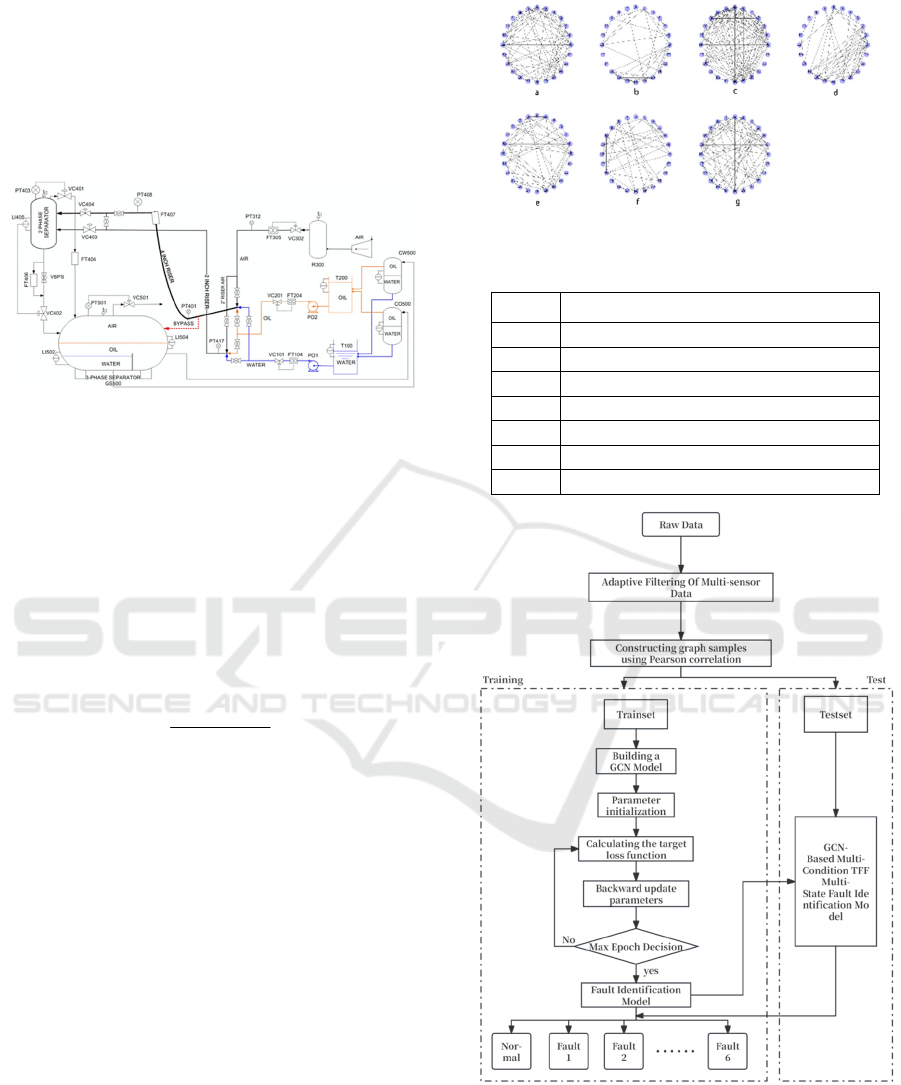
values for each state. Figure 3 shows graph-level

representations under different fault conditions,

sequentially corresponding to the faults listed

below. (a. Normal state; b. Airway blockage; c.

Water pipe blockage; d. Top separator inlet

blockage; e. Bypass valve open; f. Pressure surge;

g. System operation anomaly (manual)).

Figure 3: Display of each fault level diagram.

Table 2: Label parameters setting.

Label Fault Type

0 Normal operation

1 Gas pipe blockage

2 Water pipe blockage

3 Top separator input is blocked

4 Bypass valve open

5 Pressure surge

6 Abnormal operation (artificial)

Figure 4: Experimental step.

3.2 Setup

The experimental procedure is illustrated in

Figure 4. By utilizing different algorithms such as

PCA+SVM, MLP, CNN, and GAT (Graph

Fault Diagnosis of Process Systems Based on Graph Neural Network

Attention Networks) as benchmarks, the method

presented in this paper is compared against them,

evaluating the stability and effectiveness of fault

diagnosis on the aforementioned dataset through

various metrics.

This paper employs three metrics to evaluate

data-driven classification models: Accuracy

Estimation (Accuracy), Precision, Recall, and F1-

score. Accuracy is the most common evaluation

metric for classification problems, representing

the probability of correct predictions for all test

samples. Precision and Recall are often used

together as indicators to assess the performance of

classification models. Precision refers to the

accuracy of the classification model in predicting

positive samples correctly, that is, among the

samples predicted as positive, how many are truly

positive samples. Recall refers to the rate at which

the classification model correctly identifies all

true positive samples, indicating how many of the

actual positive samples were correctly recognized.

When precision is high, the model's analysis

results are more reliable, but it may miss some

true positive samples. On the other hand, when

recall is high, the model can effectively identify

all true positive samples, but it may mistakenly

classify some negative samples as positive. The

F1-score is the harmonic mean of precision and

recall, incorporating the performance of both

precision and recall, and is commonly used to

evaluate the performance of binary classification

models. The F1-score combines the model's

precision and recall, providing a single numerical

indicator to measure the model's overall

performance. Its value generally ranges from 0 to

1, with higher values indicating better model

performance.The F1-score includes three different

scores: micro-F1, macro-F1, and weighted-F1.

This paper uses the first two for calculating and

evaluating the classification models. Micro-F1

calculates the F1 score by aggregating the global

true positives (TP), false negatives (FN), and false

positives (FP). First, the true positives (TP), false

positives (FP), and false negatives (FN) values for

all categories are summed up, and then these

values are inserted into the F1 equation to obtain

the micro-F1 score. Macro-F1 calculates the

arithmetic mean of the F1 scores for each

category. This method treats all fault categories

equally without considering the importance of

differences between categories.

The experiment comprises a total of 3281

sample sets, with each set consisting of 10 data

points. The training and test sets account for 70%

and 30% of the total number of samples,

respectively, resulting in 2296 sets for the training

set and 985 sets for the test set. Each experimental

sample is represented by a matrix of size (10 ×

number of nodes) as the X input feature matrix. In

this paper, except for the normal state and fault

state with 6 nodes, which have 24 nodes each, all

other fault states consist of 23 nodes.In model

training, mini-batch training is employed with a

BatchSize of 16, and the maximum training epoch

is set to 100.The experimental method utilizes a

cross-entropy loss function and employs the

Adam optimizer along with model parameters,

with the learning rate set at 0.0005. In the graph

neural network model, two convolutional layers,

one Dropout layer (rate = 0.5), and one fully

connected layer are adopted, as shown in Table 3:

Table 3: Experimental model parameter setting.

arameters/Setting

Value Description Remarks

Learning Rate

0.0005

Using the

Adam

optimize

through the

gri

Batch size 16

Epoch 100

Dropout Rate 0.5

After being

applied to the

convolution

laye

Reduce

overfitting

Hidden Layer Size 64

GCN Layers 3

ctivation Functio

ReLU

Early Stop

Strateg

yes

Based on the

validation loss

Prevent

overfitting

Moreover, the experimental method is

implemented on the basis of PyTorch Geometric,

and the experimental platform is a computer

equipped with an NVIDIA RTX3070 and an Intel

i7 10th generation CPU.

4 EXPERIMENTAL

VALIDATION

This paper tests the performance of the model by

inputting a randomly assigned test dataset into the

model trained from the training set. A qualitative

analysis of each model's fault identification

classification performance is conducted visually

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

through confusion matrices, evaluating the

recognition performance for each fault category. This

analysis also identifies issues within the model in

graph classification tasks. To reduce the impact of

randomness in device computation during the

experiment, the experiment was repeated multiple

times. It was found that the results did not vary

significantly, allowing the selection of one set of

results for comparative analysis across different

algorithms. This experimental method can quickly

improve the model's classification accuracy during

the computation process, and after multiple

iterations, there is no significant fluctuation in the

loss value, indicating the model's rapidity and

stability. Table 4 assesses the performance of the

experimental method from multiple perspectives by

displaying the performance metrics of various

algorithms.

It's not difficult to see from the accuracy metric

that the model proposed in this paper significantly

outperforms traditional fault diagnosis methods and

existing popular methods, reaching up to 97%

accuracy. This is a 9.2%, 9.4%, and 15%

improvement over GAT, CNN, and MLP

respectively, and a substantial 44% improvement

compared to the traditional PCA+SVM method. In

terms of precision, recall, and F1 score, the increase

in these metrics further indicates a reduced

probability of making incorrect predictions.

Consequently, it can be intuitively judged that the

model method proposed in this paper has

improvements of 6%, 7.5%, and 9% over the CNN

method, 25%, 14%, and 20% over the MLP method,

and 5.8%, 6%, and 6% over the GAT model,

respectively. From this comparative experiment, it

can be concluded that the performance evaluation

metrics of the proposed method are the highest. This

also demonstrates that the method proposed in this

paper is effective and robust when implementing

dynamic process system fault diagnosis for different

fault classification tasks.

Table 4: Classify performance comparison of each model.

Model

Precision

(%)

Accuracy

(%)

Recall

(%)

Micro

Macro

CA+SVM 53.23 49.66 53.23 0.51 0.36

MLP 82.78 71.49 82.77 0.76 0.54

CNN 88.43 90.52 88.43 0.87 0.71

GAT 88.67 90.8 90.8 0.90 0.86

this paper 97.86 96.61 96.17 0.96 0.93

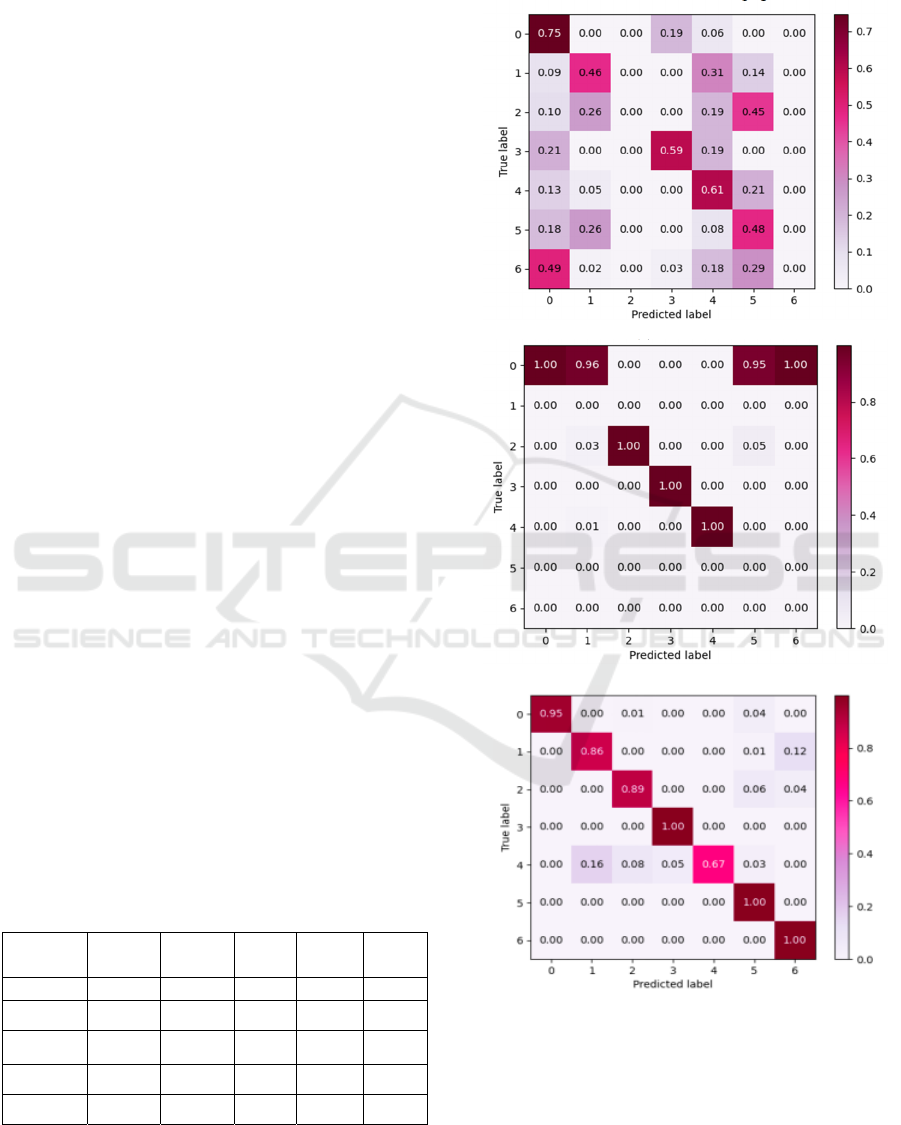
Figure 5 sequentially displays the confusion

matrix diagrams for PCA+SVM, MLP, CNN, GAT,

and the method mentioned in this paper:

(a)PCA+SVM

(b)MLP

(c)CNN

Fault Diagnosis of Process Systems Based on Graph Neural Network

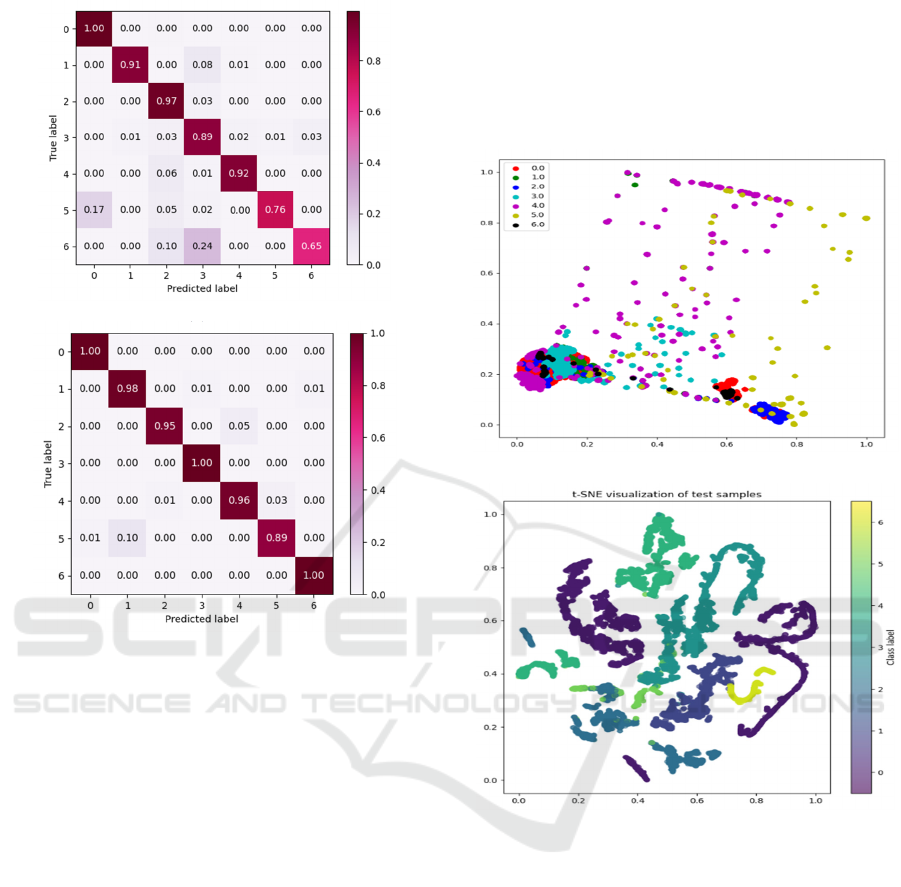
(d)GAT

(e)Methods of this paper

Figure 5: Confusion matrix diagram of each model.

In the confusion matrix, each column represents

the predicted labels, and each row represents the true

labels. The values on the main diagonal of each

model's confusion matrix represent the percentage of

samples correctly classified for each label during the

testing phase, while the off-diagonal elements

represent cases of misclassification.By comparing the

main diagonals of the five models, it is more

intuitively observed that PCA and MLP both exhibit

cases where the misidentification rate is 100%. In the

CNN model, the recognition rate for the fault of

mistakenly opening the bypass valve is relatively

low, and in the GAT model, the recognition rate for

system faults under conditions of manual

misoperation is low. The graph-structured optimized

GCN model proposed in this paper demonstrates an

accuracy rate of over 89% for the recognition of

triphasic flow data compared to other models. This

further proves the effectiveness and robustness of the

graph neural network model under graph structure

optimization for recognizing different fault

categories. It has stronger generalization capabilities

for fault recognition rates and can effectively extract

fault features.

Furthermore, this paper utilizes the t-Distributed

Stochastic Neighbor Embedding (t-SNE) method

(Van Der Maaten and Hinton, 2008) to visualize the

fault features learned by the model and the

preprocessed original data in two-dimensional feature

maps, as shown in Figures 6(a) and 6(b).

(a)Feature of Raw Data

(b)Features after model training

Figure 6: T-SNE Visualization in 2D.

It can be observed that the fault features after

model learning exhibit better clustering performance

and fault separation, effectively revealing the

inherent structure and correlations within the data.

5 CONCLUSIONS

This paper proposes a fault diagnosis method for

mechanical process industrial systems using a Graph

Convolutional Neural Network (GCN) model, which,

compared to traditional intelligent fault diagnosis

methods that heavily rely on manual feature

extraction, introduces a novel approach. The

proposed method combines multi-dimensional time-

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

series data with improved graph data obtained

through correlation calculations and original graph

data, inputting them into the network model to

extract features from different fault samples, thereby

achieving fault type diagnosis. The experiments

show a significant improvement in commonly used

metrics such as Accuracy Estimation (Accuracy),

Precision, Recall, and F1-score, as well as in the

intuitive representation of confusion matrices and t-

SNE visualizations, compared to traditional

intelligent fault diagnosis methods. This

demonstrates a certain superiority, enabling the

model to fully capture and utilize the structural

information in the data, thereby further enhancing the

model's representational capability and prediction

accuracy.

In future work, based on graph data under

continuous time-series operating conditions, effective

fault features can be extracted using weighted

windows to enhance the timeliness of fault diagnosis

by graph neural network models and to predict fault

occurrence points in advance. Applying this to actual

operations can effectively reduce maintenance costs

and labor requirements.

REFERENCES

Ma L ,Dong J ,Peng K , et al, 2019.“Hierarchical

Monitoring and Root-Cause Diagnosis Framework for

Key Performance Indicator-Related Multiple Faults in

Process Industries,” IEEE Trans. Industrial

Informatics, vol. 15, no. 4, pp. 2091-2100, 2019.

Jiang. Y.,Yin. S., 2018.“Recursive total principle

component regression based fault detection and its

application to vehicular cyber-physical systems,”

IEEE Trans.Ind.Inform., vol. 14, no. 4, pp. 1415–1423.

Yu, T.,Wang, G, 2005.“The connotation and role of

statistical process control in advanced manufacturing

environments,” Industrial Engineering and

Management, no. 03, pp. 51-54.

Wang, Q.,Wang, B, 2006, 2009.“Simulation research on

model-based fault diagnosis methods,” Journal of

Hebei University of Technology, no. 04, pp. 99-104.

Mahadevan S, Shah S L.“Fault detection and diagnosis in

process data using one-class support vector machines,”

Journal of process control, 2009 vol. 19, no. 10, pp.

1627-1639.

Gu, Y.,Yang, Z.,Zhu, F. ,2014. “Fusion analysis of rolling

bearing fault characteristics based on principal

component analysis,” In: National Academic

Exchange Conference on Reliability Technology in the

Machinery Industry and Establishment Conference of

the Fifth Committee of the Reliability Engineering

Branch. ChengDu. pp. 193-197.

Wang. C., Chen. G., Xie. Y, 2005.“Application of

multilayer perceptron in fault diagnosis of analog /

hybrid circuit,” Journal of Instrumentation, no. 06, pp.

578-581.

Chen. S.,Yu. J, 2020.“Feature learning and fault diagnosis

of convolutional neural networks,” Journal of Harbin

Institute of Technology, vol. 52, no. 07, pp. 59-67.

Gori M, Monfardini G, Scarselli F. ,2005. “A new model

for learning in graph domains,” In: Proceedings IEEE

international joint conference on neural networks. vol.

2, pp. 729-734.https://10.1109/IJCNN.2005.1555942

Wu. Z., Pan. S., Chen. F., et al, 2020.“A comprehensive

survey on graph neural networks,” IEEE transactions

on neural networks and learning systems, vol. 32, no.

1, pp. 4-24.

Li. T., Zhao. Z., Sun. C., et al, 2020.“Multireceptive field

graph convolutional networks for machine fault

diagnosis,” IEEE Transactions on Industrial

Electronics, vol. 68, no. 12, pp. 12739-12749.

Yang. C., Zhou. K., Liu. J, 2021.“SuperGraph: Spatial-

temporal graph-based feature extraction for rotating

machinery diagnosis,” IEEE Transactions on

Industrial Electronics, vol. 69, no. 4, pp. 4167-4176.

Yu. X., Tang. B., Zhang. K, 2021.“Fault diagnosis of wind

turbine gearbox using a novel method of fast deep

graph convolutional networks,” IEEE Transactions on

Instrumentation and Measurement, vol. 70, pp. 1-14.

Ding. C., et al, 2020.“Intelligent acoustic-based fault

diagnosis of roller bearings using a deep graph

convolutional network,” Measurement, vol. 156, pp.

107585-107585.

Kenning. M., Deng. J., Edwards. M., et al, 2022.“A

directed graph convolutional neural network for edge-

structured signals in link-fault detection,” Pattern

Recognition Letters, vol. 153, pp. 100-106.

Tong. H., Qiu. R.,Zhang. D., et al, 2021.“Detection and

classification of transmission line transient faults

based on graph convolutional neural network,” CSEE

Journal of Power and Energy Systems, vol. 7, no. 3,

pp. 456-471.

Tang. Y., Zhang. X.,Qin. G., et al, 2021.“Graph

Cardinality Preserved Attention Network for Fault

Diagnosis of Induction Motor Under Varying Speed

and Load Condition,” IEEE Transactions on Industrial

Informatics, vol. 18, no. 6, pp. 3702-3712.

Dominic. Edelmann., et al, 2021.“On relationships

between the Pearson and the distance correlation

coefficients,” Statistics and Probability letters, vol.

169.

Ruiz-Cárcel. C.,Cao. Y.,Mba. D., et al, 2015.“Statistical

process monitoring of a multiphase flow facility,”

Control Engineering Practice, vol. 42, pp. 74–88.

Van. Der. Maaten. L.,Hinton. G., 2008.“Visualizing data

using t-sne,” Journal of machine learning research,

vol. 9, no. 11.

Fault Diagnosis of Process Systems Based on Graph Neural Network