Identification of TITO Systems Using Modified Decentralized Relay
Feedback
M. Hofreiter
a
Department of Instrumentation and Control Engineering, Czech Technical University in Prague,
Faculty of Mechanical Engineering, Prague, Czech Republic
Keywords: System Identification, Multivariable Systems, Static Gain, Relay Control, Parameter Estimation, Frequency
Response, Feedback, Time Delay.
Abstract: The paper is devoted to the identification of systems with two inputs and two outputs (TITO systems) from
one short, decentralized relay feedback experiment. The proposed modifications help to excite the process so
that all parameters of the model describing the process can be estimated. The proposed procedure can be used
to estimate the parameters of linear models without the need to achieve a steady-state output cycle. The
proposed modification of relay feedback identification is demonstrated on a simulated TITO process.
1 INTRODUCTION
A relay feedback experiment for process
identification is often used in control design. It was
originally used for process identification by Rotač et
al. (1961) and lately also for tuning mainly
proportional-integral-derivative (PID) controllers,
e.g. Åström & Hägglund (1984); Bi et al. (1997);
Luyben (1987). A review of methods using relay
feedback identification for single-input single-output
(SISO) systems can be found in publications, e.g.
Dharmalingam & Thangavelu (2019); Liu et al.
(2013); Liu & Gao (2011); Ruderman (2019); Yu
(2006).
Although there are many publications devoted to
relay feedback identification, most of them consider
only SISO systems. However, in many industrial
processes, we often encounter systems with multiple
inputs and multiple outputs, i.e. MIMO systems. The
methods proposed for relay feedback identification of
SISO systems can be used for the identification of
MIMO systems in the case of negligible cross-
couplings. Some methods are also dedicated to
designing a proper decoupler to limit cross-couplings,
e.g. Padhy & Majhi, (2006). If cross-couplings in
MIMO systems are not negligible, then according to
Wang et al. (1997) sequential tuning or decentralized
relay feedback can be used. Sequential tuning is used,
a
https://orcid.org/0000-0001-9373-2988
for example, in Shen & Yu (1994). In the case of
decentralized relay feedback all loops are closed with
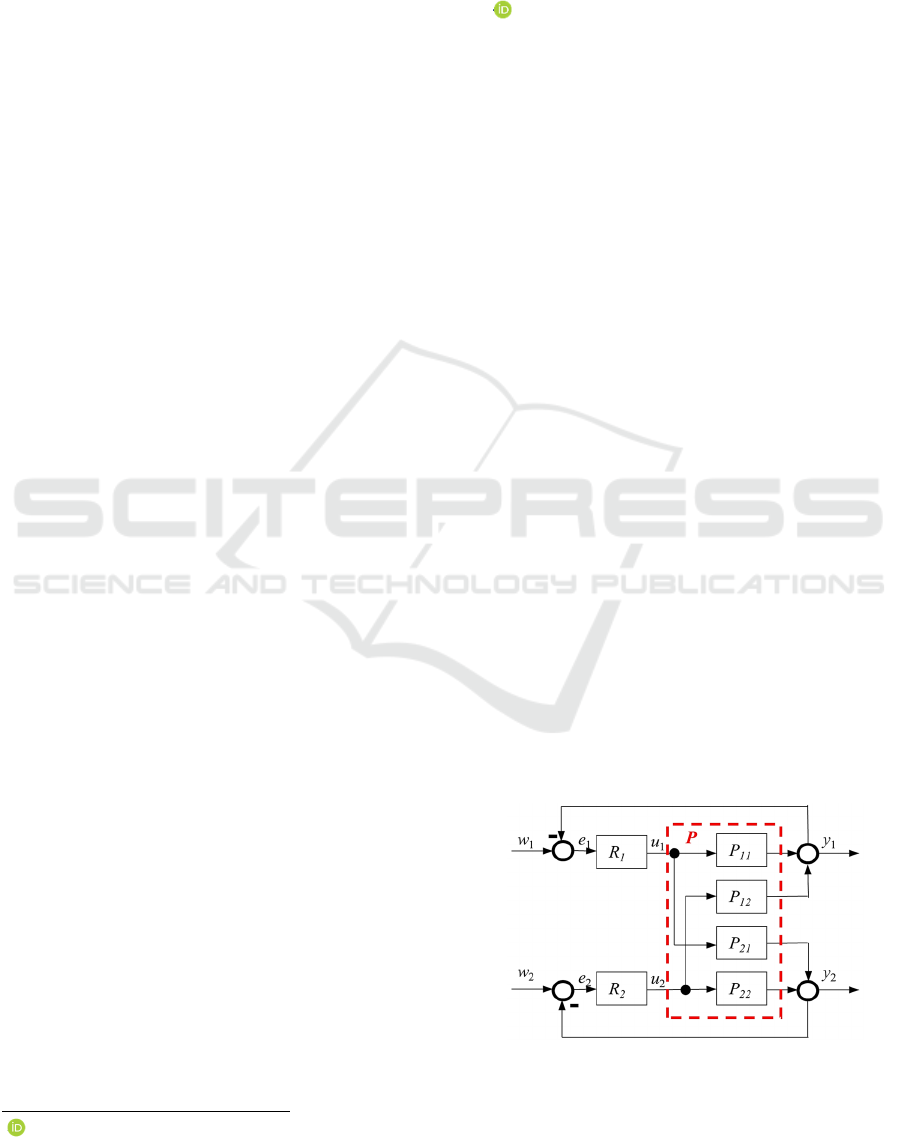
relay feedback simultaneously, see Fig. 1 for the two-
input two-output (TITO) process P. In this case, all
cross-couplings influence the process. Published
methods using the relay feedback experiment to
identify TITO systems mostly assume low-order
linear models, steady-state oscillations with the same
fundamental period, and require multiple
experiments, see e.g. Chidambaram & Sathe (2014);
Wang et al. (1997); Bajarangbali & Majhi (2012);
Hofreiter (2022). The mentioned limitations are
solved in Berner et al. (2017a); Berner et al. (2017b)
by changing the relay parameters during the relay
feedback test and the identification is solved as an
optimization problem.
Figure 1: Block diagram of the decentralized relay control
of the TITO process.
Hofreiter, M.
Identification of TITO Systems Using Modified Decentralized Relay Feedback.
DOI: 10.5220/0012887000003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 625-631
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
625

In this paper, we restrict ourselves to TITO
systems and our goal is to use a decentralized relay
test to identify the process. The aim of this paper is
not to design TITO systems control, but to obtain a
matrix of transfer functions that can be used for
control design.
This paper is organized as follows. After an
introductory section presenting the issues addressed,
Section II explains the frequency method for
identification of TITO strongly coupled systems
using a relay-based closed-loop test. Here one
recommends inserting an integrator before the relay
to improve the estimation of the TITO system's static
sensitivities. Section III demonstrates the proposed
method on a TITO strongly coupled process where
second-order time-delayed models model all
interactions. The basic properties of this method are
summarized in the Conclusions section.
2 RELAY IDENTIFICATION FOR
TITO SYSTEMS
Let us consider a time-invariant strongly coupled TITO
process, which is controlled by two biased relays R
1
, R
2
with hysteresis, see Figure 1, where y
1
, y
2
denote the
controlled variables, w
1
, w
2
are the desired variables,
e
1
, e
2
are the control errors and u
1
and u
2
are the
manipulated variables. The static characteristics of the
relays are depicted in Figure 2. The TITO process is
described by the following frequency transfer function
matrix (j is the imaginary unit).
𝑷
(
𝑗𝜔
)
=
𝑃

(
𝑗𝜔
)
𝑃

(
𝑗𝜔
)
𝑃

(
𝑗𝜔
)
𝑃

(
𝑗𝜔
)
 (1)
Figure 2: Steady-state characteristics of a biased relay with
hysteresis (i=1,2).
In the frequency domain, it holds for the TITO
process
𝑌

=𝑃

⋅𝑈

𝑃

⋅𝑈

; 𝑖=1,2 (2)
where Y
i
, U
i
are the Fourier images of y
i
, u
i
and P
i1
,
P
i2
are the frequency transfer functions of the TITO
process. We choose the model structure M
i1
, M
i2
,
i=1,2 for describing the frequency transfer functions
P
i1
, P
i2
, i=1,2 of the TITO process. The unknown
parameters of the model transfer functions M
i1
, M
i2
,
i=1,2 can be obtained by minimizing the criterion
reflecting the errors of equations (2) for individual
frequencies where P
i1
, P
i2
, i=1,2 are substituted by
M
i1
, M
i2
, i=1,2. The relationship (2) implies that we
can identify the process subsystems related to one
output separately from the subsystem related to the
other output. Therefore, the model parameters can be
obtained for i=1,2 by the criterion
( ) () ( ) ()
2
2
12
11
,,
f
n
ii i i k ilil k l k
kl
Cr Y M U θθ ω θω ω
==

=− ⋅



(3)
where θ
i1
, θ
i2
; i=1,2 are the estimated model
parameters, n
f
is the number of frequencies, and ω is
the frequency. The model parameters θ
i1
, θ
i2
; i=1,2
are estimated by iterative calculation using
()
,1 2
12 ,12
,
,argmin ,;1,2
ii
ii ii i
Cr i
θθ
θθ θ θ ==
(4)
This optimization problem was solved in the
Matlab environment using the tfest command in
System Identification Toolbox (Release 2024a). The
algorithm of the tfest command is described in
Ozdemir & Gumussoy (2017).
Asymmetric relays help to excite the process and
thus improve parameter estimation. A significant
improvement in parameter estimates can be achieved
by inserting an integration term into one input (see
Fig. 3) or both inputs. This will excite the process at
low frequencies, which significantly improves the
estimates of steady-state gains.
3 EXAMPLE
The following description of the TITO process was
taken from Wang et al. (1997). Consider the transfer
function matrix P(s) of a TITO process
𝑷
(
𝑠
)
=
.
(
.
)

(
.
)


(
.
)(
.
)


(
.
)(
.
)

.
(
.
)(
.
)

(
.
)
 (5)
(s is the complex variable in the Laplace transform).
e
i
u
Ai
u
Bi
ε
Ai
ε
Bi
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
626

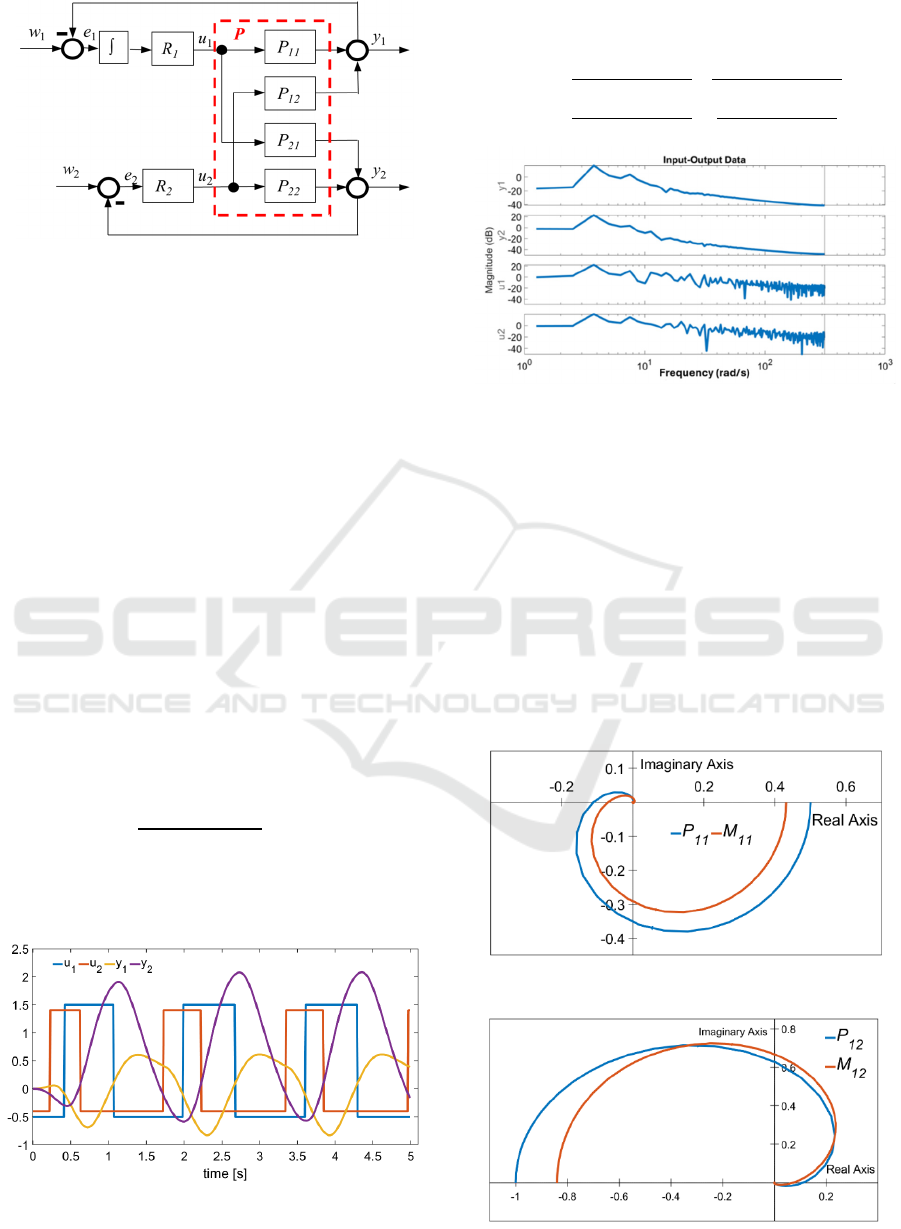
Figure 3: Block diagram of the decentralized modified relay
test of the TITO system.
The block diagram used to identify the TITO system
is shown in Fig. 1. The relays parameters in the given
example were chosen as follows.
u
A1
= 1.5, u
B1
= −0.5, ε
A1
= 0.1, ε
B1
= −0.1 (6)
u
A2
= 1.4, u
B2
= −0.4, ε
A2
= 0.1, ε
B2
= −0.1 (7)
The relay outputs u
1
, u
2
and the process outputs y
1
, y
2
obtained from the relay feedback test to identify the
TITO process are shown in Fig. 4. Input and output
data in the range of 5 s were used to estimate the
parameters of models M
i1
, M
i2
, i=1,2. Inputs and
outputs were recorded with a sampling period of 0.01
s. A fast Fourier transform was used to convert the
inputs and outputs from the time domain to the
frequency domain, see Fig. 5. Second-order time-
delayed (SOTD) models (8) were used for the model
fitting because this model is very versatile and can
describe most non-oscillating or oscillating
proportional systems with or without a transport
delay.
𝑀

(
𝑠
)
=


⋅
⋅








, m=1,2; n=1,2 (8)
Therefore, it is necessary to estimate 16 parameters
(K
mn
, τ
mn
, a
2mn
, a
1mn
, m=1,2; n=1,2) using relay
feedback identification.
Figure 4: Input and output data used to estimate model
parameters.
Model M of the TITO process was obtained using the
procedure described in Section 2 in the form
𝑴
(
𝑠
)
=
.⋅(.)


..
.⋅
(
.
)


..
.⋅
(
.
)


..
.⋅
(
.
)


..
 (9)
Figure 5: Magnitude spectrum of signals y
1
, y
2
, u
1
and u
2
.
Fig. 6 to 9 show the Nyquist frequency responses
of process P and model M. Further comparison is
made using unit step responses shown in Fig. 10 to13.
It is clear from the frequency and step responses that,
especially at lower frequencies, there is little
agreement between the frequency characteristics of
the process and the model, which is a consequence of
the small excitation of the process at lower
frequencies. At the same time, it can be stated that
with the mentioned procedure, it was possible to
estimate all 16 parameters from the transition process
by means of one short experiment using decentralized
relay control.
Figure 6: Nyquist frequency responses of P
11
and M
11
.
Figure 7: Nyquist frequency responses of P
12
and M
12
.
Identification of TITO Systems Using Modified Decentralized Relay Feedback
627

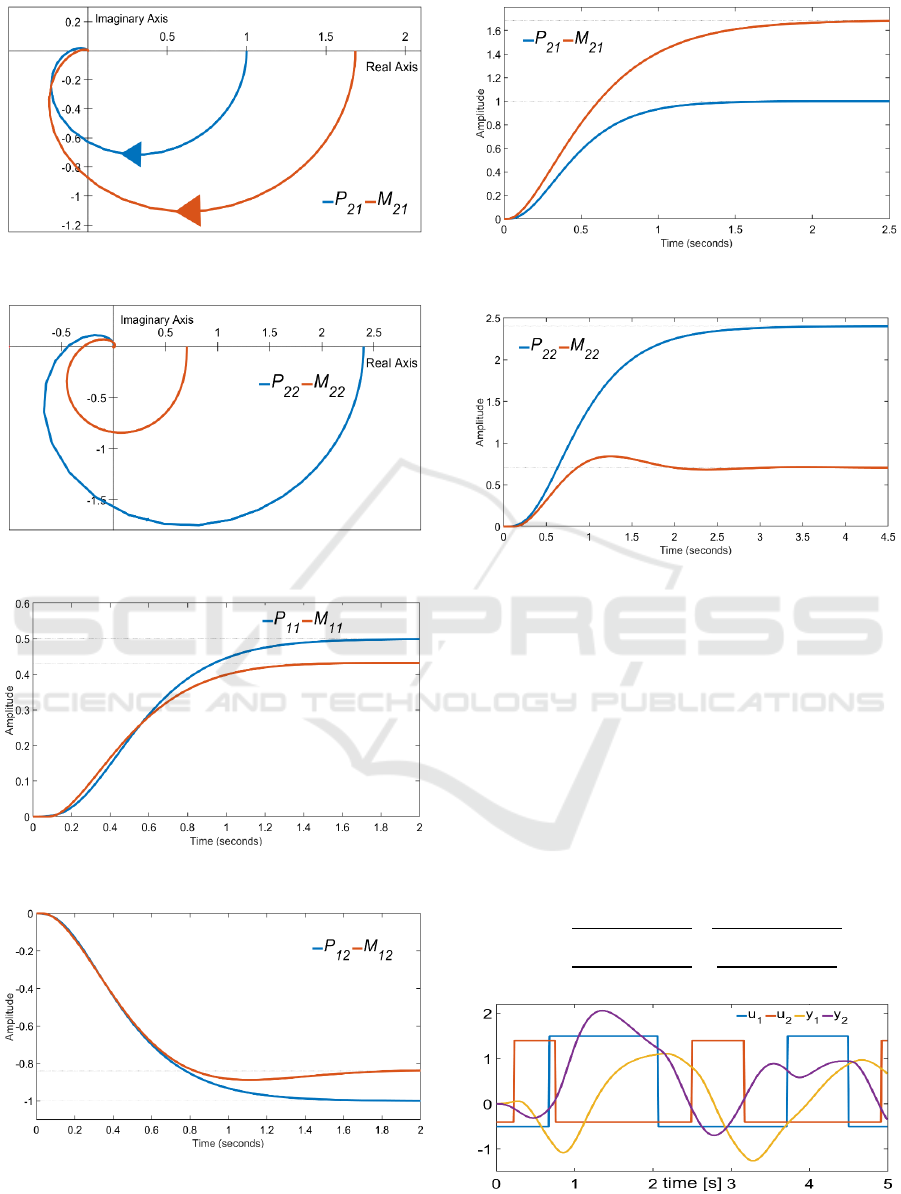
Figure 8: Nyquist frequency responses of P
21
and M
21
.
Figure 9: Nyquist frequency responses of P
22
and M
22
.
Figure 10: Unit step responses of P
11
and M
11
.
Figure 11. Unit step responses of P
12
and M
12
.
Figure 12. Unit step responses of P
21
and M
21
.
Figure 13: Unit step responses of P
22
and M
22
.
The estimation of the model parameters in the above
example can be improved by inserting an integration
term on one of the inputs (see Fig. 3) or on both
inputs. The relay outputs u
1
, u
2
and the process
outputs y
1
, y
2
obtained from the relay feedback test by
inserting an integration term into the input u
1
to
identify the TITO process are shown in Fig. 14. This
will cause a greater excitation of the process at lower
frequencies (see Fig. 15) and improve the estimation
of the model parameters. Model M of the TITO
process obtained using the modified decentralized
relay feedback is in the form
𝑴
(
𝑠
)
=
.⋅(.)


..
.⋅
(
.
)


..
.⋅
(
.
)


..
.⋅
(
.
)


..
 (10)
Figure 14: Input and output data used to estimate model
parameters.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
628

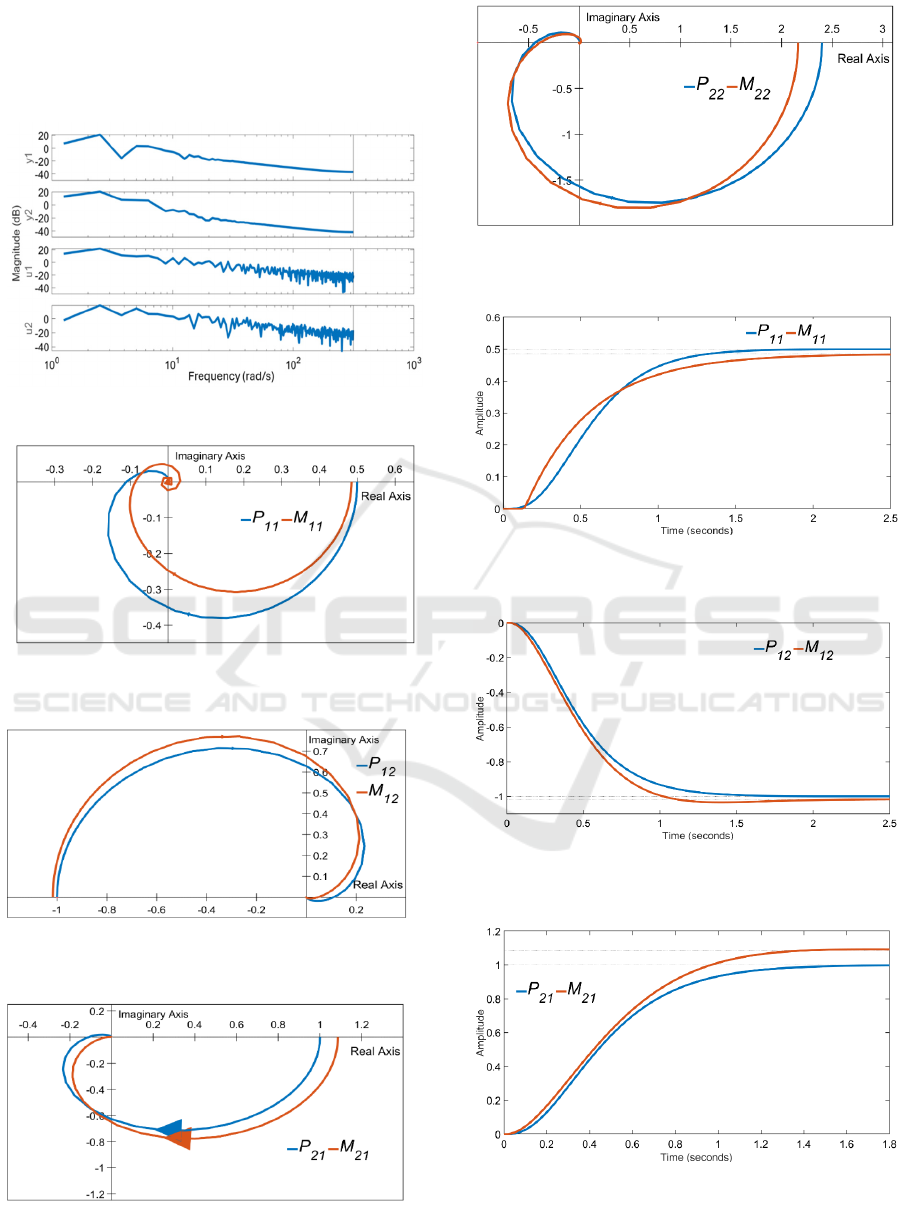
The Nyquist frequency responses of process P and
model M obtained by the modified relay feedback test
are depicted in Fig. 16 to 19. Unit step responses of
process P and model M obtained by the modified
relay feedback test are depicted in Fig. 20 to 23.
Figure 15: Magnitude spectrum of signals y
1
, y
2
, u
1
and u
2
.
Figure 16: Nyquist frequency responses of P
11
and M
11
obtained by the modified decentralized relay feedback.
Figure 17: Nyquist frequency responses of P
12
and M
12
obtained by the modified decentralized relay feedback.
Figure 18. Nyquist frequency responses of P
21
and M
21
obtained by the modified decentralized relay feedback.
Figure 19: Nyquist frequency responses of P
22
and M
22
obtained by the modified decentralized relay feedback.
Figure 20: Unit step responses of P
11
and model M
11
obtained by the modified relay feedback test.
Figure 21: Unit step responses of P
12
and model M
12
obtained by the modified relay feedback test.
Figure 22: Unit step responses of P
21
and model M
21
obtained by the modified relay feedback test.
Identification of TITO Systems Using Modified Decentralized Relay Feedback
629

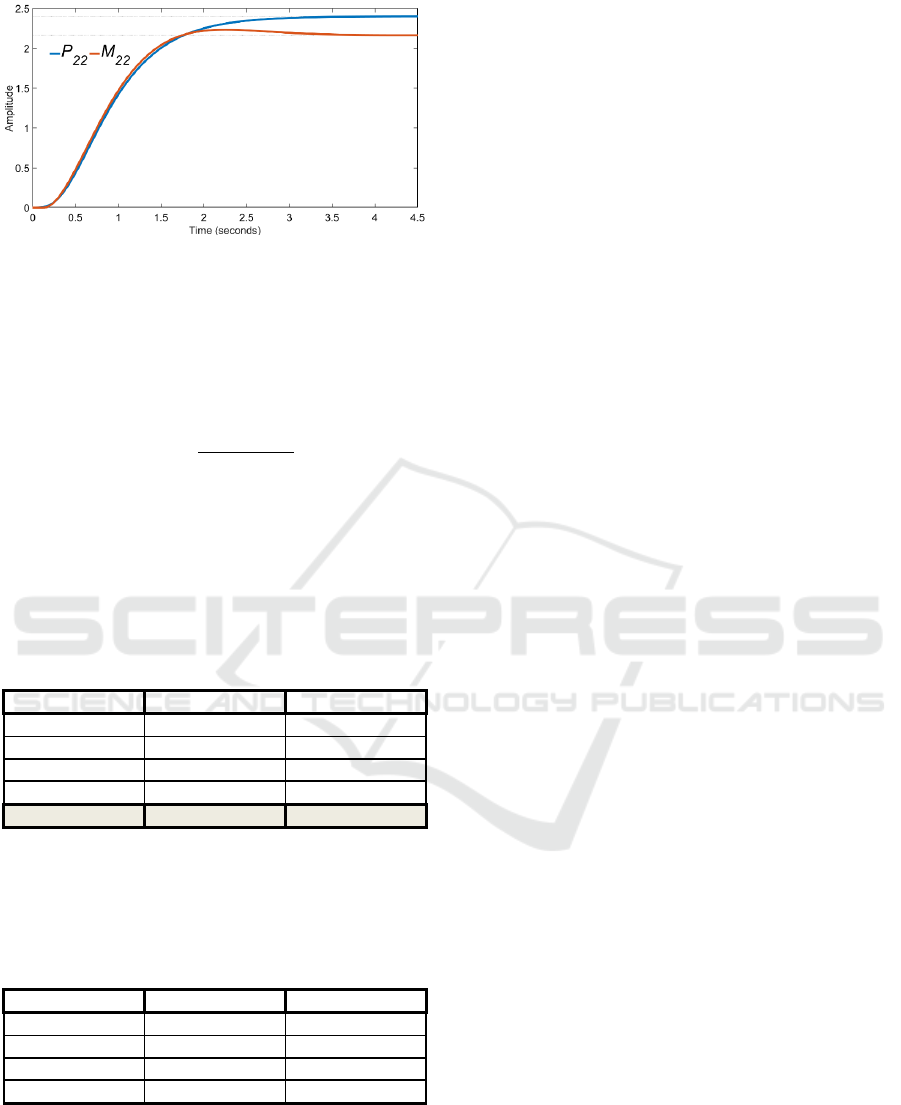
Figure 23: Unit step responses of P
22
and model M
22
obtained by the modified relay feedback test.
The percentage fit between the TITO process (5)
and the estimated TITO models (9) and (10) is shown
in Table 1. The fit between P
ij
and M
ij
is calculated
using the relationship
𝐹𝑖𝑡

=100∙1−
𝑃

−𝑀


𝑃

−𝑃



,𝑖,𝑗=1,2
where P
ij
and M
ij
are vectors where vector elements
are 128 linearly spaced frequency responses of
process P
ij
(jω) and M
ij
(jω) up to frequency 314 rad/s.
𝑃


denotes the mean value of elements of P
ij
, 𝜔∊
(
0,314
)
rad·s
-1
,
‖
𝑥
‖
is Euclidean norm of a vector x.
Table 1: The fit between the TITO process (5) and the
estimated TITO models (9) and (10).
Model
(
9
)
Model
(
10
)
Fit
11
81.67 % 77.00 %
Fit
12
82.24 % 93.13 %
Fit
21
19.06 % 89.04 %
Fit
22
14.20 % 86.76 %
mean 49.29 % 86.48 %
The steady-state gains of the TITO process (5) and
the estimated TITO models (9) and (10) are shown in
Table 2.
Table 2: The steady-state gains of the TITO process (5) and
the estimated TITO models (9) and (10).
Process
(
5
)
Model
(
9
)
Model
(
10
)
P
11
(0)=0.5
M
11
(0)=0.43
M
11
(0)=0.48
P
12
(0)=-1
M
12
(0)=-0.84
M
12
(0)=-1.02
P
21
(0)=1
M
21
(0)=1.68
M
21
(0)=1.08
P
22
(0)=2.4
M
22
(0)=0.71
M
22
(0)=2.17
4 CONCLUSIONS
Most methods using relay feedback identification for
estimating the model parameters of MIMO systems
rely on experimental determination of the steady-state
oscillation period. For cross-coupled MIMO systems,
these identification methods require the process to be
able to achieve steady-state oscillations under relay
control, which requires a significantly longer
experimental measurement period compared to relay
feedback identification of SISO systems. The
procedure presented in this paper reduces the
experimental measurement time compared to
commonly used relay identification methods because
it does not require achieving stable oscillations to
determine the fundamental period. The proposed
modification using the integration term and frequency
characteristics of the TITO system then allows better
estimation of the static gains of the individual transfer
functions. The procedure is demonstrated using the
TITO process and shows that TITO processes can be
identified from a non-stationary time course with one
decentralized relay test. Further research will be
devoted to the sensitivity of the relay feedback
method to disturbances, the identification of more
complex MIMO systems, and the control design of
real TITO systems using models obtained through the
decentralized relay test.
ACKNOWLEDGEMENTS
The presented work was supported by the
Institutional Resources of CTU in Prague for research
(RVO12000).
REFERENCES
Åström, K. J., & Hägglund, T. (1984). Automatic tuning of
simple regulators with specifications on phase and
amplitude margins. Automatica, 20(5), 645–651.
https://doi.org/10.1016/0005-1098(84)90014-1
Bajarangbali, & Majhi, S. (2012). TITO system
identification using relay with hysteresis. 2012 1st
International Conference on Power and Energy in
NERIST (ICPEN), 1–5. https://doi.org/10.1109/ICPEN.
2012.6492321
Berner, J., Soltesz, K., Astrom, K. J., & Hagglund, T.
(2017). Practical evaluation of a novel multivariable
relay autotuner with short and efficient excitation. 2017
IEEE Conference on Control Technology and
Applications (CCTA), 1505–1510. https://doi.org/10.11
09/CCTA.2017.8062671
Berner, J., Soltesz, K., Hägglund, T., & Åström, K. J.
(2017). Autotuner identification of TITO systems using
a single relay feedback experiment. IFAC-
PapersOnLine, 50(1), 5332–5337. https://doi.org/10.10
16/j.ifacol.2017.08.922
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
630

Bi, Q., Wang, Q.-G., & Hang, C.-C. (1997). Relay-based
estimation of multiple points on process frequency
response. Automatica, 33(9), 1753–1757.
https://doi.org/10.1016/S0005-1098(97)00090-3
Chidambaram, M., & Sathe, V. (2014). Relay Autotuning
for Identification and Control. Cambridge University
Press. https://doi.org/10.1017/CBO9781107415966
Dharmalingam, K., & Thangavelu, T. (2019). Parameter
estimation using relay feedback. Reviews in Chemical
Engineering, 35(4), 505–529. https://doi.org/10.1515/
revce-2017-0099
Hofreiter, M. (2022). Shifting Method for Identification of
TITO Systems using Decentralized Relay Feedback.
IFAC-PapersOnLine, 55(10), 2115–2120.
https://doi.org/10.1016/j.ifacol.2022.10.020
Liu, T.; Gao, F. (2011). Industrial process identification
and control Design: Step-test and relay-experiment-
based Methods. Springer-Verlag.
Liu, T., Wang, Q.-G., & Huang, H.-P. (2013). A tutorial
review on process identification from step or relay
feedback test. Journal of Process Control, 23(10),
1597–1623. https://doi.org/10.1016/j.jprocont.2013.08.
003
Luyben, W. L. (1987). Derivation of transfer functions for
highly nonlinear distillation columns. Industrial &
Engineering Chemistry Research, 26(12), 2490–2495.
https://doi.org/10.1021/ie00072a017
Ozdemir, A. A., & Gumussoy, S. (2017). Transfer Function
Estimation in System Identification Toolbox via Vector
Fitting. IFAC-PapersOnLine, 50 (1). 6232-6237.
https://doi.org/10.48550/ARXIV.2003.06289
Padhy, P. K., & Majhi, S. (2006). Identification of TITO
Processes. 2006 IEEE International Conference on
Industrial Technology, 664–669. https://doi.org/10.11
09/ICIT.2006.372248
Rotač, V. Ja., Arrieta,O., Vilanova, R. (n.d.). Rasčet
nastrojki promyšlenych sistem regulirovanija (Vol.
1961). Gosenergoizdat.
Ruderman, M. (2019). Relay Feedback Systems—
Established Approaches and New Perspectives for
Application. IEEJ Journal of Industry Applications,
8(2), 271–278. https://doi.org/10.1541/ieejjia.8.271
Shen, S.-H., & Yu, C.-C. (1994). Use of relay-feedback test
for automatic tuning of multivariable systems. AIChE
Journal, 40(4), 627–646. https://doi.org/10.1002/aic.69
0400408
Wang, Q.-G., Zou, B., Lee, T.-H., & Bi, Q. (1997). Auto-
tuning of multivariable PID controllers from
decentralized relay feedback. Automatica, 33(3), 319–
330. https://doi.org/10.1016/S0005-1098(96)00177-X
Yu, C.C. (2006). Autotuning of PID Controllers. Springer-
Verlag. https://doi.org/10.1007/b137042
Identification of TITO Systems Using Modified Decentralized Relay Feedback
631