
Approximated Fuzzy p-values by Bootstrapped Fuzzy Distributions and
Fuzzy Hypotheses Testing
Julien Rosset
a
and Laurent Donz
´
e
b
ASAM Group, University of Fribourg, Boulevard de P
´
erolles 90, 1700 Fribourg, Switzerland
{Julien.Rosset, Laurent.Donz
´
e}@unifr.ch
Keywords:
Fuzzy Confidence Interval, Fuzzy Hypothesis Testing Procedure, Fuzzy p-value, Fuzzy Logic, Fuzzy Methods
in Data Analysis.
Abstract:
Although we could dispute the use of p-values, it is a standard tool used by many to know if one has to reject
or not a null hypothesis. With the emergence of fuzzy data, fuzzy hypothesis testing procedures appeared.
Among these testing procedures, various methods to compute crisp or fuzzy p-values arising from fuzzy data
and hypotheses were investigated. However, we noticed that, despite calculating a fuzzy test statistic, none
of these approaches assume a fuzzy distribution. Thus, to remedy this, we tackle the problem of finding
fuzzy p-values in the context of both fuzzy data and hypotheses while considering the fuzzy distribution of
the test statistic. Finding fuzzy p-values alone is not helpful if one does not know how to use them to make a
decision. This is why we also provide a way to interpret fuzzy p-values and present a decision rule to reject
or not the fuzzy null hypothesis. Additionally, we aim to compare this decision rule to fuzzy statistical testing
procedures. We thus offer an empirical application that compares the decisions obtained from fuzzy p-values
to the results given by a fuzzy hypothesis testing procedure.
1 INTRODUCTION AND
NOTATION
It is debatable whether or not the concept of p-value
is a good tool for testing statistical hypotheses. But,
considering that it is widely used in practice, it is
not in vain to broaden this subject in the context of
fuzzy data and fuzzy hypotheses. In this regard, recall
that the classical statistics analysis can be widened by
(1) using fuzzy data, (2) using fuzzy hypotheses, and
(3) assuming a fuzzy distribution for the test statistic.
Several authors already extended the first two. To cite
a few, (Viertl, 2011) investigated the problem of find-
ing fuzzy p-values in the context of fuzzy hypothe-
ses and crisp data. (Parchami, 2020) and (Berkachy
and Donz
´
e, 2022) developed a method to find fuzzy
p-values with fuzzy data and hypotheses. Many meth-
ods to compute p-values and fuzzy p-values already
exist. Unfortunately, they are all based on the as-
sumption of a crisp and specific distribution of the test
statistic, principally for computation reasons. Thus,
to our knowledge, no one has contemplated this latter
point, for instance, using fuzzy distributions to com-
a
https://orcid.org/0000-0002-7883-1512
b
https://orcid.org/0000-0003-3522-4672
pute fuzzy p-values related to a statistical inference
case.
Consequently, in the case of fuzzy data and hy-
potheses, one major improvement is to consider the
implied fuzzy distribution of the test statistic to com-
pute fuzzy p-values. A reliable procedure should also
ensure that the obtained fuzzy p-values must be re-
duced to classical p-values when the data and hy-
potheses are crisp. At last, the p-values should be
interpretable, and thus, one needs a decision rule to
evaluate the fuzzy p-values
We recall in Section 2 the main recent develop-
ments on the subject of fuzzy inferences. Then, we
explain in Section 3 our method to compute p-values
and propose a decision rule to interpret them. On
other occasions (see e.g. (Rosset and Donz
´
e, 2024)),
we had the opportunity to present and develop fuzzy
test statistics. Thus, to compare the results of infer-
ences from fuzzy p-values and those from our fuzzy
test statistics, we will briefly recall these approaches
in Section 4. An empirical analysis is provided in Sec-
tion 5 where two case studies are given to compare the
results based on fuzzy p-values to those obtained via a
fuzzy hypothesis testing procedure and discuss them
thoroughly. Finally, we conclude in Section 6.
Rosset, J. and Donzé, L.
Approximated Fuzzy p-values by Bootstrapped Fuzzy Distributions and Fuzzy Hypotheses Testing.
DOI: 10.5220/0012888300003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 387-395
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
387

We will use the following notation and conven-
tions below. First, let us define by ˜x a fuzzy number
and by µ
˜x
(·) its membership function. We consider
also the α-cuts of ˜x denoted by ˜x
α
or by its equivalent
in interval form by (x
L,α
,x
R,α
). In practice, triangular
fuzzy numbers are often used. We denote them by a
triplet ˜x = (x
L
,x,x
R
) with x
L
≤ x ≤ x
R
∈ R.
2 LITERATURE REVIEW
p-values are standard elements of statistical infer-
ences. It is, therefore, natural to analyse the p-values
arising from fuzzy testing procedures. Many aspects
could be considered. Indeed, one could just use fuzzy
hypotheses with crisp data or crisp hypotheses with
fuzzy data or both, i.e. have fuzzy data and hy-
potheses. Traditionally, mimicking the classical case,
fuzzy p-values are computed under the assumption of
a given test statistic distribution. Researchers have
thoroughly studied this. But, in the presence of fuzzy
data and, perhaps, fuzzy hypotheses, a fuzzy distribu-
tion of the test statistic should be considered. To our
knowledge, this latter case has not yet been carefully
considered.
Regarding the traditional approach, (Viertl, 2011)
investigated fuzzy p-values from fuzzy data with crisp
hypotheses. To do so, he used a fuzzy test statis-
tic and assumed a crisp distribution for the sample.
This setting allows him to compute a p-value corre-
sponding to each of the left and right alpha-cuts of
the test statistic. This collection of p-values then cor-
responds to the alpha-cuts of a fuzzy p-value. Un-
like Viertl, (Parchami et al., 2010) analysed the case
where hypotheses are fuzzy and data are crisp. They
introduced the notion of fuzzy p-value by apply-
ing Zadeh’s extension principle. Later, (Parchami,
2020) investigated the case where both hypotheses
and data are fuzzy and studied the fuzzy p-values aris-
ing from Zadeh’s extension principle under the as-
sumption that the test statistic has a crisp distribution
despite the fuzziness of the data. Similarly, (Berkachy
and Donz
´
e, 2017) found fuzzy p-values in the case
of fuzzy data and hypotheses assuming a crisp dis-
tribution of the test statistic. We can also mention
(Hryniewicz, 2018), who developed a procedure to
find fuzzy p-values using fuzzy confidence intervals
in the sense of (Kruse and Meyer, 1987). His method
is based on finding intersection points between the
fuzzy null hypothesis and the fuzzy confidence inter-
vals of the test statistic. Despite being a very interest-
ing method, the procedure has two problems. First,
it doesn’t deal with a fuzzy distribution of the test
statistic. Secondly, when the fuzzy confidence inter-
val becomes crisp, the intersection points (p-values)
take the value 0 or 1, thus not generalising the classi-
cal approach to find p-values.
As mentioned above, the study of fuzzy p-values
involves fuzzy hypothesis testing procedures, which
are connected to the notion of fuzzy confidence in-
tervals. Hence, let us briefly review some results in
this context. (Kruse and Meyer, 1987) gave a theoret-
ical definition of a fuzzy confidence interval. Many
researchers have utilised and refined their definition
since its introduction in 1987. Indeed, (Viertl and
Yeganeh, 2016) introduced the notion of fuzzy con-
fidence regions. (Kahraman et al., 2016) and (Kahra-
man et al., 2019) studied interval-valued intuitionistic
fuzzy sets (IVIFSs) and hesitant fuzzy sets (HFS) and,
based on them, developed two methods to construct
fuzzy confidence intervals. (Wu, 2009) solved optimi-
sation problems involving a fuzzy Gaussian distribu-
tion to build fuzzy confidence intervals. (Chachi and
Taheri, 2011) proposed fuzzy confidence intervals for
the mean of a fuzzy normal distribution. These ap-
proaches involve a predefined distribution of the test
statistic, which, in practical cases, is not always possi-
ble to know. To bypass this difficulty, (Berkachy and
Donz
´
e, 2022) developed a general procedure to con-
struct fuzzy confidence intervals using the likelihood
ratio method and a bootstrap procedure extended to
the fuzzy environment to estimate the distribution of
this likelihood ratio.
Due to the seminal works of Bradley Efron, boot-
strap techniques are widely known among statisti-
cians. Then, many fuzzy bootstrap approaches were
introduced and used. Among the recent works, we
can point out (Berkachy and Donz
´
e, 2020), who gave
two algorithms to generate fuzzy bootstrapped sam-
ples with the notions of location and dispersion and
(Grzegorzewski and Romaniuk, 2021), who provided
an epistemic approach to fuzzy bootstrap techniques
for fuzzy data.
Finally, let us mention two concepts that come in
handy in constructing fuzzy confidence intervals. The
first one is the fuzzy quantile function proposed by
(Shvedov, 2016), a fuzzy extension of the classical
quantile function. The second one is the construction
of fuzzy distributions where (Arefi et al., 2012) de-
scribe how to find empirical fuzzy distributions.
3 FUZZY P-VALUES AND
INFERENCES
Statistical inferences are based on samples. Let us de-
note by X
1
,...,X
n
a random sample drawn from the
distribution of interest. Assuming the data are fuzzy,
FCTA 2024 - 16th International Conference on Fuzzy Computation Theory and Applications
388

we write as
˜
X
1
,...,
˜
X
n
, the fuzzy equivalent of the ran-
dom sample. The fuzzy realisations of the fuzzy ran-
dom sample are given by ˜x
1
,..., ˜x
n
and their α-cuts
by ˜x
α
i
, i = 1,...,n.
The fuzzy random mean is readily computable
as
˜
¯
X =
1
n
∑
n
i=1
˜
X
i
and its realisation is given by
˜
¯x =
1
n
∑
n
i=1
˜x
i
.
It’s common practice to express a fuzzy hypothe-
sis using linguistic terms. For example, we could say,
”The value of the parameter θ is more or less equal to
θ
0
”, or rewritten in terms of differences, i.e. ”The dif-
ference between the value of the parameter θ and θ
0
is more or less equal to 0”. Thus, we could write, for
instance, the following two-sided fuzzy hypotheses:
˜
H
0
: θ =
˜
0 against
˜
H
1
: θ ̸=
˜
0. (1)
Of course, in the same way, one-sided fuzzy hypothe-
ses could be written as:
˜
H
0
: θ ≤
˜
0 against
˜
H
1
: θ >
˜
0, (2)
or
˜
H
0
: θ ≥
˜
0 against
˜
H
1
: θ <
˜
0. (3)
Remark that the null fuzzy hypothesis
˜
H
0
or the al-
ternative one
˜
H
1
can be modelled by triangular num-
bers, i.e. (H
L
0
,H
0
,H
R
0
) or (H
L
1
,H
1
,H
R
1
). On the other
hand, it is common practice to implement the in-
ference process through a proper test statistic. Let
˜
T = (T
L
,T,T
R
) be a fuzzy statistic to test
˜
H
0
. For
example, if we want to test the mean of the distribu-
tion, we could use:
˜
T := (
˜
¯
X −θ
0
) ⊘
˜
σ
˜
¯x
, (4)
where ⊘ is the fuzzy division operator and
˜
σ
˜
¯x
is the
standard-error of
˜
¯
X. We note by
˜
t = (t
L
,t,t
R
) the
fuzzy realisation of
˜
T .
In a fuzzy approach, the distribution of the statistic
is difficult to know, even more so if one doesn’t want
to assume strong conditions about the form of the dis-
tribution. As we need this distribution, we propose
using a bootstrapped one instead. One of the many ad-
vantages of using this approach is that it is relatively
easy to generate a fuzzy bootstrapped distribution for
˜
T . Let B be the number of bootstrapped samples and
denote by
˜
t
⋆
1
,...,
˜
t
⋆
b
,...
˜
t
⋆
B
the bootstrapped distribution
of the test statistic. The fuzzy empirical mean is given
by
¯
˜
t
∗
= (
∑
B
1
˜
t
⋆
b
)/B = (
¯
t
∗L
,
¯
t
∗
,
¯
t
∗R
).
We consider, on one hand, the fuzzy observed
statistic
˜
t = (t
L
,t,t
R
) and its absolute value:
|
˜
t| =(t
L
abs
,t
abs
,t
R
abs
)
=
min(|t
L
|,|t|, |t
R
|),
|t|,
max(|t
L
|,|t|, |t
R
|)
,
and, on the other hand, the centred bootstrapped dis-
tribution given by
˜
t
⋆
1
−
¯
t
∗
,...,
˜
t
⋆
b
−
¯
t
∗
,...
˜
t
⋆
B
−
¯
t
∗
. We
note this distribution by
˜
F
∗
= (F
∗,L
,F
∗
,F
∗,R
). Then,
we can compute the following empirical approxima-
tion for the fuzzy p-value ˜p = (p
L
, p, p
R
) of the two-
sided hypotheses test (1):
p
L
= 2 ·
#(F
⋆,L
> t
R
abs
) + 1
B + 1
,
p = 2 ·
#(F
⋆
> t
abs
) + 1
B + 1
,
p
R
= min(2 ·
#(F
⋆,R
> t
L
abs
) + 1
B + 1
,1),
where # gives the number of cases for which the con-
dition in parentheses is true. For the one-sided hy-
potheses test (2), the fuzzy p-value ˜p = (p
L
, p, p
R
) is
calculated as:
p
L
=
#(F
⋆,L
> t
R
) + 1
B + 1
,
p =
#(F
⋆
> t) + 1
B + 1
,
p
R
= min(
#(F
⋆,R
> t
L
) + 1
B + 1
,1),
and for the second one-sided hypotheses test (3), we
have:
p
L
=
#(F
⋆,R
< t
L
) + 1
B + 1
,
p =
#(F
⋆
< t) + 1
B + 1
,
p
R
= min(
#(F
⋆,L
< t
R
) + 1
B + 1
,1).
We must underline that we centred the fuzzy
bootstrapped distribution (left, centre and right parts)
around
¯
t
∗
. Another possibility would’ve been to
centre it around
¯
˜
t
∗
by writing it as
˜
t
⋆
1
⊖
¯
˜
t
∗
,...,
˜
t
⋆
b
⊖
¯
˜
t
∗
,...
˜
t
⋆
B
⊖
¯
˜
t
∗
where ⊖ is the fuzzy substraction opera-
tor. Nevertheless, we did not choose it for empirical
reasons. The algorithm 1 summarises the computa-
tion steps to find the bootstrapped fuzzy p-values.
Fuzzy p-values ˜p = (p
L
, p, p
R
) are not always easy
to interpret, unlike their crisp counterparts. Though
a proper defuzzification method can help the inter-
pretation, we propose constructing a specific measure
whose meaning is straightforward. Let δ ∈ (0, 1) be
a chosen significance level. We expect δ ∈ [p
L
, p
R
],
but this could not be true. Let us suppose that this
is the case. Furthermore, we assume first that δ ≤ p.
In the space [0, 1]
2
, consider the point (δ, y
0
) given
by the intersection between the line x = δ and the
triangular fuzzy number (p
L
, p, p
R
) and compute the
area A of the new resulting triangle given by the
Approximated Fuzzy p-values by Bootstrapped Fuzzy Distributions and Fuzzy Hypotheses Testing
389
Algorithm 1: Fuzzy p-values by a Bootstrapped Fuzzy Dis-
tribution.
Data: ˜x
1
,..., ˜x
n
a fuzzy realisation of the
random sample.
Result: Fuzzy p-values.
begin
Compute: (
˜
t, |
˜
t |) ;
for b = 1 to B do
Draw sample ˜s
b
= { ˜x
∗
1
,..., ˜x
∗
n
} ;
Compute: (
˜
t
∗
b
) ;
end
Compute: (
¯
˜
t
∗
,
˜
F
∗
, ˜p) ;
return ˜p ;
end
three points ((p
L
,0),(δ,y
0
),(δ,0)). If δ > p, then A
is the area of the polygon given by the four points
((p
L
,0),(p, 1), (δ, y
0
),(δ,0)). On the other hand, let
P be the area of the fuzzy p-value. Then, we can pro-
pose the following crisp measure of the p-value:
r
re j
= A/P. (5)
We set r
re j
= 0 if δ < p
L
and r
re j
= 1 if δ > p
R
. The
real number r
re j
is between 0 and 1 and tells us how
much the fuzzy p-value tends to reject the null hy-
pothesis. On the opposite, r
acc
= 1−r
re j
∈ [0,1] gives
us the tendency of not rejecting the null hypothesis.
If r
re j
> 0.5, we will tend to reject the null hypothe-
sis, while if r
re j
< 0.5, we will tend not to reject it.
No decision can be taken for r
re j
= 0.5. r
re j
and r
acc
can be seen as weights to respectively reject or not to
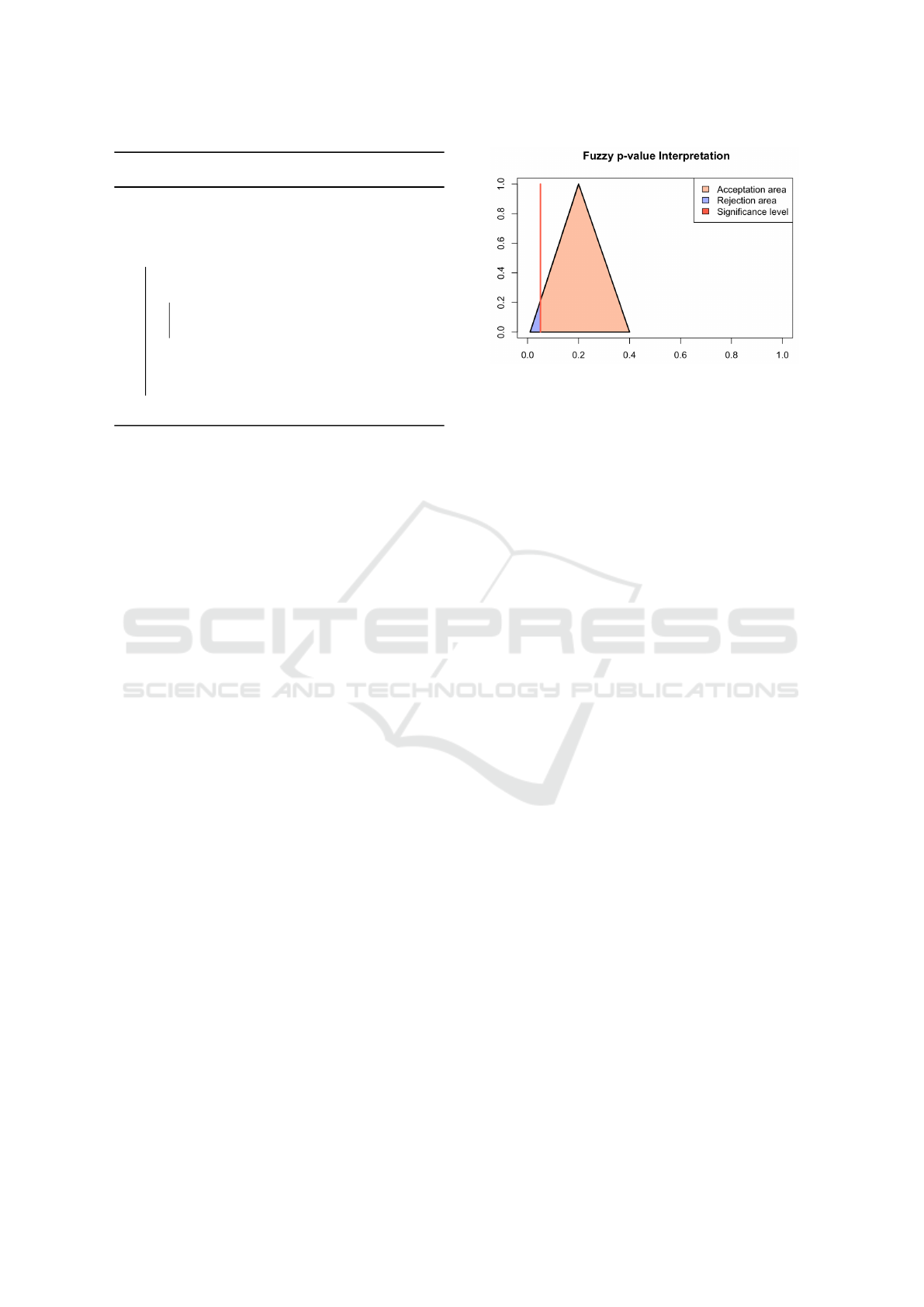
reject the null hypothesis. Figure 1 depicts the ten-
dency to reject the null hypothesis in blue. This area
equals to r
re j
= 0.22. The orange region has an area
of r
acc
= 1 − r
re j
= 0.78 and gives the tendency not to
reject the null hypothesis.
4 FUZZY TESTS AND
CONFIDENCE INTERVALS
(Rosset and Donz
´
e, 2024) proposed the following in-
ference procedure. They built two real-valued func-
tions of the fuzzy random sample
˜
X
1
,...,
˜
X
n
defined
as
˜
φ
rej
: (F
∗
c
(R))
n
→ [0,1],
˜
φ
acc
: (F
∗
c
(R))
n
→ [0,1].
It can be proven that
˜
φ
rej
and
˜
φ
acc
are two fuzzy
statistical tests on F
∗
c
(R), the class of the non-empty
compact, convex and normal fuzzy sets on R. Func-
tions of the random sample, their values are given by
the intersection of the fuzzy null hypothesis
˜
H
0
and
Figure 1: Example of a fuzzy p-value. Here ˜p =
(p
L
, p, p
R
) = (0.01,0.2, 0.4). The tendency to reject the null
hypothesis (in blue) is r = 0.22, and the tendency to not re-
ject the null hypothesis (in orange) is 1 − r = 0.78
a fuzzy confidence interval
˜
⊓ for the parameter to be
tested θ. For technical details, the reader may consult
(Rosset and Donz
´
e, 2024). The interpretation of these
statistical tests is given in the following definition:
Definition 1 (Decision rules).
Let be
L
rej
=
R
[0,1]
˜
φ
rej,α
dα and L
acc
=
R
[0,1]
˜
φ
acc,α
dα.
(6)
L
rej
and L
acc
are called, respectively, the levels of
rejection and acceptance (not rejection) of the (fuzzy)
null hypothesis
˜
H
0
.
1. If L
rej
= 1,
˜
H
0
is rejected. In this case L
acc
= 0;
2. If L
rej
= 0,
˜
H
0
is not rejected. In this case L
acc
= 1;
3. If 0 < L
rej
< 1, the test shows how strong
˜
H
0
is
rejected. The higher L
rej
is, the stronger the test
rejects
˜
H
0
;
4. If 0 < L
acc
< 1, the test shows how strong
˜
H
0
is
not rejected. The higher L
acc
is, the stronger the
test doesn’t reject
˜
H
0
;
5. If L
rej
> L
acc
,
˜
H
0
tends to be rejected;
6. If L
rej
< L
acc
,
˜
H
0
tends to be not rejected;
7. If L
rej
= L
acc
, no decision can be taken.
The fuzzy confidence interval
˜
⊓ for the parame-
ter θ of the distribution, defined at a given confidence
level 1 − δ, plays a crucial role in the construction of
the two fuzzy tests
˜
φ
re j
and
˜
φ
acc
. Hence, its construc-
tion is a key point of the inference procedure. Several
methods can be used to build such fuzzy confidence
intervals. We will use the one proposed in (Rosset
and Donz
´
e, 2024), where we introduced a method
based on bootstrap techniques. This method is attrac-
tive because no specific (fuzzy) distribution should be
assumed.
FCTA 2024 - 16th International Conference on Fuzzy Computation Theory and Applications
390
5 APPLICATIONS
5.1 Case 1
Let us test the fuzzy mean of a fuzzy distribution at
a significance level of 5%. Table 1 depicts the fuzzy
observations taken from (Berkachy and Donz
´
e, 2020)
that will be used to compute the fuzzy p-values as-
sociated with different fuzzy null hypotheses as illus-
trated in Table 2. The fuzzy mean estimation is the tri-
angular fuzzy number
¯
˜x = (1.8,2.8,3.8) and a fuzzy
confidence interval at a confidence level of 95% is
the fuzzy trapezoidal number (0.933,1.933, 3.6, 4.6).
This fuzzy confidence interval will allow us to test the
null hypotheses and compute their associated levels of
acceptance and rejection as shown in Table 2. Lastly,
we will compare the obtained fuzzy p-values to the re-
sults given by the fuzzy hypothesis testing procedure.
Let us first talk about the results given by the fuzzy
hypothesis testing procedure at a 5% significant level
in Table 2. One can easily see that in the extreme
cases (tests 1, 2, 3, 13) when the fuzzy null hypoth-
esis is outside the fuzzy confidence interval at 95%
(0.93,1.93,3.6,4.6), the levels of acceptance and re-
jection are respectively 0 and 1. Moreover, when
the fuzzy null hypothesis is entirely contained in the
fuzzy confidence interval’s core (1.93,3.6), e.g. tests
8, 9, 10, the levels of acceptance and rejection are
respectively 1 and 0. These two extreme situations
give the expected binary results one would have found
using a crisp testing procedure. Let us now anal-
yse the cases when the fuzzy null hypothesis overlaps
with the fuzzy confidence interval’s fuzzy regions, i.e.
(0.93,1.93) and (3.6,4.6). With tests 4, 5, 6 and 7 of
Table 2, when the null hypothesis overlaps the inter-
val (0.93, 1.93), we observe that the values of L
acc
and L
re j
change depending on the shape of H
0
. As
opposed to the crisp case, we see that the values L
acc
and L
re j
are between 0 and 1 and will tend to reject
or not the null hypothesis. Tests 5 and 7 depicted on
Figures 3 and 4 show how the shape of a crispier null
hypothesis (Figure 4) or fuzzier null hypothesis (Fig-
ure 3) affects the values of L
acc
and L
re j
. Lastly, when
the fuzzy confidence interval is fully overlapped (tests
11 and 12), the amount of area outside the fuzzy con-
fidence interval will dictate the value of the rejection
level. Conversely, the amount of area inside the fuzzy
confidence interval will dictate the value of the ac-
ceptance level. This situation is illustrated in Figures
2 and 5.
Let us now discuss the fuzzy p-values obtained by
the method displayed in Section 3. In extreme cases,
as in test 1 and 13, we find binary values. For test
1, we find the values, r
re j
= 0, r
acc
= 1 and for test
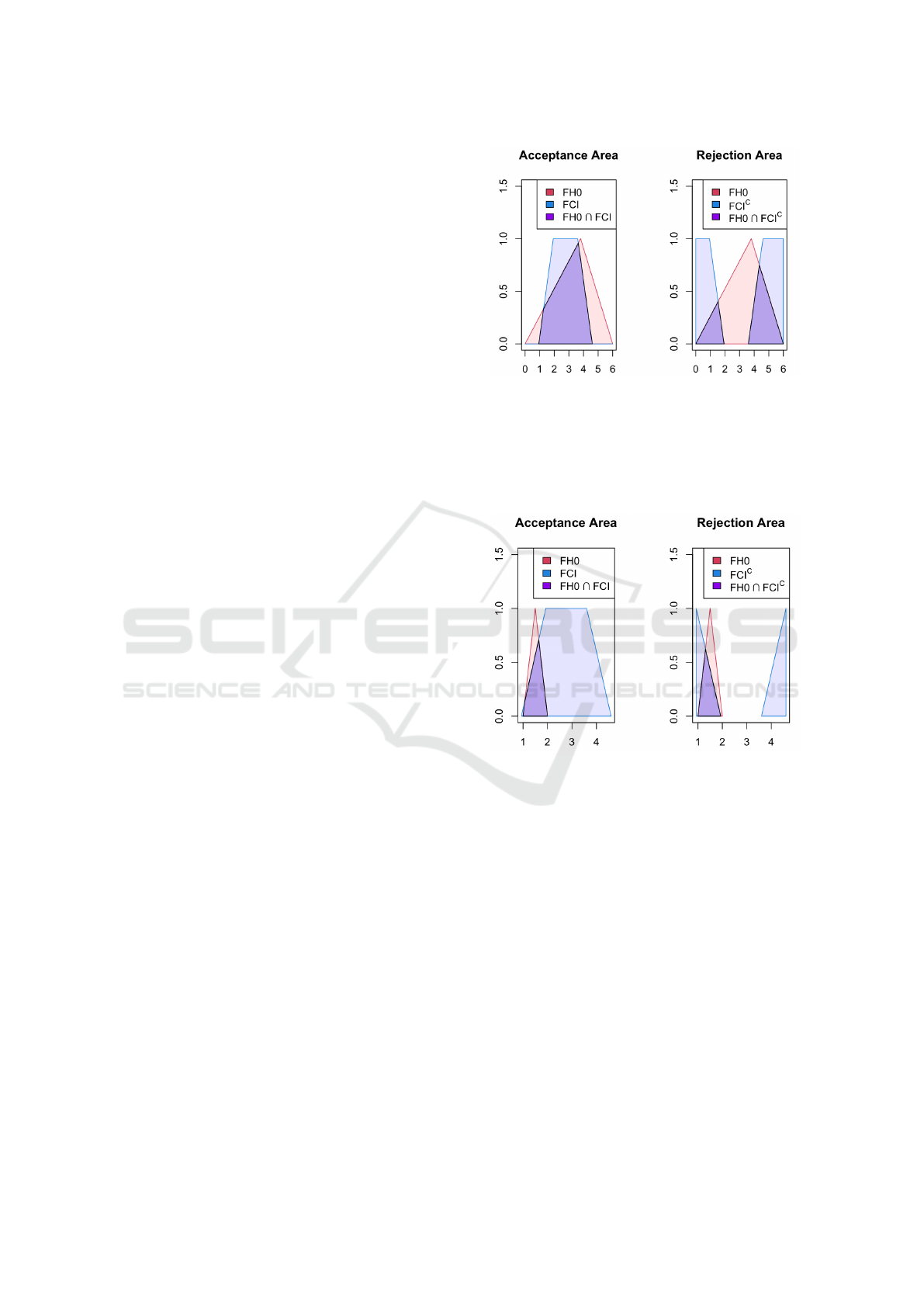
Figure 2: Fuzzy test of the mean θ,
˜
H
0
: θ = (0,3.8, 6)
against
˜
H
1
: θ ̸= (0,3.8,6). FH0 stands for ”Fuzzy Null Hy-
pothesis”, and FCI stands for ”Fuzzy Confidence Interval”.
The tendency to not reject the null hypothesis (acceptance
area in purple on the left graph) is L
acc
= 0.68. The ten-
dency to reject the null hypothesis (rejection area in purple
on the right graph) is L
re j
= 0.43.
Figure 3: Fuzzy test of the mean θ,
˜
H
0
: θ = (1,1.5, 2)
against
˜
H
1
: θ ̸= (1,1.5,2). FH0 stands for ”Fuzzy Null Hy-
pothesis”, and FCI stands for ”Fuzzy Confidence Interval”.
The tendency to not reject the null hypothesis (acceptance
area in purple on the left graph) is L
acc
= 0.75. The ten-
dency to reject the null hypothesis (rejection area in purple
on the right graph) is L
re j
= 0.58.
13, the values r
re j
= 1, r
acc
= 0. This shows that
we tend to strongly reject (respectively not reject) the
null hypothesis, which confirms the decisions taken
with L
re j
and L
acc
. However, one quickly notices that
the fuzzy p-values tends to take extreme values for
the left and right parts. Excepted tests 1, 12 and 13,
the left and right parts of every fuzzy p-value are 0
and 1. This makes the interpretation of these fuzzy
p-values quite hard. One can, however, observe that
when the null hypothesis is fully contained in the re-
gion delimited by (1.93,3.6), r
re j
is very low, and r
acc
is almost 1, which is in accordance with the results of
the fuzzy testing procedure. However, in tests 2, 3
Approximated Fuzzy p-values by Bootstrapped Fuzzy Distributions and Fuzzy Hypotheses Testing
391
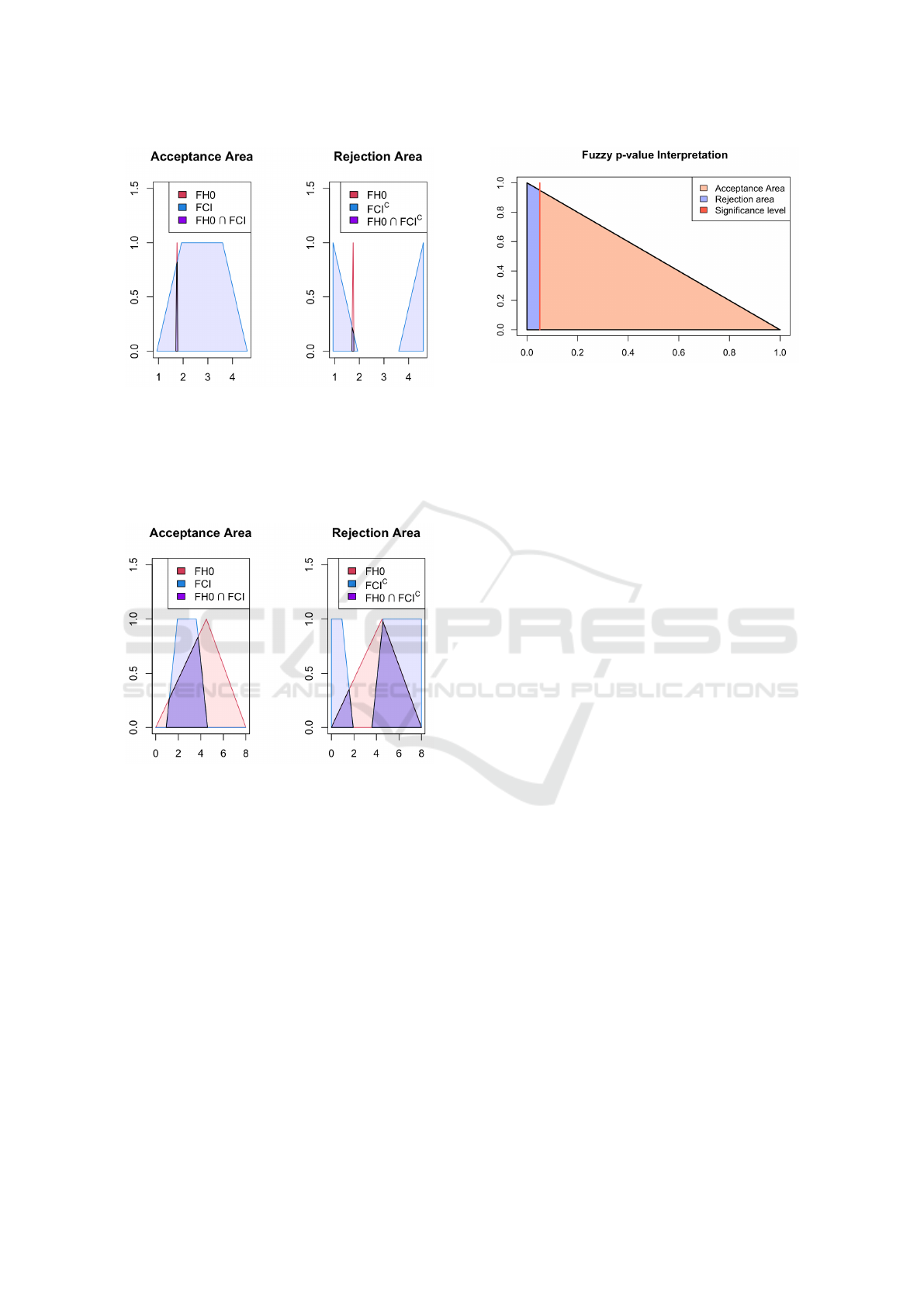
Figure 4: Fuzzy test of the mean θ,
˜
H
0
: θ = (1.7, 1.75,1.78)
against
˜
H
1
: θ ̸= (1.7,1.75,1.78). FH0 stands for ”Fuzzy
Null Hypothesis” and FCI stands for ”Fuzzy Confidence
Interval”. The tendency to not reject the null hypothesis
(acceptance area in purple on the left graph) is L
acc
= 0.96.
The tendency to reject the null hypothesis (rejection area in
purple on the right graph) is L
re j
= 0.34.
Figure 5: Fuzzy test of the mean θ,
˜
H
0
: θ = (0,4.5, 8)
against
˜
H
1
: θ ̸= (0,4.5, 8). The tendency to not reject the
null hypothesis (acceptance area in purple on the left graph)
is L
acc
= 0.44. The tendency to reject the null hypothesis
(rejection area in purple on the right graph) is L
re j
= 0.63.
and 4, when the null hypothesis should be rejected,
the fuzzy p-values give a r
acc
of 0.9025 and a r
re j
of
0.0975. While it seems surprising, it can be explained
by looking at the meaning behind these two quanti-
ties. On Figure 6,
One can see that although the left and centre parts
of the fuzzy p-value favour rejecting the null hypoth-
esis (both have a value of 0), r
acc
(orange area) is very
large because the right part of the fuzzy p-value is
1. This causes the fuzzy p-value to have a great r
acc
and low r
re j
. This result shows the limits of the use
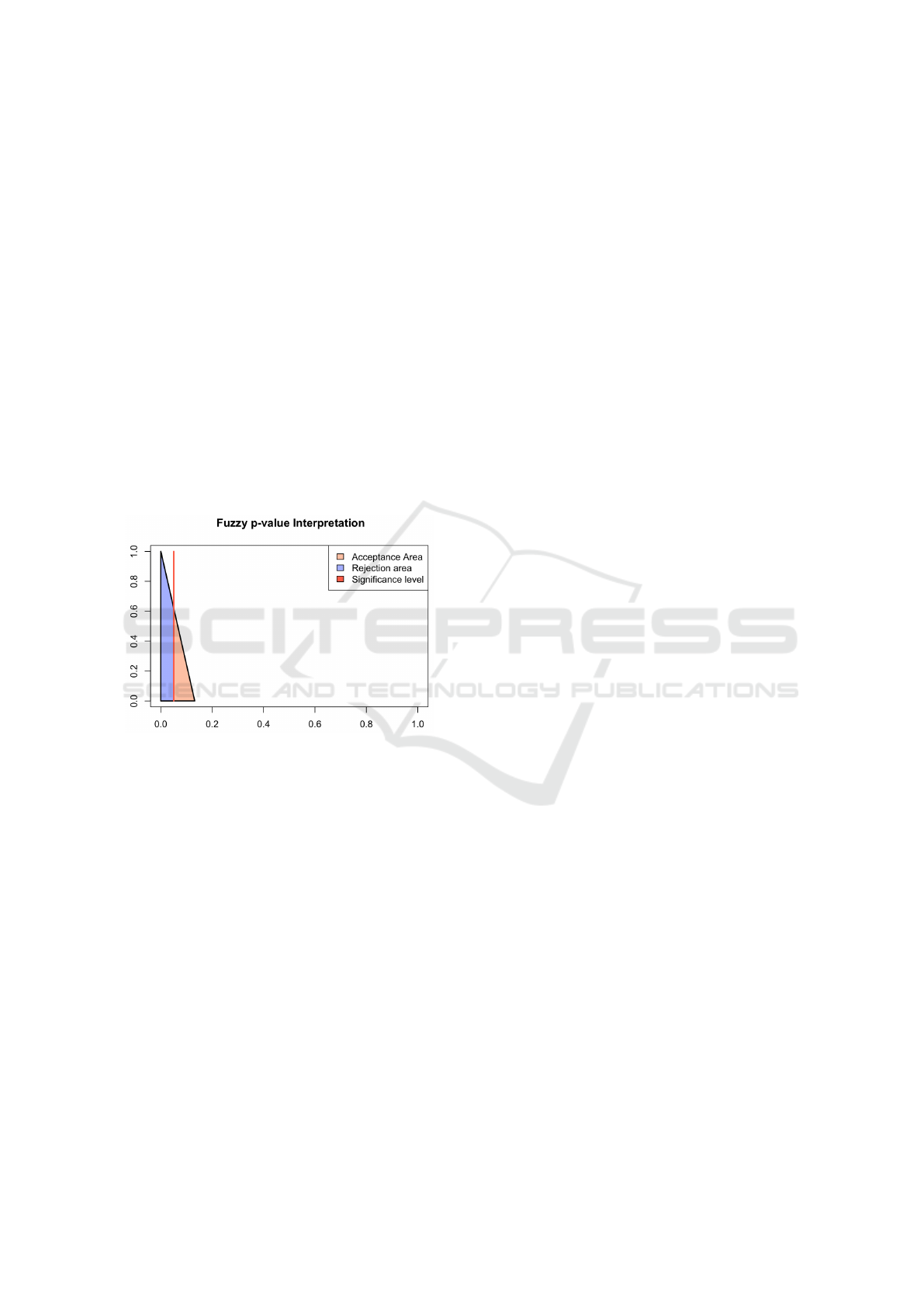
of fuzzy p-values. However, let us point out the re-
sults for test 12 depicted in Figure 7. Observe that
they are in accordance with the results found with the
Figure 6: Extreme fuzzy p-value ˜p = (0, 0,1). r
acc
=
0.9025 and r
re j
= 0.0975.
testing procedure. L
acc
is 0.44 and r
acc
is 0.39 which
tends to reject the null hypothesis. This is confirmed
by L
re j
= 0.63 and r
re j
= 0.61. This good result is
a byproduct of having a fuzzy p-value with a small
right part, which can be easily interpreted. Test 12
shows that when the fuzzy p-value is not too extreme,
i.e. does not have a right part close to 1, it holds in-
formation about whether or not to reject the null hy-
pothesis. To confirm this assumption, let us consider
another set of crispier observations that will give us
crispier p-values.
5.2 Case 2
Let X ∼ N(2.8,3), U
1
∼ Unif(0.001,0.006), U
2
∼
Unif(0.004,0.009). Let x
i
, u
1,i
, u
2,i
be realisations of
the random variables X, U
1
and U
2
respectively. We
can form fuzzy observations in the following way. Let
x
L
i
= x
i
− u
1,i
and x
R
i
= x
i
+ u
2,i
. We generate N fuzzy
triangular observations ˜x
i
= (x
L
i
,x
i
,x
R
i
), i = 1,...,N.
By generating N = 500 observations via the above
procedure, we find an estimation for the fuzzy mean
˜
¯x = (2.693,2.697, 2.704) and a fuzzy confidence in-
terval at 95% confidence level (2.44,2.45,2.94,2.95).
Table 5 displays fuzzy p-values obtained by a two-
sided test for different null hypotheses for these 500
observations. Table 3 displays fuzzy p-values ob-
tained by a one-sided test for the mean θ,
˜
H
0
: θ <
˜
θ
0
against
˜
H
1
: θ ≥
˜
θ
0
, where
˜
θ
0
is the conjectured fuzzy
triangular number used to characterise the null hy-
pothesis
˜
H
0
. Table 4 shows fuzzy p-values obtained
by a one-sided test for the mean θ,
˜
H
0
: θ >
˜
θ
0
against
˜
H
1
: θ ≤
˜
θ
0
. Now that our fuzzy observations are
crispier, the obtained fuzzy p-values are also crispier.
This allows us to compute r
acc
and r
re j
that hold in-
formation. Indeed, on Table 3, which is about the
one-sided test
˜
H
0
: θ <
˜
θ
0
against
˜
H
1
: θ ≥
˜
θ
0
, we can
see with tests 1 and 2 that the fuzzy p-value strongly
rejects the null hypothesis with a r
re j
of 1. Tests 3,
FCTA 2024 - 16th International Conference on Fuzzy Computation Theory and Applications
392
4, 5 show us how different shapes for the null hy-
pothesis yield to different non binary values r
re j
and
r
acc
. At last, Table 3 also depicts how shifting null
hypotheses from (2.25, 2.35, 2.40) to (2.5, 2.55, 2.6)
gives values r
acc
gradually going from 0 to 1 and val-
ues r
re j
gradually going from 1 to 0. Table 4 illus-
trates the same results, but this time for the opposite
side,
˜
H
0
: θ >
˜
θ
0
against
˜
H
1
: θ ≤
˜
θ
0
. Finally, for the
two-sided test illustrated by Table 5, we again observe
the same behaviour. Test 6 yields values r
acc
= 0 and
r
re j
= 1. As opposed to it, test 1 gives values r
acc
= 1
and r
re j
= 0. Tests 2, 3, 4, 5 yield non binary values
for r
acc
and r
re j
. As a whole, we observe that r
acc
gradually goes from 1 to 0 while r
re j
gradually goes
from 0 to 1 when considering the tests 1, 2, 3, 4, 5,
6. This allows us to empirically discover the fuzzy re-
gion in between (2.35,2.4,2.45) and (2.45,2.5,2.5)
where the null hypothesis is starting to be more and
more rejected, respectively less and less rejected de-
pending on the null hypothesis shape.
Figure 7: Crispier fuzzy p-value ˜p = (0, 0,0.132). r
acc
=
0.39 and r
re j
= 0.61.
6 CONCLUSION
In this paper, we introduced a new procedure to
find fuzzy p-values based on precedent works, which
generalises the computation of crisp p-values. Our
method revolves around generating a centred fuzzy
bootstrapped statistic distribution to test and count
how many of these bootstrapped observations are
greater than an observed statistic. Then, we explained
how the obtained fuzzy p-values could be interpreted
as a ratio of a rejection or acceptance area over the to-
tal area formed by the fuzzy p-value. We then enun-
ciated a fuzzy hypothesis testing procedure to be able
to compare fuzzy p-values to results obtained via this
testing procedure. The main takeaway from this com-
parison is that fuzzy p-values tend to be very impre-
cise, with the observations getting fuzzier. However,
it is still a helpful tool when the observations become
crisper. Indeed, in the latter scenario, fuzzy p-values
give us an idea of how much we’re inside the fuzzy
confidence interval or how much we’re outside of it.
In extreme cases, fuzzy p-values give the same binary
results coming from crisp p-values.
REFERENCES
Arefi, M., Viertl, R., and Taheri, S. M. (2012). Fuzzy den-
sity estimation. Metrika, 75(1):5–22.
Berkachy, R. and Donz
´
e, L. (2017). Testing Fuzzy Hy-
potheses with Fuzzy Data and Defuzzification of the
Fuzzy p-value by the Signed Distance Method. Pro-
ceedings of the 9th International Joint Conference on
Computational Intelligence, pages 255–264.
Berkachy, R. and Donz
´
e, L. (2020). Fuzzy Confi-
dence Intervals by the Likelihood Ratio with Boot-
strapped Distribution. Proceedings of the 12th Inter-
national Joint Conference on Computational Intelli-
gence, pages 231–242.
Berkachy, R. and Donz
´
e, L. (2022). Fuzzy Confidence In-
tervals by the Likelihood Ratio: Testing Equality of
Means—Application on Swiss SILC Data. SN Com-
puter Science, 3(5):374.
Chachi, J. and Taheri, S. M. (2011). Fuzzy confidence in-
tervals for mean of Gaussian fuzzy random variables.
Expert Systems with Applications, 38(5):5240–5244.
Grzegorzewski, P. and Romaniuk, M. (2021). Epistemic
Bootstrap for Fuzzy Data. Joint Proceedings of
the 19th World Congress of the International Fuzzy
Systems Association (IFSA), the 12th Conference of
the European Society for Fuzzy Logic and Technol-
ogy (EUSFLAT), and the 11th International Sum-
mer School on Aggregation Operators (AGOP), pages
538–545.
Hryniewicz, O. (2018). Statistical properties of the fuzzy p-
value. International Journal of Approximate Reason-
ing, 93(J. Am. Stat. Assoc. 95 452 2000):544–560.
Kahraman, C., Otay, I., and
¨
Oztays¸i, B. (2016). Fuzzy Ex-
tensions of Confidence Intervals: Estimation for µ, σ
2
,
and p, pages 129–154. Springer International Publish-
ing, Cham.
Kahraman, C.,
¨
Oztays¸i, B., and Onar, S. C. (2019).
Interval-Valued Intuitionistic Fuzzy Confidence Inter-
vals. Journal of Intelligent Systems, 28(2):307–319.
Kruse, R. and Meyer, K. D. (1987). Statistics with Vague
Data. D. Reidel Publishing Company.
Parchami, A. (2020). Fuzzy decision in testing hypotheses
by fuzzy data: Two case studies. Iranian Journal of
Fuzzy Systems.
Parchami, A., Taheri, S. M., and Mashinchi, M. (2010).
Fuzzy p-value in testing fuzzy hypotheses with crisp
data. Springer Stat Papers, 51:209–226.
Rosset, J. and Donz
´
e, L. (2024). New decision rules for
fuzzy statistical inferences. In Ansari, J., Fuchs, S.,
Trutschnig, W., Lubiano, M. A., Gil, M.
´
A., Grze-
gorzewski, P., and Hryniewicz, O., editors, Combin-
ing, Modelling and Analyzing Imprecision, Random-
Approximated Fuzzy p-values by Bootstrapped Fuzzy Distributions and Fuzzy Hypotheses Testing
393
ness and Dependence, pages 405–412. Springer Na-
ture Switzerland.
Rosset, J. and Donz
´
e, L. (2024). Fuzzy confidence inter-
vals by bootstrapped fuzzy distributions. IPMU 2024
LISBOA, 20th International Conference on Informa-
tion Processing and Management of Uncertainty in
Knowledge-Based Systems.
Shvedov, A. S. (2016). Quantile function of a fuzzy random
variable and an expression for expectations. Mathe-
matical Notes, 100(3-4):477–481.
Viertl, R. (2011). Statistical Methods for Fuzzy Data. John
Wiley & Sons, Ltd.
Viertl, R. and Yeganeh, S. M. (2016). Fuzzy Confidence
Regions, pages 119–127. Springer International Pub-
lishing, Cham.
Wu, H.-C. (2009). Statistical confidence intervals for fuzzy
data. Expert Systems with Applications, 36(2):2670–
2676.
APPENDIX
Table 1: Fuzzy observations from Berkachy and Donz
´
e (Berkachy and Donz
´
e, 2020).
x
i
˜x
i
x
i
˜x
i
x
i
˜x
i
x
i
˜x
i
x
i
˜x
i
4 (3,4,5) 3 (2,3,4) 3 (2,3,4) 5 (4,5,6) 3 (2,3,4)
1 (0,1,2) 2 (1,2,3) 2 (1,2,3) 2 (1,2,3) 3 (2,3,4)
Note: ¯x = 2.8,
¯
˜x = (1.8,2.8,3.8).
Table 2: Fuzzy Hypothesis testing at a 5% significant level and fuzzy p-values.
Tests
˜
H
0
L
acc
L
re j
Fuzzy p-value r
acc
r
re j
1 (-0.3,-0.2,-0.1) 0 1 (0,0,0.032) 0 1
2 (0,0.5,0.8) 0 1 (0,0,1) 0.9025 0.0975
3 (0.8,0.85,0.9) 0 1 (0,0,1) 0.9025 0.0975
4 (0.95,1,1.05) 0.12 0.99 (0,0,1) 0.9025 0.0975
5 (1,1.5,2) 0.75 0.58 (0,0,1) 0.9025 0.0975
6 (1.8,1.9,2) 0.99 0.08 (0,0.012,1) 0.914 0.086
7 (1.7,1.75,1.78) 0.96 0.34 (0,0.01,1) 0.912 0.088
8 (2,2.5,3.5) 1 0 (0,0.5,1) 0.995 0.005
9 (2.4,2.45,2.5) 1 0 (0,0.32,1) 0.992 0.008
10 (2.6,2.8,3.2) 1 0 (0,0.87,1) 0.997 0.003
11 (0,3.8,6) 0.68 0.43 (0,0.08,1) 0.91 0.09
12 (0.5,4.5,8) 0.44 0.63 (0,0,0.132) 0.39 0.61
13 (7,8,9) 0 1 (0,0,0) 0 1
This Table shows first the levels of acceptance (L
acc
) and rejection (L
re j
) given by the fuzzy testing procedure of
section 4. Then, the levels of acceptance (r
acc
) and rejection (r
re j
) of the associated fuzzy p-values are displayed.
The fuzzy trapezoidal number (0.933,1.933,3.6,4.6) is the computed fuzzy confidence interval at a 95% confi-
dence level for the distribution’s mean. The values shown in red are in contradiction with the results of the testing
procedure of section 4.
Table 3: Fuzzy statistics inferences at a 5% significance level. Fuzzy p-values for randomly generated fuzzy observations
(one-sided test for the mean, θ,
˜
H
0
: θ <
˜
θ
0
against
˜
H
1
: θ ≥
˜
θ
0
).
Tests
˜
H
0
Fuzzy p-value r
acc
r
re j
1 (2.25,2.35,2.40) (0,0.002,0.016) 0 1
2 (2.39,2.42,2.45) (0.002,0.009,0.04) 0 1
3 (2.43,2.46,2.5) (0.006,0.034,0.087) 0.32 0.68
4 (2.44,2.46,2.5) (0.009,0.039,0.088) 0.44 0.56
5 (2.45,2.48,2.52) (0.02,0.048,0.118) 0.68 0.32
6 (2.5,2.55,2.6) (0.051,0.126,0.245) 1 0
This Table shows the levels of acceptance (r
acc
) and rejection (r
re j
) of different fuzzy null hypotheses via the ob-
tained fuzzy p-values. The fuzzy mean of the dataset is (2.693,2.697,2.704) and the associated fuzzy confidence
interval at a 95% confidence level for the distribution’s mean is (2.42, 2.49, 2.94, 3.01).
FCTA 2024 - 16th International Conference on Fuzzy Computation Theory and Applications
394
Table 4: Fuzzy statistics inferences at a 5% significance level. Fuzzy p-values for randomly generated fuzzy observations
(one-sided test for the mean, θ,
˜
H
0
: θ >
˜
θ
0
against
˜
H
1
: θ ≤
˜
θ
0
)).
Tests
˜
H
0
Fuzzy p-value r
acc
r
re j
1 (2.7,2.75,2.8) (0.168,0.346,0.511) 1 0
2 (2.75,2.8,2.85) (0.1,0.208,0.354) 1 0
3 (2.8,2.85,2.9) (0.042,0.117,0.221) 0.993 0.007
4 (2.85,2.9,2.95) (0.029,0.057,0.129) 0.85 0.15
5 (2.87,2.92,2.94) (0.026,0.035,0.1) 0.52 0.48
6 (2.9,3,3.1) (0.001,0.004,0.071) 0.1 0.9
7 (3,3.1,3.2) (0,0,0.009) 0 1
This Table shows the levels of acceptance (r
acc
) and rejection (r
re j
) of different fuzzy null hypotheses via the ob-
tained fuzzy p-values. The fuzzy mean of the dataset is (2.693,2.697,2.704) and the associated fuzzy confidence
interval at a 95% confidence level for the distribution’s mean is (2.42, 2.49, 2.94, 3.01).
Table 5: Fuzzy statistics inferences at a 5% significance level. Fuzzy p-values for randomly generated fuzzy observations
(one-sided test for the mean, θ,
˜
H
0
: θ =
˜
θ
0
against
˜
H
1
: θ ̸=
˜
θ
0
).
Tests
˜
H
0
Fuzzy p-value r
acc
r
re j
1 (2.58,2.6,2.62) (0.318,0.466,0.594) 1 0
2 (2.45,2.5,2.55) (0.03,0.112,0.322) 0.984 0.016
3 (2.4,2.45,2.5) (0.01,0.052,0.134) 0.7 0.3
4 (2.37,2.4,2.44) (0.004,0.016,0.062) 0.06 0.94
5 (2.35,2.4,2.45) (0.002,0.026,0.086) 0.74 0.26
6 (2.3,2.35,2.4) (0,0.004,0.02) 0 1
This Table shows the levels of acceptance (r
acc
) and rejection (r
re j
) of different fuzzy null hypotheses through
the obtained fuzzy p-values. The fuzzy mean of the dataset is (2.693,2.697,2.704) and the associated fuzzy
confidence interval at a 95% confidence level for the distribution’s mean is (2.42, 2.49, 2.94, 3.01).
Approximated Fuzzy p-values by Bootstrapped Fuzzy Distributions and Fuzzy Hypotheses Testing
395
