Randomized Local Search for Two-Dimensional Bin Packing and a

Negative Result for Frequency Fitness Assignment

Rui Zhao

1 a

, Zhize Wu

1 b

, Daan van den Berg

2 c

, Matthias Th

urer

3 d

, Tianyu Liang

1 e

Ming Tan

1 f

and Thomas Weise

1 g

Institute of Applied Optimization, School of Artiﬁcial Intelligence and Big Data, Hefei University, Jinxiu Dadao 99, Hefei,

230601, Anhui, China

Department of Computer Science, Vrije Universiteit Amsterdam, De Boelelaan 1111, Amsterdam, 1081 HV,

The Netherlands

Professur Fabrikplanung und Intralogistik, TU Chemnitz, Str. der Nationen 62, 09111 Chemnitz, Sachsen, Germany

Keywords:

Two-Dimensional Bin Packing, Randomized Local Search, Frequency Fitness Assignment, Cutting Stock

Problem.

Abstract:

We consider a two-dimensional orthogonal bin packing problem (2BP) where rectangular items are to be

placed into rectangular bins such that their edges are parallel to those of the bins with the aim to require

as few bins as possible. Two variants of the problem are analyzed. In the 2BP|O|F, the items have a ﬁxed

orientation while in the 2BP|R|F, they can be rotated by 90 degrees. We show that on both variants, a simple

randomized local search (RLS) has surprisingly good performance – if the objective function guiding the

search is deﬁned suitably. In particular, on the 2BP|O|F, the RLS performs on par with more complicated

state-of-the-art metaheuristics. We furthermore investigate plugging Frequency Fitness Assignment (FFA)

into the RLS, obtaining the FRLS. FFA has improved the RLS performance on several classical N P-hard

optimization problems from operations research, including Max-SAT, the Job Shop Scheduling Problem, and

the Traveling Salesperson Problem. This paper is the ﬁrst negative result for FFA: it cannot improve algorithm

performance on the 2BP variants studied. This can be explained by the fact that RLS already performs very

well on the instances of the 2DPackLib benchmark set used as the basis of our experiments.

1 INTRODUCTION

Cutting stock problems (CSPs) and bin packing prob-

lems (BPs) are two closely related domains of oper-

ations research (Lodi et al., 2002; Iori et al., 2021).

CSPs ask for dividing larger chunks of material into

smaller pieces, whereas BPs require us to place

smaller items into larger containers. In many cases,

variants of both problems can be trivially transformed

into each other. Their two-dimensional orthogonal

variants, which we here jointly refer to as 2BPs,

have many important applications, ranging from ob-

https://orcid.org/0009-0002-2426-9453

https://orcid.org/0000-0001-7416-5711

https://orcid.org/0000-0001-5060-3342

https://orcid.org/0000-0002-2705-969X

https://orcid.org/0009-0004-3732-4831

https://orcid.org/0009-0004-3851-053X

https://orcid.org/0000-0002-9687-8509

vious tasks such as packing and layout to scheduling

and build formation in additive manufacturing (Pinto

et al., 2024; Li and Zhang, 2018). The goal of solving

a 2BP is to pack a set of rectangular items into as few

as possible rectangular bins. While several exact al-

gorithms for this purpose have been developed (Ma

and Zhou, 2017; Cid-Garcia and Rios-Solis, 2020;

van den Berg et al., 2016; Braam and van den Berg,

2022; Martello and Vigo, 1998; Iori et al., 2021), they

can only be one part of the answer to the 2BP due to

its N P -hard nature (Lodi et al., 2002). As a result,

several heuristic algorithms have been applied to this

problem family, ranging from one-shot constructive

heuristics (Wong and Lee, 2009; Liu and Teng, 1999;

Pejic and van den Berg, 2020) over tabu search (Lodi

et al., 2004), evolutionary (Kierkosz and Luczak,

2013; Liu and Teng, 1999; Gonc¸alves and Resende,

2013; Lee, 2008; Li et al., 2021), and memetic algo-

rithms (Blum and Schmid, 2013; Parre

no et al., 2010)

Zhao, R., Wu, Z., van den Berg, D., Thürer, M., Liang, T., Tan, M. and Weise, T.

Randomized Local Search for Two-Dimensional Bin Packing and a Negative Result for Frequency Fitness Assignment.

DOI: 10.5220/0012888500003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 15-26

ISBN: 978-989-758-721-4; ISSN: 2184-3236

to hyper-heuristics (Beyaz et al., 2015; Terashima-

Mar

ın et al., 2007).

We build on the recent work (Zhao et al.,

2024), where it was shown that a randomized local

search (RLS) can perform surprisingly well on a vari-

ant of the 2BP where item rotation is permitted, if the

objective function is deﬁned appropriately. The ﬁrst

contribution of this paper is to signiﬁcantly expand

upon these results and to show that the same RLS can

be even more competitive to the related work on the

2BP if item rotation is not permitted. In other words,

we ﬁnd that two important variants of the 2BP can

already be solved quite well with relatively simple al-

gorithms.

As our related work study in Section 3 shows,

many of the existing works on the 2BP provide re-

sults that are either normalized with different lower

bounds, are always averaged over several instances,

or use different benchmark instances. The second

contribution of our work therefore is to provide

a complete set of results on the recently published

2DPackLib benchmark (Iori et al., 2022), including

the discovered packings, the complete progress over

the runtime, and the algorithm implementations in an

immutable archive at https://doi.org/10.5281/zenodo.

13324219, to serve as basis for future research.

All of the metaheuristic algorithms for the 2BP

share the common concept that they iteratively sample

new solutions s

based on the currently retained solu-

tions s

and that they tend to retain the new solution

if it is better (or, at least, not worse) than s

. They

may maintain populations of solutions (e.g., evolu-

tionary algorithms) or introduce some diversity or ex-

ploration criterion (e.g., tabu search), but over time,

better solutions are preferred over worse ones. There

are only three iterative optimization algorithms free

of such bias: random sampling, random walks, and

exhaustive enumeration.

In (Weise et al., 2014b), a fourth optimization ap-

proach without bias towards good solutions was intro-

duced, Frequency Fitness Assignment (FFA), but its

theoretical properties were proven only relatively re-

cently (Weise et al., 2021b; Weise et al., 2023). FFA

is not an algorithm itself, but a module that can be

plugged into a wide range of iterative heuristics. It

then renders them invariant under all injective trans-

formations of the objective function value. It prefers

new solutions s

if they have a previously less fre-

quently encountered objective value z

= f (s

), re-

gardless of whether they are better or worse.

Despite this unbiasedness, FFA yields remarkable

performance on several classical N P -hard optimiza-

tion problems such as Max-SAT (Weise et al., 2021b;

Weise et al., 2023), the Job Shop Scheduling Prob-

lem (JSSP) (Weise et al., 2021a; de Bruin et al., 2023),

and on the Traveling Salesperson Problem (Liang

et al., 2022; Liang et al., 2024, TSP). Experiments

support that FFA-based algorithms tend to ﬁnd better

solutions than the objective-guided counterparts into

which they are plugged if the problem they are ap-

plied to does not have too many different objective

values (Liang et al., 2022; Liang et al., 2024).

Since the possible range of the number of bins into

which the items in a 2BP can be packed is usually

small (Zhao et al., 2024), the 2BP might be another

classical N P-hard problem where FFA could excel.

As the third contribution, we explore this idea by

plugging FFA into the RLS, yielding the FRLS, and

applying it to all the 2DPackLib instances. We ﬁnd

that FRLS cannot outperform the RLS on the 2BP.

This is the ﬁrst completely negative result for FFA

on any classical optimization task. However, when

analyzing the performance of RLS and FRLS in more

detail, the reasons for this discrepancy become clear.

The fourth contribution of our work is that we

identify the need for harder benchmark instances

based on reproducible results: RLS should not per-

form well on N P-hard problems, but it does so any-

way in our experiments on the 2BP. This means that

we have conﬁrmed that the 2DPackLib benchmark for

the 2BP, despite being well-designed and comprehen-

sive, is probably too easy and should be extended.

In the remainder of the paper, we ﬁrst introduce

the two variants of the 2BP in Section 2 and discuss

the related work on it in Section 3. We present our

approach to the 2BP, including the RLS and FRLS al-

gorithms, the encoding used, the search space, opera-

tors, and objective functions, in Section 4. The exper-

imental results are analyzed in Section 5 before we

conclude the paper with a summary and an outlook

for future work in Section 6.

2 2D BIN PACKING

In this paper, we consider two orthogonal rectangu-

lar two-dimensional bin packing problem variants,

which are deﬁned as follows. The bins and items are

both two-dimensional rectangles. All bins have the

same width W ∈ N and height H ∈ N. The number of

available bins is unlimited. There are N ∈ N items.

The item i ∈ {1..N} has width w

∈ {1..W } and

height h

∈ {1..H}. For each item i, there is a de-

mand d

, meaning that d

instances of item i need

to be packed. Thus, the goal is to pack all the

T =

∑

i=1

item instances into as few bins as possi-

ble. The edges of the item instances must be parallel

to those of the bins. There must be no overlap and all

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

item instances must be contained entirely in the bins.

In the 2BP|O|F variant, the items have a ﬁxed

orientation, must not be rotated, and are placed in

the same way they are deﬁned in the problem in-

stance (Lodi et al., 2002)

. In the 2BP|R|F problem

variant, the item instances can be rotated by 90

◦

Both variants have packing plans s as solutions,

which can be deﬁned as sets of T records s[ j] with

j ∈ {1..T }, each denoting the location of one packed

item instance in its bin. Thus, record s[ j] stores the

item s[ j].i ∈ {1..N}, the bin s[ j].b ∈ {1..T } into which

it should be packed, as well as the horizontal co-

ordinate s[ j].x

∈ {0..W − 1} and the vertical coordi-

nate s[ j].y

∈ {0..H −1} of the lower left corner of

the packed item instance. To represent whether the

item instance is rotated by 90

◦

or not, the coordi-

nates s[ j].x

∈ {1..W } and s[ j].y

∈ {1..H} of its up-

per right corner are stored as well. For s[ j].i = i,

it then either holds that s[ j].x

= s[ j].x

+ w

and

s[ j].y

= s[ j].y

+ h

if the instance of item i is not ro-

tated or s[ j].x

= s[ j].x

+ h

and s[j].y

= s[ j].y

+ w

if the item instance is rotated. Rotation is only per-

mitted in the 2BP|R|F variant.

The space of all such feasible packing plans is S.

The goal is to ﬁnd the packing plan s ∈ S that re-

quires the fewest bins among all the possible feasi-

ble plans and, hence, also has the smallest total unoc-

cupied space inside the bins, i.e., that minimizes the

following objective function:

(s) = |{s[j].b ∀ j ∈ {1..T }}| (1)

For any 2BP instance, it is not a priori clear how

many bins will be required in the optimal solution.

However, lower bounds for f

provide a limit for

the best-case scenario. The geometric or continuous

bound lb

( f

) therefore returns the rounded-up quo-

tient of the total area sum of all item instances and the

bin area (Martello and Vigo, 1998):

( f

) =



∑

i=1



/(W H)



(2)

Obviously f

(s) ≥ lb

( f

) for all s ∈ S, as it is impos-

sible to package the items into bins whose total area is

less than the total item area. The most commonly used

lower bound for f

may be lb

( f

) by (Dell’Amico

et al., 2002), which, due to its algorithmic formula-

tion, shall not be detailed here. In our work, we will

use the maximum lb

( f

) = max{lb

( f

),lb

( f

)} of

both bounds where appropriate.

The “F” stands for cutting being free if the problem is

considered from the CSP perspective.

3 RELATED WORK

A search for publications focused on these spe-

ciﬁc problem variants, in particular the 2BP|R|F,

produces signiﬁcantly fewer results (Cid-Garcia and

Rios-Solis, 2020) compared to other classical prob-

lem domains such as the Traveling Salesperson Prob-

lem or the Quadratic Assignment Problem. This may

be due to the many different problem variants, their

sometimes non-obvious naming, and, ﬁnally, due to

the comparatively higher implementation effort for

simple algorithms (see Algorithm 3). Nevertheless,

the orthogonal rectangular 2BP with and without ro-

tation did attract some research attention over the

decades, although maybe not as much as it deserves.

(Bengtsson, 1982) contributed a heuristic algo-

rithm for packing rectangular pieces in 1982. The al-

gorithm involves an initial allocation of items to bins

and then tries to iteratively reﬁne it. The goal of this

algorithm is to minimize the unused space in the bins

and it permits that some items may not be loaded,

so the results are not directly comparable to our 2BP

scenarios. The authors provide the beng benchmark

and use it in their experiments, where they achieve a

bin utilization between 95% and 98% within compu-

tational budgets of 0.5 and 1 second.

(Liu and Teng, 1999) proposed an Improved Bot-

tom Left (IBL) encoding that can translate signed per-

mutations to packings. In their work, the goal is to

minimize the packing height in a bin of inﬁnite height.

Examples are provided, but no experimental results.

However, we will adapt the IBL to the 2BP in this

work (see Algorithm 3 later on).

(Lodi et al., 2004) developed the C library TSpack

for solving two- and three-dimensional bin packing

problems with the goal of minimizing the number of

bins. It offers iterative optimization through Tabu

Search whose key aspect is the ability to switch be-

tween neighborhoods of different sizes. The goal is to

tune between intensiﬁcation and diversiﬁcation. The

authors use a dataset similar to class, but with differ-

ent instances and hence, different bounds and solu-

tions. The results thus cannot be directly compared

with such obtained on 2DPackLib. The computational

budget per run is 60s.

(Terashima-Mar

ın et al., 2007) introduce two hy-

perheuristic approaches to the 2BP|R|F. They ﬁrst

deﬁne a set of selection heuristics that choose items

and bins as well as a set of placement heuristics that

place the selected items into the selected bins. Then,

they synthesize rules that decide which of the heuris-

tics should be applied based on the current state of the

packing process. For this purpose, they both inves-

tigate an XCS-type Learning Classiﬁer System and a

Randomized Local Search for Two-Dimensional Bin Packing and a Negative Result for Frequency Fitness Assignment

dedicated Genetic Algorithm (GA). The authors show

that the hyper-heuristics can synthesize heuristics that

can outperform the best single heuristic on any in-

stance, however, no results are reported that could be

used for direct comparison.

In the MultiCrossover GA (MXGA) by (Lee,

2008), solutions are integer strings storing, for each

of the T item instances, into which bin it should be

placed. The location of the item instances is then

computed by a heuristic placement routine. As opera-

tors, single-point crossover and single-swap mutation

are applied. The work again uses the class benchmark

and grants 120 seconds per run to its C-based algo-

rithm implementations. The number of repetitions is

not given. Results are averaged over instance groups,

divided by lb

and given with a precision of two dec-

imals.

(Wong and Lee, 2009) propose two heuristic

placement algorithms, namely Improved Lowest Gap

Fill (LGFi) for the case with rotation and LGFi

for

the case where the items cannot be rotated. These

algorithms iteratively select the bin with the small-

est remaining space to place the current item until

all items are placed. LGFi is a constructive heuris-

tic that creates a single packing. It would therefore be

a possible alternative to the IBL method that we use

as the encoding scheme in our RLS and FRLS in Sec-

tion 4. Results for the class instances are reported and

normalized by lb

and another bound (Boschetti and

Mingozzi, 2003) with three decimals of precision.

(Parre

no et al., 2010) developed the GRASP/VND

algorithm for 2BP|O|F problems, which combines

the greedy randomized adaptive Search Proce-

dure (GRASP) and the variable neighborhood de-

scent (VND). GRASP is a constructive algorithm that

builds solutions incrementally by iteratively select-

ing the best available option based on randomized

greedy criteria. It aims to balance exploitation (choos-

ing the best immediate option) and exploration (di-

versifying the search space). In GRASP/VND, the

GRASP procedure generates an initial solution by it-

eratively adding items to bins based on a randomized

greedy rule. VND is a local search algorithm that

explores different neighborhoods around a given so-

lution to ﬁnd local optima. It iteratively moves from

one neighborhood to another until no further improve-

ment is possible. In GRASP/VND, the VND is applied

to the initial solution and improves it iteratively. The

algorithm is run for 50000 iterations on the class and

beng datasets. The average of the numbers of bins per

instance group is reported.

(Gonc¸alves and Resende, 2013) present the Bi-

ased Random Key GA (BRKGA) for 2D and 3D

bin packing problems with and without item rotation

(BRKGA-2r, BRKGA-aNB, respectively). The chro-

mosome encodes both the sequence in which items

are packed as well as their orientation. The authors

use the class and the beng instances, and also some

other benchmarks to evaluate their algorithm. They

conduct three runs per setup for 200 generations with

a population of 30 times the number T of item in-

stances, and report the average number of bins over

the instance groups.

The EA-LGFi for the 2BP|O|F by (Blum and

Schmid, 2013) is an Evolutionary Algorithm (EA)

that works on permutations and uses the aforemen-

tioned LGFi heuristic by (Wong and Lee, 2009) to

translate the permutations to packing plans. The pa-

per used class instances as the benchmark and found

four new best solutions. The computational budget is

FEs per run and one run is conducted per instance.

The sum of bins over all the solutions per instance

group is reported.

(Kierkosz and Luczak, 2013) developed an evolu-

tionary algorithm (EA) to select a subset of the items

and place them such that the maximum area in the sin-

gle available bin is used. None of the benchmarks in

2DPackLib are used.

(Beyaz et al., 2015) introduced their hyper-

heuristic method HHA-NO based on a Memetic Al-

gorithm, i.e., the combination of an EA with local

search. The genome contains the order of items to

be packed as well as two heuristic selections. The

ﬁrst half of the items are packed using the ﬁrst se-

lected heuristic and the second half using the sec-

ond selected heuristic. A population of 60 individ-

uals evolved for 40 generations. The algorithm is im-

plemented in C++ and the runtimes within the range

of 46s to 14.5min are reported for a selection of in-

stances. This runtime seems to be relatively high for

what should be around 60 ∗40 = 2400 objective func-

tion evaluations (FEs), raising the question of how to

fairly compare algorithms whose single steps require

vastly different runtimes (Weise et al., 2014a). The

authors use the class instances and report the sum of

the f

values over the instance set.

(Ma and Zhou, 2017) introduced two mixed-

integer programming (MIP) models for solving the

2BP. This is an exact solution approach, i.e., given

enough runtime, the optimal solution can be obtained.

The models are implemented under CPLEX. The au-

thors report the average runtime. The used bench-

mark instances are randomly generated and are not

part of an available benchmark set, and a comparison

is therefore not possible.

(Cid-Garcia and Rios-Solis, 2020) developed the

two-stage exact Positions and Covering (P&C) algo-

rithm for the 2BP with and without rotation. The

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

ﬁrst stage involves an initial placement strategy to as-

sign items to preliminary positions, which maximizes

space utilization. The second stage employs a cover-

ing algorithm to further optimize item placement and

minimize wasted space. Results are reported for the

beng and some of the class instances which, neces-

sarily, are the correct optimal solutions (but are only

given as averages, sadly). The time limit for the runs

was set to 5 hours and the algorithm could not be com-

pleted on some instances.

Most recently, (Li et al., 2021) proposed a hy-

brid adaptive GA (HAGA) for a two-dimensional rect-

angular packing problem. As in (Bengtsson, 1982),

the goal is to maximize the ﬁlling rate of the sheets,

meaning that some items may not be selected for in-

clusion. The benchmark instances used are also not in

2DPackLib.

From this brief overview, we immediately no-

tice several problems for any researcher delving into

the 2BP. The existing works have different goals

(number of bins, ﬁll rate), report results obtained on

different benchmarks, use different termination crite-

ria that can either be based on FEs or on time and then,

range from 0.5s to many days, and perform different

numbers of runs per instance. The actual solutions,

the packing plans, are almost never provided. Even

worse, the results are always averaged over bench-

mark instance sets, often normalized using different

lower bounds, and usually rounded to one or two dec-

imals. While it is possible (although error-prone) to

de-normalize the results for comparison purposes by

multiplying with the (right) lower bound, it is not pos-

sible to de-average or de-round them. . .

For a problem as important and common as the

2BP, there should be a complete set of unrounded, un-

normalized, and un-averaged results on a standard-

ized and publically available dataset. It is not neces-

sary that such a set represents the state-of-the-art or is

continuously updated. The presence of instances to-

gether with solutions and objective values alone will

allow other researchers to verify and replicate each

others’ work. And if all future publications include

complete results in immutable archives as we do here

in https://doi.org/10.5281/zenodo.13324219, the set

of best-known solutions emerges automatically.

We chose the recent 2DPackLib benchmark (Iori

et al., 2022) for our work, which has been published

by researchers who are responsible for several of the

most important milestones in the ﬁeld (Iori et al.,

2021; Dell’Amico et al., 2002; Lodi et al., 2002; Lodi

et al., 2004; Martello and Vigo, 1998; Monaci and

Toth, 2006). Unfortunately, no results or solutions

were published along with the benchmark instances.

We close this gap. Moreover, by reporting all improv-

ing moves of our algorithm for a large computational

budget, arbitrarily shorter computational budgets can

be simulated by cutting off the later improvements.

4 OUR APPROACH

4.1 RLS and FRLS

As the baseline algorithm for our study, we use the

simplest local search method available, Randomized

Local Search (RLS), often also called Hill Climbing

or (1 + 1) EA (Russell and Norvig, 2002; Neumann

and Wegener, 2007; Johnson et al., 1988). As a black-

box metaheuristic, it allows us to choose a search

space P and a search operator move : P 7→ P, a decod-

ing function decode : P 7→ S that translates the points

in the search space to packing plans, and an objective

function f : S 7→ N rating the quality of such plans.

The blueprint of this metaheuristic is illustrated

in Algorithm 1. The algorithm begins by sampling

a random point π

from the search space P, decod-

ing it to a packing plan s

, and evaluating its objective

value z

= f (s

). In a loop, a new point π

is sam-

pled as a modiﬁed copy of π

using the unary opera-

tor move, decoded, and evaluated. If π

is not worse

than π

, it replaces it. When the computational bud-

get of 10

FEs is exhausted, both the best-so-far so-

lution s

and its quality z

are returned. In our exper-

iments, the algorithm terminates after 10

objective

function evaluations (FEs).

FFA is an algorithm module that prescribes re-

placing the objective values with their encounter fre-

quencies in the selection decisions. Plugging it into

the RLS yields the FRLS sketched in Algorithm 2.

This algorithm starts like RLS, but additionally ini-

tializes a frequency table H to be ﬁlled with zeros.

Where RLS compares the objective values z

and z

decide whether π

should replace π

or be discarded,

FRLS ﬁrst increments the encounter frequencies H[z

]

and H[z

] of z

and z

and then compares these instead

of the objective values. As a result, it will accept π

if it corresponds to a solution whose objective value

has been seen less or equally often than the one cor-

responding to π

. Since FRLS does not care whether

is better than z

or not, the algorithm may lose the

best-discovered solution again and thus needs to re-

member it in an additional variable s

(Weise et al., 2021b; Weise et al., 2023) dis-

cuss the interesting theoretical features of the result-

ing algorithm that no longer optimizes towards bet-

ter solutions but, yet, will ﬁnd these nevertheless be-

cause good solutions have rare objective values. It

was shown that this scheme yields remarkable perfor-

Randomized Local Search for Two-Dimensional Bin Packing and a Negative Result for Frequency Fitness Assignment

Algorithm 1: RLS(decode : P 7→ S, f : S 7→ N).

sample π

from P u.a.r.;

← decode(π

); ▷ see Algorithm 3

← f (s

); ▷ one of the objective functions

for 10

− 1 times do ▷ our termination criterion

← move(π

); ▷ depends on problem type

← decode(π

); z

← f (s

);

if z

≤ z

then

← π

; s

← s

; z

← z

return s

, z

Algorithm 2: FRLS(decode : P 7→ S, f : S 7→ N).

H ← (0, 0,· ·· ,0); ▷ H-table initially all 0s

sample π

from P u.a.r.;

← decode(π

); ▷ see Algorithm 3

← f (s

); ▷ one of the objective functions

← s

; z

← z

; ▷ best may otherwise get lost

for 10

− 1 times do ▷ our termination criterion

← move(π

); ▷ depends on problem type

← decode(π

); z

← f (s

);

if z

< z

then s

← s

; z

← z

;

H[z

] ← H[z

] + 1; H[z

] ← H[z

] + 1;

if H[z

] ≤ H[z

] then

← π

; s

← s

; z

← z

return s

, z

▷ return preserved best

mance on the Max-SAT domain, where it can speed

up multiple algorithms several thousand times (Weise

et al., 2023), as well as on the JSSP (Weise et al.,

2021a; de Bruin et al., 2023) and on the TSP (Liang

et al., 2022; Liang et al., 2024). Whether it can re-

peat this impressive performance on the 2BP will be

investigated in our experiments.

4.2 Encoding and Search Operators

Deﬁning search operators for the packing plans s ∈ S

directly is complicated. However, when solving the

2BP|O|F, we can use permutations π with repetitions

as search space P to represent the packing orders.

Each item ID i ∈ {1..N} occurs d

times in π. The

permutations π therefore have length T .

For the 2BP|R|F, we allow the elements of π to be

signed: Each time an item ID occurs, it then can do

so either in its original (positive) value, meaning that

an instance of i is to be packed in its original orien-

tation (w

), or negated, i.e., as −i, which signiﬁes

that an instance of i is packed after a 90

◦

rotation, that

is, having dimensions (h

The decoding function decode is based on the Im-

proved Bottom Left IBL heuristic by (Liu and Teng,

1999) and adopted to the 2BP in (Zhao et al., 2024).

It accepts one such packing order π ∈ P and translates

Algorithm 3: decode(π ∈ P) 7→ S.

b ← 1; ▷ start at bin 1

for k ∈ {1..T } do ▷ iterate over all T elements

in π

i ← π[k]; ▷ get current item ID

if i < 0 then ▷ ≡ rotation in 2BP|R|F

i ← −i; w ← h

; h ← w

;

else w ← w

; h ← h

;

▷ some rotations may be invalid in 2BP|R|F

if w > W ∨ h > H then swap w and h;

▷ put item with bottom-right corner on

top-right corner of current bin

set s[k].b ← b; s[k].i ← i; s[k].x

← W − w;

s[k].y

← H; s[k].x

← W ;

s[k].y

← H +h;

move s[k] down-left as far as possible without

creating any overlap; prefer moving

down over moving left;

if s[k].y

> H then ▷ item does not ﬁt in bin?

▷ put it at bottom-left corner of a new bin

b ← b + 1;

set s[k].b ← b; s[k].x

← 0; s[k].y

← 0;

s[k].x

← w; s[k].y

← h;

return s

bin closedbin closed

new bin

item ﬁtsitem ﬁts

item does

not ﬁt

item does

not ﬁt

Figure 1: An illustrative example of the decoding Algo-

rithm 3 (read from the top-left to the bottom-right).

it to a packing plan s ∈ S. It therefore iterates over

the (potentially signed) permutation s and places the

items into the packing plan in the prescribed order. As

sketched in Figure 1, it ﬁrst places the item instance

outside on top of the bin, with its bottom-right corner

onto the top-right corner of the current bin b. It then

moves the instance downwards and leftwards as far as

possible, prioritizing the downward movement when-

ever possible. If the item instance cannot be moved

any further, we check if it is completely contained in

the bin b. If yes, it can remain there. Otherwise, a

new bin is opened (b ← b + 1) and the item instance

is placed at its bottom-left corner. Once a new bin is

opened, this bin is used for all further insertions.

For the 2BP|O|F, the unary search operator move :

P 7→ P accepts one point π

∈ P and returns a

point π

∈ P where two randomly chosen different el-

ements are swapped.

For the 2BP|R|F, where the elements of the per-

mutations π can be signed, it produces a point π

where either one value is negated or two different val-

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

ues are swapped. It therefore ﬁrst creates a copy π

and draws an index j uniformly at random (u.a.r.)

in {1..T }. It then draws a Boolean value v, which

is either True or False, u.a.r. If v = True, it tries

to swap two different elements in π

. It therefore at-

tempts for at most 10T times to draw a random in-

dex k ∈ {1..T } with π

[k] ̸= π

[ j]. If this succeeds,

it swaps the values at indices j and k in π

and re-

turns π

. Otherwise, i.e., if either no appropriate in-

dex k was found (which can happen, e.g., if all items

are identical) or if v = False, it ﬂips the sign of π

[ j]

and returns π

Finally, in (Zhao et al., 2024), several objective

functions that minimize the number of bins were dis-

cussed as alternatives to f

on the 2BP|R|F. It was

found that the function f

(see Equation 5) combining

the number of bins f

with the area under the skyline

(the top border of the packing) in the last bin yielded

the best results. An RLS using this objective function

will prefer a packing s

over a packing s

if it requires

fewer bins or, if both require the same number of bins

but s

has a lower skyline in its last bin. We will in-

vestigate both f

and f

in our experiments.

inB(s,b) = { j ∀ j ∈ {1..T } ∧ s[ j].b = b} (3)

sl(s,b) =

W −1

∑

x=0

max



s[ j].y

: ∀ j ∈ inB(s,b)∧

s[ j].x

≤ x < s[ j].x



(4)

(s) = W H( f

(s) − 1) + sl(s, f

(s)) (5)

5 EXPERIMENTS AND RESULTS

5.1 Setup

We implement our algorithms in Python 3.10 on Win-

dows 10 on an Intel64 Family 6 Model 167 CPU us-

ing the moptipy (Weise and Wu, 2023) framework, as

well as numba just-in-time compilation where pos-

sible. We conduct 3 runs per algorithm setup and

problem instance, except for the RLS- f

, for which

we conduct 5 runs. Since this algorithm performed

best, we deemed it worth to gather more data for it

as basis for future experiments. We use a computa-

tional budget of at most 10

objective function eval-

uations (FEs) per run, which is the same as in (Zhao

et al., 2024).

We use the 2DPackLib by (Iori et al., 2022), which

offers three sets of 2BP instances in a uniﬁed format:

The ten instances of type beng (Bengtsson, 1982)

have both bin and item dimensions drawn from uni-

form distributions. They have 20 to 200 items and

the largest bin size is (40,25). The class instance

set (Berkey and Wang, 1987; Martello and Vigo,

1998) is divided into ten classes based on the bin and

item dimensions, the former of which ranges from

(10,10) to (300, 300). Each class is divided into ﬁve

groups with N ∈ {20,40, 60,80, 100} items. Each

group contains ten benchmark instances. Finally, the

set A (Macedo et al., 2010) offers 43 instances with

N ∈ {13..809} and bin sizes of either (2750,1220),

(2550,2100), or (2470,2080).

Additionally to the 2DPackLib, we consider the

four non-trivial “Almost Squares in Almost Squares”

(AsqasN) instances from (van den Berg et al., 2016).

They have N ∈ {3, 8,20,34} and the widths of all

objects are one unit larger than their heights, i.e.,

= h

+ 1 ∀i ∈ {1..N} and W = H + 1. The goal is

to pack all items into a single bin, which would result

in a perfect packing without any wasted space.

5.2 Results

In Table 1 we present the results of our methods for

the 2BP|R|F (with rotation) and in Table 2 for the

2BP|O|F (without rotation).

We conducted 3 runs

per algorithm setup and problem instance for at most

objective function evaluations (FEs), except for

the RLS- f

setups, for which we performed 5 runs.

While we do present the sum of the number of bins

added up over groups of instances like the related

works do, we ﬁrst average the results over each in-

stance. The ﬁnal results are rounded to full integers.

The best values per instance group are marked with

bold face and we count how often each algorithm can

achieve the best result on the class and beng instance

groups in the bottom row (# best c&b).

Among our own four algorithm setups, the RLS

using f

can achieve the best results. On the 2BP|R|F,

it is outperformed only by the BRKGA-2r, which

achieves the best result 52 times whereas the average

result of RLS- f

is best 38 times. The third best al-

gorithm is HHA-NO(sr) (Beyaz et al., 2015), which

achieves the best result 22 times.

On the 2BP|O|F, the BRKGA-aNB scores

best 49 times, followed by the EA-LGFi

by (Blum and Schmid, 2013) (44 times) and the

GRASP/VND (Parre

no et al., 2010) (43 times). The

average results of RLS- f

are the best 41 times.

For MXGA (Lee, 2008) normalized results have been

reported. We de-normalized them, but had to use lb

in-

stead of lb

to get reasonable values. Still, due to round-

ing errors, we had to correct the values for class 1/60 and

class 1/100, which, probably due to the result of rounding

in (Lee, 2008), de-normalizing, and then rounding again,

came out slightly below the optimal result delivered by

P&C. Due to this rounding process, the comparison with

MXGA must be taken with a grain of salt. As said, this pro-

cess is error-prone.

Randomized Local Search for Two-Dimensional Bin Packing and a Negative Result for Frequency Fitness Assignment

Table 1: Average total number of bins of the RLS and FRLS

on the 2BP|R|F (with rotation) for objective functions f

and f

for 3 runs per setting in comparison to the related

work. For RLS- f

, 5 runs were conducted, for the other

settings only 3. Column RLS- f

⋆

is the best result of the 5

RLS- f

runs.

instance BRKGA HHA-NO MXGA P&C FRLS RLS

group 2r (r) (sr) f

⋆

a/small 100 99 99 97 97

a/med 203 221 198 176 174

a/large 745 867 721 651 644

beng/1-8 54 54 61 54 60 54 54

beng/9-10 13 13 15 13 14 13 13

class 1/20 66 66 66 66 66 66 66 66 66 66

class 1/40 128 131 129 129 128 132 129 131 129 128

class 1/60 195 196 195 195 195 205 195 202 195 195

class 1/80 270 270 270 270 270 283 274 278 270 270

class 1/100 313 314 313 313 313 340 325 331 313 313

class 2/20 10 10 10 10 10 10 10 10 10 10

class 2/40 19 20 19 21 19 20 19 20 19 19

class 2/60 25 25 25 25 25 29 25 28 25 25

class 2/80 31 31 31 31 31 36 31 35 31 31

class 2/100 39 39 39 39 39 42 40 42 39 39

class 3/20 47 48 48 48 47 48 47 47 47 47

class 3/40 92 95 95 94 97 94 97 94 93

class 3/60 134 137 137 136 148 142 146 134 134

class 3/80 182 186 187 184 207 206 201 183 183

class 3/100 220 225 225 223 250 253 244 220 220

class 4/20 10 10 10 10 10 10 10 10 10

class 4/40 19 19 19 19 19 19 19 19 19

class 4/60 23 25 25 25 28 25 27 24 23

class 4/80 31 32 33 32 35 33 35 31 31

class 4/100 37 38 38 38 42 40 42 37 37

class 5/20 59 59 59 59 59 59 59 59 59

class 5/40 114 116 115 114 120 118 119 114 114

class 5/60 172 175 176 177 186 191 182 174 173

class 5/80 239 240 241 241 257 271 251 239 239

class 5/100 277 284 284 279 308 330 302 278 278

class 6/20 10 10 10 10 10 10 10 10 10

class 6/40 16 18 17 21 19 17 19 16 16

class 6/60 21 22 22 21 23 22 23 21 21

class 6/80 30 30 30 30 31 30 31 30 30

class 6/100 32 34 34 34 39 37 38 32 32

class 7/20 52 52 52 52 52 52 52 52 52

class 7/40 102 106 107 104 111 109 107 103 102

class 7/60 146 152 153 147 162 164 157 146 146

class 7/80 208 216 217 213 232 244 228 208 208

class 7/100 250 260 259 255 281 298 274 250 250

class 8/20 53 53 53 53 53 53 53 53 53

class 8/40 103 106 105 105 111 111 108 104 104

class 8/60 147 155 154 149 164 166 160 148 148

class 8/80 204 213 214 209 229 240 225 207 206

class 8/100 252 261 262 255 284 302 278 253 252

class 9/20 143 143 143 143 143 143 143 143 143

class 9/40 275 275 275 275 275 275 275 275 275

class 9/60 435 435 435 436 435 435 435 435 435

class 9/80 573 573 573 574 573 573 573 573 573

class 9/100 693 693 693 695 693 693 693 693 693

class 10/20 41 41 41 43 41 41 41 41 41

class 10/40 72 73 73 73 79 73 76 73 72

class 10/60 99 101 101 101 112 107 109 99 99

class 10/80 125 129 130 129 146 144 142 126 125

class 10/100 154 161 162 159 184 185 179 158 156

asqas 6 6 6 6 6

# best c&b 52 19 22 19 13 14 22 15 38 44

However, if we consider the best results of ﬁve runs

of RLS- f

(denoted in column f

⋆

), this algorithm

achieves 50 times the best solution and would rank

ﬁrst. In other words, had we given ﬁve times the

computational budget and performed restarts, a

simple local search would have outperformed all of

the much more complicated algorithm designs on the

2BP|O|F.

The P&C (Cid-Garcia and Rios-Solis, 2020) is an

exact method that always ﬁnds the optimal solutions.

On the 2BP|R|F, the average results of RLS- f

reach

the same (optimal) quality on all but one of the in-

stance groups (class 1/40) where results of P&C are

Table 2: Average total number of bins of the RLS and FRLS

on the 2BP|O|F (without rotation) for objective functions

and f

in comparison to the related work. For RLS- f

5 runs were conducted, for the other settings only 3. Col-

umn RLS- f

⋆

is the best result of the 5 RLS- f

runs.

instance BRKGA EA GRASP P&C FRLS RLS

group aNB LGFi VND f

⋆

a/small 102 101 101 101 101

a/med 202 211 202 181 180

a/large 733 801 719 641 635

beng/1-8 54 54 54 60 54 60 55 54

beng/9-10 13 13 13 14 13 14 13 13

class 1/20 71 71 71 71 71 71 71 71 71

class 1/40 134 134 134 134 136 134 136 134 134

class 1/60 200 200 200 200 206 200 203 200 200

class 1/80 275 275 275 275 285 275 281 275 275

class 1/100 317 317 317 317 341 324 333 317 317

class 2/20 10 10 10 10 10 10 10 10 10

class 2/40 19 19 19 19 20 19 20 19 19

class 2/60 25 25 25 25 28 25 27 25 25

class 2/80 31 31 31 31 36 31 35 31 31

class 2/100 39 39 39 39 42 39 42 39 39

class 3/20 51 51 51 51 51 51 51 51 51

class 3/40 94 94 94 98 94 97 94 94

class 3/60 139 139 139 149 140 147 140 139

class 3/80 189 189 189 206 204 204 190 189

class 3/100 223 224 223 251 249 243 223 223

class 4/20 10 10 10 10 10 10 10 10

class 4/40 19 19 19 19 19 19 19 19

class 4/60 25 23 25 28 25 27 25 24

class 4/80 31 31 31 36 33 36 31 31

class 4/100 37 37 38 42 39 42 37 37

class 5/20 65 65 65 65 65 65 66 65

class 5/40 119 119 119 123 120 122 119 119

class 5/60 180 180 180 188 190 185 180 180

class 5/80 247 247 247 259 270 253 247 247

class 5/100 281 284 282 309 328 305 282 281

class 6/20 10 10 10 10 10 10 10 10

class 6/40 16 17 17 19 17 19 17 16

class 6/60 21 21 21 23 22 23 21 21

class 6/80 30 30 30 32 30 31 30 30

class 6/100 33 32 34 39 37 38 32 32

class 7/20 55 55 55 55 55 55 55 55

class 7/40 111 111 111 116 113 116 111 111

class 7/60 158 159 159 165 162 162 159 158

class 7/80 232 232 232 239 240 236 232 232

class 7/100 271 271 271 284 293 282 271 271

class 8/20 58 58 58 58 58 58 58 58

class 8/40 113 113 113 115 114 115 113 113

class 8/60 161 161 161 168 167 166 161 161

class 8/80 224 224 224 233 236 231 224 224

class 8/100 278 277 278 292 298 286 277 277

class 9/20 143 143 143 143 143 143 143 143

class 9/40 278 278 278 278 278 278 278 278

class 9/60 437 437 437 437 437 437 437 437

class 9/80 577 577 577 577 577 577 577 577

class 9/100 695 695 695 695 695 695 695 695

class 10/20 42 42 42 43 42 42 42 42

class 10/40 74 74 74 79 74 77 74 74

class 10/60 100 101 100 112 105 111 101 100

class 10/80 128 128 129 145 143 142 129 128

class 10/100 158 160 159 183 184 179 159 159

asqas 8 8 8 8 8

# best c&b 49 44 43 13 14 27 15 41 50

available. The best result of the RLS with f

(col-

umn f

⋆

) is also optimal on class 1/40. The exact same

situation can be observed on the 2BP|O|F, but now

beng/1-8 is the only instance group for which P&C

results are available where RLS- f

is worse (on aver-

age). The best of ﬁve runs of the same algorithm do

ﬁnd the optimal solutions for beng/1-8 as well.

It becomes obvious from both tables that f

leads

to much better results compared to f

. This is ex-

pected. What is unexpected is that FRLS is consis-

tently worse than RLS. RLS is prone to get stuck at

local optima. From the tables, we also know that the

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

100 200 300 400 500 600 700 800

mean life (log-scaled)

FRLS-f₁

FRLS-f₇

RLS-f₁

RLS-f₇

2BP|O|F

100 200 300 400 500 600 700 800

mean life (log-scaled)

FRLS-f₁

FRLS-f₇

RLS-f₁

RLS-f₇

2BP|R|F

Figure 2: The average over the index life of the objective function evaluation where the last improving move was made by

the different algorithms, plotted over the total number T of item instances to pack. The plot for the problem variant without

rotation (2BP|O|F) is on the left and the one for the variant with rotation (2BP|R|F) is on the right.

7 12

10 5

2BP|O|F

12 10

2BP|R|F

Figure 3: Two optimal result of RLS- f

on class 1/20-4 for the problem variant without rotation (2BP|O|F) on the left and for

the variant with rotation (2BP|R|F, on the right).

best-of-ﬁve-runs result ( f

⋆

columns) is better than the

average results ( f

columns) for RLS. One would as-

sume that this must be due to RLS getting stuck at dif-

ferent local optima. (In this case, restarting the algo-

rithm, which is equivalent to running it ﬁve times and

taking the best result, would be a good idea.) Then

why does FRLS, which has been shown to deliver

much better results in previous works on N P -hard

problems, perform worse than RLS? Should it not be

able to escape from the local optima?

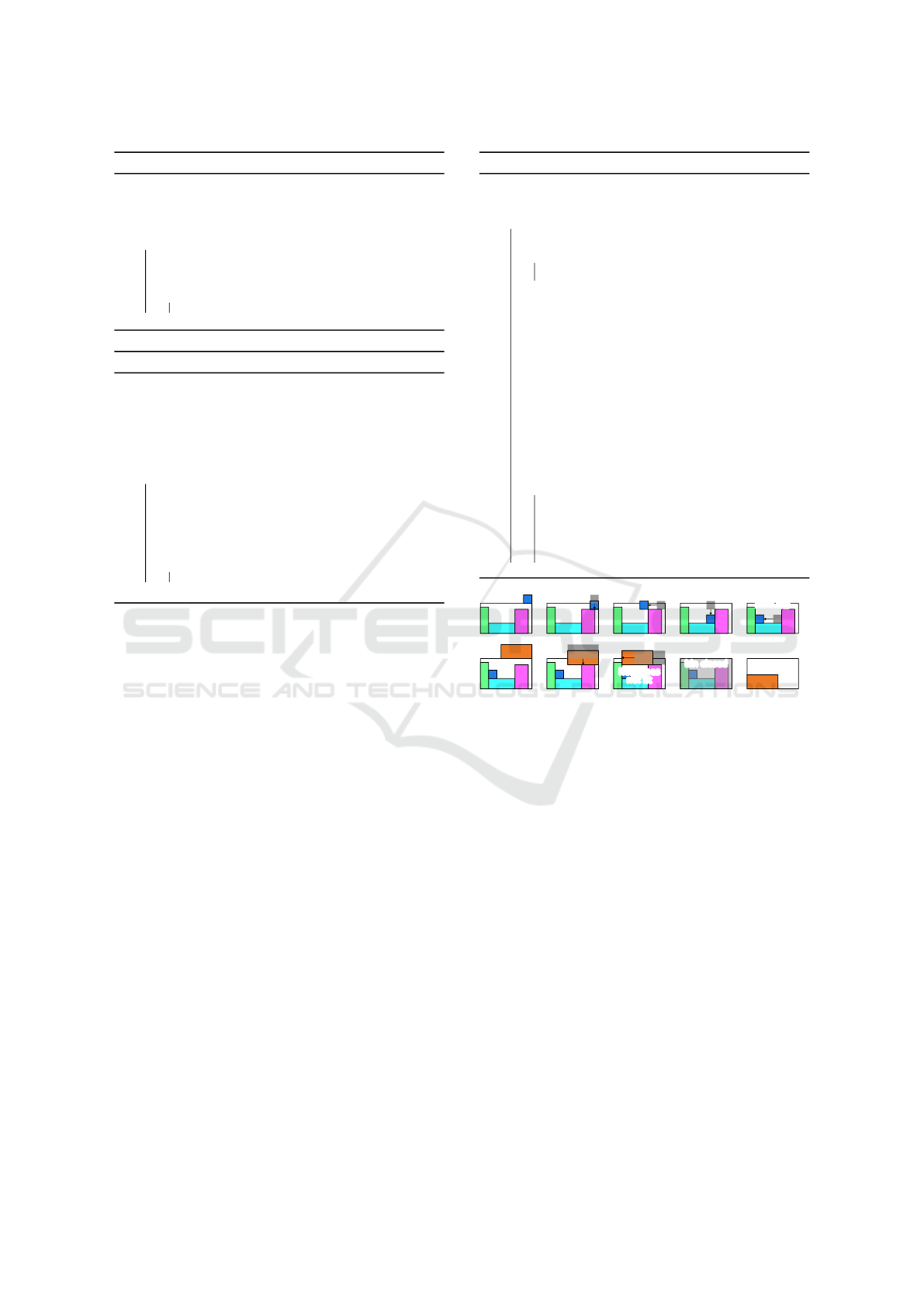
Now, in our experiments, we use a generous bud-

get of 10

objective function evaluations per run. If

RLS would get stuck at local optima, then we would

expect that it would stop improving much earlier. The

index life of the objective function evaluation where

its last improving move takes place would be much

lower than 10

. Of course, it will also be lower on

small-scale instances where it already ﬁnds the opti-

mal solution and we know that it does so on several

instances from our tables. Either way, in Figure 2 we

plot this index over the total number T of item in-

stances to pack. In stark contrast to the reasonable ex-

pectation regarding the behavior of RLS- f

, we notice

that the algorithm keeps ﬁnding improvements until

the end of the computational budget, consistently over

all not-too-small problem scales and for both investi-

gated objective functions. RLS- f

does not get stuck

in local optima. As a result, FRLS cannot outperform

it, because its strength is exactly to avoid getting stuck

at local optima and it trades in speed for obtaining this

ability.

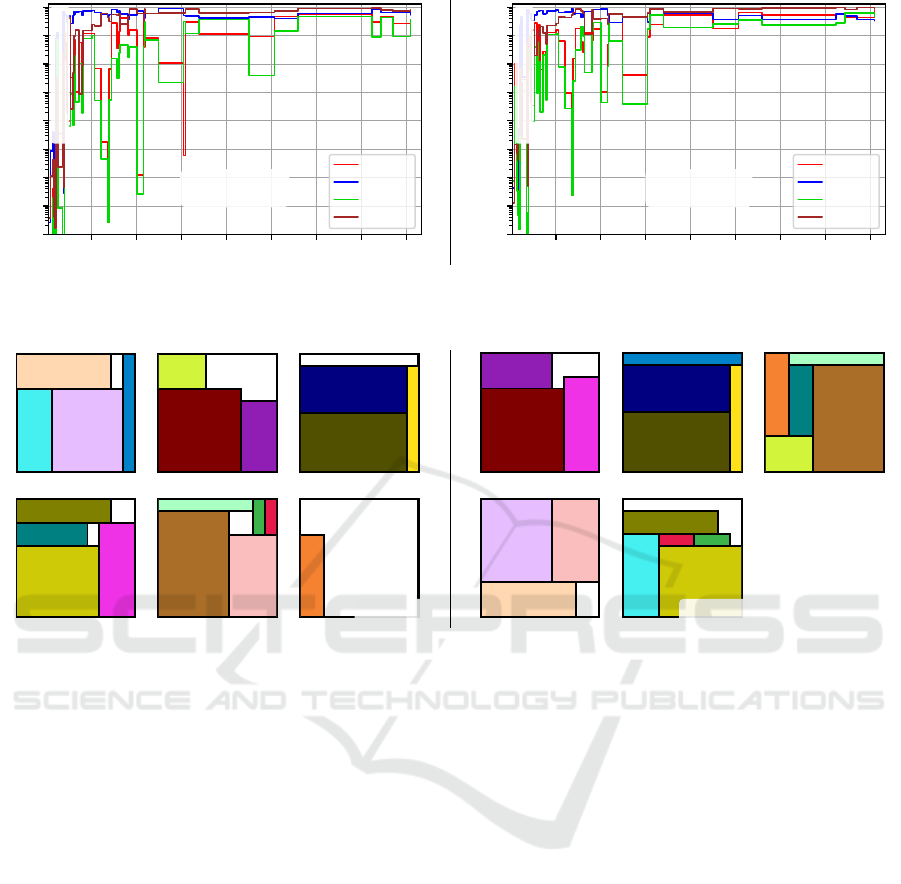
Finally, we illustrate two packings discovered by

RLS- f

on instance class 1/20-4. From Table 1 and

Table 2, we know that RLS- f

ﬁnds results of the

same average quality over all class 1/20 instances as

P&C. Since P&C is an exact method always return-

ing the optimal solution, the results of RLS- f

are

therefore also optimal in average and, hence, opti-

mal in each run on each of the class 1/20 instances.

The optimal packing in Figure 3 for the problem vari-

ant 2BP|O|F where items have a ﬁxed orientation and

cannot be rotated and requires six bins. The fact that

lots of space in the bins is left unused hints towards

the problem being rather easy, as this would proba-

bly allow us to place the items slightly differently and

still get the optimal number of bins. Figure 3 also

Randomized Local Search for Two-Dimensional Bin Packing and a Negative Result for Frequency Fitness Assignment

shows the optimal packing for the same instance but

for 2BP|R|F, illustrating that one bin can be saved if

item rotation is permitted.

6 CONCLUSIONS

Our experiments conﬁrmed that randomized local

search (RLS) performs very well on two important

variants of the 2BP, the 2BP|R|F and the 2BP|O|F.

What does this mean? Our results indicate that RLS

does not get stuck at local optima, or, at least does so

much later than one would expect. The implications

of this are interesting: If RLS does not get suck at

local optima, then any mechanism that aims to avoid

getting stuck at local optima is essentially useless. If

RLS does not get stuck at local optima, then extend-

ing it to tabu search by introducing tabu and aspira-

tion criteria to avoid local optima could not yield a

performance improvement. If RLS does not get stuck

at local optima, then sometimes accepting worse so-

lutions, as simulated annealing would do, could not

yield better results. If RLS does not get stuck at local

optima, then FRLS cannot outperform it. The latter

is what we observed in our experiments here as well,

while doing tests with tabu search and simulated an-

nealing will be part of our future work. Also, this

could be the reason why the very simple RLS seems

to be competitive to much more sophisticated algo-

rithms.

Now it seems unlikely that an N P -hard problem

does not have local optima. But maybe the bench-

mark instances in the 2DPackLib are not challenging

enough. So from this perspective, we would suggest

that creating harder instances is indeed needed. This,

too, is part of our future work.

Therefore, while this work presents a ﬁrst negative

result for Frequency Fitness Assignment (FFA), this

ﬁnding has to be taken with a grain of salt: We will

revisit the problem once we have a set of instances

of which we can conﬁrm that RLS cannot solve them

well.

ACKNOWLEDGEMENTS

The authors acknowledge support from the Project

of National Natural Science Foundation of China

62406095, the Project of Natural Science Foundation

of Anhui Province 2308085MF213, the Key Research

Plan of Anhui Province 2022k07020011, the Univer-

sity Scientiﬁc Research Innovation Team Project of

Anhui Province 2022AH010095, as well as the Hefei

Specially Recruited Foreign Expert program and the

Hefei Foreign Expert Ofﬁce program.

REFERENCES

Bengtsson, B.-E. (1982). Packing rectangular pieces

– A heuristic approach. The Computer Journal,

25(3):353–357.

Berkey, J. O. and Wang, P. Y. (1987). Two-

dimensional ﬁnite bin-packing algorithms. Journal

of the Operational Research Society, 38(5):423–429.

doi:10.1057/jors.1987.70.

Beyaz, M., Dokeroglu, T., and Cosar, A. (2015). Ro-

bust hyper-heuristic algorithms for the ofﬂine

oriented/non-oriented 2D bin packing prob-

lems. Applied Soft Computing, 36:236–245.

doi:10.1016/j.asoc.2015.06.063.

Blum, C. and Schmid, V. (2013). Solving the 2D

bin packing problem by means of a hybrid evolu-

tionary algorithm. In Alexandrov, V., Lees, M.,

Krzhizhanovskaya, V. V., Dongarra, J. J., and Sloot, P.

M. A., editors, International Conference on Computa-

tional Science (ICCS’13), June 5–7, 2013, Barcelona,

Spain, volume 18 of Procedia Computer Science,

pages 899–908, Amsterdam, The Netherlands. Else-

vier. doi:10.1016/j.procs.2013.05.255.

Boschetti, M. A. and Mingozzi, A. (2003). The two-

dimensional ﬁnite bin packing problem. Part II: New

lower and upper bounds. 4OR – the Quarterly Jour-

nal of the Belgian, French and Italian Operations Re-

search Societies, 1(2):135–147. doi:10.1007/s10288-

002-0006-y.

Braam, F. and van den Berg, D. (2022). Which rectangle

sets have perfect packings? Operations Research Per-

spectives, 9(100211). doi:10.1016/j.orp.2021.100211.

Cid-Garcia, N. M. and Rios-Solis, Y. A. (2020). Po-

sitions and covering: A two-stage methodol-

ogy to obtain optimal solutions for the 2d-bin

packing problem. PLoS ONE, 15(4):e0229358.

doi:10.1371/journal.pone.0229358.

de Bruin, E., Thomson, S. L., and van den Berg, D.

(2023). Frequency ﬁtness assignment on JSSP: A

critical review. In Correia, J., Smith, S. L., and

Qaddoura, R., editors, Proceedings of the 26th Eu-

ropean Conference on Applications of Evolutionary

Computation (EvoApplications’23), Held as Part of

EvoStar 2023, April 12-14, 2023, Brno, Czech Repub-

lic, volume 13989 of Lecture Notes in Computer Sci-

ence, pages 351–363, Cham, Switzerland. Springer.

doi:10.1007/978-3-031-30229-9 23.

Dell’Amico, M., Martello, S., and Vigo, D. (2002). A lower

bound for the non-oriented two-dimensional bin pack-

ing problem. Discrete Applied Mathematics, 118(1-

2):13–24. doi:10.1016/S0166-218X(01)00253-0.

Gonc¸alves, J. F. and Resende, M. G. (2013). A bi-

ased random key genetic algorithm for 2D and

3D bin packing problems. International Jour-

nal on Production Economics, 145(2):500–510.

doi:10.1016/j.ijpe.2013.04.019.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

Iori, M., de Lima, V. L., Martello, S., Miyazaw, F. K.,

and Monaci, M. (2021). Exact solution techniques

for two-dimensional cutting and packing. European

Journal of Operational Research, 289(2):399–415.

doi:10.1016/j.ejor.2020.06.050.

Iori, M., de Lima, V. L., Martello, S., and Monaci, M.

(2022). 2DPackLib: A two-dimensional cutting and

packing library. Optimization Letters, 16(2):471–480.

doi:10.1007/s11590-021-01808-y.

Johnson, D. S., Papadimitriou, C. H., and Yannakakis,

M. (1988). How easy is local search? Jour-

nal of Computer and System Sciences, 37(1):79–100.

doi:10.1016/0022-0000(88)90046-3.

Kierkosz, I. and Luczak, M. (2013). A hybrid evolutionary

algorithm for the two-dimensional packing problem.

Central European Journal of Operations Research,

22(4):729–753.

Lee, L.-S. (2008). A genetic algorithm for two-

dimensional bin packing problem. MathDigest: Re-

search Bulletin of Institute for Mathematical Re-

search, 2(1):34–39. http://psasir.upm.edu.my/id/

eprint/12464/1/Artikel 6 vol2 no1.pdf.

Li, X. and Zhang, K. (2018). Single batch process-

ing machine scheduling with two-dimensional

bin packing constraints. International Jour-

nal of Production Economics, 196:113–121.

doi:10.1016/j.ijpe.2017.11.015.

Li, Y., Sang, H., Xiong, X., and Li, Y. (2021).

An improved adaptive genetic algorithm for two-

dimensional rectangular packing problem. Applied

Sciences, 11(1):413. doi:10.3390/app11010413.

Liang, T., Wu, Z., L

assig, J., van den Berg, D., Thom-

son, S. L., and Weise, T. (2024). Addressing the

traveling salesperson problem with frequency ﬁtness

assignment and hybrid algorithms. Soft Computing.

doi:10.1007/s00500-024-09718-8.

Liang, T., Wu, Z., L

assig, J., van den Berg, D., and

Weise, T. (2022). Solving the traveling salesper-

son problem using frequency ﬁtness assignment. In

Ishibuchi, H., Kwoh, C., Tan, A., Srinivasan, D.,

Miao, C., Trivedi, A., and Crockett, K. A., edi-

tors, IEEE Symposium Series on Computational In-

telligence (SSCI’22), December 4–7, 2022, Singa-

pore, pages 360–367, Piscataway, NJ, USA. IEEE.

doi:10.1109/SSCI51031.2022.10022296.

Liu, D. and Teng, H. (1999). An improved BL-algorithm for

genetic algorithm of the orthogonal packing of rect-

angles. European Journal of Operational Research,

112(2):413–420. doi:10.1016/S0377-2217(97)00437-

Lodi, A., Martello, S., and Vigo, D. (2002). Recent

advances on two-dimensional bin packing problems.

Discrete Applied Mathematics, 123(1–3):379–396.

doi:10.1016/S0166-218X(01)00347-X.

Lodi, A., Martello, S., and Vigo, D. (2004).

TSpack: A uniﬁed tabu search code for multi-

dimensional bin packing problems. Annals

of Operations Research, 131(1–4):203–213.

doi:10.1023/B:ANOR.0000039519.03572.08.

Ma, N. and Zhou, Z. (2017). Mixed-integer program-

ming model for two-dimensional non-guillotine bin

packing problem with free rotation. In 4th Interna-

tional Conference on Information Science and Control

Engineering (ICISCE), July 21-23, 2017, Changsha,

China, pages 456–460, Piscataway, NJ, USA. IEEE.

doi:10.1109/ICISCE.2017.102.

Macedo, R., Alves, C., and Val

erio de Carvalho,

J. M. (2010). Arc-ﬂow model for the two-

dimensional guillotine cutting stock problem. Com-

puters & Operations Research, 37(6):991–1001.

doi:10.1016/j.cor.2009.08.005.

Martello, S. and Vigo, D. (1998). Exact solution of the two-

dimensional ﬁnite bin packing problem. Management

Science, 44(3):388–399. doi:10.1287/mnsc.44.3.388.

Monaci, M. and Toth, P. (2006). A set-covering-

based heuristic approach for bin-packing problems.

INFORMS Journal on Computing, 18(1):1–134.

doi:10.1287/ijoc.1040.0089.

Neumann, F. and Wegener, I. (2007). Randomized lo-

cal search, evolutionary algorithms, and the minimum

spanning tree problem. Theoretical Computer Sci-

ence, 378(1):32–40. doi:10.1016/j.tcs.2006.11.002.

Parre

no, F., Alvarez-Vald

es, R., Oliveira, J. F., and

Tamarit, J. M. (2010). A hybrid GRASP/VND al-

gorithm for two- and three-dimensional bin pack-

ing. Annals of Operations Research, 179(1):203–220.

doi:10.1007/s10479-008-0449-4.

Pejic, I. and van den Berg, D. (2020). Monte carlo

tree search on perfect rectangle packing problem in-

stances. In Coello, C. A. C., editor, Genetic and

Evolutionary Computation Conference (GECCO’20),

Companion Volume, July July 8-12, 2020, Canc

un,

Mexico, pages 1697–1703, New York, NY, USA.

ACM. doi:10.1145/3377929.3398115.

Pinto, M., Silva, C., Th

urer, M., and Moniz, S. (2024).

Survey in operations research and management sci-

ence. nesting and scheduling optimization of addi-

tive manufacturing systems: Mapping the territory.

Computers & Operations Research, 165(106592).

doi:10.1016/j.cor.2024.106592.

Russell, S. J. and Norvig, P. (2002). Artiﬁcial Intelligence:

A Modern Approach (AIMA). Prentice Hall Interna-

tional Inc., Upper Saddle River, NJ, USA, 2 edition.

Terashima-Mar

ın, H., Z

arate, C. J. F., Ross, P., and

Valenzuela-Rend

on, M. (2007). Comparing two

models to generate hyper-heuristics for the 2D-

regular bin-packing problem. In Lipson, H., edi-

tor, Genetic and Evolutionary Computation Confer-

ence (GECCO’07), July 7-11, 2007, London, UK,

pages 2182–2189, New York, NY, USA. ACM.

doi:10.1145/1276958.1277377.

van den Berg, D., Braam, F., Moes, M., Suilen, E., and

Bhulai, S. (2016). Almost squares in almost squares:

Solving the ﬁnal instance. In Bhulai, S. and Se-

manjski, I., editors, DATA ANALYTICS 2016: The

Fifth International Conference on Data Analytics, Oc-

tober 9-13, 2026, Venice, Italy, Wilmington, DE,

USA. International Academy, Research, and Indus-

try Association (IARIA). https://math.vu.nl/

∼

sbhulai/

publications/data analytics2016b.pdf.

Weise, T., Chiong, R., Tang, K., L

assig, J., Tsutsui, S.,

Chen, W., Michalewicz, Z., and Yao, X. (2014a).

Randomized Local Search for Two-Dimensional Bin Packing and a Negative Result for Frequency Fitness Assignment

Benchmarking optimization algorithms: An open

source framework for the traveling salesman problem.

IEEE Computational Intelligence Magazine, 9(3):40–

52. doi:10.1109/MCI.2014.2326101.

Weise, T., Li, X., Chen, Y., and Wu, Z. (2021a).

Solving job shop scheduling problems without us-

ing a bias for good solutions. In Genetic and

Evolutionary Computation Conference (GECCO’21),

July 10-14, 2021, Lille, France, Companion Vol-

ume, pages 1459–1466, New York, NY, USA. ACM.

doi:10.1145/3449726.3463124.

Weise, T., Wan, M., Tang, K., Wang, P., Devert, A.,

and Yao, X. (2014b). Frequency ﬁtness assignment.

IEEE Transactions on Evolutionary Computation,

18(2):226–243. doi:10.1109/TEVC.2013.2251885.

Weise, T. and Wu, Z. (2023). Replicable self-documenting

experiments with arbitrary search spaces and algo-

rithms. In Genetic and Evolutionary Computa-

tion Conference Companion (GECCO’23 Compan-

ion), July 15-19, 2023, Lisbon, Portugal, New York,

NY, USA. ACM. doi:10.1145/3583133.3596306.

Weise, T., Wu, Z., Li, X., and Chen, Y. (2021b). Fre-

quency ﬁtness assignment: Making optimization al-

gorithms invariant under bijective transformations

of the objective function value. IEEE Transac-

tions on Evolutionary Computation, 25(2):307–319.

doi:10.1109/TEVC.2020.3032090.

Weise, T., Wu, Z., Li, X., Chen, Y., and L

assig, J. (2023).

Frequency ﬁtness assignment: Optimization without

bias for good solutions can be efﬁcient. IEEE Transac-

tions on Evolutionary Computation, 27(4):980–992.

doi:10.1109/TEVC.2022.3191698.

Wong, L. and Lee, L. S. (2009). Heuristic placement

routines for two-dimensional bin packing problem.

Journal of Mathematics and Statistics, 5(4):334–341.

https://www.thescipub.com/pdf/jmssp.2009.334.341.

Zhao, R., Liang, T., Wu, Z., van den Berg, D., Th

urer,

M., and Weise, T. (2024). Randomized local

search on the 2D rectangular bin packing prob-

lem with item rotation. In Genetic and Evolu-

tionary Computation Conference (GECCO’24 Com-

panion), July 14–18, 2024, Melbourne, VIC, Aus-

tralia, pages 235–238, New York, NY, USA. ACM.

doi:10.1145/3638530.3654139.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications