
A Neural Network-Based Controller Towards Achieving
Near-Natural Gait in Transfemoral Amputees
Zunaed Kibria
*
and Sesh Commuri
†
Electrical and Biomedical Department, University of Nevada - Reno, Reno, Nevada, U.S.A.
Keywords: Prosthetic Control, Radial Basis Function Based Neural Network (RBFNN), Gait Analysis.
Abstract: Achieving proper post-amputation mobility in an individual is extremely important to ensure the health of the
residual limb and the quality of life of an individual. Traditionally, prosthetic limbs were designed to primarily
support the weight of the individual and replicate the look and feel of the natural limb. Powered prosthetic
devices are typically based on classical control and cannot adapt to changing user requirements. A critical
challenge in controller design is that, unlike tracking controllers, the desired trajectory for the prosthetic joint
is unknown. Improper control can lead to asymmetry in the gait of intact and amputated sides, which in turn
can have adverse health consequences. In this paper, an intelligent controller for above-knee prosthesis is
proposed that can generate pseudo-trajectories for the joints, learn the dynamics of the prosthetic limb in real-
time, and track these pseudo-trajectories to reduce the asymmetry in gait between the intact and amputated
side. Mathematical analysis shows that the method is stable and can adapt to changing user gaits. Numerical
simulations and Monte Carlo analysis show that the performance of the controller is robust to variations in
dynamics and user requirements, and results in near-natural gait for the individual.
1 INTRODUCTION
Amputation of the lower limb is performed as a
consequence of traumatic injuries or diseases such as
diabetes and vascular disorders (Gorden et al., 2022).
After amputation, the residual limb is fitted with a
socket, and a prosthetic limb is attached to the socket.
Traditionally, such prosthetic limbs are designed to
provide weight bearing and limited mobility. Modern
powered devices can help in locomotion by providing
regenerative energy as well as providing custom fit
for the individual. However, an individual seldom
regains natural locomotion as these devices cannot
recognize and adapt to changing user gait or
environmental conditions.
Effective control mechanisms are essential for
improving prosthetic gait. Passive devices, acting as
springs or dampers, provide weight support but limit
mobility and increase energy expenditure during
locomotion (Feng & Wang, 2017; Sharma et al.,
2022). Semi-active and active prostheses offer some
improvement, but they cannot adjust to different gait
patterns (Saini et al., 2020) and rely on traditional
*
https://www.linkedin.com/in/zunaed-kibria-984743107/
†
https://www.unr.edu/ebme/people/sesh-commuri
control methods which cannot compensate for system
nonlinearities (Elery et al., 2020; Lenzi et al., 2019).
Researchers also explored several adaptive control
methods (Embry & Gregg, 2021; Gao et al., 2021).
Model reference adaptive control performs best
among them but is based on a linearized model with
limited range of performance and does not provide a
symmetric gait (Pagel et al., 2017) .
In this paper, a neural network-based control
strategy is pursued to reduce the asymmetry in gait
between the intact and amputated side of an amputee.
Gait is primarily divided into two phases: stance and
swing. The stance phase is further subdivided into
phases including Heel Strike, Loading Response, Mid
Stance, Terminal Stance, and Pre-Swing, while the
swing phase comprises Toe Off, Mid Swing, and
Terminal Swing. During gait, the body weight is
supported by a single leg from ‘Loading Response’ to
‘Terminal Stance’ phases, and the time difference
between these phases is defined as ‘single support
time’. When the difference in single support time
between the intact and prosthetic side is minimized, it
promotes smoother weight transfer between the legs,
Kibria, Z. and Commuri, S.
A Neural Network-Based Controller Towards Achieving Near-Natural Gait in Transfemoral Amputees.
DOI: 10.5220/0012888700003822
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 201-208
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
201

reduces gait asymmetry, aids amputees in achieving a
more natural and balanced gait.
The following approach is adopted to implement
a learning controller that can adapt to user
requirements and guarantee near natural gait in an
individual:
• Develop the dynamical model of the prosthetic
leg system to determine the nature of unknown
nonlinear functions that influence the dynamics.
• Desired trajectories for the knee and ankle joints
are first selected based on the natural
displacement profile of these joints in an intact
individual and then parameterize in terms of the
gait speed.
• Use a visco-elastic model to estimate ground
reaction force and reaction torques at the joints,
and then compensate for them in the system
dynamics.
• A radial basis function based neural network
(RBFNN) is selected to learn the unknown
nonlinear parameters in the dynamics due to its
efficiency and lower computational cost
(Schilling et al., 2001).
• Cost function reflecting the asymmetry between
the gait of the intact and prosthetic side is used to
perform Lyapunov analysis. Weight update laws
for the neural network are determined so that the
unknown/changing dynamics are estimated
while ensuring stability of the controlled system
and minimizing the cost, i.e., the asymmetry in
the gait.
Numerical simulations are used to demonstrate
the ability of the control strategy to accommodate
variations in height, weight, gait speed, and ground
reaction force. Analysis shows that the time duration
of the single support portion of the gait is improved
with the proposed control strategy, thereby
minimizing the asymmetry in the gait.
The rest of the paper is organized as follows – in
section 2, gait requirements for transfemoral
prosthesis, detailed formulation for control
mechanism, and stability of the closed loop system
are presented. Numerical simulations and Monte
Carlo analysis to evaluate the ability of the proposed
control scheme are demonstrated in section 3. The
conclusions of the paper and future work are
presented in section 4.
2 CONTROL OF THE
PROSTHESIS JOINT
2.1 Gait Requirement for
Transfemoral Prosthesis
The nominal displacement profiles for the knee and
ankle joints in a healthy individual during normal gait
is shown in Figure 1(a). It is desirable for the
prosthetic limb to track similar displacement profile
in order to achieve near normal gait. Similar to the
technique followed in (Winter, 2009), we can
calculate the joint angles of lower limb as shown in
Figure 1(b). Assuming that the user is walking with
upright posture (q_tr = 90◦) and the joints follow the
nominal displacement profiles mentioned in Figure
1(a), we can calculate the ideal foot position relative
to the ground during gait (Figure 1(c)). Postural
balance relies on smooth weight transfer between the
legs. If a prosthetic device effectively tracks the
movements of the knee, ankle, and foot to closely
replicate those on the intact side, it would lead to
improved weight transfer and reduce gait asymmetry.
(It is to be noted that the analysis is limited to motion
in the sagittal plane.)
2.2 System Model
The dynamics of knee-ankle prosthetic system
(Figure 1(d)) can be expressed as:
M
(
q
)
q
+V
(
q,q
)
q +G
(
q
)
+F
(
q
)
+τ
=τ+τ
(1)
In “(1)”, M
(
q
)
stands for the inertia matrix of the
knee-ankle coupled dynamics. V
(
q,q
)
denotes the
coriolis/ centripetal matrix of the system, G
(
q
)
is a
vector that represents the effect of gravity, frictional
terms are represented by the matrix F
(
q
)
, and the
disturbance torque is labeled by τ
. Torque generated
by each joint is represented by τ and τ
is the ground
reaction torque which is generated as a result of the
interaction of the foot with the ground. The control
input to the system is τ+τ
=
τ
+τ
()
τ
+τ
()
∈ℝ
. Here, subscript ‘k’
stands for knee joint and subscript ‘a’ stands for ankle
joint. Detailed description of the terms in “(1)” are
given in (Kibria & Commuri, 2024). A block diagram
of the proposed neural network control system is
shown in Figure 1(e).
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
202

2.3 Parameterization of the Gait
Profiles and Ground Reaction
Torque
Nominal displacement profiles for knee and ankle
joints during gait are generated according to “(2)”,
where the subscript ‘i’ refers to either knee or ankle
joint:
𝑞
()
(𝑡) = 𝑎
()
+{𝑎
()
cos(𝑘
𝜔
()
𝑡)
+𝑏
()
sin(𝑘
𝜔
()
𝑡)};
(2)
Here, displacement profile time instance is
represented by ‘t’. We can obtain the parameters 𝑎
()
,
𝑎
()
, 𝑏
()
, 𝜔
()
through the synthesis of the Fourier
series. As the hip is under biological control, gait based
desired trajectory for ‘knee’ and ‘ankle’ can be
generated from hip joint movement and used as
kinematic reference as following:
𝑞
()
=
𝑞
()
𝑞
()
𝑞
()
; 𝑞
()
=
𝑞
𝑞
;
𝑞
()
=𝑞
𝑞
; 𝑞
()
=𝑞
𝑞
;
(3)
The gait-based profiles are labeled with superscript
(·)
and are generated by determining the user’s intent
during the gait cycle. To compute the control input τ+
τ
, the ideal kinematic profiles of knee-ankle joints
𝑞
()
=
𝑞
()
𝑞
()
𝑞
()
are not available.
The differences between the ideal kinematic
references and the gait-based references are defined as:
𝑞
()
=
𝑞
()
𝑞
()
𝑞
()
; 𝑞
()
=𝑞
()
–𝑞
()
;
𝑞
()
=𝑞
()
–𝑞
()
; 𝑞
()
=𝑞
()
–𝑞
()
;
(4)
In practice, accurate evaluation of ground reaction
torque τ
is not feasible. Therefore, gait-based ground
reaction torques τ
acting on knee and ankle joints are
estimated from known empirical models.
The estimation errors between estimated GRT τ
and actual τ
()
at the knee or ankle joints are defined
as:
τ
()
= τ
()
–τ
()
;
(5)
The actual ground reaction torque τ
()
at knee or
ankle joint can be approximated by following equation
(Mai & Commuri, 2016):
τ
()
(
t
)=d
()
F
()
(
t
)+d
()
F
()
(
t
) ;
(6)
in which ‘t’ is the gait time, F
()
indicates the
vertical ground reaction force and F
()
is the horizontal
ground reaction forces acting on the knee or ankle
joints. d
()
means the distances between knee joint or
ankle joint to the center of pressure (ground contact
point) during gait. The ground reaction forces can be
computed from a nonlinear spring-damper system
equations mentioned in (Peasgood et al., 2006):
𝐹
()
=𝜅
̅
(𝑧
)
+𝑐
𝑧
𝐹
()
=µ𝐹
𝑠𝑔𝑛(𝑥
) ;
(7)
in which, z
and z
mean foot penetration and
penetration rate at the ground contact point. 𝜅̅, e, c
, µ,
sgn(·), x
denote respectively- spring coefficient,
spring exponent, damping coefficient, friction
coefficient, signum function, and the horizontal
velocity.
Remark 1. In “(2)”, the sine and cosine functions are
bounded; it is it is assumed that the reference
kinematic pattern and the gait based kinematic pattern
q
()
are also bounded as the residual limb is under
active control of the user to follow specific periodic
gait profile to reduce the energy consumption during
a walk (Ackermann & Bogert, 2010). Hence, we can
assume that q
()
term is also bounded as it is the
difference between two bounded terms.
Remark 2. In “(7)”, the ground is assumed to be firm
and therefore present finite penetration of the foot.
Therefore, the terms F
()
and F
()
terms in equation
(7) are bounded and gait based τ
()
in (5) is also
bounded. Since weight of the individual is known, the
actual ground reaction torque τ
()
is also bounded.
Therefore, τ
()
= τ
()
–τ
()
is also bounded.
2.4 Cost Function for Single Support
Time
To evaluate the performance of the controller in terms
of single support time, a cost function is defined as:
𝐽
(t) =
𝑒
(𝑡
)
+
𝑒
(𝑡
)
(8)
Here, 𝑒
(𝑡
) and 𝑒
(𝑡
) are the foot angle
error of the prosthetic leg from desired foot angle at
‘Loading Response’ and ‘Terminal Stance’ phases.
Time lapse between these phases of the gait is
considered as the single support time 𝑡
.
𝑡
=𝑡
–𝑡
(9)
A Neural Network-Based Controller Towards Achieving Near-Natural Gait in Transfemoral Amputees
203
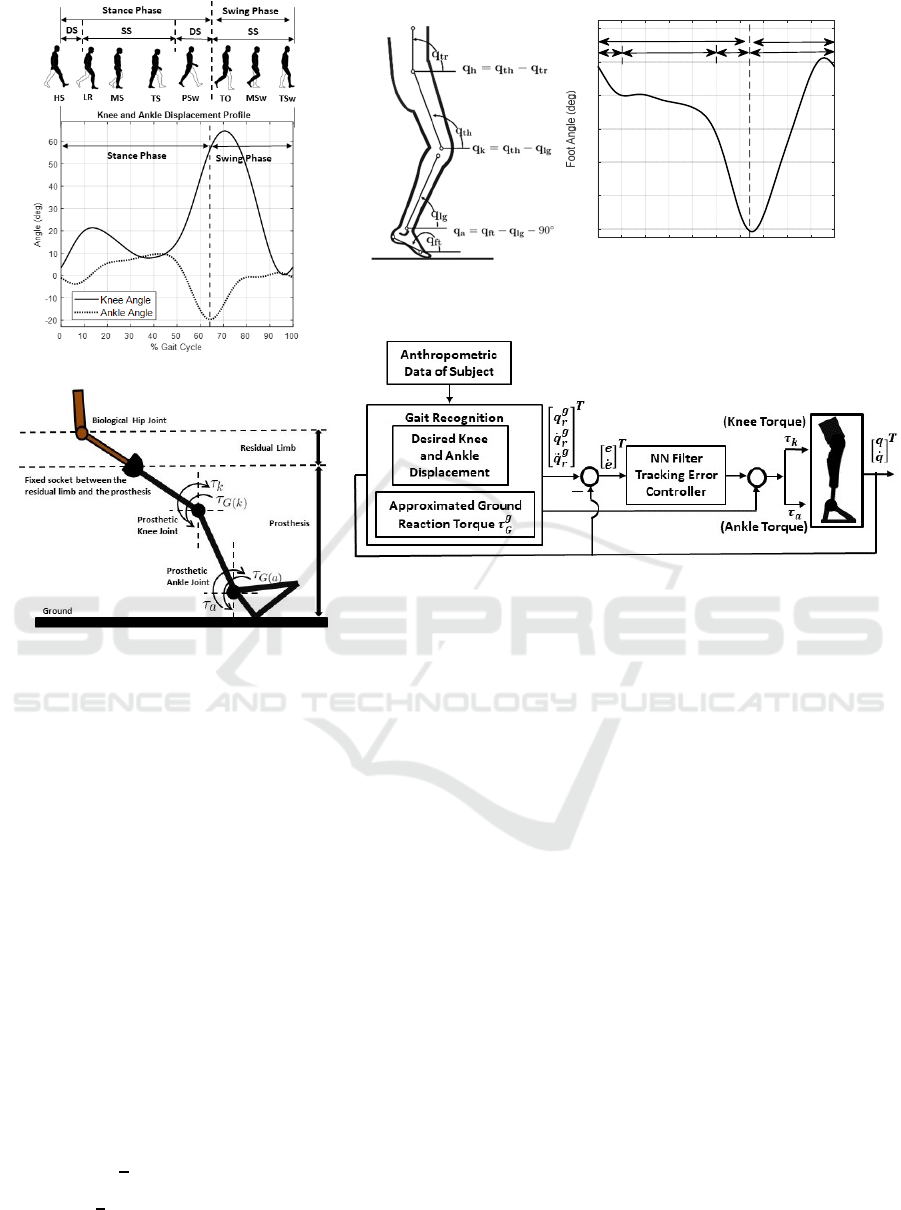
(b) (c)
(a)
(e)
(d)
Figure 1: (a) Reference gait profiles of knee and ankle joints; HS = Heel Strike, LR = Loading Response, MS = Mid Stance,
TS = Terminal Stance, PSw = Pre-Swing, TO = Toe Off, MSW = Mid Swing, TSw = Terminal Swing. DS = Double Support,
SS = Single Support.
(b) Angle calculation for leg joints during a gait. 𝑞
= trunk angle, 𝑞
= hip angle, 𝑞
= thigh angle, 𝑞
= shank angle, 𝑞
= knee angle, 𝑞
= ankle angle, 𝑞
= foot angle. 𝑞
and 𝑞
are +ve for Flexion and -ve for Extension, 𝑞
is +ve for
Dorsiflexion and -ve for Planter Flexion.
(c) Foot angle relative to the ground. DS = Dual Support, SS = Single Support.
(d) Link-segment representation of the prosthetic leg connected to the residual limb.
(e) Block diagram of NN controlled knee-ankle Prosthetic.
in which 𝑡
and 𝑡
are the time instances of the
prosthetic leg at ‘Loading Response’ and ‘Terminal
Stance’ phases. If we can minimize 𝑒
at these time
instances then it will in turn reduce the single support
time error of the prosthetic leg, thereby reducing gait
asymmetry. Since the cost function 𝐽
is a function
of 𝑒
, so minimizing the cost function will result in
reducing gait asymmetry.
Using Figure 1(b) the augmented cost function
can be written as:
J
(t)=
𝑒
(𝑡
)–𝑒
(𝑡
)
+
𝑒
(𝑡
)–𝑒
(𝑡
)
(10)
2.5 Control Equations
In order for the prosthetic system to ensure near
natural gait cost function J
needs to be small. From
(14), we see that J
= 𝑓𝑐𝑛(𝑒
,𝑒
). So, if the
controller can reduce the knee and ankle angle error
then in tern it will reduce J
. To make the prosthetic
system follow a reference trajectory 𝑞
()
, at first the
tracking error ‘e(t)’ and the filtered tracking error
‘r(t)’ is defined by (Lewis et al., 1997):
𝑒=𝑞
()
–q; 𝑟=𝑒 +𝜆𝑒
(11)
in which, 𝜆 is a positive constant, 𝑞
()
=
𝑞
𝑞
; and 𝑞=
𝑞
𝑞
; The dynamics of
0 102030405060708090100
% Gait Cycle
-80
-60
-40
-20
0
20
40
Foot Position Angle Relative To The Ground
Swing Phase
Stance Phase
DS
SS
DS
SS
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
204

the prosthesis in “(1)” can be expressed with
reference to the filtered tracking error as:
M
𝑟 =M
(𝑞
()
–q
+𝜆𝑒)
=–V
𝑟+
𝑓
+τ
–τ–τ
(12)
Where, 𝑓=M
(𝑞
()
+𝜆𝑒)+V
(𝑞
()
+𝜆𝑒)+
G
(𝑞) + F
(𝑞).
The term f comprises of the unknown nonlinear terms
in the dynamics of the system. In the next sections,
we will demonstrate the use of RBF neural network
to approximate f and implement a stable controller.
2.6 Neural Network (NN) Based
Approximation
The function 𝑓 in equation (16) is a smooth function
of the joint angles and joint velocities and can be
bounded on a compact region in ℝ
. Hence 𝑓 can be
approximated using a RBF network (Schilling et al.,
2001).
The output of the RBF network can be expressed
as:
ℎ
=𝑒𝑥𝑝
–
‖
‖
;
𝑗
=1,2,3,..𝑘
𝑓
(𝑥) =𝑊
ℎ+ε
(13)
in which, x is the input of the network,
i
is input
number of the network,
j
is the number of
hidden layer nodes in the network
, 𝜇
value
represents the center point of the Gaussian function
of the neural net 𝑘 for the 𝑖
input, 𝑏
is the width of
the Gaussian function for neural network k. Here, 𝑊
represents
optimum weight for the NN and ε is a very
small value. For an estimated value of 𝑊
, i.e. 𝑊
, the
output of the NN is expressed as 𝑊
h(x). Learning
algorithms are designed such that 𝑊
is updated
iteratively to minimize the error between f(x) and its
estimation 𝑓
(x).
𝑓
(𝑥) =𝑊
ℎ(𝑥)
(14)
Here, 𝑊
=𝑊
–𝑊
; 𝑊
≤𝑊
; so, 𝑊
=–𝑊
;
𝑓
–
𝑓
=
𝑓
=𝑊
ℎ+ε−𝑊
ℎ=𝑊
ℎ+ε
(15)
From the f(x) expression in equation (16) the
input of the RBF has been selected as:
𝑥=𝑒
𝑒
𝑒
𝑒
𝑞
𝑞
𝑞
𝑞
𝑞
𝑞
;
here, subscript k= knee, a=ankle, r = reference;
superscripts g = gait based.
2.7 Analysis of Controlled Prosthetic
Gait
The control law for the system described in “(1)” is:
τ=
𝑓
(𝑥) + 𝐾
𝑟–υ− τ
(16)
In which, 𝑓
is the estimation of f, υ=−(𝜀
+
𝑏
)𝑠𝑔𝑛(𝑟) is the robust term, and τ
is the gait-based
ground reaction torque. The corresponding neural
network adaptive law is designed as:
𝑊
=𝐹ℎ𝑟
−𝜅𝐹
‖
𝑟
‖
𝑊
(17)
Where, 𝜅, 𝐹=𝐹
≥0 are design parameters. In
“(21)” the third term is the filtering term which gives
a better tracking response for non-zero initial
condition.
Theorem II.1. The prosthetic system given in “(12)”
with the control law in “(16)” and the weight update
law for the NN in “(17)” ensure that J
is bounded
and the error between the desired and actual support
time can be made arbitrarily small. Further, the
tracking error e(t) is bounded and can be made
arbitrarily small.
Proof.
Substituting “(16)” to “(12)” we can find:
M
𝑟 =−(𝐾
+V
)𝑟 +𝑊
ℎ+ε+τ
−
τ
+
υ
(18)
Where, τ
is the difference between actual and gait-
based ground reaction torque.
First, the Lyapunov function is defined as:
𝐿=
𝑟
𝑀
𝑟 +
𝑡𝑟(𝑊
𝐹
𝑊
)
(19)
Taking derivative of “(19)” we can find:
𝐿
=𝑟
𝑀
𝑟 +
𝑟
𝑀
𝑟 + 𝑡𝑟(𝑊
𝐹
𝑊
),
(20)
Inserting “(14)”, “(18)” into “(20)”, and with the help
of “(15)”, and “(17)”we can write:
𝐿
=−r
𝐾
𝑟+𝜅
‖
𝑟
‖
𝑡𝑟{W
(𝑊−𝑊
)} +
r
(τ
−τ
+
υ
+ε) ≤−𝐾
‖
𝑟
‖
+
𝜅
‖
𝑟
‖
𝑊
(𝑊
−𝑊
) +(ε
+𝑏
)
‖
r
‖
=−
‖
r
‖
{𝐾
‖
r
‖
+𝜅𝑊
(𝑊
−𝑊
)−
(ε
+𝑏
)}
(21)
A Neural Network-Based Controller Towards Achieving Near-Natural Gait in Transfemoral Amputees
205
By setting up boundary for
‖
r
‖
and 𝑊
as:
‖
𝑟
‖
>
(𝜀
𝑁
+𝑏
𝑑
)
=
=𝐵
𝑊
>
+
𝑊
+
(𝜀
𝑁
+𝑏
𝑑
)
=𝐵
(22)
We can observe that in “(21)”, 𝐿
is negative because
the term inside the braces can be written as:
{𝐾
‖
r
‖
+𝜅𝑊
(𝑊
−𝑊
)−(ε
+𝑏
)}
=𝜅(𝑊
−
1
2
𝑊
)
−
κ
4
W
+K
‖
r
‖
−(ε
+𝑏
)}
(23)
The first and fourth terms on the right side of “(23)”
are positive and other terms are negative. The
boundary conditions of “(22)” ensure that the
derivative of the Lyapunov equation “(21)” is negative
on the region described in “(22)” and implies system
stability. The boundary conditions of “(22)” ensure the
filtered tracking error and the error in estimated NN
weights converge exponentially to the bounds
expressed in “(22)”. Now, from “(15)” and “(22)”, we
can set the bounds for error terms as:
τ=
𝑓
(𝑥) + 𝐾
𝑟–υ− τ
(24)
‖
e
‖
<
‖
r
‖
λ
<
B
λ
K
(25)
Where, λ
is the minimum design value for λ.
From “(14)” we see that the cost function J
depends on the difference between e
and e
. From
“(14)” and “(25)” we can write:
1
2
(e
−e
)
<
1
2
(
‖
e
‖
+
‖
e
‖
)
<
1
2
(
2B
λ
K
)
(26)
Which gives a bound on the cost function J
in
“(14)”:
J
<(
)
; Therefore, it can be concluded that
the cost function J
is bounded by design terms λ
and K
, and can be minimized by the choice of
design values.
3 SIMULATION RESULTS
In this section, two simulation examples are
considered to compare the performance of the
proposed controller with a standard PD controller
(τ
PD
=K
(λ
PD
e+𝑒)- τ
) which is widely used for this
type of systems. Gain parameters for both PD and NN
controllers were chosen to provide stable and
acceptable tracking performance. Lower gain values
made the system unstable and deteriorated tracking
performance. System parameters were chosen from
(Kibria & Commuri, 2024; Zhou et al., 2016).
3.1 Monte-Carlo Simulation to Study
Support Time
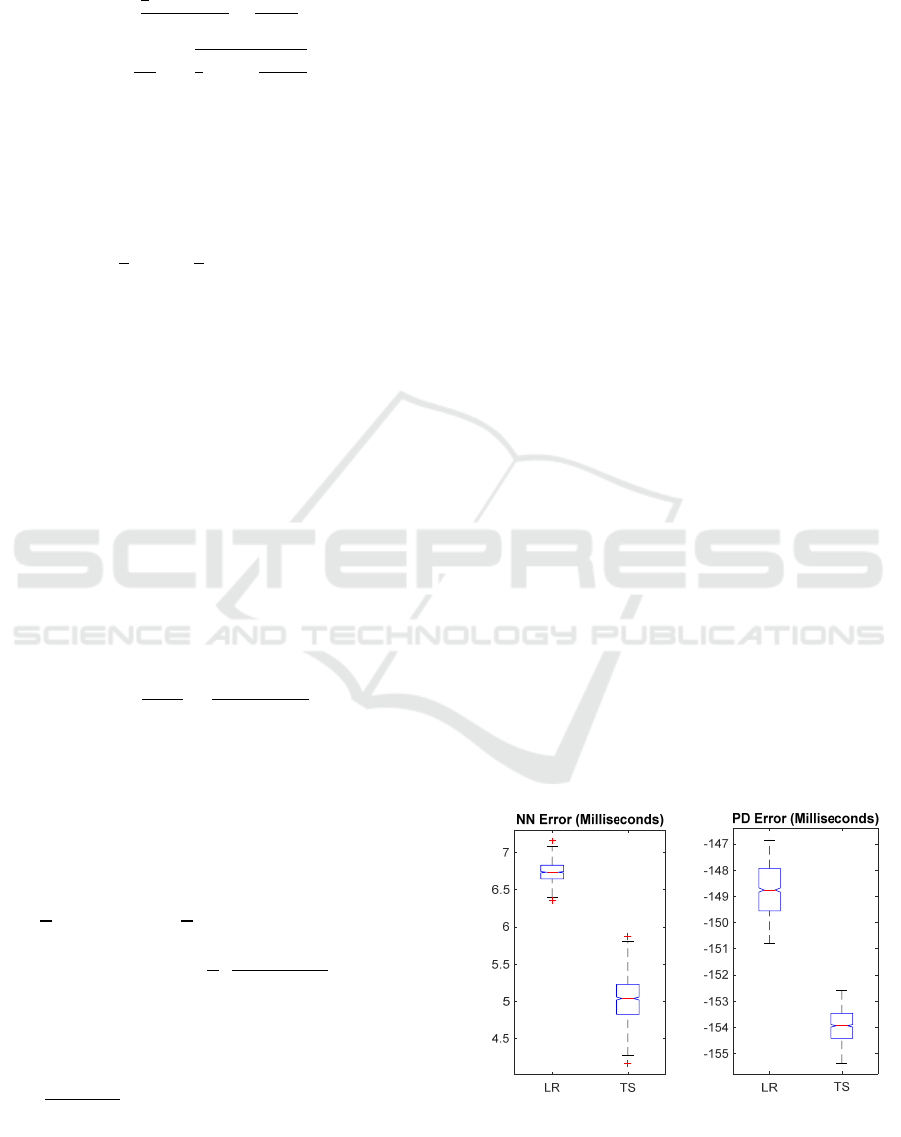
In this example, Monte Carlo simulation is performed
to study the ‘support time’ achieved by the proposed
controller. Support time is defined by the time
difference between the ‘Loading Response (LR)’ and
‘Terminal Stance (TS)’ phases of the gait. In this
example, 1000 different simulations are conducted
with the walking speed, ground reaction force,
measurement noise, disturbance torque being
randomly selected. The error between the desired
support time and the actual support time (TS and LR
time error) is shown in Figure 2. It is seen that the
proposed controller can achieve near-normal gait
despite unknown changes in user gait, terrain
conditions, or measurement noise (error in LR and TS
time is 6.74 and 5.03 milliseconds (standard deviation
of 0.13 and 0.29 milliseconds)). On the other hand,
the performance of PD controller deteriorates in the
presence of variations in desired gait, terrain
conditions, and measurement noise (error in LR and
TS time is 148.76 and 153.94 milliseconds (standard
deviation of 0.97 and 0.58 milliseconds)).
(
a
)
(
b
)
Figure 2: Monte Carlo error for NN (a) and PD (B) at
Loading Response (LR), and Terminal Stance (TS) phases.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
206
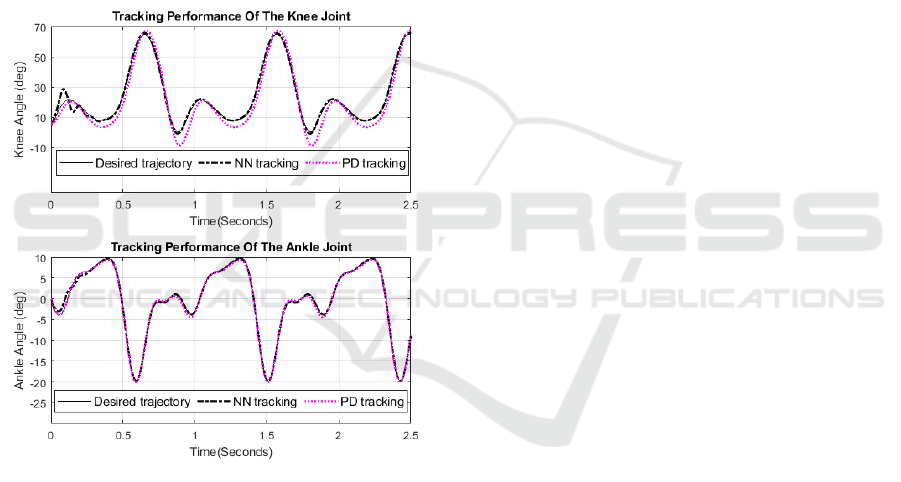
3.2 Tracking Performance
The tracking performance for nominal gait (walking
at normal self-selected pace, known ground reaction
force, and no disturbance torque) is considered in this
example. From Figure 3, it is seen that the NN
controller can track the desired knee and ankle
displacement profiles with greater accuracy than the
PD controller.
The simulation examples discussed in this section
demonstrate that the proposed NN controller can
adapt in real time to track desired joint profiles for the
prosthetic leg. More importantly, the proposed
controller ensures that the prosthetic foot reaches the
‘Loading Response’ position and maintains stipulated
‘single support time’ to provide near natural gait for
the individual.
Figure 3: Gait profile tracking of knee and ankle joints.
4 CONCLUSIONS AND FUTURE
WORKS
In this paper, a novel control strategy was proposed
to reduce the asymmetry in gait between the intact
and amputated side of an amputee. Unlike traditional
controlling approach, the proposed controlling
approach effectively addresses real time challenges
like variations in ground reaction force, measurement
noise, changes in walking speed etc., that can degrade
the performance of the system. It holds great promise
for prosthetics, potentially enhancing amputee
mobility, comfort, and overall quality of life. The
development of a prosthetic test-bed and the
validation of the control strategy discussed in this
paper are being pursued by the authors.
REFERENCES
Ackermann, M., & Bogert, A. J. (2010). Optimality
principles for model-based prediction of human gait.
Journal of Biomechanics, 43(6), 1055-1060.
https://doi.org/https://doi.org/10.1016/j.jbiomech.2009
.12.012
Elery, T., Rezazadeh, S., Nesler, C., & Gregg, R. D. (2020).
Design and Validation of a Powered Knee–Ankle
Prosthesis With High-Torque, Low-Impedance
Actuators. IEEE Transactions on Robotics, 36(6),
1649-1668. https://doi.org/10.1109/TRO.2020.30055
33
Embry, K. R., & Gregg, R. D. (2021). Analysis of
Continuously Varying Kinematics for Prosthetic Leg
Control Applications. IEEE Transactions on Neural
Systems and Rehabilitation Engineering, 29, 232-272.
https://doi.org/10.1109/TNSRE.2020.3045003
Feng, Y., & Wang, Q. (2017). Combining Push-Off Power
and Nonlinear Damping Behaviors for a Lightweight
Motor-Driven Transtibial Prosthesis. IEEE/ASME
Transactions on Mechatronics, 22(6), 2512-2523.
https://doi.org/10.1109/TMECH.2017.2766205
Gao, S., Mai, J., Zhu, J., & Wang, Q. (2021). Mechanism
and Controller Design of a Transfemoral Prosthesis
With Electrohydraulic Knee and Motor-Driven Ankle.
IEEE/ASME Transactions on Mechatronics, 23(5),
2429-2439. https://doi.org/10.1109/TMECH.2020.304
0369
Gorden, L. Y. T., Ariel, Y. F., Pei, H., Meng, L., Yi Zhen,
N. G., & Graves, N. (2022). Decision-making for early
major amputation in selected diabetic foot ulcer patients
with peripheral vascular disease. Health Care Science,
1(2), 58-68. https://doi.org/https://doi.org/10.1002
/hcs2.17
Kibria, Z., & Commuri, S. (2024). Neuro-Dynamic Control
of an Above Knee Prosthetic Leg. SN Computer
Science, 5(5), 509. https://doi.org/10.1007/s42979-024-
02817-1
Lenzi, T., Cempini, M., Hargrove, L. J., & Kuiken, T. A.
(2019). Design, Development, and Validation of a
Lightweight Nonbackdrivable Robotic Ankle
Prosthesis. IEEE/ASME Transactions on Mechatronics,
24(2), 471-482. https://doi.org/10.1109/TMECH.20
19.2892309
Lewis, F. L., Jagannathan, S., & Yeşildirek, A. (1997).
Chapter 7 - Neural Network Control of Robot Arms and
Nonlinear Systems. In L. E. Omid Omidvar and David
(Ed.), Neural Systems for Control (pp. 161-211).
Academic Press. https://doi.org/https://doi.org/10.101
6/B978-012523430-3/50008-8
Mai, A., & Commuri, S. (2016). Intelligent control of a
prosthetic ankle joint using gait recognition. Control
A Neural Network-Based Controller Towards Achieving Near-Natural Gait in Transfemoral Amputees
207

Engineering Practice, 49, 1-13. https://doi.org/https://
doi.org/10.1016/j.conengprac.2016.01.004
Pagel, A., Ranzani, R., Riener, R., & Vallery, H. (2017).
Bio-Inspired Adaptive Control for Active Knee
Exoprosthetics. IEEE Transactions on Neural Systems
and Rehabilitation Engineering, 25(12), 2355-2364.
https://doi.org/10.1109/TNSRE.2017.2744987
Peasgood, M., Kubica, E., & McPhee, J. (2006).
Stabilization of a Dynamic Walking Gait Simulation.
Journal of Computational and Nonlinear Dynamics,
2(1), 65-72. https://doi.org/10.1115/1.2389230
Saini, R. S. T., Kumar, H., & Chandramohan, S. (2020).
Semi-active control of a swing phase dynamic model of
transfemoral prosthetic device based on inverse
dynamic model. Journal of the Brazilian Society of
Mechanical Sciences and Engineering, 42(6), 294.
https://doi.org/10.1007/s40430-020-02387-2
Schilling, R. J., Carroll, J. J., & Al-Ajlouni, A. F. (2001).
Approximation of nonlinear systems with radial basis
function neural networks. IEEE Transactions on Neural
Networks, 12(1), 1-15. https://doi.org/10.1109/72.89
6792
Sharma, R., Gaur, P., Bhatt, S., & Joshi, D. (2022).
Performance Assessment of Fuzzy Logic Control
Approach for MR-Damper Based-Transfemoral
Prosthetic Leg. IEEE Transactions on Artificial
Intelligence, 3(1), 53-66. https://doi.org/10.1109/
TAI.2021.3106884
Winter, D. A. (2009). Kinematics. John Wiley and Sons
Ltd. https://doi.org/https://doi.org/10.1002/97804705
49148.ch3
Zhou, X., Chen, J., Chen, G., Zhao, Z., & Zhao, Y. (2016).
Anthropometric body modeling based on orthogonal-
view images. International Journal of Industrial
Ergonomics, 53, 27-36. https://doi.org/https://doi.org/
10.1016/j.ergon.2015.10.007
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
208
