Solving the Holed Space Budgeted Maximum Coverage Problem with a
Discrete Selection Problem
Phillip Smith
a
and Mohammad Zamani
b
Defence Science and Technology Group, Melbourne, Victoria, Australia
Keywords:
Motion and Path Planning, Collision Avoidance, Detouring, Area Coverage, Genetic Algorithm.
Abstract:
In this paper, a new heuristic for the budgeted maximum coverage problem is introduced for environments
that include obstacles (holed space). This heuristic leads to a solvable but NP-hard problem which requires a
series of discrete decisions to be made. These decisions are non-trivial as the quality of each decision option
may be impacted by the selected options of other decisions in the series and thus optimal solution formation is
NP-hard. The effectiveness of the proposed heuristic is demonstrated by empirically comparing it to another
known heuristic for the area coverage problem; finding it to be more effective at covering the space, at the cost
of requiring greater computation time.
1 INTRODUCTION
Path planning for area-coverage is a well-known
problem with numerous applications from CNC
milling to robotic environment exploration. Generally
speaking, a solution to this problem is a sequence of
coordinates p
t
∈ R
n
(where n ∈ {2, 3}) that an agent
must travel to such that coordinates c in a bounded
area B ⊂ R
n
are ‘covered’ by the agent. That is,
sup
t
∥p
t
−c∥ ≤ r, c ∈B (1)
where r is the coverage radius. As an example, an
agent equipped with a LIDAR with range r travels a
path p
t
|
t=T
t=0
(over time 0 to T ). Criterion (1) then de-
fines that all space is covered by the path and thus any
objects in B would be detected by the LIDAR. Addi-
tionally, this area-coverage path has a travel distance,
δ, found via:
δ =
T −1
∑
t=0
∥p
t+1
−p
t
∥ (2)
assuming the agent travels on a straight line between
each pair of consequent waypoints.
In this simple form (with no limit on δ), such
a path can be solved in polynomial time (P). How-
ever, the complexity is often increased with either dis-
tance minimisation (known as Shortest Tour Cover-
age (STC) (Arkin et al., 2000)) or with a constrained
a
https://orcid.org/0000-0002-5330-1830
b
https://orcid.org/0000-0003-2979-7132
distance (known as Budgeted Maximum Coverage
(BMC) (Khuller et al., 1999)). The former aims to
find the path-solution with smallest δ meeting (1),
which is NP-hard (Arkin et al., 2000). The latter lim-
its δ to a travel budget ∆, δ ≤ ∆, which is chosen in
accordance with real-world constraints such as robot
battery capacity or task time-limits. The overall opti-
misation problem becomes:
max
C⊆B
Volume(C)
s.t. δ ≤∆,
C = {c : sup
t
∥p
t
−c∥ ≤ r},
(3)
which is also NP-hard (Nemhauser et al., 1978).
Due to the fact both sub-problems are NP-hard,
many heuristic path generators have been proposed
to solve (most instances of) these problems. These
include boustrophedon paths (sweeping) (Choset and
Pignon, 1998), spiral paths (Cabreira et al., 2018)
and fractal planning such as Hilbert Curves (HCs)
(Hilbert, 1935). Due to the similarities in STC and
BMC, these heuristics may be applied to either prob-
lem. However, some heuristics are more suited to one
over the other. These heuristics produce a solution in
polynomial time at the cost of not guaranteeing global
optimally in irregular spaces. Further, these heuristics
require modification to overcome challenges such as
spaces with holes (e.g. obstacles).
In this work, a modification process for these
heuristic-based paths is derived for BMC in holed
spaces. Further, this process is demonstrated on HC
Smith, P. and Zamani, M.
Solving the Holed Space Budgeted Maximum Coverage Problem with a Discrete Selection Problem.
DOI: 10.5220/0012889300003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 15-24
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
15

paths, being found to be more coverage-effective and
tolerant of hole shapes and sizes than the holed space
path modifier found in (Nair et al., 2017). However,
the implemented method requires a set of combinato-
rial decisions to be made, which is itself an NP-hard
problem. This leads to the main problem of this paper;
a discrete, non-monotonic decision selector. It is be-
lieved this new problem will be of interest to the area-
coverage community as it produces a locally optimal
solution to the parent problem of BMC with consid-
erably less complexity. Additionally, the discrete de-
cisions of this problem pose a new benchmarking ap-
plication for numerous meta- and hyper-heuristics al-
gorithms such as Genetic Algorithm (GA) (Holland,
1992), Artificial Ant/Bee Algorithms (Dorigo and
St
¨
utzle, 2019) (Karaboga, 2005) and Particle Swarm
Optimisation (Kennedy and Eberhart, 1995).
In this paper, the background of this topic is fur-
ther discussed and a formal definition of the proposed
path-modifying heuristic is presented in Section 2 and
Section 3. In Section 4 an empirical demonstration
of this method is made by comparing it to both an-
other HC modifying technique from literature (Nair
et al., 2017) and to a tree-search (Boyd and Mattin-
gley, 2007). Finally, in Section 5 this work is con-
cluded.
2 BACKGROUND
2.1 Hilbert Curves
The Hilbert space-filling curve heuristic is a path
planner approach that aims to uniformly examine an
environment (Hilbert, 1935). The algorithm uses a
square pattern, recursively repeated to the h
th
degrees
(h ∈ Z
+
); as the degree increases both the coverage
resolution and path length increase, as shown in Fig-
ure 1. This path length, δ
HC
, is defined as:
δ
HC
= w(2
h
−2
9h
) (4)
where w is the size of the square space being cov-
ered and it can be noted that δ
HC
(h) is a monotonic
function. Additionally, it is noted that applying the
coverage circle r to this path produces the coverage
volume, which is also monotonic until (1) is satisfied.
To define an optimal h value for square area cov-
erage, (Viana and De Amorim, 2013) observes that a
Hilbert curve of degree h divides the space, B, into
2
h+1
cells, each with size l = w ·2
−h
. The resulting
path has the agent travel to each cell centre, and thus
the agent’s circular coverage of range r fully covers
the square cells if
l ≤ r
√
2 (5)
Figure 1: HC scaled to space with degrees 1 (red), 2 (blue)
and 3 (black). Each degree covers more area and has greater
length. Figure use granted under unrestricted ‘public do-
main’ licensing (Richards, 2022).
In contrast, the agent’s coverage range does not
spread into neighbouring cells (which may have al-
ready been explored) if
l ≥ 2r (6)
Substituting w and h into these limits, it is guaranteed
a Hilbert curve completely covers an area if
h ≥ ⌈log
2
(
w
r
) −0.5⌉ (7)
Similarly, it is observed that the path is guaranteed to
have no overlapping coverage (and thus no redundant
travel) if
h ≤ ⌊log
2
(
w
r
) −1⌋ (8)
From these two limits with conflicting rounding func-
tions, it is noted that the proposed h limits are always
1 apart. Further, both (7) and (8) cannot be satisfied
by a h selection simultaneously.
As an example, consider a space with w = 16 cov-
ered by a path with r = 2 and assume the path can be
executed with omnidirectional travel (ignore the cost
of rotations). Eq. (7) produces the restriction h ≥ 3
while Eq. (8) sets h ≤ 2. In Figure 2 it can be seen
that the h = 3 path covers all space within B, how-
ever, there is significant area covered multiple times
and the total path length is much longer than h = 2.
In contrast, the h = 2 has no sub-effective travel from
re-covering area but fails to cover the corners of some
HC cells.
Using these qualities, it can be observed that the
HC lends itself well to the STC and BMC problems
in square space. However, as (7) and (8) cannot be
satisfied simultaneously, h must be tuned for the spe-
cific problem variant.
In terms of STC, a locally optimal solution min-
imising h such that (7) is satisfied will also minimise
length δ
HC
as per the monotonic natures of (4). The
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
16

Figure 2: Area coverage with h=3 (left) and 2 (right).
resulting path-solution may not be globally optimal
to the STC problem but can be effectively produced
in linear time via the optimisation of a single integer.
For BMC, a locally optimal solution is generated
by combining (3) and (4) into
max(h) | (2
h
−2
9h
) ≤
∆
w
(9)
Again, this approach requires linear time and, if the h
produced by (9) can also satisfy (7), the HC is glob-
ally optimal due to the travel budget of the problem
instance being too relaxed for the give w. Similarly, if
we expand the h of (9) to h ∈R and find (8) still holds
(the real-number h is not between the neighbouring
integer limits of (8) and (7)), we can say the HC is
globally optimal, given the w and ∆ combination.
To conclude, the HC heuristic allows the path-
generating problem of STC and BMC to be com-
pressed to one degree of freedom, h. Not only is this
much cheaper in terms of computation but also makes
the constraints and objective functions monotonic and
hence makes it easier to solve using efficient optimi-
sation algorithms.
2.2 Holed Space Area Coverage
Heuristics
Several works have modified path-generating heuris-
tics for area-coverage in holed spaces, e.g. spaces
with obstacles. However, these works either compro-
mise path length efficiency to circumvent the holes
or make significant assumptions on space discretisa-
tion and hole alignment which limit the applicability
of these heuristics.
In (Choset and Pignon, 1998) and (Achat et al.,
2023) hole-tolerant variants of the boustrophedon
heuristic are proposed which segmented the environ-
ment as the path intersected holes and sequentially
swept each subsection, guaranteeing all spaces are
covered. However, in the former, travelling between
each subsection used a greedy planner, and in the lat-
ter, the subsection order follows the global sweeping
pattern. As such, agents could move through prior-
covered subsections. As a result, the total path length
would be non-optimal in STC and all sub-sections
may not be effectively swept in BMC.
Similarly, in (Gabriely and Rimon, 2001) a spi-
ral path was produced by a depth-first spanning trees
of unoccupied, unexplored cells. This work escaped
dead-ends (caused by obstacles) by reverse-travelling
the path until unexplored cell neighbours became
available. This, again, reduced the effectiveness of
the overall path, making the heuristic sub-optimal for
both STC and BMC.
Finally, (Nair et al., 2017) explored modifying
HCs by removing, adding, or rearranging path ver-
tices around obstacles with the modifying action cho-
sen via the vertices’ index in the recursive HC path.
This approach maximised the exploration of unoccu-
pied cells with minimal increase to path length. How-
ever, it also assumed the space could be easily discre-
tised, with the holes being of equal size and shape to
the occupancy cells. In this work, it was assumed h
was provided to the algorithm, though explored the
use of each quartile of the space utilising a different
h. Further, in a follow-up paper, (Joshi et al., 2019),
the heuristic was extended to overcome rectangular
obstacles, occupying two adjacent occupancy cells.
However, the rectangles still required to be aligned
to the occupancy grid and thus HC vertices.
From this review, no prior work, to the best of our
knowledge, has been found that modifies a path gen-
eration heuristic for resilience to holed spaces without
incurring similar shortcomings.
3 HILBERT CURVE FOR HOLED
SPACE
3.1 Problem Formulation
In this section, the coverage path planning problem in
holed space is revisit and the proposed path adjust-
ment process is described. For simplicity, it is as-
sumed the agent is ground based and thus the space
is two-dimensional (n = 2). Further, this study is lim-
ited to circular and rectangular obstacles. That be-
ing said, higher dimensional spaces and irregular ob-
stacles circumvention is possible with this approach.
Additionally, it should be highlighted that the obsta-
cles of this demonstration have centroids at any given
c ∈ R
2
. That is, the obstacles are not bound to a dis-
crete occupancy grid; this allows a closer representa-
tion of real-world obstacle environments.
Given a set of obstacles, the hole-space of the en-
vironment is defined as H . This H represents all ob-
stacles the agent must circumvent plus the collision-
Solving the Holed Space Budgeted Maximum Coverage Problem with a Discrete Selection Problem
17

avoiding buffer spaces around them. The remaining
free space is B\H .
3.1.1 Path Initialisation
The proposed process starts with a path not necessar-
ily robust to holes projected onto the space (ignoring
the holes). In this study, this takes the form of a h
degree HC, maximising h as in (9) to optimise for
BMC. It can be noted that this approach is not limited
to HC paths; any path planning heuristic (see Section
2) could be utilised at this initial point. As defined
in Section 1, the initial path of length T
0
, p
0
, is ex-
pressed as a series of waypoints,
p
0
= [p
0
i
∈ R
2
, i ∈Z
T
0
] (10)
and the 0 superscript is a preemptive addition for later
in this section. In this (and all further discussed)
path(s), each pair of consequent waypoints (p
j
i
, p
j
i+1
)
(where j denotes an arbitrary path p
j
) is connected via
a straight line, expressed as:
l
j
i
= {p ∈ R
2
: p = p
j
i
+t(p
j
i+1
−p
j
i
),t ∈ R
1
}. (11)
3.1.2 Path Breaks
To prevent the agent colliding with an obstacle while
travelling the path, at each point p
0
intersects H the
corresponding straight-line path is split into subpaths,
each being expressed as a subarray of waypoints. The
overall path is then the array of these subarrays, ini-
tialised as P = [p
0
].
Collision detection is sequentially performed on
each subpath, p
j
, in P. A collision occurs on p
j
if γ
exists such that:
γ = argmin
i∈Z
T
j
(l
j
i
∩H ̸=
/
0) (12)
If γ exists, the first collision-point along l
j
γ
can be
found by combining (11) and (12):
t
α
= argmin
0≤t≤1
(p
j
γ
+t ·(p
j
γ+1
−p
j
γ
)) ∈ H (13)
If t
α
> 0, it can be used to find the ‘last safe point’,
p
j
α
, on l
j
γ
:
1
p
j
α
= max
t<t
α
(p
j
γ
+t ·(p
j
γ+1
−p
j
γ
)) : p
j
α
̸∈ H (14)
The first collision-free point after t
α
is labelled p
β
and found via:
p
j
β
= min
t
α
<t≤1
(p
j
γ
+t ·(p
j
γ+1
−p
j
γ
)) : p
j
β
̸∈ H (15)
1
In relation to implementation, t may be incremented in
discrete steps,
ˆ
t. In which case p
α
= p
j
γ
+(
ˆ
t ·⌊t
α
⌋)·(p
j
γ+1
−
p
j
γ
))
original path post path-breaking
Figure 3: HC, split into four subarrays such that hole-
collisions are removed. Path presented as green lines, obsta-
cles as blue circles. Grey area around obstacles is the hole
space.
The two corner cases of this process are t
α
= 0 and
p
β
being undefined. These cases are two results of the
unmodified path having a waypoint inside H and are
addressed by (16) and (17), respectively. The former
case, t
α
= 0, occurs when l
j
γ
begins inside H and thus
only arises when γ = 0.
2
The latter case, p
j
β
being
undefined, occurs if all points of l
j
γ
after p
j
α
are inside
H and thus is coupled with the former case (t
α
= 0)
occurring in the following straight-line.
Using p
α
and p
β
, the currently examined subarray
p
j
= [p
j
0
, p
j
1
, . . . , p
j
α
, p
j
γ
, . . . , p
j
T
j
−1
] is reduced to the
waypoints prior to the collision:
p
j′
=
(
[p
j
0
, . . . , p
j
α
] , if t
α
> 0
[ ] , otherwise
(16)
and a new subarray, p
j+1
, is appended to P:
p
j+1
=
(
[p
j
β
, p
j
γ+1
, . . . , p
j
T
j
−1
], if p
j
β
is defined
[p
j
γ+1
, . . . , p
j
T
j
−1
], otherwise
(17)
From the sequential nature of this possess, the
modified subpath, p
j′
, is guaranteed to be collision
free. When (12) reports a γ does not exit for any p
j
,
the entire path is assured to be collision free and will
be in the form:
P
′
= [p
0′
, p
1′
, . . . , p
η
] (18)
where η = |P
′
| − 1. However, the set of straight
lines defining P are no longer a continuous path, i.e.
p
j
T
j
−1
̸= p
j+1
0
. This path-splitting process is demon-
strated in Figure 3.
3.1.3 Re-Joining the Path
To make the HC a continuous path once more,
heuristic-based detours are added between each sub-
2
if a > 0 (12) assures there are no collisions for l
j
0
to
l
j
γ−1
, and l
j
γ−1
(t = 1) == l
j
γ
(t = 0), therefore it is assured
that γ > 0 =⇒ t
α
̸= 0.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
18

array of P
′
. At each reconnection, µ ∈ Z
+
detour op-
tions are available, but only one may be selected per
reconnection. Here a reconnection is defined as a de-
cision, d
j
, with detour options {m
j
0
, m
j
1
, . . . , m
j
µ−1
},
where a detour is a heuristic-based array of way-
points, m
j
u
= [m
j
u,0
, m
j
u,1
, . . . , m
j
u,T
j
u
] such that p
j′
T
j
==
m
j
u,0
and p
j+1′
0
== m
j
u,T
j
u
(u denoting an arbitrary de-
tour in the option-set, with length T
j
u
+1). The result-
ing path, P
′′
, can be represented with detour option
super-positions:
P
′′
=[p
0′
, d
0
, p
1′
, d
1
, . . . , p
η−1′
, d
η−1
, p
η
]
=[p
0′
,




m
0
0
m
0
1
. . .
m
0
µ−1




⊤
, . . . ,




m
η−1
0
m
η−1
1
. . .
m
η−1
µ−1




⊤
, p
η
]
(19)
As η detour options must be selected, the detour
solution space is size µ
η
. As such, the size complexity
of this selection process grows exponentially as more
detour options are implemented and grows monoton-
ically (polynomial to µ) as the environments become
more densely filled with obstacles.
In relation to the detour options, any path-
generating heuristic that connects two points while
avoiding hole intersections may be utilised. That
said, due to the exponential complexity growth, this
demonstration will assume only a ‘left’ and ‘right’
circumvention along the borders of B and H
3
. This
reduces d
j
to:
d
j
= {m
j,left
, m
j,right
} (20)
Applying this µ = 2 option set to the example problem
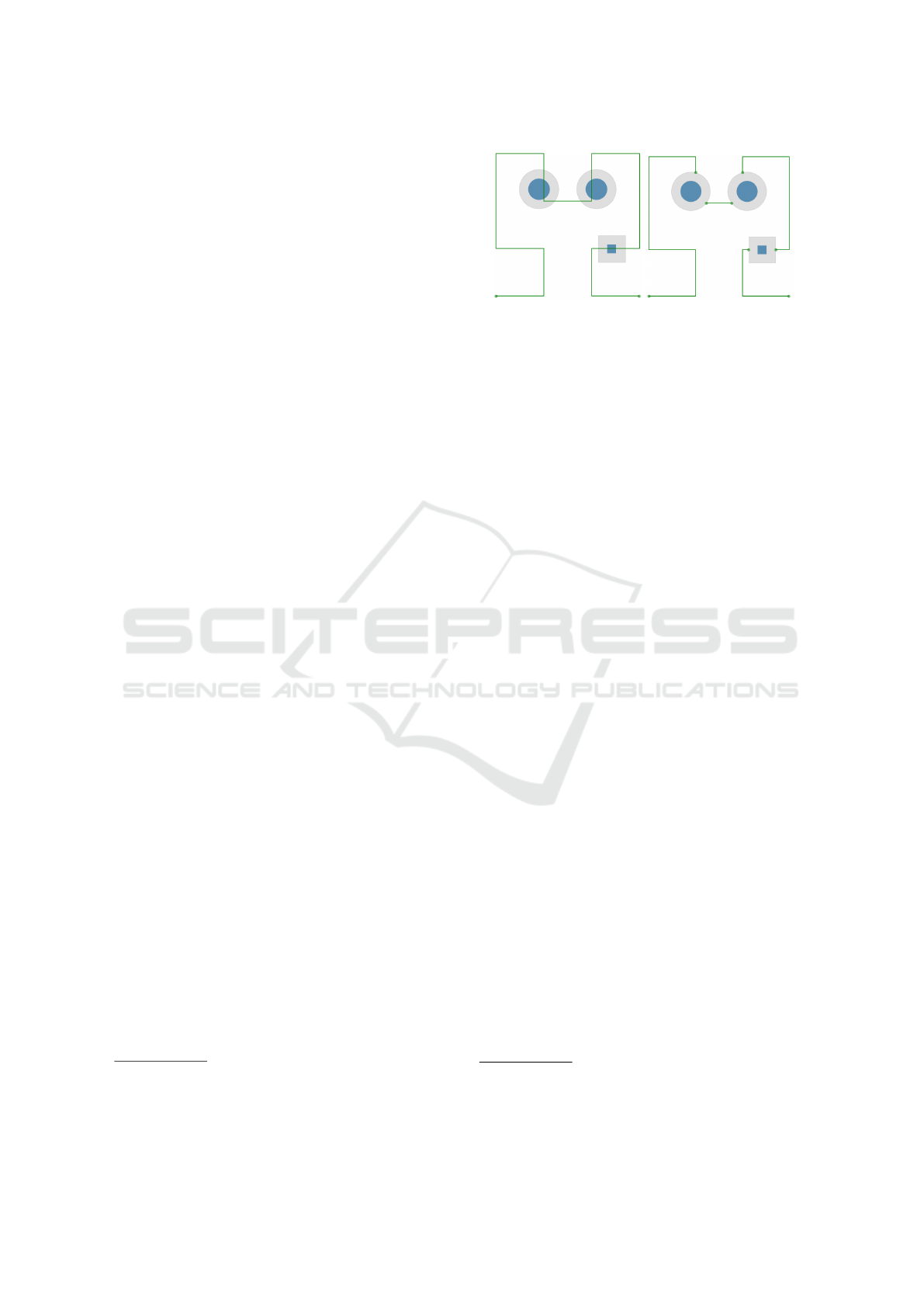
of Figure 3, the graph shown in Figure 4 is produced.
A solution to the decision-making problem, S, can
now be defined as the array of detour options chosen
to fully reconnect the HC. i.e. for the problem in Fig-
ure 4, a solution is “[left, right, left]”. This solution
collapses the super-positions of (19) into a standard,
continuous path P
′′
S
. However, discovering an effec-
tive and valid solution to this problem remains com-
plex, as discussed next.
3.2 Problem Constraints
3.2.1 Selection Limit
As stated above, a detour selection solution must have
exactly one detour option selected for each decision
3
Additional detours potentially include ‘wide-left’ and
‘wide-right’; these see the agent circumvents wider, such
that the borders of the obstacle is w from the agent, max-
imising area coverage during detour
Figure 4: All detour options added to HC, each obstacle
must select the left (red) or right (yellow) circumvention
path.
point. Formally, this is defined as the following con-
straint:
∀j ∈ {0, 1, . . . , η −1},
µ
∑
u=0
x(S, m
j
u
) = 1 (21)
x(S, m) ≜
(
1, if m ∈ S,
0, otherwise.
(22)
3.2.2 Travel Distance
As this work is exploring the BMC problem, any so-
lution path P
′′
S
must adhere to the travel budget, ∆,
∥P
′′
S
∥ ≤ ∆,
∥P
′′
S
∥ ≜
η
∑
j=0
T
j
∑
i=0
∥p
j
i+1
−p
j
i
∥
+
η−1
∑
j=0
µ
∑
u=0

x(S, m
j,u
) ·
T
j
u
∑
i=0
∥m
j
u,i+1
−m
j
u,i
∥

,
(23)
where the first sum is the remaining HC, P
′
, and the
second sum is the detour paths with x(S, m
j
u
) remov-
ing non-selected detours. As P
′
is fixed during the
detour selection process, we can simplify (23) to,
∆
′
≜ ∆ −∥P
′
∥
η−1
∑
j=0
µ
∑
u=0

x(S, m
j,u
) ·
T
j
u
∑
i=0
∥m
j
u,i+1
−m
j
u,i
∥

≤ ∆
′
(24)
3.3 Space Coverage
As the BMC problem aims to maximise the cover-
age of the path, the coverage of P
′′
S
is defined as the
union of covered areas (inside B) produced by trav-
elling along the lines of the path, l
j
i
(defined in (11)),
with the vision range r. As the geometrical calcu-
lations are beyond this discussion, the exposition is
Solving the Holed Space Budgeted Maximum Coverage Problem with a Discrete Selection Problem
19

simplified to: line l
j
i
has a given area A(l
j
i
, r) ⊂ B,
and subpath p
j
have area defined as,
A(p
j
) =
T
j
[
i=0
A(l
j
i
, r)
(25)
Here, ∪ denotes the union of the spacial subsets.
Continuing this notation, the path of solution S is
said to have area coverage:
A(P
′′
S
) = B ∩

η
[
j=0
A(p
j
)∪
η−1
[
j=0
µ
[
u=0

x(S, m
j
u
)·A(m
j
u
)


,
(26)
which, again, can be simplified by removing the P
′
constants:
˜
A(P
′
S
) ≜A(P
′′
S
) −A(P
′
)
=B ∩
η−1
[
j=0
µ
[
u=0

x(S, m
j
u
) ·

A(m
j
u
)−
A(P
′
) ∩A(m
j
u
)

(27)
This simplified space coverage value is only the
additional coverage of the detours. That is, the area
not already covered by the remains of the HC. The
coverage of the example problem in Figure 3 is shown
in Figure 5. This figure highlights the complexity of
this problem space: detour coverage areas may over-
lap, resulting in area unions less than the sum of indi-
vidual detour areas. id est, if both m
0,le f t
and m
1,le f t
are selected,
A(m
0,le f t
) ∪A(m
0,le f t
)) ≪ A(m
0,le f t
) + A(m
1,le f t
).
3.4 Problem Summary
To summarise the problem requirements, given a col-
lection of decisions [d
0
, d
1
, . . . , d
η−1
], each containing
µ heuristic-based detour paths, {m
j
0
, m
j
1
, . . . , m
j
µ−1
}, a
solution to this problem is an array of detour selec-
tions of length η. This solution aims to maximise the
area coverage while keeping the total path length be-
low a budget:
max
m
j,u
B ∩
η−1
[
j=0
µ
[
u=0

x(S, m
j
u
) ·

A(m
j
u
)−
A(P
′
) ∩A(m
j
u
)

s.t
η−1
∑
j=0
µ
∑
u=0

x(S, m
j,u
) ·
T
j
u
∑
i=0
∥m
j
u,i+1
−m
j
u,i
∥

≤ ∆
′
∀j ∈ {0, 1, . . . , η −1},
µ
∑
u=0
x(S, m
j
u
) = 1.
(28)
It can be noted that because the detour options
have no inherent ordering (the cost-reward function is
Figure 5: Space coverage of example problem. Coverage
coloured as per the line colouring of Figure 4.
not monotone), a gradient-based or greedy heuristic
can not be derived (Garrido-Merch
´
an and Hern
´
andez-
Lobato, 2020). Additionally, due to the above dis-
cussed detour area overlap, the selection process is
non-convex and thus difficult to solve in a sequential
greedy fashion, or with tree-search algorithms (such
as branch and bound (Boyd and Mattingley, 2007)).
That is, partial-solution area-coverage must be recal-
culated (from scratch) as each decision is iteratively
added to a solution with these algorithms. This results
in a worst case of
∑
η
i=1
(µ
i
) area calculations. Further,
a globally optimal solution is only guaranteed if all
valid solutions are evaluated in a combinatorial fash-
ion. This may be reduced by testing for budget vio-
lation in polynomial time, but the worst-case instance
requires all µ
η
to undergo area optimality testing, and
thus the problem is NP-hard.
As a final note on this detour problem, because
a solution is a fixed-length string of values from
a finite set, many meta-heuristics can be employed
to search such a landscape. Furthermore, the so-
lution landscape is expected to be rugged, with
both jagged cliffs (poor and good solutions close
together) and smooth concavities. Therefore, this
problem lends itself well to meta-heuristic algorithms
which effectively explore the space via both local
search (finding optima) and large leaps (escaping lo-
cal optima and crossing jagged cliffs). Such meta-
heuristics include: GA (Holland, 1992), Artificial
Bee Colony (Karaboga, 2005) , Simulated Annealing
(Van Laarhoven and Aarts, 1987), and Particle Swarm
Optimisation (Kennedy and Eberhart, 1995). As such,
this detour selecting problem is seen as both a new
heuristic for the BMC problem in holed space and as
a new application for the meta-heuristics field.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
20

4 VALIDATING THE HEURISTIC
4.1 Experiment Design
4.1.1 Corner Cutting Hilbert Curve Comparison
To validate the proposed process, a comparison is
made for both efficiency and effectiveness between
this method and the hole-tolerant HC modification of
Nair et. al (Nair et al., 2017). For conciseness, Nair
et. al’s algorithm is hereon refereed to as Corner Cut-
ting Hilbert Curve (CCHC) and the proposed detour
method as Detour Selection Hilbert Curve (DSHC).
To solve the detour selection problem, both a Brute-
Force search (BF) and GA solver are trialled. The
comparison study consists of 20 randomly generated
holed spaces for each of the 24 configurations of the
following variables:
- HC degree, h ∈ {1, 2, 3, 4}
- Budget, ∆ ∈ {δ
HC
, 1.1δ
HC
, 1.5δ
HC
}
- Hole Alignment ∈ {Aligned, Randomised}
where δ
HC
is the length of the unmodified HC as de-
fined in (4); ‘Aligned’ holes are only placed on the
vertices of the HC, sized to only restrict the path
to/from that vertex, and never adjacent to one another
(as seen in (Nair et al., 2017)); and ‘Randomised’
holes are either rectangular or circular, with size range
(0.02w, 0.05w) and randomly placed in the space with
centroid coordinates in R
2
∈ (0.025w, 0.975w). Ex-
amples of these hole alignments are presented in Fig-
ure 6. In addition to these variables, the agent has a
fixed vision range r = 1.
When generating the environments of this study,
B has width and length w = r ·2
h+1
which allow an
unmodified HC to fully cover the space (see Section
2). This choice of w is seen as the least effective use-
case for DSHC and thus presents the greatest compar-
ative challenge. That is, a B being fully covered by
the original HC causes (27) to be relatively small and
flat across the detour solution landscape, which min-
imises the impact of (28). In contrast, a B only par-
tially covered by the original HC allows the detours to
significantly contribute to the coverage and thus (28)
has greater optimisation potential. For example, in
Figure 5 the left and right detours of the first two de-
cisions produce significantly different coverage. By
using this least effective case the performance com-
parison of this study is strengthened, as any results
in favour of DSHC would only be increased in a pre-
ferred B.
For the GA implementation, a population of 100
solutions is maintained and each generation produces
10% of the population (10) new solutions. A history
Figure 6: Example of Aligned (left) and Randomised (right)
obstacle layouts.
of all explored solutions is additionally maintained,
ensuring each generation contains unexplored solu-
tions. Offspring are produced via one-point crossover,
with parents selected using roulette wheel. The re-
sulting children are added to the generation in both
mutated and unmutated forms (if not found in the
search’s history); where mutation is an element-wise
decision switch with probability
1
η
. The GA is ter-
minated after 1000 generations without a solution fit-
ness improvement or if the history contains all 2
η
so-
lutions.
To analyse the efficiency results of this compar-
ison, the CPU clock-times relative to the number of
detours (η) are plotted. For DSHC, this plotting is
done for both the time to generate the selection prob-
lem (as discussed in Section 3.1) and the full opera-
tion time (both creating the problem and solving it). A
best-fit function of type: polynomial (degree 1 to 6),
logarithmic or exponential is reported for each algo-
rithm’s run time. For fair comparisons, all algorithms
are run without multi-threading on a single i5-8365U
(1.60GHz) processor.
The effectiveness of the algorithms is quantified
via the percentage of B covered by the resulting path,
using (26). The mean and standard deviation for each
variable configuration is reported.
As CCHC is not designed for randomised-hole
locations, a marginal adjustment has been made to
CCHC when operating in random-hole environments.
This adjustment recursively decreases the h value of
path segments at any point where hole intersections
still exist after corner-cutting. It has been imple-
mented to build on Nair et. al’s use of different h val-
ues in each environment quadrant. Further, it is found
that this method performs better than repeatedly re-
moving waypoints until all obstacles are avoided on a
fixed h HC, and this adjustment is only made to give
a fairer comparison between the algorithms. Further
details of this algorithm modification are provided
upon request.
In addition to this adjustment to CCHC, both al-
gorithms are modified to strongly adhere to the travel
budget; if the modified path of CCHC or the short-
est path of all DSHC solutions exceed ∆, the end of
Solving the Holed Space Budgeted Maximum Coverage Problem with a Discrete Selection Problem
21

the respective path is trimmed to meet the budget re-
quirement. This reduces the coverage performance of
the path but prevents either approach from having an
unfair advantage or not being able to produce valid
solutions to an environment.
4.1.2 Tree-Search Comparisons
In addition to the above comparison, this study also
validates the hypothesis that tree-search algorithms,
such as Branch and Bound (B&B), are ill-suited for
solving the proposed detour selection problem. This
is confirmed by analysing the CPU clock-time and
number of area calculations for the DSHC-BF search
and a B&B search. This analysis is conducted for
budgets: ∆ = 1.1δ
HC
and ∆ = 1.5δ
HC
. For each bud-
get, 1,000 randomly generated problem instances are
solved by each algorithm. It can be noted that the
coverage results are not compared, as both algorithms
produce a globally optimal detour solution.
4.2 Experiment Results
4.2.1 DSHC vs. CCHC Computation Time
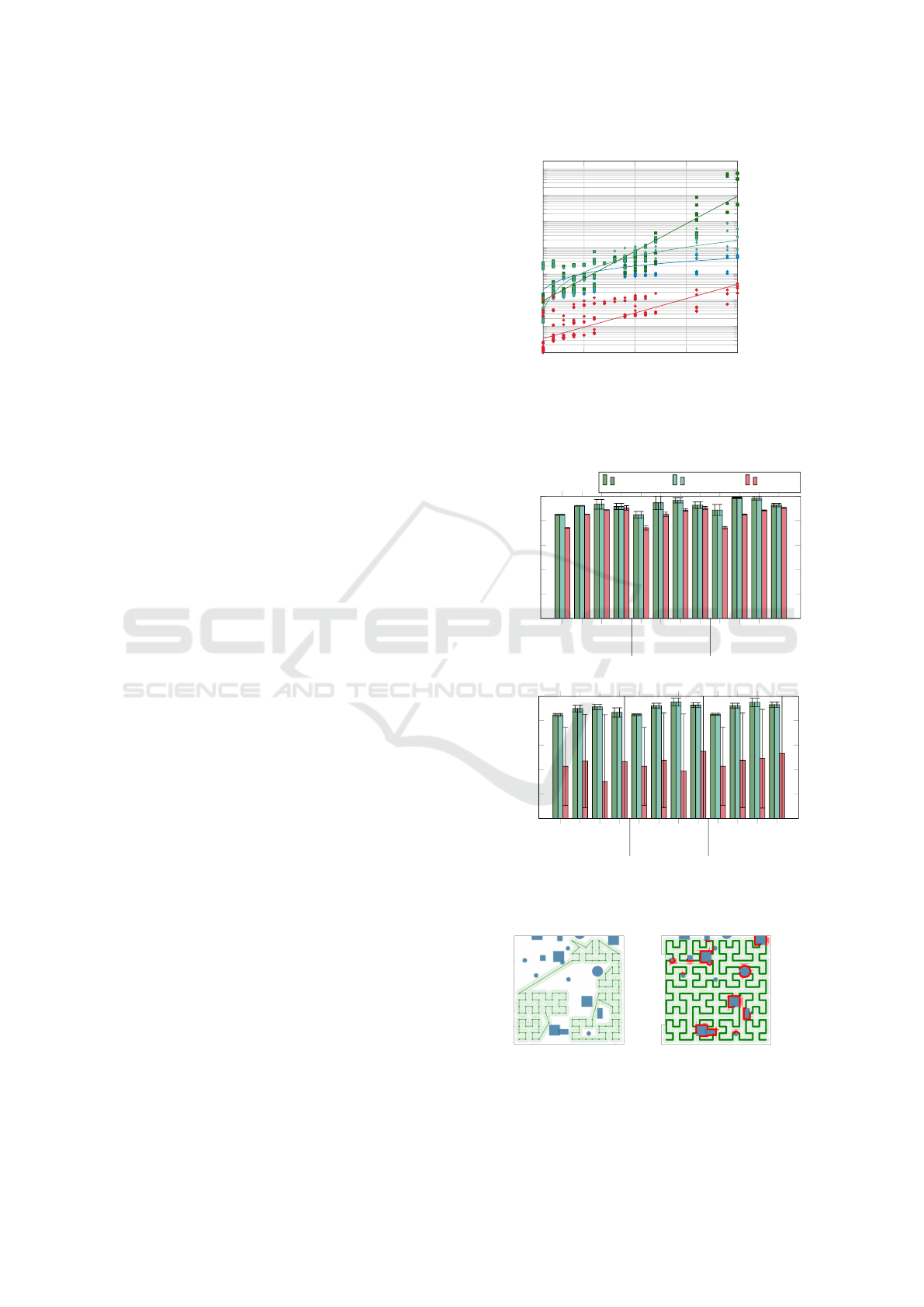
Figure 7 presents the execution times and best-fit
function for each algorithm. CCHC reported the
fastest execution times, faster than either DSHC
solver by several order of magnitude. However, these
execution times still most closely fit an exponential
growth model, despite the theoretical polynomial al-
gorithm. In contrast, the proposed detour problem can
be built in linear time and solved with a GA approach
in polynomial time. Only the BF solver grows expo-
nentially, as expected.
4.2.2 DSHC vs. CCHC Coverage
Figure 8 presents the mean coverage effectiveness of
the paths after heuristic modification.
In relation to the two solvers applied to DSHC,
equivalent coverage results are produced. As BF
is guaranteed to discover the global optima of the
detour-selection problem, it is concluded that the
GA meta-heuristic is also consistently discovering the
global optima, and is thus well suited to this problem.
In regards to DSHC and CCHC in the various
environment configurations, the former outperforms
the latter in all cases explored. DSHC is minimally
impacted by the HC degree or the placement of ob-
stacles, though sees better performance with a bud-
get significantly larger than δ
HC
. In contrast, CCHC
shows little variation from the budget but is signifi-
cantly impacted by the holes not aligning with the HC
vertices and with smaller h curves.
5 10 15 20
10
−3
10
−2
10
−1
10
0
10
1
10
2
10
3
10
4
Detours
CPU time, (seconds)
ticks on a log
10
scale
DSHC Build
t = 0. 2x + 0. 06
DSHC BF
t = 0. 06e
0. 5x
DSHC GA
t = 0. 05x
2
CCHC
t = 0. 003e
0. 25x
Figure 7: Time-detour relation between obstacle avoiding
CCHC (Red), DSHC with a BF solver (green), DSHC with
a GA solver (teal), and just the problem creation time of
DSHC (blue).
1 2 3 4 1 2 3 4 1 2 3 4
0.5
0.6
0.7
0.8
0.9
1
100% 110% 150%
Coverage
Aligned
DSHC BF DSHC GA CCHC
Budget
HC Degree
𝛿
HC
1.1 𝛿
HC
1.5 𝛿
HC
1 2 3 4 1 2 3 4 1 2 3 4
0.5
0.6
0.7
0.8
0.9
1
100% 110% 150%
Coverage
Random
Budget
HC Degree
𝛿
HC
1.1 𝛿
HC
1.5 𝛿
HC
Figure 8: Normalised coverage of B by the three meth-
ods. DSHC shows greater mean coverage in all cases than
CCHC.
CCHC. DSHC.
Figure 9: Result of removing vertices to avoid collisions in
a dense, randomly scattered, hole environment.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
22

The performance growth of DSHC relative to the
budget increase is due to δ
HC
≈∆ causing ∆
′
≈0 (see
(24)). This restricts (28) to the single shortest path so-
lution or a small subset of solutions. Further, if larger
obstacles must be circumvented, ∆
′
may become neg-
ative which triggers the path-trimming modification
discussed above.
In relation to the poor robustness of CCHC to ran-
domised obstacle placement, this is due to obstacles
intersecting the path at edges (rather than vertices)
and larger obstacles triggering multiple HC vertices
to be modified. As most of the CCHC modifications
have a vertex removed, these multiple modifications
can accumulate to large sections of the path being
discarded. This is in contrast to DSHC, which can
detour an obstacle irrespective of size or the intersec-
tion location. An extreme case of this over-removal
by CCHC is shown in Figure 9. In (a) (CCHC), the
upper left corner must be treated as a h = 1 HC and re-
moved accordingly to prevent collision with all obsta-
cles of the cluster. This results in the entire quadrant
being unexplored. In contrast (b) (DSHC), shows a
series of small detours that allow the quadrant to still
be explored as the agent weaves around the many ob-
stacles.
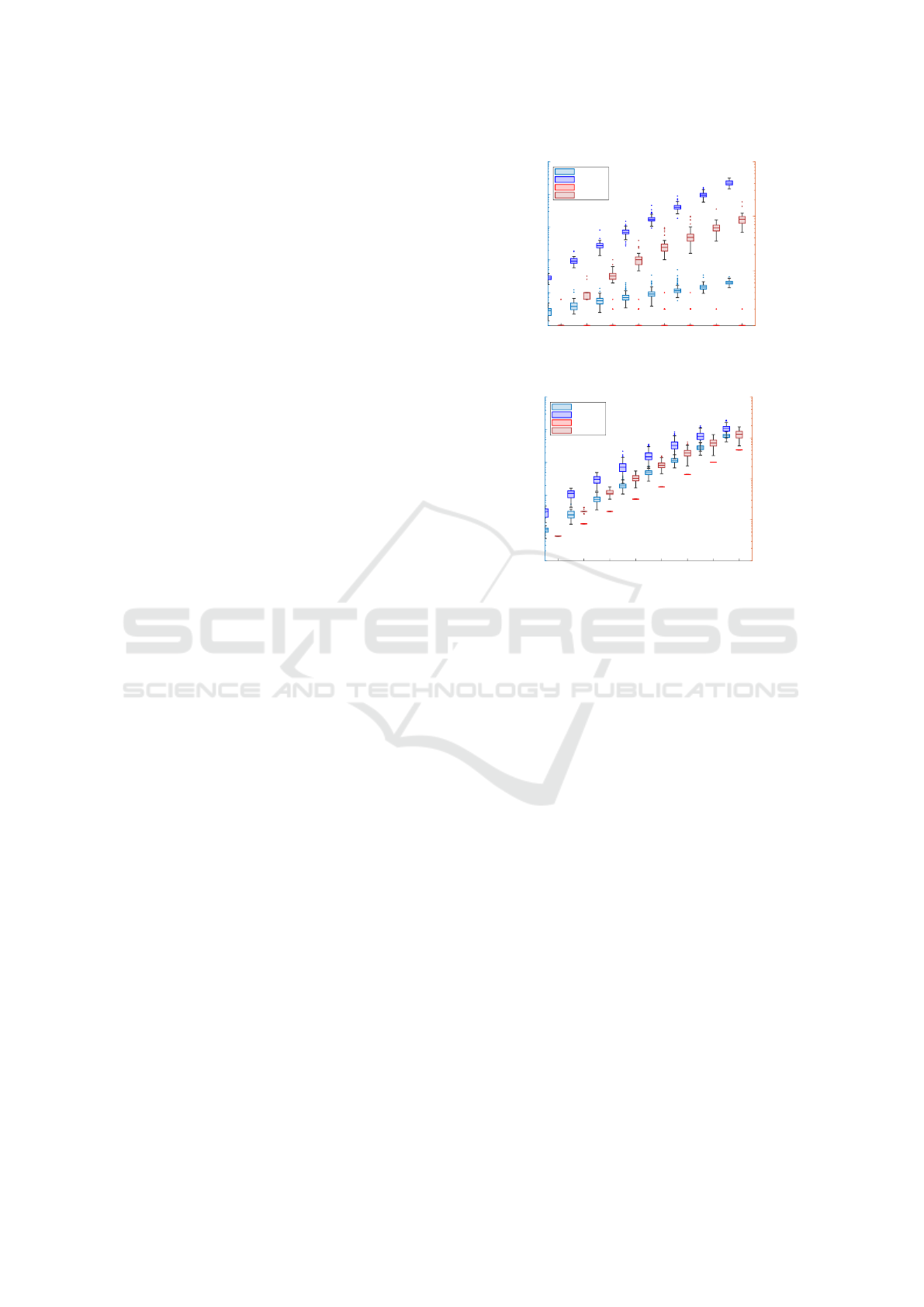
4.3 DSHC vs. B&B Computation Time
In Figure 10 the computation time (left axis) and num-
ber of area computations (right axis) are presented for
both DSHC-BF and B&B. In both instances, B&B
performs more area calculations and thus requires
more computation time; this computation time differ-
ence is more significant for low-budget cases.
For the low-budget cases, ∆ = 1.1δ
HC
, it is ob-
served that very few area calculations are performed
by DSHC-BF for all problem instances, irrespective
of η. This is due to many solutions not meeting the
small ∆
′
, and thus being filtered out prior to area cal-
culation. As such, the execution time is much faster
than B&B. In contrast, the number of area calcula-
tions performed by B&B grows exponentially to η
due to many partial solutions’ areas still being cal-
culated as the tree is expanded in order to find the
single (or small set of) valid solution(s). Due to these
partial solution explorations, the B&B search shows
rapid exponential growth relative to η.
In the high budget cases, ∆ = 1.5δ
HC
, the ma-
jority of solutions are within the travel budget and
thus the area calculations of DSHC-BF search is ex-
ponential relative to detours. As such, the variation
between the two search algorithms is reduced with
noticeable overlap at high η. That being said, the
B&B search has a much wider variation in both area
2 3 4 5 6 7 8 9
Detours
10
-4
10
-3
10
-2
10
-1
10
0
10
1
Time (log, sec)
10
0
10
1
10
2
10
3
Area Tests (log)
Brute time
Branch time
Brute exe
Branch exe
(a) ∆ = 1.1δ
HC
.
2 3 4 5 6 7 8 9
Detours
10
-4
10
-3
10
-2
10
-1
10
0
10
1
Time (log, sec)
10
0
10
1
10
2
10
3
10
4
Area Tests (log)
Brute time
Branch time
Brute exe
Branch exe
(b) ∆ = 1.5δ
HC
.
Figure 10: Time and Area calculations vs number of De-
tours for both BF DSHC and B&B with both small and large
travel budgets.
calculations performed and computation time due to
the tree search having a best-case computation count
(with complete bounding) of µ and a worst-case (with
no bounding) of
∑
η
i=1
(µ
i
).
From this experiment, it can be concluded that
tree-search algorithms, even B&B, are inappropriate
for the proposed problem, as hypothesised. This is be-
cause the repeated calculation of each node’s ‘value’
(while expanding the tree with partial detour solu-
tions) is more computationally expensive than the re-
ductions observed by bounding the search.
5 CONCLUSION
In this paper, a new heuristic was defined for mod-
ifying a space-filling path which circumvents holed
spaces. In doing so, a non-convex optimisation prob-
lem is produced which is NP-hard but simpler to
solve than the parent Budgeted Maximum Coverage
(BMC) path-planning problem. This paper demon-
strates the proposed path modification process on
the well-established Hilbert Curve (HC) path, find-
ing considerable area can be covered despite the space
Solving the Holed Space Budgeted Maximum Coverage Problem with a Discrete Selection Problem
23

having holes. That being said, it is noted that the pro-
duced solutions are not guaranteed to be globally op-
timal for the original BMC problem.
Via empirical evaluation, it has been shown that
this approach produces a path that, on average, cov-
ers more area than a HC modifying approach found
in literature (Nair et al., 2017). However, the pro-
posed approach requires considerably longer compu-
tation times.
Additionally, it has been demonstrated that the
proposed problem cannot be effectively solved via
traditional tree-search techniques due to the non-
convex nature of the detour overlapping areas.
In addition to this work acting as a new ap-
proach to the BMC problem, it is the authors’ be-
lief that the detour selection problem produced by
this method may act as a new test-bed for meta- and
hyper-heuristic research. In this initial examination,
it was shown that GA often found the global-optimal
solution in polynomial time, and there is potential for
other meta-heuristics to do likewise. Future work in
this domain aims to explore hyper-heuristics on more
challenging instances of this problem, specifically
cases with more than two detour options and hole
spaces based on real-world obstacle environments.
REFERENCES
Achat, S., Marzat, J., and Moras, J. (2023). Curved sur-
face inspection by a climbing robot: Path planning
approach for aircraft applications. In ICINCO 2023.
Arkin, E. M., Fekete, S. P., and Mitchell, J. S. (2000). Ap-
proximation algorithms for lawn mowing and milling.
Computational Geometry, 17(1):25–50.
Boyd, S. and Mattingley, J. (2007). Branch and bound meth-
ods. Notes for EE364b, Stanford University, 2006:07.
Cabreira, T. M., Di Franco, C., Ferreira, P. R., and Buttazzo,
G. C. (2018). Energy-aware spiral coverage path plan-
ning for uav photogrammetric applications. IEEE
Robotics and automation letters, 3(4):3662–3668.
Choset, H. and Pignon, P. (1998). Coverage path planning:
The boustrophedon cellular decomposition. In Zelin-
sky, A., editor, Field and Service Robotics, pages 203–
209, London. Springer London.
Dorigo, M. and St
¨
utzle, T. (2019). Ant colony optimization:
overview and recent advances. Handbook of meta-
heuristics, pages 311–351.
Gabriely, Y. and Rimon, E. (2001). Spanning-tree
based coverage of continuous areas by a mobile
robot. In Proceedings 2001 ICRA. IEEE Interna-
tional Conference on Robotics and Automation (Cat.
No.01CH37164), volume 2, pages 1927–1933 vol.2.
Garrido-Merch
´
an, E. C. and Hern
´
andez-Lobato, D. (2020).
Dealing with categorical and integer-valued variables
in bayesian optimization with gaussian processes.
Neurocomputing, 380:20–35.
Hilbert, D. (1935).
¨
Uber die stetige abbildung einer linie auf
ein fl
¨
achenst
¨
uck. In Dritter Band: Analysis· Grundla-
gen der Mathematik· Physik Verschiedenes, pages 1–
2. Springer.
Holland, J. H. (1992). Genetic algorithms. Scientific amer-
ican, 267(1):66–73.
Joshi, A. A., Bhatt, M. C., and Sinha, A. (2019). Modifica-
tion of hilbert’s space-filling curve to avoid obstacles:
A robotic path-planning strategy. In 2019 Sixth Indian
Control Conference (ICC), pages 338–343. IEEE.
Karaboga, D. (2005). An idea based on honey bee swarm
for numerical optimization. Technical report, Erciyes
University, Engineering Faculty Computer Engineer-
ing Department,Kayseri/T
¨
urkiye.
Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-
mization. In Proceedings of ICNN’95-international
conference on neural networks, volume 4, pages
1942–1948. IEEE.
Khuller, S., Moss, A., and Naor, J. S. (1999). The budgeted
maximum coverage problem. Information processing
letters, 70(1):39–45.
Nair, S. H., Sinha, A., and Vachhani, L. (2017). Hilbert’s
space-filling curve for regions with holes. In 2017
IEEE 56th Annual Conference on Decision and Con-
trol (CDC), pages 313–319. IEEE.
Nemhauser, G. L., Wolsey, L. A., and Fisher, M. L. (1978).
An analysis of approximations for maximizing sub-
modular set functions—I. Mathematical program-
ming, 14(1):265–294.
Richards, G. (2022). Hilbert curves, first to third
orders. https://commons.wikimedia.org/wiki/File:
Hilbert curve 3.svg. Last checked on Aug 09, 2024.
Van Laarhoven, P. J. and Aarts, E. H. (1987). Simulated
annealing. In Simulated annealing: Theory and ap-
plications, pages 7–15. Springer.
Viana, A. C. and De Amorim, M. D. (2013). Coverage strat-
egy for periodic readings in robotic-assisted monitor-
ing systems. Ad hoc networks, 11(7):1907–1918.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
24