Epidemic Modeling and Control: An ARX Approach for Measles
Containment
Paolo Di Giamberardino
a
and Daniela Iacoviello
b
Department of Computer, Control and Management Engineering Antonio Ruberti, Sapienza University of Rome, Italy
Keywords:
Measles, ARX Modeling, Containment Measures.
Abstract:
Measles is one of the most dangerous epidemic disease for its high reproduction number and the possible
complications on already weakened patients. Effective vaccination is available since the early 60s and a suit-
able vaccination campaign could interrupt this epidemic disease. The most common approach for the disease
description considers compartmental models, effective but requiring the identification of model parameters,
generally data consuming. A different approach is data driven, that is it consideres autoregressive modeling
with exogenous input. The autoregressive modeling is here considered describing measles evolution by using
measurable available information, like the number of infected patients and the percentage of vaccinated indi-
viduals. A penalized control is herein determined, thus taking into account also limitation in control actions.
Numerical results, based on available real data, show the effectivenes of the approach.
1 INTRODUCTION
Despite the existence of a safe and cost-effective vac-
cination since the early 60s, measles is still one of
the most dangerous epidemic disease, for the possi-
ble complications on already weakened patients and
for its high reproduction number, estimated equal to
14. According to the World Health Organization, it
is estimated that in 2022 there were 136000 measles
death globally, mostly among children under 5 years
old, unvaccinated or under-vaccinated. Immunization
activities prevented about 57 million deaths between
2000 and 2022 all over the world, (World Health Or-
ganization, 2024). Measles is caused by a virus that
infects, initially, the respiratory tract; early symptoms
(that last up to 7 days) include small white spots in-
side the cheeks, cough with runny nose and red eyes.
A prominent rash begins about 10 days after expo-
sure and it usually lasts less than a week. Most deaths
are from complications, like encephalitis, severe diar-
rhoea, ear infections and severe breathing problems.
The importance of facing measles and its com-
plications is the motivation of many research papers
focusing on modeling the evolution of the disease
and proposing possible control strategies. Generally,
the compartmental modeling results the most effec-
a
https://orcid.org/0000-0002-9113-8608
b
https://orcid.org/0000-0003-3506-1455
tive description, partitioning the population depend-
ing on the specific condition with respect to the dis-
ease; with the SEIR model, in particular, the popula-
tion is split into 4 compartments, including suscepti-
ble S, exposed E, infected I and removed R individu-
als. When considering also control actions, the classi-
cal SEIR model is further enriched by new elements,
like vaccination, as in (A. Kuddus, M. Mohiuddin and
A. Rahman, 2021), or by the class of pathogen pop-
ulation, the host of measles virus, as in (H. Alem-
neh, 2023). More complex models consider also sus-
ceptible subjects that cannot be vaccinated and pa-
tients that, along with measles, have also complica-
tions, (P. Di Giamberardino and D. Iacoviello, 2019a),
(P. Di Giamberardino and D. Iacoviello, 2019b), (P.
Di Giamberardino and D. Iacoviello, 2020). In this
case, the goals are both to provide heard immunity to
help subjects that cannot be vaccinated, and to help
patients: control actions include prevention, like in-
formative campaign and vaccination, and medication
referring both to patients with measles and patients
with measles and complications. Optimal control is
applied in (H. W. Berhe and O. D. Makinde, 2020),
where actions by vaccination, treatment, and preven-
tion by an education campaign are implemented.
The impact of preventive actions is discussed
in (O.J. Peter, H.S.Panigoro, M.A. Ibrahim,
O.M.Otunuga, T.A.Ayoola and A.O. Oladapo,
2023), where the role of the reproduction number is
632
Di Giamberardino, P. and Iacoviello, D.
Epidemic Modeling and Control: An ARX Approach for Measles Containment.
DOI: 10.5220/0012890500003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 632-639
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

faced. The numerical analysis supports and quantifies
the theoretical results, thus suggesting lowering
the effective contact with an infected person and
increasing the rate of vaccinating susceptible people.
In (Y. Xue, X. Ruan and Y. Xiao, 2021), it is in-
vestigated the influences of heterogeneity and immu-
nity on measles transmission, proposing a network
model with periodic transmission rate and examining
the threshold dynamics.
These compartmental models, while being effec-
tive, require the identification of parameters describ-
ing the transition from one condition to the others.
A possible different approach is data driven; in
this way the analysis and the control strategies are de-
termined just using the measured available data, as, in
this case, the number of infected patients and the per-
centage of vaccinated individuals. In this framework,
a useful representation is given by the autoregressive
model with exogenous input, namely the ARX and
the ARMAX models, (F. Piltan, S. Haghighi and N.
Sulaiman, 2017); starting from historical series and
by using identification methods, it is possible to de-
scribe complex phenomena. The number of infected
patients at the current time is expressed as a linear
combination of the number of patients in previous
years and of the control actions (the vaccinations) pre-
viously applied. In the ARX model the number of
infected patients is function of the current measure
noise, whereas in the ARMAX model also past errors
are considered.
In recent studies, (Y. Pei, Q.Pei, H. Lee, M. Qiu
and Y. Yang, 2022), historical epidemics data, along
with climate and economy ones, have been investi-
gated by means of autoregressive exogenous analy-
sis in the framework of human ecology; in particular,
ARX modeling has been used to simulate long-term
effects of climate change, economy and epidemics.
This approach is particularly useful in presence of
missing data, as in (M. Horner, S. Pakzad and N.
Gulcec, 2019), where structural health monitoring is
faced using also Kalman filtering.
The paper is organized as follows: in Section 2, af-
ter a brief recall of the ARX model with the penalized
optimal control and the identification of the model pa-
rameters, the specific ARX model for epidemic dis-
eases is developed. Numerical results, reported in
Section 3, are based on real data, implementing the
described procedures, from the data processing, to the
ARX model identification, to the penalized optimal
control definition and state prediction. In the conclu-
sions the obtained results are summarized, proposing
also future developments.
2 MATERIALS AND METHODS
The measles epidemic disease is usually described by
means of a compartmental model in which the pop-
ulation is partitioned into groups homogeneous with
respect to the disease conditions. For example, of-
ten the SEIR model is efficiently used, thus assuming
that an healthy subject in the susceptible class S can
be infected by an infected patient belonging to the I
class. He becomes infected but not infectious yet, thus
belonging to the E class of exposed, before the tran-
sit to the I class. Successively, he can recover, thus
leaving the I class and going to the R one. This de-
scription, while being realistic, is not easy to be im-
plemented since it requires the knowledge of the tran-
sit parameters from one class to the other. These pa-
rameters are strongly connected to the general healthy
conditions of the population under study and must be
identified considering real data, sometimes not avail-
able and consistent. Another approach is data driven,
meaning that the description of the measles diffusion
is obtained by means of the unique available informa-
tion, the number of infected patients and of adminis-
trated vaccines. The proposed approach falls within
this area, considering in particular the autoregressive
models with exogenous input, the ARX models. In
the next Subsections, this class of models is briefly
recalled and adapted to the specificity of the measles
disease.
2.1 Brief Recall of the ARX Model
The ARX is an autoregressive model with exogenous
input. It is useful the notation of the backward shift
operator z
−1
: for a given scalar process x(t), one has
z
−1
x(t) = x(t − 1). The classical ARX model can be
represented as follows:
A(z
−1
)y(t) = z
−d
B(z
−1
)u(t) +C(z
−1
)e(t) (1)
where:
A(z
−1
) = 1 + a
1
z
−1
+ .... + a
n
z
−n
(2)
B(z
−1
) = b
0
+ b
1
z
−1
+ .... + b
m
z
−m
(3)
C(z
−1
) = 1 (4)
with d > 0 denoting the delay of the system, b
0
̸=
0 and e(t) representing a white noise process, with
zero mean value and variance σ
2
; y(t) and u(t) are
jointly stationary processes representing, in the pro-
posed framework, the number of infected patients and
the applied control at time t, respectively. The control
Epidemic Modeling and Control: An ARX Approach for Measles Containment
633

process u up to t − 1 is realistically assumed indepen-
dent on the noise process e.
The system (1) represents the situation in which
the number of infected patients at time t is function of
the sequence of the number of infected patients in the
past, up to a chosen time t − n, of the applied control
actions u, from t − 1 up to the instant (t − m − 1) and
of the noise e(t).
For d = 1, it is useful to represent the current mea-
sure y(t) as:
y(t) = φ
T
(t)θ + e(t) (5)
where
φ(t) =







−y(t − 1)
...
−y(t − n)
u(t − 1)
...
u(t − m)







(6)
and
θ =







a
1
...
a
n
b
1
...
b
m







(7)
Equation (5) is already in prediction form; there-
fore, the 1–step predictor can be written as follows:
ˆy(t|t − 1) = φ
T
(t)θ (8)
with the prediction error ε, function of the current in-
stant t and of the set of coefficients θ, given by:
ε(t, θ) = y(t) − ˆy(t|t − 1) = y(t) − φ
T
(t)θ (9)
With a delay d > 1, this procedure is no longer useful;
it is necessary to solve the Diofantine equation:
C(z
−1
) = A(z
−1
)Q(z
−1
) + z
−d
¯
R(z
−1
) (10)
that is, it is necessary to solve the long division be-
tween C(z
−1
) and A(z
−1
) up to the point in which
in the remainder R(z
−1
) it appears the term z
−d
and
therefore it is possible to write R(z
−1
) = z
−d
¯
R(z
−1
).
The polynomials Q(z
−1
) and
¯
R(z
−1
) are given by:
Q(z
−1
) = q
0
+ q
1
z
−1
+ .... + q
d−1
z
−(d−1)
(11)
¯
R(z
−1
) = r
0
+ r
1
z
−1
+ .... + r
n−1
z
−(n−1)
(12)
The optimal predictor in the general case of d ≥ 1
is given by:
C(z
−1
) ˆy(t|t − d) =
¯
R(z
−1
)y(t − d)
+B(z
−1
)Q(z
−1
)u(t − d) (13)
that is, with C(z
−1
) = 1 in the ARX case:
ˆy(t|t − d) =
¯
R(z
−1
)y(t − d) + B(z
−1
)Q(z
−1
)u(t − d)
(14)
By using (11), (3), (12), the latter expression can be
explicitly written as follows:
ˆy(t|t − d) =
n−1
∑
i=0
(r
i
y(t − d − i))
+
m+(d−1)
∑
j=0
j
∑
k=0
b
k
q
j−k
u(t − d − j) (15)
2.2 Penalised Optimal Control of the
ARX Model
The choice of the control action can be done follow-
ing the goal of an optimal tracking of the variable y(t)
to a given reference y
r
(t). This can be obtained mini-
mizing the cost index:
J = E[(y(t) + βu(t − d) − y
r
(t − d))
2
] (16)
with β ≥ 0 the coefficient of a penalty control. This
implies that the optimal choice of the control is ob-
tained weighting also its cost, thus aiming at the op-
timal tracking, penalizing possible too strong control
actions. As β increases, generally the behaviour of
the control variable becomes more regular.
Let us assume that the autoregressive AR part of
the model (1) is asymptotically stable, that is the poly-
nomial A(z
−1
) has poles strictly inside the unit circle.
In this case, the minimization of the cost index (16) is
obtained once
ˆy(t|t − d) = −βu(t −d) + y
r
(t − d) (17)
The optimal predictor ˆy(t|t − d) with β = 0 is given
by (15); by substituting this expression into (17), the
expression
u
o
(t − d) =
1
β + b
0
q
0
(y
r
(t − d) −
n−1
∑
i=0
(r
i
y(t − d − i))
−
m+(d−1)
∑
j=1
j
∑
k=0
b
k
q
j−k
u(t − d − j)) (18)
is obtained or, equivalently:
u(t) =
1
β + b
0
q
0
(y
r
(t) −
n−1
∑
i=0
(r
i
y(t − i))
−
m+(d−1)
∑
j=1
j
∑
k=0
b
k
q
j−k
u(t − j)) (19)
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
634

This is the penalized optimal control to be applied
at time t to reduce the distance to the reference y
r
(t)
at time t +d.
By using the delay operator, equation (19) can be
written as:
(β + b
0
q
0
+
m+(d−1)
∑
j=1
j
∑
k=0
b
k
q
j−k
z
− j
)u(t)
= y
r
(t) −
n−1
∑
i=0
(r
i
y(t)z
−i
) (20)
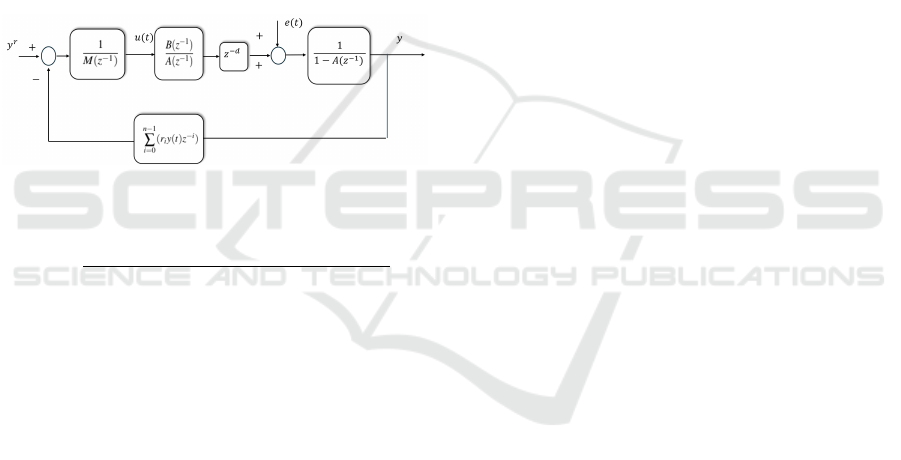
A block diagram of the ARX model is given in
Fig. 1, where the notation
M(z
−1)
) = (β + b
0
q
0
+
m+(d−1)
∑
j=1
j
∑
k=0
b
k
q
j−k
z
− j
)
is adopted.
Figure 1: Block diagram of the ARX model.
The transfer function of the loop is given by:
L(z
−1
) =
B(z
−1
)z
−d
A(z
−1
)
∑
n−1
i=0
(r
i
z
−i
)
(β + b
0
q
0
+
∑
m+(d−1)
j=1
∑
j
k=0
b
k
q
j−k
z
− j
)
(21)
with the poles of the closed loop obtained from:
∆ = 1 + L(z
−1
) (22)
that is:
B(z
−1
)z
−d
A(z
−1
)
n−1
∑
i=0
r
i
z
−i
+ β + b
0
q
0
+
m+(d−1)
∑
j=1
j
∑
k=0
b
k
q
j−k
z
− j
= 0 (23)
Note the role of the penalty term β, able to modify the
poles of the transfer function of the loop and therefore
the system behaviour. The analysis of the poles and
of their variation as β goes to infinite will be studied
in the numerical section for the specific problem at
hand.
2.3 Identification of the ARX Model
Parameters
What has been discussed up to now assumes that an
identified model ARX is available. It means that
the phenomenon under investigation (in the proposed
study, the measles evolution when vaccination strat-
egy is applied) has been described by an ARX model
with chosen order (n, m) and identified coefficients a
i
,
i = 1, ..., n and b
j
, j = 0, ..., m. Moreover, also the de-
lay with which one wants to determine the optimal
control to track a given reference must be established;
anyway, this latter can be left as a parameter to be dis-
cussed in the numerical section. The identification of
the model parameters is obtained by using the least
square estimation, minimizing the square of the dif-
ference between the model (1) and the available real
data. The order of the model is related to the amount
of available data, thus resulting from a compromise
between the requirement of a model with high order
(equivalent to long memory) and the usually limited
number N of couples of real inputs u(t) (the adminis-
tered vaccination) and of real outputs y(t) (the number
of positive patients).
Without loosing generality, assume the delay d =
1 and consider the prediction in the form (8): it is
linear in the parameter vector (7). To estimate θ, by
using the prediction error method it is minimized the
cost function:
J
N
(θ) =
N
∑
t=1
(y(t) − φ(t)
T
θ)
2
(24)
The solution is analogous to the least square estima-
tion:
ˆ
θ
N
= (
N
∑
t=1
φ(t)φ
−1
(t))
−1
(
N
∑
t=1
φ(t)y(t)) (25)
It is possible to find the solution of this identification
problem once N ≥ (n + m).
2.4 The ARX Model for
Epidemiological Environment
The availability of historical data allows the identi-
fication of the ARX model, where the measure y(t)
is the number of infected patients I(t) per million of
people at time t, and the control u(t) is the percent-
age of vaccinated individual in the population. In the
data driven approach used in this paper, the historical
series of data are split into two sets; the first one is
used for the identification of the ARX, whose order
depends on the amount N of data that can be used for
the identification, as described previously. The sec-
ond set is used to validate the identified model, thus
checking how much it adequately describes the data
not used for the identification.
Note that for the specific application in epidemiol-
ogy, a reasonable choice for the model’s order should
Epidemic Modeling and Control: An ARX Approach for Measles Containment
635

take into account the reproduction number R
0
, rep-
resenting the average number of subjects that can be
infected by a unique individual in the period in which
he is infectious. This information is important since a
low number would slow the epidemic, whereas a high
one speeds up the spread by increasing the influence
of the number of infected subjects in recent period;
in particular, the estimated reproduction number for
the measles is 14. Another important aspect is the im-
munization effects of the vaccine which, for measles,
occur almost immediately. The incubation time of the
disease, which is about 10 days, while being a fun-
damental information in a compartmental model, in
this case seems less important to be considered for
the identification purposes.
If the identification step provides acceptable fit-
ting between real data and the model outputs, a re-
liable model for the dynamics of the number of in-
fected subjects, connected with the vaccination cam-
paign, becomes available.
This allows, following the procedure of Subsec-
tion 2.2, to determine the control action u(t), possibly
penalized (by the coefficient β), to minimize the ex-
pected value given in (16), that is to make the num-
ber of infected patients, I(t), as close as possible to a
desired reference, say I
r
(t), more manageable by the
national health service.
In Subsection (2.2), it is considered also the pos-
sibility of yielding the best control at time t to reduce
the distance between the predicted number of infected
patients
ˆ
I(t + d|t), once given the information avail-
able at time t, and the desired trend I
r
.
In the next Section, the discussed ARX model is
identified on real data, showing its effectiveness and
limits.
3 NUMERICAL RESULTS
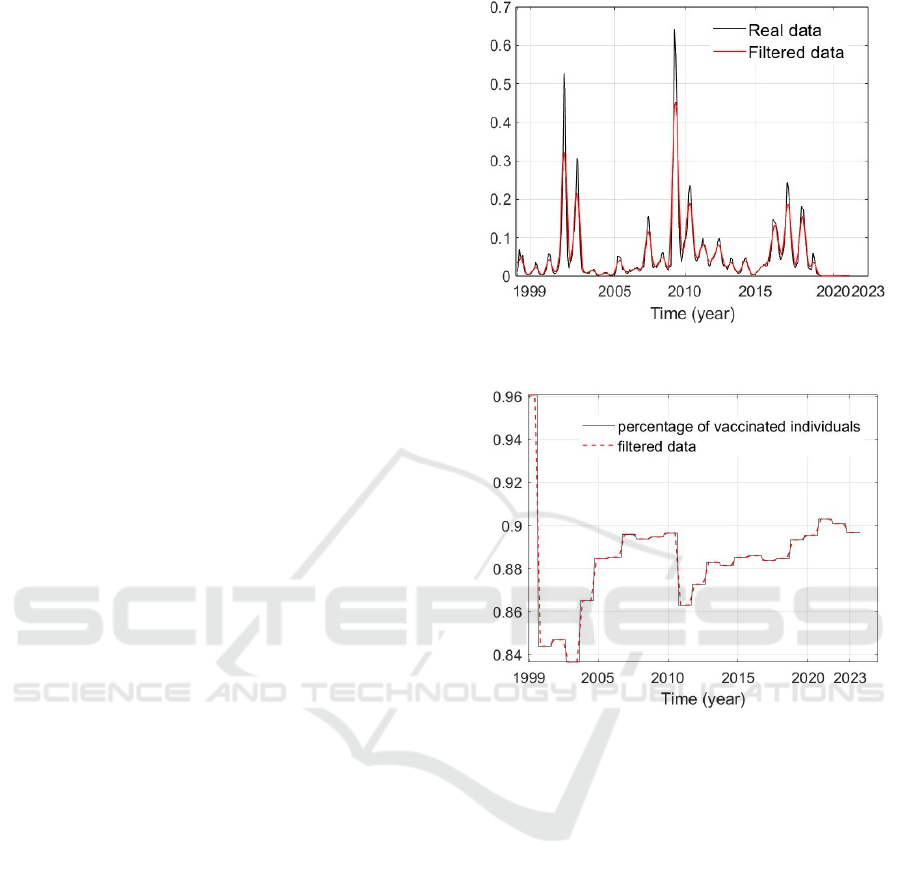
The data considered in this section are taken from
(Surveillance atlas of infectious diseases, 2024); they
are the sequence of the numbers of infected indi-
viduals, per million, in Europe (without consider-
ing United Kingdom) between 1999 and 2024, taken
monthly, see Fig.2. Moreover, with the same time
unit, it is available the percentage of vaccinated indi-
viduals, see Fig.3. Since in the ARX model the num-
ber of infected patients and the number of vaccinated
people are connected by the equation (1), it is neces-
sary to normalize the data.
To filter the real data, without loosing relevant in-
formation, a moving average of a windows of 5 sam-
ples is assumed; as seen in the cited figures, this al-
lows to cut and smooth some peaks in real data.
Figure 2: Evolution of the number of infected subjects per
million; in black, real data; in red, filtered real data.
Figure 3: Evolution of the percentage of vaccinated individ-
uals; in black, real data; in red, filtered real data.
The available data cover the period of less than 25
years; for the ARX model identification, it is chosen a
period of two years that contains the general periodi-
cal trend, thus corresponding to 24 samples. As a first
attempt it is chosen an ARX model with n = m = 3
and delay d = 1. By using the least square estimation
method, the identified model is
(1 + a
1
z
−1
+ a
2
z
−2
+ a
3
z
−3
)y(t)
= (b
1
z
−1
+ b
2
z
−2
b
3
z
−3
)u(t) (26)
that is:
(1 − 1.898z
−1
+ 1.274z
−2
− 0.1479z
−3
)y(t)
= (−1.533z
−1
+ 1.606z
−2
− 0.06802z
−3
)u(t)
(27)
In Fig.4 it is shown the comparison between the
real data used for the identification and the output of
the ARX model. An higher number of data used for
the identification yields a low quality; it is possible
to obtain higher fitting by reducing the period over
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
636

Figure 4: Comparison between real data and the ones re-
constructed by the ARX model.
which the model is identified, but the risk is to obtain
an overfitting, unable to generalize the model.
By using the model (27) it is possible to deter-
mine the characteristics of the noise present in the
data regarding two years, assuming, reasonably, that
the statistics of the noise remain almost the same in
all the control period; the mean value is estimated in
3.16 · 10
−5
with a standard deviation of 0.0015.
The availability of an ARX model allows to pre-
dict the possible behaviour of the number of infected
patients, once the penalized control (19) is adopted;
the windows on which this prediction is determined,
along with the penalized control, is chosen corre-
sponding to a period of 18 months. A longer period
could yield an unreliable prediction, being based on a
model identified on data of a window starting 24 + 18
months before, thus referring to a too long period. As
a first choice, it is simulated the identified model (27),
with no penalization (that is β = 0), and a realization
of noise with the estimated mean value and standard
deviation.
In Fig.5 it is shown the simulated behaviour of the
number of infected patients once the control (19) is
implemented, versus the real trend of infected individ-
uals; in Fig. 6 it is shown the simulated control versus
the really applied vaccination strategy. Considering
the two Figures 5 and 6, it can be noted that without
any penalization, the control can assume high values
reaching rapidly about 90% of vaccination coverage
and, consequently, the number of infected patients de-
creases almost immediately.
These results are promising, but it must be con-
sidered that no limitations in control actions are intro-
duced; moreover, it is assumed, implicitly, as refer-
ence y
r
(t) = 0, thus requiring a strong effort for a fast
reduction of the number of infected patients.
Figure 5: Comparison between real data of infected patients
(in black) and the ones reconstructed by the ARX model
under the optimal control (19), in red.
Figure 6: Comparison between real data of vaccination and
the the optimal control (19).
If these conditions are not applicable, the pro-
posed approach allows to include a penalization for
the strong control actions and, at the same time, ac-
cept a less restrictive reference y
r
. To stress the in-
fluence of β and y
r
, behind the basic situation con-
sidered, indicated for simplicity as case 1, three new
cases are analysed:
2. β = 0 with y
r
= 0.01
3. β = 0.001 with y
r
= 0.01
4. β = 0.005 with y
r
= 0.01
The situation 2 is still with a non penalized control
with the goal of tracking a low non null number of
infected patients; in case 3 it is considered also a pe-
nalization, as well as in the forth case, with a higher
weight for β.
In the non penalized case, the obtained control is
able to make the state fluctuate around the reference,
Fig. 7, with a low mean value for the tracking error,
respectively equal to 0.0065 (case 1) and 0.0077 (case
2). In the penalized control of case 4 the tracking
Epidemic Modeling and Control: An ARX Approach for Measles Containment
637

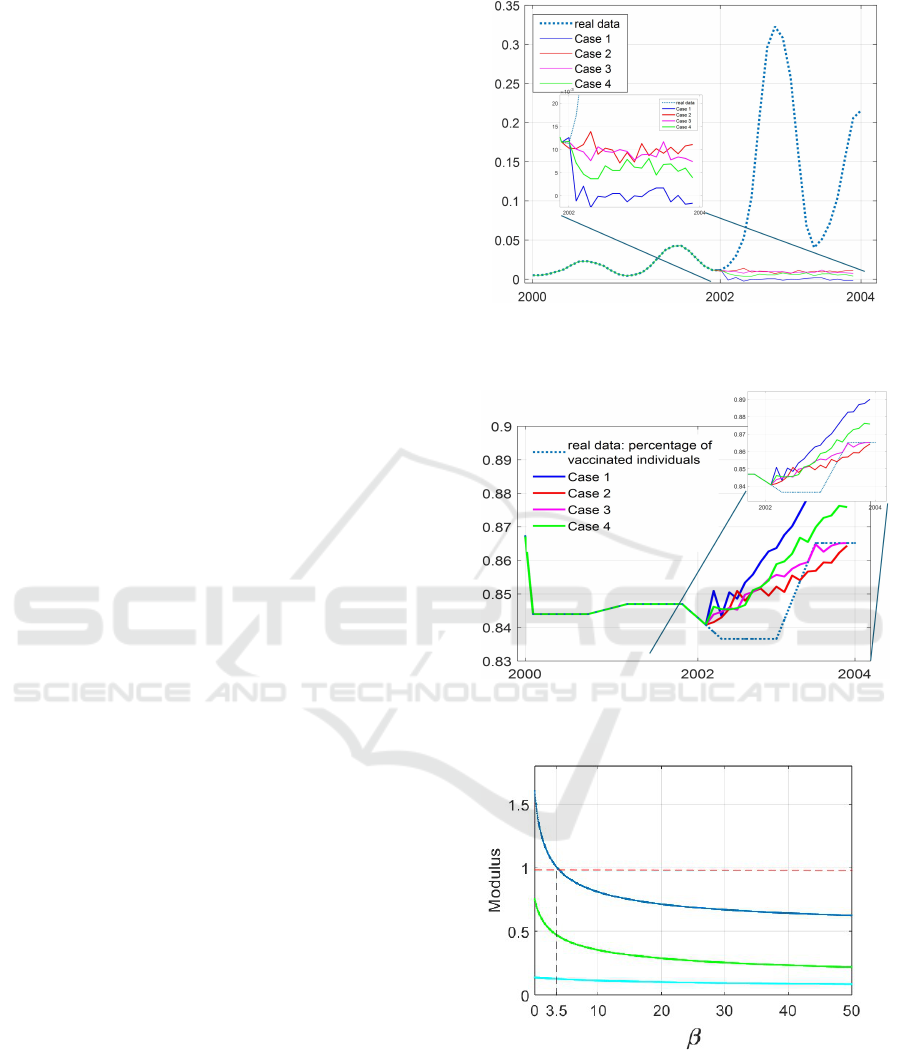
error is of one order higher, equal to 0.0119; this is
reasonable, being the control not as efficient as in the
first two cases.
Comparing the behaviours of the controls, Fig. 8,
besides the higher values obtained in case 1, it can be
noted that, for cases 2 and 4, for the first 8 months the
values of u(t) are generally higher in the non penal-
ized case, as obvious; on the other hand, from month
9 on, when the predictive control is less reliable, the
trend of the two controls are reverted. Nevertheless,
the tracking appears still acceptable. An interesting
case is the third, with an intermediate behaviour; the
tracking error is the same as in the non penalized con-
trol of case 1: this can be justified noting that for the
system it is easier the tracking to the value 0.01 of
(case 3) rather than to the value 0 of (case 1), requir-
ing, in this latter situation, a stronger action. As far as
the control, u(t), its behaviour is between the ones of
case 2 and 4.
As discussed in Subsection 2.2, it is interesting to
study the poles of the closed loop transfer function
obtained from (22); for the chosen model identified
in (27), the roots to be determined comes from the
polynomial (23), that is:
∆ =(1 + a
1
(β − b
1
))z
4
− (a
1
b
2
− a
2
(β − b
1
))z
3
−
(a
2
b
2
+ a
1
b
2
− (β − b
1
)a
3
)z
2
−
(b
2
a
3
+ b
2
a
2
)z − b
2
a
3
(28)
The stability is reached if all the roots have mod-
ulus inside the circle of unit radius.
It is interesting to note the dependency of the roots
on the values of β. In absence of penalization, that
is assuming β = 0, there are three roots with modu-
lus less than 1 and one root with modulus equal to
1.6056, thus the system is unstable. As β increases all
the roots move away from the zone of instability, as
can be noted in Fig. 9; it is shown the evolution of the
fours roots as β increases. All the roots have modu-
lus less than 1 for β ≥ 3.5. With a strongly penalized
control the system becomes stable, with a more regu-
lar action.
4 CONCLUSIONS
In this paper a data driven approach to face the
measles epidemic spread control is addressed. The
unique available and measurable information are the
number of infected patients and the vaccination cov-
erage; the autoregressive model ARX allows to repre-
sent the current measurable number of infected pa-
tients as function of the characteristics of the pan-
demics, i.e. the weighted sum of the past numbers
Figure 7: Comparison between real data of Infected patients
per million and the corresponding values obtained in Case
1, 2, 3, 4 described in the text.
Figure 8: Comparison between real data of percentage of
vaccinated patients and the corresponding values obtained
in Case 1, 2, 3, 4 described in the text.
Figure 9: Evolution of the modulus of each root of ∆ as
penalty parameter β increases. Note that two roots have
almost the same modulus and this is the reason for which
only three evolutions are evident in the figure.
of infected individuals and of the percentage of vac-
cinated subjects. It is possible to determine the pe-
nalized optimal control (i.e. the vaccination) that re-
duces the difference between the number of infected
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
638

patients and an acceptable threshold, penalising too
high values of control actions.
Some general remarks can be summarized:
• the data driven approach considered describes the
epidemic spread without using population model-
ing by means of compartmental description; this
allows to avoid identification of parameters, like
contact rate, strongly dependent on the specific
population;
• the proposed autoregressive approach with exoge-
nous input describes the data by a linear system;
this implies that the predictive approach could be
limited to few months;
• the ARX model must be identified using histori-
cal data; depending on the consistency of the col-
lected data, the identification is more or less reli-
able;
• in absence of penalization, with the proposed
model it is possible to track y
r
, with higher control
values when the goal to be pursued for infected
patients, the reference, is equal to 0;
• with a penalization term by means of the coeffi-
cient β, the tracking is in general less efficient, as
expected, being the control lower;
• with a strong penalization term the system be-
comes stable and the control should be lower and
more regular. In the proposed analysis, in the pre-
dicted evolution this occurs for about one year, as
far as the prediction becomes less reliable.
The results, determined on real data, appears
promising, showing the effectiveness of the data
driven approach, despite some possible criticisms
with respect to the ARX model identification.
ACKNOWLEDGEMENTS
The Authors wish to thank the Istituto Nazionale di
Alta Matematica Francesco Severi in Rome for its
support.
REFERENCES
A. Kuddus, M. Mohiuddin and A. Rahman (2021). Math-
ematical analysis of a measles transmission dynamics
model in bangladesh with double dose vaccination. In
Scientific Reports.
F. Piltan, S. Haghighi and N. Sulaiman (2017). Comparative
study between arx and armax system identification. In
I.J. Intelligent Systems and Applications.
H. Alemneh (2023). Modelling, analysis, and simulation of
measles disease transmission dynamics. In Discrete
dynamics in Nature and Society.
H. W. Berhe and O. D. Makinde (2020). Computational
modelling and optimal control of measles epidemic in
human population. In Biosystems.
M. Horner, S. Pakzad and N. Gulcec (2019). Parameter es-
timation of autoregressive-exogenous and autoregres-
sive models subject to missing data using expectation
maximization. In Frontiers in Built Environment. 7.
O.J. Peter, H.S.Panigoro, M.A. Ibrahim, O.M.Otunuga,
T.A.Ayoola and A.O. Oladapo (2023). Analysis and
dynamics of measles with control strategies: a mathe-
matical modeling approach. In International Journal
of dynamicsa and control. 7.
P. Di Giamberardino and D. Iacoviello (2019a). Analy-
sis, simulation and control of a new measles epidemic
model. In Proceedings of the 16th International Con-
ference on Informatics in Control, Automation and
Robotics.
P. Di Giamberardino and D. Iacoviello (2019b). Modeling
and control of measles epidemic spread with immun-
odepressed individuals and possible complications. In
Proceedings of the IEEE Conference on Decision and
Control.
P. Di Giamberardino and D. Iacoviello (2020). A new
measles epidemic model: analysis, identification and
prediction. In 28th Mediterranean Conference on
Control and Automation.
Surveillance atlas of infectious diseases (2024). In
https://atlas.ecdc.europa.eu/public/index.aspx.
World Health Organization (2024). In https://www.who.int/.
Y. Pei, Q.Pei, H. Lee, M. Qiu and Y. Yang (2022). Epi-
demics in pre-industrial europe: Impacts of climate
change, economic well-being, and population. In An-
thropocene.
Y. Xue, X. Ruan and Y. Xiao (2021). Measles dynamics
on network models with optimal control strategies. In
Advances in Continuous and Discrete Models.
Epidemic Modeling and Control: An ARX Approach for Measles Containment
639