Reducing the Transformer Architecture to a Minimum

Bernhard Bermeitinger

1,∗ a

, Tomas Hrycej

2,∗

, Massimo Pavone

2,∗∗

, Julianus Kath

2,∗∗

and Siegfried Handschuh

2,∗ b

Institute of Computer Science in Vorarlberg, University of St. Gallen (HSG), Dornbirn, Austria

Institute of Computer Science, University of St.Gallen (HSG), St. Gallen, Switzerland

∗

{ﬁrstname.lastname}@unisg.ch,

∗∗

{ﬁrstname.lastname}@student.unisg.ch

Keywords:

Attention Mechanism, Transformers, Computer Vision, Model Reduction, Deep Neural Networks.

Abstract:

Transformers are a widespread and successful model architecture, particularly in Natural Language Process-

ing (NLP) and Computer Vision (CV). The essential innovation of this architecture is the Attention Mecha-

nism, which solves the problem of extracting relevant context information from long sequences in NLP and

realistic scenes in CV. A classical neural network component, a Multi-Layer Perceptron (MLP), complements

the attention mechanism. Its necessity is frequently justiﬁed by its capability of modeling nonlinear relation-

ships. However, the attention mechanism itself is nonlinear through its internal use of similarity measures.

A possible hypothesis is that this nonlinearity is sufﬁcient for modeling typical application problems. As the

MLPs usually contain the most trainable parameters of the whole model, their omission would substantially

reduce the parameter set size. Further components can also be reorganized to reduce the number of parame-

ters. Under some conditions, query and key matrices can be collapsed into a single matrix of the same size.

The same is true about value and projection matrices, which can also be omitted without eliminating the sub-

stance of the attention mechanism. Initially, the similarity measure was deﬁned asymmetrically, with peculiar

properties such as that a token is possibly dissimilar to itself. A possible symmetric deﬁnition requires only

half of the parameters. All these parameter savings make sense only if the representational performance of the

architecture is not signiﬁcantly reduced. A comprehensive empirical proof for all important domains would be

a huge task. We have laid the groundwork by testing widespread CV benchmarks: MNIST, CIFAR-10, and,

with restrictions, ImageNet. The tests have shown that simpliﬁed transformer architectures (a) without MLP,

(b) with collapsed matrices, and (c) symmetric similarity matrices exhibit similar performance as the original

architecture, saving up to 90 % of parameters without hurting the classiﬁcation performance.

1 INTRODUCTION

Recently, Large Language Models (LLMs) have

shown impressive performance in producing complex

text answers to given questions. Their outstanding

feature is the massive size of parameter sets (up to

billions). The rapidly growing parameter number has

limited the possibility of developing such models (as

well as objectively investigating their properties) to

companies and institutions capable of making consid-

erable investments in computing the model’s parame-

ters.

This is why it is of great interest to attempt to

ﬁnd more efﬁcient conﬁgurations with fewer param-

eters without performance loss. A computing model

with an excellent success record is based on the trans-

https://orcid.org/0000-0002-2524-1850

https://orcid.org/0000-0002-6195-9034

former architecture (Vaswani et al., 2017). Their suc-

cess is due to an excellent ability to capture con-

textual information. Initially developed for language

processing, transformers have also been successfully

used in Computer Vision (CV). The analogy to lan-

guage processing is the following: the semantics of

individual words are determined by other words in

the word sequence. Frequently, the basic units are not

words but tokens (e.g., n-grams consisting of n con-

secutive letters). Since the Vision Transformer (Doso-

vitskiy et al., 2021), in an image, the tokens are repre-

sented by patches — typically square regions of pix-

els in the image. Other patches can inﬂuence or dis-

ambiguate a patch’s conceptual meaning. For exam-

ple, the environment in which an individual object is

embedded in the image may disambiguate the identi-

ﬁcation of a speciﬁc bird or mushroom species.

The fundamental concept of the transformer is that

234

Bermeitinger, B., Hrycej, T., Pavone, M., Kath, J. and Handschuh, S.

Reducing the Transformer Architecture to a Minimum.

DOI: 10.5220/0012891000003838

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 234-241

ISBN: 978-989-758-716-0; ISSN: 2184-3228

of attention (Bahdanau et al., 2016). It is based on the

insight that a particular token’s semantics are inﬂu-

enced by its close relationships with other tokens. The

tokens are encoded as real-valued vectors in a high-

dimensional space (frequently around 1,000 dimen-

sions or more). These vectors are called embeddings.

The algebraic similarity between the embedding vec-

tors measures the semantic proximity between the to-

kens. This similarity measure is the vector product or

the cosine angle between the vectors. The weighting

of tokens by such similarity measure is called atten-

tion, which, in analogy to human attention, focuses

on relevant concepts. From the computational point

of view, a transformer is a structure consisting of

• an algorithm for consideration of token context,

the attention mechanism, and

• a Multi-Layer Perceptron (MLP) for nonlinear

transformation of intermediary data.

Multi-Head Attention. For every transformer in

the stack, the following processing is done by the at-

tention mechanism (multi-head attention or MHA).

The input of a training sample in the stack’s s-th

Transformer (out of their total number S) is a se-

quence of input vectors x

. This sequence is trans-

formed into an equally long sequence of output em-

beddings z

. Each of them is, for given weights, a

formally linear transformation

∑

j=1

si j

s j

∑

j=1

si j

s j

(1)

i.e., a weighted average of input embeddings x

, lin-

early transformed by matrix W

. The weight vec-

tors a

= [a

si1

si2

,... ,a

sii

] are computed as

= Softmax (s

) (2)

The vector argument of the Softmax() function mea-

sures the similarity between a present token x

, “the

query” and another token x

, “the key”.

si j

= x

s j

(3)

This form of attention mechanism is referred to as

single-head. A popular variant consists of an exten-

sion to multiple heads indexed by h:

∑

h=1

∑

j=1

shi j

s j

(4)

Each head has its separate matrices W

, W

and W

. The weights are also computed separately as

shi

= Softmax (s

shi

) (5)

and

shi j

= x

s j

(6)

Multi-Layer Perceptron. The second component

is a standard MLP with a single hidden layer, applied

to each intermediary embedding z

= f



(1)

+ b

(1)



= h

(2)

+ b

(2)

(7)

with f () being a nonlinear function, usually the Gaus-

sian Error Linear Unit (GELU) (Hendrycks and Gim-

pel, 2023), weight matrices W

(1)

and W

(2)

as well as

bias vectors b

(1)

and b

(2)

(He and Hofmann, 2024) have investigated the

possibilities of simplifying the transformer archi-

tecture. Their focus has been increasing the sig-

nal throughput through the network. The proposed

changes primarily consist of modifying or omitting

shortcut connections and normalizing layers. In addi-

tion, they have addressed the possibility of omitting

matrices W

and W

. The last idea has also been im-

plemented in our modiﬁcations proposed in Section 3.

Our focus is different: we intend to substantially

reduce trainable parameters to accelerate the training

and improve convergence.

2 TRANSFORMER WITHOUT

THE MLP

The MLP requires the majority of the parameters to be

ﬁtted. This is justiﬁed by the argument that the MLP

is the vehicle for implementing nonlinear mappings.

However, it can be argued that the ﬁrst compo-

nent, the attention mechanism, can also capture non-

linearities. It is the variable weights that make the

mapping nonlinear. The argument of the Softmax()

function is already a quadratic function of input to-

kens, and the function itself is nonlinear. Even if the

Softmax() were linear, the multiplication of input to-

kens by the weights a

si j

(which are quadratic in these

tokens) would result in a cubic function of input to-

kens. The nonlinearity of Softmax() makes this map-

ping only more nonlinear.

So, a stack of S transformers is a chain of S at

least cubic functions of the input, resulting in a func-

tion of polynomial order of at least 3S. This makes

clear that subsequent processing by an MLP is not the

only nonlinear element of the processing. The extent

of the task’s nonlinearity cannot be assessed in ad-

vance. Still, the hypothesis that a reduced transformer

without an MLP may cover the nonlinearity needs for

Reducing the Transformer Architecture to a Minimum

235

some tasks is justiﬁed and can be validated by appro-

priate tests.

Without the MLPs, the transformer architecture

can be described in more explicit terms. This is par-

ticularly the case if a single-head option is pursued.

3 SINGLE-HEAD

CONFIGURATION

Although the matrices W

, W

, and W

can the-

oretically map the embedding vector to an arbitrary

vector width, it is common to keep this width constant

throughout the model, referring to the model width N.

Then, in the case of a single head, these matrices are

square. With square matrices, it is evident that W

can be collapsed to a single matrix W

, and, ana-

logically, W

to W

. This saves 50 % of the

attention module’s parameters, from 4SN

to 2SN

Concatenating the transformer-encoder layers

without MLP leads to the following recursion:

∑

j=1

1i j

1 j

∑

j=1

2i j

1 j

∑

k=1

2ik

∑

j=1

1k j

1 j

= W

∑

k=1

2ik

∑

j=1

1k j

1 j

·· ·

(8)

When stacking the attention modules, the matrices

concatenate to their product over s = 1,...,S.

Then, they collapse into a single matrix

∏

s=1

(9)

Since every sum

∑

j=1

si j

is equal to unity (as a re-

sult of the softmax operation), every successive trans-

former layer performs a weighted mean of stacked in-

puts x

1 j

The total number of parameters with S matrices

and a single matrix W

is (S + 1)N

, only

slightly more than 25 % of the original size without

MLP. So far, all this is possible without losing any ex-

pressive power of the single-head transformer without

MLP — only obsolete parameters are deleted.

In many NLP applications, the output of the last

transformer of the stack is expected to produce an em-

bedding of a word or a language token. These out-

put embeddings can be expected to come from the

space spanned by the input words or tokens. From

this viewpoint, it may appear questionable to trans-

form the input embeddings by matrices W

and to

re-transform them back into the word embeddings.

Then, it may be worth attempting to delete the value

transformations. This has also been the proposal

of (He and Hofmann, 2024), resulting in a simple

weighted mean

∑

j=1

si j

s j

(10)

The output embedding z

is a convex combina-

tion of input embeddings x

. In other words, it is a

member of the convex set spanned by x

This concept has been implemented in the Keras

framework by setting the matrices W

and W

unit matrices. Collapsing W

to W

has been

reached by setting the matrix W

to a unit matrix. The

newly deﬁned matrix W

replaces matrix W

4 MULTI-HEAD

CONFIGURATION

The relationships of Section 3 are valid wherever the

matrices W

, W

, and W

are square. This may

also apply to multiple heads. However, it is usual to

commit to a reduced dimension per head. With H > 1

heads, it is common to map the embedding vector to a

narrower vector of width

/H, assumed to be integer.

In such cases, the matrices W

, W

, and W

are not square but of dimension (N,

/H). Collapsing

to W

is then no longer efﬁcient since W

is of dimension (N, N) and has thus N

parameters

while W

and W

together have

/H, which is a

smaller or equal number for H > 1.

Moreover, it is impossible to equivalently concate-

nate the value/projection matrices W

to a unique

product because of varying index h along various

paths through the heads.

Nevertheless, omitting the W

at all would have

the same justiﬁcation as for single-head conﬁgura-

tion: the output embedding z

would become a con-

vex combination of input embeddings x

, which can

be expected to correspond to a meaningful word or

token.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

236

5 SYMMETRY OF SIMILARITY

The expression Eq. (3) measures the similarity be-

tween queries and keys. The general concept of char-

acterizing similarity between vectors by their product

is symmetric: a is equally similar to b as is b to a.

However, the similarity between a key and a query

evaluated with the help of x

s j

is asymmet-

ric. This is because the matrices W

and W

are po-

tentially different.

This asymmetry leads to different similarities be-

tween x

and x

s j

in the roles of key and query: x

not as similar to x

s j

as is x

s j

to x

. The vector x

also not the most similar to itself. The matrix product

is generally not positive deﬁnite, so it is not

even guaranteed that the similarity of x

to itself is

positive.

The asymmetry can be deliberate and justiﬁed

from some viewpoints. It is not a matter of course that

the roles of queries and keys are symmetric. How-

ever, some of the mentioned properties can make its

use harmful.

The symmetry can be guaranteed by simply set-

ting W

= W

. Then, half of the parameters ded-

icated to the query and key matrices can be econo-

mized. In the single-head case, the same effect is

reached by a symmetric matrix W

, with identical

parameters mirrored over the diagonal, i.e., w

si j

s ji

. Another possibility is to parameterize a lower

triangular matrix T

and to multiply it by its trans-

pose, getting

= T

QKT

(11)

This amounts to the well-known Cholesky decompo-

sition (Cholesky, 1924) of a symmetric matrix.

With both methods, the number of parameters is

N(N+1)

instead of N

, or even 2N

of the original ver-

sion without collapsing W

and W

The symmetry is implemented by reusing W

, omitting the use of W

at all.

6 SETUP OF COMPUTING

EXPERIMENTS

The benchmarks for the evaluation have been chosen

from the CV domain. They are medium-sized prob-

lems that can be run for a sufﬁcient number of exper-

iments. This would not be possible with large models

such as those used in language processing.

For the experiments, two well-known image clas-

siﬁcation datasets MNIST (LeCun et al., 1998) and

CIFAR-10 (Krizhevsky, 2009) were used. MNIST

contains grayscale images of handwritten digits (0–9)

while CIFAR-10 contains color images of exclusively

ten different mundane objects like “horse”, “ship”, or

“dog”. They contain 60,000 (MNIST) and 50,000

(CIFAR-10) training examples. Their respective pre-

conﬁgured test split of each 10,000 examples are used

as validation sets. While CIFAR-10 is evenly dis-

tributed among all classes, MNIST can be considered

almost equally distributed.

An important criterion is that the training set size

is sufﬁcient for good generalization. The training size

(as related to the number of model parameters) must

be large enough for the model not to be underdeter-

mined so that we can fairly assess the models’ per-

formances. As a criterion for this, the overdetermina-

tion ratio of each benchmark candidate has been eval-

uated (Hrycej et al., 2023):

Q =

(12)

with K being the number of training examples, M be-

ing the output vector length (usually equal to the num-

ber of classes), and P being the number of trainable

model parameters.

This formula justiﬁes itself by ensuring that the

numerator KM equals the number of constraints to be

satisﬁed (the reference values for all training exam-

ples). This number must be larger than the number of

trainable parameters for the system to be sufﬁciently

determined. (Otherwise, there is an inﬁnite number

of solutions, most of which do not generalize.) This

is equivalent to the requirement for the overdetermi-

nation ratio Q to be larger than unity.

The losses and accuracies in Table 1 show that

the performance with 12 encoders is not superior to

that with 6 encoders. The parameter set sizes with 12

encoders have been 563,242 with MLP and 198,100

without MLP. This is substantially more than 287,686

and 101,470, respectively, with 6 encoders. Conse-

quently, the latter variant has been adopted as a base-

line.

6.1 Results for MNIST

Following the arguments of Sections 2 to 5, the fol-

lowing reduced transformer variants have been tested:

• with and without an MLP in each transformer-

encoder,

• with 1 and 4 heads,

• with the original matrix conﬁguration as well ma-

trix pair W

and W

collapsed into one matrix,

and W

omitted (one head variants only), and

Reducing the Transformer Architecture to a Minimum

237

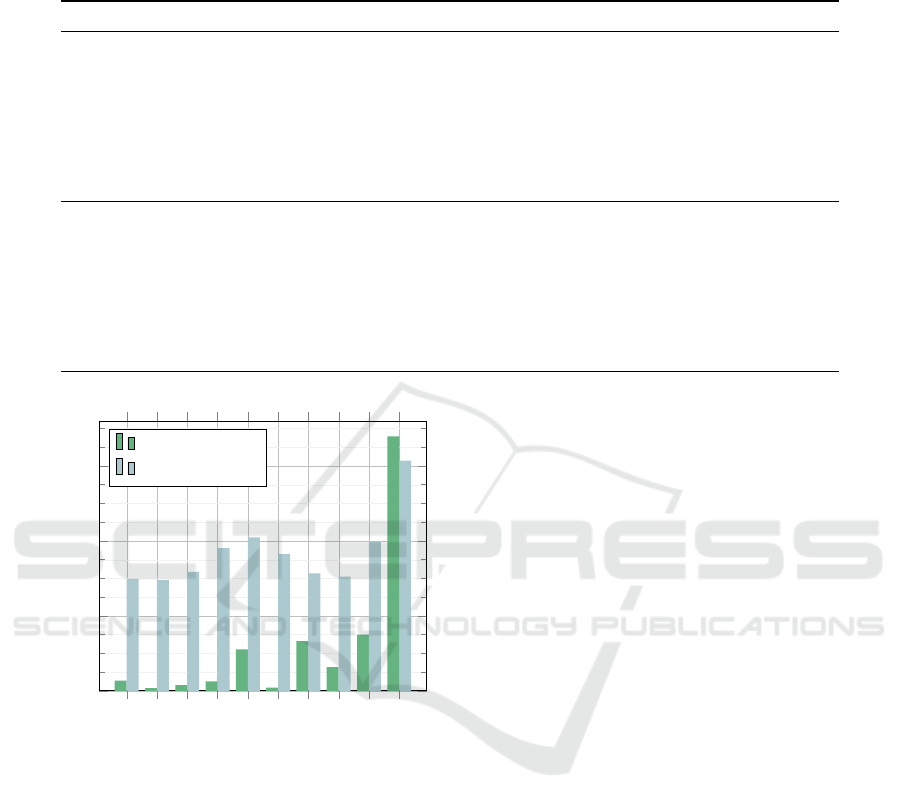
Table 1: Results of 16 experiments on the two datasets MNIST and CIFAR-10 with 6 or 12 consecutive transformer encoders

and 1 or 4 attention heads per encoder layer either with the default MLP inside each encoder layer or skipping it entirely. The

loss and accuracy for the training and validation sets are reported after each model is trained for exactly 500 epochs.

Dataset #Encs-#Heads MLP? Q Train loss Val. loss Train. acc. [%] Val. acc. [%]

MNIST

6-1 yes 2.15 0.0067 0.0747 99.78 98.38

6-1 no 6.46 0.0277 0.1023 99.07 97.49

6-4 yes 2.09 0.0018 0.0739 99.95 98.26

6-4 no 5.91 0.0021 0.0912 99.92 98.29

12-1 yes 1.08 0.0052 0.0652 99.81 98.71

12-1 no 3.29 0.0117 0.0970 99.62 97.94

12-4 yes 1.08 0.0025 0.0656 99.92 98.70

12-4 no 3.29 0.0026 0.1002 99.93 98.10

CIFAR-10

6-1 yes 1.74 0.1533 2.2418 94.63 60.24

6-1 no 4.93 0.9341 1.3590 66.16 55.30

6-4 yes 1.74 0.1109 2.4033 96.01 60.46

6-4 no 4.92 0.5621 1.6984 80.82 52.37

12-1 yes 0.89 2.3026 2.3026 9.82 10.00

12-1 no 2.52 0.5604 1.7219 79.48 54.06

12-4 yes 0.89 0.0632 2.6379 97.92 58.02

12-4 no 2.52 0.1787 2.3200 93.59 55.60

1H/MLP/unchanged

4H/MLP/unchanged

1H/MLP/Wqk

1H/MLP/Wqk+noWv.Vo

1H/NoMLP/unchanged

4H/NoMLP/unchanged

1H/NoMLP/symmetry

4H/NoMLP/symmetry

1H/NoMLP/Wqk

1H/NoMLP/Wqk+noWv.Vo

0.00

0.05

0.10

0.15

Loss

Train loss

Validation loss

Figure 1: Training and validation losses attained by vari-

ous reduced transformer-encoders with six encoder layers

on MNIST.

• with asymmetric and symmetric similarity mea-

sures.

The variants depicted refer to the matrix options:

• unchanged corresponds to the original attention

module matrix variety;

• Wqk variants use a single matrix for the product

; these variants are only available for a

single attention head, and their similarity measure

is asymmetric as in the original version;

• noWv.Vo denotes omitting the value matrices W

as well as the projection matrices W

; also, these

variants imply a single attention head and asym-

metric similarity measurement;

• symmetric variants are committed to symmetric

similarity measures; W

and W

are left un-

touched.

The performances of the individual variants are

given in Table 2. For better comparability, the losses

are additionally depicted in Fig. 1.

The following observations can be made:

• The original variants with MLPs perform better

than those without MLPs on the training set.

• By contrast, their advance disappears on the vali-

dation set, particularly if the symmetric similarity

metrics are used.

• The variant with asymmetric similarity without

MLP is inferior to the analogical one with sym-

metric similarity.

• The minimum variant with query and key matri-

ces W

collapsed to W

= W

and ad-

ditionally omitted value and projection matrices

show a higher loss than other variants. This may

be due to its dramatically reduced parameter num-

ber, which may lead to an insufﬁcient capacity to

capture nonlinearities.

As MNIST is a relatively easy benchmark, the

accuracy results are very close to each other. The

parameter numbers are substantially different. The

symmetric variant without MLP has only about 25 %

of the parameter number of the original, full variant

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

238

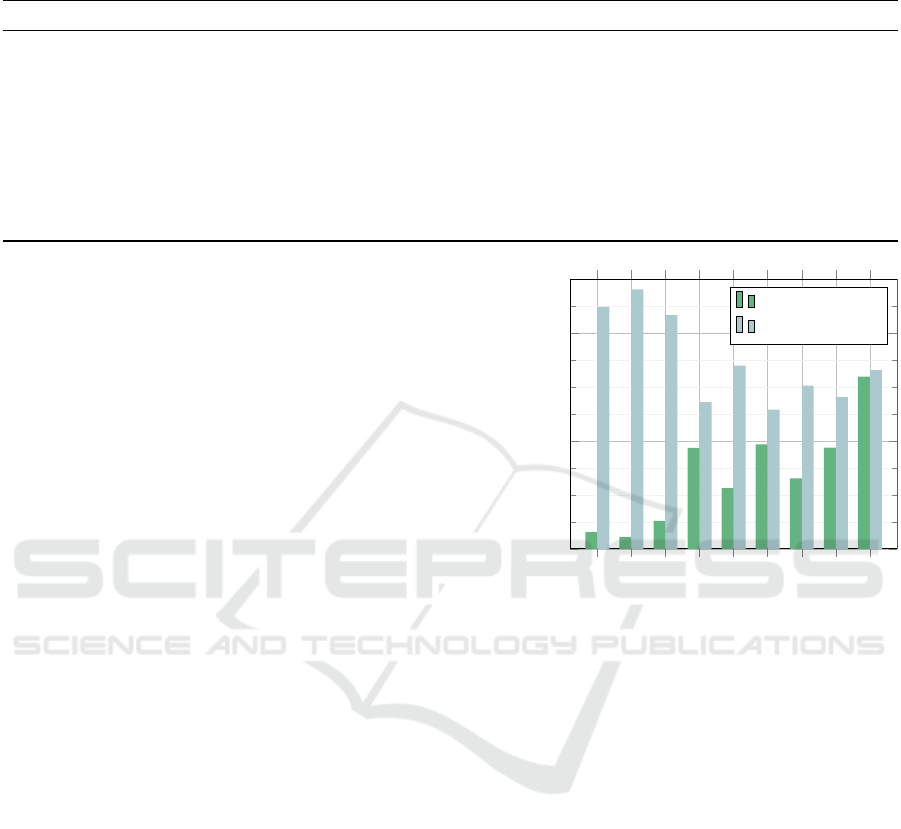
Table 2: Loss and accuracy for different variants of transformer-encoder modiﬁcations on MNIST: 1 or 4 heads, with or

without the MLP, with a single W

matrix, no value and projection matrices, or a symmetric similarity measurement.

# Heads MLP? Modiﬁcation # Parameters Q Train loss Val. loss Train. acc. [%] Val. acc. [%]

1 yes unchanged 279,106 2.15 0.0067 0.0747 99.78 98.38

4 yes unchanged 287,746 2.09 0.0018 0.0739 99.95 98.26

1 yes Wqk 257,506 2.33 0.0037 0.0794 99.89 98.43

1 yes Wqk+noWv,Vo 212,866 2.82 0.0063 0.0951 99.78 98.27

1 no unchanged 92,890 6.46 0.0277 0.1023 99.07 97.49

4 no unchanged 101,530 5.91 0.0021 0.0912 99.92 98.29

1 no symmetry 69,910 8.58 0.0331 0.0783 98.85 97.80

4 no symmetry 69,910 8.58 0.0158 0.0762 99.46 98.24

1 no Wqk 70,570 8.50 0.0374 0.0996 98.70 97.60

1 no Wqk+noWv,Vo 26,650 22.51 0.1697 0.1536 94.82 95.32

with MLP. The variant with collapsed matrices has

about 33 % of the original parameters. The parame-

ters include, in addition to the attention modules of all

transformer-encoders, the embedding matrix reducing

the image patch to the embedding vector.

The number of parameters has a strong effect on

the generalization capability of the model. This can

be quantiﬁed with the help of the overdetermination

ratio from Eq. (12) in column Q of Table 2. The

loss gap between the training and validation sets is the

largest for the original version with Q close to unity

while it shrinks towards the symmetric version with-

out MLPs.

6.2 Results for CIFAR-10

The variants tested are analogical to those for MNIST.

The losses and accuracies attained after 500 epochs

are given in Table 3, the losses additionally in Fig. 2.

The result characteristics are similar to those for

MNIST but more distinct:

• The original variant with MLP reaches the best

training set loss but the worst validation set loss.

• Compared to the original variant, the reduced

variants without MLP and with symmetric simi-

larity are superior in generalization.

• This also applies to the variant with collapsed key

and query matrices.

• Even the minimum variant with all considered

matrix reductions (except for symmetry), whose

parameter count is only a tenth of the original ver-

sion with MLP, shows a better validation set per-

formance than the original variant with all matri-

ces and MLP.

The measured accuracies are roughly consistent

with the losses on the training set. On the validation

set, some of them follow, paradoxically, a different

ranking. However, the fact that the loss, not the ac-

1H/MLP/unchanged

4H/MLP/unchanged

1H/MLP/Wqk+noWv.Vo

1H/NoMLP/unchanged

4H/NoMLP/unchanged

1H/NoMLP/symmetry

4H/NoMLP/symmetry

1H/NoMLP/Wqk

1H/NoMLP/Wqk+noWv.Vo

0.00

1.00

2.00

Loss

Train loss

Validation loss

Figure 2: Training and validation losses attained by vari-

ous reduced transformer-encoders with six encoder layers

on CIFAR-10.

curacy, is explicitly trained justiﬁes the arguments via

loss rather than accuracy.

6.3 Trials with ImageNet

Several trials on the ImageNet dataset (Russakovsky

et al., 2015) have been conducted to support the hy-

potheses with a larger benchmark. Unfortunately, the

baseline run with the original transformer architec-

ture, including MLP, has not been successful. In all

trials, Adam failed to ﬁnd a substantial improvement

in the initial parameter state. By contrast, without

MLP, it has been converging at least to a state with

a moderate classiﬁcation performance. This is why

we cannot present a serious study on ImageNet. It

can only be concluded that discarding MLP is helpful

Reducing the Transformer Architecture to a Minimum

239

Table 3: Loss and accuracy for different variants of transformer-encoder modiﬁcations on CIFAR-10: 1 or 4 heads, with or

without MLP, with a single W

matrix, no value and projection matrices, or a symmetric similarity measurement.

# Heads MLP? Modiﬁcation # Parameters Q Train loss Val. loss Train. acc. [%] Val. acc. [%]

1 yes unchanged 287,686 1.74 0.1533 2.2418 94.63 60.24

4 yes unchanged 287,746 1.74 0.1109 2.4033 96.01 60.46

1 yes Wqk+noWv,Vo 221,446 2.26 0.2597 2.1659 90.53 54.98

1 no unchanged 101,470 4.93 0.9341 1.3590 66.16 55.30

4 no unchanged 101,530 4.92 0.5621 1.6984 80.82 52.37

1 no symmetry 78,490 6.37 0.9686 1.2885 64.80 55.85

4 no symmetry 78,490 6.37 0.6521 1.5125 76.10 55.52

1 no Wqk 79,150 6.32 0.9364 1.4057 66.03 53.70

1 no Wqk+noWv,Vo 35,230 14.19 1.5961 1.6565 40.52 39.17

for convergence. The proof that this variant’s perfor-

mance is acceptable is still pending, and further work

will be required to provide it.

7 CONCLUSIONS AND

LIMITATIONS

The experiments presented have shown limited utility

of some parameter-extensive components of the trans-

former architecture. In particular, the following ﬁnd-

ings can be formulated:

• The MLP component is frequently presented as

necessary for capturing nonlinearities in the mod-

eled relationship. However, the inherent nonlin-

earity of the similarity measures seems powerful

enough in many practical cases.

• While the classiﬁcation performance without the

MLPs is not signiﬁcantly inferior to that with

MLPs, a substantial beneﬁt is saving the param-

eters. With model size N, the attention mecha-

nism requires 4N

parameters in the form of ma-

trices W

, W

, and W

. The size of the

MLP is usually chosen as an integer multiple of

h of the model size. Then, the MLP consists

of weights and biases of two layers, with a total

of hN(N + 1) + N(hN + 1) = 2hN

+ hN + N ≈

2hN

. If the multiple is h = 4, MLP has double

the number of parameters as the attention mech-

anism. Consequently, omitting MLP reduces the

parameters to 33 % of the original size.

• Symmetric similarity measures tend to perform

better than asymmetric ones, with 50 % fewer

query and key matrix parameters. This improve-

ment may be reached by excluding undesirable

freedoms, such as a token being dissimilar to it-

self. The parameter reduction can be expected to

constrain the search for the optimum ﬁt fruitfully.

• Collapsing the value and the key matrix into one

is another possibility of reducing the parameter set

of these matrices by 50 %.

• Omitting the value matrix W

and the projection

matrix W

reduces the parameters of the whole

attention module by 50 %. This variant has also

been proposed by (He and Hofmann, 2024), with

the observation of no signiﬁcant performance loss

in NLP benchmarks.

• Both preceding reductions amount to a reduction

to 25 % of the original attention module size.

• In our experiments, the variants with the collapsed

query/key matrices, omitted value, and projection

matrices are slightly inferior for MNIST but equal

for CIFAR-10. These minimum variants have less

than 10 % of parameters compared with the clas-

sical transformers, including MLP. Compared to

the architecture with 12 encoders, it is as little as

5 %.

The savings in computing time have been propor-

tional to the savings in parameter numbers.

Our research has been limited to image process-

ing benchmarks MNIST, CIFAR-10, and ImageNet.

The experiments with the last benchmark have par-

tially failed due to computing problems. Empirical

evidence with the help of two medium-sized bench-

marks and an incomplete test of a larger one is not

satisfactory. This requests further research with more

robust algorithms. There is considerable potential for

second-order optimization methods such as the con-

jugate gradient algorithm of (Fletcher and Reeves,

1964), thoroughly described in (Press et al., 1992).

This algorithm’s convergence is excellent, but im-

plementing the stopping rule in widespread packages

seems to improve its ability to prevent early stops be-

fore reaching the minimum region.

Limitations to image processing suggest further

extension. The proper domain of transformers is

NLP. An obstacle to its investigation is the size of

benchmark problems, so most published investiga-

tions consist of observing the performance of ﬁne-

tuning pre-trained models. To use pre-trained param-

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

240

eter sets, these ﬁne-tuned models must be identical

or almost identical to the pre-trained models. This

makes the testing of different architectures difﬁcult.

A possibility is to use a large model used for pre-

training as a teacher and a medium-sized model as

student, mimicking its performance. This procedure,

referred to as knowledge distillation, has been pro-

posed by (Hinton et al., 2015) and used, e.g., by (Sun

et al., 2019).

These will be important focuses soon.

REFERENCES

Bahdanau, D., Cho, K., and Bengio, Y. (2016). Neural

Machine Translation by Jointly Learning to Align and

Translate. ICLR.

Cholesky, A.-L. (1924). Note Sur Une M

ethode de

esolution des

equations Normales Provenant de

L’Application de la M

eThode des Moindres Carr

a un Syst

eme D’

equations Lin

eaires en Nombre

Inf

erieur a Celui des Inconnues. — Application

de la M

ethode a la R

esolution D’un Syst

eme

Deﬁni D’

eQuations Lin

eAires. Bulletin G

eod

esique,

2(1):67–77.

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn,

D., Zhai, X., Unterthiner, T., Dehghani, M., Min-

derer, M., Heigold, G., Gelly, S., Uszkoreit, J., and

Houlsby, N. (2021). An image is worth 16x16 words:

Transformers for image recognition at scale. In In-

ternational Conference on Learning Representations,

page 21, Vienna, Austria.

Fletcher, R. and Reeves, C. M. (1964). Function minimiza-

tion by conjugate gradients. The Computer Journal,

7(2):149–154.

He, B. and Hofmann, T. (2024). Simplifying Transformer

Blocks. arXiv:2311.01906 [cs].

Hendrycks, D. and Gimpel, K. (2023). Gaussian Error Lin-

ear Units (GELUs). arXiv:1606.08415 [cs].

Hinton, G., Vinyals, O., and Dean, J. (2015). Distilling the

Knowledge in a Neural Network. arXiv:1503.02531

[cs, stat].

Hrycej, T., Bermeitinger, B., Cetto, M., and Handschuh,

S. (2023). Mathematical Foundations of Data Sci-

ence. Texts in Computer Science. Springer Interna-

tional Publishing, Cham.

Krizhevsky, A. (2009). Learning Multiple Layers of Fea-

tures from Tiny Images. Dataset, University of

Toronto.

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2324.

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flan-

nery, B. P. (1992). Numerical recipes in C (2nd ed.):

the art of scientiﬁc computing. Cambridge University

Press, USA.

Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,

Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bern-

stein, M., Berg, A. C., and Fei-Fei, L. (2015). Ima-

geNet Large Scale Visual Recognition Challenge. In-

ternational Journal of Computer Vision, 115(3):211–

252.

Sun, S., Cheng, Y., Gan, Z., and Liu, J. (2019). Patient

Knowledge Distillation for BERT Model Compres-

sion. arXiv:1908.09355 [cs].

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, L., and Polosukhin, I.

(2017). Attention is all you need. In Proceedings of

the 31st International Conference on Neural Informa-

tion Processing Systems, NIPS’17, pages 6000–6010,

Red Hook, NY, USA. Curran Associates Inc.

Reducing the Transformer Architecture to a Minimum

241