Randomized Local Search vs. NSGA-II vs. Frequency Fitness

Assignment on The Traveling Tournament Problem

Cao Xiang

1 a

, Zhize Wu

1 b

, Daan van den Berg

2 c

and Thomas Weise

1 d

Institute of Applied Optimization, School of Artiﬁcial Intelligence and Big Data,

Hefei University, Jinxiu Dadao 99, Hefei, 230601, Anhui, China

Department of Computer Science, Vrije Universiteit Amsterdam, De Boelelaan 1111, Amsterdam, 1081 HV,

The Netherlands

Keywords:

Traveling Tournament Problem, NSGA-II, Randomized Local Search, Frequency Fitness Assignment.

Abstract:

The classical compact double-round robin traveling tournament problem (TTP) asks us to schedule the games

of n teams in a tournament such that each team plays against every other team twice, once at home and

once away (doubleRoundRobin constraint). The maxStreak constraint prevents teams from having more than

three consecutive home or away games. The noRepeat constraint demands that, before two teams can play

against each other the second time, they must at least play one other game in between. The goal is to ﬁnd a

game plan observing all of these constraints and having the overall shortest travel length. We deﬁne a game-

permutation based encoding that allows for representing game plans with arbitrary numbers of constraint

violations and tackle the TTP as a bi-objective problem minimizing both the number of constraint violations

and the travel length by applying the well-known NSGA-II. We combine both objectives in a lexicographic

prioritization scheme and also apply the randomized local search RLS to this single-objective variant of the

problem. We realize that Frequency Fitness Assignment (FFA), which makes algorithms invariant under all

injective transformations of the objective function value, would also make optimization algorithms invariant

under all lexicographic prioritization schemes for multi-objective problems. The FRLS, i.e., the RLS with

FFA plugged in, would therefore solve both possible prioritizations of our TTP variants at once. We thus also

explore its performance on the TTP. We ﬁnd that RLS performs surprisingly well and can ﬁnd game plans

without constraint violations reliably until a scale of 36 teams, whereas FRLS and NSGA-II have an advantage

on small- and mid-scale problems.

1 INTRODUCTION

The Traveling Tournament Problem (TTP) is the com-

binatorial optimization problem of efﬁciently and

fairly organizing a tournament of n teams that play

against each other in a pairwise fashion (Easton et al.,

2001). The efﬁcient part boils down to arranging the

games such that the total travel length

is short, which

is somewhat similar to the classical Traveling Sales-

https://orcid.org/0009-0006-4811-7824

https://orcid.org/0000-0001-7416-5711

https://orcid.org/0000-0001-5060-3342

https://orcid.org/0000-0002-9687-8509

Initially, each team is at its home location. On each

day, a team needs to travel if its scheduled game is not at

its present location. On the last day, each team may need

to travel back home unless their last game is a home game.

The total travel length sums up the lengths of all travels over

all teams.

person Problem (TSP). The fair part is represented in

several constraints. Compared to classical N P -hard

problems like the TSP, the Job Shop Scheduling Prob-

lem (JSSP), or Max-SAT, these constraints are what

make the TTP (more) challenging, as (Verduin et al.,

2023) pointed out at last year’s IJCCI. This problem

is indeed very hard and therefore, very interesting.

We focus on the classical compact double round

robin instances from the RobinX benchmark by (Van

Bulck et al., 2018; Van Bulck, 2024), where the fol-

lowing constraints apply (Van Bulck et al., 2020):

• doubleRoundRobin (2RR): Each team i plays

twice against every other team j, once at home

(home game) and once at the place of j (away

game). Therefore, there are g = n(n − 1) games

in the tournament.

• compactness: Each team has one game in ev-

ery slot and thus, the whole tournament lasts d =

Xiang, C., Wu, Z., van den Berg, D. and Weise, T.

Randomized Local Search vs. NSGA-II vs. Frequency Fitness Assignment on The Traveling Tournament Problem.

DOI: 10.5220/0012891500003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 38-49

ISBN: 978-989-758-721-4; ISSN: 2184-3236

g/(n/2) = 2(n − 1) days.

• maxStreak: Each team has at most three away

and at most three home games in each consecu-

tive four time slots, i.e., the maximum lengths for

home and away streaks are both 3.

• noRepeat: Each pair of teams has at least one

different game between two consecutive mutual

games.

The ﬁrst contribution of our work is to treat the TTP

as a bi-objective problem that can be approached with

metaheuristics. We deﬁne the two objective functions

(s), counting all constraint violations of a solution s

across the board, and f

(s), evaluating the total travel

length over all teams. If both objectives are mini-

mized, the result would be the game plan without any

constraint violation that also has the shortest possible

travel length among all such plans. The question is

how to achieve this goal.

An important ingredient to this end is to deﬁne a

proper search space P amenable to metaheuristic opti-

mization and a decoding decode which translates it to

the solution space S containing the game plans s. In

our work, we apply a game-based encoding where the

search space consists of permutations π of length g =

n(n − 1) where each element identiﬁes one of the

g games. The decoding then processes such a permu-

tation π from beginning to end and places the games

into the earliest slot in the game plan s where both

involved teams do not yet have another game sched-

uled. Games that cannot be placed are omitted, so

the game plans can have so-called “byes” (Van Bulck,

2024; Thielen and Westphal, 2011; Brand

ao and Pe-

droso, 2014), i.e., days at which a team does not have

a game scheduled, which, of course, are considered

in f

. With the exception of this last detail, which

makes the implementation more efﬁcient, this encod-

ing is very similar to the one presented by (Choubey,

2010).

Having reduced the TTP to ﬁnding good permu-

tations π in the space P, we must now tackle the

question of how to go about conducting this search.

Since we consider the TTP as a multi-objective

problem with two objective functions, applying the

most famous multi-objective optimization algorithm,

NSGA-II (Deb et al., 2000; Deb et al., 2002) would be

an obvious approach. NSGA-II tries to push a popula-

tion of candidate solutions towards the Pareto frontier,

i.e., the trade-off curve where any further improve-

ment in f

would require an increase in f

and vice

versa. To the best of our knowledge, we are the ﬁrst

to explicitly approach the TTP as a multi-objective

problem.

Then again, we are not really interested in obtain-

ing the Pareto frontier: The objective f

is more im-

portant than f

. Thus, we can turn the TTP into a

single-objective problem by deﬁning a new objective

function

f (s) = (UB[ f

] + 1)∗ f

(s) + f

(s) (1)

where UB[ f

] is the upper bound of f

. In other words,

even an improvement or loss of 1 in terms of f

would

outweigh even the largest loss or improvement of f

(which could never be more than UB[ f

]), meaning

that the objectives are lexicographically ordered (An-

derson, 2000; George et al., 2015; Volgenant, 2002;

Zhang et al., 2023). This problem can then be ap-

proached by a single-objective technique. We pick

the randomized local search (RLS) for this purpose.

The question now arises whether RLS or NSGA-II

can ﬁnd shorter error-free game plans. Will RLS get

trapped in local optima of f and the multi-objective

approach will pay off by ﬁnding a way around them?

Or will spreading out the search pressure over the

Pareto frontier consume more objective function eval-

uations (FEs) and the efﬁciency of RLS focusing all

FEs towards feasible game plans and then such with

short travel lengths lead to the better results? Answer-

ing this question is an interesting second contribu-

tion of our work.

In (Weise et al., 2014), a mechanism called Fre-

quency Fitness Assignment (FFA) was proposed.

FFA renders optimization processes invariant under

all injective transformations of the objective function

value (Weise et al., 2021b) and, as a result, removes

the bias towards better solutions (Weise et al., 2023).

By replacing the objective value f (s) of a solution s

with its encounter frequency H[ f (s)], an algorithm

that uses FFA does no longer prefer better solutions

over worse ones, i.e., FFA breaks with the most fun-

damental principle inherent in all metaheuristic opti-

mization methods.

The only iterative optimization algorithms that

have similar properties are random walks, random

sampling, and exhaustive enumeration. FFA has been

shown to improve the performance of RLS on clas-

sical N P -hard problems like the Max-SAT prob-

lem (Weise et al., 2021b; Weise et al., 2023), the

JSSP (Weise et al., 2021a; de Bruin et al., 2023), and

on TSP instances (Liang et al., 2022; Liang et al.,

2024). The third contribution is to also apply FFA

to the TTP, extending our comparison to RLS vs.

NSGA-II vs. FRLS, i.e., the RLS with FFA plugged

in.

But there is another reason for us to include FFA

into our experiments: We stated above that FFA ren-

ders algorithms invariant under injective transforma-

tions of the objective function value. What does this

mean in a multi-objective scenario? If we consider

our original multi-objective formulation of the TTP,

Randomized Local Search vs. NSGA-II vs. Frequency Fitness Assignment on The Traveling Tournament Problem

then f

and f

span a two-dimensional space O ⊂ N

Inspecting the construction of f in Equation 1, one re-

alizes that it is actually a bijective mapping of O 7→ N.

Indeed, each unique combination of a value of f

and

a value of f

will map to a unique value of f . Applying

the invariance transitively means that FRLS will be in-

variant – i.e., traverse the exactly same path through

the search space P – regardless of which of the two

original objectives is prioritized. If we would favor

travel length over game plan correctness instead, the

FRLS would still visit the same solutions. If FFA is

applied to one lexicographic prioritization scheme of

a k-objective problem, it will optimize all the k! possi-

ble orders of the objective functions at once. Finding

this puzzling property is the fourth contribution and

the deeper reason for us to explore what kind of re-

sults FRLS will yield on our TTP formulation.

Finally, as the ﬁfth contribution, we publish not

just all of our results, but also all of the source code of

all involved algorithms, and all scripts for generating

the tables and ﬁgures in this paper in an immutable

archive at https://doi.org/10.5281/zenodo.13329107,

making our work fully reproducible.

The remainder of this paper is structured as fol-

lows. In Section 2, we will discuss the related works

on the TTP before introducing our approach and the

involved algorithms in detail in Section 3. We then

present our experiments and results in Section 4. We

conclude our paper in Section 5 with a summary and

outlook to future work.

2 RELATED WORK

(Anagnostopoulos et al., 2006) applied simulated an-

nealing to the TTP. Their ﬁve search operators work

directly on the game plans s ∈ S and thus, are more

complicated than the simple swap-2 unary operator

used in our work. Like in our work, the solutions may

violate the maxStreak and noRepeat constraints but

different from us, they always observe the doubleR-

oundRobin and compactness constraints. This forces

them to generate a starting solution that adheres to

these constraints as well, whereas we can just sample

a permutation uniformly at random (u.a.r.). Further-

more, like us when using the RLS and FRLS, they

construct a single summary objective function min-

imizing both constraint violations and travel length.

Different from us, this summary objective is not

a strict prioritization scheme but instead a penalty-

based method. They do not tackle problems larger

than n = 16.

(Chen et al., 2007) develop a hyper-heuristic

based on the ant colony optimization (ACO) where

ants travel through a graph whose nodes represent

heuristics. When visited, the heuristics correspond-

ing to the nodes are applied to the current solution

and transform it to a new game plan. The nodes can

be visited multiple times by the ants, allowing them

to better explore the solution space and try out differ-

ent combinations of heuristics. The article uses the

NLn instances in the experiment, i.e., does not inves-

tigate problems with more than 16 teams. While their

method cannot outperform the related works, this ﬁrst

attempt to tackle the TTP with ACO did yield good

results on NL4 and NL6.

(Choubey, 2010) presents an encoding scheme for

tackling the TTP with GAs. The games to be sched-

uled are represented as symbols which are arranged in

a sequence and decoded to game plans. While some

details are not fully clear, it can be assumed that this

encoding will basically work like ours with some mi-

nor deviations: Games that cannot be scheduled due

to conﬂicts within the d tournament days are added to

the end of the game plan and thus expanding it, vio-

lating the compactness constraint. In our case, they

are simply omitted. In their work and ours, these

situations add to the number of errors. (Choubey,

2010) use a weighted sum as objective that penalizes

scheduling errors, but theirs is not a lexicographic pri-

oritization like ours. Their GA is applied to RobinX

instances with no more than n = 8 teams.

In (Khelifa and Boughaci, 2016), a harmony

search (HS) algorithm is hybridized with variable

neighborhood search (VNS) and applied to the mir-

rored TTP with reversed venues. The polygon

method (de Werra, 1988) is used to generate single-

round robin game plans and the encoding applied in

the HS maps teams to the abstract teams in this poly-

gon heuristic. The numerical results are limited to

instances with n ≤ 16.

(Khelifa et al., 2017) applied a Genetic Al-

gorithm (GA) whose initial population consists

of feasible game plans generated by the polygon

method (de Werra, 1988) The search operators work

directly on (feasible) game plans and minimizing f

As a result, they (and in particular, the binary

crossover operator), are much more complicated than

ours. No instance with more than n = 10 teams is

tacked in (Khelifa et al., 2017).

(Khelifa and Boughaci, 2018) ﬁnally apply a co-

operative search method for the TTP that handles the

constraints and travel length separately. They start by

generating a 2RR solution, similar to (Anagnostopou-

los et al., 2006). Then, however, they only search for

a feasible solution satisfying all constraints and ig-

nore the travel length using simulated annealing and

variable neighborhood search. Once a feasible solu-

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

tion is found, they apply a Stochastic Local Search

to minimize the travel length f

while only consid-

ering feasible solutions. The selection criterion used

in this last step is very similar to our prioritization

scheme f from Equation 1. We, however, always

only apply one algorithm (either only RLS or only

FRLS) to f , and the algorithm used is also much

simpler compared to those in (Khelifa and Boughaci,

2018). Different from (Khelifa and Boughaci, 2018),

we also do not work on the game plans directly but

on our game-permutation based representation, which

also allows for simpler search operators. Finally, the

largest instance used in (Khelifa and Boughaci, 2018)

has n = 24.

From this survey, we ﬁnd that, to the best of

our knowledge, only (Choubey, 2010) applies an

encoding-based approach working directly on game

permutations. This is somewhat surprising, as such a

game-permutation based encoding has, at least from

the perspective of simplicity, several advantages. It

allows us to basically use all operators and algorithms

that work with permutations off-the-shelf. As a draw-

back, it permits solutions that violate any number of

constraints. Also, to the best of our knowledge, we

are the ﬁrst to tackle the TTP explicitly as a multi-

objective problem, to apply a multi-objective algo-

rithm (NSGA-II) to it, and to apply a lexicographic

prioritization of the objectives in a weighted sum ap-

proach to let a local search sort out all types of con-

straint violations. Finally, we are the ﬁrst to apply

FFA to the TTP, or, actually, to any multi-objective

problem, and to reveal its odd characteristics in this

domain.

3 OUR APPROACH

3.1 Algorithms

In our study, we apply three different algorithms,

RLS, FRLS, and NSGA-II. Let us begin by outlin-

ing the simplest one of them, the Randomized Lo-

cal Search (RLS), often also called Hill Climbing or

(1 + 1) EA (Russell and Norvig, 2002; Neumann and

Wegener, 2007; Johnson et al., 1988). As a black-box

metaheuristic, it allows us to choose a search space P

(in our case, permutations) and a unary search oper-

ator, a decoding function decode : P 7→ S that trans-

lates the points in the search space to game plans, and

an objective function f : S 7→ N rating the quality of

game plans (see Equation 1).

The blueprint of this metaheuristic is given in Al-

gorithm 1. The algorithm begins by sampling a ran-

dom point π

from the search space P, decoding it to

Algorithm 1: RLS(decode : P 7→ S, f : S 7→ N).

sample π

from P u.a.r.; s

← decode(π

);

← f (s

); ▷ see Equation 1

for 10

− 1 times do ▷ our termination criterion

← swap 2 values in π

u.a.r.;

← decode(π

); z

← f (s

);

if z

≤ z

then

← π

; s

← s

; z

← z

return s

, z

Algorithm 2: FRLS(decode : P 7→ S, f : S 7→ N).

H ← (0, 0,·· · ,0); ▷ H-table initially all 0s

sample π

from P u.a.r.; s

← decode(π

);

← f (s

); ▷ see Equation 1

← s

; z

← z

; ▷ best may otherwise get lost

for 10

− 1 times do ▷ our termination criterion

← swap 2 values in π

u.a.r.;

← decode(π

); z

← f (s

);

if z

< z

then s

← s

; z

← z

;

H[z

] ← H[z

] + 1; H[z

] ← H[z

] + 1;

if H[z

] ≤ H[z

] then

← π

; s

← s

; z

← z

return s

, z

▷ return preserved best

a game plan s

, and evaluating its objective value z

f (s

). In a loop, a new point π

is sampled as a

modiﬁed copy of π

using the unary operator, is de-

coded, and evaluated. If π

is not worse than π

, it re-

places it. When the computational budget of 10

FEs

is exhausted, both the best-so-far solution s

and its

quality z

are returned. In our experiments, the algo-

rithm terminates after 10

objective function evalua-

tions (FEs).

FFA is an algorithm module that prescribes re-

placing the objective values with their observed en-

counter frequencies in the selection decisions. Plug-

ging FFA into the RLS yields the FRLS sketched in

Algorithm 2. This algorithm starts like RLS, but ad-

ditionally initializes a frequency table H to be ﬁlled

with zeros. Where RLS compares the objective val-

ues z

and z

to decide whether π

should replace π

or be discarded, FRLS ﬁrst increments the encounter

frequencies H[z

] and H[z

] of z

and z

and then com-

pares these instead of the objective values. As a re-

sult, it will accept π

if it corresponds to a solution

whose objective value has been seen less or equally

often than the one corresponding to π

. Since it no

longer matters whether z

is a better objective value

than z

or not, the algorithm may lose the best discov-

ered solution again and thus needs to remember it in

an additional variable s

(Weise et al., 2021b; Weise et al., 2023) showed

that the FRLS will be invariant under all injective

Randomized Local Search vs. NSGA-II vs. Frequency Fitness Assignment on The Traveling Tournament Problem

transformations of the objective function values. In

our case, f itself is a bijective transformation of the

space spanned by the possible pairs of return values of

the two original objective functions f

and f

. In fact,

any lexicographic/prioritization scheme implemented

as weighted sum is such a bijective transformation.

Therefore, the FRLS will be invariant, i.e., visit the

exact same candidate solutions in the exact same se-

quence, under all lexicographic approaches to solv-

ing the original problem (or any other multi-objective

problem). This bafﬂing feature of such a simple algo-

rithm is worth exploring, which is what we will do in

this paper.

The third algorithm in our study, NSGA-II (Deb

et al., 2000; Deb et al., 2002), is the most well-known

multi-objective evolutionary algorithm. If the popu-

lation size is set to K, then this algorithm starts by

sampling a population containing 2K random initial

points in the search space and mapping them to game

plans, in the same way RLS and FRLS do. For each

solution, both objective functions f

and f

are evalu-

ated.

At the beginning of its main loop, NSGA-II will se-

lect K of the 2K points in the population and discard

the rest. This selection step proceeds in two phases.

Iteratively, the “fronts” of all solutions that are non-

dominated in the population are extracted from the

population. If the current front ﬁts entirely into the

new population without exceeding K total solutions,

it is put into there and the selection continues. If it

does not ﬁt entirely, then in the second phase, the new

population is ﬁlled up to size K by choosing the solu-

tions that have the farthest-away nearest neighbors to

both sides in each objective function (i.e., those with

the largest crowding distance).

It will then create K new points from the selected

ones. NSGA-II therefore uses a binary and a unary op-

erator, among which it chooses based on the crossover

rate cr. Each new solution is created by using, with

probability cr, a binary operator combining two per-

mutations. The solutions not created by the binary

operator are generated using the same unary search

operator as RLS and FRLS. Then, the K selected and

the K new solutions are put together to form the joint

population to undergo the selection at the beginning

of the next iteration.

3.2 Encoding, Objectives, and Search

Operators

A 2RR tournament involves n teams competing over

d = 2(n − 1) days. In our work, a game plan s ∈ S

therefore is a d × n matrix where the item s[i, j] ∈

−n..n denotes the opponent that team j plays on day i.

If s[i, j] > 0, then team j plays against team s[i, j] in the

home stadium of team j and if s[i, j] < 0, it has an away

game against team −s[i, j] at their stadium. s[i, j] = 0

indicates that no game is scheduled for team j on

day i, i.e., a “bye,” which constitutes a scheduling er-

ror.

The f

objective function counts all such byes (as

they imply violations of the compactness constraint),

as well as all violations of the doubleRoundRobin,

maxStreak, and noRepeat constraints mentioned in

the introduction. The f

objective computes the total

round trip travel length summed up over each team

(which start from and, ﬁnally, return to their home

location). If a team has a bye scheduled for a cer-

tain day, the travel length for this day can be con-

sidered as undeﬁned

and is replaced by a penalty

value which equals 2Ω + 1, where Ω is the maxi-

mum distance between any two teams in the tour-

nament. This function can never exceed the upper

bound UB[ f

] = 2nd(2Ω + 1) used in Equation 1.

The search space P consists of the permutations π

of the ﬁrst g = n(n − 1) natural numbers, correspond-

ing to the g games to be scheduled. Each number

in 1..g uniquely identiﬁes a game with one home

team α and one away team β. The permutations π

are processed from front to end and are used to trans-

late a matrix s initially ﬁlled with 0 to a game plan.

When the element π[k] at index k of π is processed,

the decoding function decode ﬁrst extracts the corre-

sponding α and β values. It will then ﬁnd the smallest

index i such that s[i, α] = s[i,β] = 0. If such i exists, it

will set s[i, α] ← β and s[i,β] ← −α. This may violate

the maxStreak and noRepeat constraints, but we hope

that the search will correct such errors over time. If

no day exists where both teams α and β have byes,

the game is discarded, i.e., not scheduled. This will

always lead to an increase of f

and, eventually, re-

sult in a two byes somewhere in the game plan, also

causing an increase of f

It can immediately be seen that any feasible game

plan s can be represented as a permutation. One

would start with an empty permutation π and simply

translate s it iteratively from day i = 1 to i = d and,

for each day, process columns j = 1 to j = n. If the

team α = s[i, j] > 0 has a home game scheduled, one

would look for the necessarily existing other team β

playing against it on the same day i and append the

value identifying (α,β) to π. Eventually, one ends up

with a permutation π such that decode(π) = s. There-

fore, our encoding allows for representing and hope-

fully also ﬁnding the globally optimal solution.

If a team was not already at home, it would not be

a priori clear whether it would travel home or to the next

location.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

The unary search operator used in all three op-

timization algorithms swaps two elements in a per-

mutation u.a.r. NSGA-II requires a binary crossover

operator which takes two permutations π

and π

input and produces another permutation π

as out-

put. Here we apply a generalized version of the Al-

ternating Position Crossover operator AP for the TSP

by (Larra

naga et al., 1997; Larra

naga et al., 1999).

The original AP operator creates π

by selecting al-

ternately the next element of π

and the next element

of π

, omitting the elements already present in the

offspring. For example, if π

= 12345678 and π

37516824, the AP operator gives π

= 13275468. Ex-

changing π

and π

results in π

= 31725468. Our

generalized version randomly decides, u.a.r., at each

step of ﬁlling π

, from which of the two parent permu-

tations a value should be copied. This should hope-

fully result in a greater variety of possible results. Our

operator also does not skip over a parent if its next el-

ement is already used, but instead picks the next not-

yet-used element from that parent.

4 EXPERIMENTS AND RESULTS

4.1 Setup

We implement our algorithms in Python 3.10 on Win-

dows 10 using the moptipy (Weise and Wu, 2023)

framework, as well as numba just-in-time compila-

tion where possible. We use the 118 classical com-

pact 2RR instances from the RobinX benchmark by

(Van Bulck et al., 2018; Van Bulck et al., 2020; Van

Bulck, 2024):

• bra24 is based on the 24 teams in the main divi-

sion of the 2003 edition of the Brazilian soccer

championship,

• circn (Easton et al., 2001) with n ∈ 4, 6,8,. .., 40

where all teams are distributed equidistantly on a

circle,

• conn (Urrutia and Ribeiro, 2006) with n ∈

4,6,8,... ,40 where all distances are 1,

• galn (Uthus et al., 2013) with n ∈ 4, 6,8,. .., 40

uses the distances between Earth and exoplanets,

• incrn with n ∈ 4,6,8, ... ,40 has teams situated on

a straight line with the distance between teams i

and i + 1 being i

• linen with n ∈ 4, 6,8,...,40 has teams situated on

a straight line with neighbors being one distance

unit apart,

• nﬂn with n ∈ 16, 18,20,. .., 44 based on the on the

National Football League

• nln (Easton et al., 2001) with n ∈ 4,6,8,... ,16

based on the teams in the National League of the

Major League Baseball, and

• supn with n ∈ 4,6, 8,...,14

We investigate RLS and FRLS, which do not have

any parameters. We also apply the NSGA-II with a

crossover rate of cr = 1/16 and three different pop-

ulation sizes K ∈ {4,16,64}, which we refer to as

NSGA-II

, NSGA-II

, and NSGA-II

, respectively.

We conduct 7 runs per algorithm setup and problem

instance for at most 10

objective function evalua-

tions (FEs).

4.2 Results

Table 1 and Table 2 list the best f values found by the

different algorithms, averaged over the 7 runs per in-

stance. The best values are marked with bold face and

the last row, # best, counts how often each algorithm

reaches the best result. From this row, we immedi-

ately see that RLS performs best, yielding the best

result 72 times, followed by NSGA-II

(36 times),

and FRLS (21 times best). Among the NSGA-II se-

tups, larger populations are better as NSGA-II

beats

NSGA-II

beats NSGA-II

, so in future we will try

even larger populations. The NSGA-II and FRLS can

beat RLS on smaller problems. For example, FRLS

is best on circ4 to circ10, NSGA-II is best on circ12 to

circ20, whereas RLS is best on the remaining circn in-

stances. Interestingly, NSGA-II and FRLS also yield

the best results on all of the supn and nln instances

except for the smallest ones with n = 4, where RLS

wins. At this stage, we can summarize that the pop-

ulation of NSGA-II and the FFA component of FRLS

offer a clear advantage, but only if the instances are

not big.

If these best- f values are less than the upper

bound UB[ f

] of the travel length objective func-

tion f

, then this means that the discovered game

plans s have no error ( f

(s) = 0). In this case,

f (s) = f

(s), i.e., the printed values are actually the

travel lengths of the plans. The average solutions of

RLS are error-free on bra24, circ4 to circ36, con4 to

con38, gal4 to gal36, incr4 to incr34, on incr38, line4

to line36, and on all nﬂn, nln, and subn instances. We

therefore can conclude that, at least up to a scale n

of 36, RLS with our simple encoding and budget of

FEs can reliably ﬁnd violation-free game plans

of the 2RR TTP. This means that given more time, it

would probably have found error-free game plans for

all of the RobinX instances used in our study. Recall

that the earlier studies usually use only instances with

n up the low twenties at most, usually in the middle-

tens.

Randomized Local Search vs. NSGA-II vs. Frequency Fitness Assignment on The Traveling Tournament Problem

Table 1: The best f values found by the different algorithms, averaged over the 7 runs per instance with 10

FEs each. We

also provide the upper bound UB[ f

] of f

and the upper bound UB-opt for the optimal tour length, taken from (Van Bulck,

2024) at the time of this writing. The best values are marked with bold face and counted in the last row (# best). Continued

in Table 2.

instance UB[ f

] UB-opt RLS NSGA-II

NSGA-II

FRLS

bra24 7 093 200 538 866 688 630 81 904 796 35 246 018 703 411 537 039 600

circ4 120 20 20 20 20 20 20

circ6 420 64 65 69 66 66 64

circ8 1 008 132 146 163 144 146 135

circ10 1 980 242 286 329 280 285 276

circ12 3 432 400 491 591 482 494 501

circ14 5 460 616 793 923 805 782 863

circ16 8 160 898 1 186 10 750 1 231 1 159 1 445

circ18 11 628 1 268 1 684 33 608 6 844 1 676 5 645

circ20 15 960 1 724 2 353 62 145 20 851 2 340 110 399

circ22 21 252 2 366 3 171 173 883 55 141 3 214 368 743

circ24 27 600 3 146 4 159 513 812 83 573 8 136 853 588

circ26 35 100 3 992 5 355 502 946 211 752 15 475 1 642 139

circ28 43 848 4 642 6 790 991 604 346 019 69 524 2 740 632

circ30 53 940 5 842 8 401 1 682 421 679 980 139 661 4 527 256

circ32 65 472 7 074 10 443 2 575 350 666 393 300 591 6 972 901

circ34 78 540 8 042 12 539 3 291 243 1 438 983 439 302 10 114 965

circ36 93 240 9 726 15 153 4 680 108 1 908 173 774 723 14 698 709

circ38 109 668 11 424 378 500 5 739 472 2 385 512 1 115 263 20 594 348

circ40 127 920 12 752 459 834 8 906 144 3 513 490 1 867 497 27 822 677

con4 72 17 17 17 17 17 17

con6 180 43 43 43 43 43 43

con8 336 80 80 82 80 80 80

con10 540 124 124 133 126 126 127

con12 792 181 183 198 186 188 189

con14 1 092 252 254 274 262 261 266

con16 1 440 327 334 2 219 351 343 361

con18 1 836 416 428 7 820 719 439 474

con20 2 280 520 535 12 317 4 160 548 2 565

con22 2 772 626 653 20 920 6 645 668 20 159

con24 3 312 747 786 49 614 11 259 2 695 60 529

con26 3 900 884 928 79 045 29 979 5 407 114 757

con28 4 536 1 021 1 084 123 696 49 129 10 186 204 120

con30 5 220 1 177 1 256 183 371 59 516 14 712 305 013

con32 5 952 1 359 1 434 249 907 93 375 26 138 468 538

con34 6 732 1 512 1 634 296 112 122 935 47 846 665 550

con36 7 560 1 703 1 841 415 699 132 639 65 621 909 426

con38 8 436 1 918 2 062 543 426 186 582 98 547 1 232 937

con40 9 360 2 099 19 684 652 410 244 466 128 071 1 622 050

gal4 2 280 416 416 423 417 416 416

gal6 6 180 1 365 1 416 1 459 1 393 1 407 1 366

gal8 14 448 2 373 2 674 2 897 2 498 2 499 2 394

gal10 29 340 4 535 5 222 5 720 4 981 5 031 5 342

gal12 55 704 7 135 8 569 9 615 8 333 8 256 9 888

gal14 76 804 10 840 13 420 26 011 13 581 12 920 16 897

gal16 108 960 14 583 18 552 99 099 35 273 18 020 444 554

gal18 146 268 20 205 25 405 593 209 90 095 25 070 1 870 983

gal20 201 400 25 401 33 220 1 332 743 208 980 32 849 5 164 274

gal22 244 860 33 901 44 359 2 359 260 537 884 78 948 9 466 587

gal24 389 712 44 260 58 246 4 854 406 1 677 874 280 886 21 953 367

gal26 536 900 58 968 76 655 7 910 227 3 074 931 690 326 39 981 434

gal28 697 032 75 276 100 600 16 743 963 6 881 086 1 297 734 68 335 459

gal30 997 020 95 158 127 694 29 486 387 13 099 851 2 267 234 119 802 775

gal32 1 251 904 119 665 1 234 343 46 682 652 21 099 566 5 708 124 185 483 935

gal34 1 546 116 143 298 199 392 59 640 798 29 150 579 9 922 914 271 702 974

gal36 1 862 280 169 387 241 169 93 918 510 35 376 235 19 403 519 384 992 916

gal38 2 319 900 204 980 6 922 941 130 247 268 56 985 534 29 465 761 558 133 816

gal40 2 886 000 241 908 9 428 405 188 818 884 81 189 254 38 298 839 797 804 204

incr4 312 48 48 48 48 48 48

incr6 1 860 228 255 266 254 254 250

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

Table 2: Continued from Table 2.

instance UB[ f

] UB-opt RLS NSGA-II

NSGA-II

FRLS

incr8 6 384 638 714 824 697 701 670

incr10 16 380 1 612 1 778 2 043 1 712 1 730 1 755

incr12 35 112 3 398 3 735 4 313 3 644 3 626 4 312

incr14 66 612 6 488 7 063 27 652 7 236 6 821 9 593

incr16 115 680 10 332 12 023 163 460 12 635 11 786 315 443

incr18 187 884 17 278 19 470 534 396 48 252 19 368 2 149 226

incr20 289 560 25 672 29 948 2 064 999 282 106 29 845 6 746 265

incr22 427 812 40 944 44 746 3 844 540 1 334 966 45 275 16 385 851

incr24 610 512 56 602 63 017 7 495 505 1 469 070 152 351 33 325 005

incr26 846 300 81 866 88 979 15 952 802 3 972 629 332 892 63 000 386

incr28 1 144 584 106 870 121 563 28 604 791 9 952 208 778 753 108 752 856

incr30 1 515 540 136 810 163 877 52 816 362 12 960 999 2 550 410 180 585 600

incr32 1 970 112 177 990 212 346 71 755 110 22 764 475 5 568 153 285 130 008

incr34 2 520 012 222 082 2 438 961 101 145 675 48 918 770 16 486 326 436 356 818

incr36 3 177 720 278 060 3 075 541 138 435 016 51 241 361 23 971 265 647 384 186

incr38 3 956 484 336 008 437 733 222 669 638 112 416 041 46 812 515 946 779 972

incr40 4 870 320 406 960 9 599 136 274 093 532 157 865 646 51 366 137 1 345 652 388

line4 168 24 24 24 24 24 24

line6 660 76 85 89 85 86 84

line8 1 680 162 183 203 175 182 167

line10 3 420 370 356 419 350 352 347

line12 6 072 584 618 729 602 615 640

line14 9 828 918 1 007 1 239 998 996 1 159

line16 14 880 1 320 1 503 16 751 3 703 1 485 1 981

line18 21 420 1 926 2 163 51 654 11 553 2 142 39 959

line20 29 640 2 548 2 988 228 273 16 077 3 008 313 491

line22 39 732 3 684 4 094 368 448 67 048 4 118 914 082

line24 51 888 4 732 5 331 770 377 147 056 5 468 1 868 418

line26 66 300 6 382 6 940 1 296 961 263 622 54 516 3 344 085

line28 83 160 7 778 8 762 1 876 289 865 566 56 562 5 810 457

line30 102 660 9 312 10 970 2 580 140 965 839 275 173 9 445 912

line32 124 992 11 234 13 422 4 302 373 1 443 644 370 949 13 768 626

line34 150 348 13 190 16 319 5 711 951 2 316 826 918 949 20 857 072

line36 178 920 15 536 19 657 8 893 440 3 191 630 1 349 717 29 804 800

line38 210 900 17 862 385 004 11 959 570 6 293 569 2 344 401 41 127 949

line40 246 480 20 546 978 543 14 223 932 7 108 618 3 761 441 56 340 615

nﬂ16 2 575 200 231 483 305 783 3 668 565 325 792 298 438 37 199 678

nﬂ18 3 283 380 282 258 385 630 9 831 069 1 817 916 377 761 82 614 298

nﬂ20 4 077 400 332 041 453 985 28 517 178 4 588 157 451 007 164 899 817

nﬂ22 4 957 260 400 636 554 380 21 185 780 14 068 063 553 708 281 914 620

nﬂ24 5 922 960 463 657 641 449 67 606 634 22 724 195 653 214 445 953 536

nﬂ26 6 974 500 536 792 760 150 119 472 514 34 729 015 1 777 608 658 635 398

nﬂ28 8 111 880 598 123 882 061 149 361 098 75 166 343 7 858 029 950 306 569

nﬂ30 9 509 100 739 697 1 094 695 258 024 414 97 663 698 20 136 400 1 347 689 293

nﬂ32 10 842 560 914 620 1 371 006 412 089 659 128 529 608 35 478 556 1 826 481 460

nl4 44 616 8 276 8 276 8 287 8 276 8 276 8 276

nl6 165 660 23 916 24 773 25 758 24 917 24 472 23 916

nl8 309 232 39 721 43 792 46 971 42 047 41 876 44 243

nl10 496 980 59 436 67 619 76 609 65 619 66 872 80 222

nl12 908 424 110 729 132 423 145 180 128 863 128 534 165 868

nl14 1 885 884 188 728 235 944 547 804 241 993 231 053 8 938 940

nl16 2 486 880 261 687 337 449 4 313 728 719 253 327 340 38 836 517

sup4 364 152 63 405 63 405 63 612 63 405 63 405 63 405

sup6 910 380 130 365 143 164 147 208 135 228 136 631 130 395

sup8 1 699 376 182 409 203 163 260 895 193 428 190 643 254 361

sup10 2 731 140 316 329 366 130 439 820 341 093 345 553 521 457

sup12 4 005 672 458 810 531 185 653 431 528 485 511 240 5 435 891

sup14 5 522 972 567 891 735 259 1 732 923 759 361 719 889 43 792 093

# best 72 3 14 36 21

Randomized Local Search vs. NSGA-II vs. Frequency Fitness Assignment on The Traveling Tournament Problem

10 20 30 40

mean life (log-scaled)

RLS

NSGA-II₄

NSGA-II₁₆

NSGA-II₆₄

FRLS

Figure 1: The average life index of the objective function

evaluation (FE) where the last improving move was made,

plotted in log-scale over the problem scale n.

From the RobinX website (Van Bulck, 2024), we

take the current upper bound UB-opt of the optimal

tour length for a feasible tour, i.e., the best result to

date delivered by any heuristic or exact method. We

ﬁnd that the travel lengths delivered by our method

are not yet competitive. However, especially FRLS

can sometimes hit the upper bound UB-opt of the op-

timal travel length for a feasible tour. Most notably

on the instance line10, it dips below UB-opt of 370

by delivering a solution with travel length 347. Sadly,

while we were writing this text, the RobinX website

had been updated, moving the upper bound to 302.

Either way one question arises: Are these re-

sults the limit of what our algorithms and setups can

achieve?

The answer to this question is clearly No. In Fig-

ure 1, we plot the average life index of the objec-

tive function evaluation (FE) where the last improv-

ing move was made over the problem scale n. As-

tonishingly, all three algorithms keep improving until

the very end of the computational budget of 10

FEs

on all but the smallest problems. This means that, if

we had used a larger computational budget, we would

very likely have obtained better results.

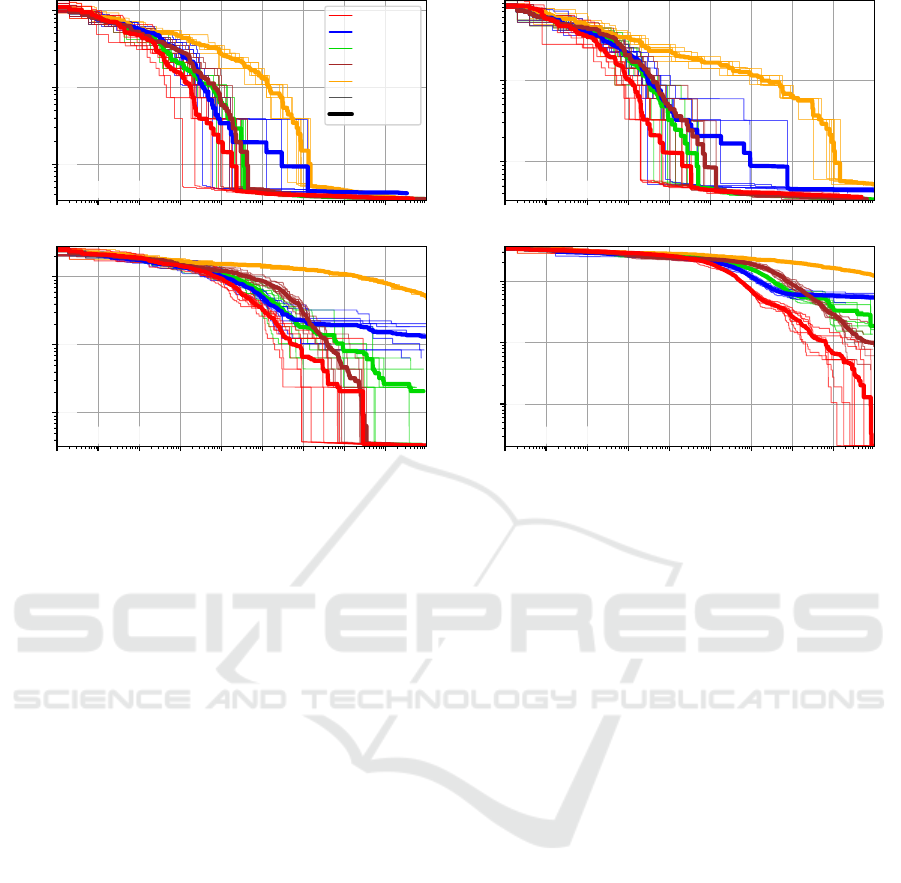
This is conﬁrmed in Figure 2, where the progress

of the algorithm setups in terms of their best-so-far

f -value over time measured in FEs is illustrated on

four selected RobinX instances. On all four instances,

the initial larger improvements of the algorithms are

due to removing errors and the corresponding large

penalties in f . Once they cannot remove further er-

rors, their curves begin to ﬂatten. Interestingly, the

curves for the two NSGA-II setups with smaller popu-

lations tend to become ﬂatter more quickly than RLS.

NSGA-II

keeps improving long, but even it seem-

ingly begins to slow down at least on the large con38

instance before RLS. Despite these slowdowns, a

close inspection shows that all algorithms keep im-

proving until the very end of the budget, conﬁrm-

ing the conclusions from Figure 1. FRLS is visibly

slower than the other algorithms, but the curves also

show that if more budget was given, it could have had

a good chance to outperform them. Notice that ear-

lier studies gave a computational budget of 10

FEs,

compared to the 10

used here (Weise et al., 2021b;

Weise et al., 2023; Liang et al., 2022; Liang et al.,

2024).

The two ﬁgures explain why RLS performs best:

The simple randomized local search has no means to

escape from local optima. The advantage of NSGA-II

with a large population, i.e., NSGA-II

, or of FRLS,

would be that they are probably much less likely to

get stuck at local optima, can keep improving long af-

ter RLS gets stuck, and will, hence, eventually ﬁnd

better solutions. But it takes a long time until the

RLS stops improving, even on small problems. In-

deed, only on problems with up to six teams, it stops

improving before consuming 10

FEs in average! It

usually kept ﬁnding better solutions until the whole

budget was consumed. Interestingly, NSGA-II

and

NSGA-II

seem to not be better than RLS in their ex-

ploration ability. While NSGA-II

and FRLS may be

better in this respect, they pay for it by being slower in

exploitation, i.e., need longer to ﬁnd solutions of the

same quality as RLS. Nevertheless, we expect that

had we used an even larger budget, FRLS and maybe

an NSGA-II setup with a bigger population would have

outperformed RLS eventually. On smaller and mid-

sized problems, they do ﬁnd better results already.

5 CONCLUSIONS

The goal of solving the classical double-round robin

traveling tournament problem (2RR TTP) is to sched-

ule games in a fair and efﬁcient way. Several meta-

heuristic approaches have been designed for it. The

majority of them work on the game plans directly and

only (Choubey, 2010) investigated an encoding based

on game permutations. We too, construct game plans

from permutations and search in the much simpler

space of permutations, allowing us to apply different

heuristics off-the-shelf.

We are, to the best of our knowledge, the ﬁrst

to explicitly tackle the 2RR TTP as a bi-objective

problem, minimizing both constraint violations f

and

travel length f

as distinct objective functions. We

did this by applying the multi-objective NSGA-II al-

gorithm, as well as a randomized local search RLS

working on a lexicographical prioritization f of the

constraint violations f

over the travel length f

. We

furthermore plug frequency ﬁtness assignment (FFA)

into the RLS, obtain the FRLS, and apply it to the

same prioritization scheme. This algorithm will opti-

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

time in FEs

best-so-far f on line10

RLS

NSGA-II₄

NSGA-II₁₆

NSGA-II₆₄

FRLS

single run

mean

time in FEs

best-so-far f on sup10

time in FEs

best-so-far f on gal20

time in FEs

best-so-far f on con38

Figure 2: The progress of the ﬁve algorithm setups in terms of f over time (measured in FEs) on line10, sup10, gal20, and

con38 (top-left to bottom-right). All axes use a log scale.

mize all possible prioritizations of a multi-objective

problem at once (which is a pleasing theoretically

property but otherwise of no relevance here).

Our experiments showed clearly that the encoding

we use is a feasible way to approach the 2RR TTP

even at larger scales and even if used in very dif-

ferent algorithms. The simple RLS can reliably ﬁnd

game plans without errors for problem instances with

a scale n of 36 within our computational budget. This

is remarkable as most related works using metaheuris-

tics tackle problems of a smaller scale only.

We also found that RLS performed better than

NSGA-II and FRLS on larger problems while often

losing out on smaller scales. All algorithms can

keep improving during the complete computational

budget of 10

objective function evaluations that we

granted in the experiment (with the exception of re-

ally small problems). Unexpectedly, RLS did not con-

verge within this budget on all but the very smallest

instances but instead kept improving.

On the smaller instances, where RLS indeed con-

verged, both FRLS and NSGA-II could reach better

solutions. To be fair, what we refer to as “smaller

instances” are instances of scales n up to about 20,

which are already larger than what most related works

tackle. So had we limited our work to these scales,

we would probably have concluded that NSGA-II and

FRLS are better choices across the board. Therefore,

maybe a sixth contribution of our work is to ﬁnd

that, while more sophisticated methods can beat crude

local search on small instances, big instances pose

a challenge so hard that even a primitive algorithm

can be competitive, even on a fairly large budget of

FEs.

In our future work, we will try to improve upon

the encoding scheme. If we can get it to produce

fewer constraint violations, we could probably reach

feasible solutions without error earlier in the search

and more search pressure would result on the travel

length f

. This would then also likely increase the im-

pact of the exploration power of FRLS and NSGA-II.

Of course, we also want to apply different metaheuris-

tics to the problem, but this only makes sense after

the encoding is improved: Any other method for pre-

venting convergence to local optima (e.g., in simu-

lated annealing) would currently likely not fare better

than FRLS or NSGA-II.

ACKNOWLEDGEMENTS

The authors acknowledge support from the Project

of National Natural Science Foundation of China

62406095, the Project of Natural Science Foundation

of Anhui Province 2308085MF213, the Key Research

Plan of Anhui Province 2022k07020011, the Univer-

sity Scientiﬁc Research Innovation Team Project of

Anhui Province 2022AH010095, as well as the Hefei

Specially Recruited Foreign Expert program and the

Hefei Foreign Expert Ofﬁce program.

Randomized Local Search vs. NSGA-II vs. Frequency Fitness Assignment on The Traveling Tournament Problem

REFERENCES

Anagnostopoulos, A., Michel, L., Van Hentenryck, P., and

Vergados, Y. (2006). A simulated annealing approach

to the traveling tournament problem. Journal of

Scheduling, 9(2):177–193. doi:10.1007/S10951-006-

7187-8.

Anderson, J. (2000). A survey of multiobjective optimiza-

tion in engineering design. Technical Report LiTH-

IKP-R-1097, Link

oping University, Department of

Mechanical Engineering, Link

oping, Sweden. https:

//www.researchgate.net/publication/228584672.

Brand

ao, F. and Pedroso, J. P. (2014). A complete search

method for the relaxed traveling tournament problem.

EURO Journal on Computational Optimization, 2(1-

2):77–86. doi:10.1007/s13675-013-0010-3.

Chen, P., Kendall, G., and Vanden Berghe, G. (2007). An

ant based hyper-heuristic for the travelling tournament

problem. In IEEE Symposium on Computational Intel-

ligence in Scheduling (CISched’07), April 2–4, 2007,

Honolulu, HI, USA, pages 19–26, Piscataway, NJ,

USA. IEEE. doi:10.1109/SCIS.2007.367665.

Choubey, N. S. (2010). A novel encoding scheme for travel-

ing tournament problem using genetic algorithm. In-

ternational Journal of Computer Applications (IJCA),

Special Issue on “Evolutionary Computation for Op-

timization Techniques” (ECOT’10)(2):79–82. https:

//www.ijcaonline.org/ecot/number2/SPE139T.pdf.

de Bruin, E., Thomson, S. L., and van den Berg, D.

(2023). Frequency ﬁtness assignment on JSSP: A

critical review. In Correia, J., Smith, S. L., and

Qaddoura, R., editors, Proceedings of the 26th Eu-

ropean Conference on Applications of Evolutionary

Computation (EvoApplications’23), Held as Part of

EvoStar 2023, April 12-14, 2023, Brno, Czech Repub-

lic, volume 13989 of Lecture Notes in Computer Sci-

ence, pages 351–363, Cham, Switzerland. Springer.

doi:10.1007/978-3-031-30229-9

23.

de Werra, D. (1988). Some models of graphs for scheduling

sports sompetitions. Discrete Applied Mathematics,

21(1):47–65. doi:10.1016/0166-218X(88)90033-9.

Deb, K., Agrawal, S., Pratab, A., and Meyarivan, T. (2000).

A fast elitist non-dominated sorting genetic algorithm

for multi-objective optimization: NSGA-II. In Schoe-

nauer, M., Deb, K., Rudolph, G., Yao, X., Lutton, E.,

Merelo-Guerv

os, J. J., and Schwefel, H., editors, Pro-

ceedings of the 6th International Conference on Paral-

lel Problem Solving from Nature (PPSN VI), Septem-

ber 18–20, 2000, Paris, France, volume 1917/2000

of Lecture Notes in Computer Science (LNCS), pages

849–858, Berlin, Germany. Springer-Verlag GmbH.

doi:10.1007/3-540-45356-3 83.

Deb, K., Agrawal, S., Pratap, A., and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm:

NSGA-II. IEEE Transactions on Evolutionary Com-

putation, 6(2):182–197. doi:10.1109/4235.996017.

Easton, K., Nemhauser, G. L., and Trick, M. A. (2001).

The traveling tournament problem description and

benchmarks. In Walsh, T., editor, Proceedings

of the 7th International Conference on Principles

and Practice of Constraint Programming (CP’01),

November 26–December 1, 2001, Paphos, Cyprus,

volume 2239 of Lecture Notes in Computer Sci-

ence, pages 580–584, Berlin/Heidelberg, Germany.

Springer. doi:10.1007/3-540-45578-7 43.

George, A., Razak, A., and Wilson, N. (2015). The

comparison of multi-objective preference inference

based on lexicographic and weighted average mod-

els. In 27th IEEE International Conference on

Tools with Artiﬁcial Intelligence (ICTAI’15), Novem-

ber 9–11, 2015, Vietri sul Mare, Italy, pages 88–

95, Piscataway, NJ, USA. IEEE Computer Society.

doi:10.1109/ICTAI.2015.26.

Johnson, D. S., Papadimitriou, C. H., and Yannakakis,

M. (1988). How easy is local search? Jour-

nal of Computer and System Sciences, 37(1):79–100.

doi:10.1016/0022-0000(88)90046-3.

Khelifa, M. and Boughaci, D. (2016). Hybrid harmony

search combined with variable neighborhood search

for the traveling tournament problem. In Nguyen,

N. T., Manolopoulos, Y., Iliadis, L. S., and Traw-

inski, B., editors, Computational Collective Intel-

ligence - 8th International Conference (ICCCI’16),

September 28–30, 2016, Halkidiki, Greece, Part I,

volume 9875 of Lecture Notes in Computer Sci-

ence, pages 520–530, Cham, Switzerland. Springer.

doi:10.1007/978-3-319-45243-2 48.

Khelifa, M. and Boughaci, D. (2018). A cooperative lo-

cal search method for solving the traveling tournament

problem. Computing and Informatics, 37(6):1386–

1410. doi:10.4149/CAI 2018 6 1386.

Khelifa, M., Boughaci, D., and A

ımeur, E. (2017). An en-

hanced genetic algorithm with a new crossover oper-

ator for the traveling tournament problem. In 4th In-

ternational Conference on Control, Decision and In-

formation Technologies (CoDIT’17), April 5–7, 2017,

Barcelona, Spain, pages 1072–1077, Piscataway, NJ,

USA. IEEE. doi:10.1109/CODIT.2017.8102741.

Larra

naga, P., Kuijpers, C. M. H., Murga, R. H., Inza, I.,

and Dizdarevic, S. (1999). Genetic algorithms for the

travelling salesman problem: A review of represen-

tations and operators. Artiﬁcial Intelligence Review,,

13(2):129–170. doi:10.1023/A:1006529012972.

Larra

naga, P., Kuijpers, C. M. H., Poza, M., and Murga,

R. H. (1997). Decomposing bayesian networks:

Triangulation of the moral graph with genetic al-

gorithms. Statistics and Computing, 7(1):19–34.

doi:10.1023/A:1018553211613.

Liang, T., Wu, Z., L

assig, J., van den Berg, D., Thom-

son, S. L., and Weise, T. (2024). Addressing the

traveling salesperson problem with frequency ﬁtness

assignment and hybrid algorithms. Soft Computing.

doi:10.1007/s00500-024-09718-8.

Liang, T., Wu, Z., L

assig, J., van den Berg, D., and

Weise, T. (2022). Solving the traveling salesper-

son problem using frequency ﬁtness assignment. In

Ishibuchi, H., Kwoh, C., Tan, A., Srinivasan, D.,

Miao, C., Trivedi, A., and Crockett, K. A., edi-

tors, IEEE Symposium Series on Computational In-

telligence (SSCI’22), December 4–7, 2022, Singa-

pore, pages 360–367, Piscataway, NJ, USA. IEEE.

doi:10.1109/SSCI51031.2022.10022296.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

Neumann, F. and Wegener, I. (2007). Randomized lo-

cal search, evolutionary algorithms, and the minimum

spanning tree problem. Theoretical Computer Sci-

ence, 378(1):32–40. doi:10.1016/j.tcs.2006.11.002.

Russell, S. J. and Norvig, P. (2002). Artiﬁcial Intelligence:

A Modern Approach (AIMA). Prentice Hall Interna-

tional Inc., Upper Saddle River, NJ, USA, 2 edition.

Thielen, C. and Westphal, S. (2011). Complexity

of the traveling tournament problem. Theo-

retical Computer Science, 412(4-5):345–351.

doi:10.1016/J.TCS.2010.10.001.

Urrutia, S. and Ribeiro, C. C. (2006). Maximizing breaks

and bounding solutions to the mirrored traveling tour-

nament problem. Discrete Applied Mathematics,

154(13):1932–1938. doi:10.1016/j.dam.2006.03.030.

Uthus, D. C., Riddle, P. J., and Guesgen, H. W.

(2013). Solving the traveling tournament prob-

lem with iterative-deepening A*. In Borrajo, D.,

Kambhampati, S., Oddi, A., and Fratini, S., edi-

tors, Proceedings of the Twenty-Third International

Conference on Automated Planning and Scheduling

(ICAPS’13), June 10–14, 2013, Rome, Italy, pages

488–489. AAAI. http://www.aaai.org/ocs/index.php/

ICAPS/ICAPS13/paper/view/6030.

Van Bulck, D. (2024). Minimum travel objective repos-

itory: Website of the RobinX benchmark. https:

//robinxval.ugent.be/RobinX/travelRepo.php, visited

on 2024-05-10.

Van Bulck, D., Goossens, D., Sch

onberger, J., and Gua-

jardo, M. (2018). RobinX: An xml-driven classiﬁ-

cation for round-robin sports timetabling. In Pro-

ceedings of the 12th International Conference on

the Practice and Theory of Automated Timetabling

(PATAT’18), August 28–31, 2018, Vienna, Aus-

tria, pages 481–484, Leuven, Belgium. EURO

Working Group on Automated Timetabling (EWG-

PATAT). https://patatconference.org/patat2018/ﬁles/

proceedings/paper39.pdf.

Van Bulck, D., Goossens, D., Sch

onberger, J., and

Guajardo, M. (2020). RobinX: A three-ﬁeld

classiﬁcation and uniﬁed data format for round-

robin sports timetabling. European Jour-

nal of Operational Research, 280(2):568–580.

doi:10.1016/J.EJOR.2019.07.023.

Verduin, K., Thomson, S. L., and van den Berg, D. (2023).

Too constrained for genetic algorithms. Too hard

for evolutionary computing. The traveling tournament

problem. In van Stein, N., Marcelloni, F., Lam,

H. K., Cottrell, M., and Filipe, J., editors, Proceedings

of the 15th International Joint Conference on Com-

putational Intelligence (IJCCI’23), November 13-15,

2023, Rome, Italy, pages 246–257, Set

ubal, Portugal.

SciTePress. doi:10.5220/0012192100003595.

Volgenant, A. (2002). Solving some lexicographic

multi-objective combinatorial problems. European

Journal of Operational Research, 139(3):578–584.

doi:10.1016/S0377-2217(01)00214-4.

Weise, T., Li, X., Chen, Y., and Wu, Z. (2021a).

Solving job shop scheduling problems without us-

ing a bias for good solutions. In Genetic and

Evolutionary Computation Conference (GECCO’21),

July 10-14, 2021, Lille, France, Companion Vol-

ume, pages 1459–1466, New York, NY, USA. ACM.

doi:10.1145/3449726.3463124.

Weise, T., Wan, M., Tang, K., Wang, P., Devert, A.,

and Yao, X. (2014). Frequency ﬁtness assignment.

IEEE Transactions on Evolutionary Computation,

18(2):226–243. doi:10.1109/TEVC.2013.2251885.

Weise, T. and Wu, Z. (2023). Replicable self-documenting

experiments with arbitrary search spaces and algo-

rithms. In Genetic and Evolutionary Computa-

tion Conference Companion (GECCO’23 Compan-

ion), July 15-19, 2023, Lisbon, Portugal, New York,

NY, USA. ACM. doi:10.1145/3583133.3596306.

Weise, T., Wu, Z., Li, X., and Chen, Y. (2021b). Fre-

quency ﬁtness assignment: Making optimization al-

gorithms invariant under bijective transformations

of the objective function value. IEEE Transac-

tions on Evolutionary Computation, 25(2):307–319.

doi:10.1109/TEVC.2020.3032090.

Weise, T., Wu, Z., Li, X., Chen, Y., and L

assig, J. (2023).

Frequency ﬁtness assignment: Optimization without

bias for good solutions can be efﬁcient. IEEE Transac-

tions on Evolutionary Computation, 27(4):980–992.

doi:10.1109/TEVC.2022.3191698.

Zhang, S., Jia, F., Wang, C., and Wu, Q. (2023). Targeted

hyperparameter optimization with lexicographic pref-

erences over multiple objectives. In The Eleventh In-

ternational Conference on Learning Representations

(ICLR’23), May 1-5, 2023, Kigali, Rwanda, MA,

USA. OpenReview.net. https://openreview.net/pdf?

id=0Ij9 q567Ma.

Randomized Local Search vs. NSGA-II vs. Frequency Fitness Assignment on The Traveling Tournament Problem