Two-Stage Fault Detection and Control Approach for DFIG-Based

Wind Energy Conversion System

Daison Stallon

, Ichrak Eben Zaid

and Yolanda Vidal

1,3 c

Control, Data, and Artificial Intelligence (CoDAlab), Department of Mathematics, Escola d’Enginyeria de Barcelona

Est (EEBE), Universitat Politécnica de Catalunya (UPC), Barcelona, Spain

Commande Numérique des Procédés Industriels (CONPRI) National School of Engineers of Gabes,

University of Gabes, Tunisia

Institut de Matemátiques de la UPC, BarcelonaTech, IMTech, Pau Gargallo 14, 08028 Barcelona, Spain

Keywords: Wind Turbines, Wind Speed, Fault Diagnosis, Wind Energy Conversion Systems, Control Monitoring,

Doubly Fed Induction Generators, Machine Learning.

Abstract: Doubly-Fed Induction Generator (DFIG)-based Wind Energy Conversion Systems (WECS) are critical in

modern electricity generation due to their ability to enhance energy capture and seamlessly integrate with

the electrical grid. However, maintaining reliability and minimizing maintenance costs are essential to

ensure consistent energy production. This research presents an innovative method for fault detection and

diagnosis in DFIG-based WECS. The approach leverages independent component analysis-based

correlation coefficient for precise fault identification. Additionally, an enhanced multihead cross attention

with bi-directional long short term memory classifier is employed to accurately categorize different fault

types. To further improve classifier’s performance, the multi-strategy enhanced orchard algorithm is

implemented, focusing on regulating active and reactive power variations, harmonics in rotor current, and

voltage in the DC link. The proposed method is evaluated using MATLAB working platform and

demonstrates a high accuracy rate of 98% compared to other techniques.

https://orcid.org/0000-0002-1339-6919

https://orcid.org/0000-0001-5066-3601

https://orcid.org/0000-0003-4964-6948

INTRODUCTION

The increasing use of fossil fuels and growing

environmental concerns highlight the urgent need for

clean and sustainable energy sources. Wind energy

has become a vital part of the global energy

landscape, providing 20% of the world’s electricity,

with Wind Turbines (WT) at its core. Consequently,

efficient problem diagnosis and maintenance are

necessary to ensure that WT operates dependably

(Ding et al., 2019; Heilari et al., 2016). Power

electronic converters' fault-tolerant performance in a

variety of applications, including electrical drives,

has been extensively studied in recent years. Zhang et

al. (2014), for instance, talk about fault-tolerant

techniques for multilevel and two-level converters.

Furthermore, Riera-Guasp et al. (2014) offer

information on condition monitoring and fault-

tolerant operation for electric drives and other

equipment.

Moreover, a fault-tolerant control strategy for a

T-type three-level inverter is presented which

guarantees a decrease in power and output voltage

distortions in the event of an open circuit fault.

Despite the paucity of research on fault tolerance in

Wind Energy Conversion Systems (WECSs),

provides a fault-tolerant topology using a five-leg

converter configuration for the grid side converter’s

post-fault operation in PMSG-based systems. An

alternative approach is presented, wherein the output

phases are connected to the dc-link post-fault

detection midway.

Practicality is limited, though, as this arrangement

causes grid-side converter switch voltages to double

in the post-fault mode (Li, Y et al. 2020; Tumari, M

et al. 2022; Dou, B et al. 2020). To eliminate current

Stallon, D., Zaid, I. and Vidal, Y.

Two-Stage Fault Detection and Control Approach for DFIG-Based Wind Energy Conversion System.

DOI: 10.5220/0012891900003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 209-216

ISBN: 978-989-758-717-7; ISSN: 2184-2809

209

distortion post-fault, research suggests faulttolerant

control for open-switch faults in three-level neutral

point clamped converters of Permanent Magnet

Synchronous Generator (PMSG) based systems by

using d-axis current injection. References (SaeKok et

al., 2010), examined the reconfiguration post-fault

diagnosis and converter defects in DFIG. Kanjiya et

al. (2013) presented a fault-tolerant Power Electronic

(PE) structure by substituting a nine-switch Grid Side

Converter (GSC).

While grid failures are covered in (Li et al.,

2014), converter faults are not mentioned. Shi and

Patton (2015) explain current sensor malfunctions

and introduce a new current observer to enhance fault

detection. In order to overcome these problems, Gao

et al. (2015a) investigate malfunctions in pitch and

generator speed sensors and suggest an observer-

based active fault-tolerant control technique.

Timely defect detection is critical to all fault-

tolerant

systems. A wealth of information on defect

diagnostic techniques has been published recently,

including surveys such as (Gao et al., 2015b).

Various research papers have existed in the

literature

based on fault analysis in wind energy using

various techniques and aspects. Tuerxun et al.

(Tuerxun et al., 2021) introduced the SSA-SVM

(Sparrow Search Algorithm-Support Vector

Machines) model, an efficient approach that

outperforms existing methods for enhancing

diagnostic accuracy and applicability of WT. Zhang

et al. (Zhang et al., 2022) introduced a CVAE-GAN

(Conditional Variational Generative Adversarial

Network)-based strategy, enhancing the diagnostic

precision of WT in complex scenarios.

Kong et al. (Kong et al., 2021) introduced an

adaptive noise reduction technique known as

CDWPSO (Chaotic Dynamic Weight Particle Swarm

Optimization with Sigmoid-Based Acceleration

Coefficients), aimed at enhancing the diagnosis of

bearing faults in WT.

Hsu et al. (Hsu et al., 2020) employed a statistical

process control and machine learning on 2.8 million

sensor data to diagnose WT faults and predict

maintenance needs with high accuracy, improving

operational efficiency and reducing downtime. Qi et

al. (Qi et al., 2023) presented the WJDAN (Weighted

Joint Domain Adversarial Network) as an innovative

approach for improving cross-domain fault diagnosis

in WT. This research makes the following significant

contributions:

• To handle the non-stationary nature of vibration

signals originating from WECS, the research

uses the Independent Component Analysis-

based Correlation Coefficient (ICA-CC)

method, particularly within the timefrequency

domains.

• The research encompasses the process of

training an Enhanced Multihead Cross

Attention with BiLSTM (EMCABN) classifier,

that is specifically designed for categorizing

different types of faults in WECS.

• Furthermore, the research involves the

optimization of critical parameters within the

EMCABN model.

• This optimization is carried out using the Multi-

strategy Enhanced Orchard Algorithm

(MSEOA)

for controlling the variations in

active and reactive powers, harmonics in rotor

current, and the voltage in the dc-link.

The research is organized into distinct sections:

Section 2 outlines the proposed control methodology

mechanism, Section 3 discusses implementation

results, and Section 4 offers a comprehensive

conclusion summarizing the entire work.

PROPOSED SYSTEM UNDER

INVESTIGATION

The data processing system depicted in Figure 1 for

WT fault detection and classification represents a

cutting-edge and comprehensive approach to

ensuring the reliability and safety of WT while also

mitigating maintenance costs.The present framework

comprises the following primary steps for the goal of

defect identification and classification:

DFIG

Rotor side

converter

Grid s ide

converter

Interconnection

transfor mer

Grid

Filter

Independent

Component Analysis

based C orrelation

Coefficient (ICA-CC)

method

Enhanced

Multihead Cross

Attention with

BiLSTM Network

(EMCABN)

Optimization of

EMCABN parameters

using Multi-strategy

Enhanced Orchard

Algorithm (MSEOA)

Data collection and

signal processing

Power signal (active

and reactive)

DC link

capacitor

Stage 1

Fault control phase

Fault classification

phase

Fault identification

phase

Phase C grid current

Phase B grid current

Phase A grid current

Phase C rotor current

Phase B rotor current

Phase A rotor current

DC link voltage

Figure 1: Structure of proposed methodology.

Data Collection: Under various operating

conditions, the process records different

measurements. The gathered data depicts both

optimal and several potentially flawed scenarios that

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

210

may arise during the process. It can be split into two

sets, one for testing and the other for training.

Denoising Process: Firstly, use the wavelet threshold

denoising method to denoise the defected voltage

signal, then the denoised voltage signal is subjected

to ICA-CC model to produce a series of components.

Feature Extraction: When the system is functioning

normally, an ICA-CC model is constructed solely

from the training data set. The ICA-CC model

extracts a collection of characteristics where the

original data's information becomes less and less

important. As a result, the features that are most

frequently caught are retained and show how the data

is projected onto a subspace that is determined

by fewer total projector directions. Given that it has a

substantial impact on the classification performance,

this quantity was chosen with sufficient care. The

combined probabilities of the chosen features across

the various process scenarios are computed. An ICA-

CC model with five directions has been built based

on the most important information that was projected

from the data.

Fault Detection and Classification: During the

training phase, EMCABN demonstrates a potential

capacity to identify each of the WT's various

operating circumstances. The quantity of situations

determines the EMCABN structure. As a result, each

scenario is given a matching state. The intermediate

transitions between all EMCABN states are defined

manually based on certain requirements and for

large-sized data. Conversely, estimating the

transition probabilities is more feasible in the

univariate scenario. The EMCABN parameter triplet

is defined once it has been trained, and its

effectiveness is evaluated using a testing setup.

Fault Control: Wind speed, rotor speed, generator

temperature, voltage, and current are the inputs of

the system. Using these inputs, fault control actions

are implemented, such as adjusting pitch angle, yaw

control, braking, or activating protection

mechanisms to mitigate fault effects and ensure safe

and efficient WECS operation. The mechanism is

done using MSEOA.

2.1

Fault Identification Phase Using

ICA-CC

In the fault detection phase of the DFIG-based

WECS, the independent component analysis-based

correlation coefficient (ICA-CC) is used to isolate

and identify fault signatures from the system's

operational data. The ICA-CC method effectively

separates the mixed signals into independent

components, allowing for precise detection of

anomalies indicative of faults.

Monitoring statistics include active and reactive

power variations, harmonics in rotor currents, and

voltage fluctuations in the DC link. These

parameters are continuously monitored to establish

baselines and identify deviations that may signal a

fault. Thresholds for each parameter are set based on

historical data, and any significant deviation triggers

an alert. The enhanced multihead cross attention

with BiLSTM classifier then categorizes the fault

type based on the identified patterns, ensuring

accurate and timely diagnosis. The monitoring

statistics are crucial in this phase, as they provide the

necessary data to detect and classify faults

efficiently.

Fault Detection:

Input Parameters: Decrease in wind speed, abnormal

generator temperature rise, and fluctuations in

electrical grid voltage.

Output: Detection of anomalies in the system’s

behavior, triggering an alarm for further

investigation.

Based on this, the measured data matrix is

represented in the following:

EASX +=

(1)

Where X represents the measured data matrix, S

represents the independent component matrix, and A

represents the mixing matrix. To find the separation

matrix W, the reconstructed matrix S

is derived as

follows:

WXS =

(2)

To derive the detection logic, the thresholds are

established first, followed by the application of the

corresponding logic:











−≥≥

−<<

occurredfaultJSPEJI

freefaultJSPEJI

thSPE

(3)

where estimated thresholds are expressed as J

and

SPE,th

, the unit matrix is expressed as I.

2.2 Fault Classification Phase Using

EMCABN

The fault classification phase in DFIG-based WECS

leverages the Enhanced Multihead Cross Attention

with BiLSTM Network (EMCABN) to accurately

categorize various fault types (Leng, X.L et al.

2021). This advanced model combines the strengths

of multihead attention mechanisms and BiLSTM

Two-Stage Fault Detection and Control Approach for DFIG-Based Wind Energy Conversion System

211

networks. The model can focus on various input data

points at once thanks to the multihead cross attention

method, which helps it identify complex patterns

linked to various defects. The BiLSTM component,

with its bidirectional processing, ensures that

temporal dependencies in the data are effectively

utilized, leading to a more accurate fault

classification.

EMCABN excels in handling complex, nonlinear

relationships within the system, enabling it to

differentiate between subtle fault signatures. By

integrating this approach, the model can classify

faults with high precision, which is essential for

timely intervention and maintenance in WECS. The

performance of EMCABN is further enhanced by

optimizing its parameters using the Multi-strategy

Enhanced Orchard Algorithm (MSEOA), ensuring

robust classification under various operational

conditions.

Fault Classification:

Input Parameters: Detected anomalies and historical

fault data.

Output: Classification of faults into categories such

as mechanical faults (e.g., bearing failure), electrical

faults (e.g., short-circuit in the generator), or

gridrelated faults (e.g., voltage instability).

It incorporates the forward hidden layer denoted

as L

, the backward hidden layer L

and the output

GHI

for network updates. The network undergoes

iterative updates, proceeding both in the backward

direction, beginning T to 1 and in the forward

direction, beginning 1 to T. The mathematical

expression for the layers of the EMCABN technique

is formulated as follows:

Lfifw

bLwtGHIwL ++=

−121

)((

(4)

Lbibw

bLwtGHIwL ++=

−153

)((

(5)

GHIfOp

bLwLwGHI ++=

(6)

where, L

represents forward bias, L

represents

backward pass, GHI

represents the final output

layers. σ represents standard deviation, w represents

the weight coefficients, and b

, b

, and b

GHI

defines the biases in the model.

2.3 Fault Control Phase Using MSEOA

The practical implementation of a multi-objective

framework for WT fault detection is discussed in

this section. This framework's main goal is to

maximise EMCABN. The objective function for the

proposed system is formulated in the following.

],,,,,,[

)(min

,,,,

QPVIVIVE

EfunctionObjective

abcgabcgabcrabcrDC

(7)

where, error is specified as E which mainly defines

the minimization of voltage, current and power

variation in the WECS. V

represents dc-link

voltage, I

r,abc

, V

r,abc

represents three phase rotor

current and voltage, I

g,abc

, V

g,abc

represents three

phase grid current and voltage, P represents active

power, Q represents reactive power, ’min’ represents

minimize.

Fault Control:

Input Parameters: Identified fault types and system

configuration.

Output: Implementation of control actions such as

adjusting pitch angle to reduce load on the turbine or

activating protection mechanisms to isolate faulty

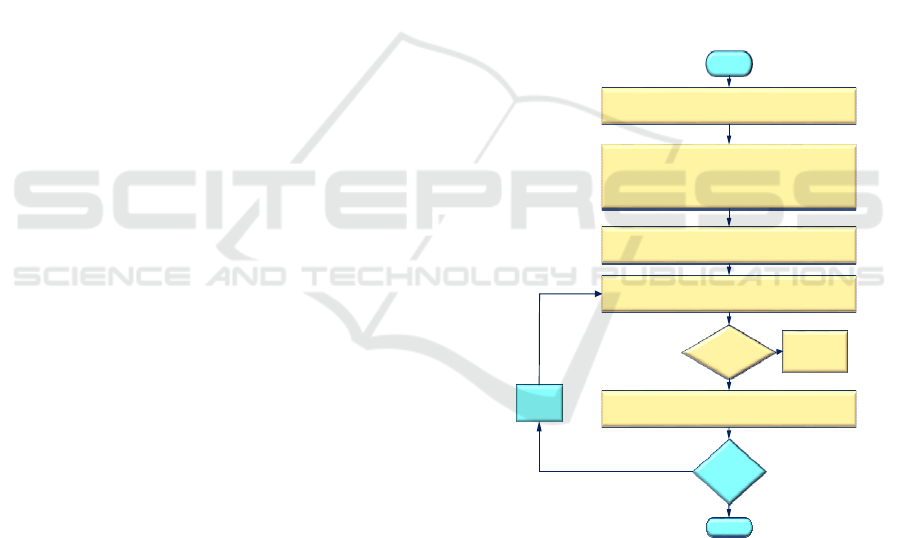
components. Pseudocode and flowchart of MSEOA

is shown in Figure 2 respectively.

Begin

Initialize Objective function

Calculate the optimal fitness position

The optimal solution is replaced

Update the orchard seedlings

If the growth years

number finished?

Replace the seedlings of weak-one with new one

If condition

statisfied?

End

t=t+1

Update the growth

of new seedlings

Yes

],,,,,,[

)(min

,,,,

QPVIVIVError

ErrorfunctionObjective

abcgabcgabcrabcrDC

Figure 2: Flowchart of MSEOA Algorithm.

2.4 Step-by-Step Explanation of

Multi-Strategy Enhanced Orchard

Algorithm (MSEOA)

According to the Orchard Algorithm (OA),

exploration is the movement of candidate

individuals in the direction of the ocean current,

whereas exploitation is the movement of candidate

individuals within the swarm. Temporal control

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

212

−

parameters regulate how these two phases transition

into one another. In Kaveh et al., 2023.

In order to find potential areas, the OA focusses on

exploration in the beginning of an iteration.

Ultimately, though, the OA favors exploitation to

identify the optimal spot inside the designated

region.

The algorithm's capacity for local exploration

and convergence are enhanced by the sine and

cosine learning factors approach. The ability to

participate in global exploitation and to break free

from the trap of local optimization is both improved

by the local escape operator method. Opposition

Based Learning (OBL) and Quasi Oppositional

Learning (QOL) approaches increase the population

solution quality and expand the pool of possible

persons, which improves optimization competency.

An MSEOA is created by integrating the OA with

these three tactics. In order to solve optimisation

difficulties, MSEOA integrates multiple

sophisticated methodologies, building upon the

fundamentals of OA. To improve the OA, it

combines generalised oppositional learning,

quadratic interpolation, and orthogonal learning.

Generalised oppositional learning enhances initial

population quality and convergence, quadratic

interpolation improves the accuracy of global

searches, and orthogonal learning helps escape local

optima. When combined, these tactics improve OA

performance, especially for high-dimensional and

complicated issues. The comprehensive steps of the

MSEOA are summed up in the following to

represent the aforementioned phases.

Step 1. Start by initializing a population of

solutions randomly. Each solution represents a

potential answer to the optimization problem, and

the population size determines the number of

solutions considered at each iteration. Define

necessary parameters, such as the number of

iterations, the search space boundaries, and the

learning rates. Initialize specific parameters for each

strategy used within the algorithm. Establish N =

300 and T = 200, specify the fitness function, and

use the logistic maps provided by to create the

starting locations of N seedlings in the solution search

space. P

i+1

= αP

(1 P

), 0 ⩽ P

⩽ 1 and let t = 1.

Step 2. Assess and contrast the objective value of

every contender, and record the best location thus far

along with the matching optimal objective value.

Evaluate the fitness of each solution using an

objective function. This function quantifies how well

each solution solves the problem. In DFIG-based

WECS, for instance, it could measure how well the

algorithm controls power variations and harmonics.

Rank the solutions based on their fitness. The better

the solution, the higher its rank.

Step 3. Growth of the seedlings. Compute the time

control function C(t). If C(t) > 0.5, the candidate

individual

()

tracts the growth for each seedling,

screening of the seedlings and graft for each seedling

()

1+tP

is renewed using

() ()

(

)

μβ

××−×+=+

∗

221 rPrtPtP

Where constants is denoted as

, random

number is expressed as

, deviated updated

position is denoted as

∗

Step 4. Replacement of the weak seedlings by the

new ones. If

() ()()

tC11,0rand −>

, Type A

movement is performed by the candidate, and the

new position is determined using

() () ( )

LbUbrtPtP

−××+=+ 31

Otherwise, the candidate engaged in Type B

movement, and the updated position makes use of

() ()

(

)

()

tPPsteptPtP

iii

−++=+

..1

ωω

Where, upper bound and lower bound is expressed

LbUb,

, constant for seedlings is expressed as

step

is expressed as step function.

Step 5. Verify the modified individual solution to

see if it exceeds the boundary condition. If it is

outside the scope of the search,













−+

PUbLb

UbLb

randP ,



is used to

return to the opposite boundary.

Step 6. Examine the current location's objective

cost both before and after upgrading. Replace the

site if the grafted seedlings are more fit than the

existing one. Next, compare the ideal fitness value to

the objective value of the existing place. Renew the

best location so far found and the accompanying

ideal objective value if the objective value at the

current position is superior.

Step 7. If t < T, go back to Step 3, otherwise,

perform Step 8.

Step 8. The optimal solution is the one that

remains after the algorithm converges and finds the

best solution. Next, this solution is implemented in

the problem domain, e.g., DFIG-based WECS fault

categorisation. In order to confirm the solution's

Two-Stage Fault Detection and Control Approach for DFIG-Based Wind Energy Conversion System

213

resilience, evaluate the outcomes once more and, if

necessary, validate the results against different

benchmarks.

RESULTS AND DISCUSSION

The research uses a benchmark model that uses the

MATLAB software to simulate a modern WT in

order to evaluate the efficacy of this strategy

(Xiahou, K.S et al 2020). The dataset consisting of

images related to these fault scenarios, is divided

into two subsets through a random split. Details on

the number of variables assessed, the total number of

samples, and the percentage of data allotted to

training and testing should all be included in the

EMCABN dataset.

Usually, 80% of the data is used for training and

20% is used for testing; however, this could change

depending on the study. The Multihead Cross

Attention mechanism improves the model's focus on

pertinent portions of the input data, enhancing

overall performance in tasks like time series

prediction or classification. The EMCABN catches

both past and future information in the sequence.

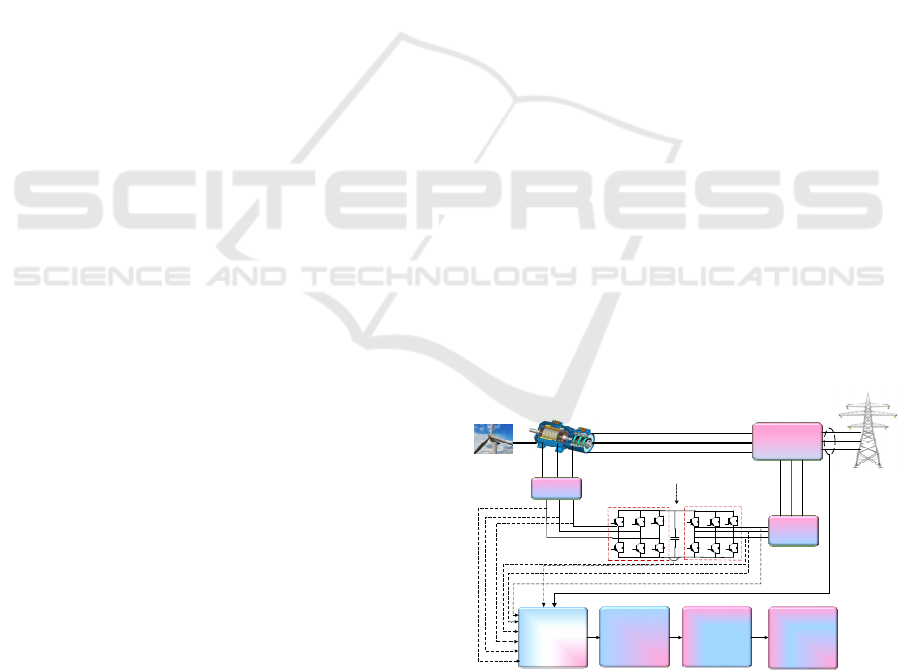
Simulink block setup of the proposed system is

shown in Figure 3.

Approximately 75% of these images are

allocated for detection within the EMCABN, while

the remaining 25% are reserved for the classification

task.

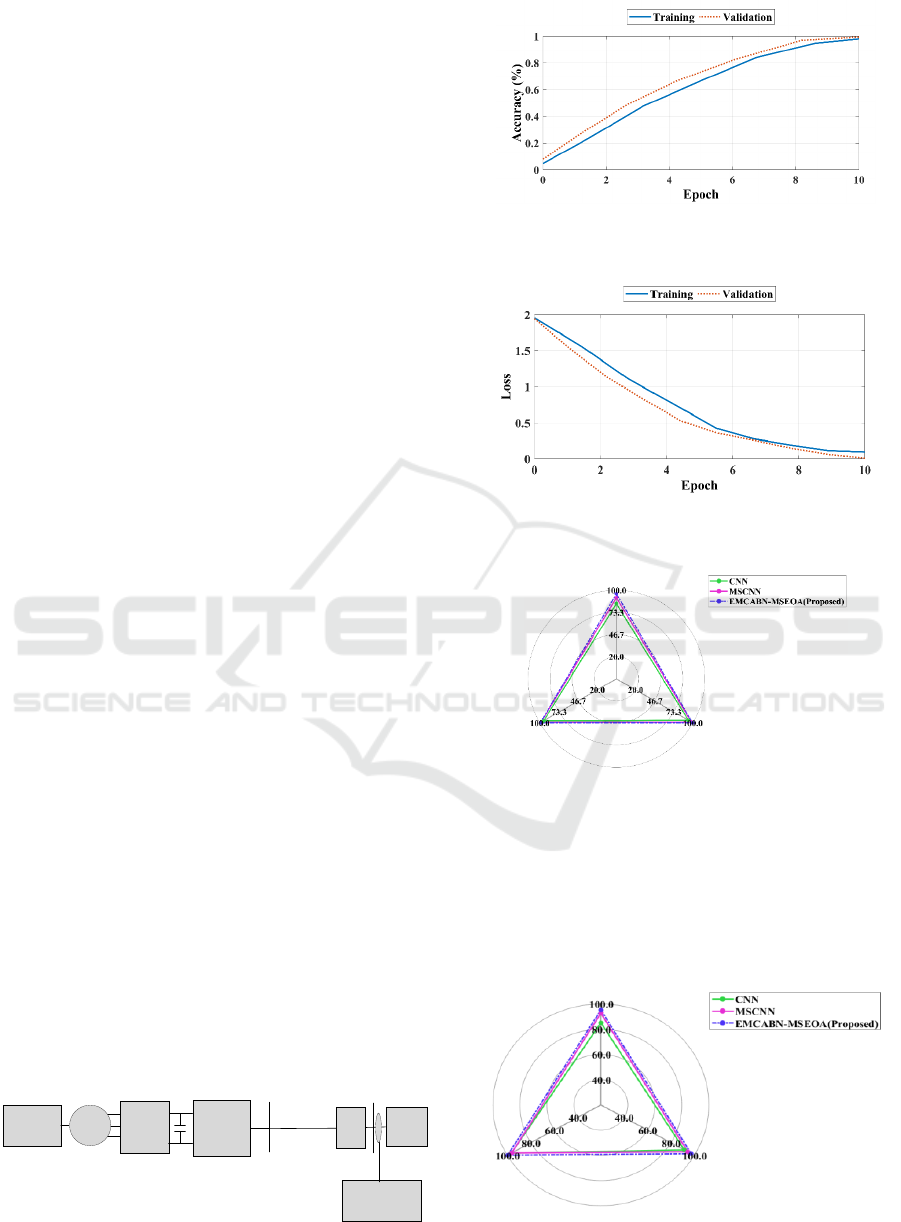
Figure 4 shows the average accuracy of the

EMCABN-MSEOA machine learning model over

the course of training. The validation accuracy

reaches a maximum of about 98% at around epoch

10. The proposed EMCABN detects the WT faults

with remarkable average accuracy of 98%. The

Figure 5 shows the training and validation loss of a

machine learning model over the course of training.

The results, shown in Figure 6, indicate that

EMCABN-MSEOA benefit from increased depth.

Notably, EMCABN-MSEOA models with two or

three layers achieved performance, reaching an F1

score of about 98%. This represents a substantial 7%

improvement over the single-layer

EMCABNMSEOA model.

Wind Turbine

Grid

Grid sid e

converter

Rotor side

converter

Proposed algorithm

Filter

Grid

Figure 3: Simulink block setup of the proposed system.

Figure 4: Average accuracy of the EMCABN-MSEOA

model.

Figure 5: Average losses of the EMCABN-MSEOA

model.

Figure 6: Comparison for efficient diagnosis of WT fault

with proposed and conventional techniques.

In Figure 7, the evaluation compares

EMCABNMSEOA, MSCNN, and CNN using

average F1 scores across eight conditions as the

evaluation metric. Table 1 offers a comprehensive

and wellrounded analysis by synthesizing the results

from 50 randomly conducted trials.

Figure 7: Comparison for efficient diagnosis of noise with

proposed and conventional techniques.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

214

Table 1: Comparison of solution techniques for 50 random

trails.

Techniques F

Score (%) Detection time (s)

CNN (Zare and Ayati, 2021) 98.82±0.0050 36.7318±0.2197

MSCNN (Zare and Ayati, 2021) 98.57±0.0038 14.5388±0.2247

EMCABN-MSEOA 98.05±0.0058 14.5995±0.1756

Techniques

Classification

time (ms)

Control time(s)

CNN (Zare and Ayati, 2021) 0.4884±0.0023 6.56

MSCNN (Zare and Ayati, 2021) 0.1806±0.0025 4.19

EMCABN-MSEOA 0.1814±0.0022 2.65

Table 2: Comparison of solution techniques for 50 random

trails.

Techniques Control level 1 Control level 2 Control level 3

CNN

(

Zare and A

ati, 2021

)

80.41±4.32 86.92±2.84 72.50±5.40

MSCNN

(

Zare and A

ati, 2021

)

71.01±1.04 70.42±2.32 62.70±3.04

EMCABN-

MSEOA

97.34±0.96 98.20±0.72 96.76±1.46

Techniques

Control

level 4

Control

level 5

Average

CNN

(

Zare and A

ati, 2021

)

96.93±2.99 78.95±3.21 84.31

MSCNN

(Zare and Ayati, 2021)

72.09±1.97 71.30±1.57 72.71

EMCABN-

MSEOA

98.94±0.85 99.05±0.69 98.33

Within Table 2, a comprehensive comparative

assessment is presented, utilizing percentage scores

as the evaluative metric. Statistical comparative

analysis is shown in Table 3. The performance of

proposed technique is compared with existing

approaches (Dhibi, K et al. 2022) such as NN-based

EL (NN-EL), Reduced NN-EL, Neural Network

(NN), Bagging ensemble, Random Forest ensemble,

Cascade Forward Neural Network (CFNN), Multiple

Layers (MNN), Feed-Forward Neural Network

(FFNN), and Generalized Regression Neural

Network (GRNN).

The proposed method gives better results in

terms of statistical analysis.

Table 3: Statistical comparative analysis.

Methods

Global performances

Accuracy Recall Precision

Computational

time (s)

Proposed 99.98 99.987 99.987 27.01

GRNN 97.01 97.01 97.01 99.14

FFNN 97.17 97.18 97.17 126.45

MNN 93.58 93.58 93.58 51.30

CFNN 97.41 97.41 97.40 186.82

Random Forest

ensemble

98.41 98.41 98.42 261.3

Bagging ensemble 98.31 98.31 98.31 197.12

NN 93.70 93.71 93.70 47.01

Reduced NN-EL 99.95 99.95 99.95 141

NN-EL 99.97 99.97 99.97 386

Table 4 displays the results of the Wilcoxon

signed-rank test comparison (Fathy, A. et al., 2022).

The suggested approach differs dramatically, with a

95% confidence level.

Table 4: Wilcoxon signed-rank test comparison results.

Method Negative

ranks

Positive

ranks

Ties Z Decision regard (30 runs)

GA-PSO 5

-3.918

a. GA < PSO

b. GA > PSO

c. GA = PSO

d. Based on ne

ative ranks

FPA-GA 30

-4.782

a. FPA < GA

b. FPA > GA

c. FPA = GA

d. Based on

ositive ranks

FPA-PSO 30

-4.782

a. FPA < PSO

b. FPA > PSO

c. FPA = PSO

d. Based on

ositive ranks

Proposed 35

-5

a. Proposed<FPA-GA

b. Proposed >FPA-GA

c. Proposed=FPA-GA

d. Based on

ositive ranks

CONCLUSIONS

This work confirms the efficacy of the

EMCABNMSEOA method in processing signal

images for intelligent WT fault diagnosis, which

improves system reliability and reduces the need for

human interpretation. The methodology is shown to

be proficient at detecting faults and accelerating the

decision-making process, thereby decreasing the

dependence on human expertise for signal feature

extraction. Variable wind speeds, a significant factor

influencing WT performance, are incorporated into

the analysis. Utilizing data across various wind

speeds ensures that the approach reflects real-life

scenarios. When compared to other artificial neural

networks, the Independent Component Analysis-

based Correlation Coefficient (ICA-CC) is notable

for its ability to directly extract optimal features

from raw data, although it does necessitate a

considerable amount of training data. Additionally,

the EMCABN-MSEOA method is characterized by

its computational efficiency and an impressive

classification accuracy rate of 98%, representing a

notable improvement. Future works are planned to

apply this method to actual vibration data from WT

gearboxes in wind farms to confirm its practical

value in improving operational WT fault diagno sis.

ACKNOWLEDGEMENTS

This work was supported by the Spanish Agencia

Two-Stage Fault Detection and Control Approach for DFIG-Based Wind Energy Conversion System

215

Estatal de Investigacio´n (AEI) Ministerio de

Econom´ıa, Industria y Competitividad (MINECO),

and the Fondo Europeo de Desarrollo Regional

(FEDER) through the research projects

PID2021122132OB-C21 and TED2021-129512B-

I00; and by the Generalitat de Catalunya through the

research project 2021-SGR-01044.

REFERENCES

Dou, B., Qu, T., Lei, L. and Zeng, P., (2020). Optimization

of wind turbine yaw angles in a wind farm using a

three-dimensional yawed wake model. Energy, 209,

p.118415.

Ding, P., Wang, H., Bao, W., and Hong, R. (2019).

Hygpmsam based model for slewing bearing residual

useful life prediction. Measurement, 141:162–175.

Dhibi, K., Mansouri, M., Bouzrara, K., Nounou, H. and

Nounou, M., (2022). Reduced neural network based

ensemble approach for fault detection and diagnosis of

wind energy converter systems. Renewable Energy,

194, pp.778-787.

Fathy, A., Rezk, H., Yousri, D., Kandil, T. and Abo-Khalil,

A.G., (2022). Real-time bald eagle search approach for

tracking the maximum generated power of wind energy

conversion system. Energy, 249, p.123661.

Gao, Z., Cecati, C., and Ding, S. X. (2015a). A survey of

fault diagnosis and fault-tolerant techniques—part i:

Fault diagnosis with model-based and signal-based

approaches. IEEE transactions on industrial

electronics, 62(6):3757–3767.

Gao, Z., Cecati, C., and Ding, S. X. (2015b). A survey of

fault diagnosis and fault-tolerant techniques—part i:

Fault diagnosis with model-based and signal-based

approaches. IEEE transactions on industrial

electronics, 62(6):3757–3767.

Heidari, M., Homaei, H., Golestanian, H., and Heidari, A.

(2016). Fault diagnosis of gearboxes using wavelet

support vector machine, least square support vector

machine and wavelet packet transform. Journal of

Vibroengineering, 18(2):860–875

Hsu, J.-Y., Wang, Y.-F., Lin, K.-C., Chen, M.-Y., and Hsu,

J. H.-Y. (2020). Wind turbine fault diagnosis and

predictive maintenance through statistical process

control and machine learning. Ieee Access, 8:23427–

23439.

Kanjiya, P., Ambati, B. B., and Khadkikar, V. (2013). A

novel fault-tolerant dfig-based wind energy conversion

system for seamless operation during grid faults. IEEE

Transactions on Power Systems, 29(3):1296– 1305.

Kaveh, M., Mesgari, M.S. and Saeidian, B., (2023).

Orchard Algorithm (OA): A new meta-heuristic

algorithm for solving discrete and continuous

optimization problems. Mathematics and Computers in

Simulation, 208, pp.95-135.

Kong, X., Xu, T., Ji, J., Zou, F., Yuan, W., and Zhang, L.

(2021). Wind turbine bearing incipient fault diagnosis

based on adaptive exponential wavelet threshold

function with improved cpso. Ieee Access, 9:122457–

122473.

Leng, X.L., Miao, X.A. and Liu, T., (2021). Using

recurrent neural network structure with enhanced

multi-head self-attention for sentiment analysis.

Multimedia Tools and Applications, 80, pp.12581-

12600.

Li, Y., Wei, K., Yang, W. and Wang, Q., (2020).

Improving wind turbine blade based on multi-objective

particle swarm optimization. Renewable Energy, 161,

pp.525-542

Li, H., Yang, C., Hu, Y., Zhao, B., Zhao, M., and Chen, Z.

(2014). Fault-tolerant control for current sensors of

doubly fed induction generators based on an improved

fault detection method. Measurement, 47:929–937.

Qi, H., Han, Y., Tuo, S., and Zhao, Q. (2023). Fault

diagnosis in wind turbines based on weighted joint

domain adversarial network under various working

conditions. IEEE Sensors Journal.

Riera-Guasp, M., Antonino-Daviu, J. A., and Capolino, G.

A. (2014). Advances in electrical machine, power

electronic, and drive condition monitoring and fault

detection: State of the art. IEEE Transactions on

Industrial Electronics, 62(3):1746–1759.

Sae-Kok, W., Grant, D., and Williams, B. (2010). System

reconfiguration under open-switch faults in a doubly

fed induction machine. IET Renewable Power

Generation, 4(5):458–470.

Shi, F. and Patton, R. (2015). An active fault tolerant

control approach to an offshore wind turbine model.

Renewable Energy, 75:788–798.

Tuerxun, W., Chang, X., Hongyu, G., Zhijie, J., and

Huajian, Z. (2021). Fault diagnosis of wind turbines

based on a support vector machine optimized by the

sparrow search algorithm. Ieee Access, 9:69307–69315.

Tumari, M.Z.M., Ahmad, M.A., Suid, M.H. and Ghazali,

M.R., (2022), December. Data-driven control based on

marine predators algorithm for optimal tuning of the

wind plant. In 2022 IEEE International Conference on

Power and Energy (PECon) (pp. 203-208). IEEE.

Xiahou, K.S., Liu, Y., Li, M.S. and Wu, Q.H., (2020).

Sensor fault-tolerant control of DFIG based wind

energy conversion systems. International Journal of

Electrical Power & Energy Systems, 117, p.105563.

Zare, S. and Ayati, M. (2021). Simultaneous fault diagnosis

of wind turbine using multichannel convolutional

neural networks. ISA transactions, 108:230–239.

Zhang, L., Zhang, H., and Cai, G. (2022). The multiclass

fault diagnosis of wind turbine bearing based on

multisource signal fusion and deep learning generative

model. IEEE Transactions on Instrumentation and

Measurement, 71:1–12.

Zhang, W., Xu, D., Enjeti, P. N., Li, H., Hawke, J. T., and

Krishnamoorthy, H. S. (2014). Survey on fault-tolerant

techniques for power electronic converters. IEEE

Transactions on Power Electronics, 29(12):6319–6331.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

216