SportsNGEN: Sustained Generation of Realistic Multi-Player Sports

Gameplay

Lachlan Thorpe

, Lewis Bawden

, Karanjot Vendal

, John Bronskill

and Richard E. Turner

Hawk-Eye Innovations Ltd., U.K.

University of Cambridge, U.K.

Keywords:

Sports Simulation, Tennis, Football, Coaching.

Abstract:

We present a transformer decoder based sports simulation engine, SportsNGEN, trained on sports player and

ball tracking sequences, that is capable of generating sustained gameplay and accurately mimicking the deci-

sion making of real players. By training on a large database of professional tennis tracking data, we demon-

strate that simulations produced by SportsNGEN can be used to predict the outcomes of rallies, determine the

best shot choices at any point, and evaluate counterfactual or what if scenarios to inform coaching decisions

and elevate broadcast coverage. By combining the generated simulations with a shot classiﬁer and logic to

start and end rallies, the system is capable of simulating an entire tennis match. We evaluate SportsNGEN by

comparing statistics of the simulations with those of real matches between the same players. We show that the

model output sampling parameters are crucial to simulation realism and that SportsNGEN is probabilistically

well-calibrated to real data. In addition, a generic version of SportsNGEN can be customized to a speciﬁc

player by ﬁne-tuning on the subset of match data that includes that player. Finally, we show qualitative results

indicating the same approach works for football.

1 INTRODUCTION

The application of machine learning methods has

proven beneﬁcial to many sports applications (Zhao

et al., 2023). In particular, sports simulation and

analysis can provide valuable insights to sports teams

when attempting to understand how small changes to

player formation or playing style could impact the

next period of play, or their chances of winning (Hauri

and Vucetic, 2022; Teranishi et al., 2022; Wang et al.,

2023). In addition, realistic gameplay simulation is

critical in computer gaming scenarios (Kurach et al.,

2020).

Tremendous progress has been made in the area of

sports trajectory prediction (Yue et al., 2014; Zheng

et al., 2016; Le et al., 2017b; Zhan et al., 2019; Li

et al., 2021; Tang et al., 2021; Wu et al., 2021; Alcorn

and Nguyen, 2021; Omidshaﬁei et al., 2022), how-

ever it is difﬁcult to precisely mimic training data over

long periods of time. Figure 18 shows how the pre-

diction error of the player and ball positions increases

with time when simulated tennis data from our sys-

tem is compared to the training data. Sports are inher-

ently unpredictable over time scales longer than sev-

eral seconds and as a result, deterministic prediction

is not possible or useful in many scenarios. Instead, it

is important to capture the different ways a match will

evolve in a statistically accurate manner by modelling

the complete distribution of player decision making.

We propose that generated sports simulations

should be: (i) highly realistic and capture the com-

plete distribution of real player behaviour; (ii) sus-

tained for the duration between natural breaks in the

gameplay; (iii) customizable via ﬁne-tuning or other

method to emulate the style of play of a particular

player and/or team; and (iv) measurable in that met-

rics are available to evaluate the quality of the simu-

lations (as opposed relying on a human expert) such

that the simulations can be improved by optimizing

the metrics.

Recently, the transformer architecture (Vaswani

et al., 2017) has been applied to multi-agent spa-

tiotemporal systems problems to generate realistic

sports simulations and understand player behavioural

patterns (Alcorn and Nguyen, 2021). Instead of gen-

erating words as in natural language processing, tem-

poral player and ball movements can be generated by

training a transformer model to predict the next posi-

tion from a sequence of tracking data.

However, to the best of our knowledge, no pre-

Thorpe, L., Bawden, L., Vendal, K., Bronskill, J. and Turner, R.

SportsNGEN: Sustained Generation of Realistic Multi-Player Sports Gameplay.

DOI: 10.5220/0012892000003828

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 12th International Conference on Sport Sciences Research and Technology Support (icSPORTS 2024), pages 119-130

ISBN: 978-989-758-719-1; ISSN: 2184-3201

119

a) t = 0 s b) t = 2.0 s c) t = 3.1 s

d) t = 4.1 s e) t = 5.2 s f) t = 7.0 s

Figure 1: Frames from a football match simulated using SportsNGEN. The panels depict a passing sequence involving 3 play-

ers. The ball is in the red circle, with an arrow depicting the play that follows. Link to video: https://youtu.be/M0kkKiGVNzk.

Figure 2: Simulated tennis rally between 2 players using 3 shots of training data as input. Frames a) - c): Training data shots.

Frames d) - f) Simulated rollout. Red and blue markings indicate player movement. The lines indicate shot trajectories. The

current shot is opaque while earlier shots are more transparent. The purple line is the ﬁrst simulated shot. Link to video:

https://youtu.be/A1_vv12V5q0.

vious work has been successful in generating realis-

tic, sustained, and customizable simulations, learned

from player and ball tracking data, for more than a

few seconds. In this work we present Sports Neu-

ral Generator or SportsNGEN that realizes the goals

of realistic, sustained, customizable and measurable

sports gameplay. Figure 1 and Figure 2 depict foot-

ball

and tennis sequences, respectively, generated by

our approach along with links to simulation videos.

Our contributions: (i) A transformer decoder

based simulation engine, SportsNGEN, trained on

player and ball tracking data as well as match meta-

data, capable of simulating the movement of all play-

ers and the ball simultaneously in a sports game sce-

nario. The simulations are sustained between breaks

in play. (ii) Training and evaluating SportsNGEN on

a large database of professional tennis tracking data.

SportsNGEN is capable of simulating an entire ten-

nis match by combining the generated simulations

with a shot classiﬁer and logic to start and end ral-

lies. (iii) We show that our model can be used to

inform tennis coaching decisions and best shot op-

tions by evaluating counterfactual or what if options.

We use the term football to refer European football or

soccer.

(iv) We demonstrate through ablations that the follow-

ing enhancements signiﬁcantly improve convergence

and generated simulations: a) extending the player

and ball representations to include relative velocity,

distance to the ball, and time into the game or se-

quence; b) adding small perturbations to the ball po-

sitions during training to allow the model to correct

for errors; and c) Adding context tokens to allow the

model to adapt to different playing surfaces. (v) We

devise a novel optimization method by deﬁning met-

rics to statistically evaluate the quality of generated

tennis data. By altering simulation hyperparameters,

we show that the simulations can be optimized to

be statistically similar to the behaviour of real play-

ers. (vi) We demonstrate that a generic version of our

model can be customized to a speciﬁc tennis player

by ﬁne-tuning on match data that includes that player.

2 RELATED WORK

In this section, we discuss related work in the cate-

gories of sports analytics, and game simulation, and

trajectory prediction.

icSPORTS 2024 - 12th International Conference on Sport Sciences Research and Technology Support

120

Group Activity Recognition and Sports Analyt-

ics. Miller et al. (2014) develop an approach to rep-

resent and analyze the underlying spatial structure

that governs shot selection among professional bas-

ketball players. Le et al. (2017a) employ an imitation

learning approach to analyze football defensive strate-

gies. Hauri and Vucetic (2022) propose a transformer-

based architecture with a Long Short-Term Memory

(LSTM) embedding to recognize basketball group ac-

tivities from player and ball tracking data. Teranishi

et al. (2022) evaluate football players who create off-

ball scoring opportunities by comparing actual move-

ments with the reference movements generated via

trajectory prediction. Chen et al. (2023) use a proba-

bilistic diffusion approach to model basketball player

behavior. The model only considers player movement

and no other metadata. Wang et al. (2023) present

a football tactics assistant that focuses on analyzing

corner kicks which allows coaches to explore player

setup options and use those with the highest likeli-

hood of success.

Game Simulation. Kurach et al. (2020) introduce a

game engine that simulates football gameplay with an

environment for evaluating RL algorithms. Liu et al.

(2021) demonstrate an RL approach, where the agents

progressively learn to play football initially from ran-

dom behavior, to simple ball chasing, to showing ev-

idence of cooperation. Braga and Barros (2022) in-

troduce a simulator for robot football optimized for

performing RL experiments. Yu et al. (2023) intro-

duce a RL environment where agents are trained to

play basketball.

Finally, Yuan et al. (2023) describe a method to

learn simulated tennis skills from broadcast videos.

However, this approach only models one shot cycle at

a time, using statistical analysis to predict the desired

shot location for speciﬁc players. There is no cou-

pling between the current shot and previous shots, so

strategic play is limited. Also, the players are only al-

lowed to move on the baseline, so no volleys or inner

court play is permitted, restricting realism.

Our approach is not RL based. It instead learns in

a discriminative fashion from sequences of gameplay

tracking data, which obviates the need to use physics

based models of gameplay or learning gameplay from

scratch with RL. This also enables us to build pre-

dictive models for speciﬁc players which can be im-

portant for analysis and gaming scenarios. Overall,

our work is distinct from the above works in that our

goal is to generate sports gameplay that captures the

complete distribution of player behaviour, where the

aggregation of non-deterministic simulations is statis-

tically similar to real data. This acts as a powerful tool

for strategic analysis, evaluating how player decision

making affects the outcome of a period of play.

Sports Trajectory Prediction. There is a rich lit-

erature on trajectory prediction in general, and sports

trajectory prediction in particular. Yue et al. (2014)

learn predictive models for basketball play prediction

given the current game state. Zheng et al. (2016)

model spatiotemporal trajectories over long time hori-

zons using expert demonstrations capable of gener-

ating realistic, but short rollouts. Le et al. (2017b)

present an LSTM based imitation learning approach

for learning multiple policies for team defense in pro-

fessional football. However, no policy is learned

for the position of the ball. Zhan et al. (2019) de-

scribe a hierarchical framework for sequential gener-

ative modeling that can generate high quality trajec-

tories and encode coordination between agents. How-

ever, their framework cannot generate entire games.

Li et al. (2021) describes an approach for multi-agent

trajectory prediction using a graph neural network.

When evaluated on basketball data, only short trajec-

tories were considered. Tang et al. (2021) propose the

concept of collaborative uncertainty, to model the un-

certainty in interaction in multi-agent trajectory fore-

casting. Wu et al. (2021) propose a generative ad-

versarial network (GAN) to generate short basket-

ball player and ball trajectories. Alcorn and Nguyen

(2021) introduce baller2vec, a multi-entity trans-

former that can model coordinated agents. It em-

ploys a special self-attention mask to learn the dis-

tributions of statistically dependent agent trajectories

and is shown to generate realistic trajectories for bas-

ketball players or the ball itself for short durations.

Our work builds upon baller2vec to enable sus-

tained gameplay simulations by simultaneously sim-

ulating both the player and the ball. Omidshaﬁei et al.

(2022) study the problem of multiagent time-series

imputation in the context of football in order to pre-

dict the behaviors of off-screen players.

3 METHODOLOGY

In this section we provide a complete description of

our approach to generating sports simulations. A ﬂow

diagram of SportsNGEN is shown in Figure 3.

3.1 Input Data

We index the N players and the ball in a match with

n ∈ {1, . . . , N, ball}. We then deﬁne an object token

τ,n

at index τ to represent the state of nth player or

SportsNGEN: Sustained Generation of Realistic Multi-Player Sports Gameplay

121

Initialize starting

tokens 𝐶 and 𝑂

Compute next

token using 𝑓

Classify events

using 𝑔

End-of-play

conditions met?

Update Match State

True

False

Increment

token

“Winner – Cross court”

2 Games 3

1 Sets 1

Figure 3: Left: SportsNGEN ﬂow diagram. Right: Cartoons

from a simulated tennis match corresponding to the ﬂow

chart steps.





 



 



 



 



 



  



 



 



Context Tokens Object Tokens

Token Sequence of Length  for =3 Context Tokens, =2 Players, and a Ball

Object Token for Player or Ball 



Position





 



, 





Identity



Distance to Ball





 



 





Velocity





 



 





Elapsed Time



Figure 4: Top: Layout of an object token O

τ,n

. Bottom:

Sequence of T tokens for M=3 context tokens, N=2 players,

and a ball.

ball as:

τ,n

= {I

, (p

x,τ,n

, p

y,τ,n

, p

z,τ,n

), (v

x,τ,n

, v

y,τ,n

, v

z,τ,n

x,τ,n

, d

y,τ,n

, d

z,τ,n

), e}

where p denotes position, v velocity, d distance to the

ball, I ∈ R

a learned identity for a player that can

capture their style of play, e ∈ R elapsed time into

the game or sequence depending on the sport, and

x, y, z ∈ R

are components in a 3D coordinate sys-

tem. The position data are typically supplied as the

center of mass (COM) of the ball or player from a

sports tracking system. For all players, position is 2D

only i.e. p

z,τ,n

= v

z,τ,n

= 0 and for the ball, distance d

is set to 0. The e component of the feature vector is

useful to model long-term dependencies due to player

fatigue and team strategy or for ensuring simulated

tennis rallies are realistic in length. We normalize the

p, v, and d components of O by appropriate values for

each sport.

As a crucial step in generating sustained simula-

tions, we add a small amount of uniform noise to the

position p and velocity v of the ball. We ﬁnd that

training on noise-free ball trajectories does not lead

to stable simulations as any errors in the prediction

lead to out-of-distribution inputs at the next time step,

which the model cannot correct.

In addition to the object tokens, we also deﬁne

a set of context tokens {C

, . . . , C

} speciﬁc to each

sport that contain information that would inﬂuence

gameplay such as the score, the identity of the oppos-

ing team, the location of the game, and the weather.

We convert each piece of contextual information into

feature vectors, either through learned encodings for

discrete information such as the stadium, or training a

network to convert a representation of the score into a

feature vector. Figure 4 depicts the components of a

token and the order of tokens in a training sequence.

Cropping Sequences. We crop the input training

sequences to eliminate data outside of actual game-

play. The data removed includes players getting into

position for the next play or switching sides which are

not essential for simulation. To train the model efﬁ-

ciently using batches, we deﬁne a maximum sequence

length of tokens T and cut any sequences longer than

this into multiple sequences. Shorter sequences are

padded to make up the remainder of the maximum

length. The sequence length T depends on the sam-

ple rate of the data, and the length of previous data

relevant to predicting the next time step. Tracking

data can be sampled up to 50 Hz. Although this pro-

vides extremely ﬁne detail, for team sports like foot-

ball with 23 objects on the pitch, a period of 5 seconds

at 50 Hz would produce a sequence length of 5750

tokens, making the model impractical to train. Since

many of the dynamics in matches are longer than 5

seconds, we make a compromise between sample rate

and computational cost.

3.2 Transformer Decoder Model

We use a transformer decoder model f that is an ex-

tended implementation of baller2vec (Alcorn and

Nguyen, 2021) to predict future player and ball states

given the current and recent history of states. We

make a signiﬁcant update to the baller2vec exper-

iments by modelling both the ball and the players si-

multaneously.

The model f is run in an auto-regressive mode

with a rolling window of length T , using a speciﬁed

period of previous predictions to predict the ball and

player state at the next step. We use the same atten-

tion method as baller2vec, permitting each object

token to attend to every object token up to and includ-

ing its own time step. We adjust the attention mask

so that each object token can attend to the context to-

kens, inﬂuencing the predictions for player and ball

icSPORTS 2024 - 12th International Conference on Sport Sciences Research and Technology Support

122

movement.

We treat the update step as a classiﬁcation as op-

posed to a regression or diffusion problem, by split-

ting the area of possible next locations for the ball and

players into a 3D and 2D grid, respectively, of discrete

bins that indicate the relative offset ρ from the current

position p as this is easier to learn and can bound mo-

tion to physically possible values. A depiction of a

grid for a football player and the ball is shown in Fig-

ure 5.

Figure 5: Visualization of the 2D and 3D classiﬁcation grids

used to predict the position of a player and the ball at the

next time step.

We use nucleus sampling (Holtzman et al., 2020)

to sample the location in the output grid based on the

output probabilities of f . When the grid location has

been selected, we turn the discrete value into a contin-

uous value by sampling from a uniform distribution

across the bin. If the initial conditions for the player

or ball have zero velocity, this helps to force the sim-

ulation into motion by avoiding continuous velocity

predictions of zero.

To enable the model to learn the behavior of in-

dividual players, the bin size must be ﬁne grained

enough for predictions to capture distinguishing fea-

tures. In many sports, important statistics include how

fast a player can run, or how far they can hit, throw or

kick the ball. Formally, the probability distribution of

predicting a particular bin location k for an object n at

step τ + 1 is

p(ρ

τ+1,n

= k|O

1:τ,n

) = f (O

1:τ,n

, k).

The value of ρ is then sampled from the distribution:

τ+1,n

∼ p(ρ

τ+1,n

= k|O

1:τ,n

Based on the sampled value of ρ and the mapping

between bins and physical distance, the updated val-

ues of position p

τ+1,n

, velocity v

τ+1,n

, and distance

to the ball d

τ+1,n

can be computed. Since we use

the baller2vec attention mask, the positions of the

ball and each player can be updated simultaneously at

each time step.

We detect the end of a simulation or break in a

play with logic speciﬁc to each sport. For example,

we can end simulations if a ball goes out of bounds

or in some sports if the ball makes contact with the

ground, or if the time in the period of play runs out.

When generating simulations, we set a maximum in-

put sequence length of T tokens. For a player and

ball state update at step τ + 1, we input from τ − T to

τ steps of initial token data into the model f . If T time

steps of data are not yet simulated, the missing tokens

are padded with zeros and masked. Speciﬁcally, sim-

ulations are rolled autoregressively out at the ith step

∼ p(ρ

= k|O

i−1

, O

i−2

. . . O

i−T

3.3 Event Classiﬁcation

We also train an event classiﬁer g which is run after

a break in gameplay. Examples of events would be

passes, runs, fouls, goals, the type of shot played, and

so on. The event classiﬁer g has the same input and

architecture as f , but does not use attention masking,

and uses separate prediction heads for each different

type of event. The event classiﬁer can be used for

deﬁning the initial conditions for the next play and

gathering statistics about the period of play.

4 TENNIS IMPLEMENTATION

DETAILS

In this section, we detail the implementation of Sport-

sNGEN for tennis. Initial rally conditions, boundary

logic and relevant player statistics are well deﬁned, so

we can demonstrate the capabilities of the system.

We use a proprietary dataset of tennis tracking

data for approximately 15,000 tennis matches con-

taining 7.6 million rally sequences. The data contain

COM locations for each player and the ball sampled

at 25 Hz, with the center of the court at (x, y, z) =

(0, 0, 0), whose components refer to the length, width,

and vertical directions, respectively.

The data also contains metadata about each match

and rally, including: the players in the rally, the tour-

nament and court, the rally winner, whether the rally

was a ﬁrst or second serve, and what shots were

played. The tracking data set is cut up into individual

sequences that start at the toss before a serve and end

shortly after the rally is ﬁnished. We set a maximum

sequence length of input data to be 6 seconds. We

found that increasing the sequence length to be more

than 6 seconds became computational impractical and

did not improve the model accuracy. This suggests

that professional tennis players’ decision making is

not strongly affected by information further than 6

seconds into the past. We also double the size of the

SportsNGEN: Sustained Generation of Realistic Multi-Player Sports Gameplay

123

data set by ﬂipping the data along the x and y axes

simultaneously.

We allow for ±25 mm of uniform position and

per unit time velocity noise in the x dimension and

±12.5 mm of noise in the y and z dimensions. If the

added noise is any smaller than this, the simulations

start to break down. For output classiﬁcation, we use

61 bins for each dimension, scaled for the ball such

that the maximum velocity is fractionally faster than

the current fastest serve speed. This results in 61 ×

61 = 3721 and 61 × 61 × 61 = 226981 possible bin

locations for the player and ball output, respectively.

At 25 Hz, this equates to a ball bin size of {x, y, z} =

{46, 13, 10} mm.

The playing surface is important contextual infor-

mation when predicting rallies in tennis. The expec-

tation is that hard and grass courts have the fastest

bounces, and clay courts absorb more momentum

from the impact resulting in slightly slower bounces

and longer rallies. We learn context vectors for each

surface and tournament in the dataset, and also en-

courage the model to learn the difference between ﬁrst

and second serve types by including context vectors

for both.

We generate initial conditions based on historical

examples from the data when particular players are

serving ﬁrst or second serves from speciﬁc sides. We

take the initial condition as the start of the toss move-

ment during the serve. This initial condition includes

the positions and velocities in all dimensions for both

players and the ball. We can detect the end of the rally

through simple logic on the movement of the ball. If

the ball continues past a player, is close to stationary

near the net, bounces out of bounds or bounces twice

on one side of the net, then we can deem the rally to

have ﬁnished. At this point, we stop the simulation

and collect the rally data using the event classiﬁer.

To understand who won the rally, and for analysis

of the point, we train the event classiﬁer to classify

the type of shot being played at every step within the

simulation. This includes the type of stroke (ground-

stroke, serve, volley, etc.), the direction of the shot

(cross court, down the line, etc.), whether the shot is

a winner, error, or a continuation of the point, and if

an error is forced or unforced.

The event classiﬁer g receives as input a simpli-

ﬁed version of the input token, without any identity

I or context C components. In the training data, shot

type labels are consistent across time steps between

shots. The model is expected to predict the same,

only varying its prediction when the ball contacts a

racket. When a rally is ﬁnished, we convert the track-

ing data from the rally into the shot type classiﬁer in-

put, run the model once to identify where the changes

in shot type are, and take the model shot type between

changes as the ﬁnal label for each shot. The winner or

error classiﬁcation for the ﬁnal shot of the rally tells

us who won the point, and the shot type labels help us

break down the shots for statistical analysis. To com-

bine rallies together to simulate an entire match, all

that is left to do is implement logic to increment the

score, calculate who is serving, from which end and

which side. These can be used to obtain the initial

conditions for the next point.

Tennis Network Architecture. The input tokens

τ,n

are embedded with a 3 layer MLP with input size

30, hidden sizes 256 and 512, and output size 2048.

The transformer decoder, f , has 4 layers, 2048 em-

bedding dimension, 8 heads, 4 expansion factor, and

0.2 dropout. The shared player output network is a

single linear layer with input size 2048 output size

equal to 61 × 61 bins. The ball output network is

a single linear layer with input size 2048 and output

size equal to 61 × 61 × 61 bins.

5 EXPERIMENTS

For the tennis experiments, we selected 3 male profes-

sional players with varying styles to evaluate Sport-

sNGEN and simulated 6 matches between each com-

bination of two players. Each match was the best

of 3 sets. We repeat this experiment across 3 dif-

ferent tournaments, one for each surface type: hard,

clay and grass. For comparison, we then collect data

where these players have played each other on these

surfaces. Using both real and simulated data, we com-

pute relevant statistics and deﬁne an evaluation metric

for each statistic as the difference between the two.

For physical metrics, we compare the median,

inter-quartile range (IQR), and Wasserstein distance

between the distributions of real and simulated data

for the following quantities collected across all

matches:

• Toss contact height: Height of the ball at the con-

tact point with the racket during serving.

• First and second serve speeds: Maximum

recorded speed during the serve.

• Return speeds: Maximum speed of a return of

serve.

• Groundstroke speeds: Maximum speed of all

groundstrokes.

We also compute additional relevant statistics based

on aggregated data. For these quantities, a scalar

value is aggregated over many rallies for each player.

icSPORTS 2024 - 12th International Conference on Sport Sciences Research and Technology Support

124

The absolute difference between the real and simu-

lated aggregated scalars is compared.

• First serve %: Percentage of ﬁrst serves that are

in bounds.

• Double fault %: Percentage of second serves that

are out of bounds.

• First and second serve win %: Percentage of ral-

lies won when serving on ﬁrst and second serve,

respectively.

• Ace %: Percentage of ﬁrst serves that are aces.

• Serve points won %: Percentage of rallies won

as server.

Figure 6: Bin probabilities for the ball projected into the

xy plane during a) mid-ﬂight and b) - d) at time of impact

(ToI) for 3 values of top-p. The center of each diagram, bin

(x, y) = (30, 30), corresponds to no movement. Yellow in-

dicates a probability of 0 while progressively darker colors

indicate higher probabilities.

Varying the Top-p Sampling Parameter. Figure 6

shows typical output probability distributions, pro-

jected into the xy plane, for an update step of the ball

in mid-ﬂight, and at the moment the ball is about to

be hit. The peaks in intensity for the mid-ﬂight pre-

dictions (a) are distributed over very few bins since

the model has learned the physical constraints of the

system (e.g. drag, gravity), and can therefore be very

conﬁdent in how to update the ball state. The remain-

ing panels (b)-(d) depict the probability distributions

for the ball at the time of impact (ToI) – the point

at which a player hits the ball for various values of

top-p. The distributions in these cases contain multi-

ple separated peaks in intensity in the xy plane. This

corresponds to different decisions a player may make

when choosing to play the shot either down the line or

across the court. By sampling from these two modes,

we are able to perform counterfactual analysis (see

Section 5). As top-p decreases, the probability of

sampling a cross court shot decreases, demonstrating

the need to optimize top-p in order to accurately cap-

ture the player behaviour in the simulations. In gen-

eral, we will see that a low top-p value will result in

less variety in playing style, but a high top-p value

will result in many outliers.

We see the similar patterns in Figure 7a), the cu-

mulative probability for the player and ball at ToI for a

return and during mid-ﬂight for a shot as a percentage

of number of contributing bins. For mid-ﬂight predic-

tions of the ball, the probability distribution is con-

centrated over few bins, with 90% of the distribution

contained within 0.002% of the total bins. When pre-

dicting changes in direction (e.g. at ToI), the probabil-

ity distribution is spread over more bins, up to 0.5%

of the bins are required to populate 90% of the cumu-

lative probability.

Figure 7b) and (c) show how the various metrics

vary with top-p. In (b), the number of non-realistic

rallies (rallies that must be discarded based on logi-

cal checks) increases with a value of top-p both that

is too high, and too low. Increasing top-p increases

the probability that the ball trajectory may be updated

in a way that deﬁes physical constraints and would

be forced to be removed. With too low top-p there

may be too few options for the ball and player to up-

date in a way that leads to a realistic rally. In (c), we

see that with the exception of double fault percentage,

the metrics reach optimal values when top-p is in the

range of 0.8 to 0.9.

Object Token Component Ablation Study. In

Figure 8, we quantify how the additional components

in the token vector O affect the convergence and ﬁ-

nal accuracy of the physical metrics when compared

to a baseline model that does not use velocity v, dis-

tance to the ball d, elapsed time e, or context tokens C

(similar to that used in baller2vec). The plots show

that SportsNGEN converges faster and reaches better

results than the baseline model when averaged across

all physical metrics. We also see faster convergence

to ∼20% non-realistic rallies.

Varying the size ι of the player encoding vector I

in Figure 9, we ﬁnd that the accuracy increases until

ι =20 where there are diminishing returns for further

increases. This is also supported by Figure 10 d)-f),

where the data with no player ID I has a much broader

distribution of serve speeds, and a nearly identical

median serve speed for all three players.

Context Token Study. We add context tokens to

encode the tournament, court surface type, and

SportsNGEN: Sustained Generation of Realistic Multi-Player Sports Gameplay

125

Figure 7: A) Cumulative probability for the player and ball at ToI for a return and during mid-ﬂight for a shot as a percentage

of number of contributing bins. b) Proportion of non-realistic rallies that are discarded during match simulation. c) Absolute

difference between aggregated statistics in the training data and the simulations as a function of top-p.

Figure 8: A comparison of convergence for SportsNGEN against a Baseline model without v, d, e and context tokens C, for

a) An average of the 4 physical metrics, and b) Non-realistic rallies as a function of training iterations.

Figure 9: Varying the player ID I size ι to show how various

metrics can be improved with a larger ι. As a control, we

train a generic model without player ID I.

whether the serve is the player’s ﬁrst or second. Typ-

ically the second serve is expected to be slower since

players will prioritize accuracy over speed to avoid

losing a point through double fault. Figure 10 shows

that the addition of a serve context token C

serve

as well

as the player ID component I in O reduce the dif-

ference between real and simulated serve speeds and

produce narrower distributions between ﬁrst and sec-

ond serve speeds.

Figure 10: The distribution of ﬁrst and second serve speeds

for all three players for the following models: (top) Sport-

sNGEN, (middle) a model with no player ID vector I, (bot-

tom) a model with no serve context token C

serve

To quantify the effect of the playing surface, we

use the coefﬁcient of restitution by taking the ratio of

icSPORTS 2024 - 12th International Conference on Sport Sciences Research and Technology Support

126

Figure 11: Ratio of speed after to before the ball bounce.

Each row contains results for a different court surface type.

The columns are real (left), and simulated (right) data. The

last row is surface type agnostic, containing a weighted av-

erage of the data for each court.

the speed after to before the bounce. A value less than

1 means the ball has lost momentum and indicates a

slower surface. Figure 11 shows this metric for three

court types and for the surface agnostic case, for both

real and simulated data. The median value for each

court type follows the expected trend: typically clay

courts have the slowest bounces, and hard courts have

the fastest, which is better represented when we intro-

duce the surface token into the model.

We also demonstrate that SportsNGEN is realistic

throughout the rally with Figure 12 showing the dis-

tribution of rally lengths for real data, and simulations

from SportsNGEN. Although we see a slightly higher

peak in rally lengths in (b), we see both distributions

with a peak at a small number of shots per rally, and

tailing off towards 15 shots.

Figure 12: Length of rallies in number of shots for a) the

original training data for the given three players on hard

surfaces, b) simulated data using SportsNGEN.

Transfer Learning. As an extension to training a

model capable of capturing the behavior of all play-

ers, we also train a generic model f

gen

which learns

a single feature vector I

gen

, called the generic player

vector where I

= I

gen

, n ∈ N. We then ﬁne-tune f

gen

with matches containing a speciﬁc player, and transfer

learn a new set of I

∈ N for the player that can rep-

resent their behavior against a generic opponent. This

could be used for quickly customizing a pretrained

model to a new player on the circuit.

Figure 13 shows various metrics as a function of

the number of training sequences that are required to

ﬁne-tune f

gen

such that the generic player ID vector I

is adapted to a new player. In the simulations, f

gen

the opponent for the ﬁne-tuned model. The ground-

stroke and return metrics improve as the number of

training samples increases whereas the serve metrics

ﬂuctuate with the ﬁrst serve speed getting worse. This

can be explained by the low variability of the serve

distribution being easier to learn when compared to

highly variable groundstroke patterns.

Figure 13: Learning features of a speciﬁc player by ﬁne-

tuning a generic model, showing a) the Wasserstein distance

for physical data, and b) difference to training data for sta-

tistical metrics.

6 APPLICATIONS

In this section we explore SportsNGEN applications.

Predicting Rally Outcomes. A key intended ap-

plication of SportsNGEN is generating insights for

coaching and sports broadcasts. To prove it’s valid-

ity for these applications, the model should accurately

forecast the probability that each player wins a rally

as it develops.

We can test SportsNGEN’s ability to do this in the

following way. We sample random rallies from the

training data, and roll out the model from a given ran-

dom time step 100 times, to generate a win percentage

for both players. Repeating this for a large number of

starting points, we form a histogram of predictions by

stratifying the predictions into bins.

SportsNGEN: Sustained Generation of Realistic Multi-Player Sports Gameplay

127

Figure 14 shows the histogram of events contribut-

ing to the win percentage calibration plot. For each

event, 100 simulated rollouts are used to generate the

win percentage. The mean win percentage generated

by the model is close to 50% which is to be expected

for tennis rallies. In addition there are situations in

which the winner is very likely already determined

(if the random time chosen is close to the end of the

rally, for example). As a result, the bins close to 0

and 100% are also more populated which explains the

higher error in the more sparsely populated bins close

to 20% and 80%.

For each prediction, we also have the ground truth

of who won the rally in the training data. Taking the

90% bin for example, if the model is well-calibrated,

the corresponding ground truth rallies should be won

by the player in 90% of cases. Figure 15 shows that

the win percentages generated by the SportsNGEN

are well-calibrated, with deviations where data are

sparse.

Figure 14: Histogram of win percentages output by the

model when simulating rollouts in a random rally at a ran-

dom point.

Figure 15: Predicted win percentages vs. observed win per-

centages for SportsNGEN. The solid line shows ideal cal-

ibration. The win percentages output by SportsNGEN are

well calibrated.

Counterfactuals. Figure 16 demonstrates one way

the SportsNGEN can be used to inform coaching de-

cisions. A point indicated by the red dot in a real rally

is chosen as a branch point in time, just as a player

is about to play a shot. In the real rally, the shot af-

ter the branch point goes straight down the middle –

indicated by the purple line in (a).

We can force alternative shot selection by sam-

pling from the cross court mode in Figure 6 and

analysing how the rally would have played out. In (b)

and (c), two alternatives are depicted. We quantify the

strength of each shot selection by running 100 simula-

tions until the end of the rally, sampling equally from

both modes at this branch point. We then aggregate

statistics to calculate a win percentage for each shot

choice.

Playing a shot to either of the two corners gave the

player roughly equal probability of winning at 58%,

whereas the original choice of hitting to the middle

reduced the probability below 50%. Pushing the op-

ponent farther to the edge of the court may explain

this advantage. Figure 6 shows that the probability

of the cross court mode is lower, highlighting that the

player would more often opt for the safer shot down

the middle.

Figure 17 shows the results of many simulations

forcing a certain type of shot for the shot shown in

purple. It shows that even if there are constraints im-

posed on the type of shot, there can still be variability

in play. Running this simulation for many shots and

aggregating win percentages can give insight into the

kinds of tactics that would be advantageous, and since

the player and court can be speciﬁed and trained on

real data, it could be speciﬁcally useful for improving

the play style of a player in a particular situation.

Football. Though we focused this work on tennis,

we have had success using SportsNGEN to simu-

late football matches with a high degree of realism

using the same model architecture. Click on https:

//youtu.be/M0kkKiGVNzk for a video demonstration

of sustained passing sequences. The player and ball

positions are derived from COM data.

7 LIMITATIONS

An important limitation of SportsNGEN is that it is

not designed to handle out of distribution situations.

Unconventional initial conditions can produce unreli-

able results. This extends to unseen players in which

the model will default to a “generic” player represen-

tation. This method is also computationally intensive,

requiring 2 days to train on an NVIDIA A100 GPU.

While we believe our method is applicable to many

sports, we have only trained models for football and

tennis. Other sports may introduce difﬁculties.

icSPORTS 2024 - 12th International Conference on Sport Sciences Research and Technology Support

128

Figure 16: A real rally, and two simulated rallies for a different shot type, where the color transparency indicates time into the

rally (with opaque being the end). The ball trajectory is orange, with the shot at which the simulations start shown in purple.

The point at which the two simulations are branched is denoted by a red dot. The players are shown as blue and red traces.

Figure 17: A real rally a), and many simulated rallies for two different shot types b), c). In the real rally, the increasing color

opacity indicates time into the rally. The ball trajectory is orange, with the shot at which the simulations start shown in purple,

the point at which this is branched is denoted by a red dot. The players are shown as blue and red traces. In the simulations,

only the shots after the decision are shown to highlight the possibilities arising from the simulation engine.

8 DISCUSSION

In this work, we detailed SportsNGEN that is capable

of generating realistic sports gameplay when trained

on player and ball tracking sequences. A unique as-

pect of the system is the ability to customize game-

play in the style of a particular player via ﬁne-tuning.

Also, it is straightforward to use SportsNGEN to in-

form coaching decisions and game strategy through

counterfactuals. In the future, we plan to adapt Sport-

sNGEN to sports beyond tennis and football.

ACKNOWLEDGEMENTS

The authors would like to thank Beyond Sports B.V.

for the visualisations and Sports Interactive for syn-

thetic football data. We also thank Anirban Mishra,

Tristan Fabes, and Pavlo Sharhan for their helpful

contributions.

REFERENCES

Alcorn, M. A. and Nguyen, A. (2021). baller2vec: A

multi-entity transformer for multi-agent spatiotempo-

ral modeling. arXiv preprint arXiv:2102.03291.

Braga, P. H. and Barros, E. S. (2022). rsoccer: A framework

for studying reinforcement learning in small and very

small size robot soccer. RoboCup 2021: Robot World

Cup XXIV, 13132:165.

Chen, X., Wang, W.-Y., Hu, Z., Chou, C., Hoang, L.,

Jin, K., Liu, M., Brantingham, P. J., and Wang, W.

(2023). Professional basketball player behavior syn-

thesis via planning with diffusion. arXiv preprint

arXiv:2306.04090.

Hauri, S. and Vucetic, S. (2022). Group activity recognition

in basketball tracking data–neural embeddings in team

sports (nets). arXiv preprint arXiv:2209.00451.

Holtzman, A., Buys, J., Du, L., Forbes, M., and Choi, Y.

(2020). The curious case of neural text degeneration.

In International Conference on Learning Representa-

tions.

Kurach, K., Raichuk, A., Sta

nczyk, P., Zaj ˛ac, M., Bachem,

O., Espeholt, L., Riquelme, C., Vincent, D., Michal-

ski, M., Bousquet, O., et al. (2020). Google re-

search football: A novel reinforcement learning en-

vironment. In Proceedings of the AAAI conference on

artiﬁcial intelligence, volume 34, pages 4501–4510.

Le, H. M., Carr, P., Yue, Y., and Lucey, P. (2017a). Data-

driven ghosting using deep imitation learning.

Le, H. M., Yue, Y., Carr, P., and Lucey, P. (2017b). Coordi-

nated multi-agent imitation learning. In International

Conference on Machine Learning, pages 1995–2003.

PMLR.

Li, L., Yao, J., Wenliang, L., He, T., Xiao, T., Yan, J., Wipf,

D., and Zhang, Z. (2021). Grin: Generative relation

and intention network for multi-agent trajectory pre-

diction. Advances in Neural Information Processing

Systems, 34:27107–27118.

Liu, S., Lever, G., Wang, Z., Merel, J., Eslami, S., Hennes,

SportsNGEN: Sustained Generation of Realistic Multi-Player Sports Gameplay

129

D., Czarnecki, W. M., Tassa, Y., Omidshaﬁei, S., Ab-

dolmaleki, A., et al. (2021). From motor control

to team play in simulated humanoid football. arXiv

preprint arXiv:2105.12196.

Miller, A., Bornn, L., Adams, R., and Goldsberry, K.

(2014). Factorized point process intensities: A spa-

tial analysis of professional basketball. In Xing, E. P.

and Jebara, T., editors, Proceedings of the 31st Inter-

national Conference on Machine Learning, volume 32

of Proceedings of Machine Learning Research, pages

235–243, Bejing, China. PMLR.

Omidshaﬁei, S., Hennes, D., Garnelo, M., Wang, Z., Re-

casens, A., Tarassov, E., Yang, Y., Elie, R., Con-

nor, J. T., Muller, P., et al. (2022). Multiagent off-

screen behavior prediction in football. Scientiﬁc re-

ports, 12(1):8638.

Tang, B., Zhong, Y., Neumann, U., Wang, G., Chen, S., and

Zhang, Y. (2021). Collaborative uncertainty in multi-

agent trajectory forecasting. Advances in Neural In-

formation Processing Systems, 34:6328–6340.

Teranishi, M., Tsutsui, K., Takeda, K., and Fujii, K. (2022).

Evaluation of creating scoring opportunities for team-

mates in soccer via trajectory prediction. In Interna-

tional Workshop on Machine Learning and Data Min-

ing for Sports Analytics, pages 53–73. Springer.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. Advances in neural

information processing systems, 30.

Wang, Z., Veli

ckovi

c, P., Hennes, D., Tomašev, N.,

Prince, L., Kaisers, M., Bachrach, Y., Elie, R., Wen-

liang, L. K., Piccinini, F., et al. (2023). Tacticai:

an ai assistant for football tactics. arXiv preprint

arXiv:2310.10553.

Wu, G., Zhao, S., Lin, J., and Silva, C. (2021). Basketball

gan: Sportingly acceptable trajectory prediction.

Yu, C., Yang, X., Gao, J., Chen, J., Li, Y., Liu, J., Xi-

ang, Y., Huang, R., Yang, H., Wu, Y., and Wang,

Y. (2023). Asynchronous multi-agent reinforcement

learning for efﬁcient real-time multi-robot coopera-

tive exploration. In Proceedings of the 2023 Interna-

tional Conference on Autonomous Agents and Multia-

gent Systems, AAMAS ’23, page 1107–1115, Rich-

land, SC. International Foundation for Autonomous

Agents and Multiagent Systems.

Yuan, Y., Makoviychuk, V., Guo, Y., Fidler, S., Peng, X.,

and Fatahalian, K. (2023). Learning physically simu-

lated tennis skills from broadcast videos. ACM Trans.

Graph, 42(4).

Yue, Y., Lucey, P., Carr, P., Bialkowski, A., and Matthews,

I. (2014). Learning ﬁne-grained spatial models for

dynamic sports play prediction. In 2014 IEEE inter-

national conference on data mining, pages 670–679.

IEEE.

Zhan, E., Zheng, S., Yue, Y., Sha, L., and Lucey, P. (2019).

Generating multi-agent trajectories using program-

matic weak supervision. In International Conference

on Learning Representations.

Zhao, Z., Chai, W., Hao, S., Hu, W., Wang, G., Cao, S.,

Song, M., Hwang, J.-N., and Wang, G. (2023). A

survey of deep learning in sports applications: Per-

ception, comprehension, and decision. arXiv preprint

arXiv:2307.03353.

Zheng, S., Yue, Y., and Hobbs, J. (2016). Generating long-

term trajectories using deep hierarchical networks.

Advances in Neural Information Processing Systems,

29.

APPENDIX

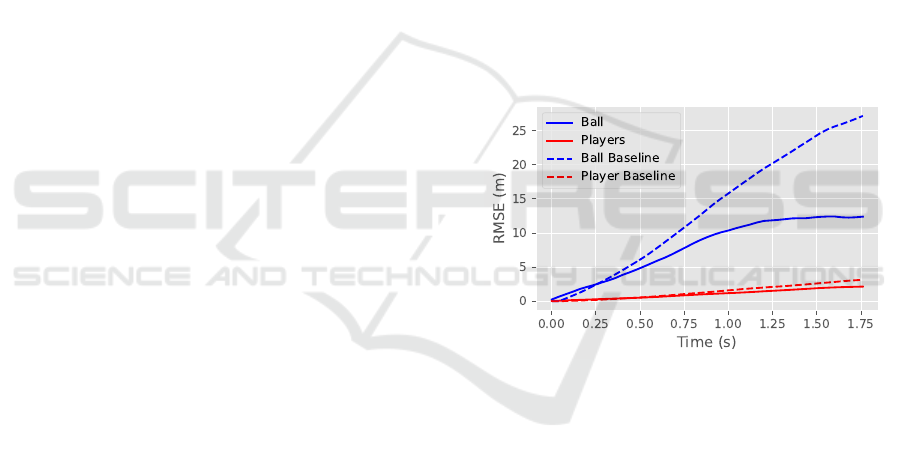
Prediction Error Versus Time. Figure 18 shows the

results from 200 simulations initialized from a ran-

dom point in a random rally. The simulations are

evolved for 1.75 seconds and the RMSE is plotted

compared with the ground truth data for the ball and

players. The baseline is taken as a linear extrapolation

of the velocity of the player and ball frozen at the time

the simulation begins. Our simulation performs better

than a linear extrapolation over a short time, indicat-

ing it has learned how to sensibly predict and update

the state vectors as a function of time.

Figure 18: Root Mean Squared Error (RMSE) compared

to real tennis data as a function of time, for both ball and

player positions when simulating forward from a random

in a rally. SportsNGEN performs better than a baseline of

linear extrapolation.

icSPORTS 2024 - 12th International Conference on Sport Sciences Research and Technology Support

130