Fitness Landscape Analysis of a Cell-Based Neural Architecture
Search Space
Devon Tao
a
and Lucas Bang
b
Computer Science Department, Harvey Mudd College, Claremont, CA, U.S.A.
Keywords:
Neural Architecture Search, Fitness Landscape, Neural Networks.
Abstract:
Neural Architecture Search (NAS) research has historically faced issues of reproducibility and comparability
of algorithms. To address these problems, researchers have created NAS benchmarks for NAS algorithm evalu-
ation. However, NAS search spaces themselves are not yet well understood. To contribute to an understanding
of NAS search spaces, we use the framework of fitness landscape analysis to analyze the topology search
space of NATS-Bench, a popular cell-based NAS benchmark. We examine features of density of states, local
optima, fitness distance correlation (FDC), fitness distance rank correlations, basins of attraction, neutral net-
works, and autocorrelation in order to characterize the difficulty and describe the shape of the NATS-Bench
topology search space on CIFAR-10, CIFAR-100, and ImageNet16-120 image classification problems. Our
analyses show that the difficulties associated with each fitness landscape could correspond to the difficulties of
the image classification problems themselves. Furthermore, we demonstrate the importance of using multiple
metrics for a nuanced understanding of an NAS fitness landscape.
1 INTRODUCTION
Neural networks have performed well in tasks such
as image classification (He et al., 2016; Krizhevsky
et al., 2012), speech recognition (Abdel-Hamid et al.,
2014), and object detection (Szegedy et al., 2013).
However, achieving state-of-the-art performance has
traditionally required expert knowledge of neural ar-
chitecture design. This poses a challenge for non-
computer scientists who wish to use neural net-
works but lack the specific neural network expertise
(Sheikhtaheri et al., 2014). One recent solution is
Neural Architecture Search (NAS), where a neural ar-
chitecture is algorithmically engineered as opposed to
hand-designed. NAS has shown to be an effective ar-
chitecture design method, in some cases outperform-
ing hand-designed architectures (Zoph and Le, 2016).
While NAS has achieved state-of-the-art perfor-
mance, it has also faced reproducibility issues due
to algorithmic complexity and expensive computation
(Li and Talwalkar, 2020). Furthermore, differences in
training procedures and search spaces make it diffi-
cult to compare across methods (Ying et al., 2019).
To combat these problems, researchers have created
a
https://orcid.org/0009-0003-0507-0489
b
https://orcid.org/0000-0003-2711-5548
NAS benchmarks, which provide common baselines
for comparing algorithms and significantly reduce the
costs of NAS evaluation (Ying et al., 2019; Dong and
Yang, 2020; Siems et al., 2020). One popular bench-
mark is NATS-Bench, a cell-based NAS search space
(Dong et al., 2021).
Although there have been analyses of NAS search
spaces as a whole (White et al., 2023; Chitty-Venkata
et al., 2023), there currently do not exist many deep
analyses of specific NAS search spaces. While NAS
algorithms have performed well on these spaces (Mel-
lor et al., 2021; Chen et al., 2021), there is a lack
of understanding of the search spaces themselves.
We aim to fill this gap by analyzing the NATS-
Bench topology search space through the framework
of fitness landscape analysis, a concept originating
from biology (Wright et al., 1932) that has since
been applied to optimization problems (Merz and
Freisleben, 2000; Tavares et al., 2008). We exam-
ine fitness landscape components of density of states,
local optima, fitness distance correlation (FDC), fit-
ness distance rank correlations, basins of attraction,
neutral networks, and autocorrelation in order to
characterize the difficulty of the NATS-Bench topol-
ogy search space on three popular image classifi-
cation datasets CIFAR-10, CIFAR-100 (Krizhevsky
and Hinton, 2009), and ImageNet16-120, which is a
Tao, D. and Bang, L.
Fitness Landscape Analysis of a Cell-Based Neural Architecture Search Space.
DOI: 10.5220/0012892400003886
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Explainable AI for Neural and Symbolic Methods (EXPLAINS 2024), pages 77-86
ISBN: 978-989-758-720-7
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
77

downsampled version of ImageNet (Chrabaszcz et al.,
2017). We summarize our contributions as follows:
• We build upon previous NATS-Bench analyses
(Ochoa and Veerapen, 2022; Thomson et al.,
2023) by analyzing the fitness landscapes of the
NATS-Bench topology search space test accura-
cies.
• We calculate and analyze several components of
the NATS-Bench topology fitness landscape, aug-
menting previous NATS-Bench analyses of den-
sity of states, Spearman fitness distance corre-
lation, and local optima networks (Ochoa and
Veerapen, 2022) with additional characteristics of
Pearson’s fitness distance correlation, basins of
attraction, neutral networks, and autocorrelation.
To our best knowledge, we are the first to cal-
culate these metrics for the NATS-Bench topol-
ogy search space. Due to the complexity of fit-
ness landscapes, it is important to analyze many
different metrics in order to create a deeper un-
derstanding of the fitness landscape (Pitzer and
Affenzeller, 2012). To that end, the inclusion of
these additional metrics reveals novel insights into
the NATS-Bench topology search space.
2 RELATED WORK
The first NAS method used reinforcement learning
(Zoph and Le, 2016). Since then, researchers have
developed a variety of approaches, such as neuroevo-
lution (Stanley et al., 2019), differentiable architec-
ture search (Liu et al., 2018), one-shot NAS (Dong
and Yang, 2019; Guo et al., 2020), and training-free
methods (Mellor et al., 2021; Chen et al., 2021).
As for the search spaces themselves, there have
been a number of established benchmarks for im-
age classification problems such as NAS-Bench-101
(Ying et al., 2019), NAS-Bench-201 (Dong and Yang,
2020), NAS-Bench-301 (Siems et al., 2020), and
NATS-Bench (Dong et al., 2021). More recently,
there have also been NAS benchmarks in other ar-
eas such as automated speech recognition (Mehrotra
et al., 2020) and natural language processing (Klyuch-
nikov et al., 2022).
Prior fitness landscape analyses of NAS search
spaces include analyses of local optima networks
(Potgieter et al., 2022; Rodrigues et al., 2022), FDC
(Rodrigues et al., 2022), autocorrelation, entropic
measure of ruggedness, fitness clouds, density clouds,
and overfitting (Rodrigues et al., 2020). There addi-
tionally exist some analyses for specific benchmark
datasets. The authors of NAS-Bench-101 analyze the
FDC, locality, and autocorrelation of their benchmark
(Ying et al., 2019). Traor
´
e et al. expand on this work
with additional characteristics of ruggedness, cardi-
nality of optima, and persistence (Traor
´
e et al., 2021).
A few studies have examined the NATS-Bench
benchmark specifically. Thomson et al. examine the
local optima networks of the NATS-Bench size search
space (Thomson et al., 2023) and Ochoa and Veer-
apen analyze the density of states, Spearman fitness
distance correlation, and local optima networks of
the NATS-Bench topology search space (Ochoa and
Veerapen, 2022).
We expand on Ochoa and Veerapen’s work by
analyzing the test accuracies rather than the valida-
tion accuracies of the NATS-Bench topology search
space and by providing additional analyses. In addi-
tion to the Spearman correlation coefficient between
fitnesses and distances, we also include Kendall and
Pearson correlation coefficients. Notably, the Pearson
correlation coefficient is the most established corre-
lation coefficient in the literature (Jones et al., 1995),
but it is missing from Ochoa and Veerapen’s analy-
sis.
1
Moreover, Ochoa and Veerapen’s analysis fo-
cuses on local optima, whereas our analysis also pro-
vides insight into neutral areas. Furthermore, Ochoa
and Veerapen’s analysis of ruggedness is entirely in-
formed by the number of modes, while we provide an
additional perspective by including autocorrelation.
Overall, we corroborate Ochoa and Veerapen’s exist-
ing analyses while also providing a more nuanced un-
derstanding with additional metrics.
3 BACKGROUND
In this section, we introduce NATS-Bench, a repeated
cell-based neural architecture search space. We then
define a fitness landscape and its components and de-
scribe the specific fitness landscapes for the NATS-
Bench topology search space.
3.1 NATS-Bench
NATS-Bench is a repeated-cell neural architecture
benchmark that consists of a size search space S
s
and
a topology search space S
t
(Dong et al., 2021). We
analyze the topology search space S
t
, which is the
same as NAS-Bench-201 (Dong and Yang, 2020).
The macro structure of each neural architecture be-
gins with a 3-by-3 convolution with 16 output chan-
nels and a batch normalization layer. It is then fol-
1
We note that Ochoa and Veerapen use “FDC” to re-
fer to Spearman’s correlation coefficient, however the tra-
ditional use of “FDC” in the literature refers to Pearson’s
correlation coefficient (Jones et al., 1995)
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
78

image conv con ×N cell
residual
block
stride=2
con ×N cell
residual
block
stride=2
con ×N cell
global
avg pool
Figure 1: Macro structure of a neural architecture in the topology search space of NATS-Bench. Visual based on original
paper (Dong et al., 2021).
1
2
3
4
5
6
zeroize
skip-connect
1×1 conv
3×3 conv
3×3 avg pool
Operations
Figure 2: DAG representation of an individual cell. Visual
based on original paper (Dong et al., 2021).
lowed by three stacks of N = 5 cells with a residual
block between each cell stack. The number of out-
put channels are 16, 32, and 64 for the three stacks
respectively. These cell stacks are then followed by a
global average pooling layer. The NATS-Bench archi-
tectures are trained on CIFAR-10, CIFAR-100, and
ImageNet16-120, which is a downsampled version of
ImageNet. Performance data for architectures in S
t
trained on 12 or 200 epochs of data can be accessed
via the NATS-Bench API.
2
Further, architectures un-
dergo many trials. For our analysis, our fitness values
are the test accuracies of architectures trained on 200
epochs of data, averaging over all trials.
Each cell in S
t
can be represented as a densely-
connected DAG with four vertices, where there is an
edge from the ith node to the jth node if i < j for
a total of six edges. Each edge is selected from one
of five operations: zeroize, skip connection, 1-by-1
convolution, 3-by-3 convolution, and 3-by-3 average
pooling layer, where the zeroize operation represents
dropping the edge. Then, there are 5
6
= 15625 total
architectures. However, some architectures are iso-
morphic, so there are only 6466 unique architectures
(Dong and Yang, 2020).
3.2 Fitness Landscape Analysis
3.2.1 Definition
We use the definition of fitness landscape provided by
Pitzer and Affenzeller (Pitzer and Affenzeller, 2012).
There is a solution space S and an encoding of the so-
lution space S . There is also a fitness function f :
S → R that assigns a real-valued number to a solu-
tion candidate, and a distance metric d : S ×S → R.
2
https://github.com/D-X-Y/NATS-Bench
Then, a fitness landscape is defined as the tuple
F = (S , f , d). (1)
3.2.2 Fitness Landscape of NATS-Bench
Topology Search Space
Each architecture in the NATS-Bench topology search
space can be represented as a string of length six
where each character represents an edge operation for
a corresponding edge in the DAG representation of
the cell. Then for S
t
, S is the set of all possible neu-
ral architecture string representations. The distance
function d is the Hamming distance between two such
strings. We define the neighborhood of a solution
candidate as N (x) = {y ∈ S |d(x, y) = 1}, that is, the
set of architecture strings that represent a change of
one edge operation from the architecture of x. We
have three fitness functions, corresponding to average
test accuracies of architectures trained on 200 epochs
of data on CIFAR-10, CIFAR-100, and ImageNet16-
120. Thus, we have three fitness landscapes, one for
each image classification dataset.
For the purposes of analysis on NATS-Bench, we
deviate from Pitzer and Affenzeller’s definitions of
phenotype and genotype. Because some architectures
are isomorphic, in addition to the string representa-
tion of the architecture, each architecture also has a
string representation of the unique isomorph. We con-
sider the string representation of the architecture the
genotype, and the string representation of the unique
isomorph the phenotype. Due to numerical error, two
architectures with the same phenotype may have dif-
ferent fitnesses (Dong and Yang, 2020).
3.2.3 Density of States
A density of states analysis examines the number of
solution candidates with a certain fitness value. The
density of states can tell us how likely it is to find a
“good” solution via random search (Ros
´
e et al., 1996).
For example, a fitness landscape with many fitnesses
near the global optimum will be relatively easy for
random search.
3.2.4 Fitness Distance Correlations
One measure of problem difficulty is the correlation
between distances to the nearest global optimum (in
Fitness Landscape Analysis of a Cell-Based Neural Architecture Search Space
79

our case, maximum) and the fitnesses of solution can-
didates. This correlation can help us measure the ex-
tent to which there is a “gradient” of fitness to a global
optimum. One established metric is fitness distance
correlation (FDC), which is a measure of problem dif-
ficulty for genetic algorithms (Jones et al., 1995). If
we let F represent a list of fitnesses of S and D repre-
sent the corresponding distances to the nearest global
optimum, then the FDC is the Pearson correlation co-
efficient between F and D:
FDC =
cov(F, D)
σ
F
σ
D
, (2)
where cov(F, D) is the covariance of F and D, and σ
F
and σ
D
are the standard deviations of F and D, respec-
tively. In addition to FDC, we also examine Spearman
and Kendall rank correlations between F and D. The
Spearman fitness distance rank correlation is
ρ =
cov(R(F), R(D))
σ
R(F)
σ
R(D)
, (3)
where R(F) and R(D) are F and D converted to ranks,
respectively. Then, the Kendall fitness distance rank
correlation is
τ =
2
n(n − 1)
∑
i< j
sgn( f
i
− f
j
)sgn(d
i
− d
j
), (4)
where n = |S | = |F| = |D| and f
i
and d
i
are the ith
elements of F and D, respectively.
We clarify that while the Spearman and Kendall
correlations are correlations between fitness and dis-
tance, the term “fitness distance correlation” or FDC
specifically refers to Pearson’s correlation, as estab-
lished in the literature (Jones et al., 1995).
3.2.5 Local Optima
A solution candidate x is a local optimum if it is
the fittest among its neighborhood (Pitzer and Affen-
zeller, 2012):
local optima(x) ⇐⇒ ∀y ∈ N (x), f (x) > f (y). (5)
We clarify that while this definition may sometimes
be referred to as a strict local optimum, we use the
term local optimum to be consistent with Pitzer and
Affenzeller’s definitions. The number of local optima
can tell us about the global ruggedness of a fitness
landscape, for instance, a multi-modal landscape is
more globally rugged than a unimodal one. Further-
more, correlations between local optima fitness and
distance to a global optimum can tell us the extent to
which there is a progression of fitness from local op-
tima to a global optimum.
3.2.6 Basins of Attraction
Related to local optima is the concept of basins of
attraction. Although the fitness landscape of NATS-
Bench is a maximization problem, we use the term
basins of attraction to remain consistent with the lit-
erature. To understand basins of attraction, we must
first understand an upward path to a local maximum.
We adapt this definition from the definition of a down-
ward path by Pitzer et al. (Pitzer et al., 2010). An up-
ward path p
↑
from candidate x
0
to x
n
is the sequence
{x
i
}
n
i=0
where (∀i < j), f (x
i
) ≤ f (x
j
), f (x
0
) < f (x
n
),
and x
i+1
∈ N (x
i
), that is, each solution candidate in
the upward path is at least as fit as the previous one.
Then, the weak basin of local optimum o is defined as
b(o) := {x|x ∈ S , p
↑
(x, o)}, (6)
which is the subset of the search space that has an
upward path leading to o. A strong basin of a local
optimum o is defined as
ˆ
b(o) := {x|x ∈ b(o), (∄o
′
̸= o ∈ O) with x ∈ b(o
′
)}
(7)
where O is the set of all local optima. In other words,
the strong basin of a local optimum o is the subset of
the search space that has an upward path only to o.
The relative fitnesses of the local optima com-
bined with the relative sizes of their basins of attrac-
tion can indicate problem difficulty, as local optima
with larger basins are more likely to be found via lo-
cal search methods.
3.2.7 Neutral Networks
A neutral network is a set of connected solution can-
didates with equal fitness and can be intuitively de-
scribed as a “plateau” of fitness (Pitzer and Affen-
zeller, 2012).
3.2.8 Autocorrelation and Correlation Length
Autocorrelation and correlation length are two mea-
sures for ruggedness of a fitness landscape (Wein-
berger, 1990). The autocorrelation function for some
lag i is the Pearson correlation coefficient between a
random walk on the landscape and the same walk with
time delay i. Then for a random walk F
t
and a lag i,
the autocorrelation function is
ρ(i) =
cov(F
t
, F
t+i
)
σ
F
t
σ
F
t+i
. (8)
where F
t+i
is F
t
with a lag of i, cov(F
t
, F
t+i
) is the
covariance of F
t
and F
t+i
, and σ
F
t
and σ
F
t+i
are the
standard deviations of F
t
and F
t+i
, respectively. Cor-
relation length is defined as τ =
−1
ln|ρ(1)|
for ρ(1) ̸= 0,
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
80

which is the expected distance between points be-
fore they become “uncorrelated” (Weinberger, 1990;
Tavares et al., 2008).
4 RESULTS
We compare the difficulty and shape of the NATS-
Bench topology search space for three different
fitness landscapes of CIFAR-10, CIFAR-100, and
ImageNet16-120 test accuracies. We calculate, ana-
lyze, and visualize characteristics of density of states,
FDC and fitness distance rank correlations, local op-
tima, basins of attraction, neutral networks, and au-
tocorrelation. Our analysis could indicate that the
problem difficulty for the NAS search problems cor-
respond to the difficulties of the image classification
problems themselves, with the nuance that the use of
different metrics results in different orderings of dif-
ficulty for the three fitness landscapes.
While analyses of larger search spaces may need
to use sampling to approximate fitness landscape
characteristics (Nunes et al., 2021; Traor
´
e et al.,
2021), S
t
in NATS-Bench is relatively small, so we
are able to exhuastively evaluate the search space for
most of our metrics. To estimate autocorrelation, we
average 200 random walks of length 100 on the search
space with random starting points. Our data and code
are publicly available online.
3
4.1 Density of States
As seen in Figure 3, CIFAR-10 has the most architec-
tures near the global optimum, followed by CIFAR-
100, then ImageNet16-120. This may indicate that
NAS on architectures for CIFAR-10 image classifi-
cation is the easiest, followed by CIFAR-100 and
lastly ImageNet16-120. This order of difficulty for
the NATS-Bench fitness landscapes matches the or-
der of difficulty for the image classification problems
themselves. Our density of states analysis of the
NATS-Bench topology space test accuracies is con-
sistent with Ochoa and Veerapen’s analysis of the val-
idation accuracies.
4.2 Fitness Distance Correlations
FDC can be used to characterize problem difficulty
for genetic algorithms and can divide problems into
three broad categories. FDC ≥ 0.15 is considered
misleading, because solution candidates decrease in
fitness as they approach a global optimum. −0.15 <
3
https://github.com/v-tao/nats-bench-landscape
Table 1: Correlations between architecture fitness and dis-
tance to the global optimum.
CIFAR-10 CIFAR-100 ImageNet
FDC -.2199 -.3090 -.3163
ρ -.4144 -.4666 -.3270
τ -.3200 -.3630 -.2502
FDC < 0.15 is difficult because there is weak to
no correlation between fitnesses and distances to the
global optimum, and FDC ≤ −0.15 is straightfor-
ward, as solution candidates approaching the global
optimum increase in fitness (Jones et al., 1995). From
the rank correlations in Table 1, the CIFAR-100 land-
scape appears the most straightforward, followed by
CIFAR-10 and then ImageNet16-120, which is con-
sistent with Ochoa and Veerapen’s analyses. How-
ever, examining FDC which is Pearson’s correla-
tion, the ImageNet16-120 landscape appears the most
straightforward, followed by CIFAR-100 and then
CIFAR-10. Thus, we demonstrate how different met-
rics can cause different interpretations of problem dif-
ficulty.
4.3 Local Optima
Table 2: Correlations between architecture fitness and dis-
tance to global optimum of local optima.
CIFAR-10 CIFAR-100 ImageNet
# optima 17 24 36
FDC -.8741 -.8225 -.6172
ρ -.8650 -.7916 -.6311
τ -.7223 -.6845 -.5050
For the test accuracies, ImageNet16-120 has the most
local optima, followed by CIFAR-100 and CIFAR-
10 (see Table 2), corroborating Ochoa and Veerapen’s
modality analysis of the validation accuracies. In con-
trast to the whole search space, which has a weak neg-
ative correlation between fitness and distance to the
global optimum (see Table 1 and Figure 4), the subset
of just local optima has a strong negative correlation
between these features, as seen in Table 2 and Fig-
ure 5. This suggests there is a progression of fitnesses
from local optima to the global optimum for all three
fitness landscapes.
4.4 Basins of Attraction
From Table 3, we see that for each fitness landscape,
the vast majority of the search space is in a weak basin
of attraction, meaning almost any starting architecture
can reach a local optimum via local search. Combined
with Figure 5, this demonstrates that search on S
t
for
CIFAR-10 is easy, as the local optima for CIFAR-10
Fitness Landscape Analysis of a Cell-Based Neural Architecture Search Space
81

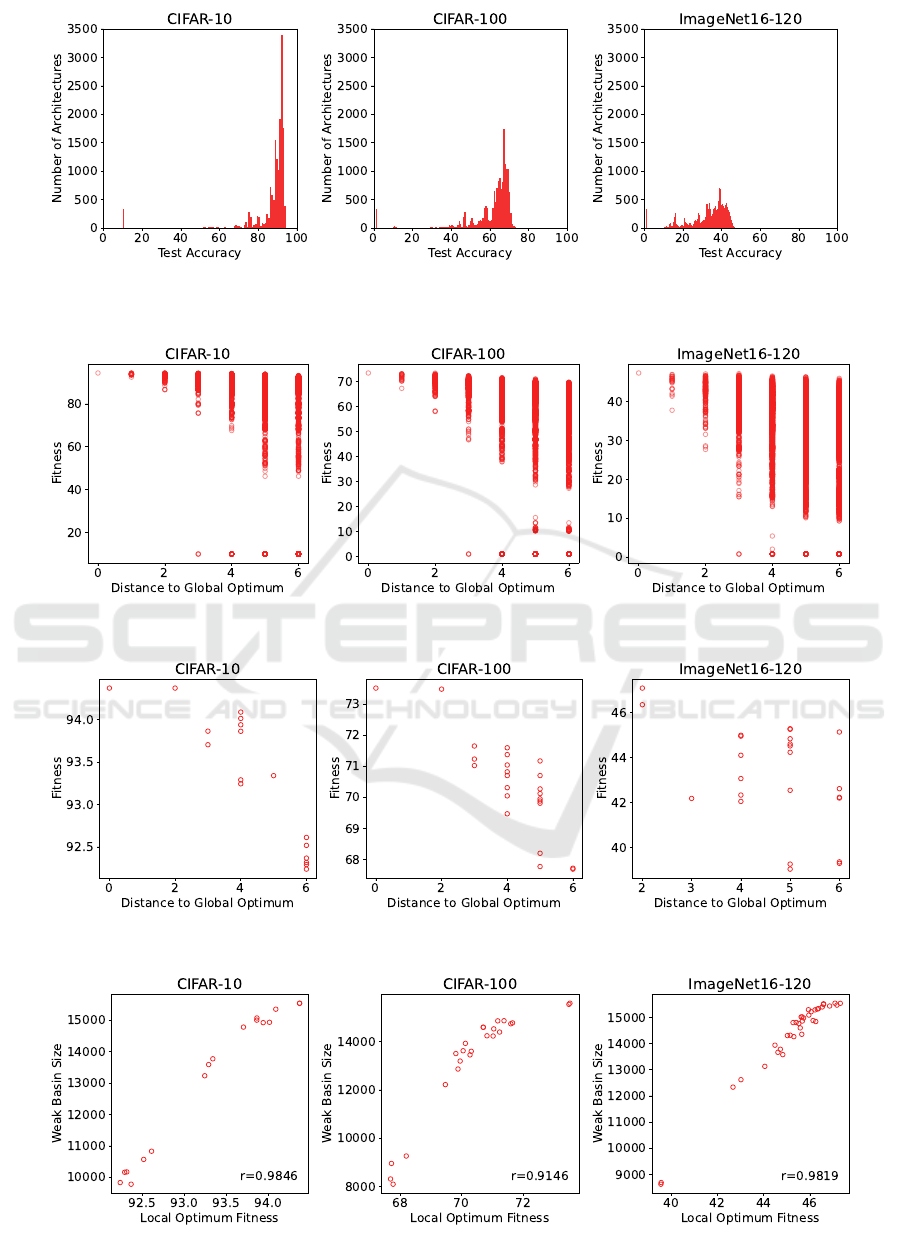
Figure 3: Density of states of NATS-Bench topology search space test accuracies. The maximum fitness for each fitness
landscape is 94.37, 73.51, and 47.31 for CIFAR-10, CIFAR-100, and ImageNet16-120, respectively.
Figure 4: Fitness vs. distance to the global optimum.
Figure 5: Fitness vs. distance to the global optimum for local optima.
Figure 6: Fitness vs. size of weak basin for local maxima.
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
82

Table 3: Summary statistics of weak basins of attraction.
CIFAR-10 CIFAR-100 ImageNet
# basins 17 24 36
Avg. size 13122.06 13245.08 14337.81
Extent .9989 .9984 .9977
Table 4: Summary statistics of strong basins of attraction.
CIFAR-10 CIFAR-100 ImageNet
# basins 4 8 14
Avg. size 10.00 7.88 2.29
Extent .0026 .0040 .0020
are close in fitness to the global optimum. While the
ranges in local optima fitness are greater for CIFAR-
100 and ImageNet16-120, all three fitness landscapes
show a strong correlation between local optima fit-
ness and weak basin extent. This may also indicate
problem easiness, as fitter optima are more likely to
be achieved via local search.
4.5 Neutral Networks
Table 5: Neutral network summary statistics.
CIFAR-10 CIFAR-100 ImageNet
# nets 249 35 46
Avg. size 3.41 7.46 5.41
Max. size 341 63 67
Only a small fraction (< .01) of the search space
belongs to a neutral network (see Table 5). From
Figure 7, we observe most neutral networks contain
only a handful of architectures and are the worst-
performing architectures in the search space. These
architectures correspond to the “spikes” on the left of
each histogram in Figure 3.
Close inspection of the largest neutral network in
each fitness landscape reveals that these neutral net-
works consist entirely of architectures where the input
node and output node are disconnected, resulting in an
architecture that performs equal to random choice. In
some cases, large neutral networks may be beneficial
because they allow exploration of a large space while
maintaining the same fitness (Pitzer et al., 2010; Wag-
ner, 2008). Although our data in Table 6 indicate that
exploring these neutral networks do provide access to
genetic diversity, these neutral networks consist of the
worst architectures in the search space, so it may not
be desirable to remain in these neutral networks over
many iterations.
4.6 Autocorrelation
The correlation lengths are 1.53, 1.71, and 2.23 for
CIFAR-10, CIFAR-100, and ImageNet16-120, re-
spectively. Furthermore, we can see from Figure 8
that the autocorrelation function for ImageNet16-120
decays slower than for CIFAR-10 or CIFAR-100.
Both the correlation length and the autocorrelation
function indicate that at the local level, ImageNet16-
120 is the smoothest out of the three fitness land-
scapes.
5 DISCUSSION
Our fitness landscape analyses could indicate that
the difficulties associated with the three fitness land-
scapes of CIFAR-10, CIFAR-100, and ImageNet16-
120 on the NATS-Bench topology search space cor-
respond to the difficulties of the image classification
problems themselves. This is reflected in the den-
sity of states, as CIFAR-10 has the greatest propor-
tion of architectures close to the global optimum, fol-
lowed by CIFAR-100 and ImageNet16-120. In ad-
dition, while all three fitness landscapes have similar
weak and strong basin extents, both the number of lo-
cal optima and the range of fitness values for local op-
tima is smallest for CIFAR-10, then CIFAR-100, then
ImageNet16-120. This means that for CIFAR-10, not
only is the global optimum more likely to be reached
via local search, but also any local optimum reached
is closer in fitness to the global optimum than for the
other two fitness landscapes. Previous work indicates
that ImageNet16-120 is the most difficult for valida-
tion accuracies of S
t
(Ochoa and Veerapen, 2022), and
our work shows a similar case for the test accuracies.
However, our data contains some discrepancies
which would at first appear to be contradictions.
The progression of difficulty from CIFAR-10 to
ImageNet16-120 is not supported by our data on cor-
relations between architecture fitness and distance to
the global optimum. By FDC, ImageNet16-120 is
the most straightforward, while the rank correlations
point to CIFAR-100 as the most straightforward. We
can resolve this discrepancy by considering the dif-
ferent algorithms that may be applied to the optimiza-
tion problem. As FDC is a measure of problem dif-
ficulty for genetic algorithms (Jones et al., 1995), the
lowest FDC may indicate that ImageNet16-120 is the
most straightforward for a genetic algorithm whereas
the lowest rank correlation may indicate that CIFAR-
100 is the most straightforward for algorithms like hill
climbing that only use relative fitness values.
Previous work has used number of local op-
Fitness Landscape Analysis of a Cell-Based Neural Architecture Search Space
83

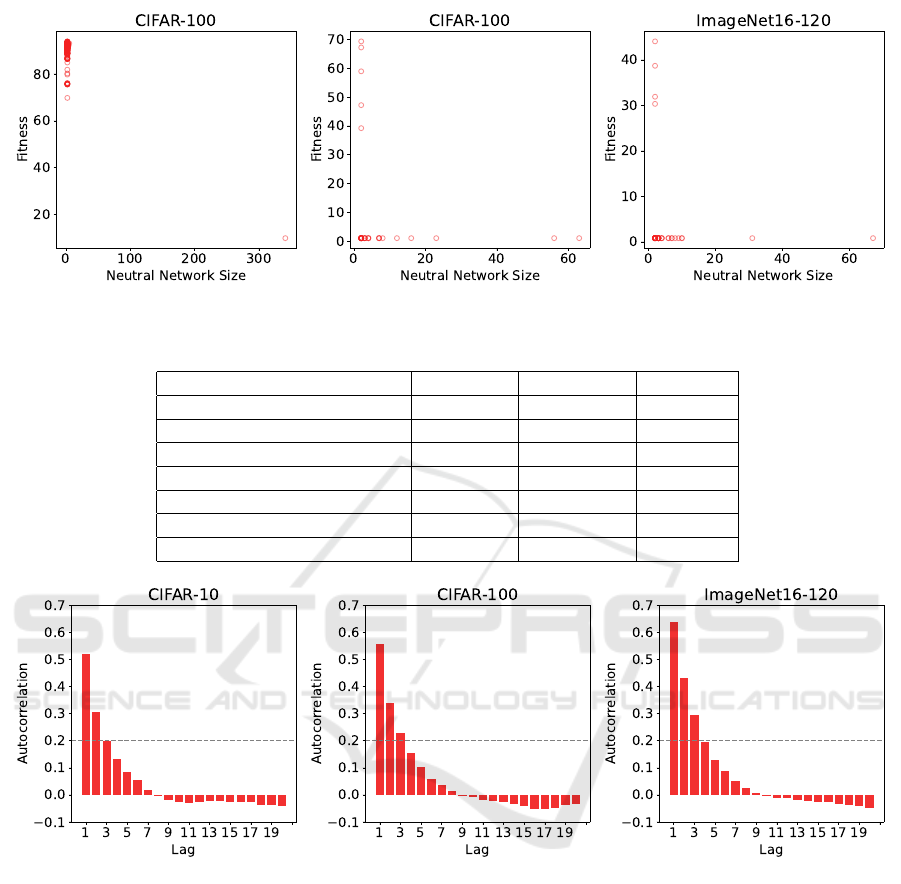
Figure 7: Fitness vs. size of neutral networks.
Table 6: Properties of largest neutral network and its neighbors.
CIFAR-10 CIFAR-100 ImageNet
Size 341 63 67
Fitness 10.00 1.00 .83
Max. edit distance 6 6 6
Avg. edit distance 4.8031 4.8249 4.8318
Unique phenotypes 5 5 5
Unique neighbor genotypes 2868 917 974
Unique neighbor phenotypes 513 177 182
Figure 8: Autocorrelation functions sampled from 200 random walks of length 100.
tima to describe the ruggedness of the NATS-Bench
topology fitness landscapes (Ochoa and Veerapen,
2022). While our own analysis of local optima sup-
port these claims of ruggedness, we should be more
careful in describing this as global ruggedness. As
ImageNet16-120 has the most local optima, followed
by CIFAR-100 and CIFAR-10, ImageNet16-120 ap-
pears the most rugged on a global level. However, our
autocorrelation and correlation length analyses point
to the reverse order of ruggedness on a local level.
These discrepancies demonstrate that the fitness land-
scape of an NAS search problem is multi-faceted, and
many metrics are required to paint a fuller picture
of the NAS fitness landscape. Furthermore, a fitness
landscape analysis should be done with nuance, and
consider the different implications of metrics for dif-
ferent algorithms.
Our fitness landscape analysis contributes to a
growing body of work aimed at combining evolution-
ary computation and explainable AI. As an intersec-
tion between explainable AI and NAS, our work di-
rectly addresses a challenge mentioned by Bacardit
et al.’s recent position paper on the subject (Bacardit
et al., 2022). With the rise in popularity of NAS, we
illustrate how evolutionary computation methods can
contribute to understanding NAS search spaces.
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
84

6 CONCLUSION
We performed a fitness landscape analysis of the
NATS-Bench topology search space, analyzing and
visualizing features of density of states, FDC and fit-
ness distance rank correlations, local optima, basins
of attraction, neutral networks, and autocorrelation.
Our analyses indicated that the problem difficulty of
search on the topology search space of NATS-Bench
for architectures that can perform well on CIFAR-10,
CIFAR-100, and ImageNet16-120 datasets may cor-
respond to the difficulties of the image classification
problems themselves. We also demonstrated the im-
portance of multiple metrics and nuance in the inter-
pretation of an NAS fitness landscape.
While these metrics can help to characterize the
fitness landscape, ultimately they are not exact. Fu-
ture work may include the comparison of different
algorithms on NATS-Bench in order to discern how
useful these metrics are for describing the true fitness
landscape of NATS-Bench. As our current under-
standing of NAS search spaces is limited, future work
may also include fitness landscape analyses of other
NAS search spaces, such as non-tabular search spaces
(Siems et al., 2020) or for problems other than im-
age classification (Klyuchnikov et al., 2022; Mehrotra
et al., 2020). Another possible direction is to investi-
gate what properties of the architectures themselves
cause the fitness landscapes to appear this way.
REFERENCES
Abdel-Hamid, O., Mohamed, A.-r., Jiang, H., Deng, L.,
Penn, G., and Yu, D. (2014). Convolutional neural
networks for speech recognition. IEEE/ACM Trans-
actions on audio, speech, and language processing,
22(10):1533–1545.
Bacardit, J., Brownlee, A. E., Cagnoni, S., Iacca, G., Mc-
Call, J., and Walker, D. (2022). The intersection of
evolutionary computation and explainable ai. In Pro-
ceedings of the Genetic and Evolutionary Computa-
tion conference companion, pages 1757–1762.
Chen, W., Gong, X., and Wang, Z. (2021). Neural ar-
chitecture search on imagenet in four gpu hours:
A theoretically inspired perspective. arXiv preprint
arXiv:2102.11535.
Chitty-Venkata, K. T., Emani, M., Vishwanath, V., and So-
mani, A. K. (2023). Neural architecture search bench-
marks: Insights and survey. IEEE Access, 11:25217–
25236.
Chrabaszcz, P., Loshchilov, I., and Hutter, F. (2017). A
downsampled variant of imagenet as an alternative to
the cifar datasets. arXiv preprint arXiv:1707.08819.
Dong, X., Liu, L., Musial, K., and Gabrys, B. (2021). Nats-
bench: Benchmarking nas algorithms for architecture
topology and size. IEEE transactions on pattern anal-
ysis and machine intelligence, 44(7):3634–3646.
Dong, X. and Yang, Y. (2019). One-shot neural architecture
search via self-evaluated template network. In Pro-
ceedings of the IEEE/CVF International Conference
on Computer Vision, pages 3681–3690.
Dong, X. and Yang, Y. (2020). Nas-bench-201: Extending
the scope of reproducible neural architecture search.
arXiv preprint arXiv:2001.00326.
Guo, Z., Zhang, X., Mu, H., Heng, W., Liu, Z., Wei, Y.,
and Sun, J. (2020). Single path one-shot neural ar-
chitecture search with uniform sampling. In Com-
puter Vision–ECCV 2020: 16th European Confer-
ence, Glasgow, UK, August 23–28, 2020, Proceed-
ings, Part XVI 16, pages 544–560. Springer.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 770–778.
Jones, T., Forrest, S., et al. (1995). Fitness distance corre-
lation as a measure of problem difficulty for genetic
algorithms. In ICGA, volume 95, pages 184–192.
Klyuchnikov, N., Trofimov, I., Artemova, E., Salnikov,
M., Fedorov, M., Filippov, A., and Burnaev, E.
(2022). Nas-bench-nlp: neural architecture search
benchmark for natural language processing. IEEE Ac-
cess, 10:45736–45747.
Krizhevsky, A. and Hinton, G. (2009). Learning multiple
layers of features from tiny images. Technical Re-
port 0, University of Toronto, Toronto, Ontario.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. Advances in neural information processing
systems, 25.
Li, L. and Talwalkar, A. (2020). Random search and re-
producibility for neural architecture search. In Un-
certainty in artificial intelligence, pages 367–377.
PMLR.
Liu, H., Simonyan, K., and Yang, Y. (2018). Darts:
Differentiable architecture search. arXiv preprint
arXiv:1806.09055.
Mehrotra, A., Ramos, A. G. C., Bhattacharya, S., Dudziak,
Ł., Vipperla, R., Chau, T., Abdelfattah, M. S., Ishtiaq,
S., and Lane, N. D. (2020). Nas-bench-asr: Repro-
ducible neural architecture search for speech recogni-
tion. In International Conference on Learning Repre-
sentations.
Mellor, J., Turner, J., Storkey, A., and Crowley, E. J. (2021).
Neural architecture search without training. In In-
ternational Conference on Machine Learning, pages
7588–7598. PMLR.
Merz, P. and Freisleben, B. (2000). Fitness landscape anal-
ysis and memetic algorithms for the quadratic assign-
ment problem. IEEE Transactions on Evolutionary
Computation, 4(4):337–352.
Nunes, M., Fraga, P. M., and Pappa, G. L. (2021). Fitness
landscape analysis of graph neural network architec-
ture search spaces. In Proceedings of the Genetic and
Evolutionary Computation Conference, pages 876–
884.
Fitness Landscape Analysis of a Cell-Based Neural Architecture Search Space
85

Ochoa, G. and Veerapen, N. (2022). Neural architecture
search: a visual analysis. In International Conference
on Parallel Problem Solving from Nature, pages 603–
615. Springer.
Pitzer, E. and Affenzeller, M. (2012). A comprehensive sur-
vey on fitness landscape analysis. Recent advances in
intelligent engineering systems, pages 161–191.
Pitzer, E., Affenzeller, M., and Beham, A. (2010). A closer
look down the basins of attraction. In 2010 UK work-
shop on computational intelligence (UKCI), pages 1–
6. IEEE.
Potgieter, I., Cleghorn, C. W., and Bosman, A. S. (2022).
A local optima network analysis of the feedforward
neural architecture space. In 2022 International Joint
Conference on Neural Networks (IJCNN), pages 1–8.
IEEE.
Rodrigues, N. M., Malan, K. M., Ochoa, G., Vanneschi, L.,
and Silva, S. (2022). Fitness landscape analysis of
convolutional neural network architectures for image
classification. Information Sciences, 609:711–726.
Rodrigues, N. M., Silva, S., and Vanneschi, L. (2020). A
study of generalization and fitness landscapes for neu-
roevolution. IEEE Access, 8:108216–108234.
Ros
´
e, H., Ebeling, W., and Asselmeyer, T. (1996). The den-
sity of states — a measure of the difficulty of optimisa-
tion problems. In Voigt, H.-M., Ebeling, W., Rechen-
berg, I., and Schwefel, H.-P., editors, Parallel Prob-
lem Solving from Nature — PPSN IV, pages 208–217,
Berlin, Heidelberg. Springer Berlin Heidelberg.
Sheikhtaheri, A., Sadoughi, F., and Hashemi Dehaghi, Z.
(2014). Developing and using expert systems and neu-
ral networks in medicine: a review on benefits and
challenges. Journal of medical systems, 38:1–6.
Siems, J., Zimmer, L., Zela, A., Lukasik, J., Keuper, M.,
and Hutter, F. (2020). Nas-bench-301 and the case for
surrogate benchmarks for neural architecture search.
arXiv preprint arXiv:2008.09777, 4:14.
Stanley, K. O., Clune, J., Lehman, J., and Miikkulainen, R.
(2019). Designing neural networks through neuroevo-
lution. Nature Machine Intelligence, 1(1):24–35.
Szegedy, C., Toshev, A., and Erhan, D. (2013). Deep neu-
ral networks for object detection. Advances in neural
information processing systems, 26.
Tavares, J., Pereira, F. B., and Costa, E. (2008). Multi-
dimensional knapsack problem: A fitness landscape
analysis. IEEE Transactions on Systems, Man, and
Cybernetics, Part B (Cybernetics), 38(3):604–616.
Thomson, S. L., Ochoa, G., Veerapen, N., and Michalak,
K. (2023). Channel configuration for neural architec-
ture: Insights from the search space. In Proceedings
of the Genetic and Evolutionary Computation Confer-
ence, pages 1267–1275.
Traor
´
e, K. R., Camero, A., and Zhu, X. X. (2021). Fit-
ness landscape footprint: A framework to compare
neural architecture search problems. arXiv preprint
arXiv:2111.01584.
Wagner, A. (2008). Robustness and evolvability: a paradox
resolved. Proceedings of the Royal Society B: Biolog-
ical Sciences, 275(1630):91–100.
Weinberger, E. (1990). Correlated and uncorrelated fitness
landscapes and how to tell the difference. Biological
cybernetics, 63(5):325–336.
White, C., Safari, M., Sukthanker, R., Ru, B., Elsken, T.,
Zela, A., Dey, D., and Hutter, F. (2023). Neural ar-
chitecture search: Insights from 1000 papers. arXiv
preprint arXiv:2301.08727.
Wright, S. et al. (1932). The roles of mutation, inbreeding,
crossbreeding, and selection in evolution. Proceed-
ings of the Sixth International Congress of Genetics.
Ying, C., Klein, A., Christiansen, E., Real, E., Murphy, K.,
and Hutter, F. (2019). Nas-bench-101: Towards repro-
ducible neural architecture search. In International
conference on machine learning, pages 7105–7114.
PMLR.
Zoph, B. and Le, Q. V. (2016). Neural architecture
search with reinforcement learning. arXiv preprint
arXiv:1611.01578.
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
86