H
∞
Type Control of Periodic Stochastic Systems Subject to Multiplicative
White Noises: Application to Satellite AOCS Design
Adrian-Mihail Stoica
a
University Politehnica of Bucharest, Romania
Keywords:
Stochastic Systems with Multiplicative White Noises, Periodic Coefficients, H
∞
Type Control, Systems of
Linear Matrix Inequalities.
Abstract:
The paper presents an H
∞
state feedback type design method for a class of periodic discrete-time stochastic
systems subject to multiplicative white noises. It is shown that the gains of the control law for the considered
problem may be expressed in terms of the solution of a specific system of linear matrix inequalities with
periodic coefficients. The design method is illustrated by an application for the detumbling subsystem of a
cubesat in which a linearized model with parametric modeling uncertainties is considered.
1 INTRODUCTION
The design of the satellites AOCS (Attitude and Or-
bit Control System) is an important direction of re-
search in aerospace applications due to the wide mis-
sion profiles and the specific requirements in their dif-
ferent stages. One of the effective approaches to de-
sign control laws used in such applications is based
on the so-called H
∞
type techniques which became
over the last decades a mature design method for
a large number of engineering applications (see e.g.
(Doyle,1989, Skelton, 1998, Zhou, 1999) for theoret-
ical fundamentals) and for instance, (Simplicio, 2016,
La Ballois, 1996, Souza, 2019), for some applications
in aerospace engineering. Early results concerning
the H
∞
norm minimization referred to the case when
the controlled system dynamics is approximated by
linear models with constant coefficients. Further, the
H
∞
type design methodology was extended to other
classes of dynamic systems, including models with
time-varying parameters, stochastic systems and non-
linear systems (see e.g. (Dragan, 2010, Zhang, 2017,
Coutinho, 2002, Aliyu, 2017)).
In the present paper, an H
∞
type control prob-
lem is considered for stochastic discrete-time linear
systems with periodic time-varying parameters cor-
rupted with multiplicative white noises. This class
of systems extend the results presented for instance
in (Lovera, 2000, Lovera, 2002), derived in the ab-
sence of the stochastic terms. The interest for stochas-
a
https://orcid.org/0000-0001-5369-8615
tic models including multiplicative white noise terms
is motivated both for specific applications in which
such terms naturally appear (see e.g. (Gershon, 2005,
Xing, 2020, Avital, 2023)) but also in the representa-
tion of parametric modeling uncertainties (Petersen,
2017). The design approach presented in this paper
aims to determine a state feedback control law ensur-
ing an H
∞
performance for systems with time peri-
odic coefficients subject to multiplicative noises. It is
shown that the gains of this H
∞
control law depend
on the solution of a specific system of coupled linear
matrix inequalities (LMIs) with periodic coefficients.
The theoretical results are illustrated for the design of
the detumbling subsystem of a cubesat.
Throughout the paper, the following notations will
be used: R denotes the set of real numbers, Z
+
is the
set of nonnegative integers, E[·] stands for the expec-
tation, |x| represents the Euclidean norm of the vector
x and P(·) denotes the probability of an event.
2 PROBLEM FORMULATION
Consider the discrete-time stochastic system
x(k +1) = (A
0
(k) +
∑
r
ℓ=1
w
ℓ
(k)A
ℓ
(k)) x(k)
+

B
10
(k) +
∑
r
ℓ=1
w
ℓ
(k)B
1ℓ(k)

u
1
(k)
+

B
20
(k) +
∑
r
ℓ=1
w
ℓ
(k)B
2ℓ(k)

u
2
(k)
y
1
(k) = C(k)x(k) +D(k)u
2
(k);
y
2
(k) = x(k), k = 0, 1,...
(1)
where x ∈ R
n
denotes the state vector, u
1
∈ R
m
1
is the exogenous input, u
2
∈ R
m
2
stands for the
Stoica, A.
H ∞ Type Control of Periodic Stochastic Systems Subject to Multiplicative White Noises: Application to Satellite AOCS Design.
DOI: 10.5220/0012892700003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 217-221
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
217

control variable, y
1
∈ R
p
1
is the quality output
and y
2
denotes the measured output. w(k) =

w
1
(k) .. . w
r
(k)

T
are random vectors which
components w
ℓ
(k), ℓ = 1,...,r are independent, zero
mean variables on a probability space (Ω,F , P ) with
sup
k∈Z
+
E[|w(k)|
2
] < ∞ and E[w(k)w
T
(k)] = I
r×r
for
all k ∈ Z
+
. Throughout the paper it will be assumed
that all matrices are time-periodic functions with the
positive integerperiod N. A motivation for the consid-
ered model will be given in Section 4 where an appli-
cation for the periodic control law design of a cubesat
detumbling is presented.
Remark 1. In the above stochastic system (1) the
same noises w
ℓ
,ℓ = 1, ...,r were considered in the ex-
pressions of the state and the control matrices. In the
situation when these matrices are perturbed with dif-
ferent independent multiplicative noises, one may de-
fine a vector w obtained by concatenating all noises
in a single vector w and setting accordingly the coef-
ficients A
ℓ
, B
ℓ
, ℓ = 1,...,r.
The problem consists in determining a periodic
state feedback gain F(k), k = 0,1... such that the re-
sulting system obtained with u
2
(k) = F(k)x(k) is ex-
ponentially stable in mean square (ESMS) and it sat-
isfies for a given γ > 0, the H
∞
type condition
∞
∑
k=0
E

|y
1
(k)|
2
− γ
2
|u
1
(k)|
2

< 0 (2)
for all u
1
∈ L
2
[0,∞; R
m
1
], where L
2
denotes the
space of all sequences u
1
with
∑
∞
k=0
|u
1
(k)|
2
< ∞.
It is reminded that a discrete-time stochastic system
with time varying coefficients of form x(k + 1) =
(A
0
(k) +
∑
r
ℓ=1
w
ℓ
(k)A
ℓ
(k)) x(k), k ∈ Z
+
is ESMS if
there exist α ∈ (0, 1) and β ≥ 1 such that E[|x(k)|
2
] ≤
βα
k
|x
0
|
2
for all x
0
∈ R
n
(see e.g. (Morozan, 1997, El
Bouhtouri, 1999)).
3 TIME-PERIODIC H
∞
STATE
FEEDBACK CONTROL LAW
The next result which proof may be found in (Mo-
rozan, 1999) is a version of the Bounded Real Lemma
for discrete-time time-varying systems with multi-
plicative noises.
Theorem 1. The following assertions are equivalent
i) The system
x(k + 1) = (A
0
(k) +
∑
r
ℓ=1
w
ℓ
(k)A
ℓ
(k)) x(k)
(B
0
(k) +
∑
r
ℓ=1
w
ℓ
(k)B
ℓ
(k)) u(k)
y(k) = (C
0
(k) +
∑
r
ℓ=1
w
ℓ
(k)C
ℓ
(k)) x(k)
+(D
0
(k) +
∑
r
ℓ=1
w
ℓ
(k)D
ℓ
(k)) u(k)
is ESMS and its associated input-output operator has
the norm less than γ;
ii) The system of linear matrix inequalities

R
11
(k, k + 1) R
12
(k, k + 1)
R
T
12
(k, k + 1) R
22
(k, k + 1)

< 0 (3)
where
R
11
(k, k + 1) =
∑
r
ℓ=0

A
T
ℓ
(k)X(k + 1)A
ℓ
(k)
+C
T
ℓ
(k)C
ℓ
(k)

− X (k)
R
12
(k, k + 1) =
∑
r
ℓ=0

A
T
ℓ
(k)X(k + 1)B
ℓ
(k)
+C
T
ℓ
(k)D
ℓ
(k)

R
22
(k, k + 1) = −

γ
2
I −
∑
r
ℓ=1

D
T
ℓ
(k)D
ℓ
(k)
+B
T
ℓ
(k)X(k + 1)B
ℓ
(k)

has a bounded positive definite solution {X(k)}
k∈Z
+
.
Moreover, if the coefficients are periodic then the sys-
tem (3) has a periodic positive definite solution with
the same period. □
Based on the above theorem, the state feedback
periodic gain solving the H
∞
type control problem is
given by the following result.
Theorem 2. If there exist Y (k) ∈ R
n×n
, Y (k) > 0 and
Z(k) ∈ R
n×m
2
, k = 0,1,...,N with Y (N) = Y (0) solv-
ing the system of linear matrix inequalities




−Y(k) 0 M (k) N (k)
0 −γ
2
I
m
1
B 0
M
T
(k) B
T
−Y (k + 1) 0
N
T
(k) 0 0 −I
p
1




< 0, (4)
k = 0,1,..., N − 1 where
M (k) :=

Y (k)A
T
0
(k) + Z(k)B
T
20
(k)

,. . .
.. . ,

Y (k)A
T
r
(k) + Z(k)B
T
2r
(k)

N (k) := Y (k)C
T
(k) + Z(k)D
T
(k)
B :=

B
T
10
,. . .,B
T
1r

Y (k + 1) := diag (Y(k + 1),... ,Y (k + 1)) ,
then the stabilizing state feedback periodic gains for
which the H
∞
type condition (2) is fulfilled are given
by F(k) = Z
T
(k)Y
−1
(k), k = 0,1,...N − 1.
Proof. For u
2
(k) = F(k)x(k), the system (1) becomes:
x(k + 1) = [A
0
(k) + B
20
(k)F(k)
+
∑
r
ℓ=1
w
ℓ
(A
ℓ
(k) + B
2ℓ
(k)F(k))]x(k)
+(B
10
(k) +
∑
r
ℓ=1
w
ℓ
B
1ℓ
(k)) u
1
(k)
y(t) = (C(k) + D(k)F(k)) x(k), k = 0, 1,...
Using Theorem 1 for the above closed loop system,
direct algebraic computations based on Schur com-
plements arguments, give (4) after multiplication of
the equivalent inequality to the left and the right
with diag(Y (k), I,...,I), where one denoted Y (k) :=
X
−1
(k) and Z(k) := X
−1
(k)F
T
(k). □
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
218

4 CUBESAT DETUMBLING
TIME-PERIODIC CONTROL
LAW
The attitude dynamics of a rigid satellite is expressed
by the known angular momentum equation (see e.g.
(Wertz, 1978, Wie, 1998))
˙
ω(t) = −ω(t)× Iω(t)+ T
c
(t)+ T
d
(t)
(5)
where ω ∈ R
3
denotes the angular rate expressed in
the body frame, I ∈ R
3×3
is the inertia matrix, T
c
∈ R
3
stands for the control torques and T
d
∈ R
3
includes the
exogenous disturbances torques. The control torque is
given by the cross product between the geomagnetic
field vector B and the magnetic dipole moment gener-
ated by magnetic coils of the magnetorquer actuator.
The external disturbances are generated by the forces
acting on a satellite in low-earth orbit as gravity gradi-
ent, solar radiation pressure, magnetic torques and air
drag (see e.g. (Wisniewski, 1999, Wallado, 2001)).
The attitude kinematics is parametrized as follows
(Wertz, 1978, Wie, 1998)
˙
q(t) =
1
2
W(ω)q(t),
(6)
where q ∈ R
4
is the quaternion vector with unit Eu-
clidian norm and the skew matrix W ∈ R
4×4
has the
expression
W(ω) =



0 ω
z
−ω
y
ω
x
−ω
z
0 ω
x
ω
y
ω
y
−ω
x
0 ω
z
−ω
x
−ω
y
−ω
z
0



in which ω
x
, ω
y
and ω
z
denote the components of the
angular rate ω. An important phase of the satellite
mission after its ejection from the launch vehicle is
the so-called ”detumbling”, consisting in reducing its
angular rate to a value close to zero. A linear ap-
proximation of the dynamics and kinematics equa-
tions (5) and (6) around equilibrium conditions for
the state x := [q
T
ω
T
]
T
, namely for q = [0 0 0 1]
T
and
ω = [0 0 0]
T
, respectively, leads to the following ap-
proximative model with time-varying coefficients
˙x(t) = Ax(t) + B(t)u(t) (7)
where one denoted by u the magnetic dipole moment
vector generated by the magnetic coils aligned with
the principal inertia axes and where (see e.g. Lovera,
2000, Silano, 2005)
A =
"
∂
˙
q
∂q
∂
˙
q
∂ω
∂
˙
ω
∂q
∂
˙
ω
∂ω
#
=

0
3×4
1
2
I
3×3
0
4×4
0
4×3

B(t) =

0
4×3
I
−1

B(b(t))
where
∂
˙
q
∂q
,
∂
˙
q
∂ω
,
∂
˙
ω
∂q
,
∂
˙
ω
∂ω
represent the derivatives of the
right hand sides of equations (6) and (5), respectively,
and
B(b(t)) =


0 b
z
(t) −b
y
(t)
−b
z
(t) 0 b
x
(t)
b
y
(t) −b
x
(t) 0


in which b
x
(t), b
y
(t) and b
z
(t) are time-periodic com-
ponents of the geomagnetic field vector. They may
be measured on board using magnetometers but they
also be determined using the International Geomag-
netic Reference Field (IGRF) models based on the lat-
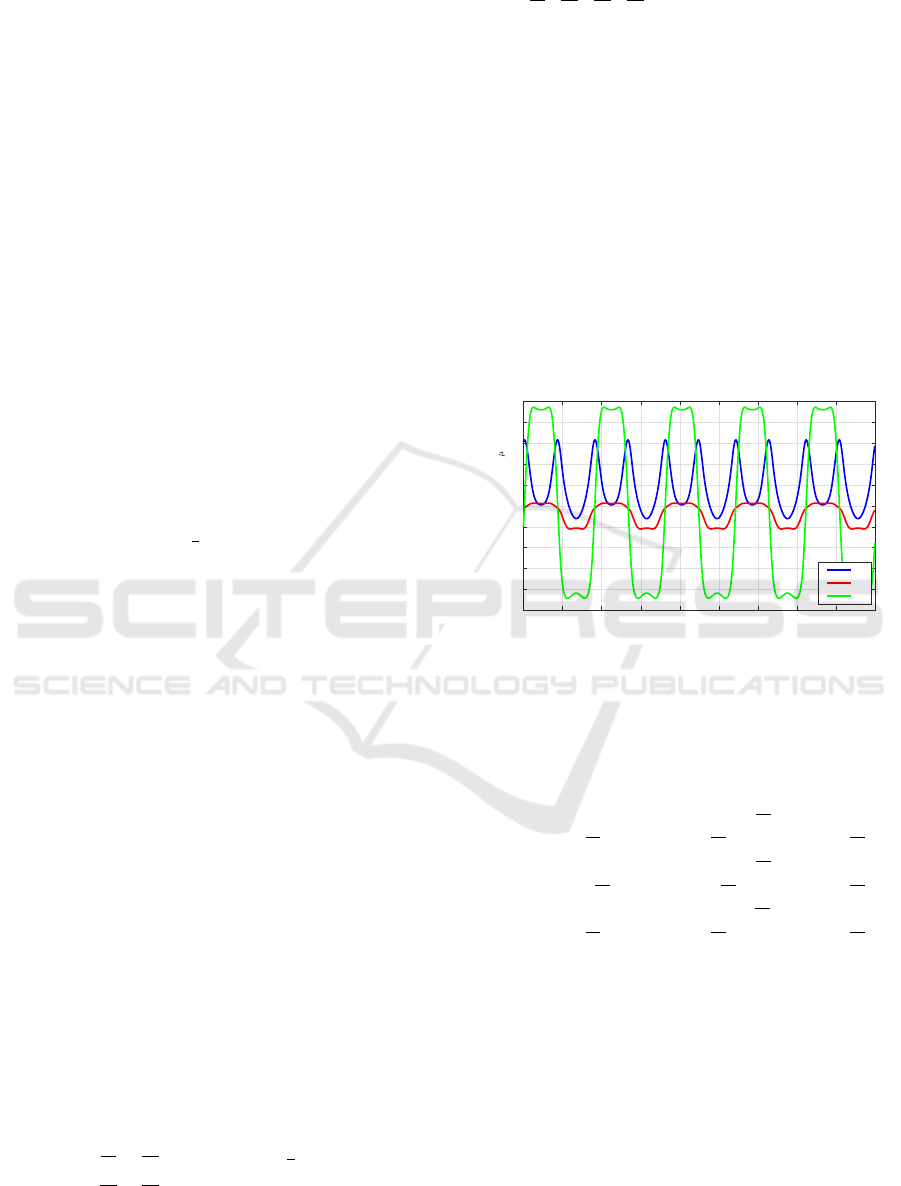
itude, longitude and altitude of the satellite. In Figure
1, the time variation of the components of the Earth
magnetic field are presented, corresponding to a polar
low Earth orbit (LEO) of a cubesat at 500 km altitude
and 87
o
longitude.
0 50 100 150 200 250 300 350 400 450
Time [min]
-50
-40
-30
-20
-10
0
10
20
30
40
50
Geomagnetic field components [ Tesla]
b
x
b
y
b
z
Figure 1: Geomagnetic field components for a polar orbit at
500 km altitude and 87
o
longitude.
These components of the magnetic field may be
approximated by simplified expressions derived us-
ing the Fourier coefficients, for an orbital period T =
90min, as follows
b
x
(t) = 10
−6

10.7150 + 2.4674 sin
2π
90
t
+4.1390 cos
2π
90
t − 9.7118 sin
4π
90
t + 11.5496 cos
4π
90
t

b
y
(t) = 10
−6

−34927 + 5.9779 sin
2π
90
t
+42.7726 cos
2π
90
t − 1.8465 sin
4π
90
t + 1.0177 cos
4π
90
t

b
z
(t) = 10
−6

1.2491 + 48.5761 sin
2π
90
t
+20.594 cos
2π
90
t − 3.7489 sin
4π
90
t + 11.5496 cos
4π
90
t

.
For the application presented in Sec-
tion 4, a cubesat with the inertia matrix
I = diag(0.005,0.005,0.002)kg m
2
has been consid-
ered, for which the time varying control matrix B(t)
has the expression
B(t) =



0
4×1
0
4×1
0
4×1
0 200b
z
(t) −200b
y
(t)
−200b
z
(t) 0 200b
x
(t)
500b
y
(t) −500b
x
(t) 0



.
One can see that in the above model, the con-
trol matrix B(t) is time periodic with the orbital pe-
riod T . Another aspect taken into account in the
H ∞ Type Control of Periodic Stochastic Systems Subject to Multiplicative White Noises: Application to Satellite AOCS Design
219

considered application is the influence of the para-
metric modeling uncertainties. One may represent
such uncertainties using white multiplicative noise
terms. Thus, if for instance, the element B(5, 2) which
equals 200b
z
(t), has a variation of ±10% around its
nominal amplitude
¯
b
52
= 200 due to modeling un-
certainties or to the satellite mass change, then this
uncertainty may be represented as b
52
=
¯
b
52
+ ξ
1
(t)
where ξ
1
is a Gaussian white noise. Its variance
σ
2
ξ
1
may be determined using the 3σ rule stating that
P

|b
52
−
¯
b
52
| ≤ 3 σ
ξ
1

≥ 0.997 from which it results
that σ
ξ
1
= 6.67. Similarly, for b
63
=
¯
b
63
+ ξ
2
(t) and
b
71
=
¯
b
71
+ ξ
3
(t), where
¯
b
63
= 200 and
¯
b
71
= 500,
considering the same level of uncertainty ±10%, one
obtains the following representation of the control
matrix B
u
(t) with modeling uncertainties
B
u
(t) = B(t) + ξ
1
(t)B
1
(t) + ξ
2
(t)B
2
(t)
+ξ
3
(t)B
3
(t)
(8)
where
B
1
(t) =



0
4×1
0
4×1
0
4×1
0 200b
z
(t) −200b
y
(t)
0 0 0
0 0 0



B
2
(t) =



0
4×1
0
4×1
0
4×1
0 0 0
−200b
z
(t) 0 200b
x
(t)
0 0 0



.
and
B
3
(t) =



0
4×1
0
4×1
0
4×1
0 0 0
0 0 0
500b
y
(t) −500b
x
(t) 0



,
and where the noises have the standard deviations
σ
ξ
1
= σ
ξ
2
= 6.67 and σ
ξ
3
= 11.67, respectively. For
this application, the matrices B
2ℓ
, ℓ = 0,...,3 of the
generalized discrete-time model (1) were obtained
by discretization of the above matrices A, B(t) and
B
ℓ
(t),ℓ = 1, 2,3 with a sampling period T
s
= 15 min.
Taking into account the average magnitude of the dis-
turbances torques (see e.g. (Wisnievski, 1999, Wal-
lado, 2001)), the matrix coefficients of u
1
(k) in (1)
where considered 10
−2
B
2ℓ
,ℓ = 0,...,3. As concerns
the quality output, one defined
y
1
(k) =

W
1
ω(k)
W
2
u
2
(k)

with the positive scalar weights W
1
and W
2
. Solv-
ing the system of LMIs (4) one obtained for W
1
=
100, W
2
= 1 and for an attenuation level γ = 0.5,
the following time-varying gains for an orbital period
T = 90min:
F(1) =


0
1×4
−0.0001 0.00301 −0.0011
0
1×4
−0.0225 0.0001 0.0776
0
1×4
0.0006 −0.0415 0


F(2) =


0
1×4
0 0.0467 −0.0021
0
1×4
−0.0467 0.0000 0.0017
0
1×4
0.0008 −0.0007 0


F(3) =


0
1×4
−0.0009 0.0438 −0.0031
0
1×4
−0.0345 0.0009 0.0308
0
1×4
0.0016 −0.0157 0


F(4) =


0
1×4
−0.0059 −0.0403 0.0117
0
1×4
0.0213 0.0059 0.0410
0
1×4
−0.0100 −0.0352 0


F(5) =


0
1×4
−0.0022 −0.0505 0.0299
0
1×4
0.0484 0.0022 −0.0188
0
1×4
−0.0108 0.068 0


F(6) =


0
1×4
−0.0080 −0.0435 0.0159
0
1×4
0.0302 0.0079 0.0336
0
1×4
−0.0113 −0.0240 0


,
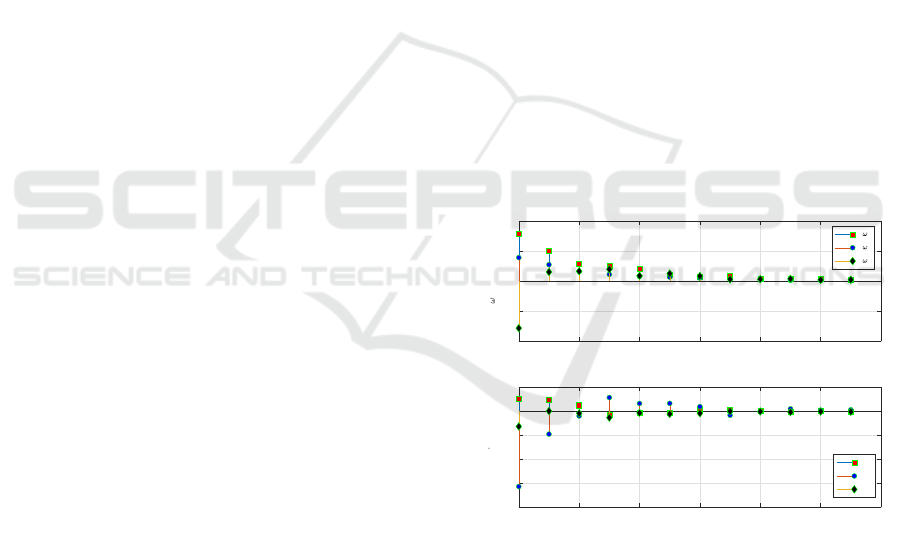
corresponding to the moments of time
{0;15;30; 45; 60; 75}min. With the above time-
periodic gains, the following time responses of
the angular rates and of coil’s magnetic dipoles
illustrated in Figure 2, have been obtained. These
-0.4
-0.2
0
0.2
0.4
[rad/sec]
0 2 4 6 8 10 12
Time [x15 min]
x
y
z
-0.04
-0.03
-0.02
-0.01
0
0.01
u [A m
2
]
0 2 4 6 8 10 12
Time [x15 min]
u
x
u
y
u
z
Figure 2: Angular velocities and dipoles moments at the
sampling instants for two orbits.
time-responses indicate the cubesat stabilization with
a reduced control effort together with disturbances
attenuation. The time response performance may be
adjusted by changing the ratio between the weights
W
1
and W
2
in the quality outputs according with the
AOCS requirements.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
220

5 CONCLUDING REMARKS
The problem of stable feedback H
∞
-control of linear
discrete-time systems with periodic coefficients and
corrupted with state dependent noise has been ana-
lyzed and illustrated for a small satellite using only
magnetic coils as actuators. The main result states
that the time-varying optimal state feedback gains are
periodic functions expressed in terms of the solution
of a specific system of linear matrix inequalities. The
theoretical result is used for a detumbling application
of a cubesat subject to parametric modeling uncertain-
ties, aiming to stabilize it with a low control effort.
Further developments will be devoted to synthesis of
time-periodic optimal control laws for satellite forma-
tion.
REFERENCES
John Comstock Doyle, Keith Glover, Pramod Khargonekar
and Bruce Francis, ”State-Space Solutions to Standard
H
2
and H
∞
Control Problems”, IEEE Transactions on
Automatic Control, Vol. 34, pp. 831-846, 1989
Robert E. Skelton, Tetsuya Iwasaki and Karalos Grigori-
adis, ”A Unified Algebraic Approach to Linear Con-
trol Design”, Taylor & Francis, 1998
Kemin Zhou and John Comstock Doyle, ”Essential of Ro-
bust Control”, Prentice Hall, 1999
Pedro Simplicio, Samir Bennani, Andres Marcos,
Christophe Roux and Xavier Lefort, ”Structured
Singular-Value Analysis of the Vega Launcher in
Atmospheric Flight”, Journal of Guidance, Control
and, Dynamics, Vol. 39, No. 6, pp. 1342-1355, 2016
Sandrine La Ballois and Gilles Duc, ”H
∞
Control of Earth
Observation Satellite”, Journal of Guidance, Control
and, Dynamics, Vol. 19, No. 3, pp. 628-635, 1996
Alain Giacobini Souza and Luiz Carlos Gadelha De Souza,
”Design of a controller for rigid-flexible satellite us-
ing H-infinity method considering parametric uncer-
tainty”, Mechanical Systems and Signal Processing,
Vol. 116, pp. 641-650, 2019
Vasile Dragan, Toader Morozan and Adrian-Mihail Sto-
ica, ”Mathematical Methods in Robust Control of
Discrete-Time Linear Stochastic Systems”, Springer,
2010
Weihai Zhang, Lihua Xie and Bor-Sen Chen, ”Stochastic
H
2
/H
∞
Control”, Taylor & Francis, 2017
Ferreira Coutinho, Alexandre Trofino and Minyue Fu,
”Nonlinear H-infinity control: A LMI Approach”,
IFAC Proceeding Volumes, Vol. 35, Issue 1, 2002
Mohammad Dikko S Aliyu, ”Nonlinear H-infinity Con-
trol Hamiltonian Systems and Hamilton-Jacobi Equa-
tions”, Taylor and Francis, 2017
Marco Lovera, ”Periodic H
∞
Attitude Control for Satellites
with Magnetic Actuators”, In Proceedings of the 3rd
IFAC Symposium on robust control design, Prague,
Czech Republic, 2000
Marco Lovera, Eliana De Marchi and Sergio Bittanti, ”Pe-
riodic Attitude Control Techniques for Small Satel-
lites with Magnetic Actuators”, IEEE Transactions on
Control Systems Technology, Vol. 10, No. 1, pp. 90-
95, 2002
Eli Gershon, Uri Shaked and Isaac Yaesh, ” H
∞
Control and
Estimation of State-multiplicative Linear Systems”,
Springer, 2005
Yu Xing, Ben Gravell, Xingkang He, Karl Henrik Johans-
son and Tyler Sommers, ”Linear System Identification
Under Multiplicative Noise from Multiple Trajectory
Data”, In Proceedings of American Control Confer-
ence, 1-3 July, Denver-CO, USA, 2020
Irina Avital, Isaac Yaesh and Adrian-Mihail Stoica, ”Po-
sition/Velocity Aided Leveling Loop - Continuous-
Discrete Time State Multiplicative-Noise Filter Case”,
In Proceedings of ICINCO Conference, Rome, Italy,
2023
Ian R. Petersen Matthew R. James M.R. and Paul Dupuis,
”Minimax optimal control of stochastic uncertain sys-
tems with relative entropy constraints”, Proceedings
of the 36th IEEE Conference on Decision and Con-
trol, San Diego, 1997
Toader Morozan, ”Stability Radii for Some Systems
with Independent Random Perturbations”, Stochastic
Analysis and. Applications, Vol. 15, No. 3, pp. 375-
386, 1997
Abdelmoula El Bouhtouri, Diederich Hinrichsen and An-
thony J. Pritchard, ”H
∞
type control for discrete-time
stochastic systems”, International Journal of Robust
and Nonlinear Control, Vol. 9, pp. 923-948, 1999
Rafael Wisniewski and Mogens Blancke, ”Fully magnetic
attitude control for spacecraft subject to gravity gradi-
ent”, Automatica, Vo. 35, No, 7, 1999
David A. Wallado, ”Fundamentals of astrodynamics and ap-
plications, Vol. 12, Springer, 2001
James R. Wertz, editor, ”Spacecraft Attitude Determination
and Control”, Kluwer Academic Publishers, 1978
Bong Wie, ”Space Vehicle Dynamics and Control”, Ameri-
can Institute of Aeronautics and Astronautics, 1998
Enrico Silani. and Marco Lovera, ”Magnetic spacecraft atti-
tude control: a survey and some new results”, Control
Engineering Practice, Vol. 13, p. 357-371, 2005
H ∞ Type Control of Periodic Stochastic Systems Subject to Multiplicative White Noises: Application to Satellite AOCS Design
221