Multiple Model Iterative Learning Control of FES Electrode Arrays

Lucy Hodgins

, Chris T. Freeman

and Zehor Belkhatir

School of Electronics and Computer Science, University of Southampton, Southampton, U.K.

Keywords:

Iterative Learning Control, Functional Electrical Stimulation, Multiple Model Switched Adaptive Control,

Stroke Rehabilitation.

Abstract:

Stroke is a common cause of hand and upper limb disability, but current rehabilitation approaches do not ade-

quately support successful recovery. Functional electrical stimulation (FES) is the most widely used assistive

technology, and is able to support accurate hand and wrist motion when applied using multi-element electrode

arrays. However, accurate movements have only been possible using an iterative learning control (ILC) ap-

proach involving many repeated model identiﬁcation tests. This lengthy process limits wide-spread use. This

paper presents a solution for FES electrode array control using estimation-based multiple-model ILC (EM-

MILC), in which a set of parameterised models is used to automatically update the stimulation applied to each

array element every time a task is carried out. This removes the need for model identiﬁcation, signiﬁcantly

improving system usability whilst maintaining high performance. Experimental results demonstrate that EM-

MILC reduces the average number of tests from 16 to 3, compared to the most accurate existing approach.

1 INTRODUCTION

Stroke is a leading cause of disability worldwide, with

over 12 million new cases each year (Feigin et al.,

2022). Approximately half of suffers are left with

some form of hand or upper limb impairment, which

signiﬁcantly impacts their quality of life (Persson

et al., 2012). Movement can be regained through con-

tinued repetitive practice of functional tasks, which

strengthens neural connections in the brain (Hebbian

learning (Hebb, 1949)). However, the level of support

provided by conventional physiotherapy is typically

inadequate (Stockley et al., 2019), and 62% of people

with severe impairment fail to regain dexterous hand

motion within six months (Kwakkel et al., 2003).

This motivates the use of assistive technologies,

the most common of which is functional electrical

stimulation (FES) (Hughes et al., 2014), in which

nerves are stimulated via surface electrodes to arti-

ﬁcially contract the underlying muscles. Hand move-

ment requires the coordinated motion of a large num-

ber of different muscles, which makes FES control

challenging. In recent years electrode arrays have en-

abled more selective stimulation of hand and wrist

https://orcid.org/0000-0001-6109-0546

https://orcid.org/0000-0003-0305-9246

https://orcid.org/0000-0001-7277-3895

muscles (Schill et al., 2009; Salchow et al., 2016;

O’Dwyer et al., 2006), with the best results arising

through use of iterative learning control (ILC) (Free-

man, 2014; Sun and Freeman, 2024). ILC utilises the

repetitive nature of rehabilitation to improve perfor-

mance by updating the control signal using data from

previous attempts. However, existing ILC approaches

require lengthy identiﬁcation procedures, meaning

they have not yet translated into clinical practice.

The need for model identiﬁcation can be mitigated

by fusing ILC with adaptive control. One adaptive

approach that has previously shown promise in the

context of FES is multiple model switched adaptive

control (MMSAC) (Brend et al., 2015), in which a set

of controllers are designed based on a set of system

models that capture the presumed uncertainty. The

framework determines which plant most closely ﬁts

the system behaviour at a given point in time, be-

fore switching the corresponding controller into the

closed-loop. The MMSAC framework was adapted

for use with ILC in (Freeman and French, 2015) to

create a framework termed estimation-based multiple

model ILC (EMMILC).

This work extends the EMMILC architecture for

use with a general class of non-linear systems. This

involves deﬁning a principled design framework for

speciﬁcation of the plant model set and controller

properties, together with a computationally efﬁcient

Hodgins, L., Freeman, C. and Belkhatir, Z.

Multiple Model Iterative Learning Control of FES Electrode Arrays.

DOI: 10.5220/0012892900003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 537-544

ISBN: 978-989-758-717-7; ISSN: 2184-2809

537

estimator structure to determine the controller switch-

ing. The EMMILC framework is then applied to con-

trol hand and wrist motion using an FES electrode

array. Experimental results compare it with the best

existing approach, and conﬁrm its practical efﬁcacy.

This paper is structured as follows. Section 2 in-

troduces the necessary background, including a com-

prehensive model of the hand and wrist stimulated by

an FES array, and an overview of ILC. The nonlin-

ear EMMILC framework is developed in Section 3,

and Section 4 applies it to FES array based hand and

wrist control. Experimental results are then presented

in Section 5 before Section 6 concludes the paper.

2 PROBLEM DESCRIPTION AND

PRELIMINARIES

FES electrode arrays are composed of n separate elec-

trodes pads, that are arranged in ﬁxed pattern. They

are typically printed on polycarbonate and have a hy-

drogel layer that is placed on the surface of the skin.

An FES sequence u(t) ∈ R

is applied to these elec-

trodes over time instances t = 0,1,...,N, and the aim

is to precisely assist the patient’s movement. This

is done by selecting a set of q clinically-relevant

joint angles y(t) ∈ R

and requiring they track a pre-

deﬁned reference signal trajectory y

(t) ∈ R

Since stroke rehabilitation requires repeated task

practice, each attempt or ‘iteration’ of a task is de-

noted by introducing an additional argument, with

variable k = 1,2,.... The control aim is to compute

input u(k,t) such that the error e(k,t) = y

(t)−y(k,t)

decreases with each sucessive iteration, i.e.

lim

k→∞

e(k,t) = 0, t = 0,1,...,N − 1. (1)

2.1 Hand and Wrist Structure

The dynamics of the electrically stimulated hand and

wrist consists of four key components: the electrode

array, the muscle dynamics, the non-linear tendon net-

work, and the rigid body dynamics. Their connection

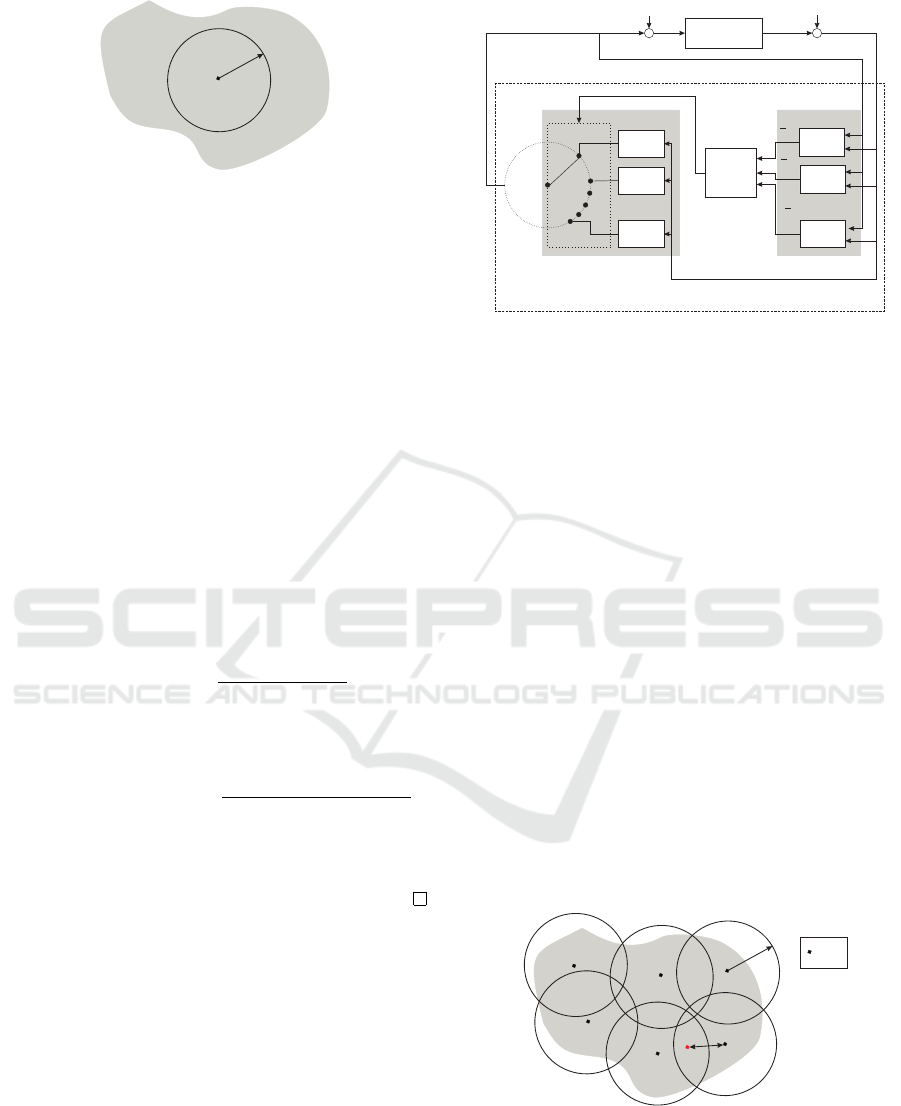
is shown in Figure 1, denoted using operator G

∗

IRC

LAD

Tendon

network

R(y)

Muscles

Rigid

Body

Dynamics

Electrode array

..............

...

}

Figure 1: Hand and wrist model structural components.

The stimulation experienced by the ith muscle can

be modelled as a linear combination of the FES ap-

plied to each element of the n channel electrode array.

The stimulation signal v(k,t) ∈ R

experienced by the

l underlying muscles therefore has elements

(k,t) =

∑

j=1

i, j

(k,t), i = 1,...,l (2)

where a

i, j

∈ R

is the contribution of the jth array

element to the ith muscle (Freeman et al., 2016).

The dynamics of the ith muscle can be accu-

rately modelled by a Hammerstein structure, com-

prising a static function h

IRC,i

(k,t)) which mod-

els the isometric recruitment curve (IRC), cascaded

with linear activation dynamics (LAD) (Le et al.,

2010). The latter are denoted by the state-space triple

A,i

B,i

C,i

} with state ˜x

(k,t). The generated

force F

(k,t) then feeds into a tendon network which

generates a moment about each joint angle. The

moment arm of the ith muscle about the pth joint

is computed using

)

where continuous function

E is the associated tendon excursion (Feldman and

Latash, 2005). Therefore the overall moment vec-

tor generated by stimulating all muscles is τ(k,t) =

R(y(k,t))F(k,t) where the (p,i)th element of moment

arm matrix R(y(k,t)) ∈ R

q×l

)

(k,t).

The moment vector actuates the passive rigid body

dynamics of the system which take the general form

M(y(k,t)) ¨y(k,t) +C(y(k,t), ˙y(k,t)) + G(y(k,t))

+ K(y(k,t), ˙y(k,t)) = τ(k,t) (3)

where M(·) denotes the inertia matrix, C(·,·) is the

Coriolis matrix, G(·) the gravity vector, and K(·,·)

captures joint stiffness, damping and friction effects.

Combining the above four components yields the

overall dynamic system

dx(k,t)







(k,t)

M(x

(k,t))

−1

X(x(k,t))

A,1

˜x

(k,t)

A,l

˜x

(k,t)













B,1

IRC,1

( ¯a

u(k,t))

B,l

IRC,l

( ¯a

u(k,t))







, (4)

y(k,t) =



I 0 ... 0



x(k,t) := h(x(k,t)), (5)

where state vector x(k,t) =

(k,t)

⊤

(k,t)

⊤

, ˜x

(k,t)

⊤

,··· , ˜x

(k,t)

⊤

]

⊤

and

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

538

output y(k,t) = [θ

(k,t),..., θ

(k,t)]

⊤

, with x

:= y,

:= ˙y. In addition, ¯a

= [a

i,1

,...,a

i,n

] and

X(x(k,t)) = R(x

(k,t))







C,1

˜x

(k,t)

C,l

˜x

(k,t)







− G(x

(k,t))

−C(x

(k,t),x

(k,t))− K(x

(k,t),x

(k,t)).

State-space system (4) is then discretised to give

x(k,t + 1) = f (x(k,t),u(k,t)), x(k, 0) = x

y(k,t) = h(x(k,t)), t = 0,1,...,N − 1.

(6)

2.2 ILC Background

Since stroke rehabilitation requires repeated move-

ments, ILC is a natural choice and has been used suc-

cessfully in ﬁve clinical trials (focusing on elbow and

shoulder motion) (Freeman, 2016). ILC is designed to

be applied to tasks carried out repeatedly, and uses er-

ror information from each previous iterations to suc-

cessively improve tracking performance.

To apply ILC, the system dynamics are efﬁciently

packaged using the ‘lifted’ supervector notation

u(k) = [u(k,0)

⊤

,u(k,1)

⊤

,...,u(k,N − 1)

⊤

]

⊤

, (7)

y(k) = [y(k,1)

⊤

,y(k,2)

⊤

,...,y(k,N)

⊤

]

⊤

, (8)

= [y

(1)

⊤

(2)

⊤

,...,y

(N)

⊤

]

⊤

, (9)

so that dynamics (6) can be equivalently written as

y(k) = g(u(k)), such that (10)

g(u(k)) = [g

(u(k))

⊤

,...,g

(u(k))

⊤

]

⊤

, (11)

with elements i = 1, 2,...,N given by

(x(k, 0),u(k,0),...,u(k,i − 1))

= h( f ( f (... f ( f (x(k,0),u(k,0)),u(k, 1)), ...

...,u(k,i − 2)),u(k,i − 1)))). (12)

The most common form of ILC update is

u(k + 1) = u(k) + Le(k), (13)

in which e(k) = y

− y(k) and L ∈ R

nN×qN

is a suit-

able learning operator. For linear systems there are

numerous options to design L to balance convergence

and robustness, and these have been extended to the

non-linear case by linearising the system between

each trial about its current operating point (Freeman,

2014; Lin et al., 2006). For example, when applied to

gradient-based ILC, the learning operator is given by

L = γ(g

′

(u(k)))

⊤

, (14)

The two-argument form u(k,t) will be used to denote

the along-the-trial form of a signal, with a single argument

denoting the lifted form.

where g

′

(u(k)) is the Jacobian of g(u(k)), given by

′

(u(k)) :=

∂g(u)

∂u



u=u(k)







∂g

(u)

∂u(k)

...

∂g

(u)

∂u(k)

∂g

(u)

∂u(k)

∂g

(u)

∂u(k)







(15)

2.3 Robust Stability of Standard ILC

Identifying g(u(k)) is exceptionally challenging due

to the complexity of the human hand, which is sensi-

tive to minor changes in electrode position and phys-

iology. It also varies signiﬁcantly between individu-

als, and over time due to fatigue. The approach used

by (Freeman, 2014) was to identify g

′

(u(k)) between

each iteration by carrying out an identiﬁcation test on

the patient, however this took over 10 minutes to track

a single reference movement, making it unsuitable for

practical use. One possible solution is to design L to

maximise robustness, potentially using a single nom-

inal model. The remainder of this section demon-

strates the limitations of such an approach.

Deﬁne G

∗

as a lifted operator representing the

true plant with the general dynamic form (10). De-

ﬁne C as the lifted operator corresponding to ILC

scheme (13). These are conﬁgured as shown in Fig-

ure 2, where the signals have been renamed to account

for the external disturbances (u

(k), y

(k))

⊤

. Hence

(k), y

(k)) denotes the plant input and output, and

(k), y

(k))

⊤

the ILC update and measured error

signals. The operators can then be deﬁned as

Figure 2: True plant and ILC feedback conﬁguration.

∗

: u

7→ y

, y

(k) = g(u

(k)), (16)

and

C : y

7→ u

, u

(k + 1) = u

(k) + L

(k).

(17)

Since the true plant is unknown, the designer only

has access to a non-linear model g

(u(k)), giving

: u

7→ y

, y

(k) = g

(k)), (18)

which is used to design a stabilising ILC law

: y

7→ u

, u

(k + 1) = u

(k) + L

k,p

(k),

(19)

Multiple Model Iterative Learning Control of FES Electrode Arrays

539

|| ||Π

Gp/Cp

-1

Figure 3: Uncertainty space showing stability region using

a single ILC update designed for model G

where L

k,p

is designed based on the linearisation (15)

of the model G

The difference between plant model G

and the

true system G

∗

can be captured by the well-known

gap metric, denoted δ(G

∗

), which is a bound on

a mapping between their graphs. Using this metric,

the following theorem lays out the conditions under

which C

is able to stabilise the true plant G

∗

Theorem 1. Let ILC update C

be designed such

that the closed-loop system [G

] is gain stable, i.e.

the map Π

//C

: (u

)

⊤

→ (u

)

⊤

from exter-

nal disturbances to internal signals has a ﬁnite bound.

Then the true closed-loop system [G

∗

] will be gain

stable if the model mismatch satisﬁes

δ(G

∗

) < ∥Π

//C

∥

−1

. (20)

Furthermore, the gap can be directly related to the

underlying vector function forms as

δ(G

∗

) ≤ sup

∥u∦=0

∥g

(u) − g

∗

(u)∥

∥u∥

, (21)

and if ILC is designed based on the sequence of lin-

earised models {g

′

(u(k))}

k∈N

, this equates to

δ(G

∗

) ≤ sup

k∈N, ∥u∦=0

∥(g

′

(u(k)) − g

∗

u(k)

)u∥

∥u∥

where g

∗

u(k)

u := g

∗

(u + u(k)) − g

∗

(u(k)).

Proof. Adapted from (Georgiou and Smith, 1997)

This states that ILC stabilises a ‘ball’ of plants

with radius ∥Π

//C

∥

−1

centred around G

, as

shown in Figure 3. However, if the model mismatch is

too large, this region may not include G

∗

and [G

∗

]

will be unstable. This motivates multiple-model ILC,

in which extra models and corresponding controllers

are added to stabilise any possible true plant.

3 EMMILC STRUCTURE

EMMILC builds on the more general multiple

model switched adaptive control (MMSAC) frame-

work (Buchstaller and French, 2016). This section

argmin

y+y

0 d

C X

...

EMMILC controller

Figure 4: EMMILC block diagram.

extends it for application to nonlinear systems. The

idea of EMMILC is to design a set of plant models

G = {G

,...,G

} with associated ILC controllers C =

,...,C

} such that a plant located anywhere within

a user-deﬁned uncertainty space U will be stabilised

by one of these controllers. Switching between con-

trollers is determined using a bank of estimators,

,...,X

, which compute a residual for each plant

model. Each residual measures how closely a par-

ticular model matches the measured signals (u

and the model with smallest residual is switched into

closed-loop. Figure 4 shows the overall structure.

Based on the underlying theory in (Freeman and

French, 2015), there are two conditions that must be

satisﬁed to guarantee overall stability:

(i)

∃ G

∈ G, s.t. δ(G

∗

) < ρ(G,C,U). (22)

(ii)

∃ C

∈ C , s.t. ∥Π

G//C

∥ < ∞ ∀G ∈ U. (23)

where ρ(·) is deﬁned in (Freeman and French, 2015).

These ensure that the models {G

,...,G

} are sufﬁ-

ciently close together, and that there exists a controller

within the set C able to stabilise all plants within the

uncertainty space, as illustrated in Figure 5.

|| ||Π

Gp/Cp

-1

< ( , , )ρ GCU

∈G

Figure 5: Model set requirements (22) and (23).

3.1 Estimator Design

Estimator X

: (u

)

⊤

7→ r

computes the smallest

disturbance estimate (u

) needed to explain the

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

540

observed signals (u

) under the assumption that

model G

is the true plant. Let N

[a,b]

p,k

) be

the set of all possible disturbances compatible with

and observed signals (u

(k), y

(k)) over iterations

a,a + 1, . ..,b. Then the residual is computed as

(k) := inf

{r ≥ 0 | r = ∥w

∥, w

∈ N

[0,k]

p,k

)}

(24)

The next theorem shows how this can be com-

puted recursively, and provides a computationally

tractable upper bound which can replace r

(k).

Theorem 2. Residual computation (24) can be solved

recursively using

(k) = ∥r

(k − 1),i

(k)∥, r

(0) = 0, (25)

where the residual calculation for only iteration k is

(k) = inf

{r ≥ 0 | r = ∥w

∥, w

∈ N

[k,k]

p,k

)}

(26)

Furthermore, i

(k) has the upper bound

∥y

(k) − g

(k))∥ (27)

so that an upper bound, ˜r

(k), can be computed as

˜r

(k) =

∑

i=0

∥y

(i) − g

(i))∥

(28)

Proof. Relations (25), (26) follows from the l

iden-

tify ∥∥x∥,∥y∥∥ = ∥(x, y)∥ for x, y ∈ l

, and the fact that

the dynamics of one ILC trial do not affect the next.

From Fig. 4, the signals compatible with G

satisfy

(k) = g

(k) + u

(k)) + y

(k). An upper bound

on (26) is achieved by setting u

= 0 to obtain

(k) ≤ inf

{r ≥ 0 | r = ∥w

∥, w

∈ N

[k,k]

p,k

)}

= inf

{r ≥ 0 | r =





(k)





= y

(k) − g

(k) + u

(k))},

= ∥y

(k) − g

(k))∥ (29)

and (28) follows by combining (29) and (25).

Remark 1. Lifted residual calculation (28) can be

modiﬁed to account for parameter variation, e.g. due

to muscle fatigue, by introducing a discount factor

0 ≤ λ < 1 such that

˜r

(k) =

∑

i=1

k−i

∥y

(i) − g

(i))∥

(30)

4 FRAMEWORK APPLICATION

EMMILC is now applied to FES array motion control.

4.1 EMMILC Design Procedure

The following steps outline the practical implementa-

tion of the EMMILC framework.

1. Model structure: Establish a suitable parame-

terised form to capture the true plant g

∗

(u).

2. Uncertainty space U: Identify the range in

model parameters necessary to capture the vari-

ation in the true dynamics. The set union is U.

3. Controller design procedure: Formulate an ILC

design procedure K : G

→ C

that stabilises the

closed-loop [G

]. This will balance conver-

gence with robustness, as measured by (20).

4. Model set G: Construct a model set G with cor-

responding controller set C to give sufﬁcient cov-

erage of the uncertainty space. Criteria (22) and

(23) can be combined into a single condition

∀ G

, ∃G

∈ G, G

̸= G

, s.t. δ(G

) < ∆,

(31)

where parameter ∆ deﬁnes the maximum distance

between neighbouring models. Smaller values

will improve the likelihood of a stable design but

will have a higher computational cost.

5. Estimator set: For each model, implement esti-

mator X

using (30). Tune λ to balance sensitivity

against adaptability to changing dynamics.

The following subsections apply this design frame-

work using the model form introduced in Section 2.1.

4.2 Speciﬁc Model Structure

The human hand and wrist contains 15 joints actu-

ated by over 20 muscles, however 42% of functional

movements involve only four ﬁngers moving in uni-

son (Ingram et al., 2008). Furthermore, the spastic-

ity commonly experienced by stroke patients makes

the extensor muscles a critical target for rehabilitation

(American Stroke Association, 2022). Therefore, the

model used in this work contains l = 4 extrinsic mus-

cles of the hand, namely the extensor communis (EC),

Extensor carpi radialis brevis (ECRB), Extensor indi-

cis (EI), and Extensor carpi ulnaris (ECU). The wrist

and metacarpophalangeal (MCP) joints were actively

controlled, and are deﬁned in Figure 6, resulting in

the output vector y(k,t) = [θ

(k,t),θ

(k,t)]

⊤

Stimulation was applied using a 6 × 4 element

electrode array (such as that used in (Freeman et al.,

2016)), giving a total of 24 elements. Preliminary

experiments revealed that all four muscles of inter-

est could be activated using only two electrode ele-

ments. The optimal location of these was determined

heuristically for each participant, and the pulse-width

Multiple Model Iterative Learning Control of FES Electrode Arrays

541

Finger

Thumb

Wrist

Figure 6: Joint angle deﬁnitions.

applied to these elements was used as the input to the

system, giving n = q = 2.

The IRC form was chosen as

= a

− 1

+ a

. (32)

which has been been shown to accurately capture

muscle dynamics using only a small number of pa-

rameters a

-a

(Freeman et al., 2009). Similarly,

the LAD were modelled as a second order, critically

damped system with natural frequency ω

The forms of M(y), C(y, ˙y), and R(y) were equiva-

lent to those given in (Theodorou et al., 2011), whilst

gravity was integrated within K(y, ˙y). This then as-

sumed a simple linear friction form, in which each

joint is represented as a spring with stiffness k

, damp-

ing b

, and zero elongation at the initial position θ

0,i

K(y, ˙y) =







(θ

0,1

− θ

) + b

(θ

0,q

− θ

) + b







. (33)

The physiological constraints of the joint were mod-

elled by increasing joint stiffness k as the angle θ ap-

proaches a cutoff value θ

cuto f f

. This is expressed by

(θ

) =

0.1k

n,i

(θ

thres,i

− θ

cuto f f ,i

)

− θ

cuto f f ,i

+ k

n,i

, i = 1,...,q

(34)

where k

n,i

is the nominal joint stiffness of joint i, and

thres,i

the threshold angle at which the stiffness be-

gins to increase. Implementation was simpliﬁed by

selecting a large value of T

and setting N = 1. In this

context the output y(k) represents the steady-state re-

sponse to input u(k). This approach has been used

previously in (Sun and Freeman, 2024), and is appli-

cable to the FES rehabilitation setting, in which dy-

namics are slow and the overall shape of the trajectory

is more important than the movement speed.

4.3 EMMILC Design

After establishing the model structure, the next step is

to deﬁne the uncertainty space U. Preliminary exper-

iments revealed that parameters k

, θ

0,i

, and θ

cuto f f ,i

i = {1, 2} had the most impact on model performance,

however, θ

0,i

and θ

cuto f f ,i

could be easily measured

experimentally (see Section 5). The joint stiffness k

0 0.5 1 1.5 2

0.5

1.5

Figure 7: Model set distribution, with key models labelled.

and k

were therefore selected to deﬁne the uncer-

tainty space, with bounds k

∈ [0.2,2] correspond-

ing to the range of values measured in (Park et al.,

2017). Preliminary experiments revealed that this was

a sufﬁcient range to cover possible parameter varia-

tion.

The control design procedure K was selected as

linearisation-based gradient ILC, as given by (13),

(14), due to its favourable robustness properties.

Preliminary tests were carried out in which EM-

MILC design parameters were tuned heuristically to

give optimal values of γ = 10,000, ∆ = 0.0007, and

λ = 0.4. Parameter γ was selected to ensure robust

convergence within 15 iterations, whilst ∆ was se-

lected as a trade-off between minimising computation

time (mean of 3.7s per trial) and ensuring stability.

The resulting model set distribution is shown in Fig-

ure 7. The low λ value allowed the system to quickly

adapt to unforeseen changes in system dynamics.

5 EXPERIMENTAL TESTING

Extensive simulation was ﬁrst undertaken using in-

silico data to demonstrate system feasibility. Results

are omitted for brevity but can be found online at

https://doi.org/10.5258/SOTON/D3186. Experimen-

tal tests were then carried out on four unimpaired par-

ticipants, following ethical approval from the Univer-

sity of Southampton (ERGO: FEPS 91636).

5.1 Method

Code was written in Matlab 2024a and deployed in

realtime onto a Raspberry Pi 3B. This provided PWM

outputs that were ampliﬁed using a 4-channel stim-

ulator (Odstock Medical Ltd, Salisbury UK), whilst

joint angles were recorded using a contactless motion-

capture sensor (Ultraleap Stereo IR 170). The setup

is shown in Figure 8.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

542

Figure 8: Experimental setup showing motion tracking.

Table 1: EMMILC and ID-based ILC performance.

Participant y

Error norm k

∗

ID-based [65.4,-9.8] 0.1065 13

EMMILC 0.0236 4

ID-based [79.9, -9.3] 0.3958 >24

EMMILC 0.1801 4

ID-based [80.2,-20.0] 0.2727 10

EMMILC 0.2304 2

ID-based [57.5, -7.7] 1.372 19

EMMILC 0.3141 2

For each participant a feasible reference was ﬁrst

determined, as given in Table 1, corresponding to a

pointing posture. The values of θ

were recorded as

the resting joint angles, before the maximum stim-

ulation pulsewidth (300µs, in accordance with FES

safety protocols) was applied to both channels, with

the resulting angles giving θ

cuto f f

. These values were

then used to deﬁne the model.

The performance of EMMILC was compared to

the best existing electrode array control approach, in

which the ILC algorithm employs a linearised model

that is identiﬁed between trials using tests on the

physical patient (Sun and Freeman, 2024). Each iter-

ation of identiﬁcation-based (ID-based) ILC requires

n + 1 tests (1 ILC update and n identiﬁcation tests).

5.2 Results

Table 1 compares the performance of EMMILC to

that of ID-based ILC, in terms of the error norm af-

ter 15 tests, deﬁned by

Error norm = ∥y

− y(15)∥

, (35)

and the number of iterations (denoted k

∗

) required for

the error to converge to 30% of its initial value.

This reveals that the average error norm over all

participants after 15 iterations is 65% lower when us-

ing EMMILC as compared with ID-based ILC, re-

quiring on average 13 fewer tests to converge.

Figure 9a gives an example of the convergence

of EMMILC and ID-based ILC for one participant,

demonstrating that EMMILC convergence requires

signiﬁcantly fewer tests. EMMILC switching is

shown in Figure 9b, which reveals that the algorithm

quickly switches to a stabilising model and stays there

for the remaining trials. The key models that the sys-

tem switches to are shown in Figure 7.

0 2 4 6 8 10 12 14

Iterations

0.2

0.4

0.6

0.8

1.2

1.4

Error norm

ID-based ILC

EMMILC

(a) Error convergence

0 5 10 15

Iteration

Selected model

(b) EMMILC switching

Figure 9: Example performance for participant 1.

6 CONCLUSIONS AND FUTURE

WORK

This paper has presented a novel approach to the con-

trol of electrode arrays using multiple-model iterative

learning control. It ﬁrst extended EMMILC for ap-

plication to nonlinear systems, and then developed

a transparent framework for the design of a suitable

model-set, estimator, and controller. It then demon-

strated the effectiveness of EMMILC in experiments

with unimpaired participants. These revealed that it

could reduce the average number of tests for con-

vergence by 13 compared to standard identiﬁcation-

based ILC algorithms.

Areas for future work include carrying out experi-

mental tests on stroke patients, increasing the number

of inputs in order to activate a carefully-chosen subset

of electrodes, and improving EMMILC performance

by increasing the dimension of the uncertainty space.

REFERENCES

American Stroke Association (2022). Let’s talk about spas-

ticity after stroke.

Brend, O., Freeman, C., and French, M. (2015). Multiple-

model adaptive control of functional electrical stimu-

lation. IEEE Transactions on Control Systems Tech-

nology, 23(5):1901–1913.

Buchstaller, D. and French, M. (2016). Robust stabil-

ity for multiple model adaptive control: Part i—the

Multiple Model Iterative Learning Control of FES Electrode Arrays

543

framework. IEEE Transactions on Automatic Control,

61(3):677–692.

Feigin, V. L., Brainin, M., Norrving, B., Martins, S., Sacco,

R. L., Hacke, W., Fisher, M., Pandian, J., and Lindsay,

P. (2022). World stroke organization (wso): Global

stroke fact sheet 2022. International journal of stroke.

Feldman, A. G. and Latash, M. (2005). Testing hypotheses

and the advancement of science: recent attempts to

falsify the equilibrium point hypothesis. Brain Res,

145(91–103).

Freeman, C. and French, M. (2015). Estimation based mul-

tiple model iterative learning control. In 2015 54th

IEEE Conference on Decision and Control (CDC),

pages 6070–6075.

Freeman, C., Hughes, A.-M., Burridge, J., Chappell, P.,

Lewin, P., and Rogers, E. (2009). A model of the up-

per extremity using fes for stroke rehabilitation. Jour-

nal of biomechanical engineering, 131:031011.

Freeman, C., Yang, K., Tudor, J., and Kutlu, M.

(2016). Feedback control of electrical stimulation

electrode arrays. Medical Engineering and Physics,

38(11):1185–1194.

Freeman, C. T. (2014). Electrode array-based electrical

stimulation using ILC with restricted input subspace.

Control Engineering Practice, 23:32–43.

Freeman, C. T. (2016). Control System Design for

Electrical Stimulation in Upper Limb Rehabilitation.

Springer International Publishing. Springer Interna-

tional Publishing.

Georgiou, T. T. and Smith, M. C. (1997). Robustness anal-

ysis of nonlinear feedback systems: An input–output

approach. IEEE Transactions on Automatic Control,

42(9):1200–1221.

Hebb, D. O. (1949). Organization of Behavior. Psychology

Press.

Hughes, A.-M., Burridge, J., Demain, S., Ellis-Hill, C.,

Meagher, C., Tedesco Triccas, L., Turk, R., and

Swain, I. (2014). Translation of evidence-based as-

sistive technologies into stroke rehabilitation: Users’

perceptions of the barriers and opportunities. BMC

health services research, 14:124.

Ingram, J., Kording, K., Howard, I., and Wolpert, D. (2008).

The statistics of natural hand movements. Experimen-

tal brain research. Experimentelle Hirnforschung. Ex-

périmentation cérébrale, 188:223–36.

Kwakkel, G., Kollen, B. J., van der Grond, J., and Prevo, A.

J. H. (2003). Probability of regaining dexterity in the

ﬂaccid upper limb: impact of severity of paresis and

time since onset in acute stroke. Stroke, 34 9:2181–6.

Le, F., Markovsky, I., Freeman, C. T., and Rogers, E.

(2010). Identiﬁcation of electrically stimulated mus-

cle models of stroke patients. Control Engineering

Practice, 18(4):396–407.

Lin, T., Owens, D., and Hatonen, J. (2006). Newton

method based iterative learning control for discrete

non-linear systems. International Journal of Control,

79(10):1263–1276.

O’Dwyer, S., O’Keeffe, D., Coote, S., and Lyons, G.

(2006). An electrode conﬁguration technique using

an electrode matrix arrangement for fes-based upper

arm rehabilitation systems. Medical Engineering &

Physics, 28(2):166–176.

Park, K., Chang, P.-H., and Kang, S. H. (2017). In vivo

estimation of human forearm and wrist dynamic prop-

erties. IEEE Transactions on Neural Systems and Re-

habilitation Engineering, 25(5):436–446.

Persson, H. c., Parziali, M., Danielsson, A., and Sunnerha-

gen, K. (2012). Outcome and upper extremity func-

tion within 72 hours after ﬁrst occasion of stroke in

an unselected population at a stroke unit. a part of the

salgot study. BMC neurology, 12:162.

Salchow, C., Valtin, M., Seel, T., and Schauer, T. (2016). A

new semi-automatic approach to ﬁnd suitable virtual

electrodes in arrays using an interpolation strategy.

European Journal of Translational Myology, 26(2).

Schill, O., Rupp, R., Pylatiuk, C., Schulz, S., and Reischl,

M. (2009). Automatic adaptation of a self-adhesive

multi-electrode array for active wrist joint stabiliza-

tion in tetraplegic sci individuals. In 2009 IEEE

Toronto International Conference Science and Tech-

nology for Humanity (TIC-STH), pages 708–713.

Stockley, R., Peel, R., Jarvis, K., and Connell, L. (2019).

Current therapy for the upper limb after stroke: a

cross-sectional survey of uk therapists. BMJ Open,

9(9).

Sun, X. and Freeman, C. T. (2024). Parameterised function

ILC with application to stroke rehabilitation. Control

Engineering Practice, 145.

Theodorou, E., Todorov, E., and Valero-Cuevas, F. J.

(2011). Neuromuscular stochastic optimal control

of a tendon driven index ﬁnger model. In Proceed-

ings of the 2011 American Control Conference, page

348–355. IEEE.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

544