Efficient Neural Network Training via Subset Pretraining
Jan Sp
¨
orer
1,∗ a
, Bernhard Bermeitinger
2,∗ b
, Tomas Hrycej
1,∗
, Niklas Limacher
1,∗∗
and Siegfried Handschuh
1,∗ c
1
Institute of Computer Science, University of St.Gallen (HSG), St.Gallen, Switzerland
2
Institute of Computer Science in Vorarlberg, University of St.Gallen (HSG), Dornbirn, Austria
∗ ∗∗
Keywords:
Deep Neural Network, Convolutional Network, Computer Vision, Efficient Training, Resource Optimization,
Training Strategies, Overdetermination Ratio, Stochastic Approximation Theory.
Abstract:
In training neural networks, it is common practice to use partial gradients computed over batches, mostly
very small subsets of the training set. This approach is motivated by the argument that such a partial gradient
is close to the true one, with precision growing only with the square root of the batch size. A theoretical
justification is with the help of stochastic approximation theory. However, the conditions for the validity of
this theory are not satisfied in the usual learning rate schedules. Batch processing is also difficult to combine
with efficient second-order optimization methods. This proposal is based on another hypothesis: the loss
minimum of the training set can be expected to be well-approximated by the minima of its subsets. Such
subset minima can be computed in a fraction of the time necessary for optimizing over the whole training set.
This hypothesis has been tested with the help of the MNIST, CIFAR-10, and CIFAR-100 image classification
benchmarks, optionally extended by training data augmentation. The experiments have confirmed that results
equivalent to conventional training can be reached. In summary, even small subsets are representative if the
overdetermination ratio for the given model parameter set sufficiently exceeds unity. The computing expense
can be reduced to a tenth or less.
1 INTRODUCTION
Neural networks as forecasting models learn by fit-
ting the model forecast to the desired reference out-
put (e.g., reference class annotations) given in the data
collection called the training set. The fitting algorithm
changes model parameters in the loss function’s de-
scent direction, measuring its forecast deviation. This
descent direction is determined using the loss function
gradient.
The rapidly growing size of neural networks (such
as those used for image or language processing) mo-
tivates striving for a maximum computing economy.
One widespread approach is determining the loss
function gradient from subsets of the training set,
called batches (or mini-batches). Different batches
are alternately used to cover the whole training set
during the training.
There are some arguments supporting this proce-
dure. (Goodfellow et al., 2016, Section 8.1.3) refers
a
https://orcid.org/0000-0002-9473-5029
b
https://orcid.org/0000-0002-2524-1850
c
https://orcid.org/0000-0002-6195-9034
to the statistical fact that random standard deviation
decreases with the square root of the number of sam-
ples. Consequently, the gradient elements computed
from a fraction of
1
/K training samples (with a given
positive integer K) have a standard deviation equal to
the factor
√
K multiple of those computed over the
whole training set, which seems to be a good deal.
Another frequent justification is with the help of
stochastic approximation theory. The stochastic ap-
proximation principle applies when drawing training
samples from a stationary population generated by a
fixed (unknown) model. (Robbins and Monro, 1951)
discovered this principle in the context of finding the
root (i.e., the function argument for which the func-
tion is zero) of a function g(x) that cannot be directly
observed. What can be observed are randomly fluc-
tuating values h(x) whose mean value is equal to the
value of the unobservable function, that is,
E [h(x)] = g(x) (1)
The task is to fit an input/output mapping to data
by gradient descent. For the parameter vector w of
this mapping, the mean of the gradient h(w) with re-
spect to the loss function computed for a single train-
242
Spörer, J., Bermeitinger, B., Hrycej, T., Limacher, N. and Handschuh, S.
Efficient Neural Network Training via Subset Pretraining.
DOI: 10.5220/0012893600003838
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 242-249
ISBN: 978-989-758-716-0; ISSN: 2184-3228
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

ing sample is expected to be equal to the gradient g(w)
over the whole data population. The local minimum
of the loss function is where the gradient g(w) (i.e.,
the mean value of h(w)) is zero. (Robbins and Monro,
1951) have proven that, under certain conditions, the
root is found with probability one (but without a con-
crete time upper bound).
However, this approach has some shortcomings.
For different batches, the gradient points in different
directions. So, the descent for one batch can be an
ascent for another. To cope with this, (Robbins and
Monro, 1951) formulated the convergence conditions.
They require that if the update rule for the parameter
vector is
w
t+1
= w
t
−c
t
h(w
t
) (2)
which corresponds to the usual gradient descent with
step size c
t
, the step size sequence c
t
has to satisfy the
following conditions:
∞
∑
t=1
c
t
= ∞ (3)
and
∞
∑
t=1
c
2
t
< ∞ (4)
Condition Eq. (3) is necessary for the step not to
vanish prematurely before reaching the optimum with
sufficient precision. Condition Eq. (4) provides for
decreasing step size. With a constant step size, the so-
lution would infinitely fluctuate around the optimum.
This is because, in the context of error minimization,
its random instance h(w) will not diminish for indi-
vidual samples, although the gradient g(w) = E[h(x)]
will gradually vanish as it approaches the minimum.
Finally, the gradients of individual samples will not
vanish even if their mean over the training set is zero.
At the minimum, g(w) = 0 will result from a balance
between individual nonzero vectors h(w) pointing to
various directions.
2 SHORTCOMINGS OF THE
BATCH ORIENTED APPROACH
The concept of gradient determination using a subset
of the training set is mostly satisfactory. However,
several deficiencies from theoretical viewpoints sug-
gest an enhancement potential.
2.1 Violating the Conditions of the
Stochastic Approximation
The conditions Eq. (3) and Eq. (4) for convergence
of the stochastic approximation procedure to a global
(or at least local) minimum result from the stochas-
tic approximation theory. Unfortunately, they are al-
most always neglected in the neural network train-
ing practice. This may lead to a bad convergence (or
even divergence). The common Stochastic Gradient
Descent (SGD) with a fixed learning step size vio-
lates the stochastic approximation principles. How-
ever, even popular sophisticated algorithms do not
satisfy the conditions. The widespread (and success-
ful) Adam (Kingma and Ba, 2015) optimizer uses a
weight consisting of the quotient of the exponential
moving average derivative and the exponential mov-
ing average of the square of the derivative
w
t+1,i
= w
t,i
−
cm
t,i
p
d
t,i
∂E (w
t,i
)
∂w
t,i
m
t,i
= β
1
d
t−1,i
+ (1 −β
1
)
∂E (w
t−1,i
)
∂w
t−1,i
d
t,i
= β
2
d
t−1,i
+ (1 −β
2
)

∂E (w
t−1,i
)
∂w
t−1,i

2
(5)
with metaparameters c, β
1
, and β
2
, network weights
w
t,i
, and the loss function E. β
1
is the decay factor
of the exponential mean of the error derivative, β
2
is
the decay factor of the square of the error derivative,
and c is the step length scaling parameter. Their val-
ues have been set to the framework’s sensible defaults
c = 0.001, β
1
= 0.9, and β
2
= 0.999 in the following
computing experiments.
Normalizing the gradient components by the mov-
ing average of their square via
p
d
t,i
is the opposite of
the decreasing step size required in the stochastic ap-
proximation theory. If the gradient becomes small (as
expected at the proximity of the minimum), the nor-
malization increases them. This may or may not be
traded off by the average gradient m
t,i
.
2.2 “Good” Approximation of Gradient
Is not Sufficient
The quoted argument of (Goodfellow et al., 2016,
Section 8.1.3) that the standard deviations of gradi-
ent components are decreasing with the square root
√
K of number of samples used while the computing
expense is increasing with K is, of course, accurate
for independent samples drawn from a population.
However, this relationship is only valid if the
whole statistical population (from which the training
set is also drawn) is considered. This does not account
for the nature of numerical optimization algorithms.
The more sophisticated among them follow the de-
scent direction. The gradient’s statistical deviation is
relatively small with respect to the statistical popula-
tion, but this does not guarantee that a so-determined
Efficient Neural Network Training via Subset Pretraining
243

estimated descent direction is not, in fact, an ascent
direction. The difference between descent and ascent
may easily be within the gradient estimation error —
the batch-based gradient is always a sample estimate,
with standard deviation depending on the unknown
variance of the individual derivatives within the train-
ing set. By contrast, optimizing over the training set
itself, the training set gradient is computed determin-
istically, with zero deviation. Then, the descent direc-
tion is certain to lead to a decrease in loss.
The explicit task of the optimization algorithm is
to minimize the loss over the training set. If the goal
of optimizing over the whole (explicitly unknown)
population is adopted, the appropriate means would
be biased estimates that can have lower errors over the
population, such as ridge regression for linear prob-
lems (van Wieringen, 2023). The biased estimate the-
ory provides substantial results concerning this goal
but also shows that it is difficult to reach because of
unknown regularization parameters, which can only
be determined with computationally expensive exper-
iments using validation data sets.
Even if the loss is extended with regularization
terms to enhance the model’s performance on the
whole population (represented by a validation set), the
optimized regularized fit is reached at the minimum of
the extended loss function once more over the given
training set. Thus, as mentioned above, it is incorrect
from the optimization algorithm’s viewpoint to com-
pare the precision of the training set gradient with that
of the batches, which are subsamples drawn from the
training set. The former is precise, while the latter are
approximations.
The related additional argument frequently cited
is that what is genuinely sought is the minimum for
the population and not for the training set. However,
this argument is somewhat misleading. There is no
method for finding the true, exact minimum for the
population only based on a subsample such as the
training set — the training set is the best and only
information available. Also, the loss function val-
ues used in the algorithm to decide whether to accept
or reject a solution are values for the given training
set. Examples in (Hrycej et al., 2023) show that no
law guarantees computing time savings through in-
cremental learning for the same performance.
2.3 Convexity Around the Minimum Is
not Exploited
Another problem is that in a specific environment of
the local minimum, every smooth function is con-
vex — this directly results from the minimum defi-
nition. Then, the location of the minimum is not de-
termined solely by the gradient; the Hessian matrix
also captures the second derivatives. Although using
an explicit estimate of the Hessian is infeasible for
large problems with millions to billions of parame-
ters, there are second-order algorithms that exploit the
curvature information implicitly. One of them is the
well-known conjugate gradient algorithm (Hestenes
and Stiefel, 1952; Fletcher and Reeves, 1964), thor-
oughly described in (Press et al., 1992), which re-
quires only the storage of an additional vector with
a dimension equal to the length of the plain gradi-
ent. However, batch sampling substantially distorts
the second-order information more than the gradi-
ent (Goodfellow et al., 2016). This leads to a con-
siderable loss of efficiency and convergence guaran-
tee of second-order algorithms, which is why they are
scarcely used in the neural network community, pos-
sibly sacrificing the benefits of their computing effi-
ciency.
Second-order algorithms cannot be used with the
batch scheme for another reason. They are usually de-
signed for continuous descent of loss values. Reach-
ing a specific loss value with one batch cannot guar-
antee that this value will not become worse with
another batch. This violates some assumptions for
which the second-order algorithms have been devel-
oped. Mediocre computing results with these algo-
rithms in the batch scheme seem to confirm this hy-
pothesis.
3 SUBSTITUTING THE
TRAINING SET BY A SUBSET
To summarize the arguments in favor of batch-
oriented training, the batch-based procedure is justi-
fied by the assumption that the gradients for individ-
ual batches are roughly consistent with the gradient
over the whole training set (epoch). So, a batch-based
improvement is frequently enough (but not always,
depending on the choice of the metaparameters) also
an improvement for the epoch. This is also consistent
with the computing experience record. On the other
hand, one implicitly insists on optimizing over the
whole training set to find an optimum, as one batch
is not expected to represent the training set fully.
Batch-oriented gradient optimization hypothe-
sizes that the batch-loss gradient approximates the
training set gradient and the statistic population gra-
dient well enough.
By contrast, the hypothesis followed here is re-
lated but essentially different. It is assumed that the
optimum of the loss subset is close to the optimum of
the training set.
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
244

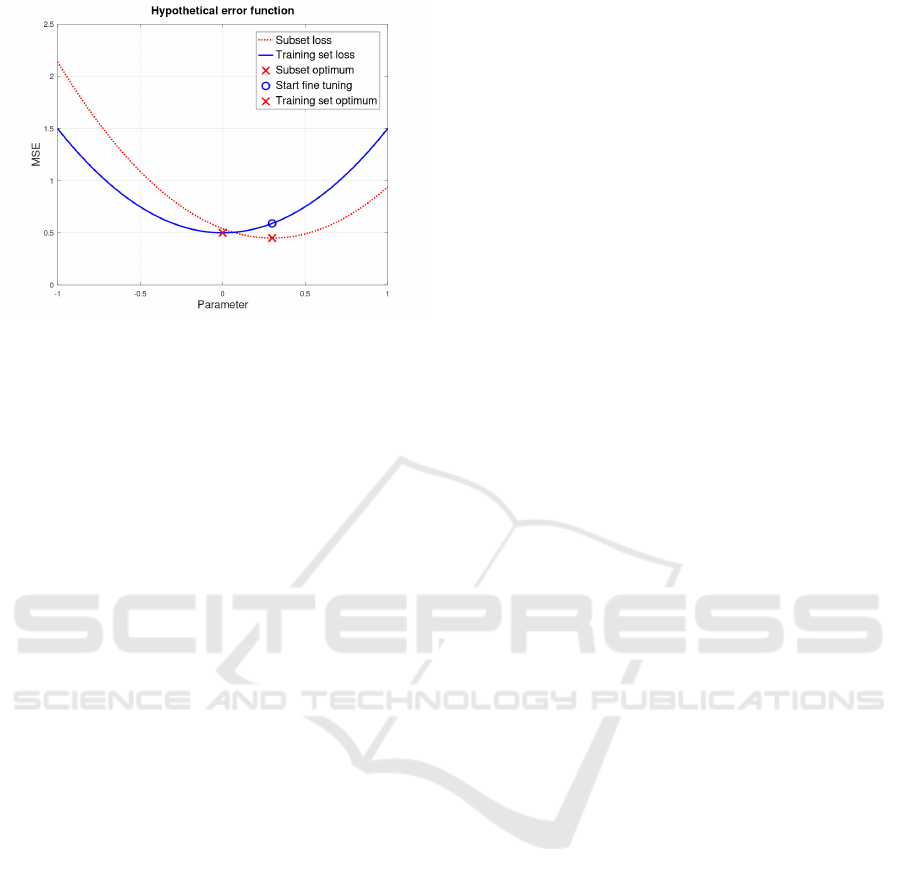
Figure 1: Optima for a subset and the whole training set.
Even if the minimum approximation is imperfect,
it can be expected to be a very good initial point for
fine-tuning the whole training set so that a few iter-
ations may suffice to reach the true minimum. This
principle is illustrated in Fig. 1. The subset loss func-
tion (red, dotted) is not identical to the training set
loss function (blue, solid). Reaching the minimum
of the subset loss function (red cross) delivers an ini-
tial point for fine-tuning on the training set (blue cir-
cle). This initial point is close to the training set loss
minimum (blue cross) and is very probably within a
convex region around the minimum. This motivates
using fast second-order optimization methods such as
the conjugate gradient method (Press et al., 1992).
Another benefit of such a procedure is that for a
fixed subset, both the gradient and the intermediary
loss values are exact. This further justifies the use of
second-order optimization methods.
Of course, the question is how large the subset has
to be for the approximation to be sufficiently good.
As previously noted, a smooth function is always lo-
cally convex around a minimum. If the approximate
minimum over the training subset is in this environ-
ment, conditions for efficient minimization with the
help of second-order algorithms are satisfied. Then,
a fast convergence to the minimum over the whole
training set can be expected.
Consequently, it would be desirable for the mini-
mum of the subset loss to be within the convex region
of the training set loss.
4 SETUP OF COMPUTING
EXPERIMENTS
The following computing experiments investigate
the support of these hypotheses. The experimental
method substitutes the training set with representative
subsamples of various sizes. Subsequently, a short
fine-tuning on the whole training set has been per-
formed to finalize the optimum solution. The model
is trained on the subsamples for exactly 1,000 epochs,
while the fine-tuning on the whole training set is lim-
ited to 100 epochs.
4.1 Benchmark Datasets Used
The benchmarks for the evaluation have been cho-
sen from the domain of computer vision. They are
medium-sized problems that can be run for a suffi-
cient number of experiments. This would not be pos-
sible with large models such as those used in language
modeling.
For the experiments, three well-known image
classification datasets MNIST (LeCun et al., 1998),
CIFAR-10, and CIFAR-100 (Krizhevsky, 2009) were
used. MNIST contains grayscale images of handwrit-
ten digits (0–9) while CIFAR-10 contains color im-
ages of exclusively ten different mundane objects like
“horse”, “ship”, or “dog”. CIFAR-100 contains the
same images; however, they are classified into 100
fine-grained classes. They contain 60,000 (MNIST)
and 50,000 (CIFAR-10 and CIFAR-100) training ex-
amples. Their respective preconfigured test split of
each 10,000 examples are used as validation sets.
While both CIFAR-10 and CIFAR-100 are evenly dis-
tributed among the classes, MNIST is roughly evenly
distributed. We opted to proceed without mitigating
the slight class imbalance.
4.2 The Model Architecture
The model is a convolutional network inspired by the
VGG architecture (Simonyan and Zisserman, 2015).
It uses three consecutive convolutional layers with
the same kernel size of 3 ×3, 32/64/64 filters, and
the ReLU activation function. Each is followed by a
maximum pooling layer of size 2 ×2. The last fea-
ture map is flattened, and after a classification block
with one layer of 64 units and the ReLU activation
function, a linear dense layer classifies it into a soft-
max vector. All trainable layers’ parameters are ini-
tialized randomly from the Glorot uniform distribu-
tion (Glorot and Bengio, 2010) with a unique seed
per layer such that all trained models throughout the
experiments have an identical starting point. The bi-
ases of each layer are initialized by zeros. The num-
ber of parameters for the models differs only because
MNIST has one input channel, while CIFAR-10 and
CIFAR-100 have three, and CIFAR-100 has 100 class
output units instead of 10.
Efficient Neural Network Training via Subset Pretraining
245

4.3 Preventing Underdetermination of
Model Parameters
An important criterion is that the training set size is
sufficient for this procedure. The size of the training
subsets (as related to the number of model parame-
ters) must be large enough for the model not to be
underdetermined. This should be true for most of the
subsets tested so that we can fairly compare subsets
that are a relatively small fraction of the training set.
As a criterion for this, the overdetermination ratio of
each benchmark candidate has been evaluated (Hrycej
et al., 2023):
Q =
KM
P
(6)
with K being the number of training examples, M be-
ing the output vector length (usually equal to the num-
ber of classes), and P being the number of trainable
model parameters.
This formula justifies itself by ensuring that the
numerator KM equals the number of constraints to be
satisfied (the reference values for all training exam-
ples). This product must be larger than the number of
trainable parameters for the system to be sufficiently
determined. (Otherwise, there are infinite solutions,
most of which do not generalize.) This is equivalent
to the requirement for the overdetermination ratio Q
to be larger than unity. It is advisable that this is sat-
isfied for the training set subsets considered, although
subsequent fine-tuning on the whole training set can
“repair” a moderate underdetermination.
The two datasets MNIST and CIFAR-10 have ten
classes. This makes the number of constraints KM
in Eq. (6) too small for subsets with b > 4. This
is why these two datasets have been optionally ex-
panded by image augmentation. This procedure im-
plies slight random rotations, shifts, and contrast vari-
ations. So, the number of training examples has been
increased tenfold by augmenting the training data.
With CIFAR-100 containing 100 classes, this prob-
lem does not occur, and it was not augmented.
4.4 Processing Steps
The processing steps for every given benchmark task
and a tested algorithm have been the following:
• The number of subsets b such that a subset is
the fraction
1
/b of the training set has been de-
fined. These numbers have been: b ∈ B with
B =
{
2,4,8, 16,32,64,128
}
. With a training set
size K, a subset contains
K
/b samples. For exam-
ple, a value of b = 2 results in a subset with half
of the samples from the original training set.
• All b subsets of size
K
/b have been built to sup-
port the results statistically. Each subset B
bi
,i =
1,... ,b, consists of training samples with index
i selected so that the subsets partition the entire
training set. The number of experiments is exces-
sive for larger values of b, so only five random
subsets are selected. All randomness is seeded
such that each experiment receives the same sub-
set.
• For every b ∈ B and every i = 1,.. . ,b, the sub-
set loss E
bi
has been minimized using the selected
training algorithm. The number of epochs has
been set to 1,000. Additionally, the losses for
the whole training set (E
BT bi
) and validation set
(E
BV bi
) have been evaluated. Subsequently, a fine-
tuning on the whole training set for 100 epochs
has been performed, and the metrics for the train-
ing set (E
T bi
) and validation set (E
V bi
) have been
evaluated. In summary, the set of loss character-
istics E
bi
, E
BT bi
, E
BV bi
, E
T bi
, and E
V bi
have repre-
sented the final results.
• For comparison, the typical training on the origi-
nal training set is given by choosing b = 1.
The conjugate gradient algorithm would be the fa-
vorite for optimizing the subset (because of its rela-
tively small size) and fine-tuning (because of its ex-
pected convexity in the region containing the initial
point delivered by the subset training). Unfortunately,
this algorithm is unavailable in deep learning frame-
works like Keras. This is why the popular Adam algo-
rithm has been used. For reproducibility and remov-
ing additional hyperparameters, a fixed learning rate
of 0.001 was employed for all training steps.
5 RESULTS
5.1 Dataset MNIST
The results for the non-augmented MNIST dataset are
depicted in Figs. 2 and 3. The training has two phases:
1. the subset training phase, in which only a fraction
of the training set is used; and
2. the fine-tuning phase, in which the optimized pa-
rameters from the subset training phase are fine-
tuned by a (relatively short) training over the
whole training set.
On the x-axis, fractions of the complete training set
are shown as used for the subset training. The axis is
logarithmic, so the variants are equally spaced. These
are
1
/2,
1
/4,
1
/8,
1
/16,
1
/32,
1
/64, and
1
/128, as well as the
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
246

baseline (fraction equal to unity). This baseline cor-
responds to the conventional training procedure over
the full training set.
The plotted magnitudes in Figs. 2 and 3 refer to
• the loss or accuracy reached for the given subset
(Subset pre-training);
• the loss or accuracy over the whole training set in
the subset training optimum (Tr.set pre-training);
• the loss or accuracy over the validation set in the
subset training optimum (Valid.set pre-training);
• the loss or accuracy over the whole training set at-
tained through fine-tuning (Tr.set fine-tuning); and
• the loss or accuracy over the validation set in the
fine-tuning optimum (Valid.set fine-tuning).
All of them are average values over the individual
runs with disjoint subsets.
The dotted vertical line marks the subset fraction
with overdetermination ratio Eq. (6) equal to unity. To
the left of this line, the subsets are underdetermined;
to the right, they are overdetermined.
Both loss (Fig. 2) and accuracy (Fig. 3) suggest
similar conjectures:
• The subset training with small subsets leads to
poor training set and validation set losses. This
gap diminishes with the growing subset fraction.
• Fine-tuning largely closes the gap between the
training and validation sets. The optimum value
for the training set tends to be lower for large frac-
tions (as they have an “advance” from the subset
training, but this does not lead to a better valida-
tion set performance. The baseline loss (the right-
most point) exhibits the highest validation set loss.
The overdetermination ratio delivers, together with
the mentioned vertical lines in Fig. 2 and Fig. 3, an
additional finding: The gap between the performance
on the subset and on the whole training set after the
subset training is very large for Q < 1 (the left side of
the plot) and shrinks for Q > 1 (the right side).
The results for the augmented data are depicted in
the plots Fig. 4 and Fig. 5. As the augmented data
are more challenging to fit, their performance char-
acteristics are generally worse than those of the non-
augmented dataset. However, an important point can
be observed: the performance after the pre-training
(particularly for the validation set) does not differ to
the same extent as it did with non-augmented data.
As with the non-augmented dataset, the baseline loss
(the rightmost point) exhibits the highest validation
set loss. There, the difference between the lowest and
the highest subset losses has been tenfold, while it is
roughly the same for all subset fractions with the aug-
mented data.
Figure 2: Dataset MNIST (not augmented), loss optima for
a pre-trained subset and the whole training set in depen-
dence from the subset size (as a fraction of the training set).
Figure 3: Dataset MNIST (not augmented), accuracy op-
tima for a pre-trained subset and the whole training set in
dependence from the subset size (as a fraction of the train-
ing set).
Figure 4: Dataset MNIST (augmented), loss optima for a
pre-trained subset and the whole training set in dependence
from the subset size (as a fraction of the training set).
The ten times larger size of the augmented dataset
leads to overdetermination ratios Q mostly (except for
the fraction
1
/128) over unity. Then, even the small-
fraction subsets generalize acceptably (which is the
goal of sufficient overdetermination).
Efficient Neural Network Training via Subset Pretraining
247

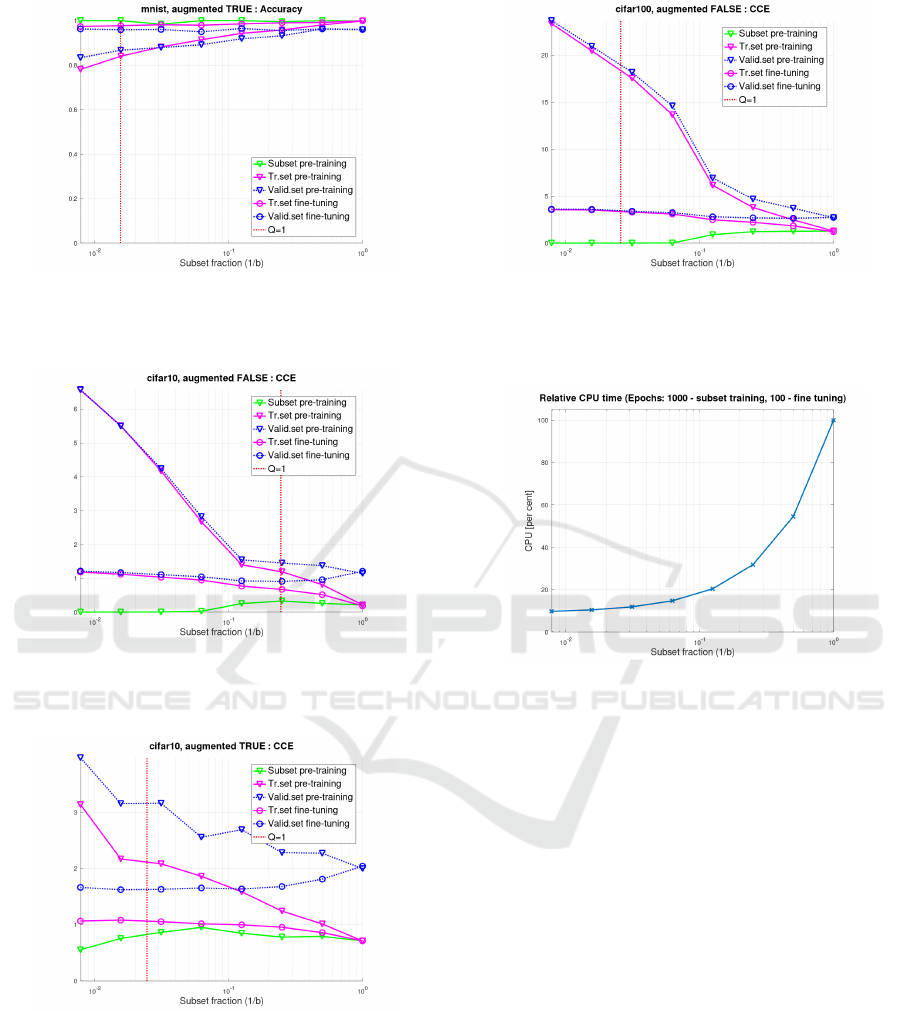
Figure 5: Dataset MNIST (augmented), accuracy optima
for a pre-trained subset and the whole training set in depen-
dence from the subset size (as a fraction of the training set).
Figure 6: Dataset CIFAR-10 (non-augmented), loss optima
for a pre-trained subset and the whole training set in depen-
dence from the subset size (as a fraction of the training set).
Figure 7: Dataset CIFAR-10 (augmented), loss optima for a
pre-trained subset and the whole training set dependent on
the subset size (as a fraction of the training set).
5.2 Dataset CIFAR-10
The results for non-augmented CIFAR-10 data are de-
picted in Fig. 6, those for augmented data in Fig. 7.
Due to the size of CIFAR-10 being close to MNIST,
the overdetermination ratios are also very similar.
Figure 8: Dataset CIFAR-100 (non-augmented), loss op-
tima for a pre-trained subset and the whole training set in
dependence from the subset size (as a fraction of the train-
ing set).
Figure 9: Training time relative to the conventional training
in dependence from the subset size (in percent).
Since CIFAR-10 is substantially harder to classify,
losses and accuracies are worse.
The accuracy is a secondary characteristic (since
the categorical cross-entropy is minimized), and its
explanatory power is limited. For this and the
space reasons, accuracies will not be presented for
CIFAR-10 and CIFAR-100.
Nevertheless, the conclusions are similar to those
from MNIST. The gap between the subset’s and the
entire training set’s fine-tuning performance dimin-
ishes as the subset grows. This gap is large with non-
augmented data in Fig. 6 because of low to overde-
termination ratios Q but substantially smaller for aug-
mented data in Fig. 7 where overdetermination ratios
are sufficient. The verification set performance after
both training phases is typically better with subsets of
most sizes than with the whole training set.
5.3 Dataset CIFAR-100
The results for (non-augmented) CIFAR-100 data are
depicted in Fig. 8. This classification task differen-
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
248

tiates 100 classes so that there are only 500 exam-
ples per class. Optimum losses for this benchmark
are higher than for the previous ones.
For small subset fractions, the representation of
the classes is probably insufficient. This may explain
the large gap between the subset loss and the train-
ing set loss after the subset training with small subset
fractions. These may contain, on average, even as few
examples per class as four. Nevertheless, the loss for
the validation set with various subset sizes is close to
the baseline loss for the conventional full-size train-
ing.
6 CONCLUSION
The experiments presented support the concept of
subset training. We demonstrated the following ele-
ments.
• The subset training leads to results comparable
with conventional training over the whole training
set.
• The overdetermination ratio Q (preferably above
unity) should determine the subset size. Never-
theless, even underdetermined subsets may lead to
a good fine-tuning result, although they put more
workload on the fine-tuning (to close the large
generalization gap).
• To summarize, even small subsets can be repre-
sentative enough to approximate the training set
loss minimum well whenever the overdetermina-
tion ratio sufficiently exceeds unity.
The most important achievement is the reduction of
computing expenses. Most optimizing iterations are
done on the subset, where the computational time per
epoch is a fraction of that for the whole training set. In
our experiments with ten times more subset training
epochs than fine-tuning epochs, the relative comput-
ing time in percent of the baseline is shown in Fig. 9.
Computational resource savings of 90 % and more are
possible.
This empirical evaluation using five benchmarks
from the CV domain is insufficient for making gen-
eral conclusions. Large datasets such as ImageNet
are to be tested in the future. They have been omit-
ted because many experiments are necessary to pro-
duce sufficient statistics. Furthermore, these experi-
ments can be extended to language benchmarks and
language models.
It is also important to investigate the behavior
of the second-order optimization algorithms such
as conjugate gradient (Hestenes and Stiefel, 1952;
Fletcher and Reeves, 1964). Their strength can de-
velop only with a sufficient number of iterations. This
is an obstacle if very large training sets are a part of
the task. Appropriately chosen subsets can make such
training feasible and help to reach good performance
even with models of moderate size.
REFERENCES
Fletcher, R. and Reeves, C. M. (1964). Function minimiza-
tion by conjugate gradients. The Computer Journal,
7(2):149–154.
Glorot, X. and Bengio, Y. (2010). Understanding the diffi-
culty of training deep feedforward neural networks. In
Proceedings of the 13th International Conference on
Artificial Intelligence and Statistics, volume 9, pages
249–256, Sardinia, Italy. PMLR.
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep
Learning. Adaptive computation and machine learn-
ing. The MIT Press, Cambridge, Massachusetts.
Hestenes, M. R. and Stiefel, E. (1952). Methods of conju-
gate gradients for solving linear systems, volume 49.
NBS Washington, DC.
Hrycej, T., Bermeitinger, B., Cetto, M., and Handschuh,
S. (2023). Mathematical Foundations of Data Sci-
ence. Texts in Computer Science. Springer Interna-
tional Publishing, Cham.
Kingma, D. P. and Ba, J. (2015). Adam: A Method for
Stochastic Optimization. 3rd International Confer-
ence on Learning Representations.
Krizhevsky, A. (2009). Learning Multiple Layers of Fea-
tures from Tiny Images. Dataset, University of
Toronto.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).
Gradient-based learning applied to document recogni-
tion. Proceedings of the IEEE, 86(11):2278–2324.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flan-
nery, B. P. (1992). Numerical recipes in C (2nd ed.):
the art of scientific computing. Cambridge University
Press, USA.
Robbins, H. and Monro, S. (1951). A Stochastic Approx-
imation Method. Annals of Mathematical Statistics,
22(3):400–407. 3515 citations (Crossref) [2021-08-
17].
Simonyan, K. and Zisserman, A. (2015). Very Deep Con-
volutional Networks for Large-Scale Image Recogni-
tion. ICLR.
van Wieringen, W. N. (2023). Lecture notes on ridge re-
gression. arXiv:1509.09169 [stat].
Efficient Neural Network Training via Subset Pretraining
249