Optimizing Small-Scale Surgery Scheduling with Large Language
Model
Fang Wan
1a
, Julien Fondrevelle
1b
, Tao Wang
2c
, Kezhi Wang
3d
and Antoine Duclos
4e
1
INSA LYON, Université Lyon2, Université Claude Bernard Lyon1, Université Jean Monnet Saint-Etienne, DISP UR4570,
Villeurbanne, France
2
Université Jean Monnet Saint-Etienne, INSA LYON, Université Lyon2, Université Claude Bernard Lyon, DISP UR4570,
Roanne, France
3
Department of Computer Science, Brunel University London, Uxbridge, Middlesex, U.K.
4
Research on Healthcare Performance RESHAPE, INSERM U1290, Université Claude Bernard, Lyon 1, France
Keywords: Surgery Scheduling, Large Language Model, Combinatorial Optimization, Multi-Objective.
Abstract: Large Language Model (LLM) have recently been widely used in various fields. In this work, we apply LLMs
for the first time to a classic combinatorial optimization problem—surgery scheduling—while considering
multiple objectives. Traditional multi-objective algorithms, such as the Non-Dominated Sorting Genetic
Algorithm II (NSGA-II), usually require domain expertise to carefully design operators to achieve satisfactory
performance. In this work, we first design prompts to enable LLM to directly solve small-scale surgery
scheduling problems. As the scale increases, we introduce an innovative method combining LLM with
NSGA-II (LLM-NSGA), where LLM act as evolutionary optimizers to perform selection, crossover, and
mutation operations instead of the conventional NSGA-II mechanisms. The results show that when the
number of cases is up to 40, LLM can directly obtain high-quality solutions based on prompts. As the number
of cases increases, LLM-NSGA can find better solutions than NSGA-II.
1 INTRODUCTION
Recent advancements in large language model (LLM)
have shown impressive performance in various fields
(Thirunavukarasu et al., 2023; Chang et al., 2024;
Kasneci et al., 2023). By learning from extensive
textual data, these models have acquired substantial
human knowledge, displaying notable capabilities in
reasoning and decision-making (Ge et al., 2024; Yao
et al., 2024). Consequently, a question arises: Can
LLM be used to solve complex combinatorial
optimization problems, or assist evolutionary
algorithms in tackling such problems? By harnessing
the vast knowledge base and reasoning abilities of
LLM, we can potentially revolutionize the way we
approach complex optimization challenges.
This work pioneers the use of LLM to solve multi-
objective combinatorial optimization problems--
a
https://orcid.org/0000-0003-1049-4959
b
https://orcid.org/0000-0002-8505-0212
c
https://orcid.org/0000-0001-8100-6743
d
https://orcid.org/0000-0001-8602-0800
e
https://orcid.org/0000-0002-8915-4203
surgery scheduling. Firstly, we designed prompts to
allow the LLM to directly solve small-scale surgery
scheduling problems. As the scale increases, we
introduce an innovative method that combines LLM
and Non-Dominated Sorting Genetic Algorithm II
(NSGA-II) (LLM-NSGA). During the evolutionary
search process, LLM-NSGA guides the LLM to
perform crossover and mutation to generate new
solutions, replacing the traditional selection,
crossover, and mutation of NSGA-II (Ruiz-Vélez et
al., 2024).
From the design perspective of NSGA-II, LLM-
NSGA has two appealing features. Firstly, by altering
the problem description and solution specifications in
the prompt, LLM-NSGA optimization can quickly
adapt to different optimization problems. This
method is more direct and flexible compared to
traditional programming, requiring minimal domain
222
Wan, F., Fondrevelle, J., Wang, T., Wang, K. and Duclos, A.
Optimizing Small-Scale Surgery Scheduling with Large Language Model.
DOI: 10.5220/0012894400003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 222-228
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

knowledge and manpower. Secondly, the zero-shot
learning capability of LLM-NSGA is particularly
noteworthy, as it reduces the computational overhead
associated with training AI models on specific tasks.
This is a significant advantage in scenarios where
resources are limited or where rapid adaptation to
new problems is required.
2 LITERATURE REVIEW
Over the past three years, the scaling of LLM has led
to groundbreaking achievements across a myriad of
tasks (Kirk et al., 2024; Schwitzgebel et al., 2024),
particularly planning and mathematical problem.
Gundawar et al., (2024) delves into the practical
application of LLM within the domain of travel
planning, and uses the Travel Planning benchmark by
the OSU NLP group. Their operationalization of the
LLM-Modulo framework for Travel Planning
domain provides a remarkable improvement,
enhancing baseline performances by 4.6x for GPT4-
Turbo and even more for older models like GPT3.5-
Turbo from 0% to 5%. Chen et al., (2024) used LLM
as general adaptive mutation and crossover operators
for an evolutionary neural architecture search (NAS)
algorithm. While NAS still proves too difficult a task
for LLM to succeed at solely through prompting, but
combination of evolutionary prompt engineering,
consistently finds high performing models.
“Prompts” refers to instructions designed to
guide LLM to complete a specific task. These
instructions are usually given in natural language to
tell the model what to do or how to process the given
information. A large number of studies have shown
that the format of the prompt can significantly impact
the quality of the LLM's output (Qi et al., 2023; Liu
et al., 2024). Wang et al., (2024a) evaluated LLM
with various prompting approaches on the Natural
Language Graph benchmark and then propose two
new Prompts, which enhance LLM in solving natural
language graph problems. Wang et al., (2024b)
explore the application of prompt engineering in
LLMs, designing and using different styles of
prompts to ask LLMs professional medical questions.
They assessed the reliability of different prompts by
asking the same question 5 times. The results showed
that GPT-4-Web with prompting had the highest
overall consistency.
In this work, by designing appropriate prompts,
LLM can directly solve small-scale operating room
(OR) allocation, and at the same time combine the
classic multi-objective algorithm NSGA-II to solve
large-scale OR allocation. The success of LLM in
surgery scheduling not only demonstrates its
effectiveness in a practical application but also opens
the door for further exploration into other
combinatorial optimization problems.
3 MATHEMATICAL MODEL
The surgery scheduling problem discussed involves:
first, assigning ORs to elective patients, and after the
surgeries are completed, some patients require
recovery in Intensive Care Unit (ICU) beds. Our
model primarily addresses how to allocate ORs to
elective patients to minimize overtime hours, meet
the patients' time window requirements, and
simultaneously reduce the peak demand for ICU
beds.
Set
I : Set of elective patient
J : Set of operating room
T: Set of planning horizon
Parameters
Q: Regular opening hours per OR
α
:Unit overtime cost for over regular hours
C: The opening costs per OR,
Variables
B
t
: Number of ICU beds on day t,
O
jt
: Opening hours in OR j on day t,
Cu
t
: All ICU patients not discharged on day t,
D
i
: Surgery duration for elective patient i,
Tw
i
: Expected surgery date for elective patient i,
Lel
i
: LOS of elective patient i,
Decision Variables:
Bf(m, A): If the element m belongs to the set A, it is
0, otherwise 1.
x
ijt
: If elective patient i is scheduled to be operated
in OR j on day t, it is 1, otherwise 0.
y
jt
: If OR j is open on day t, it is 1, otherwise 0.
Z
i
: If elective patient i needs an ICU bed, it is 1,
otherwise 0.
Mathematical Model:
11 1 1
min 1 (max( , 0)
*
TJ T J
jt
jt
tj t j
fC y OQ α
== = =
=∗ + −
  
(1)
111
min 2 ( )
ITJ
ijtk
itj
f
Ix
===
=−


(2)
()
111
min 3 ,
*
TJI
ijt i
tji
f
xBftTw
===
=

(3)
()
1
min 4 ,..., ,...,
t
T
f
max B B B=
(4)
Optimizing Small-Scale Surgery Scheduling with Large Language Model
223

Sub
j
ec
t
to
1
*,,
*
I
jt jt i ijt
i
Oy Dxtj
=
=∀

(5)
111
*,
t
t
i
It Y
tit
o
ij
iotLeljS
Cu Z x B t
==− +=+
=≤∀
 
(6)
11
1,
TJ
ijt
tj
x
i
==
≤∀

(7)
,,,
jijt
t
yx tji≥∀∀∀
(8)
{0,1}, , ,
ijt
x
tji∈∀∀∀
(9)
{0,1}, ,
j
t
ytj∈∀∀
(10)
{0,1},i
Z
i∈∀
(11)
Eqs. (1-4) are the four objective functions: f1
minimizes the total cost, including OR opening costs
and overtime costs; f2 and f3 are the number of
elective patients rejected and not operated within their
time window. f4 is the peak number of ICU beds over
all the periods.
Constraint (5) is the opening time of OR.
Constraint (6) calculates the total ICU bed demand
for elective patients. Constraint (7) indicates that
elective patients are scheduled only once during the
planning horizon. Constraint (8) represents the
relationship between two decision variables.
Constraints (9-11) shows the domain of variables.
4 METHODS AND RESULTS
To better demonstrate the effectiveness of LLM in
solving surgery scheduling, we employ three
frameworks to address this problem. Each framework
leverages different strategies and methodologies to
optimize surgery scheduling, which can lead to varied
outcomes and insights.
We have prepared 5 ORs, open for a week, to
schedule surgeries for 300 elective patients. Opening
an OR costs 1000, and each one is normally open for
8 hours. The overtime cost is 200 per hour. The details
of these patients are presented in Table 1. It contains
5 columns, "No." is the patient number. "Exe." is the
expected date for patient undergoing surgery. "Sur."
is the surgery duration in minutes. "LOS" is the length
of stay after surgery in days. "Stay" represents
whether the patient needs ICU bed after surgery
(1 represents yes and 0 represents no).
Table 1: The Information for elective patients.
No. Exe. Sur. LOS Sta
y
1 6 114 5 0
2 5 118 5 1
3 7 179 1 0
4 7 122 5 0
5 4 102 5 0
6 2 105 5 0
7 5 157 4 0
8 5 67 4 1
9 1 124 4 1
10 6 164 5 0
……
3005853 1
4.1 LLM Approach
This framework uses LLM to understand and solve
the OR allocation issue. The process is shown in
Figure 1. The LLM is given a thorough explanation
of the scheduling rules and goals. This allows the
model to create solutions that consider the complex
interdependencies of OR and ICU bed, such as
duration, LOS, and resource availability. The LLM
then gives steps to find a solution based on what it's
asked (called prompts) and makes a list of how to
schedule ORs using patient information and the
limitations given.
Figure 1: LLM approach framework.
To facilitate the display of results, Figure 2 shows
the OR and ICU bed arrangements by the LLM for
the first 10 elective patients listed in Table 1.
- f1 = 6000: The total cost includes the cost of
opening the ORs and overtime if the surgeries
extended beyond the regular hours. All surgeries were
completed within the regular operating hours, thus
avoiding overtime costs.
- f2 = 0: This indicates that none of the elective
patients were turned away due to OR constraints,
meaning the schedule was successful in
accommodating all patients.
Prompt for LLM
LLM
Develop a 7-day sche dule for operating room (OR) allocation and ICU bed utilization for elective patients
Constraints:
1.5 ORs, each open 8 hours da ily, c osting 1,000 to open, with a 200 hourly charge for overtime up to 8
hours.
2.Elective pa tients are assigned to ORs based on their expected dates, surgery duration, and OR availability.
3.After surgery, determine if patients need ICU beds, and track daily ICU bed requirements. This inc ludes
patients newly admitted and those still in the ICU.
Objectives:
1.Minimize total OR costs, including daily and overtime expenses.
2.Reduce the number of elective patients turned away due to OR constraints.
3.Ensure as many elective patients as possible have surgery on their sche duled date.
4.Minimize the peak number of ICU beds needed at period.
We need to perform a simplified approach to plan the 7-day OR allocation and ICU bed, which will involve
several steps:
Step 1: Sort Patients
Arrange patients by their planned surgery dates.
Step 2: Allocate OR Time
Place surgeries in ORs based on duration, aiming to fit within an 8-hour day.If the total surgery time exceeds
40 hours, we schedule some surgeries on other days or incur over time.
Step 3: Calculate ICU Beds
After scheduling sur geries, compute daily ICU bed needs based on patient LOS.
Step 4: Optimize
Continuously refine the schedule to balance OR use, minimize costs, and manage ICU beds efficiently.
Detailed steps
allocation plan
LLM: Output
Problem description
Data display
You: Input
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
224

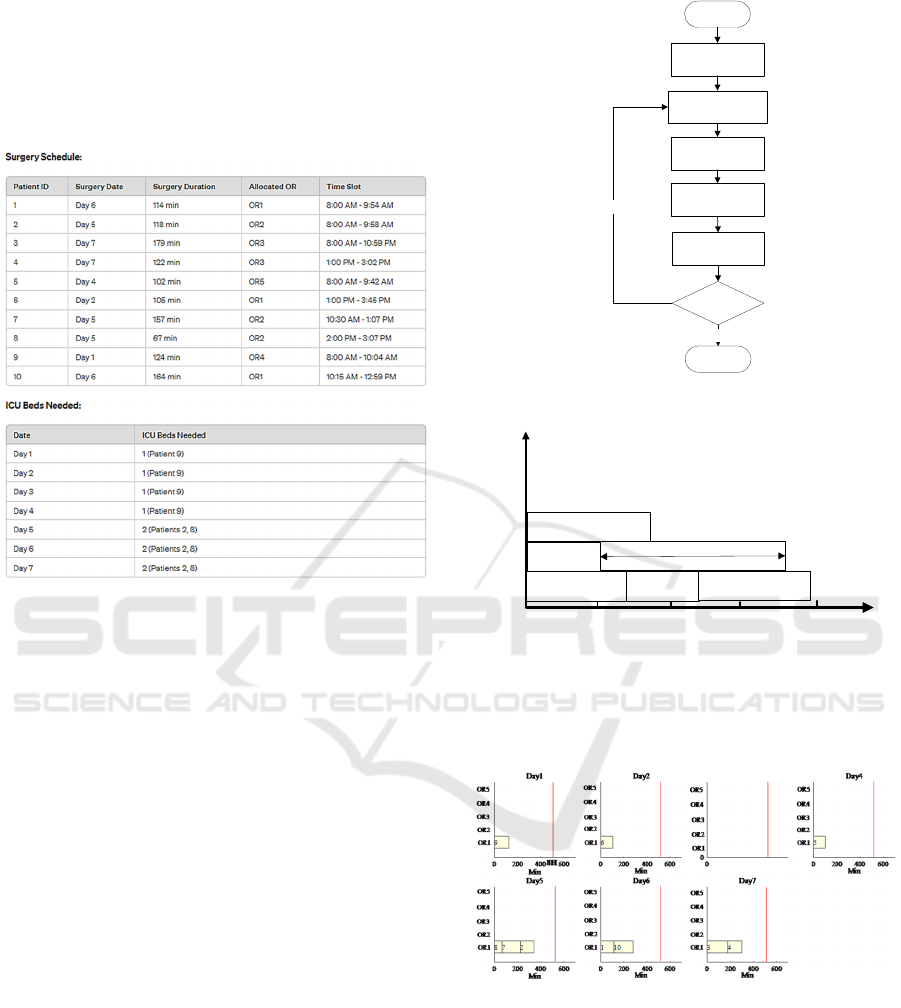
- f3 = 0: This suggests that all surgeries were
performed on their patients' expected dates, with no
rescheduling required.
- f4 = 2: This shows that, according to the plan, a
maximum of two ICU beds were needed at any given
time during the planning period.
Figure 2: LLM approach results.
This outcome suggests that the LLM performed
very well in creating an allocation plan that met all
the objectives for the given scenario. It managed to
schedule all elective surgeries on their expected dates,
without incurring any additional costs or rejecting any
patients, while also minimizing the peak number of
ICU beds required.
4.2 Traditional Approach: NSGA-II
This framework extends the NSGA-II to address the
allocation of OR and ICU beds for elective surgeries,
as illustrated in Figure 3. NSGA-II could maintain a
diverse set of solutions and its efficiency in handling
multiple objectives simultaneously (Harane et al.,
(2024); Altanany et al., (2024)), ensuring optimized
resource allocation and improved operational
efficiency in healthcare settings.
The traditional NSGA-II method was used to
assign ORs to these ten elective patients. The coding
method is shown in Figure 4. When allocating ORs to
elective patients, on the premise of avoiding overtime
in the OR and delaying elective patients, open ORs as
little as possible and arrange ICU beds at staggered
times.
Figure 3: Traditional approach framework: NSGA-II.
Figure 4: The coding method of NSGA-II.
Figure 5 shows the OR allocation results. The
corresponding four objectives are f1 = 6000, f2 = 0, f3
= 0, and f4 = 2.
Figure 5: ORs assignment of NSGA-II.
4.3 Approach Combining LLM and
NSGA-II
This is a hybrid framework that combines the
strengths of LLM and NSGA-II. LLM-NSGA
integrates LLM as evolutionary operators in a zero-
shot learning context. This means that the LLM is
utilized without any additional training specific to the
task at hand. The process involves the LLM in
Initialization
Selection,Crossover,
Mutation
Merging
populations
Pareto sorting
New population
Termination?
No
End
Start
Yes
3
...
OR1
OR2
OR3
2H
4H
6H
8H
Time
10
6
Avoid working overtime and
Avoid postponing patients
5
1
Surgery duration
...
Optimizing Small-Scale Surgery Scheduling with Large Language Model
225

performing key genetic algorithm operations such as
parent selection and genetic variation (crossover and
mutation) through an in-context learning approach
facilitated by carefully designed prompts. Figure 6
displays the prompts structured for solving the OR
and ICU bed allocation problem using LLM-NSGA.
Figure 6: LLM-NSGA approach framework.
Figure 7: Crossover and mutation of LLM-NSGA.
LLM-NSGA is that it does not program the
evolutionary operators step-by-step as it is
traditionally done. Instead, it provides high-level
instructions using natural language, reducing the need
for in-depth domain-specific knowledge.
To facilitate the presentation of results, this plan
only allocates OR and ICU beds to the first ten
elective patients in Table 1. Based on the randomly
generated initial allocation (as shown in Table 2), the
Table 2: The initial allocation solution.
Date OR Patients sequence
Da
y
1 1 [9]
Da
y
2 1 [2]
Da
y
3 1 []
Da
y
4 1 [5]
Da
y
5 1 [8,7,6]
Da
y
6 1 [10]
Da
y
7 1 [4,3]
four objectives are f1 = 6000, f2 = 1, f3 = 2, and f4 =
2, where elective patient 1 is not assigned OR and
elective patients 2 and 6 do not undergo surgery on
the desired date.
The LLM-NSGA then refines this initial plan by
performing crossover and mutation operations to
enhance the allocation, as shown in Figure 7. The
LLM effectively took into account the needs of
patients 1, 2, and 6, guided by the model's constraints
and objectives. The process is analogous to the
mutation and crossover steps in the NSGA-II
algorithm.
Table 3 displays the "Final Allocation" that results
from these operations starting from the initial plan.
The final objectives are: f1 = 6000, f2 = 0, f3 = 0, and
f4 = 2. With the goal of minimizing all four objectives,
the crossover and mutation process successfully
improved objectives f2 and f3 to zero.
Table 3: The final allocation solution.
Date OR Patients sequence
Da
y
11 [9]
Da
y
21 [6]
Da
y
31 []
Da
y
41 [5]
Da
y
5 1 [8,7,2]
Da
y
6 1 [10,1]
Da
y
71 [4,3]
4.4 Comparative Analysis
The parameters for NSGA-II were meticulously
calibrated through experimental tests and
implemented in MATLAB R2023a on Windows 10
(X64). We utilized the chat-turbo-0613 version of the
GPT-4.0 API as our LLM. The model and algorithm
parameters are shown in Table 4.
Table 4: The parameters of the model and NSGA-II.
Paramete
r
Value Ex
p
lanation
T 7 Planning horizon
Q 8 Regula
r
hours of OR
Qmax 10 Maximu
m
hours of OR
a 200 Overtime fee of OR
OR 5 Numbe
r
of OR
C 1000 O
p
enin
g
fee of OR
P 100 Population size
Ite
r
200 Numbe
r
of iterations
M
r
0.1 Mutation rate
C
r
0.7 Crossove
r
rate
These three methods can allocate ORs for the 10
elective and find the optimal solution. However, as
the number of elective patients increases, for example,
In-context examples
Below are some i nitial a llocation s olution and their obj ectives. The objectives includes: OR
costs, the number of elective patients rejected due to OR constraints, surgeries not conduc ted on
expected dates, and the peak number of ICU beds r equired. The lower these values, the better
the outcom e.
{Allocation plan 1} {objectives 1}
{Allocation plan 2} {objectives 2}
……
{Allocation plan N} {objectives N}
Probl em Description
Create a one-week plan for surgery and ICU bed needs with these constraints:5 ORs, each open
8 hours daily. Schedule surgeries based on expected dates, duration, and OR availability. Then,
calculate daily ICU bed needs for new and ongoing patients.
Task instructions
Please follow the instruction step-by-step to generate new allocations:
1. Select a allocation from the above allocations.
2. Crossover allocation: Switch the OR assignments of two elective patients, within the same
day or across different days, while aiming to adhere to their expected surgery dates.
3. Mutation allocation: Add an unsc heduled elective patient into an available OR slot on their
expected date to create a new allocation.
Prompt for LLM
Initialization
Selection
Crossover
Mutation
Termination
LLM
Evaluation
Pareto sorting
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
226

when it reaches 50, LLM cannot balance the
constraints and goals effectively. Instead, it is
recommended to use linear programming or genetic
algorithms for specific calculations and optimization.
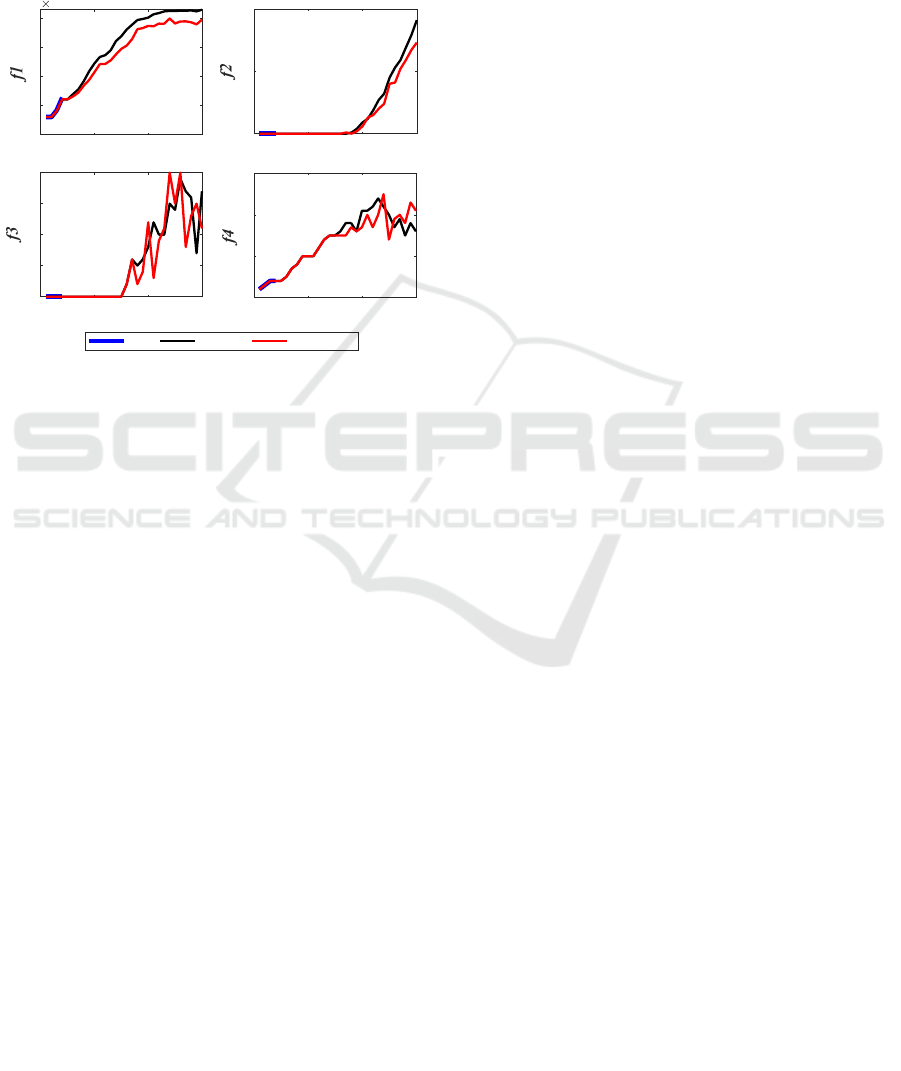
Figure 8 shows how the four optimization objectives
of the three methods change as the number of elective
patients increases.
Figure 8: Four objectives of the three methods.
The LLM ceases to provide allocation plans once
the patient count exceeds 40. When the number of
elective patients is less than 150, the effects of LLM-
NSGA and NSGA-II on f2, f3, and f4 are same, but
the f1 of NSGA-II is higher. This indicates that both
methods can schedule surgeries for all patients on
their expected dates, but they differ in how patients
are ordered within the ORs. LLM-NSGA arranges
patients more efficiently, resulting in lower overtime
costs. When the number of patients exceeds 150,
LLM-NSGA finds better allocation plans, rejecting
fewer patients. Although this may lead to more
patients not having surgeries on their expected dates,
the peak number of ICU beds required is also reduced.
5 CONCLUSIONS
In this work, we explore how LLM can directly
provide solutions for small-scale surgery scheduling
problems and can also serve as evolutionary
optimizers, where the LLM generates new solutions
based on the current population, providing high-
quality solutions for large-scale cases. Nonetheless,
LLM still has limitations in handling relatively large
problems. By adjusting the prompts given to LLM, it
may be possible for LLM to solve large-scale
problems step by step based on the prompts.
ACKNOWLEDGEMENTS
This work is partially supported by HarmonicAI -
Human-guided collaborative multi-objective design
of explainable, fair and privacy-preserving AI for
digital health distributed by European Commission
(Call: HORIZON-MSCA-2022-SE-01-01, Project
number: 101131117 and UKRI grant number
EP/Y03743X/1)
The authors sincerely acknowledge the financial
support (n°23 015699 01) provided by the Auvergne
Rhône-Alpes region.
REFERENCES
Altanany, M. Y., Badawy, M., Ebrahim, G. A., & Ehab, A.
(2024). Modeling and optimizing linear projects using
LSM and Non-dominated Sorting Genetic Algorithm
(NSGA-II). Automation in Construction, 165, 105567.
Chang, Y., Wang, X., Wang, J., Wu, Y., Yang, L., Zhu, K.,
... & Xie, X. (2024). A survey on evaluation of large
language model. ACM Transactions on Intelligent
Systems and Technology, 15(3), 1-45.
Chen, A., Dohan, D., & So, D. (2024). Evoprompting:
Language models for code-level neural architecture
search. Advances in Neural Information Processing
Systems, 36.
Ge, Y., Hua, W., Mei, K., Tan, J., Xu, S., Li, Z., & Zhang,
Y. (2024). Openagi: When llm meets domain experts.
Advances in Neural Information Processing Systems,
36.
Gundawar, A., Verma, M., Guan, L., Valmeekam, K.,
Bhambri, S., & Kambhampati, S. (2024). Robust
Planning with LLM-Modulo Framework: Case Study in
Travel Planning. arxiv preprint arxiv:2405.20625.
Harane, P. P., Unune, D. R., Ahmed, R., & Wojciechowski,
S. (2024). Multi-objective optimization for electric
discharge drilling of waspaloy: A comparative analysis
of NSGA-II, MOGA, MOGWO, and MOPSO.
Alexandria Engineering Journal, 99, 1-16.
Kasneci, E., Seßler, K., Küchemann, S., Bannert, M.,
Dementieva, D., Fischer, F., ... & Kasneci, G. (2023).
ChatGPT for good? On opportunities and challenges of
large language model for education. Learning and
individual differences, 103, 102274.
Kirk, H. R., Vidgen, B., Röttger, P., & Hale, S. A. (2024).
The benefits, risks and bounds of personalizing the
alignment of large language model to individuals.
Nature Machine Intelligence, 1-10.
Liu, Z., He, X., Tian, Y., & Chawla, N. V. (2024, May).
Can we soft prompt LLMs for graph learning tasks?. In
Companion Proceedings of the ACM on Web
Conference 2024 (pp. 481-484).
Qi, S., Cao, Z., Rao, J., Wang, L., ao, J., & Wang, X. (2023).
What is the limitation of multimodal llms? a deeper
look into multimodal llms through prompt probing.
Information Processing & Management, 60(6), 103510.
0 100 200 300
Number
0
1
2
3
4
10
4
0 100 200 300
Number
0
50
100
0 100 200 300
Number
0
5
10
15
20
0 100 200 300
Number
0
10
20
30
LLM NSGA-II LLM-NSGA
Optimizing Small-Scale Surgery Scheduling with Large Language Model
227

Ruiz-Vélez, A., García, J., Alcalá, J., & Yepes, V. (2024).
Enhancing Robustness in Precast Modular Frame
Optimization: Integrating NSGA-II, NSGA-III, and
RVEA for Sustainable Infrastructure. Mathematics,
12(10), 1478.
Schwitzgebel, E., Schwitzgebel, D., & Strasser, A. (2024).
Creating a large language model of a philosopher. Mind
& Language, 39(2), 237-259.
Thirunavukarasu, A. J., Ting, D. S. J., Elangovan, K.,
Gutierrez, L., Tan, T. F., & Ting, D. S. W. (2023).
Large language model in medicine. Nature medicine,
29(8), 1930-1940.
Wang, H., Feng, S., He, T., Tan, Z., Han, X., & Tsvetkov,
Y. (2024a). Can language models solve graph problems
in natural language?. Advances in Neural Information
Processing Systems, 36.
Wang, L., Chen, X., Deng, X., Wen, H., You, M., Liu, W.,
... & Li, J. (2024b). Prompt engineering in consistency
and reliability with the evidence-based guideline for
LLMs. npj Digital Medicine, 7(1), 41.
Yao, Y., Duan, J., Xu, K., Cai, Y., Sun, Z., & Zhang, Y.
(2024). A survey on large language model (llm)
security and privacy: The good, the bad, and the ugly.
High-Confidence Computing, 100211.
Zhao, Z., Lee, W. S., & Hsu, D. (2024). Large language
model as commonsense knowledge for large-scale task
planning. Advances in Neural Information Processing
Systems, 36.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
228