A Decentralized Guaranteed Collision Avoidance Control Framework for

Multi-Vehicle Systems in Highly Constrained Spaces

Erick J. Rodr

ıguez-Seda

Department of Weapons, Robotics, and Control Engineering,

United States Naval Academy, Annapolis, MD, U.S.A.

Keywords:

Artiﬁcial Potential Field, Collision Avoidance, Multi-Agent Systems, Unmanned Vehicles.

Abstract:

Collision avoidance methods based on artiﬁcial potential ﬁeld functions generally assume vehicles and ob-

stacles to have circular or elliptical shapes, which hinders mobility through narrow and cluttered spaces. To

counteract this problem, this paper presents a decentralized, cooperative control framework for vehicles of

unicycle type that considers the non-circular shape and relative orientation of vehicles and obstacles, increas-

ing their maneuverability through tight spaces. The control framework proposes the use of a continuously

differentiable time-varying minimum safe distance that agents need to enforce based on their shape and rel-

ative orientation and modulates the avoidance maneuvers and reaction forces based on the collision threat,

increasing the reaction forces when the vehicles are fast approaching and relaxing the forces when they are

moving away. The resulting closed-form control inputs are continuously smooth and bounded and are rigor-

ously proven to guarantee collision avoidance at all times.

1 INTRODUCTION

Nowadays, unmanned vehicles operate in complex

and dynamic environments such as disaster relief

zones, border control, and warehouses, to name a few.

Oftentimes, they need to navigate through highly con-

strained zones while sharing the space with other ve-

hicles and obstacles. The latter tends to compromise

mobility in lieu of safety (Xiao et al., 2021). There-

fore, it is mission-critical to design control algorithms

that allow these vehicles to have higher mobility and

performance while maintaining safety.

1.1 Related Work

Collision avoidance control algorithms for unmanned

vehicles have been studied for decades (Hoy et al.,

2014; Raibail et al., 2022). They typically lie in one of

two categories: motion planning and reactive control.

Motion planning methods can lead to optimal trajec-

tories, but their implementation is mostly centralized,

demanding information from all other agents, or re-

quires an accurate model of the environment (Hoy

et al., 2014). Real-time reactive collision avoidance

methods, on the other hand, can be decentralized and

respond to unexpected obstacles, making these strate-

https://orcid.org/0000-0003-1108-4329

gies more suitable for unknown and dynamic spaces.

A popular branch among real-time reactive con-

trol methods is the use of artiﬁcial potential ﬁeld

(APF) functions (Khatib, 1986). APF-based methods

allow one to build provably safe collision avoidance

control laws that can not only guarantee safety but can

be implemented in a decentralized way and for an ar-

bitrarily large number of vehicles (Stipanovi

c et al.,

2007). Recent examples of decentralized methods for

multi-vehicle systems include (Du et al., 2019; Mel-

chiorre et al., 2022; Gao et al., 2024). Yet, most APF-

based approaches rely on the conservative assump-

tion that agents, that is, vehicles and obstacles, are

of circular or elliptical shape, or a collection of them

(Stipanovi

c et al., 2007; Braquet and Bakolas, 2022).

This worst-case scenario assumption simpliﬁes the

analysis at the expense of making the agents occupy a

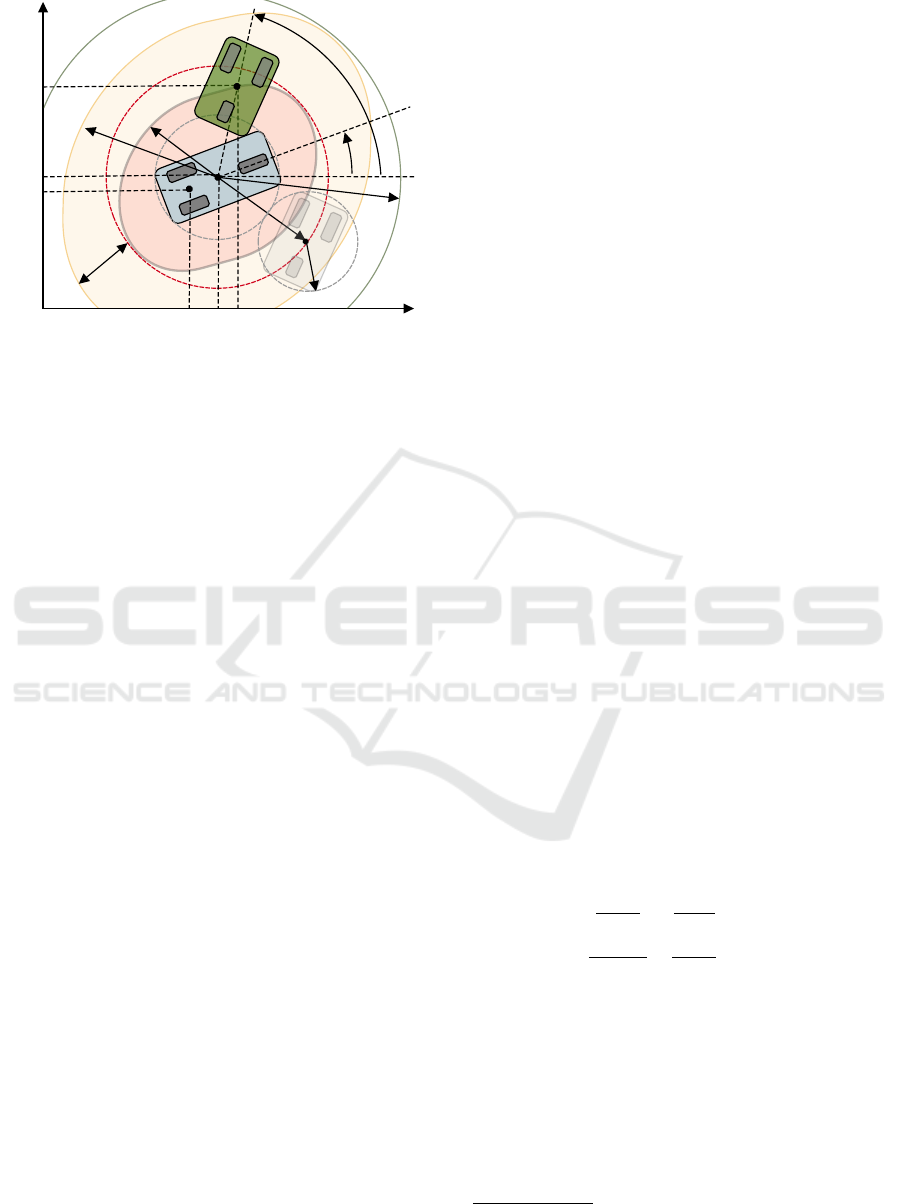
larger space. For instance, consider the two vehicles

of rectangular shape in Figure 1. The circular body as-

sumption will require both vehicles to keep a distance

from each other equal to or larger than the summa-

tion of their circumradii, r

max

i j

= h

+ h

, regardless of

their relative orientation. Instead, one could take their

shape and orientation into consideration and reduce

the distance, r

i j

, that agents need to keep from each

other, as shown in Figure 1. A recent APF-based ap-

proach that takes into consideration their orientation

and shape is presented in (Rodr

ıguez-Seda, 2024b).

Rodríguez-Seda, E.

A Decentralized Guaranteed Collision Avoidance Control Framework for Multi-Vehicle Systems in Highly Constrained Spaces.

DOI: 10.5220/0012900300003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 229-236

ISBN: 978-989-758-717-7; ISSN: 2184-2809

229

i,2

j,2

∆

i j

max

i j

i,1

j,1

Figure 1: Minimum safe distance. Traditional approaches

assume vehicles to have circular shapes and enforce a con-

stant minimum distance equal to or greater than the sum of

their circumradii r

max

i j

= h

+ h

Another common drawback of most APF-based

methods is the equal treatment of obstacles that are

moving away and those approaching. This is due to

the sole reliance on relative position among agents

while ignoring the direction of motion or velocity.

Recent research efforts that integrate relative velocity

information into the APF formulation include (Zhang

et al., 2020; Ginesi et al., 2021). These approaches,

however, require the obstacle’s velocity, which might

not be available or difﬁcult to estimate. As an alter-

native, the work in (Rodr

ıguez-Seda and Stipanovi

2020; Rodr

ıguez-Seda, 2024a) proposes an APF-

based framework that only uses the vehicle’s velocity

information and not the obstacle’s, relaxing the APF

force if the vehicle is moving away from the obstacle

and increasing it if the vehicle is moving closer to it.

1.2 Contributions

This paper builds on (Rodr

ıguez-Seda and Stipanovi

2020) and (Rodr

ıguez-Seda, 2024b) to propose a de-

centralized, cooperative APF-based control law for

nonholonomic vehicles of unicycle type that guaran-

tees collision avoidance at all times while increas-

ing maneuverability through dynamic and highly clut-

tered spaces. The proposed control law takes into

consideration the shape and relative orientation of

vehicles and obstacles to yield non-circular, tighter

avoidance zones. In contrast to other collision avoid-

ance methods for non-circular obstacles (Zimmer-

mann et al., 2022), the proposed framework yields

closed-form controllers that generate smooth and con-

tinuous forces and torques. Furthermore, the vehi-

cle’s avoidance response is modulated based on the

collision threat: it increases or decreases the repul-

sive force and activation distance if the vehicle is ap-

proaching the obstacle or moving away. To demon-

strate the performance of the control framework, a

simulation example is presented and compared with

the use of constant avoidance and reaction zones.

2 PROBLEM

2.1 Multi-Vehicle System Dynamics

Consider a group of N nonholonomic vehicles of uni-

cycle type with dynamic equations governed by

˙x

(t) = v

(t)cosφ

(t), m

˙v

(t) = f

(t)

˙y

(t) = v

(t)sinφ

(t), J

(t) = τ

(t)

(t) = ω

(t),

(1)

where x

(t) and y

(t) are the position coordinates,

(t) is the orientation, v

(t) and ω

(t) are the linear

and angular velocities, m

is the mass, J

is the iner-

tia, and f

(t) and τ

(t) are the control force and torque

inputs for the ith robot (see Figure 1). The control

objective is to design

and τ

such that the ith ve-

hicle follows a desired path while avoiding collisions

with other vehicles and obstacles. Unfortunately, it

is well known that the position and orientation of (1)

cannot be simultaneously stabilized at a desired value

using a continuous static state feedback control law

(Brockett, 1983). Therefore, this paper proposes the

use of input-output feedback linearization, where the

control task shifts to regulating the position of a ref-

erence point in front of (x

) given by

i,1

+ L

cosφ

, z

i,2

+ L

sinφ

(2)

where L

> 0 is a constant parameter and z

i,1

i,2

]

are the Cartesian coordinates of the refer-

ence point. Now, differentiating twice equation (2)

and applying the following control force and torque











cosφ

sinφ

−sinφ

cosφ









i,1

+ v

sinφ

+ L

cosφ

i,2

−v

cosφ

+ L

sinφ



(3)

one can show that (1) reduces to

(4a)

−1



−sinφ

cosφ



(4b)

where u

= [u

i,1

i,2

]

is the new control input for the

linearized system. While the internal dynamics (4b)

In what follows, the time argument of signals will be

omitted unless it is deemed necessary.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

230

can only be shown to be Lagrange stable (Rodr

ıguez-

Seda et al., 2014), the linear dynamics of the reference

point (4a) are controllable. That is, for a any desired

position z

∈R

, one can design a state feedback con-

trol law u

such that z

→ z

as t → ∞.

2.2 Problem Formulation

The main control objective is to design a decen-

tralized cooperative control framework that guaran-

tees the safe navigation of multiple vehicles through

highly constrained spaces. To this end, consider the

interaction of a pair of agents ith and jth, as illustrated

in Figure 1. Note that the minimum safe distance (or

envelope) between the agents, denoted as r

i j

, is not

only a function of their shapes and dimensions but

also of their relative position and orientations

i j

:= r

i j

−z

,φ

) = r

−z

,φ

). (5)

That is, r

i j

depends on how the jth agent or obstacle

is positioned with respect to the ith vehicle. One then

says that a collision takes place if



−z



≤ r

i j

for

some time t. In what follows, it is assumed that one

can ﬁnd an envelop function r

i j

that is continuously

differentiable with bounded derivative. Finally, it is

assumed that the vehicles can detect, either via com-

munication or onboard sensors, the relative position

and orientation of other agents within a bounded de-

tection radius R > sup

i, j̸=i

i j

} = r

max

i j

Having deﬁned the minimum safe distance and the

detection radius, one can formulate the control objec-

tive as follows. Design a control strategy u

such that

→ z

as t → ∞ and



−z



> r

i j

∀ i, j ̸= i,t ≥ 0,

where z

is the desired ﬁnal position.

3 CONTROL FRAMEWORK

3.1 Collision Avoidance Control

To achieve the control objective, this paper proposes

the use of the following control law

= K

−z

) −K

+ u

(6)

where K

and K

are positive constants and u

is the

collision avoidance control input given by

= −

∑

j∈N

∂V

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂φ



−sin φ

cosφ



(7)

The group N

= {j ∈ {1,··· , N}/i,



−z



≤ R} is

the set of neighbors of the ith agent and V

i j

and V

i j

are

avoidance functions (Stipanovi

c et al., 2007) given by

i j

:=V

i j

min

(



−z



−R

i j



−z



−r

i j

:= V

i j

). (8)

The reaction radius R

i j

represents the distance at

which the ith vehicle starts avoiding the jth agent.

Ideally, this radius should be larger if the ith vehi-

cle is approaching the jth agent at a large speed and

smaller if it is moving away. Therefore, similar to

(Rodr

ıguez-Seda and Stipanovi

c, 2020), this paper

proposes the use of

i j

:=R

i j

(λ

i j

) = r

i j

+ ∆

i j

(λ

i j

) (9a)

∆

i j

:=∆

i j

(λ

i j

) =

∆



tan

−1

(αλ

i j

+ σ)



(9b)

where ∆

i j

denotes the reaction gap distance (i.e., the

distance at which the ith vehicle starts reacting to ob-

stacles), 0 <

∆ ≤ R −sup

i, j

max

i j

} deﬁnes the maxi-

mum reaction gap distance, α and σ are two control

parameters, and λ

i j

= (z

−z

)

represents the rate

at which the ith vehicle either increases (λ

i j

> 0) or

decreases (λ

i j

< 0) its distance to the jth agent. Note

that ∆

i j

→ 0, R

i j

→ r

i j

if λ

i j

→ −∞ (i.e., if the ith

vehicle is rapidly distancing itself from the jth agent)

and ∆

i j

→

∆, R

i j

→ r

i j

∆ if λ

i j

→ −∞ (i.e., if the

vehicle is fast approaching). The radius

i j

=: R

i j

(0) = r

i j

∆ +

∆ tan

−1

(σ) (10)

denotes the reaction radius when λ

i j

= 0. Note that

i j

≡R

, yet R

i j

and R

i j

are, in general, not the same.

Similarly, R

i j

̸≡ R

for j ̸= k.

Now, returning to (7) one can show that

∂V

i j

∂z

4(R

i j

−r

i j

))(



−z



−R

i j

)(z

−z

)

(



−z



−r

i j

)

∂V

i j

∂r

i j

4∆

i j

−



−z



)(R

i j



−z



)

(



−z



−r

i j

)

if r

i j



−z



≤ R

i j

, undeﬁned if



−z



= r

i j

and zero otherwise. Similarly, one can show that

∂V

i j

∂z

∂V

∂z

∂V

i j

∂z

= −

∂V

i j

∂z

∂V

i j

∂r

i j

∂V

∂r

i j

. (11)

Theorem 1. Consider the system in (1) with con-

trol law (3) and (6). Assume that z

is constant

and that



(0) −z

(0)



> r

i j

∀ i, j ̸= i. Then,



(t) −z

(t)



> r

i j

∀ t ≥ 0.

Proof. Consider the following Lyapunov function

W =

∑

i=1



−z



∥

∑

i=1

∑

j∈N

i j

. (12)

A Decentralized Guaranteed Collision Avoidance Control Framework for Multi-Vehicle Systems in Highly Constrained Spaces

231

Differentiating (12) with respect to time yields

W =

∑

i=1



−K

−z

)

+ (K

−z

) −K

)



−

∑

i=1

∑

j∈N

∂V

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂φ



−sin φ

cosφ



∑

i=1

∑

j∈N

∂V

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂φ

∑

i=1

∑

j∈N

∂V

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂φ

(13)

Now, canceling the ﬁrst two terms and noting that

∑

i=1

∑

j∈N

∂V

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂φ

∑

i=1

∑

j∈N

∂V

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂φ

∂V

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂z

∂V

i j

∂r

i j

∂r

i j

∂φ

(14)

along with

[−sinφ

,cosφ

]

, yields

W = −K

∑

i=1

∥

−

∑

i=1

∑

j∈N

∂V

i j

∂z

−

∂V

i j

∂z

≤−

∑

i=1

∑

j∈N

i j

(15)

where

i j

−r

)(



−x



−R

i j

)

(



−x



−r

)

−4

−r

)(



−x



−R

)

(



−x



−r

)

. (16)

Note that if λ

i j

≥ 0, then R

i j

≤ R

, which implies

that Λ

i j

≥ 0 and, hence Λ

i j

≥ 0. Similarly, if

i j

< 0, then R

i j

> R

⇒Λ

i j

< 0 ⇒Λ

i j

> 0. There-

fore,

W ≤ 0 for all t ≥ 0. The latter implies that

W (t) is non-increasing and bounded ∀ t ≥ 0. Now,

suppose that for some pair i, j ̸= i one have that



(t) −z

(t)



→r

i j

for some t > 0. The latter would

imply that W (t) → ∞, which is a contradiction. Since

the solutions of (4a) are continuous, one must have

that



(t) −z

(t)



̸→ r

i j

for all i, j ∈ N

,t > 0 and

the proof is complete.

Theorem 1 guarantees that if all agents start at a

safe distance from each other, they will remain at a

safe distance for all time. Note that it does not say

anything about convergence to the agents’ desired po-

sitions. Results on convergence are given next.

Theorem 2. Assume that z

is constant and that



(0) −z

(0)



> r

i j

∀ i, j ̸= i. Then, z

−z

and

are uniformly ultimately bounded (UUB). Further-

more, if ∃T

such that u

= 0 ∀t ≥T

, then z

−z

and

vanish exponentially as t → ∞.

Proof. From Theorem 1 one have that W is bounded,

which implies that V

i j

and V

i j

are also bounded ∀ i, j ̸=

i,t ≥ 0. Boundedness of V

i j

and V

i j

, along with

the fact that r

i j

is continuously differentiable with

bounded derivative by construction, implies that ∃¯u <

∞ such that u

≤ ¯u ∀ i,t ≥ 0. Now, let e

= z

−z

= −

, and

= −

= −K

−K

−u

be the

tracking error, velocities, and accelerations, and con-

sider the following Lyapunov candidate function

W =K

∥

−K

∥

. (17)

Taking the time derivative of W yields

W =2K

+ (

+ K

)

(

+ K

)

= −K

∥

−K

∥

−2

−K

≤−aK



]



+ b ¯u



]



(18)

where a = min{1,K

} and b = max{2,K

}. Since

W < 0 for all



]



> b ¯u/(aK

), one can con-

clude that [e

]

is UUB (Khalil, 2002), and from

(4b), that

is also UUB.

Now, assume that ∃T

such that u

= 0 ∀ t ≥ T

Then,

W ≤−aK



]



∀t ≥T

from which one

can conclude that [e

]

converges asymptotically to

zero. The latter implies that

→ 0 as t → 0.

The theoretical results presented so far guarantee

collision avoidance when the desired position is con-

stant and when all agents apply the same control (or

remain static). A natural extension is the use of way-

points to drive the vehicles through a desired path or

trajectory. Additionally, the results presented so far

cannot guarantee the convergence of the tracking er-

ror to zero in all scenarios, i.e., agents may ﬁnd them-

selves trapped in a deadlock. The next section will

discuss implementing way-points in the control law

and avoiding deadlocks.

3.2 Way-Points and Deadlocks

A main drawback of decentralized APF methods is

the occurrence of deadlocks (Melchiorre et al., 2022).

A vehicle is said to reach a deadlock if it can not

reach the desired position due to a persistent interac-

tion with another agent or obstacle. This is oftentimes

the result of symmetries between the attractive poten-

tial forces (i.e., the ﬁrst term in (6)) and the avoidance

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

232

control (Rodr

ıguez-Seda et al., 2016). That is, when

→ K

−z

). To break these symmetries, one

can temporarily change the desired position along a

vector that is perpendicular to the avoidance control.

Consider an ordered sequence of unobstructed M

way-points, z

∈{z

,··· ,z

}, in the ith vehicle’s de-

sired path separated by at least a distance D

> 0 of

each other. The idea is to go to the next way-point

k+1

whenever the distance of the vehicle to the kth

way-point is smaller than some positive parameter

≪D

. Since the agents’ velocities are bounded, the

times between switches are lower bounded by some

positive constant τ

> 0. The latter is a necessary con-

dition for stability and avoidance of Zeno behavior.

Now, due to the presence of obstacles and other

agents, the ith vehicle may not reach the kth way-

point and may end up circulating around it for an in-

deﬁnite time. To escape the deadlock, the vehicle may

temporarily switch to a new way-point,

. The new

way-point can be chosen in a direction that is perpen-

dicular to the avoidance control, i.e.,

= z

+ µ

R (π/2)u

, if



+ K

−z

)



≤U

(19)

where µ

is a non-zero constant parameter, U

> 0 is

a small constant, and R (π/2) is the 2 ×2 rotational

matrix that rotates u

by π/2 radians. This tempo-

rary way-point can last for a pre-determined amount

of time T

in order to avoid multiple switching in a

short time frame. After T

, the vehicle may go back

to the original way-point z

or switch to another way-

point using (19) if the conﬂict has not been resolved.

The complete algorithm is given in Algorithm 1.

4 EXAMPLES

This section presents examples of vehicles of rectan-

gular shape with rectangular and circular obstacles.

4.1 Minimum Safe Distance

Let the shape of the ith vehicle be approximated by a

rectangle of length ℓ

and width w

. Similarly, let the

jth vehicle or obstacle be approximated by a rectangle

of length ℓ

and width w

. Without loss of generality,

let their lengths be aligned with the x-axis (i.e., when

= 0) and deﬁne the following functions

i j

ℓ

+ cos

i j

+ sin

i j

(20a)

i j

ℓ

+ sin

i j

+ cos

i j

(20b)

where ε > 0 is a small constant such that the deriva-

tives of (20) are well-deﬁned and

i j

= φ

−φ

is the

Algorithm 1: Way-Point Selection.

Constants: d

,µ

Input: k,z

k+1

Output: z

if k < M

and



−z



< d

← z

k+1

/* Pick Next Way-Point */

k ← k + 1

else if



−z



≥ d

and



+ K

−z

)



≤U

← z

+ µ

R (π/2)u

⋆

←t

while t ≤t

⋆

+ T

←

/* Switch temporarily */

else:

← z

i j

max

i j

max

i j

Figure 2: Comparison of the minimum safe distance be-

tween the proposed control framework (in red) and the tra-

ditional circular assumption (in blue). The left ﬁgure illus-

trates the case when the vehicle and obstacle have a rect-

angular shape. The right ﬁgure depicts the case when the

obstacle has a circular shape.

relative orientation. Let θ

i j

= atan2(z

j,2

−z

i,2

j,1

−

i,1

) be the angle between z

and z

. Then, the equa-

tion for a rectangle with sides β

i j

and γ

i j

in polar co-

ordinates ρ

i j

and θ

i j

, rotated by φ

and centered at z

can be approximated by

i j

+(γ

i j

cos(θ

i j

−φ

) + β

i j

sin(θ

i j

−φ

))

(21a)

i j

+(γ

i j

cos(θ

i j

−φ

) −β

i j

sin(θ

i j

−φ

))

(21b)

i j

2β

i j

+ η

i j

−2ε

. (21c)

Following the same procedure for the jth agent

and using the continuous differentiable approxima-

tion of the minimum function (Stipanovi

c et al.,

2012), one can obtain a smooth approximation of r

i j

= r

=(2)



−δ

i j

+ ρ

−δ



−

, δ ≥ 2 (22)

that is continuously differentiable and bounded.

Choosing smaller ε →0 and larger δ →∞ yields more

compact envelopes. The left side of Figure 2 illus-

trates r

i j

for different relative positions between two

rectangular agents of different sizes and different ori-

A Decentralized Guaranteed Collision Avoidance Control Framework for Multi-Vehicle Systems in Highly Constrained Spaces

233

−15

−12 −9

−6

−3 0 3

9 12

−9

−6

−3

t = 0.0 s

(t)

x (m)

y (m)

Figure 3: Simulated scenario with four vehicles and several

static obstacles represented as squares and circles.

entations. The red-dotted line represents the mini-

mum safe distance that the center of the jth agent can

come from the ith vehicle, which is generally shorter

than the constant minimum distance scenario.

The case of an obstacle of circular shape can be

similarly addressed. Consider an obstacle with radius

. The rectangle obtained by moving the circular ob-

stacle around the vehicle as seen in Figure 2 has half-

length ℓ

i j

ℓ

+ h

and half-width w

i j

+ h

Then, similar to (21), one can deﬁne this rectangle in

polar coordinates r

i j

and θ

i j

= atan2(z

j,2

−z

i,2

j,1

−

i,1

), where r

i j

is given by

i j

+(w

i j

cos(θ

i j

−φ

) + ℓ

i j

sin(θ

i j

−φ

))

(23a)

i j

+(w

i j

cos(θ

i j

−φ

) −ℓ

i j

sin(θ

i j

−φ

))

(23b)

i j

ℓ

i j

+ s

i j

−2ε

. (23c)

Figure 2 illustrates r

i j

for different relative orienta-

tions between the ith vehicle and the jth agent.

4.2 Simulations

Consider a group of four identical vehicles (1) of

rectangular shape, with length ℓ

= 2 m and width

= 1 m, traveling through a highly obstructed en-

vironment, as shown in Figure 3. Each vehicle is

tasked with following a series of way-points by im-

plementing (6) and Algorithm 1. The system and con-

trol parameters are given as m

= 1 Kg, J

= 1 Kg m

= 1 N/m, K

= 2 Ns/m, L

= 2/3 m, D

= 1.5 m,

= 0.2 N, and µ

= 2

√

2 N,

∆ = 4 m, α = 0.4,

σ = −0.3, δ = 6, and ε = 0.05. The static obsta-

cles are assumed to be squares of side ℓ

= w

= 5 m,

while circular obstacles have radius h

= 1.5 m.

The response of the multi-vehicle system is given

in Figure 4. The vehicles are able to follow the way-

points and navigate smoothly through the narrow cor-

ridor while avoiding collisions and deadlocks, despite

−9

−6

−3

t ∈ [0.0s,7.0s]

(t)

y (m)

−9

−6

−3

t ∈ [7.0s,15.0s]

y (m)

−15

−12 −9

−6

−3 0 3

9 12

−9

−6

−3

t ∈ [15.0s,26.0s]

x (m)

y (m)

Figure 4: Sequential motion of the multi-vehicle system un-

der proposed avoidance control. Newer positions are over-

imposed and time-spaced by 0.5 s.

having symmetric desired paths with obstacles in their

way. Note also that the leading vehicles, 2nd and 3rd,

are able to avoid the last circular obstacles in their

paths while being closely followed by another agent.

For comparison, the vehicles are also simulated

using the proposed control law (7) but with a con-

stant reaction gap distance of ∆

i j

= ∆

i j

(0) = 0.41 m.

This approach is equivalent to the one proposed in

(Rodr

ıguez-Seda, 2024b). The results are presented

in Figure 5. Note that, for the ﬁrst 15 s, the vehicles’

response is very similar to the previous case. How-

ever, once the vehicles reach the last obstacles and

are encircled by another vehicle closely behind, the

second and third vehicles experience a forceful reac-

tion that leads them outside of the plotted area. This is

due to the smaller reaction gap, which requires more

drastic maneuvers in order to avoid collisions.

Finally, the multi-vehicle system is also simulated

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

234

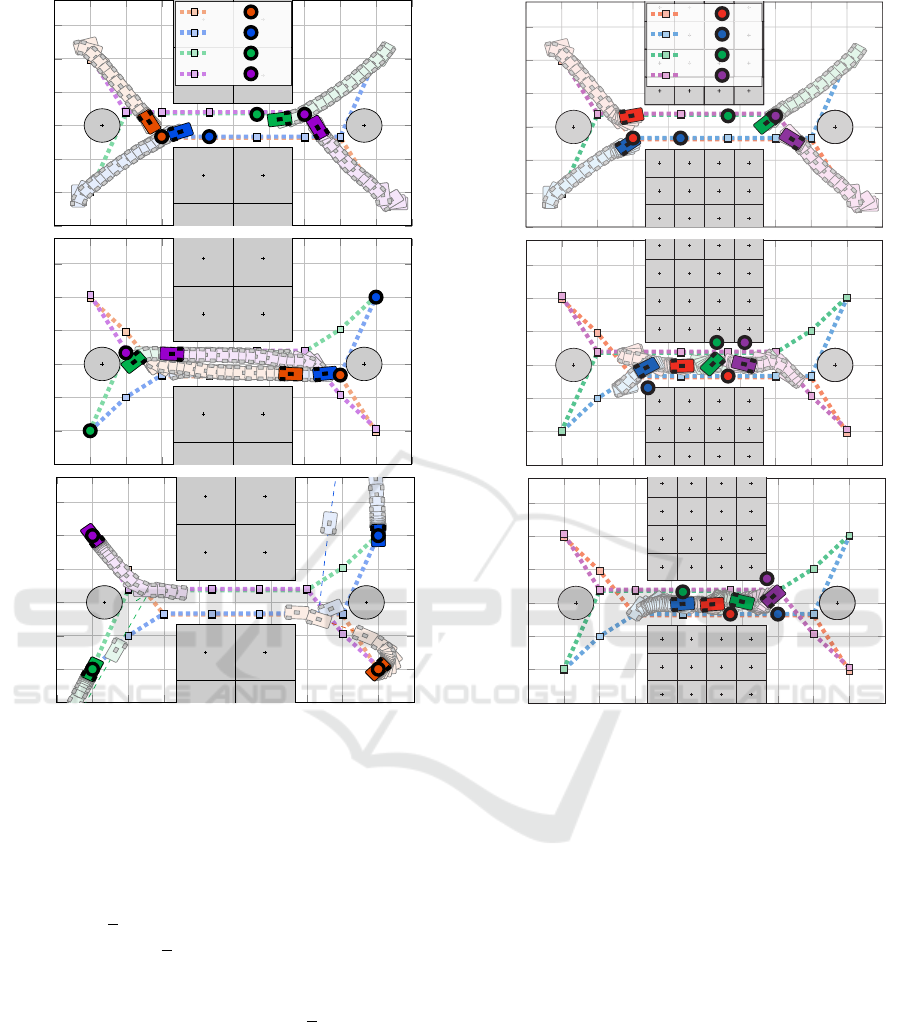
−9

−6

−3

t ∈ [0.0s,7.0s]

(t)

y (m)

−9

−6

−3

t ∈ [7.0s,14.8s]

y (m)

−15

−12 −9

−6

−3 0 3

9 12

−9

−6

−3

t ∈ [14.8s,26.0s]

x (m)

y (m)

Figure 5: Sequential motion of the multi-vehicle system

with constant detection gap distance. Newer positions are

over-imposed and time-spaced by 0.5 s.

using a constant minimum safe distance radius and a

constant reaction gap distance of ∆

i j

= 0.41 m. When

avoiding other vehicles, the minimum safe distance is

chosen as the sum of their circumradii, i.e., r

i j

= r

+ h

= 2

√

2 m. For circular obstacles, it is chosen

as r

i j

= h

+ h

√

2 + 1.5 m. All other obstacles are

divided into smaller 2.5 ×2.5 m

squares to allow the

transit of vehicles over the narrow corridor. For these

obstacles, r

i j

is chosen as r

i j

= 2.25

√

2 m. Note that,

since r

i j

is constant, the avoidance control reduces to

= −

∑

j∈N

∂V

i j

/∂z

, which is the traditional APF

approach. The results are illustrated in Figure 6. Note

that the vehicles are able to enter the narrow corridor,

where they reach a deadlock. The z

points out-

side the desired path illustrate how the vehicles try to

evade the deadlock but are unsuccessful.

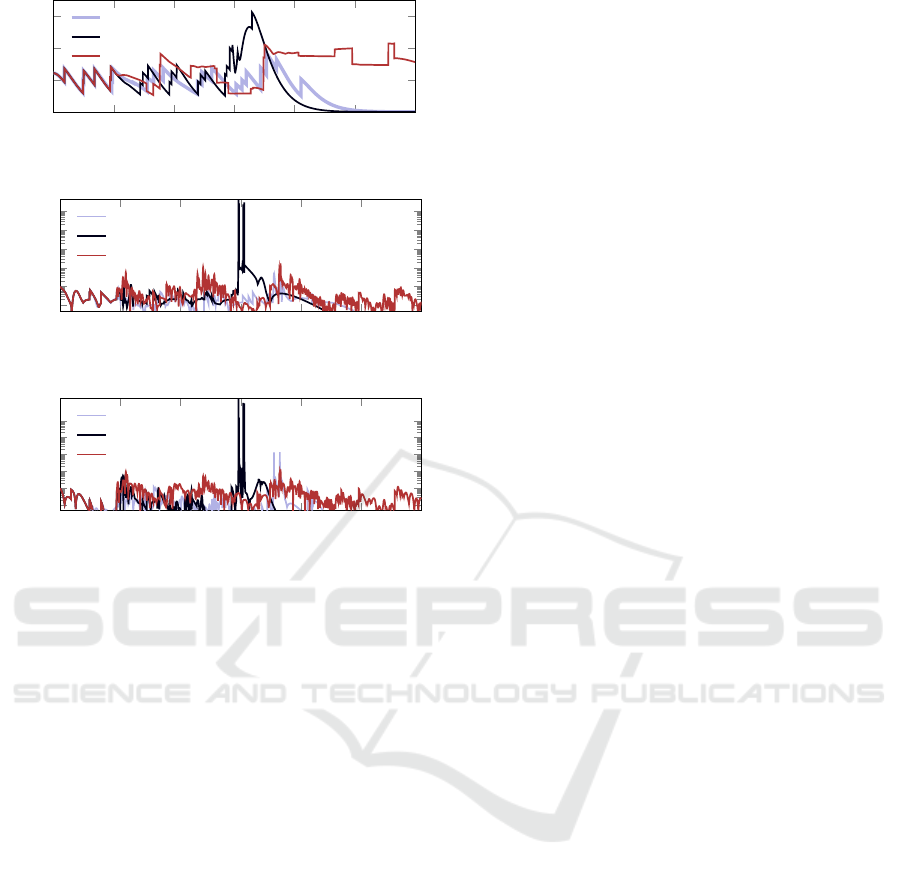
Figures 7, 8, and 9 show the cumulative instan-

taneous error, force, and torque for the case of the

−9

−6

−3

t ∈ [0.0s,7.0s]

(t)

y (m)

−9

−6

−3

t ∈ [7.0s,15.0s]

y (m)

−15

−12 −9

−6

−3 0 3

9 12

−9

−6

−3

t ∈ [15.0s,26.0s]

x (m)

y (m)

Figure 6: Sequential motion of the multi-vehicle system

with constant minimum safe distance and constant reaction

gap distance.

proposed controller (Proposed Control), the case of a

constant reaction gap (Constant ∆

i j

), and for the case

of a constant minimum safe distance and reaction gap

(Constant r

i j

and ∆

i j

). Note that errors are, in gen-

eral, smaller for the proposed avoidance control. Sim-

ilarly, note that the forces and torques are, in general,

one and four orders in magnitude larger for the use of

constant reaction gaps.

5 CONCLUSIONS

This paper presented a decentralized, cooperative,

APF-based control framework for multi-vehicle sys-

tems of unicycle type that is rigorously proven to

guarantee collision avoidance for an arbitrarily large

number of agents at all times. The control framework

deﬁnes a continuously differentiable time-varying

A Decentralized Guaranteed Collision Avoidance Control Framework for Multi-Vehicle Systems in Highly Constrained Spaces

235

t (s)

∑

i=1

||z

−z

|| (m)

Proposed Control

Constant ∆

i j

Constant r

i j

& ∆

i j

Figure 7: Cumulative tracking error.

t (s)

∑

i=1

||f

|| (m)

Proposed Control

Constant ∆

i j

Constant r

i j

& ∆

i j

Figure 8: Cumulative linear force (in logarithm scale).

t (s)

∑

i=1

||τ

|| (m)

Proposed Control

Constant ∆

i j

Constant r

i j

& ∆

i j

Figure 9: Cumulative torque (in logarithm scale).

minimum safe distance that agents need to enforce,

taking into consideration the shape and orientation

of vehicles and obstacles and, therefore, reducing

the conservatism introduced by traditional APF-based

methods. Furthermore, the framework modulates the

avoidance maneuvers and reaction forces based on

the collision threat level that obstacles might repre-

sent. The synthesis of both approaches is a contin-

uously smooth and bounded control force provided

in analytical closed-form. Simulation results demon-

strated that the proposed avoidance control can in-

crease the maneuverability of vehicles through highly

constrained spaces when compared to the use of con-

stant minimum safe distance and reaction radii.

REFERENCES

Braquet, M. and Bakolas, E. (2022). Vector ﬁeld-based

collision avoidance for moving obstacles with time-

varying elliptical shape. In Proc. AACC MECC, pages

587–592.

Brockett, R. W. (1983). Asymptotic stability and feedback

stabilization. In Brockett, R. W., Millman, R. S., and

Sussmann, H. J., editors, Differential Geometric Con-

trol Theory, pages 181–191. Birkhauser, Boston.

Du, Y., Zhang, X., and Nie, Z. (2019). A real-time colli-

sion avoidance strategy in dynamic airspace based on

dynamic artiﬁcial potential ﬁeld algorithm. IEEE Ac-

cess, 7:169469–169479.

Gao, Y., Li, D., et al. (2024). Trajectory planning and

tracking control of autonomous vehicles based on im-

proved artiﬁcial potential ﬁeld. IEEE Trans. Veh.

Technol., pages 1–16.

Ginesi, M., Meli, D., et al. (2021). Dynamic movement

primitives: Volumetric obstacle avoidance using dy-

namic potential functions. J. Intell. Robot. Syst.,

101:1–20.

Hoy, M., Matveev, A. S., and Savkin, A. V. (2014). Algo-

rithms for collision-free navigation of mobile robots in

complex cluttered environments: A survey. Robotica,

33(3):463–497.

Khalil, H. K. (2002). Nonlinear Systems. Prentice Hall,

New Jersey.

Khatib, O. (1986). Real-time obstacle avoidance for manip-

ulators and mobile robots. Int. J. Robot. Res., 5(1):90–

98.

Melchiorre, M., Scimmi, L. S., et al. (2022). Robot collision

avoidance based on artiﬁcial potential ﬁeld with local

attractors. In Proc. ICINCO, pages 340–350.

Raibail, M., Rahman, A. H. A., et al. (2022). Decentralized

multi-robot collision avoidance: A systematic review

from 2015 to 2021. Symmetry, 14(3).

Rodr

ıguez-Seda, E. J. (2024a). Decentralized low-energy

avoidance control framework for multiple mobile

agents using irregular observations. IEEE Trans. Con-

trol Syst. Technol., 32(3):1027–1039.

Rodr

ıguez-Seda, E. J. (2024b). Reactive collision avoid-

ance control for nonholonomic vehicles and obstacles

of arbitrary shape. ASME. Letters Dyn. Sys. Control,

4(3):031005.

Rodr

ıguez-Seda, E. J., Stipanovi

c, D. M., and Spong,

M. W. (2016). Guaranteed collision avoidance for

autonomous systems with acceleration constraints

and sensing uncertainties. J. Optim. Theory Appl.,

168(3):1014–1038.

Rodr

ıguez-Seda, E. J. and Stipanovi

c, D. M. (2020). Coop-

erative avoidance control with velocity-based detec-

tion regions. IEEE Control Syst. Lett., 4(2):432–437.

Rodr

ıguez-Seda, E. J., Tang, C., et al. (2014). Trajec-

tory tracking with collision avoidance for nonholo-

nomic vehicles with acceleration constraints and lim-

ited sensing. Int. J. Robot. Res., 33(12):1569–1592.

Stipanovi

c, D. M., Hokayem, P. F., et al. (2007). Coopera-

tive avoidance control for multiagent systems. J. Dyn.

Syst. Meas. Control, 129:699–707.

Stipanovi

c, D. M., Tomlin, C. J., and Leitmann, G. (2012).

Monotone approximations of minimum and maxi-

mum functions and multi-objective problems. Appl.

Math. Optim., 66(3):455–473.

Xiao, X., Liu, B., et al. (2021). Toward agile maneuvers in

highly constrained spaces: Learning from hallucina-

tion. IEEE Rob. Autom. Lett., 6(2):1503–1510.

Zhang, W., Rodr

ıguez-Seda, E. J., et al. (2020). Avoid-

ance control with relative velocity information for la-

grangian dynamics. J. Intell. Robot. Syst., 99:229–

244.

Zimmermann, S., Busenhart, M., et al. (2022). Differen-

tiable collision avoidance using collision primitives.

In Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst.,

pages 8086–8093.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

236