Feature Importance for Deep Neural Networks: A Comparison of

Predictive Power, Inﬁdelity and Sensitivity

Lars Fluri

Department of Computational Economics and Finance, Department of Management Accounting

University of Basel, Peter Merian-Weg 6, Basel, Switzerland

ﬂ

Keywords:

XAI, XML, SHAP, Shapley Value Sampling, DeepLIFT, LIME, Integrated Gradients, GradientSHAP,

Deep Learning, Neural Networks, Finance.

Abstract:

This paper evaluates the effectiveness of different feature importance algorithms employed on a neural net-

work, focused on target prediction tasks with varying data complexities. The study reveals that the feature

importance algorithms excel with data featuring minimal correlation between the attributes. However, their

determination considerably decreases with escalating levels of correlation, while the inclusion of irrelevant

features has minimal impact on determination. In terms of predictive power, DeepLIFT surpasses other meth-

ods for most data cases, but falls short in total inﬁdelity. For more complex cases, Shapley Value Sampling

outperforms DeepLIFT. In an empirical application, Integrated Gradients and DeepLIFT demonstrate lower

sensitivity and lower inﬁdelity, respectively. this paper highlights interesting dynamics between predictive

power and ﬁdelity in feature importance algorithms and offers key insights for their application in complex

data scenarios.

1 INTRODUCTION

While machine learning techniques, particularly neu-

ral networks, have demonstrated tremendous poten-

tial across various applications, their adoption in aca-

demic research has been hindered by their ”black

box” nature (Castelvecchi, 2016). Despite their con-

siderable predictive power, these models often have

non-transparent functional forms. This is especially

challenging in ﬁelds like economics, ﬁnance, and so-

cial sciences, where understanding the relationships

between variables is crucial (Molnar, 2020). This

study aims to address this gap by investigating the ef-

fectiveness of feature importance methods in provid-

ing interpretable insights for machine learning mod-

els. Speciﬁcally, it contributes to the literature by as-

sessing these methods in a controlled simulation with

known ground truth and comparing their performance

in an empirical case study. By doing so, it seeks to

enable both academic researchers and industry prac-

titioners to interpret machine learning models and ex-

plain their predictions in understandable terms. The

opacity of machine learning models has driven re-

search in explainable machine learning (XML) and

explainable artiﬁcial intelligence (XAI). Feature im-

https://orcid.org/0009-0005-0031-8355

portance methods, developed to calculate the signiﬁ-

cance of individual features, have gained popularity,

especially in image analysis and pattern recognition.

However, a thorough examination of their explana-

tory power in economics and ﬁnance is lacking. This

study’s ﬁndings are crucial for advancing the inter-

pretability of machine learning in these domains by

highlighting strengths, weaknesses, and possible pit-

falls of various feature importance methods..

2 LITERATURE REVIEW

Using methods for explainability and interpretability

is widespread in the current research literature — this

subsection mentions the most relevant works. There

is a plethora of feature importance methods for neu-

ral networks and machine learning models in gen-

eral. Examples include Integrated Gradients (Sun-

dararajan et al., 2017), Shapley Additive Explana-

tions (Lundberg and Lee, 2017), Local Interpretable

Model-Agnostic Explanations (Ribeiro et al., 2016),

and Deep Learning Important FeaTures (Shrikumar

et al., 2017). Additional measures include RelA-

Tive cEntrality to prioritise candidate genetic variants

(Crawford et al., 2019). This framework was also ex-

Fluri, L.

Feature Importance for Deep Neural Networks: A Comparison of Predictive Power, Inﬁdelity and Sensitivity.

DOI: 10.5220/0012903300003886

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Explainable AI for Neural and Symbolic Methods (EXPLAINS 2024), pages 15-26

ISBN: 978-989-758-720-7

tended for highly collinear predictors (Ish-Horowicz

et al., 2019). Applications of feature importance

methods and neural networks in the ﬁelds of eco-

nomics and ﬁnance are widespread. Convolutional

neural networks (CNN) have been shown to be effec-

tive methods when it comes to ﬁnancial time-series

prediction tasks (Chen et al., 2016). In the ﬁeld of

feature importance, comparisons of feature selection

methods based on importance calculations for solv-

ing classiﬁcation problems in ﬁnance exist (Xiaomao

et al., 2019). Research in ﬁnance also started to incor-

porate feature selection for ﬁnancial stress predictions

(Liang et al., 2015). However, the current literature is

suffering from an interesting knowledge gap. Speciﬁ-

cally, it is assumed that the feature importance attribu-

tion appropriately reﬂects the true underlying causal

link between the input features and the output predic-

tion. However, in empirical data, the true underlying

relationships between the target and the features are

generally not observable, and most of the time com-

pletely unknown. Therefore, feature importance at-

tributions are necessarily only approximations of the

underlying relationships. To gauge the relative deter-

mination and predictive power of feature importance

attribution, further research is therefore necessary. In

this paper, a synthetic data generating process (DGP)

is used to test various feature importance methods in

terms of predictive power, inﬁdelity, and sensitivity.

This paper thus provides a comprehensive analysis

of the predictive power of various feature importance

methods. This paper also closes a methodological gap

by offering a comparative setup to justify the chosen

importance methods.

3 METHODS FOR FEATURE

IMPORTANCE ATTRIBUTION

This section provides an overview over some of the

most important feature importance attributions cur-

rently in use. Subsection 3.1 provides a general in-

troduction to the methodology, while Subsection 3.2

highlights the speciﬁc methods used in this study.

Subsection 3.3 brieﬂy discusses limitations and draw-

backs.

3.1 General Overview

Feature importance methods are tools used to mea-

sure how much inﬂuence each feature in the data has

on the model’s predictions. This subsection brieﬂy

highlights general concepts. More in-depth analyses

and reviews can be found in the surrounding litera-

ture (Gevrey et al., 2003), which reviews and com-

Table 1: Importance attribution method overview can gen-

erally be categorised by model-agnosticism and mechanism

of importance computation.

method agnosticism mechanism

IG no gradient

GSHAP yes perturbation

(gradient-boosted)

LIME yes perturbation

DeepLIFT no gradient-like

SVS yes perturbation

pares different feature selection methods, including

those based on neural networks, decision trees, and

regression models. Since this study is concerned with

(deep) neural networks, neural-network speciﬁc as

well as model-agnostic importance attribution meth-

ods are introduced. Feature importance methods

are divided into backward-based and forward-based

methods. Forward-based methods move from the in-

put to the output through the neural network, while

backward-based methods move backwards from the

output to input to compute importance. Forward-

based methods compute the importance of a feature as

the difference in the output between a trained model

where the feature is present versus a trained model

where the feature is missing. This can be under-

stood as a leave-one-out calculation of importance.

Backward-based methods measure the importance of

a feature through the gradient (or a gradient-similar

measure) of the output with respect to the inputs. Sub-

section 3.2 brieﬂy introduces the relevant methods

and their theoretical frameworks.

3.2 Method Overview

The selected methods for this study are Integrated

Gradients (IG), GradientSHAP (GSHAP), Local In-

terpretable Model-Agnostic Explanations (LIME),

ShapleyValueSampling (SVS), and DeepLIFT. They

were chosen due to their concept heterogeneity and

popularity in previous applications. The follow-

ing paragraphs brieﬂy discuss their methodological

frameworks.

IG. IG was proposed as a framework for interpret-

ing the predictions of deep neural networks by assign-

ing attribution scores to input features (Sundararajan

et al., 2017). IG back-propagates and calculates im-

portance through gradients. Assume that f : R

→ R

is a function that represents a neural network, x is the

input at hand, and x

is a baseline input. In terms of

a single observation and considering the straight line

(in R

) from the baseline x

to the input x, one can

compute the gradients at all points along the path. In-

tegrated gradients are obtained by integrating over the

EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods

computed gradients. The integrated gradient IG

(x)

along the i

dimension for a single observation input

x and baseline x

is deﬁned as



− x



∂ f



+ α ·



x − x



∂x

dα, (1)

where

∂F(x)

∂X

is the gradient of f (x) along the i

feature

dimension (Sundararajan et al., 2017).

LIME. LIME is a model-agnostic method that of-

fers local explanations for the prediction of any clas-

siﬁer (Ribeiro et al., 2016). LIME learns an inter-

pretable model around the prediction with the goal of

faithfully replicating the classiﬁer’s behaviour in the

local region. The attribution method deﬁnes an expla-

nation model g ∈ G in order to explain the function f ,

where G is a class of potentially interpretable models.

LIME then produces a local explanation obtained by

ξ(x

) = argmin

g∈G

L ( f ,g,π

) + Ω(g). (2)

L is a measure of how unfaithful a simpliﬁed expla-

nation model g is in explaining the function f in the

neighbourhood π

and Ω(g) is a measure of com-

plexity of the explanation model. LIME can be used

with different model classes G, ﬁdelity functions L ,

and complexity measures Ω. LIME is designed to be

model-agnostic and therefore does not make any as-

sumptions about f . Furthermore, it is a local method,

because it computes the importance of a feature with

respect to a prediction on a single observation. LIME

can also be aggregated to create a global understand-

ing of feature importance, as will be shown in Sec-

tion 4.6.

DeepLIFT. DeepLIFT was introduced as a tech-

nique to decompose the output prediction of a neu-

ral network by back-propagating the contributions of

all neurons in the network to every feature of the input

(Shrikumar et al., 2017). It assigns contribution C

∆x

∆t

scores based on difference-from-reference neuron ac-

tivations. As described previously, reference activa-

tions are synonymous to baseline activations. For the

feature along the i

feature dimension, the difference-

from-reference between observation x and the refer-

ence x

is denoted by by ∆x

. The difference in the

neuron output is given as

∆t = t − t

, (3)

where t is the activation of a neuron at x and t

is the

reference activation of the neuron at x

. DeepLIFT

requires completeness of the form

∑

i=1

∆x

∆t

= ∆t, (4)

indicating that the sum of attributions must be

equivalent to the difference-from-reference activa-

tion. DeepLIFT is not model-agnostic because it is

only applicable to neural networks.

SHAP. SHAP is a forward-based importance

method that computes importance using perturbations

and differences in model outputs (Lundberg and Lee,

2017). SHAP is based on Shapley values from coop-

erative game theory, and it has several desirable theo-

retical properties. SHAP assigns importance by train-

ing two different models, one with the feature present

S∪{d}

and one with the feature withheld f

. It then

compares predictions from the two models

S∪{d}



S∪{d}



− f

). (5)

Since the effect of one feature depends on other fea-

tures in the set S, the difference described before-

hand is computed for all possible subsets S ⊆ F\{d},

where F is the complete set of all features. The Shap-

ley values φ

are a weighted average of all possible

differences

∑

S⊆F\{d}

|S|!(|F| −|S| − 1)!

|F|!



S∪{d}



S∪{d}



− f

)



(6)

and used as a proxy for feature importance. Due to the

computational complexity of Shapley values, multiple

approximations and boosted methods have been intro-

duced. Shapley Value Sampling (SVS) (Strumbelj and

Kononenko, 2010) is a sampling-based approach to

the calculation of SHAP that reduces computational

burden (Castro et al., 2009). In this study, it is used as

a proxy for SHAP values. GradientSHAP (GSHAP)

is an extension of the original SHAP method. It cal-

culates the gradient of outputs with respect to a cho-

sen baseline and input observation. The SHAP val-

ues can then be estimated using the expected values

of these gradients times the difference between inputs

and baselines.

3.3 Limitations, Drawbacks and

Extensions

Both forward-based and backward-based attribution

methods suffer from drawbacks and limitations. Gen-

erally speaking, all methods require baselines to cal-

culate the importance attribution of features, where

the baseline represents the normal or typical be-

haviour of the model. These baselines are crucial for

the calculation of importance attribution and must be

chosen carefully. Previous research has explored pos-

sible (dis-)advantages of different baselines for im-

age analysis (Sturmfels et al., 2020). Backward-based

Feature Importance for Deep Neural Networks: A Comparison of Predictive Power, Inﬁdelity and Sensitivity

methods are limited by multiple issues. First, they

struggle with some activation functions of neural net-

works, for example the ReLu. ReLu zeroes out gradi-

ents which makes it hard to approximate importance.

Additionally, gradient-based methods often struggle

with modelling saturation, meaning that once a fea-

ture reaches a certain threshold where its importance

to the target stays the same, it may incorrectly be

given an importance score of zero. Forward-based

methods can be computationally expensive because

they require training of the model for every possible

subset of features. Sampling mechanisms, i.e. SVS,

or boosting procedures such as GradientSHAP may

be reduce the computational burden. However, the

analysis of high-dimensional still introduces signif-

icant computational burden. Additionally, forward-

based methods generate an out-of-distribution (OOD)

problem for the neural network because they force the

model to extrapolate it to a point of the multivari-

ate distribution that does not naturally occur in the

data. Finally, forward-based methods have from the-

oretical constraints. For example, SHAP assumes that

features are independent for the calculation of feature

importance. This is a strong assumption in the case

of a real-world application that is criticised in (Kumar

et al., 2020).

4 EXPERIMENTAL SETUP

This section explains the setup for the simulation

study. Subsection 4.1 elaborates on the general setup,

while Subsections 4.2, 4.3, and 4.4 discuss speciﬁc

details of the DGP, the neural network, and the impor-

tance attribution methods. Subsection 4.6 describes

the performance measurement for the synthetic and

empirical data.

4.1 General Setup

The setup of the simulation study in this paper con-

sists of three steps. In the ﬁrst step, synthetic data

is generated from a pre-speciﬁed DGP. In the second

step, the neural network is trained on the synthetic

data. The third and last step consists of the computa-

tion of the importance attribution and the analysis of

determination. The goal of the data generation is to

create a data set where the underlying characteristics

are known in order to evaluate how well the impor-

tance attribution performs. Table 2 shows the differ-

ent cases of the DGP. The process for generating syn-

thetic data starts by creating a sample of features X

and a discriminator D as the underlying causal rela-

tionship between X and Y . A more detailed explana-

tion of the feature creation is found in Subsection 4.2.

The target variable is created as a noisy linear combi-

nation of the discriminator D and the features sample

X, formulated as

T = D · X + ε, (7)

where D is a vector of random integers and

ε ∼ N



ˆµ



where c is a scaling factor for the variance of the

Gaussian noise term. The scaling factor is set to

c = 0.4. This level of noise in the DGP leads to a true

of between 0.8 and 0.9, which is an appropriate

level of disturbance in the data, especially considering

that additional disturbances such as marginal transfor-

mations as well as spurious and irrelevant features are

added. The discriminant D is sampled from a discrete

uniform distribution U{−10,10}. This means that the

features with a negative (positive) discriminant coefﬁ-

cient have a negative (positive) inﬂuence on the target

T . To create regression targets, T is transformed us-

ing a logit transformation of the form

logit

) = y

1 + e

∀i ∈ {1,.. ., n}, (8)

to map the target to [0,1]. In order to introduce non-

linearity to the marginal distributions of the features,

the generated sample are transformed using a quan-

tile transformation of an arbitrary distribution. After

the target is created using the combination mentioned

in Equation (8), the features are transformed using a

column-wise quantile transformation

−1

) = U

∀ j ∈ {1, .. .,m} (9)

where F

−1

is the inverse of the row-wise cumula-

tive distribution function. This maps the normally-

distributed variables to [0, 1]. Afterwards, the stan-

dard uniform sample is transformed by applying a

transformation on U such that

= F

) ∀ j ∈ {1, .. .,m}. (10)

These two steps are a common procedure in sim-

ulation and data generation that allow an arbitrary

marginal distribution of the features while still pre-

serving the multivariate dependency between fea-

tures. This increases the data complexity and makes

the training process as well as the importance attribu-

tion more challenging.

4.2 Feature Creation

Three distinct types of features can be created in the

simulation study: Relevant, spurious, and irrelevant

EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods

features. Relevant features are either continuously

or discretely distributed, while spurious and irrele-

vant features are always continuously distributed. The

continuously distributed features are sampled from a

multivariate normal distribution given by

p(X, µ,Σ) =

(2π)

n/2

|Σ|

1/2

−

(X−µ)

′

−1

(X−µ)

, (11)

where is Σ a randomly generated covariance matrix

and µ is a mean vector. The covariance matrix Σ is

used to control the correlation between the synthetic

features. The constraints for the maximum level of

allowed covariance depend on the speciﬁcation of the

DGP. These features are at a later stage transformed

via a quantile transformation of a χ

distribution to

introduce non-linearity to the classiﬁcation task. Cat-

egorical features are created through converting some

numerical variables into distinct categories. The case

probabilities convert the numerical features into cate-

gorical ones and preserve the underlying dependence

structure of the data. To keep the DGP as close to a

real-world application as possible, these features are

encoded as dummy variables for use in the neural net-

work and are also multiplied with the discriminator D

in dummy form. The rationale is that these features

should represent an indicator, for example group or

sector membership, not linearly additive factors. In

addition to the relevant features described above, the

data-generating process also includes spurious fea-

tures in certain settings. Spurious features are corre-

lated to the relevant features through the multivariate

normal distribution described in Equation (11), but

do not inﬂuence the target variable via the discrim-

inant D. This increases the complexity of the pre-

diction or classiﬁcation task for the neural network

and the feature importance attribution. Irrelevant fea-

tures are sampled from an independent distribution

and therefore are statistically independent from the

relevant and spurious features. They do not inﬂuence

the target variables Y and can therefore be considered

completely irrelevant. This differentiates them from

spurious features which do not inﬂuence the target di-

rectly but may not be statistically independent from

it. In theory, uncorrelated feature with an importance

score of zero should be easy to detect.

4.3 Neural Network

Hyperparameterisation

The neural network trained on the data is a three-

layer, fully-connected neural network. It consists of

three hidden layers with 5,4,2 nodes respectively, and

a batch normalisation layer before every hidden layer.

It is trained on 80% of the data set. The remaining

Table 2: The DGP can reﬂect six different cases with in-

creasing data complexity. The columns specify the number

of total, spurious, and irrelevant features as well as the cor-

relation bounds.

case features spurious irrelevant correlation

I 20 0 0 [-0.3,0.3]

II 20 0 0 [-1,1]

III 30 10 0 [-0.3,0.3]

IV 30 10 0 [-1,1]

V 35 10 5 [-0.3,0.3]

VI 35 10 5 [-1,1]

20% are used for testing and as input for the feature

importance algorithms. The network is trained for

200 epochs per experiment. The sigmoid activation

function is used in every layer. As described in Sec-

tion 3, the sigmoid function is chosen because other

activation functions may not be suited for all feature

importance methods . An overview of the hyperpa-

rameterisation is provided in Table 3.

4.4 Importance Attribution Methods

Most of the feature importance methods require some

hyperparameterisation, for example the setting of

baseline values against which the importance attribu-

tion is calculated. In this example, the baseline is set

to 1, because a χ

distribution has mean k (in this case,

k = 1). Additional possible conﬁgurations include us-

ing the training data as baselines for importance at-

tribution in the test set. The perturbation function

passed to the inﬁdelity and sensitivity calculation is

given as

pert

) = ˜x

= x

− η ∀i ∈ {1,..., n} (12)

where x

is one observation of the input and

η ∼ N(0,0.0009). (13)

The perturbation function has been chosen in ac-

cordance with the usage tutorials of the software

package used for feature importance calculation. Nu-

merical experiments show that the choice of perturba-

tion function does not signiﬁcantly affect the compu-

tations and results.

Table 3: Hyperparameters for the neural network trained on

the synthetic and empirical data.

hyperparameter parameterisation

hidden layers and nodes 5,4,2

learning rate 0.003

batch size 50

epochs 200

dropout probability 0.2

activation function sigmoid

Feature Importance for Deep Neural Networks: A Comparison of Predictive Power, Inﬁdelity and Sensitivity

4.5 Data Cases

There are six different scenarios for data creation and

the underlying DGP. The general idea is to replicate

data structures and anomalies that are most prominent

in real-world data with the two most frequent anoma-

lies being high levels of correlation and spurious fea-

tures. Table 2 shows an overview of the relevant char-

acteristics. Case I data is weakly correlated with cor-

relation bounds given through the covariance matrix Σ

with every off-diagonal entry being ∈ [−0.3,0.3]. The

total number of features is 20 with 17 discretely dis-

tributed features, three categorical ones and no redun-

dancies. Case II data has 20 variables with no spuri-

ous features and correlation bounded by [−1,1]. Case

III data has 30 features, 17 relevant continuous ones,

3 relevant discrete ones, and 10 spurious features. Be-

cause of the constraints of positive semi-deﬁnite ma-

trices for the covariance, the maximum correlation in

the off-diagonals is lower than the numerical bounds.

Case IV data combines complications and character-

istics from case II and III such that the data is cor-

related and the some of the numerical features are

spurious. This should imitate the presence of both

data anomalies, as would most likely be expected in

a real-world application. The last data anomaly — as

represented in case V and VI — is the presence of

irrelevant features. These features are statistically in-

dependent from the relevant and spurious X and the

target Y . The features are drawn from a separate mul-

tivariate distribution.

4.6 Performance Evaluation

This section brieﬂy explains how the performance of

the feature importance methods is measured in the

synthetic and the empirical setup. In the study of syn-

thetic data with known ground truth, the performance

of the feature importance methods can be evaluated

directly. In the empirical application, the importance

attribution performance cannot be measured directly

because the causal link between Y and X is unknown.

Synthetic Data. This paragraph summarises how

performance is measured when the neural network is

trained on synthetic data. Four different components

are of interest: The ﬁrst one is the performance of

the neural network in the prediction task. The sec-

ond component is the determination of the feature

importance methods with respect to the true under-

lying causal link D. The two remaining components

are the inﬁdelity and sensitivity of the importance at-

tribution. To ensure the robustness of results, the

experiment described in the previous section is con-

ducted repeatedly. The neural network is retrained

and the importance attributions are calculated 100

times on a resampled or newly generated data set. The

ﬁrst component can be measured using R

— as one

usually would in the context of any regression task.

The second component (feature importance determi-

nation) is evaluated by regressing the discriminant D

on Θ = {θ

,. .. ,θ

}, which is a vector containing the

importance attributions of every feature. These attri-

butions can be calculated as

∑

i=0

i,d

∑

i=0

|θ

i,d

∀i ∈ {1,.. ., D} (14)

which is an aggregation of individual attributions to

obtain a global impression of the data. The numerator

is the sum of the attributions, while the denominator

is the L1 norm of the attributions. This gives the nor-

malised sum of attributions. Given that D represents

the underlying causal structure of the DGP, the score

or the coefﬁcient of determination

= 1 −

∑

i=1

(θ

− d

)

∑

i=1



−



, (15)

where φ

is the attribution of an individual feature, d

is the true importance of the synthetic feature, and

is the mean importance. This approximates how

well the average importance attribution serves as a

proxy of true global importance if φ

is the impor-

tance attribution for an individual feature, whereas d

is the true causal importance of the feature. Ideally,

the R

of the regression on the determinant should

be as close to 1 as possible, assuming that the fea-

ture importance coefﬁcients describe the underlying

data structure sufﬁciently well. To determine the reli-

ability of the importance attribution, two components

have to be studied further. First, the ﬁdelity of the at-

tributions with respect to the original model. Second,

the sensitivity of the attributions with respect to input

perturbations. Two appropriate measures, inﬁdelity

and sensitivity of explanations, have been introduced

in previous research (Yeh et al., 2019). Inﬁdelity is

the expected mean-squared error between the expla-

nation multiplied by a meaningful input perturbation

and the differences between the predictor function at

its input and its perturbed input. Inﬁdelity is derived

from the completeness property, a property or axiom

all importance methods share. It requires that the dif-

ference between the output of f at input x and x

must

be equivalent to the importance attributions. The inﬁ-

delity INFD(Φ, f ,x) is formally deﬁned as

η∼N



Φ( f ,x) − ( f (x) − f (x − η))



(16)

for a black-box function f , an explanation function

Φ, a random variable η distributed as described in

EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods

Equation (13). The explanation function Φ is one

of the feature importance methods introduced be-

forehand. The calculation of inﬁdelity requires the

trained model, the attribution, a perturbation func-

tion for the inputs, and the attributions calculated by

the importance method. Another interesting measure

is sensitivity, which measures the extent of expla-

nation change when the input is slightly perturbed.

The relevant metric here is so-called maximum sen-

sitivity which is computed using a black-box func-

tion f , an explanation function Φ, and a given input

neighbourhood radius r. The maximum sensitivity

SENS

MAX

(Φ, f ,x,r) is deﬁned as

max

∥ ˜x−x∥⩽r

∥(Φ( f , ˜x) − Φ( f ,x))∥, (17)

where ˜x is a slightly perturbed variation of the input x

in the neighbourhood of x with radius r. ∥...∥ is the

Frobenius norm. In this application, the perturbation

∆( ˜x,x) is distributed as the random variable described

in Equation (13). Ideally, attribution methods should

exhibit low amounts of inﬁdelity and sensitivity. A

lower inﬁdelity score means that the explanation pro-

vided by the feature importance method closely aligns

with the actual behaviour of the model, which is desir-

able. Sensitivity measures how much the explanation

changes when small changes are made to the input. A

lower sensitivity score means that the explanation is

stable and does not drastically change due to minor

changes in input, which is also desirable. For the dis-

cussion of results in Section 5, the results are reported

as total inﬁdelity and total sensitivity. Total inﬁdelity

and maximum sensitivity are computed for every fea-

ture of every observation and to make results compa-

rable, these results are summed up and summarised as

total inﬁdelity and total sensitivity.

Empirical Data. This subsection summarises how

performance is measured when the neural network is

trained on empirical data. In the empirical applica-

tion, a measure of predictive power is not available.

Since the underlying causal link D cannot be mea-

sured and is unknown, the determination of the impor-

tance attribution cannot be computed. The other three

measures (neural network performance, importance

attribution inﬁdelity and sensitivity) can be computed

nonetheless. The latter two are used to compare the

performance of the attribution methods in an empiri-

cal application.

5 SIMULATION STUDY RESULTS

This simulation study with known ground truth serves

as a benchmarking tool for the capabilities of the im-

Table 4: R

of neural network for 100 experiments includ-

ing true R

shows satisfying in- and out-of-sample perfor-

mance, as compared to the true R

of the DGP.

training validation test true

case I 0.759 0.480 0.500 0.858

case II 0.811 0.605 0.610 0.856

case III 0.802 0.433 0.437 0.859

case IV 0.825 0.527 0.533 0.852

case V 0.804 0.405 0.423 0.866

case VI 0.835 0.509 0.501 0.862

portance attribution methods. The performance of the

feature importance methods is measured as described

in Subsection 4.6, while the neural network perfor-

mance is summarised in Table 4. The column for the

true R

shows the R

achieved by Maximum Likeli-

hood Estimation (MLE) when the underlying func-

tional form is known and the determinant D is es-

timated from the data. This estimated optimal R

should theoretically be smaller than the training R

(due to overﬁtting) and larger than the test R

(due to

bias). The methods should ideally achieve high coef-

ﬁcients of determination and low levels of inﬁdelity

and sensitivity. The coefﬁcients of determination for

the feature importance calculation are presented here-

after for the different setups of the data-generating

process. To ensure robustness of results, the experi-

ment as described in Section 4 is repeated 100 times.

For every experiment, a sample of synthetic data with

1000 observations is generated. The parameter speci-

ﬁcations for the individual data cases can be found in

Table 2.

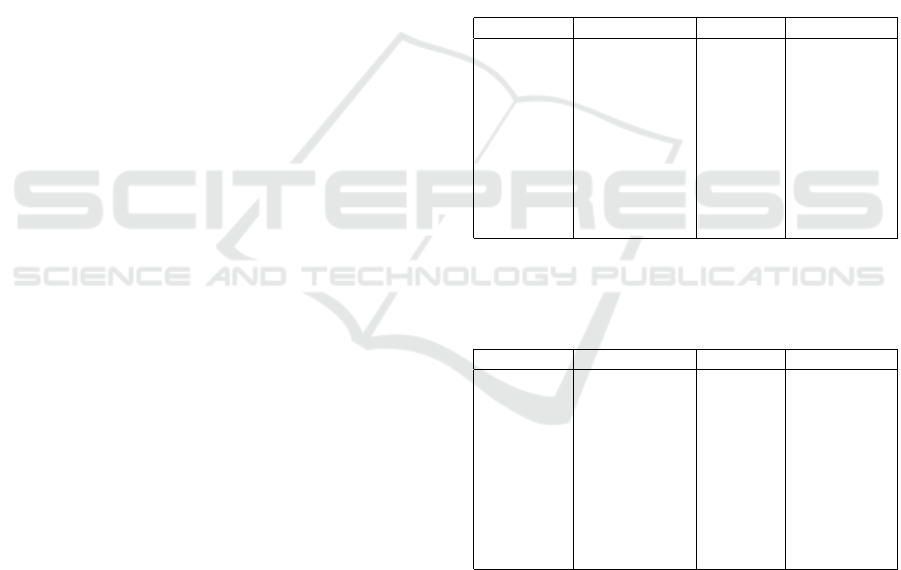
Case I. For the ﬁrst conﬁguration, the correlation

levels are low. This should make it easier for a cor-

rect importance attribution since multicollinearity is

not an issue. The network’s performance in terms

of training, validation, and testing can be assessed

from Table 4. The data appears to be well compre-

hended by the feature importance methods used. As

can be inferred from Table 7, DeepLIFT shows the

highest determination, closely followed by SVS. In

terms of total inﬁdelity, LIME stands out with the best

performance among the methods. DeepLIFT, despite

its strong determination, also presents noticeable inﬁ-

delity. Regarding sensitivity, IG is best-in-class.

Case II. The second conﬁguration does not gener-

ate any spurious features and allows for high corre-

lation levels between the features in the data. As

observed from Table 8, the network performance is

not signiﬁcantly impacted by the strong correlation

in training, validation, and testing phases. Review-

ing the results from Table 8, introducing correlation

Feature Importance for Deep Neural Networks: A Comparison of Predictive Power, Inﬁdelity and Sensitivity

has a discernible impact on attribution performance.

DeepLIFT maintains its lead in terms of determina-

tion. IG presents the lowest sensitivity, while LIME

shows the lowest inﬁdelity. Notably, there is a tan-

gible drop in performance across all methods when

compared to non-correlated data conﬁgurations. Fur-

thermore, inﬁdelity levels rise considerably for all

methods. Total sensitivity, as well, sees an uptick.

Backward-based methods such as DeepLIFT and IG

remain less sensitive to perturbations, while forward-

based methods, including GradientSHAP, LIME, and

SVS, show increased sensitivity.

Case III. For the third conﬁguration, 10 additional

features are added. These continuously distributed

features have an importance score in the discrimina-

tor vector D of 0 and therefore do not inﬂuence the

target directly. Since the features are weakly corre-

lated, it is possible that there is non-zero correlation

between the spurious features and the target. As seen

in Table 4, the neural network performance for the

training data slightly decreases from case II, and the

validation and test performance decrease more sig-

niﬁcantly compared to case II. This decrease shows

a wider performance gap between the training, vali-

dation, and testing stages. Despite this performance

decrease, when comparing Table 8 and Table 9, the

determination score does not decrease signiﬁcantly.

Most notably, DeepLIFT still outperforms the other

methods in this category. Interestingly, determination

increases slightly for all methods except LIME. This

is most likely due to the fact that all methods can suf-

ﬁciently well differentiate spurious features from im-

portant ones. In terms of inﬁdelity, LIME exhibits the

best performance, followed by IG. GradientSHAP has

the highest sensitivity.

Case IV. Case IV data introduces 10 spurious fea-

tures as well as possibly strongly correlated data. As

is shown in Table 4, the delta between training and test

performance is smaller compared to previous cases.

When correlation is high and 10 of the 30 original

features are spurious, determination — as measured

by feature importance R

— decreases signiﬁcantly.

DeepLIFT still performs best, closely followed by

SVS. Total inﬁdelity does not change signiﬁcantly

from case III (Table 9) to case IV (Table 10). To-

tal sensitivity signiﬁcantly increases from case III to

case IV data for GradientSHAP and LIME. Integrated

Gradients and DeepLIFT show the smallest sensitiv-

ity, while the sensitivity of LIME and GradientSHAP

is largest.

Case V. In case V, the data set is expanded to ad-

ditionally include 5 irrelevant features. This change

leads to diminution in the model’s test and valida-

tion performance, compared to both cases II and III,

as per Table 4. For determination of feature impor-

tance, SVS overtakes DeepLIFT and now performs

best. When analysing total inﬁdelity, DeepLIFT and

GradientSHAP show the highest levels of inﬁdelity,

while SVS and LIME are the methods with the high-

est ﬁdelity. Sensitivity shows comparable results to

previous cases: Integrated Gradients and DeepLIFT

perform well, while GradientSHAP and LIME are ex-

tremely sensitive.

Case VI. Case VI data is comparable to case IV

data since both sets are created using comparable lev-

els of correlation between relevant and irrelevant fea-

tures. Case VI data also introduces irrelevant features.

Determination, as shown in Table 12, decreases for

all methods except LIME. SVS performs best with

DeepLIFT as a close second. Integrated Gradients

and GradientSHAP are close, while LIME performs

worst. Total inﬁdelity and total sensitivity remain un-

changed in relative terms:

Summary. Table 5 shows the results for all experi-

ments on synthetic and empirical data. For synthetic

data, it is clear that neural network-speciﬁc methods,

namely DeepLIFT and IG, perform best in terms for

determination and sensitivity. LIME shows the low-

est inﬁdelity out of all the methods, even though the

difference to other methods is not that big. Tables 7 to

12 show that spurious features, with zero causal im-

portance, are less problematic than highly correlated

data. Correlated data cause a signiﬁcant drop in deter-

mination coefﬁcients, as seen in Table 8, even when

all features are relevant predictors. In contrast, case

III, despite having one-third spurious features, still

produced higher determination scores than case II. A

similar pattern was found in case V (Table 11), where

irrelevant features had little effect on the determina-

tion score. However, a mix of spurious features and

high correlation in case IV caused a drop in impor-

tance scores (Table 8 IV). This suggests the methods

used are robust against spurious features but strug-

gle with correlated data. Irrelevant features, while

not signiﬁcantly impacting R

, do affect the sensitiv-

ity of some methods, highlighting the need for pre-

processing and dimensionality reduction to improve

feature importance methods in practice.

EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods

Table 5: Best-in-class performance for synthetic and empir-

ical data.

case determination inﬁdelity sensitivity

I DeepLIFT LIME IG

II DeepLIFT LIME IG

III DeepLIFT LIME IG

IV DeepLIFT LIME IG

V SVS LIME IG

VI DeepLIFT LIME IG

Ames DeepLIFT IG

California DeepLIFT IG

FF5 GSHAP LIME

Table 6: R

of neural network for 100 iterations shows sat-

isfying performance and no signiﬁcant overﬁtting.

dataset training validation test

Ames 0.699 0.693 0.698

California 0.603 0.570 0.592

FF5 0.195 0.131 0.133

6 EMPIRICAL RESULTS

The importance attribution methods previously used

on synthetic data are applied to empirical data to pro-

vide further insights. The data sets used are the Cali-

fornia house price dataset (Dheeru and Casey, 2017),

the Ames house price data set (Cock, 2010), and the

daily Fama-French-5 (FF5) factor dataset (Fama and

French, 2024). Since Section 5 showed that impor-

tance attribution is challenged by high levels of cor-

relation, it is worthwhile to analyse correlation in the

data at hand. As can be seen in the supplementary

documents to this study, most of the features do not

exhibit signiﬁcant levels of correlation. However,

some combinations of features do show high levels

of correlation. Table 6 summarises the neural net-

work performance for all datasets in training, valida-

tion, and testing. To compute and compare inﬁdelity

and sensitivity, the data from the corresponding data

sets is resampled for 100 repeated experiments. The

model is retrained for every resampling.

The results for 100 experiments on a sample with

1000 observations are shown in Tables 13 to 15. The

table shows that while the inﬁdelity is almost identical

for all methods, the total sensitivity varies substan-

tially. While the maximum sensitivity of DeepLIFT

and IG is small, GSHAP and SVS show considerably

higher total sensitivity. This is again in line with the-

oretical ﬁndings: Forward-based methods are much

more sensitive to small input perturbations.

7 SUMMARY

This study shows that the ﬁve importance attribution

methods that were reviewed in the paper generally

perform sufﬁciently well at identifying relevant and

spurious features as well as their magnitude. In a sim-

ulation study with underlying ground truth, the meth-

ods are able to approximate the underlying connection

between the features and the target. Nonetheless, the

simulation study shows that even in a simple neural

network, the computed importance scores cannot per-

fectly explain the underlying causal structure. Addi-

tionally, not all methods are alike, and DeepLIFT pre-

dictive performance outperforms the other methods

for most data cases with SVS coming in as a close sec-

ond. For more complex cases, SVS sometimes out-

performs DeepLIFT. Total inﬁdelity of DeepLIFT and

Integrated Gradients is usually higher, while the other

methods show a somewhat lower inﬁdelity. It is es-

pecially noteworthy that inﬁdelity of Integrated Gra-

dients and GSHAP sharply increased for more com-

plicated data structures. Total sensitivity of LIME,

GSHAP, and SVS is extremely high for all classes

under observation. On the other hand, DeepLIFT

and Integrated Gradients show low sensitivity for all

four data cases. This means that the attributed impor-

tance of the features varies less when the inputs are

slightly perturbed. This is in line with the current lit-

erature. Forward-based methods are more sensitive

to input perturbations than backward-based methods.

Adding irrelevant features to the data substantially in-

creases sensitivity of GSHAP and LIME. In the em-

pirical application, these results are partly replicated.

While neural network-speciﬁc methods, namely IG

and DeepLIFT perform well for the California house

price and the Ames house price data set, they are not

best-in-class for the FF5 data. On the one hand, this

shows that model-speciﬁc attribution methods can

provide substantial advantages over model-agnostic

methods. On the other hand, the suitability of the

method heavily depends on the speciﬁc task at hand

as well as the neural network hyperparameters. The

results discussed in Section 5 and 6 suggest that the

feature importance methods work well in understand-

ing the relationships between variables in synthetic

data. However, complex patterns in the data make it

difﬁcult to accurately determine which variables are

most important, especially in real-world data. This is

particularly problematic for data with a high degree

of correlation. In more general terms, it is important

to observe that feature importance methods are not a

one-size-ﬁts all toolbox. Before deciding on which

feature importance algorithms to use, it is necessary

to consider the underlying model speciﬁcations.

Feature Importance for Deep Neural Networks: A Comparison of Predictive Power, Inﬁdelity and Sensitivity

7.1 Limitations

This research paper is only a limited analysis of

the aspect of feature importance in deep neural net-

works. Multiple things should be considered. First,

the choice of baseline values signiﬁcantly inﬂuences

the feature importance calculation. In the case of im-

age analysis, research has shown how heavily the im-

pact of a feature attribution baseline inﬂuences the

computed importance scores (Sturmfels et al., 2020).

This is no different for data such as the one used in

this paper. Additionally, the data generation process

used in this paper leads to limited generalisability -

some of the results may be different for differing se-

tups. Finally, the neural network architecture heavily

inﬂuences the predictive power of a neural network.

For example, choosing a ReLu activation function (in-

stead of the sigmoid function in this paper) can lead

to signiﬁcant problems for the utilised gradient-based

attribution methods. Another component to consider

is the computational burden implied by feature im-

portance attributions. The computations in this paper

were done on small-scale model. For bigger mod-

els, the computational complexity increases drasti-

cally. For large-scale, industry-standard applications,

this is an important factor to consider.

7.2 Extensions and Practical

Implications

This paper has given valuable insights into the predic-

tive power, inﬁdelity, and sensitivity of various fea-

ture importance methods. Future research could im-

plement the insights gathered into practical research

in economics and ﬁnance. For example, adding met-

rics of uncertainty to feature importance can enhance

the insights gathered. Furthermore, seeing the robust-

ness of feature importance calculations over repeated

experiments can also be beneﬁcial in the realm of

variable selection. Additionally, it creates a baselines

for researchers to understand that feature importance

methods are not one-size-ﬁts-all solutions and should

therefore be chosen and calibrated carefully. Addi-

tionally, It is important to note that most current stud-

ies of feature importance focus mainly on image data.

In these cases, it is easy to visually check if the im-

portant areas identiﬁed by the network make sense.

But this kind of validation does not work for purely

numerical data. This means that feature importance

in ﬁnance and economics requires additional sanity

checks. Paths for new research in these ﬁelds could

concentrate on feature importance validation using

domain-speciﬁc knowledge. Looking forward, the

ﬁeld of user-friendly and explainable machine learn-

ing can additionally beneﬁt from studying the balance

between performance, complexity, and explainability.

As neural networks get more complex with deeper ar-

chitecture, they become harder to understand. This

is not in the best interest of the researchers and gen-

eral stakeholders if model predictions should also

stay explainable. This implies that future research

could focus on smaller, sparse models, that still of-

fer a certain level of interpretability. Looking beyond

feature-based attribution methods, researchers should

also focus on more high-level, human-friendly XAI

and XML methods. For example, Testing with Con-

cept Activation Vectors (TCAV) (Kim et al., 2018),

which explain importance not by features, but by so-

called concepts. Instead of focusing on single fea-

tures, TCAV analyses higher level ideas in the data.

In TCAV, these concepts are typically identiﬁed using

a separate model. This model is often a different neu-

ral network which is trained speciﬁcally to recognise

the concepts in the model’s internal representations

of the data. This can bring XAI closer to explanations

that are easily understandable and therefore human-

centric. Especially for high-dimensional input data,

the importance of a single feature may not be impor-

tant for humans to understand the prediction model.

They would probably be much more interested in the

importance of a concept for predictions. Since this

methodology is not yet popular in research in ﬁnance

and economics, it may be worthwhile to pursue re-

search concerning concept importance.

ACKNOWLEDGEMENTS

I thank Prof. Dr. Dietmar Maringer and Prof. Dr.

Sabine B

ockem for their valuable feedback and sug-

gestions on the paper.

REFERENCES

Castelvecchi, D. (2016). Can we open the black box of AI?

Nature News, 538(7623):20–23.

Castro, J., G

omez, D., and Tejada, J. (2009). Polynomial

calculation of the shapley value based on sampling.

Computers & Operations Research, 36(5):1726–

1730.

Chen, J.-F., Chen, W.-L., Huang, C.-P., Huang, S.-H., and

Chen, A.-P. (2016). Financial time-series data anal-

ysis using deep convolutional neural networks. In

2016 7th International Conference on Cloud Comput-

ing and Big Data (CCBD), pages 87–92. IEEE.

Cock, D. D. (2010). Housing prices in Ames, Iowa.

https://www.openintro.org/data/index.php?data=ames.

Accessed: 2024-09-12.

EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods

Crawford, L., Flaxman, S. R., Runcie, D. E., and West, M.

(2019). Variable prioritization in nonlinear black box

methods: A genetic association case study. The An-

nals of Applied Statistics, 13(2):958.

Dheeru, D. and Casey, G. (2017). UCI machine learning

repository. Accessed: 2024-09-12.

Fama, E. F. and French, K. R. (2024). Fama/French 5

factors. https://mba.tuck.dartmouth.edu. Accessed:

2024-09-12.

Gevrey, M., Dimopoulos, I., and Lek, S. (2003). Review

and comparison of methods to study the contribution

of variables in artiﬁcial neural network models. Eco-

logical Modelling, 160(3):249–264.

Ish-Horowicz, J., Udwin, D., Flaxman, S., Filippi, S., and

Crawford, L. (2019). Interpreting deep neural net-

works through variable importance. arXiv preprint

arXiv:1901.09839.

Kim, B., Wattenberg, M., Gilmer, J., Cai, C., Wexler, J.,

Viegas, F., et al. (2018). Interpretability beyond fea-

ture attribution: Quantitative testing with concept acti-

vation vectors (TCAV). In Proceedings of the 35th In-

ternational Conference on Machine Learning, pages

2668–2677. PMLR.

Kumar, E. I., Venkatasubramanian, S., Scheidegger, C., and

Friedler, S. (2020). Problems with Shapley-value-

based explanations as feature importance measures. In

Proceedings of the 37th International Conference on

Machine Learning, pages 5491–5500. PMLR.

Liang, D., Tsai, C.-F., and Wu, H.-T. (2015). The effect

of feature selection on ﬁnancial distress prediction.

Knowledge-Based Systems, 73:289–297.

Lundberg, S. M. and Lee, S.-I. (2017). A uniﬁed approach

to interpreting model predictions. Advances in Neural

Information Processing Systems, 30.

Molnar, C. (2020). Interpretable Machine Learning.

Lulu.com.

Ribeiro, M. T., Singh, S., and Guestrin, C. (2016). Why

should I trust you? Explaining the predictions of any

classiﬁer. In Proceedings of the 22nd ACM SIGKDD

International Conference on Knowledge Discovery

and Data Mining, pages 1135–1144.

Shrikumar, A., Greenside, P., and Kundaje, A. (2017).

Learning important features through propagating ac-

tivation differences. In Proceedings of the 34th In-

ternational Conference on Machine Learning, pages

3145–3153. PMLR.

Strumbelj, E. and Kononenko, I. (2010). An efﬁcient expla-

nation of individual classiﬁcations using game theory.

The Journal of Machine Learning Research, 11:1–18.

Sturmfels, P., Lundberg, S., and Lee, S.-I. (2020). Visualiz-

ing the impact of feature attribution baselines. Distill.

Published: 2020-01-10, Accessed: 2024-09-12.

Sundararajan, M., Taly, A., and Yan, Q. (2017). Axiomatic

attribution for deep networks. In Proceedings of the

34th International Conference on Machine Learning,

pages 3319–3328. PMLR.

Xiaomao, X., Xudong, Z., and Yuanfang, W. (2019). A

comparison of feature selection methodology for solv-

ing classiﬁcation problems in ﬁnance. In Journal of

Physics: Conference Series, volume 1284, pages 12–

16. IOP Publishing.

Yeh, C.-K., Hsieh, C.-Y., Suggala, A. S., Inouye, D. I.,

and Ravikumar, P. (2019). On the (in)ﬁdelity

and sensitivity for explanations. arXiv preprint

arXiv:1901.09392.

APPENDIX

The appendix contains the experiment results de-

scribed in the paper. Note that the results are rounded

to three decimals unless a higher grade of granularity

is required for comparisons (most often for the inﬁ-

delity metrics).

Table 7: Mean results (Standard Deviation) for 100 repeated

experiments on case I data. Best-in-class values are marked

with *.

determination inﬁdelity sensitivity

IG 0.186 0.0035 2.782*

(0.118) (0.0020) (0.822)

GSHAP 0.183 0.0037 21808.902

(0.118) (0.0021) (41842.360)

LIME 0.107 0.0025* 921.865

(0.093) (0.0012) (5259.562)

SVS 0.223 0.0028 142.402

(0.144) (0.0013) (87.815)

DeepLIFT 0.236* 0.0040 7.512

(0.114) (0.0019) (1.200)

Table 8: Mean results (Standard Deviation) for 100 repeated

experiments on the case II data. Best-in-class values are

marked with *.

determination inﬁdelity sensitivity

IG 0.129 0.0033 2.872*

(0.108) (0.0018) (0.911)

GSHAP 0.126 0.0036 24776.439

(0.106) (0.0018) (118520.80)

LIME 0.101 0.0026* 434.697

(0.089) (0.0012) (545.340)

SVS 0.146 0.0029 144.623

(0.119) (0.0014) (79.661)

DeepLIFT 0.174* 0.0041 7.537

(0.108) (0.0020) (1.441)

Feature Importance for Deep Neural Networks: A Comparison of Predictive Power, Inﬁdelity and Sensitivity

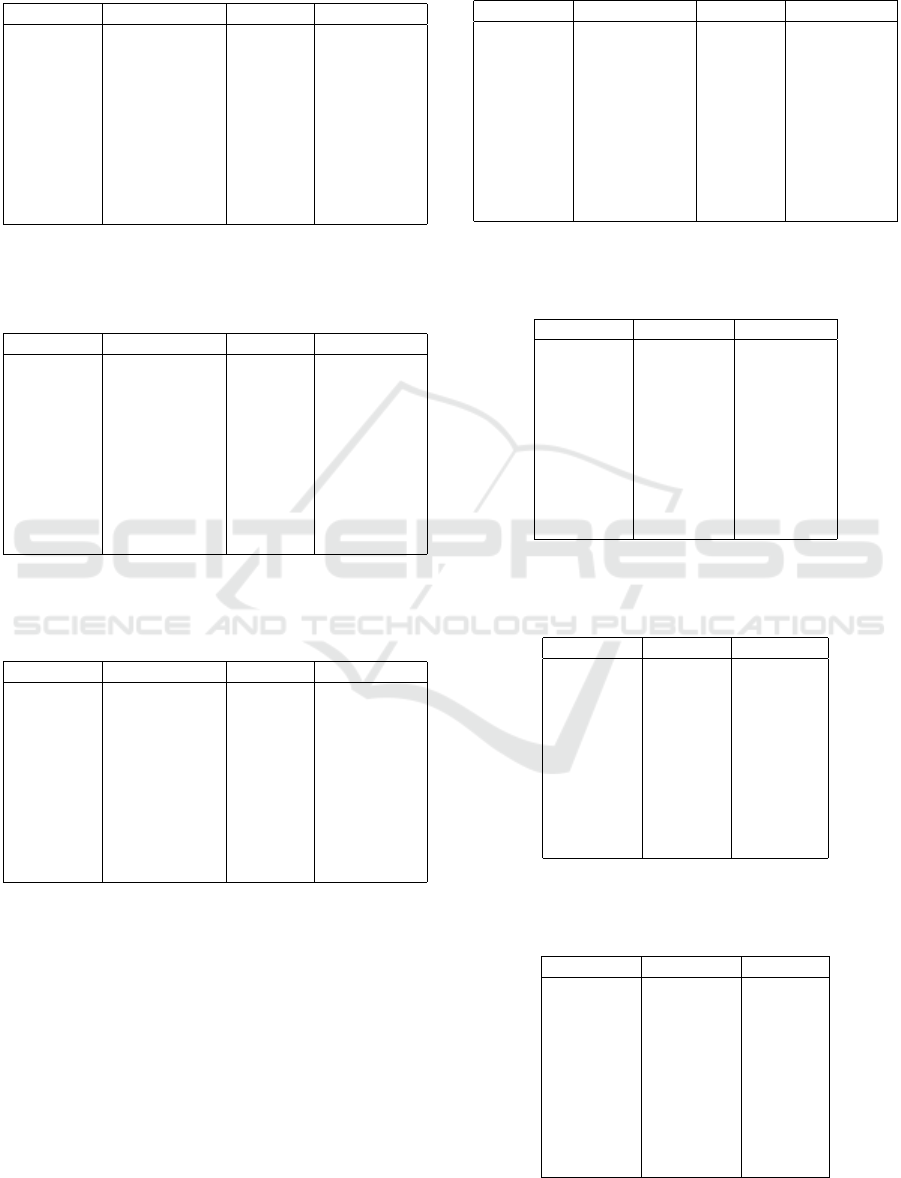
Table 9: Mean results (Standard Deviation) for 100 re-

peated experiments on case III data. Best-in-class values

are marked with *.

determination inﬁdelity sensitivity

IG 0.153 0.0030 2.816*

(0.117) (0.0010) (0.812)

GSHAP 0.148 0.0030 30712.477

(0.116) (0.0010) (77256.110)

LIME 0.066 0.0020* 446.402

(0.071) (0.0010) (451.300)

SVS 0.174 0.0030 176.937

(0.136) (0.0010) (135.055)

DeepLIFT 0.183* 0.0040 7.269

(0.111) (0.0010) (1.217)

Table 10: Mean results (Standard Deviation) for 100 re-

peated experiments on case IV data. Best-in-class values

are marked with *.

determination inﬁdelity sensitivity

IG 0.116 0.0030 2.591*

(0.104) (0.0014) (0.674)

GSHAP 0.118 0.0032 71441.851

(0.103) (0.0014) (492030.40)

LIME 0.069 0.0022* 970.022

(0.066) (0.0009) (4515.176)

SVS 0.137 0.0025 173.937

(0.112) (0.0010) (120.617)

DeepLIFT 0.142* 0.0035 6.835

(0.101) (0.0015) (0.996)

Table 11: Mean results (Standard Deviation) for 100 re-

peated experiments on case V data. Best-in-class values are

marked with *.

determination inﬁdelity sensitivity

IG 0.141 0.0029 2.517*

(0.112) (0.0013) (0.752)

GSHAP 0.139 0.0031 93285.070

(0.114) (0.0015) (599034.40)

LIME 0.052 0.0020* 549.692

(0.058) (0.0009) (1091.150)

SVS 0.179* 0.0023 165.701

(0.137) (0.0010) (119.806)

DeepLIFT 0.154 0.0032 6.700

(0.086) (0.0016) (1.035)

Table 12: Mean results (Standard Deviation) for 100 re-

peated experiments on case VI data. Best-in-class values

are marked with *.

determination inﬁdelity sensitivity

IG 0.153 0.0030 2.816*

(0.117) (0.0015) (0.812)

GSHAP 0.148 0.0032 30712.477

(0.116) (0.0015) (77256.110)

LIME 0.066 0.0023* 446.402

(0.071) (0.0009) (451.300)

SVS 0.174 0.0025 176.937

(0.136) (0.0010) (135.055)

DeepLIFT 0.183* 0.0036 7.269

(0.111) (0.0015) (1.217)

Table 13: Mean results (Standard Deviation) for 100 re-

peated experiments on the Ames housing price data. Best-

in-class values are marked with *.

inﬁdelity inﬁdelity

IG 0.000591 10.586*

(0.00020) (1.751)

GSHAP 0.000597 309.495

(0.00020) (230.412)

LIME 0.000591 321.872

(0.00020) (1171.460)

SVS 0.000596 32.218

(0.00020) (5.283)

DeepLIFT 0.000587* 17.458

(0.00021) (3.197)

Table 14: Mean results (standard deviation) for 100 re-

peated experiments on the California housing price data.

Best-in-class values are marked by *.

inﬁdelity sensitivity

IG 0.093 26.609*

(0.053) (14.956)

GSHAP 0.092 655.637

(0.054) (885.336)

LIME 0.092 260.244

(0.053) (252.150)

SVS 0.093 62.229

(0.055) (21.680)

DeepLIFT 0.091* 64.089

(0.055) (28.282)

Table 15: Mean results (Standard Deviation) for 100 re-

peated experiments on the FF5 data. Best-in-class values

are marked with *.

inﬁdelity inﬁdelity

IG 0.000151 23.564

(0.00006) (2.209)

GSHAP 0.000149* 312.104

(0.00006) (78.938)

LIME 0.000150 0.887*

(0.00006) (3.714)

SVS 0.000152 51.652

(0.00006) (12.362)

DeepLIFT 0.000152 33.935

(0.00006) (4.978)

EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods