Separating the Yes- from the No-Instances in the Number Partitioning

Problem

Ruben Horn

1 a

, Reitze Jansen

4 b

, Okke van Eck

4 c

and Daan van den Berg

2,3 d

Helmut-Schmidt-University, Hamburg, Germany

Department of Computer Science, University of Amsterdam, The Netherlands

Department of Computer Science, VU Amsterdam, The Netherlands

Independent Researcher

Keywords:

Number Partitioning Problem, NP-hard, Branch-and-Bound Algorithm, Greedy Algorithms.

Abstract:

The (two-way) number partitioning problem (NPP) is a well known NP-complete decision problem in which a

set of (positive) integers must be split in such a way that the sum of both resulting subsets is equal. However, its

optimization problem variant is even harder, since the veriﬁcation of partitions is only possible in polynomial

time for instances which have a perfect partition. We investigate the distribution of instances that have and

that do not have a perfect partition, and ﬁnd that they are not randomly distributed in the instance space. Thus,

the hardness of any given instance might be predictable to some extent. We demonstrate that it is possible

to separate these two instance types visually using a linear time embedding into R

for instances of the same

template. Furthermore, we compare three greedy heuristic algorithms (greedy captains, greedy coach, and

greedy tyrant) and their difference to the solution from an exact branch-and-bound (BB) algorithm.

1 INTRODUCTION

The (two-way) number partitioning problem (NPP),

also known as “the easiest hard problem” (Brian

Hayes, 2002; Schreiber et al., 2018; Stephan Mertens,

2003), is the well-known NP-complete (Karp, 1972)

problem of partitioning a set of positive integers such

that both resulting subsets sum up to the same value.

This problem is a special case of the subset sum prob-

lem (SSP) where the aim is ﬁnding A ⊆ S such that

∑

A = t. For the NPP, t =

⌈

∑

⌉

, meaning the set

must be split in two equally valued subsets. Com-

ing up with such a partition is hard, but veriﬁcation

can be done in polynomial time for the decision vari-

ant of this problem. For many instances, however, no

perfect partition exists and yet, the optimization vari-

ant of the NPP might be relevant. For example, even

when it is impossible to split a group of football play-

ers into perfectly equal teams, the match should be

as fair as possible (cf. Brian Hayes, 2002). For the

decision variant, instances of the NPP which have a

perfect partition are referred to as yes-instances and

https://orcid.org/0000-0001-6643-5582

https://orcid.org/0009-0007-0029-2882

https://orcid.org/0000-0002-3600-5183

https://orcid.org/0000-0001-5060-3342

those that do not as no-instances. For yes-instances,

the NP-hard optimization variant of the NPP is easy

in many cases, but for no-instances it is almost al-

ways hard, requiring many steps for an exact algo-

rithm. It is trivial to verify if a partition is perfect,

but not whether an imperfect one is optimal. An opti-

mization algorithm may terminate early upon ﬁnding

any single one of potentially many perfect partitions,

but only for yes-instances. Thus, separating yes- from

no-instances presents an interesting problem with po-

tential implications for the hardness classiﬁcation of

the NPP.

It is known that the ratio between the number of

informational bits that represent the integers and their

value inﬂuence the hardness of an instance (Brian

Hayes, 2002; Richard Korf, 1998; Stephan Mertens,

2003). Recently, the inﬂuence of the distribution

of informational bits on the hardness of an instance

has been shown (Van den Berg and Adriaans, 2021;

Sazhinov et al., 2023). Obviously, a distribution

where one integer is larger than the sum of all oth-

ers yields a trivial no-instance. Larger instances with

integers in the same range are more likely to have

many perfect partitions, because the number of parti-

tions grows faster than the number of possible subset

sums (Richard Korf, 1998). For practical applications

such as scheduling (Seenu S. Reddi, 2008) or in the

Horn, R., Jansen, R., van Eck, O. and van den Berg, D.

Separating the Yes- from the No-Instances in the Number Partitioning Problem.

DOI: 10.5220/0012907000003837

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 181-188

ISBN: 978-989-758-721-4; ISSN: 2184-3236

181

container-trucking industry (Coslovich et al., 2006),

the use of heuristic algorithms for the optimization

variant of the NPP may arguably be admissible in or-

der to obtain a partition that is good enough in reason-

able time. Therefore, the optimization variant of the

NPP and speciﬁcally its hardness warrants investiga-

tion.

Section 2 tackles our question about the separabil-

ity of yes- and no-instances. In Section 2.1, we ﬁrst

explain our method of generating suitable datasets for

our experiments. We describe both an exact algorithm

and an easy heuristic approach to the NPP: greedy al-

gorithms. Then, in Section 2.2, we present the re-

sults of our algorithm comparison and investigation

whether the instance type (yes- or no-instance) can

be predictable using the previously generated dataset.

Based on these results, in Section 3, we propose and

demonstrate a visualization approach to gain insight

into this property in Section 3.1 and Section 3.2 re-

spectively. Finally, we end with a discussion of our

ﬁndings and conclusion in Section 4.

The dataset and all source code is provided in an

online repository (Horn et al., 2024a).

The problem instances for the NPP were gener-

ated, solved and analyzed using Python 3, NumPy

(Harris et al., 2020), Pandas (The Pandas devel-

opment team, 2020) and swifter (Jason Carpenter,

2023), which is based on Dask (Matthew Rocklin,

2015), for parallel execution. For the visualization

of our results, we used Matplotlib (John D. Hunter,

2007) and seaborn (Michael L. Waskom, 2021). All

experiments were executed on the cluster HSUper us-

ing a single compute node running Linux 4.18 with

two CPUs for a total of 72 physical cores at 2.4 GHz

and with 256 GB of DDR4 memory. Generating and

analyzing the dataset took roughly 1.5 hours on this

system.

2 PREDICTABILITY OF THE NPP

Our conjecture is that, for the NPP, yes- and no-

instances are often very similar. If this is true, then

it may be impossible to efﬁciently distinguish them

without solving the instance. If, however, it is false,

then it might be worth it to assess the hardness of yes-

and no-instances separately.

2.1 Methods

2.1.1 Generating the Dataset

To investigate this conjecture, we randomly generate

a dataset expected to contain as many yes-instances

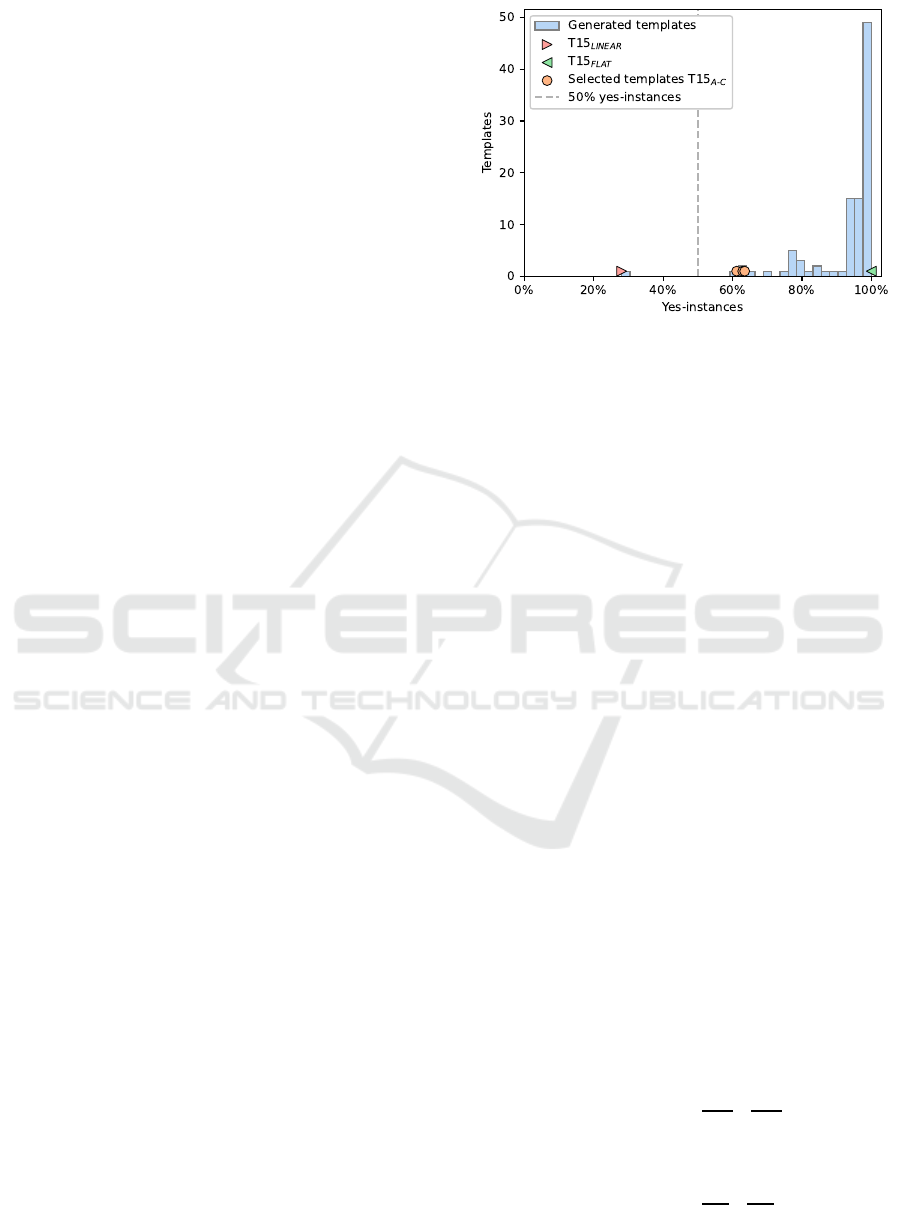
Figure 1: Histogram over the fraction of yes-instances for

100 templates generated, which have an informational bit

distribution slope between 0 and 1. Most templates produce

almost exclusively yes-instances. This can be partially at-

tributed to the small ratio of informational bits per integer

m to the number of integers n of

/n =

/15 ≈ 0.53.

as no-instances. To this end, we use the template

approach by Van den Berg and Adriaans (2021) to

generate similar instances of n = 15 integers with the

same distribution of informational bits for the same

template. A template consists of a list of numbers

which indicate the exact number of bits required to

represent the individual integers in a corresponding

instance, and therefore the range of possible integer

values from which to sample. For example, a value

of 3b in a template indicates that the corresponding

integer in an instance generated from it may have any

value between 4 = (100)

and 7 = (111)

. Thus, from

the template (3b,3b,4b,9b) for example, we might

generate the instance {4,7,8,405} or {5,6,13, 270}.

All generated templates and instances are sorted lists,

which is a prerequisite for the methods described in

this paper.

Since we suspect a correlation between the hard-

ness of instances and their instance type (yes- or

no-instance), we consider all so-called non-eccentric

templates between the linearly increasing template

T15

LINEAR

with a slope of 1 and ﬂat template T15

FLAT

with a slope of 0, which generate both instance types

(Van den Berg and Adriaans, 2021; Sazhinov et al.,

2023) and can all be represented by the binary string

corresponding to their derivative:

T15

LINEAR

′

= (1,1,1,..,1)

| {z }

14 local slopes

...

T15

FLAT

′

= (0,0,0..,0)

| {z }

14 local slopes

Conversely, by integrating all possible bit strings with

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

182

a length of n − 1 = 14, one obtains all non-eccentric

templates with n integers and

∑

i=1

i = mn bits:

T15

LINEAR

= (1b,2b,3b,..,15b)

| {z }

120 bits over 15 integers

...

T15

FLAT

= (8b,8b,8b,..,8b)

| {z }

15×8=120 bits

We take 100 templates in regular intervals over all

enumerated template derivatives and compute the yes-

instance ratio by solving 1000 instances generated

from each selected template with an exact branch-

and-bound (BB) algorithm (Van den Berg and Adri-

aans, 2021). The distribution of yes-instances of the

templates is visualized in Figure 1. Since the ratio

/n of informational bits per integer m to the number

of integers n is small, most templates generate almost

exclusively yes-instances (cf. Brian Hayes, 2002).

We select three out of the 100 templates where the

probability of yes- and no-instances is between 35%

and 65% (Figure 1) and generate a dataset of 10,000

instances for each. From every problem instance, a

d1-mutant is created by ﬂipping a single random bit

that is not the most signiﬁcant bit (MSB) of an in-

teger, such that the distribution of informational bits

remains the same as in the original instance. This is

done by

1. selecting a random integer index i,

2. determining its number of bits m

3. selecting a random bit index i

< m

and

4. ﬂipping bit i

of integer i.

If the distribution of yes- and no-instances is not

predictable (they could be thought of as being well-

mixed), then the instance type of the mutant instances

should not depend on the instance type of the origi-

nal instance and have a roughly equal probability of

being either a yes- or no-instance in both cases.

The bit distribution of the selected template T15

is given in Equation (1) and although 61.16% of

instances generated from this template were yes-

instances, it is as close as possible to an even split

between yes- and no-instances in our dataset. To im-

prove the soundness of our experiment, we also select

two other templates T15

in Equation (2) and T15

Equation (3) with 62.92% and 63.48 % yes-instances

respectively.

T15

= (3b,4b,5b,6b,6b, 7b,8b, 8b,9b,9b, (1)

9b,10b, 11b,12b,13b)

T15

= (4b,5b,6b,6b,6b, 6b,7b, 7b,8b,9b, (2)

10b,10b, 11b,12b,13b)

T15

= (4b,5b,5b,6b,6b, 6b,7b, 8b,8b,9b, (3)

10b,10b, 11b,12b,13b)

2.1.2 Hypothesis Formulation

Since yes- and no-instances are not very balanced in

any of the generated templates (Figure 1), we apply

a margin of ±15% in our experiments, so any ratio

of yes- and no-instances between 35/65 and 65/35 is

considered to have about the same of either. Thus,

our pessimistic assumption for the null hypothesis is

that yes- and no-instances must be not separable if

instances have only a 35% chance of changing their

instance type under mutation of a single bit.

2.1.3 Algorithms

Heuristic algorithms for NP-complete problems may,

in practice, be a preferable alternative to exact ones.

Sazhinov et al. (2023) investigated the performance

of three heuristic algorithms for the NPP by comput-

ing their heuristic deﬁciency, deﬁned by Equation (4).

This metric determines the performance of a heuristic

algorithm H in relation to and exact method gener-

ating the optimal partition, such as the BB algorithm

described in Algorithm 1. Here A

and A

are sub-

sets corresponding to the ﬁnal partitions p

and p

that are returned by the respective algorithms for an

instance S of the NPP.

Algorithm 1: Recursive pseudocode adaptation for

the NPP of the exact BB algorithm for the SSP by

Van den Berg and Adriaans (2021).

Data: Descending integer list S, index i ≤ |S|,

partition masks p, p

best

(initially

⃗

Result: Optimal partition for S

if p better than p

best

then

best

:= p;

if p

best

imperfect and

∑

< ⌈

∑

S⌉ then

recurse with i := i + 1 and p

:= 1;

if p

best

imperfect and

∑

< ⌈

∑

S⌉ then

recurse with i := i + 1 and p

:= 0;

We perform this analysis across all generated in-

stances and, in addition to this metric for the quality

of the partition given by a heuristic algorithm, also in-

vestigate the similarity to the optimal partition, com-

puted from the Hamming distance between the binary

strings describing the corresponding partitions.

deﬁciency

(S,A

) =

∑

S −

∑

S −

∑

(4)

We choose the greedy algorithm due to its simplic-

ity and intuitiveness, and also because of its relatively

Separating the Yes- from the No-Instances in the Number Partitioning Problem

183

good performance (Sazhinov et al., 2023). However,

one can come up with different variants of a greedy

algorithm for the NPP which may, borrowing the ex-

ample by Brian Hayes (2002), represent different ap-

proaches to partitioning a group of children into two

football teams. This is reﬂected in the names that we

gave to the different variants:

1. The greedy captains algorithm, described ini-

tially by Brian Hayes (2002) (and probably most

widely used among children), in which the titular

captains take turns selecting the largest remaining

integer, always produces the same binary partition

greedy captains

= (1,0,1,0,1, ...).

2. The variation actually used by Brian Hayes (2002)

and Sazhinov et al. (2023) may be called the

greedy coach algorithm, since the largest integer

is assigned to the subsets with the smaller sum re-

gardless of turn.

3. Finally, the greedy tyrant algorithm is just the

greedy algorithm for the SSP with t =

⌈

∑

⌉

and thereby for the NPP. The next largest integer

is assigned to the subset as long as the current sub-

set sum is smaller than t.

2.2 Results

2.2.1 Performance of Greedy Algorithms

Table 1 shows that this last variant, the greedy tyrant

algorithm, performs best over all instances from all

templates generated in Section 2.1.1 when compared

to the optimal partition, because it has the lowest

mean heuristic deﬁciency and its partition is struc-

turally closest to that of the exact algorithm having the

lowest Hamming distance. However, the large stan-

dard deviation of the difference in Table 1 shows that

the partition by even the greedy tyrant variant may be

completely different from that by the exact algorithm.

This indicates that applying a linear time greedy al-

gorithm may not be a useful preprocessing step for an

exact algorithm.

2.2.2 Instance Type Under Mutation

Contrary to the assumption of our null hypothesis in

Section 2.1.2, and as shown in Table 2, the over-

whelming majority of neighboring instances have the

same instance type after mutation instead of having

a roughly equal probability of being a yes- or no-

instance.

Since every problem instance has 120 −

15 = 105 bits that can potentially be ﬂipped and thus

We omit reporting the results of the statistical test here

due to the unambiguity of these results.

Table 1: The tyrant variant of the greedy algorithm on av-

erage performs best in terms of similarity of the integer as-

signments to the subsets compared to the BB approach and

heuristic deﬁciency.

Variant Captains Coach Tyrant

Hamming distance between p

and p

µ 5.99023 5.57089 4.02619

σ 1.09324 1.66666 2.24574

min 1 0 0

max 7 7 7

Heuristic Deﬁciency

µ 1.23877 1.00390 1.00373

σ 0.14108 0.00649 0.00719

min 1.01593 1.0 1.0

max 1.93036 1.07699 1.18914

a corresponding number of possible d1-mutants, one

can use the obtained probabilities to estimate the aver-

age number of neighboring instances with a different

instance type. Given that the ﬂip bit index was sam-

pled with uniform distribution, the almost symmetry

between instance changing from yes- to no-instance

under mutation and vice versa conﬁrms the clustering

of instance types, considering that they were initially

somewhat unbalanced. Since the original instances

are slightly more likely to be yes-instances than no-

instances, the number of instances changing from no-

to yes-instances under mutation is just slightly higher

than the other way around.

Table 2: Analysis of the instance type of the originally gen-

erated instances and the corresponding instances derived us-

ing mutation over 10,000 pairs of instances per template.

Template T15

T15

Initially

yes-instance

60.46 % 63.01 % 64.15 %

Yes-instance to

no-instance

6.64 % 6.38 % 6.81 %

No-instance to

yes-instace

7.43 % 7.47 % 7.95 %

Unchanged 85.93 % 86.15 % 85.24 %

3 VISUAL SEPARATION BY

INSTANCE TYPE

The results in Section 2.2.2 suggests that it might af-

ter all be possible to (somewhat) separate yes- and

no-instances, and we therefore investigate the prob-

ability of each variable bit of an instance to change

the instance type. A rudimentary visualization of the

inﬂuence of the bits on the instance type is given in

the bar plots in Figure 2 using the same dataset as be-

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

184

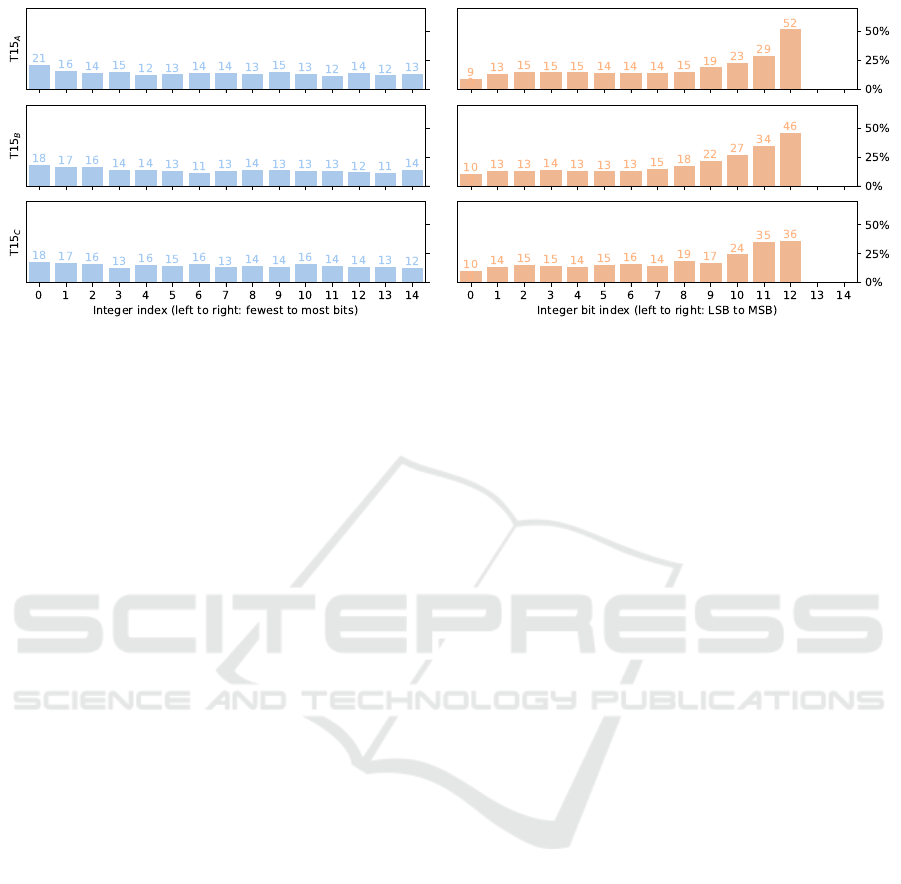
Figure 2: Probability of a one bit mutation to affect the instance type for all integer indices (left) and integer bit indices (right)

across the selected templates T15

, T15

, and T15

fore. The probability of a single bit mutation affect-

ing the instance type appears to be roughly the same

across all integers indices. Only for T15

does the in-

teger with the fewest bits have a considerably larger

inﬂuence, with 7.23 %pt. more compared to the av-

erage bit. On the level of integer bits, however, it ap-

pears that the inﬂuence of the mutation on the instance

type increases signiﬁcantly with the bit index towards

the end. The bit just below the MSB of the integer

with the most bits thus appears to have the highest im-

pact on the instance type of between 36 % and 52 %,

depending on the template. Likewise, the least sig-

niﬁcant bit (LSB) of any integer would be expected

to generally have a low effect on the instance type

because instances with an odd sum over all integers

are considered optimally partitioned with a difference

of 1 between both summed subsets (Schreiber et al.,

2018). However, it might also turn a yes-instance with

an odd sum into a no instance with a difference of 2

between the subset sums, therefore this bit can some-

times still inﬂuence the instance type.

Since the distribution of these bits over the inte-

gers (the template) is not captured by this represen-

tation, it is only valid for instances of the same tem-

plate. Therefore, our proposed method for embedding

instances into R

in such a way as to separate yes-

and no-instances, which we describe in the following

section, must be applied to instances of the same tem-

plate.

3.1 Proposed Embedding

There seems to be at least some hierarchical struc-

ture to the inﬂuence of the bit on the instance type of

the corresponding instance. We do not see the same

clear hirarchy for the integers, but also order them

from most to fewest bits to group integers with more

signiﬁcant bits. Using this, it may be possible to vi-

sually separate yes- and no-instances to some extent.

Inspired by the quad tree data structure (Finkel and

Bentley, 1974), we apply binary space partitioning

going from MSB to LSB to embed all generated in-

stances belonging to the same template into R

. The

MSBs of all integers are skipped because they are not

variable. At every index the initial unit square is split

further, alternating between vertical and horizontal,

where the upper or right half is selected if the bit is

1 and the lower or left if it is 0. This yields a unique

point in linear time for the corresponding instance.

Note again that the distribution of the bits over the

integers is not captured by this embedding, so all em-

bedded instances must belong to the same template.



⃗

b,c



= 0.5 +

dim

⃗

b÷2

∑

i=0

−i



⃗

2i+c

− 0.5



x(S) = f



⃗



y(S) = f



⃗



(5)

Equation (5) describes the formula for the polyno-

mial for both Cartesian coordinates in the range of

[0;1] where

⃗

is the binary representation of the in-

stance S without MSBs from the integer with the

most bits to that with the fewest and from MSB

to LSB for each integer. For example, given S =

{4,6, 7} = {(100)

,(110)

,(111)

}, we obtain the

following representation:

⃗

= ( 11

|{z}

)

which is embedded at (0.8125,0.5625). Unlike

other dimensionality reduction approaches like t-SNE

(van der Maaten and Hinton, 2008), our approach is

Separating the Yes- from the No-Instances in the Number Partitioning Problem

185

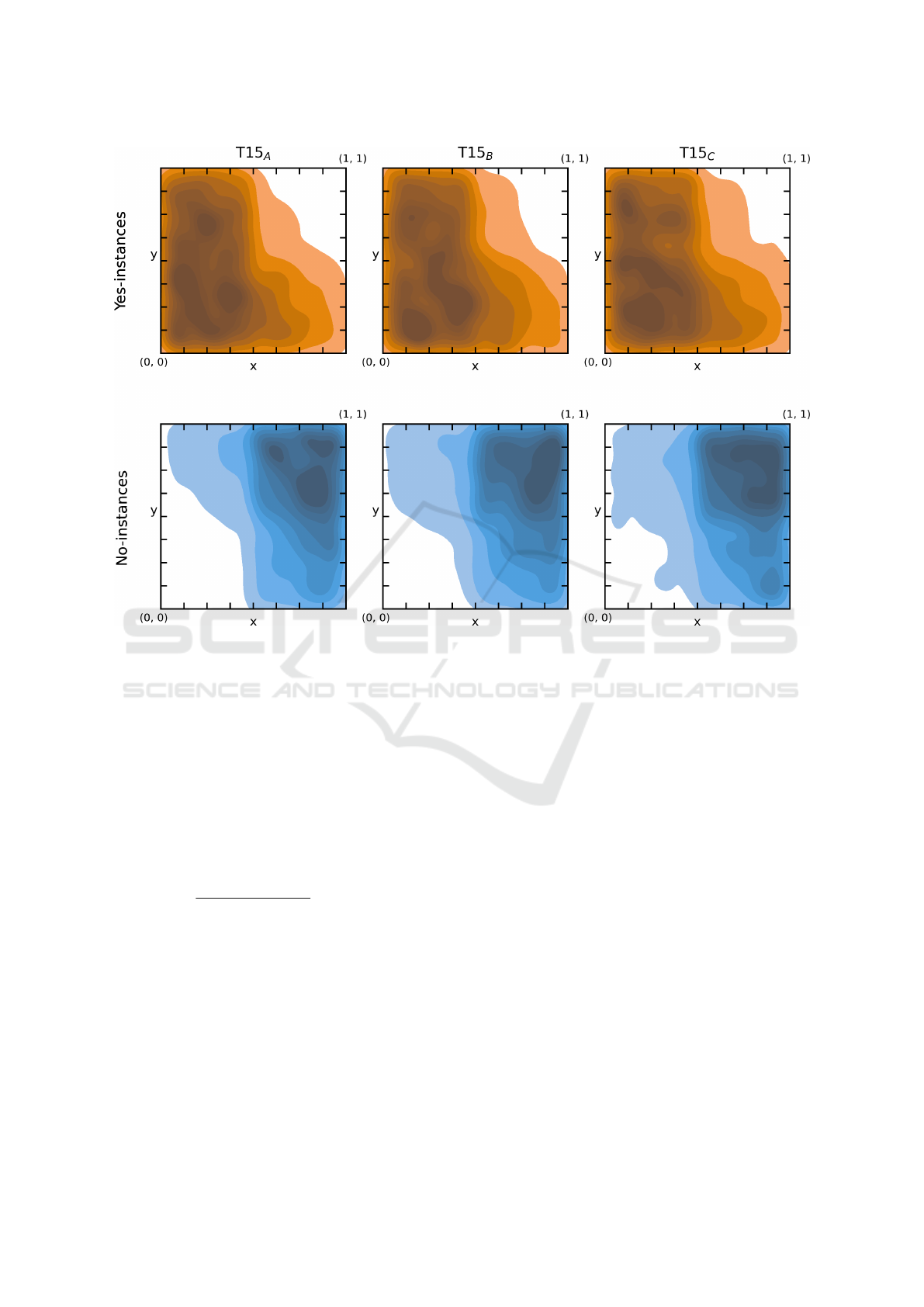
Figure 3: Density plot of the embeddings using Equation (5) of yes-instances (ﬁrst row) and no-instances (second row)

generated from the templates T15

A-C

(columns). The distribution of yes- and no-instances seems to vary along somewhat of

a semi-diagonal for the R

-embedding.

linear, interpretable and a complete representation of

the underlying instance.

One may suspect a correlation between the in-

stance type and its hardness, the number of recursions

required to solve it. In order to see, whether this ex-

tends to the optimality of the optimal (imperfect) par-

tition, we additionally compute the relative discrep-

ancy given in Equation (6), which indicates the devi-

ation of the optimal from the perfect partition in per-

cent.

|⌈

∑

⌉

−

∑

⌈

∑

⌉

× 100% (6)

3.2 Visualization of the Dataset

The density plot in Figure 3 of the previously

generated instances for T15

A-C

yields an imperfect

yet strong visual separation between yes- and no-

instances. Even though Figure 2 shows no apparent

inﬂuence of the integer index on the instance type, us-

ing the average bit values (R) over all integers as co-

efﬁcients for f only yields a less clean separation of

yes- and no-instances. The hierarchical inﬂuence of

the integer bits means that the pattern emerging from

the embedding mostly persists even when only taking

a subset of less signiﬁcant bits into account, discard-

ing up to two bits per integer. Thus, it appears that

instances are more likely to be a yes-instance if the

integers are similar to 2

and more likely to be a no-

instance if they are similar to 2

− 1.

Figure 4 shows the corresponding relative dis-

crepancy given by Equation (6) of the embedded in-

stances. Interestingly, the pattern is quite similar to

that of the distribution of instance types. Thus, it

seems that in regions where the probability of in-

stances being a yes-instance is lower, the optimality of

the optimal partition is probably also lower. The two

properties of the templates therefore appear somewhat

correlated in Figure 3 and 4.

4 DISCUSSION & CONCLUSION

Richard Korf (1998) and Brian Hayes (2002) showed

that the hardness of the NPP depends on the magni-

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

186

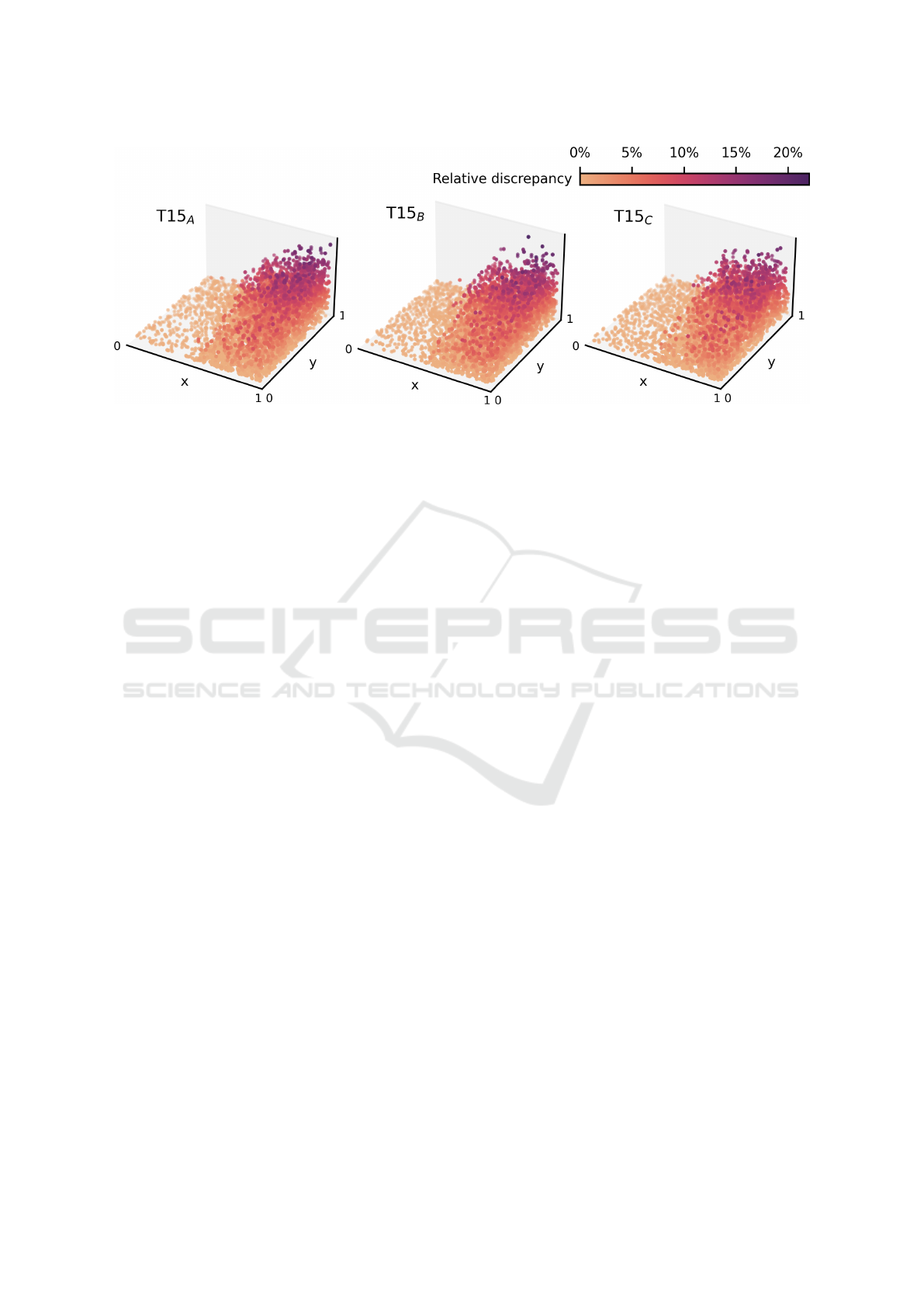
Figure 4: The relative discrepancy from Equation (6) of the optimal (imperfect) partitions for the corresponding instances

embedded into R

seems to also increase with the probability of being a no-instance from Figure 3.

tude of integers in the instances, as expressed by the

number of (informational) bits that represent them.

Van den Berg and Adriaans (2021) and Sazhinov et al.

(2023) recently extended this to also include the dis-

tribution of these bits over the instance for a ﬁxed

number of bits and investigated the performance of

heuristic algorithms. We build on the work by Sazhi-

nov et al. (2023) and ﬁnd that among three versions

of the greedy algorithm, the tyrant version, which is

equivalent to a backtracking free variant of the BB

algorithm by Van den Berg and Adriaans (2021), per-

forms best, but still deviates signiﬁcantly from the op-

timal partition.

Regarding the hardness of the NPP, in this pa-

per we have looked at a different side of the same

coin: veriﬁcation of the solution. We have investi-

gated the predictability of the instance type for three

selected templates. It is not the case that similar in-

stances are independent with respect to their instance

type, meaning that any yes-instance is more likely to

be surrounded by yes-instances in its 1-bit neighbor-

hood and a no-instance more likely to be surrounded

by no-instances.

Based on this insight, we propose a method which

provides a noticeable visual separation between yes-

and no-instances along the values of bits in order of

signiﬁcance by embedding them into R

. However,

while the preliminary results presented in this study

suggest that the diagonal position of an instance in

may be an indicator for its probability of being

a yes-instance, the instance type density maps vary

between templates. This can even be seen between the

three templates with similar yes-instance probabilities

in Figure 3. In cases where the template produces

mostly either yes- or no-instances (e.g. T15

FLAT

T15

LINEAR

), such a separation is not possible.

Yes-instances are easy to verify, no-instances not.

One might argue that yes-instances, especially those

with many perfect partitions, are easier to solve as

well, since the algorithm can likely terminate after

fewer recursions upon ﬁnding any single one of them.

It thus seems that, to fully predict the hardness (ex-

pected number of recursions) of any given instance,

one must consider all three of the following features:

1. the amount of information it contains via the num-

ber of bits, 2. their distribution, and 3. the embedding

into R

as proposed in Section 3.1. Using these three

features, it may be possible to predict the hardness

of any given instance by creating a statistical model

to predict the number of recursions required to solve

it. Something similar has recently been done for in-

stances of the NPP with uniform bit distribution by

modeling the number of perfect partitions that exist

(Horn et al., 2024b). Perhaps it is time to revisit other

NP-complete problems and investigate them along the

dimension of yes-instance probability, since at least

for the asymmetric traveling salesperson problem its

hardness is known to be affected by the other two fea-

tures (Zhang and Korf, 1996) and also for the Hamil-

tonian cycle problem no-instances are harder than

yes-instances (Sleegers and Van den Berg, 2020).

As already mentioned by Van den Berg and Adri-

aans (2021), there appear to exist non-eccentric tem-

plates (having a binary derivative) which contain both

the easiest and hardest instances, probably both yes-

and no-instances respectively. This is similar to the

Hamiltonian cycle problem (Sleegers et al., 2022;

Sleegers and Van den Berg, 2022). One might as-

sume that easy and hard instances correspond to yes-

and no-instances, but it is not yet clear to us, whether

yes-instances are never harder than no-instances. Like

Sleegers and Van den Berg (2020, 2022) we might in-

Separating the Yes- from the No-Instances in the Number Partitioning Problem

187

vestigate this by evolving ever harder (yes-)instances

of the NPP using evolutionary algorithms (EAs). The

success of an EA approach to ﬁnding such instances,

however, hinges on the fabric of the search space. If

the relative discrepancy of the no-instances in Fig-

ure 4 is also an indicator for the hardness function

of the yes-instances, the latter might have a very high

frequency randomness and thus be particularly chal-

lenging for an EA.

ACKNOWLEDGEMENTS

Computational resources (HPC-cluster HSUper) have

been provided by the project hpc.bw. hpc.bw is

funded by dtec.bw – Digitalization and Technology

Research Center of the Bundeswehr. dtec.bw is

funded by the European Union – NextGenerationEU.

REFERENCES

Brian Hayes (2002). Computing Science: The Easiest Hard

Problem. American Scientist, 90(2):113–117.

Coslovich, L., Pesenti, R., and Ukovich, W. (2006). Large-

scale set partitioning problems: Some real-world in-

stances hide a beneﬁcial structure. Ukio Technologinis

ir Ekonominis Vystymas, 12(1):18–22.

van den Berg, D. and Adriaans, P. (2021). Subset Sum

and the Distribution of Information. In Proceedings

of the 13th International Joint Conference on Compu-

tational Intelligence, pages 134–140.

Finkel, R. and Bentley, J. (1974). Quad trees: A data struc-

ture for retrieval on composite keys. Acta Inf., 4:1–9.

Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers,

R., Virtanen, P., Cournapeau, D., Wieser, E., Taylor,

J., Berg, S., Smith, N. J., Kern, R., Picus, M., Hoyer,

S., van Kerkwijk, M. H., Brett, M., Haldane, A., del

ıo, J. F., Wiebe, M., Peterson, P., G

erard-Marchant,

P., Sheppard, K., Reddy, T., Weckesser, W., Abbasi,

H., Gohlke, C., and Oliphant, T. E. (2020). Array pro-

gramming with NumPy. Nature, 585(7825):357–362.

Horn, R., Jansen, R., van Eck, O., and van den Berg, D.

(2024a). Separating the Yes- from the No-Instances in

the Number Partitioning Problem. https://anonymous.

4open.science/r/NPP-24/. (Replication package).

Horn, R., Thomson, S. L., van den Berg, D., and Adriaans,

P. (2024b). The easiest hard problem: Now even eas-

ier. In Proceedings of the Genetic and Evolutionary

Computation Conference Companion, GECCO ’24

Companion, page 97–98, New York, NY, USA. As-

sociation for Computing Machinery.

Jason Carpenter (2023). swifter. https://github.com/

jmcarpenter2/swifter/tree/1.4.0.

John D. Hunter (2007). Matplotlib: A 2d graphics environ-

ment. Computing in Science & Engineering, 9(3):90–

95.

Karp, R. M. (1972). Reducibility among Combinatorial

Problems, pages 85–103. Springer US, Boston, MA.

Matthew Rocklin (2015). Dask: Parallel computation with

blocked algorithms and task scheduling. In Huff,

K. and Bergstra, J., editors, Proceedings of the 14th

Python in Science Conference, pages 130–136.

Michael L. Waskom (2021). seaborn: statistical data visual-

ization. Journal of Open Source Software, 6(60):3021.

Richard Korf (1998). A complete anytime algorithm

for number partitioning. Artiﬁcial Intelligence,

106(2):181–203.

Sazhinov, N., Horn, R., Adriaans, P., and van den Berg,

D. (2023). The partition problem, and how the dis-

tribution of input bits affects the solving process. In

Proceedings of the 15th International Conference on

Evolutionary Computation Theory and Applications.

Schreiber, E. L., Korf, R. E., and Mofﬁtt, M. D. (2018). Op-

timal Multi-Way Number Partitioning. J. ACM, 65(4).

Seenu S. Reddi (2008). Graham’s schedules and the number

partition problem.

Sleegers, J., Thomson, S., and van Den Berg, D. (2022).

Universally hard hamiltonian cycle problem instances.

In Proceedings of the 14th International Joint Confer-

ence on Computational Intelligence. SCITEPRESS -

Science and Technology Publications.

Sleegers, J. and Van den Berg, D. (2020). Looking for the

hardest hamiltonian cycle problem instances. In Pro-

ceedings of the 12th International Joint Conference

on Computational Intelligence (IJCCI 2020) - ECTA,

pages 40–48. INSTICC, SciTePress.

Sleegers, J. and Van den Berg, D. (2022). The hardest

hamiltonian cycle problem instances: The plateau of

yes and the cliff of no. SN Comput. Sci., 3(5).

Stephan Mertens (2003). The easiest hard problem: Num-

ber partitioning.

The Pandas development team (2020). pandas-dev/pandas:

Pandas.

van der Maaten, L. and Hinton, G. (2008). Visualizing data

using t-SNE. Journal of Machine Learning Research,

9:2579–2605.

Zhang, W. and Korf, R. E. (1996). A study of complex-

ity transitions on the asymmetric traveling salesman

problem. Artiﬁcial Intelligence, 81(1):223–239. Fron-

tiers in Problem Solving: Phase Transitions and Com-

plexity.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

188