Iterative Learning Control for Linear Time-Varying Systems in the
Presence of Iteration-Varying Disturbance
Yu Dou
1 a
, Lanlan Su
2 b
and Emmanuel Prempain
1 c
1
School of Engineering, University of Leicester, Leicester, U.K.
2
Department of Automatic Control and Systems Engineering, University of Sheffield, Sheffield, U.K.
Keywords:
Iterative Learning Control, Linear Time-Varying Systems, 2D Roesser Model.
Abstract:
This paper presents an innovative Iterative Learning Control (ILC) strategy for Linear Time-Varying (LTV)
systems subject to uncertainties. In a real-world environment, implementing ILC causes the uncertainties to
vary concerning both time and iteration. To address this challenge, we introduce a metric to quantify the impact
of the uncertainties on the tracking error’s variation. First, an equivalent 2D Roesser model is established for
the uncertain ILC system. It has uncertain parameters and is subject to an external disturbance caused by the
time-varying model uncertainties of the original system. Then, a Linear Matrix Inequality (LMI) condition
is proposed to design the ILC law to provide an upper metric bound. The strategy aims to lower this bound,
thereby reducing the impact of uncertainties on the system. Finally, preliminary numerical simulation verifies
the effectiveness and robustness of the proposed strategy.
1 INTRODUCTION
Iterative Learning Control (ILC) is a control method
for repetitive processes that continuously adjusts the
current control signal by learning from historical op-
erations (Bristow et al., 2006; Ahn et al., 2007; Wang
et al., 2009; Owens and H
¨
at
¨
onen, 2005; Lee and Lee,
2007). Specifically, based on the errors of previous
iterations, it brings the system output closer to the ex-
pected trajectory in subsequent iterations. ILC has
become an important subject of academic research
since Arimoto et al. first proposed the concept of
it (Arimoto et al., 1984). The self-learning char-
acter gives ILC a unique advantage in applications
that perform repetitive tasks, such as robotics (Zhao
et al., 2015), precision manufacturing (Hoelzle and
Barton, 2014), aerospace (Yao, 2021), and power sys-
tems (Zanchetta et al., 2013). Disturbances caused by
unwanted forces, torques, or environmental changes
are common in practice. The ILC strategy can re-
sist repeatable disturbance well, but iteration-varying
disturbance will seriously affect the system’s perfor-
mance (Merry et al., 2005; Norrl
¨
of and Gunnarsson,
2001). Therefore, suppressing the effect of iteration-
a
https://orcid.org/0000-0002-1773-3847
b
https://orcid.org/0000-0002-6489-3253
c
https://orcid.org/0000-0001-8954-1265
varying disturbance becomes an important topic in the
field of ILC.
Recently, some innovative methods have been
proposed to cope with iteration-varying disturbance.
Chin et al. presented a control framework that com-
bines real-time feedback control and ILC to handle
real-time disturbance in repetitive processes more ef-
ficiently (Chin et al., 2004). This combination is de-
signed to separate the performance of the ILC from
the effects of real-time disturbance, thereby improv-
ing the effectiveness of the control strategy. Maeda
et al. gave a control structure that combines itera-
tive learning control and disturbance observer (Maeda
et al., 2015). The disturbance of the previous itera-
tion is used as a partial preview of the next distur-
bance, thus effectively resisting near-repetitive dis-
turbances. Sun et al. proposed a composite con-
trol scheme combining a P-type ILC scheme with
extended state observer (Sun et al., 2014). Among
them, the observer is used for disturbance estimation
to improve the performance of systems with iteration-
varying disturbance. The disturbances can be atten-
uated from the system output by properly selecting
the compensation gain. These studies investigate the
challenges of non-repetitive disturbance to ILC and
highlight ongoing research efforts to address these is-
sues. However, the above method may have the short-
comings of slow response or constrained disturbance,
Dou, Y., Su, L. and Prempain, E.
Iterative Learning Control for Linear Time-Varying Systems in the Presence of Iteration-Varying Disturbance.
DOI: 10.5220/0012908100003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 645-650
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
645

so the implementation might have some difficulties.
This paper considers another ILC strategy for Lin-
ear Time-Varying (LTV) systems. Our objective is to
design a suitable ILC law to mitigate the effect of the
varying uncertainty on the tracking error. The strat-
egy is based on the 2D Roesser model, which can
accurately describe the bidirectional information flow
and integrate the disturbance observer into the ILC
process. This uncertain model is subject to an ex-
ternal disturbance caused by the time-varying model
uncertainty of the original linear system. A similar
ILC design in a 2D setting can be found in the pa-
pers (Shi et al., 2005a; Shi et al., 2005b). Then, we
introduce a metric that measures the impact of the in-
duced iteration-varying disturbance on the system. A
Linear Matrix Inequality (LMI) condition is proposed
to design the ILC law to provide an upper bound of
the metric using the Schur complement and the S-
procedure (Scherer and Weiland, 2000; Zhang, 2006;
P
´
olik and Terlaky, 2007). Compared to the above-
mentioned research, our approach adopts a simpler
framework and, therefore, is easier to apply. Prelimi-
nary numerical simulations validate the effectiveness
and robustness of the strategy, suggesting its potential
applicability in practical scenarios.
This paper uses the following notations: R
n
rep-
resents an n-dimensional Euclidean space. ||x|| de-
notes the norm of a vector x. R
n×m
is the set of
all n by m matrices with real number entries. Given
M ∈ R
n×n
, M ≻ 0 indicates that M is positive definite.
M
⊤
represents the transpose of matrix M. The nota-
tions “:=” and “≡” mean “defined as” and “equiv-
alent to”, respectively. The notation “*” in matrix
representations indicates that the off-diagonal block
is the transpose of the corresponding lower-diagonal
block.
The rest of the paper is structured as follows: In
Section 2, we introduce the original system model,
formulate the 2D equivalent model, and define the
metric followed by the main result. Section 3 presents
numerical simulation results, verifying our proposed
strategy’s effectiveness and robustness. Section 4 pro-
vides a brief summary and some final remarks.
2 METHODOLOGY
2.1 Discrete-Time State-Space Model
In this study, we investigate a linear time-varying sys-
tem. This system captures the parameter uncertain-
ties inherent in a process executed repetitively over
multiple cycles. The model is given by the following
equations (Shi et al., 2005a; Shi et al., 2005b):
x
k
[t + 1] = (A + δA
k
[t])x
k
[t] + (B + δB
k
[t])u
k
[t],
y
k
[t] = Cx
k
[t]
(1)
where t ∈ [0, 1, 2, . . . , T ] is the time index, and k ∈ Z
+
is the iteration index
1
. The variables u
k
[t] ∈ R
m
,
y
k
[t] ∈ R
l
, and x
k
[t] ∈ R
n
represent the input, output,
and state at time t in the k-th iteration, respectively.
The nominal system matrices A, B, and C define the
ideal behavior of the system.
In practical applications, modeling uncertainties
of the system parameters are common. In this work,
we assume the modelling uncertainties of A and B
can be represented by δA
k
[t] and δB
k
[t] respectively,
which are defined as follows (Shi et al., 2005a; Shi
et al., 2005b):
δA
k
[t] = E
1
∆
k
[t]F
1
,
δB
k
[t] = E
2
∆
k
[t]F
2
.
(2)
The matrices E
1
, E
2
, F
1
, and F
2
are known and
of suitable dimensions, capturing the structures of the
uncertain parameter perturbations. The matrix ∆
k
[t]
represents the unknown perturbation matrix, which is
subject to the norm-bounded condition ∆
T
k
[t]∆
k
[t] ≤ I
for all t ≥ 0 and k > 0.
To improve the process performance over it-
erations, we employ the following updating law
(Aarnoudse et al., 2025):
u
k
[t] = u
k−1
[t] + r
k
[t] (3)
where the term r
k
[t] signifies the learning update at
time t in the k-th iteration. By default, the term u
0
[t]
is assumed to be a zero sequence.
2.2 Formulation of 2D Roesser System
ILC is a strategy designed for repetitive tasks charac-
terized by a two-dimensional system with time and it-
eration as two independent coordinates. The Roesser
model, a 2D system model, is well suited for repre-
senting ILC because it can depict information flow in
two directions. By employing this model, one can
combine the evolution of the state variable in the do-
mains of time and iteration. The combination aids
in developing efficient learning algorithms and robust
system convergence and stability analysis.
In what follows, we use f (t, k) to denote
f
k
[t], and define d( f (t, k)) := f (t, k) − f (t, k − 1).
Applying this definition to the set of quantities
{
x, u, y, r, e, δA, δB, ∆
}
, we can derive from equations
(1) and (3) the following:
1
The index of k can be dropped in terms of describing
the linear time-varying plant. k is added to facilitate the
analysis with ILC in the following.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
646

d(x(t +1, k)) = (A + δA(t, k))d(x(t, k))
+ (B + δB(t, k))r(t, k) + w(t, k)
(4)
where
w(t, k) = d(δA(t, k))x(t, k − 1)
+ d(δB(t, k))u(t, k − 1).
(5)
In the case of repeatable parameter perturbation,
i.e., d(δA(t, k)) ≡ 0 and d(δB(t, k)) ≡ 0, the term
w(t, k) reduces to w(t, k) ≡ 0. In general, the time-
varying modeling uncertainties are non-repeatable
2
,
and therefore d(δA(t, k)) ̸= 0 and d(δB(t, k)) ̸= 0. The
induced term w(t, k) is non-trivial and referred to as
an iteration-varying disturbance in this work.
Let us denote the tracking error at time t + 1 in
the k-th iteration as e(t + 1, k), i.e., e(t + 1, k) :=
y
r
(t + 1) − y(t + 1, k). It can be shown that e(t + 1, k)
is related to e(t + 1, k − 1) by the following equation:
e(t + 1, k) = −C(A + δA(t, k))d(x(t, k))
−C(B + δB(t, k))r(t, k)
−Cw(t, k) + e(t + 1, k −1).
(6)
Note from the above equation that the variation of
tracking error d(e(t + 1, k)) is affected by the unpre-
dictable varying perturbation w(t, k). It is important
to design a learning law to mitigate the effect of the
perturbation on the tracking error.
Combining equations (4) and (6), we obtain the
2D model denoted as:
Σ :

d(x(t +1, k))
e(t + 1, k)

= (
¯
A + δ
¯
A)

d(x(t, k))
e(t + 1, k − 1)

+ (
¯
B + δ
¯
B)r(t, k) +
¯
Dw(t, k)
(7)
where
¯
A =

A 0
−CA I

,
¯
B =

B
−CB

,
¯
D =

I
−C

,
δ
¯
A =

δA(t, k) 0
−CδA(t, k) 0

=
¯
E
1
∆(t, k)
¯
F
1
=

E
1
−CE
1

∆(t, k)

F
1
0

,
δ
¯
B =

δB(t, k)
−CδB(t, k)

=
¯
E
2
∆(t, k)
¯
F
2
=

E
2
−CE
2

∆(t, k)F
2
.
(8)
2
For example, δA, δB may be modeling error caused
by the linearization approximation, which is trajectory-
dependent. The trajectory in different iterations is variant,
and hence δA, δB varies with respect to k.
Let us interpret [d(x(t +1, k)), e(t +1, k)]
⊤
, r(t, k),
and w(t, k) be the state, input, and disturbance, re-
spectively. Then, the system Σ can be viewed as a 2D
Roesser model that incorporates uncertain parameter
perturbation and external disturbance. This model is
particularly advantageous as it effectively captures the
dynamics of convergence and tracking performance
within the ILC system. Hence, we refer to this model
as the equivalent 2D model for the ILC system.
Now, consider a 2D state feedback controller:
r(t, k) = G

d(x(t, k))
e(t + 1, k − 1)

(9)
where G ∈ R
m×(n+l)
is the feedback gain matrix to be
determined. Then, combining the 2D model Σ in (7)
and the feedback controller in (9) yields the closed-
loop model:
Σ
c
:

d(x(t +1, k))
e(t + 1, k)

= (
¯
A +
¯
BG + δ
¯
A + δ
¯
BG)

d(x(t, k))
e(t + 1, k − 1)

+
¯
Dw(t, k).
(10)
This 2D model encapsulates the system’s conver-
gence and tracking performance. It also considers the
uncertainties within the system parameters and pro-
vides a framework for potential algorithm develop-
ment.
2.3 Metric for Bounding Error
It is necessary to monitor the variation of tracking er-
rors to ensure the system’s desired behavior in the
presence of iteration-varying disturbances. Our ob-
jective is to minimize its sensitivity to such distur-
bances. Hence, a specific metric is defined as:
γ = max
k∈Z
+
∑
T +1
t=1
∥e(t, k)∥
2
−
∑
T +1
t=1
∥e(t, k − 1)∥
2
∑
T
t=0
∥w(t, k)∥
2
(11)
where γ represents the maximum ratio of the varia-
tion in tracking error energy to the disturbance energy
across all iterations.
In essence, γ provides a measurable way to see
how the tracking error’s variation responds to distur-
bances in the system. Reducing γ helps lessen the
impact of disturbances, improving the system’s sta-
bility and strengthening the system’s robustness. This
is important in engineering applications that require
precise control when faced with iteration-varying dis-
turbances. Note that a negative γ would imply that the
tracking error’s norm decreases as the number of iter-
ations increases regardless of the disturbance, which
Iterative Learning Control for Linear Time-Varying Systems in the Presence of Iteration-Varying Disturbance
647

is a strongly desired property for uncertain systems:
robust monotonic convergence of tracking error.
A natural goal is to find the feedback gain G that
minimizes metric γ. In this work, we provide an LMI
condition for simultaneously finding an upper bound
of γ and the associated G. Consider the following in-
equality for any k ∈ Z
+
:
∑
T +1
t=1
∥e(t, k)∥
2
−
∑
T +1
t=1
∥e(t, k − 1)∥
2
∑
T
t=0
∥w(t, k)∥
2
≤ γ. (12)
Theorem 1. For any k ∈ Z
+
, inequality (12) is guar-
anteed if there exists a scalar ε > 0 such that the fol-
lowing LMI holds:




−diag(I, γI) ∗ ∗

¯
A +
¯
BG
¯
D

ε
−1
(
¯
E
1
¯
E
⊤
1
+
¯
E
2
¯
E
⊤
2
) − I ∗

¯
F
1
0
¯
F
2
G 0

0 −ε
−1
I




⪯ 0
(13)
The proof can be found in Appendix B.
3 RESULTS
To solve LMI (13), we use the optimization toolbox
YALMIP (Lofberg, 2004) and solver MOSEK (ApS,
2022). The key is to determine the decision variables
G and ε in LMI (13) that minimize γ, which is the
upper bound of the measure of the resilience of the
tracking error to disturbance. We conduct a numeri-
cal simulation to validate the proposed strategy’s ef-
fectiveness.
Consider the system represented by the following
matrices:
A =

0.4 −0.3
0.1 0

, B =

1
0

, C =

1 1

,
E
1
=

0.01 0.01
0 0

, F
1
=

1 0
0 1

,
E
2
=

0.01
0

, F
2
= 1.
(14)
The reference trajectory is given by:
y
r
(t) = sin(
2π
25
t), t ∈ [0, 100]. (15)
Solving LMI (13) with YALMIP and MOSEK
gives a minimum γ value of 3.0033 with a feedback
gain G of [−0.4999, 0.29999, 0.6663] and an ε value
of 0.41.
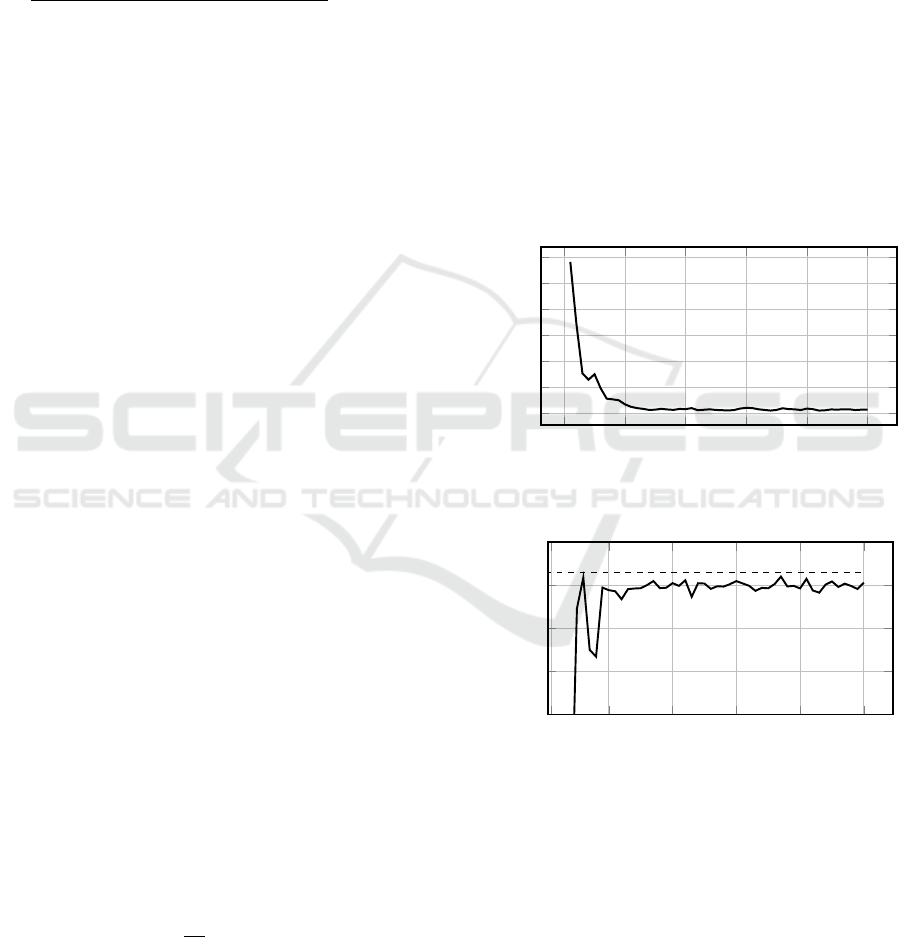
Figure 1 shows the Root Mean Square Error
(RMSE) of tracking as the iteration changes. RMSE
value obviously decreases as the number of iterations
increases. However, the tracking error cannot con-
verge perfectly to zero due to the iteration-varying
disturbances. The residual error indicates that despite
mitigations, the system experiences fluctuations that
hinder precise tracking, likely due to the influence of
disturbances that vary with each iteration.
Figure 2 shows the γ value as the iteration
changes. The energy of the error may increase at
some stages due to the presence of iteration-varying
disturbances, but this effect (measured by γ) is lim-
ited to 3.0033 or less. This bounded increase in en-
ergy indicates that the control system is able to miti-
gate the impact of disturbances up to a certain level,
maintaining overall stability and preventing excessive
error growth.
0 10 20 30 40
50
0
0.2
0.4
0.6
0.8
1
1.2
·10
−3
Iteration
RMSE
Figure 1: Tracking error convergence with iteration.
1
10 20 30 40
50
−30
−20
−10
0
10
3.0033
Iteration
γ
Figure 2: γ value variation with iterations.
4 CONCLUSIONS
In the field of ILC, addressing the challenges of time-
varying modeling uncertainty and non-repeatable dis-
turbances has been a persistent issue. This study in-
troduces a unique metric and proposes an LMI con-
dition to determine an upper bound for this metric
based on the 2D Roesser modeling formulation. The
Roesser model provides a robust framework for cap-
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
648

turing the dynamics of processes that exhibit both
temporal and iterative dependencies.
However, the proposed approach is limited to find-
ing a positive upper bound of the metric, which does
not guarantee robust monotonic convergence of the
tracking error. Ensuring that the tracking error con-
sistently decreases with each iteration is also impor-
tant for robust ILC performance. Our future research
direction will focus on addressing this limitation.
Additionally, while the theoretical analysis pro-
vides a solid foundation for our approach, further
practical validation is necessary. Preliminary numer-
ical simulation results are reasonable, demonstrating
potential resistance to iteration-varying disturbances.
This indicates that our approach can effectively han-
dle variability and unpredictability, improving the ro-
bustness and reliability of the ILC system.
REFERENCES
Aarnoudse, L., Pavlov, A., and Oomen, T. (2025). Non-
linear iterative learning control for discriminating be-
tween disturbances. Automatica, 171:111902.
Ahn, H.-S., Chen, Y., and Moore, K. L. (2007). Itera-
tive learning control: Brief survey and categorization.
IEEE Transactions on Systems, Man, and Cybernet-
ics, Part C, 37(6):1099–1121.
ApS, M. (2022). The MOSEK optimization toolbox for
MATLAB manual. Version 10.0.
Arimoto, S., Kawamura, S., and Miyazaki, F. (1984). Bet-
tering operation of robots by learning. Journal of
Robotic Systems, 1(2):123–140.
Boyd, S., El Ghaoui, L., Feron, E., and Balakrishnan, V.
(1994). Some standard problems involving lmis. Lin-
ear matrix inequalities in system and control theory,
pages 7–24.
Bristow, D., Tharayil, M., and Alleyne, A. (2006). A survey
of iterative learning control. IEEE Control Systems
Magazine, 26(3):96–114.
Chin, I., Qin, S., Lee, K. S., and Cho, M. (2004). A two-
stage iterative learning control technique combined
with real-time feedback for independent disturbance
rejection. Automatica, 40(11):1913–1922.
Du, C. and Xie, L. (1999). Stability analysis and sta-
bilization of uncertain two-dimensional discrete sys-
tems: an lmi approach. IEEE Transactions on Circuits
and Systems I: Fundamental Theory and Applications,
46(11):1371–1374.
Hoelzle, D. J. and Barton, K. L. (2014). A new spatial iter-
ative learning control approach for improved micro-
additive manufacturing. In 2014 American Control
Conference, pages 1805–1810.
Lee, J. H. and Lee, K. S. (2007). Iterative learning con-
trol applied to batch processes: An overview. Control
Engineering Practice, 15(10):1306–1318.
Lofberg, J. (2004). Yalmip : a toolbox for modeling and
optimization in matlab. In 2004 IEEE International
Conference on Robotics and Automation (IEEE Cat.
No.04CH37508), pages 284–289.
Maeda, G. J., Manchester, I. R., and Rye, D. C. (2015).
Combined ilc and disturbance observer for the rejec-
tion of near-repetitive disturbances, with application
to excavation. IEEE Transactions on Control Systems
Technology, 23(5):1754–1769.
Merry, R., van de Molengraft, R., and Steinbuch, M. (2005).
The influence of disturbances in iterative learning con-
trol. In Proceedings of 2005 IEEE Conference on
Control Applications, 2005. CCA 2005., pages 974–
979.
Norrl
¨
of, M. and Gunnarsson, S. (2001). Disturbance aspects
of iterative learning control. Engineering Applications
of Artificial Intelligence, 14(1):87–94.
Owens, D. and H
¨
at
¨
onen, J. (2005). Iterative learning con-
trol — an optimization paradigm. Annual Reviews in
Control, 29(1):57–70.
P
´
olik, I. and Terlaky, T. (2007). A survey of the s-lemma.
SIAM Review, 49(3):371–418.
Scherer, C. and Weiland, S. (2000). Linear matrix inequali-
ties in control. Lecture Notes, Dutch Institute for Sys-
tems and Control, Delft, The Netherlands, 3(2).
Shi, J., Gao, F., and Wu, T.-J. (2005a). Integrated design and
structure analysis of robust iterative learning control
system based on a two-dimensional model. Industrial
& Engineering Chemistry Research, 44(21):8095–
8105.
Shi, J., Gao, F., and Wu, T.-J. (2005b). Robust design of
integrated feedback and iterative learning control of a
batch process based on a 2d roesser system. Journal
of Process Control, 15(8):907–924.
Sun, J., Li, S., and Yang, J. (2014). Iterative learn-
ing control with extended state observer for iteration-
varying disturbance rejection. In Proceeding of the
11th World Congress on Intelligent Control and Au-
tomation, pages 1148–1153.
Wang, Y., Gao, F., and Doyle, F. J. (2009). Survey on it-
erative learning control, repetitive control, and run-to-
run control. Journal of Process Control, 19(10):1589–
1600.
Yao, Q. (2021). Robust adaptive iterative learning con-
trol for high-precision attitude tracking of spacecraft.
Journal of Aerospace Engineering, 34(1):04020108.
Zanchetta, P., Degano, M., Liu, J., and Mattavelli, P. (2013).
Iterative learning control with variable sampling fre-
quency for current control of grid-connected convert-
ers in aircraft power systems. IEEE Transactions on
Industry Applications, 49(4):1548–1555.
Zhang, F. (2006). The Schur complement and its applica-
tions, volume 4. Springer Science & Business Media.
Zhao, Y. M., Lin, Y., Xi, F., and Guo, S. (2015). Calibration-
based iterative learning control for path tracking of in-
dustrial robots. IEEE Transactions on Industrial Elec-
tronics, 62(5):2921–2929.
Iterative Learning Control for Linear Time-Varying Systems in the Presence of Iteration-Varying Disturbance
649

APPENDIX A
Lemma 1. (Du and Xie, 1999) Assume A, E, F and
Q = Q
⊤
are given matrices with appropriate dimen-
sions. For all matrix ∆, satisfying ∆∆
⊤
⩽ I, there ex-
ists a positive definite matrix P ≻ 0 satisfying
(A + E∆F)
⊤
P(A + E∆F) − Q ≺ 0 (16)
if and only if there exist a scalar ε > 0 and a posi-
tive definite matrix P ≻ 0 such that


−Q + εF
⊤
F A
⊤
P 0
PA −P PE
0 E
⊤
P −εI


≺ 0. (17)
Lemma 2. (Boyd et al., 1994) Assume W , L and V are
given matrices with appropriate dimensions, where W
and V are positive definite symmetric matrices. Then
L
⊤
V L −W ≺ 0 (18)
if and only if

−W L
⊤
L −V
−1

≺ 0 (19)
or

−V
−1
L
L
⊤
−W

≺ 0. (20)
APPENDIX B
Assume the boundary condition is maintaining zero
state transition between consecutive iterations at t =
0, which implies d(x(0, k)) = x(0, k)−x(0, k −1) = 0.
This condition is trivial and can be ensured, for in-
stance, by keeping the system state x(0, k) unchanged
across all iterations k ∈ Z
+
.
Recall that the upper bound inequality for γ is
given by:
∑
T +1
t=1
∥e(t, k)∥
2
−
∑
T +1
t=1
∥e(t, k − 1)∥
2
∑
T
t=0
∥w(t, k)∥
2
≤ γ. (21)
Firstly, observe that inequality (21) is satisfied by:
∥d(x(T + 1, k))∥
2
+
∑
T +1
t=1
∥e(t, k)∥
2
≤ ∥d(x(0, k))∥
2
+
∑
T +1
t=1
∥e(t, k − 1)∥
2
+ γ
∑
T
t=0
∥w(t, k)∥
2
.
(22)
Given that d(x(0, k)) = x(0, k) − x(0, k − 1) = 0
and ∥d(x(T +1,k))∥
2
≥ 0, the above inequality holds.
Next, we show that inequality (22) can be guaran-
teed by the following system of inequalities:
∥d(x(1, k))∥
2
+ ∥e(1,k)∥
2
≤ ∥d(x(0, k))∥
2
+ ∥e(1,k − 1)∥
2
+ γ∥w(0,k)∥
2
,
∥d(x(2, k))∥
2
+ ∥e(2,k)∥
2
≤ ∥d(x(1, k))∥
2
+ ∥e(2,k − 1)∥
2
+ γ∥w(1,k)∥
2
,
.
.
.
∥d(x(T, k))∥
2
+ ∥e(T, k)∥
2
≤ ∥d(x(T − 1, k))∥
2
+ ∥e(T, k − 1)∥
2
+ γ∥w(T −1, k)∥
2
,
∥d(x(T + 1, k))∥
2
+ ∥e(T +1, k)∥
2
≤ ∥d(x(T, k))∥
2
+ ∥e(T +1, k − 1)∥
2
+ γ∥w(T, k)∥
2
.
(23)
We obtain inequality (22) by summing the above
system of inequalities (23). Notice that the system of
inequalities (23) can be derived from:
∥d(x(t + 1, k))∥
2
+ ∥e(t +1, k)∥
2
≤ ∥d(x(t, k))∥
2
+ ∥e(t +1, k −1)∥
2
+ γ∥w(t, k)∥
2
, t = 0, 1, . . . ,T.
(24)
Construct the Lyapunov function as:
V

d(x(t +1, k))
e(t + 1, k)

= ∥d(x(t +1, k))∥
2
+ ∥e(t +1, k)∥
2
(25)
and
V

d(x(t, k))
e(t + 1, k − 1)

= ∥d(x(t, k))∥
2
+ ∥e(t + 1, k − 1)∥
2
.
(26)
With the defined Lyapunov function, inequality
(24) can be transformed into:
V

d(x(t + 1, k))
e(t + 1, k)

≤ V

d(x(t, k))
e(t + 1, k − 1)

+ γ∥w(t, k)∥
2
.
(27)
It follows from model (10) that inequality (27) can
be transformed into:
∥(
¯
A +
¯
BG + δ
¯
A + δ
¯
BG)

d(x(t, k))
e(t +1, k −1)

+
¯
Dw(t, k))∥
2
≤ ∥d(x(t, k))∥
2
+ ∥e(t +1, k − 1)∥
2
+ γ∥w(t, k)∥
2
.
(28)
Rewrite inequality (28) in matrix form:


d(x(t, k))
e(t +1, k −1)
w(t, k)


⊤

(
¯
A +
¯
BG + δ
¯
A + δ
¯
BG)
⊤
(
¯
A +
¯
BG + δ
¯
A + δ
¯
BG) − I ∗
¯
D
⊤
(
¯
A +
¯
BG + δ
¯
A + δ
¯
BG)
¯
D
⊤
¯
D − γI



d(x(t, k))
e(t +1, k −1)
w(t, k)


⪯ 0.
(29)
According to the definition of the negative semi-
definite matrix, inequality (29) holds if and only if the
matrix in the middle is negative semi-definite, that is,

(
¯
A +
¯
BG + δ
¯
A + δ
¯
BG)
⊤
(
¯
A +
¯
BG + δ
¯
A + δ
¯
BG) − I ∗
¯
D
⊤
(
¯
A +
¯
BG + δ
¯
A + δ
¯
BG)
¯
D
⊤
¯
D − γI

⪯ 0.
(30)
Substitute δA with E
1
∆F
1
and δB with E
2
∆F
2
,
where ∆
T
∆ ≤ I. After making these substitutions, in-
equality (30) transforms into:

(
¯
A +
¯
BG +
¯
E
1
∆
¯
F
1
+
¯
E
2
∆
¯
F
2
G)
⊤
(
¯
A +
¯
BG +
¯
E
1
∆
¯
F
1
+
¯
E
2
∆
¯
F
2
G) −I ∗
¯
D
⊤
(
¯
A +
¯
BG +
¯
E
1
∆
¯
F
1
+
¯
E
2
∆
¯
F
2
G)
¯
D
⊤
¯
D −γI

⪯ 0.
(31)
Using Lemma 1, inequality (31) can be guaran-
teed if and only if there exists a scalar ε > 0 such that:




−diag(I, γI) + ε

¯
F
1
0
¯
F
2
G 0

⊤

¯
F
1
0
¯
F
2
G 0

∗ ∗

¯
A +
¯
BG
¯
D

−I ∗
0

¯
E
1
¯
E
2

⊤
−εI




⪯ 0.
(32)
Then, by applying Lemma 2 (Schur complement),
inequality (32) can be guaranteed if and only if:




−diag(I, γI) ∗ ∗

¯
A +
¯
BG
¯
D

ε
−1
(
¯
E
1
¯
E
⊤
1
+
¯
E
2
¯
E
⊤
2
) − I ∗

¯
F
1
0
¯
F
2
G 0

0 −ε
−1
I




⪯ 0.
(33)
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
650