Automated Design of a Genetic Algorithm for Image Segmentation Using

the Iterated Local Search

Thambo Nyathi

Department of Computer Science, University of Pretoria, Hatﬁeld Campus, Pretoria, South Africa

Keywords:

Genetic Algorithm, Automated Design, Image Segmentation, Iterated Local Search.

Abstract:

Image thresholding is a fundamental technique used in image processing for segmentation. This is the process

of determining optimal thresholds for an image. When the number of thresholds exceeds two, that is, multi-

level thresholding, the computational complexity of the process increases exponentially. This has resulted in

the popularity of addressing this problem by using metaheuristic methods. However, metaheuristics are pa-

rameterised and their effectiveness depends on their conﬁguration, which is often performed manually using

an iterative trial-and-error approach. This leads to less effective designs that yield less accurate thresholds

and longer design times. This study proposes using an Iterated Local Search to conﬁgure a low-level meta-

heuristic, namely, a Genetic Algorithm(GA), to solve the multilevel threshold problem. The performance of

the proposed approach was compared with that of a manually designed standard GA approach, and evaluated

using T2 weighted Magnetic Resonance images of the brain. Furthermore, the proposed approach is compared

with two other metaheuristic algorithms for the same problem. The results showed that the automatically de-

signed genetic algorithm signiﬁcantly outperformed the standard genetic algorithm approach and the other two

algorithms on the set objective function. Although the runtimes were higher than those of the manual design

approach, better thresholds were obtained.

1 INTRODUCTION

Image segmentation is an essential process for image

analysis. It involves techniques used to partition an

image into distinct regions, with the hope that each

partitioned part belongs to a different object within

the image. Segmentation is prominent in facial recog-

nition and pedestrian detection among the numerous

image-processing techniques. Image segmentation

processes are predominantly preprocessing steps. Im-

age segmentation aims to simplify image data to en-

able ease of manipulation. Image thresholding is an

image-segmentation technique that separates an im-

age into two or more regions based on the intensity

values of the pixels. The most common thresholding

techniques are based on manipulating the histograms

of grayscale-level images (Amiriebrahimabadi et al.,

2024). Thresholding attempts to discriminate an ob-

ject from the background or other objects based on

the pixel intensity values of the object. There are

two approaches to thresholding: bi-level threshold-

ing and multilevel thresholding. The approaches are

https://orcid.org/0000-0003-4676-6063

categorised by the number of thresholds k. For bi-

level thresholding, there is one threshold (k=1), one

class is the range of pixel intensity values represent-

ing the object and the other representing the back-

ground. In multilevel thresholding, k > 1 and deter-

mining the optimal multilevel threshold value(s) is not

trivial (Abualigah et al., 2023).

Several techniques are used to determine opti-

mal threshold values for bi-level thresholding with

Otsu’s method (Ostu, 1979) and Kapur’s entropy

method (Kapur et al., 1985) being the most widely

used. These non-parametric exhaustive methods have

proved to be highly effective for bi-level threshold-

ing. However, as threshold levels increase beyond the

bi-level, Otsu and Kapur’s methods become computa-

tionally expensive. As a result, the use of metaheuris-

tic methods, speciﬁcally genetic algorithms (Holland,

1973) to solve multilevel thresholding problems has

gained prominence in recent years(Abualigah et al.,

2023). However, the effectiveness of metaheuristics

depends signiﬁcantly on their conﬁguration (Mart

ın-

Santamar

ıa et al., 2024). Therefore, this study pro-

poses automating the design of metaheuristics to

solve the multilevel thresholding problem. The pro-

Nyathi, T.

Automated Design of a Genetic Algorithm for Image Segmentation Using the Iterated Local Search.

DOI: 10.5220/0012908500003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 189-196

ISBN: 978-989-758-721-4; ISSN: 2184-3236

189

posed approach uses the Iterated Local Search (ILS)

algorithm (Lourenc¸o et al., 2019) to search the de-

sign space for the best GA design that solves the MLT

problem. To demonstrate its effectiveness the pro-

posed approach used a threshold of ten T2-weighted

pulse sequences (Tsushima et al., 2003) Magnetic

Resonance brain images for k = 2,3 and 4. The results

are compared to a manually designed approach, the

results of the Particle Swarm Optimisation (Kennedy

and Eberhart, 1995), and a real number encoded ge-

netic algorithm obtained from the literature. The con-

tributions of this study are as follows:

• To propose a novel ILS approach to conﬁguring

GAs that can be used to solve the MLT problem.

• To demonstrate that the proposed ILS approach

conﬁgures GAs more effectively than a manually

conﬁgured GA.

• To demonstrate that using ILS to search for GA

designs is beneﬁcial and improves the results ob-

tained from the GA.

This paper is arranged as follows: Section 2 out-

lines the ﬁeld of automated design. Section 3 presents

the multilevel thresholding problem, and Section 4 is

an outline of the GA. The Iterated Local Search is

presented in Section 5. Section 6 is the proposed ap-

proach followed by the experimental setup in Section

7 and the results in Section 8. The conclusion and

future research are outlined in Section 9.

2 AUTOMATED DESIGN OF

METHAHEURISTICS

The design of metaheuristics has long been viewed

as a combinatorial optimisation problem. It is still

driven by human expertise, which is inﬂuenced by

intuition and bias and is evaluated through trial-and-

error approaches (Mart

ın-Santamar

ıa et al., 2024). It

involves trial runs in which parameter values are it-

eratively changed. The parameter values that yield

the best objective value outputs are used in the ﬁ-

nal conﬁguration. The manual design search space

is usually restricted based on the experience of al-

gorithm designers. The development of automated

design techniques for metaheuristics is a specialized

ﬁeld that aims to create or customize metaheuristic

algorithms for speciﬁc optimisation problems. The

goal is to enhance the efﬁciency of the design pro-

cess by automating some or all aspects of it, result-

ing in potentially more effective algorithms. The lit-

erature presents two approaches to automated design:

ofﬂine and online (Zhao et al., 2023). In ofﬂine ap-

proaches, the automated design process occurs inde-

pendently of the problem that needs to be solved. On-

line design involves the adaptation of a metaheuristic

during execution. Ofﬂine approaches are simpler to

implement and less computationally expensive (Zhao

et al., 2023). Several approaches for the conﬁguration

of metaheuristics have been proposed, such as irace

opez-Ib

nez et al., 2016) and ParamsILS (Hutter

et al., 2007) although none have been widely adopted.

In its most basic form of automated design, an algo-

rithm is decomposed into its basic design components

and possible values, and placed at a low level. A de-

signer algorithm operates at a higher level and com-

bines different low-level components into a valid al-

gorithm. The designed algorithms are evaluated on

a problem, and the best-performing algorithm is pro-

posed as the solution.

In this study the automated design of a genetic al-

gorithm is proposed. Genetic algorithms are one of

the most popular evolutionary algorithms; thus, it is

not surprising that the automated design of GAs has

been previously proposed. In the earliest study on au-

tomating a GA, a GA was used at a higher level to

conﬁgure a lower-level GA (Grefenstette, 1986). Sub-

sequently, several studies have proposed using vari-

ous other algorithms to conﬁgure genetic algorithms.

Despite the potential beneﬁts of automated design, it

is still an evolving ﬁeld, and manual approaches may

outperform automated methods. The time and ef-

fort required to develop effective metaheuristics can

be signiﬁcantly reduced using automated design tech-

niques. The high-level algorithm can also suffer from

the same design ﬂaws as the low-level algorithm. In

this study, we propose using an Iterated Local Search

algorithm as the high-level algorithm. The ILS algo-

rithm replaces an algorithm designer and searches in

a search space of GA designs. This algorithm has the

advantage of being simple to implement. ILS has a

low computational cost and very few parameters to

conﬁgure. The next section reviews the multilevel

thresholding problem.

3 MULTILEVEL

THRESHOLDING

Multilevel thresholding is a systematic way of

segmenting a greyscale image I into k+1 subre-

gions/classes. In this case k thresholds are required

and are deﬁned as {t

,.....,t

= g(x, y) ∈ I|0 ≤ g(x, y) ≤ t

− 1 (1)

= g(x, y) ∈ I|t

≤ g(x, y) ≤ t

− 1 (2)

= g(x, y) ∈ I|t

≤ g(x, y) ≤ L − 1 (3)

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

190

In Equations 1, 2 and 3 c

represents the k

sub-

region, while L represents the number of greyscale

levels. This problem involves searching for the best

threshold values within the space of thresholds in the

range of 0 - L. This is an NP problem and the use of

exact methods leads to the search complexity growing

exponentially as the number of thresholds increases as

O(L

k−1

). The effectiveness of the determined thresh-

olds is generally evaluated by minimizing or max-

imizing an objective function. While Kapur’s en-

tropy and Otsu’s methods are primarily used for bi-

nary thresholding, with modiﬁcations, they can both

be extended to multilevel thresholding. This study

used Kapur’s method as the objective function be-

cause of its calculation speed. The objective is to

achieve optimal class separation by maximizing intra-

class entropy and minimizing inter-class information

leakage. The Kapur’s entropy can be extended for the

MLT problem as follows: If k values from the follow-

ing threshold values {t

,.....,t

} dissect the image

into distinct regions. The probability p

can be deﬁned

as:

h(i)

∑

L−1

i=0

h(i)

(4)

where h(i) represents the grey scale level and

∑

L−1

i=0

h(i) is the total number of pixels, while L is the

number of levels. Kapur’s entropy is given as follows:

f (t

, .....t

) = H

+ H

+ ..... + H

(5)

To evaluate multilevel problems Kapur’s entropy

is extended as follows.

= −

∑

−1

i=0

, where ω

∑

−1

i=0

(6)

= −

∑

L−1

i=t

, where ω

∑

L−1

i=k

(7)

Numerous metaheuristics have been employed to

solve the multilevel thresholding problems. In a

recent survey (Amiriebrahimabadi et al., 2024) de-

scribes the use of evolutionary algorithms such as

genetic algorithms. In the early years, metaheuris-

tics were commonly used independently; however, to

improve performance, the latest approaches employ

hybridised metaheuristics (Amiriebrahimabadi et al.,

2024).

The next section reviews genetic algorithms.

4 GENETIC ALGORITHMS

Algorithm 1 outlines a genetic algorithm.

Genetic Algorithms have been widely applied in

multilevel thresholding owing to their computational

Data: Population P, Fitness function F,

Crossover rate p

, Mutation rate p

Result: Optimal solution

Initialize population P;

Evaluate the ﬁtness of each individual;

while termination condition not met do

Select parents for crossover;

Apply crossover with probability p

;

Apply mutation with probability p

;

Evaluate the ﬁtness of new individuals;

Update the population;

end

return best individual from ﬁnal population;

Algorithm 1: Genetic Algorithm (Holland, 1973).

efﬁciency. When applied to MLT problems, inte-

ger encoding is the most commonly used encoding

method (Manikandan et al., 2014). Each individual

is a complete solution to an MLT problem, in which

each gene is an integer that represents a threshold.

The general mode of operation of most techniques

that employ GAs begins by generating random thresh-

olds. The thresholds are iteratively adjusted using

variation operators to improve the objective function.

Genetic algorithms have been used to threshold mag-

netic resonance brain scan images(Manikandan et al.,

2014). Binary encoding has been used to thresh-

old a subset of benchmark problems (de Oliveira and

Yamanaka, 2018). Studies in the literature employ

a wide range of population sizes. Ranging from a

population size of 20 and 30 (de Oliveira and Ya-

manaka, 2018). Fitness proportionate and tourna-

ment selections are the most commonly used parent

selection methods. Otsu’s and Kapur’s methods are

the most commonly used ﬁtness functions. The most

commonly applied variation operators are crossover

and mutation operators. Single-point crossover has

been widely used at a rate of 10%. Another widely

used crossover method is simulated binary crossover

(SBX) (Manikandan et al., 2014). A study (Sun

et al., 2016) used ﬁtness proportionate selection and

discrete mutation as genetic operators to threshold

benchmark images at levels 2,3,4 and 5, using Otsu

and Kapur’e entropy as ﬁtness functions. In the fol-

lowing study, 100 generations were set as the ter-

mination criteria. Most studies (Hammouche et al.,

2008) have used the generational approach to update

the population. In that study, a population size of 100

was used, with Kapur entropy conﬁgured as the ﬁt-

ness function. Single point crossover was used at a

rate of 90% and mutation rate of 1%. In another study

(Abbasgholipour et al., 2011), a GA was used to solve

the thresholding problem by using string encoding

with a population size of 12. Tournament selection

Automated Design of a Genetic Algorithm for Image Segmentation Using the Iterated Local Search

191

was performed, using, a tournament size of 4. Single

point crossover (80%), mutation (16%), and 400 gen-

erations were the termination criteria. Medical image

segmentation is an important area where threshold-

ing algorithms are applied such as a study (Manikan-

dan et al., 2014) where a GA was used to threshold

the MRI brain scan images using real number encod-

ing. Simulated binary crossover (SBX) was applied

at a probability rate of 80% and mutation probability

rate of 1 %. A population size of 50 was used and

the termination criteria was 10000 generations. Vari-

ations in GAs for solving the MLT problem can also

be found in the literature (Lai and Tseng, 2004).

5 ITERATED LOCAL SEARCH

Iterated Local Search is a metaheuristic algorithm

which is effective at solving a wide range of optimi-

sation problems. It involves three steps: perturbation,

local search and evaluation of an acceptance criterion.

Data: Initial solution s

, perturb function N,

Iteration limit T

Result: Improved solution

best

← s

;

′

← s

;

t ← 0;

while t < T do

′

← perturb(s

′

) ; // Generate a

neighbour solution

′

← localSearch(s

′

) ; // Apply local

search to s

′

if ﬁtness(s

′

) > ﬁtness(s

best

) then

best

← s

′

;

end

t ← t +1;

end

return s

best

;

Algorithm 2: Iterated Local Search (Lourenc¸o et al.,

2003).

Algorithm 2 presents the outline of the ILS algo-

rithm. The algorithm begins by creating a random ini-

tial solution s

using a constructive heuristic. The al-

gorithm then goes through a cycle of applying three

operators, perturbation, local search, and acceptance

criteria, until a stopping criterion is achieved. Pertur-

bation accepts a solution and makes changes that be-

come new starting points of the local search. This en-

ables the ILS to escape local optima (Lourenc¸o et al.,

2003). In the next step, a local search is applied to

the initial solution. This involves searching the neigh-

bourhood of the current solution, in this case s’, by

making small changes to s’. The acceptance criterion

determines whether a new solution should replace the

current optimal solution.

5.1 Automated Design Using Iterated

Local Search

Previous studies have shown that an ILS algorithm

effectively conﬁgures other algorithms. In one of

the earliest uses of ILS as an algorithm conﬁgura-

tor, (Hutter et al., 2007) proposed an approach called

ParamsILS. This approach was used to conﬁgure four

algorithms and was shown to outperform the man-

ually conﬁgured algorithms. Variants of ParmaILS,

namely BasicILS and FocusedILS, have been pro-

posed. A concise review of the applications of the

ILS algorithm is presented in (Lourenc¸o et al., 2019).

6 PROPOSED APPROACH

The challenge of designing an evolutionary algorithm

that can achieve optimal performance in solving the

multilevel thresholding problem involves ﬁnding a

design that can balance exploration and exploitation

effectively. To achieve this, an ILS algorithm was

used to search the conﬁguration space of the GA. The

proposed approach was based on the ILS algorithm

presented in Section 5. The ﬁrst step of the ILS for

the GA, herein termed ILSGA, was to create an ini-

tial solution s

. An initial solution was randomly cre-

ated from the GA design components, as presented

in Table 1. An ILSGA solution was represented as a

chromosome of nine genes. Each gene (G) represents

a design decision as speciﬁed in Table 1.

Table 1: GA Design Decisions.

G Parameter Range of Possible Values

0 popSize 50–200

1 selection 0-tourn,1-ﬁt prop, 2- rank

2 crossover 0-1point,1-SBXT, 2-BLXT

3 crossrate 0-100%

4 mutation 0-bit ﬂip, 1- gauss, 2-cauchy

5 mutrate 0-100%

6 termination 50-150

7 control ﬂow 0 – none, 1- create

8 init 0 – random, 1- sensible

The ﬁrst column indexes the design-decision

genes of the genetic algorithm. The second column

describes the design decisions. Column 3 presents

the range of possible values for each design deci-

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

192

sion. Each range of values represents the values

found in the literature commonly used to conﬁgure

a GA. Gene 0 determines the GA population size

from within the range of 50 to 200. Gene 1 spec-

iﬁes the parent selection method from one of three

possible methods i.e. tournament selection, ﬁtness

proportionate and rank selection. Gene 2 is used

to determine the crossover operator. Three options

are available: 0-uniform crossover, 1-Simulated Bi-

nary Crossover (SBX, eta = 0.2, mu = rand(0,1), and

2- Blend Crossover (BLX, alpha =0.5) (Manikandan

et al., 2014). Gene 3 speciﬁes the crossover rate, and

gene 4 speciﬁes the mutation operator. Gene 4 options

are uniform mutation, gaussian mutation and Cauchy

mutation(Rudolph, 1997). The mutation rate is speci-

ﬁed by gene 5. Gene 6 determines the number of gen-

erations, which is also the termination criterion from

a value of 50 to 200. Gene 7 speciﬁes the control ﬂow

of the GA. If this gene is conﬁgured to be a value of

0, the evolution of the GA runs normally; however,

if it is conﬁgured to a value of 1, the algorithm will

abruptly create a new population at a random point

during the run. This behaviour allows the algorithm

to escape a local optimum. Gene 8 determines the

starting position of the algorithm. If the gene is set

to 0, the thresholds of the initial population are ran-

domly selected from the range of 0 – 255. If the gene

is set to a value of 1, bounded sensible initialisation is

used for example, for a 2-level threshold GA individ-

ual, the two thresholds are randomly obtained from

bounded ranges as follows: threshold one 0-127 and

threshold two 128-255.

6.1 Iterated Local Search Genetic

Algorithm- ILSGA

An initial ILSGA solution is randomly created from

a range of possible values. The ILSGA solution is

a GA conﬁguration used to solve the MLT problem.

Kapur’s entropy presented in Section 3 was used as

the ﬁtness function of the underlying GA, which was

subsequently used as the objective function of the

ILSGA. The initial solution is used to conﬁgure a GA

applied to an MLT problem, and the ﬁtness value of

the best-performing GA is assigned to the ILSGA as

its objective value. A local search was then conducted

on the ILSGA solution. The number of neighbours

considered was randomly selected from 2 to 9. In

this study, a neighbour was considered as a single al-

teration to any of the nine genes of an ILSGA solu-

tion, without considering the value of the gene in the

change. The algorithm may consider two or all nine

neighbours. The selected neighbouring solution was

applied to the MLT problem. The acceptance criterion

used was the improving only criterion (Best(s,s”))

and is given by Equation 8:

s = Best(s, s”) = s”if f (s”) > f (s)else = s (8)

Where f(s) is the objective function. The best-

performing becomes the new solution. Therefore, a

new ILSGA solution is accepted only if it outperforms

the current solution. After this step, a perturbation

was applied. The perturbation operator mutates one

or more genes in the solution. This perturbed solution

becomes the new starting point for the local search.

This cycle was continued for a ﬁxed number of itera-

tions until convergence was achieved.

7 EXPERIMENTAL SETUP

To evaluate the effectiveness of the proposed ap-

proach ten T2-weighted MRI images obtained from

the Harvard Medical School web-based medical im-

age repository were used as test images speciﬁcally

Slices 22,32,42,52,62,72,82,92,102 and 112. Six ex-

periments were conducted for each of the ten images.

A manually designed standard GA was used to es-

tablish 2-level, 3-level and 4-level thresholds. Simi-

larly, the ILSGA algorithm was applied to solve for

the 2-level, 3-level and 4-level thresholds. To estab-

lish the parameter values for each threshold level for

the standard GA design, test runs were conducted us-

ing values from the literature as the starting points.

An iterative trial-and-error parameter tuning approach

was applied until the best-performing set of parame-

ters, based on the test runs, was established. These

are presented in Table 2

The simulations were conducted at the Centre for

High-Performance Computing (CHPC) Lengau Clus-

ter. Java 1.8 was used as the software development

platform on the Netbeans 8.1 Integrated Development

Environment.

Table 2: Standard GA Parameters.

Param 2T 3T 4T

Popsize 200 200 200

Selection Tourn Tourn Tourn

Tourn size 8 10 10

Crossover 1-point 1-point Uniform

Crossrate 0.85 0.80 0.70

Mutation Random Random Uniform

MutRate 0.25 0.30 0.25

Termination 200 200 200

Automated Design of a Genetic Algorithm for Image Segmentation Using the Iterated Local Search

193

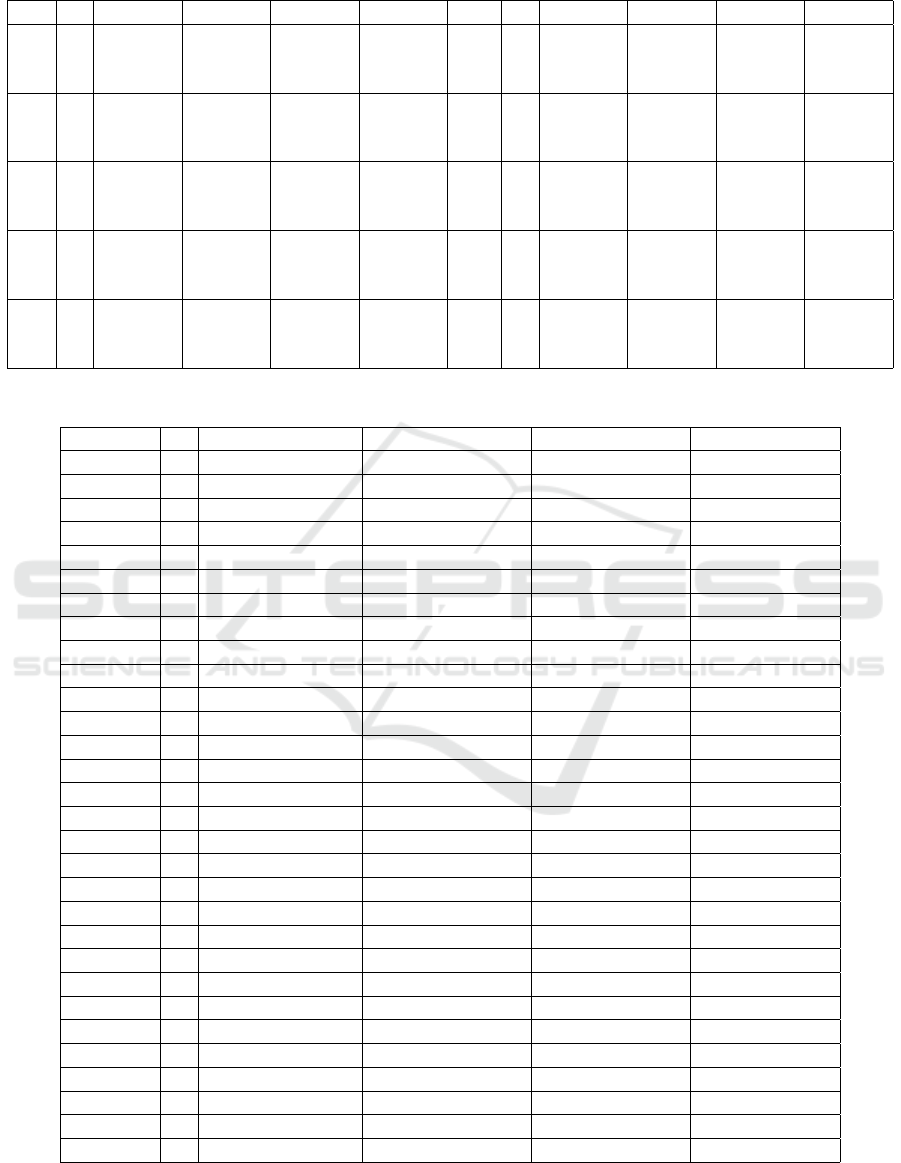
Table 3: Kapur’s Entropy Results.

Im T ILSGA SGA PSO RGA Im T ILSGA SGA PSO RGA

22 2 11.1665 11.1665 9.2136 9.2155 72 2 11.5713 11.5707 9.4163 9.4205

3 14.3145 14.3145 11.3290 11.7333 3 14.5270 14.5227 11.4144 11.6935

4 17.1510 17.1387 13.5003 13.9555 4 17.3750 17.3257 13.5094 13.8463

32 2 11.3694 11.3694 9.2617 9.2645 82 2 11.3492 11.3492 9.1847 9.1910

3 14.4216 14.4209 11.3367 11.6835 3 14.3630 14.3612 11.0248 11.4269

4 17.3015 17.3038 13.4849 13.9406 4 17.1757 17.1531 13.2558 13.5191

42 2 11.4938 11.4916 9.2568 9.2585 92 2 10.6614 10.6612 8.7750 8.7906

3 14.4656 14.4641 11.3036 11.5779 3 13.5962 13.5763 10.6335 11.1640

4 17.3378 17.3291 13.5556 13.865 4 16.3146 16.2432 12.9568 13.2974

52 2 11.3897 11.3888 9.2433 9.2447 102 2 10.3586 10.3586 8.5127 8.5283

3 14.4421 14.4390 11.2299 11.5795 3 13.4379 13.4335 10.6913 10.9277

4 17.2938 17.2021 13.3646 13.7502 4 16.1471 16.1337 12.5920 13.1320

62 2 11.4731 11.4717 9.3073 9.3367 112 2 9.7462 9.7462 8.1308 8.1476

3 14.5211 14.4960 11.3313 11.6745 3 12.6918 12.6776 10.0312 10.6029

4 17.3975 17.3223 13.4960 13.7812 4 15.7416 15.7128 12.3148 13.0591

Table 4: Image Thresholds.

Image T ILSGA GA PSO RGA

Slice 22 2 95,177 95,177 97,184 96,184

3 61,115,178 61, 115, 229 69,138,207 58,115,185

4 56 ,108 ,159 ,189 58 ,113, 182, 246 83,116,175,207 44,87,131,186

Slice 32 2 110,185 110, 185 107,185 109,185

3 56 ,115 ,185 60, 118 ,247 74,157,192 53,116,185

4 56 ,114 ,175 ,207 55,113,230,250 95,125,164,194 39,84,131,189

Slice 42 2 112 ,182 113, 182 111,183 114,183

3 83 ,130 ,183 83,131,222 80,148,178 84,132,187

4 76 ,120 ,169 ,214 58,112,236,250 81,125,164,197 30,75,127,188

Slice 52 2 118,181 120,181 119,186 118,185

3 112 ,167 ,204 111,167,237 89,113,187 109,165,203

4 92 ,128 ,170 ,205 82, 122, 182, 248 79,111,141,208 91,131,174,209

Slice 62 2 120,182 119,183 109,186 121,187

3 110 ,166 ,213 115,162,205 112,167,187 101,147,196

4 98 ,136 ,176 ,213 87,127,151,235 85,134,180,203 94,134,175,211

Slice 72 2 116,175 118,177 116,177 117,179

3 98 ,139 ,184 97,140,233 96,178,207 99,141,187

4 96,133 ,174 ,212 98,139,151,213 96,124,161,187 99,140,179,213

Slice 82 2 113,173 113,173 110,170 111,169

3 109 ,158 ,203 109,158,225 103,136,198 103,146,190

4 98 ,134 ,173 ,213 95,138,190,192 100,129,167,188 98,133,169,210

Slice 92 2 108,168 109,168 109,175 109,174

3 102 ,144 ,186 98,146,242 115,134,178 94,142,190

4 98 ,135 ,168 ,199 105, 139,170, 230 77,107,149,194 97,136,173,211

Slice 102 2 114,168 114, 168 98,166 107,174

3 95 ,142 ,186 95, 142, 242 113,145,180 94,142,190

4 91 ,131 ,164 ,201 90,125,128,248 84,124,165,189 1,63,120,174

Slice 112 2 100,150 100, 150 109,162 106,163

3 94 ,135 ,173 94, 138, 247 104,163,216 1,70,142

4 6 ,62 ,122 ,169 5, 56, 209, 233 63,130,153,206 1,65,123,172

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

194

8 RESULTS

Table 3 presents the performance results of the

four algorithms using Kapur’s entropy as a metric.

Columns 1 and 7 present the image problem in-

stances. Columns 2 and 8 present the thresholds

considered 2,3 and 4, respectively. The remaining

columns present the algorithms used in this study.

Columns 3 and 9 show the results obtained by the

ILS GA and columns 4 and 10 show the results of the

standard GA. The results of two algorithms, namely

PSO and the real genetic algorithm (RGA), applied to

the same images obtained from (Manikandan et al.,

2014) are also presented. Columns 5 and 11 show

the PSO results and columns 6 and 12 show the RGA

results. The best result from 30 independent runs is

reported for each image for each of the three thresh-

old levels considered for the ILSGA and SGA algo-

rithms. From the results across all images, on the 2-

level thresholds, the ILSGA algorithm performed bet-

ter than SGA on ﬁve images and equivalently on the

other ﬁve images. On the 3-level thresholds, ILSGA

performed better on nine images and equivalently on

one image, slice22. On the 4-level thresholds, the

ILS GA algorithm performed better on nine images

and worse on slice 32. From the presented values, the

ILSGA and SGA algorithms perform better than the

PSO and RGA algorithms reported in the literature.

However, this assertion is cautionary, as differences

in experimental settings and image sizes may lead to

disparities in the results. Table 4 presents the thresh-

old values achieved for each image by each algorithm

at the considered threshold level. An analysis of the

threshold values revealed that the values obtained for

the 2-level threshold were almost identical across all

algorithms. For the 3-level and 4-level thresholds, the

differences are wider than for the 2-level but the val-

ues are within the same range. To evaluate the sig-

niﬁcance of the differences in performance between

ILSGA and SGA, the Wilcoxon rank sum test at a 5%

signiﬁcance level was used (Wilcoxon, 1992). The

differences in performance were found to be signiﬁ-

cant where ILSGA performed signiﬁcantly better than

the standard GA approach.

Table 5 presents a sample of GA designs that were

evolved using the ILSGA algorithm. The ﬁrst and

second columns show the image and threshold lev-

els, respectively. The third column presents the pa-

rameters of the GA design, as listed in Table 1. The

numbers in brackets indicate the number of times the

ILS algorithm accepts a new set of parameters. The

fourth column shows the design time (in millisec-

onds). For example, in the ﬁrst row for the image

slice 22 2-level threshold, the population size is 77

Table 5: ILSGA Designs.

Im T GA Design Time

22 2 77,1,2,60,0,10,87,1,0 (4) 18721

3 152,1,2,70,2,20,119,1,1 (12) 58341

4 99,2,1,80,1,10,102,1,0 (4) 51656

62 2 159,2,0,30,0,80,98,1,0 (3) 65154

3 189,1,0,20,0,60,144,1,1 (6) 47705

4 77,2,2,80,1,50,51,0,1 (6) 56301

102 2 172,0,2,50,2,10,120,1,0 (3) 60953

3 184,1,1,30,2,20,144,0,1 (5) 57887

4 179,0,2,50,2,40,153,1,1(5) 54139

and the ﬁtness proportionate is selected as the selec-

tion method. The crossover operator is set to BLXT

at a probability rate of 60%. A bit-ﬂip mutation was

applied at a probability rate of 10 %. ILSGA was ap-

plied for 87 iterations. The process runs for 18721

milliseconds and four perturbations were accepted as

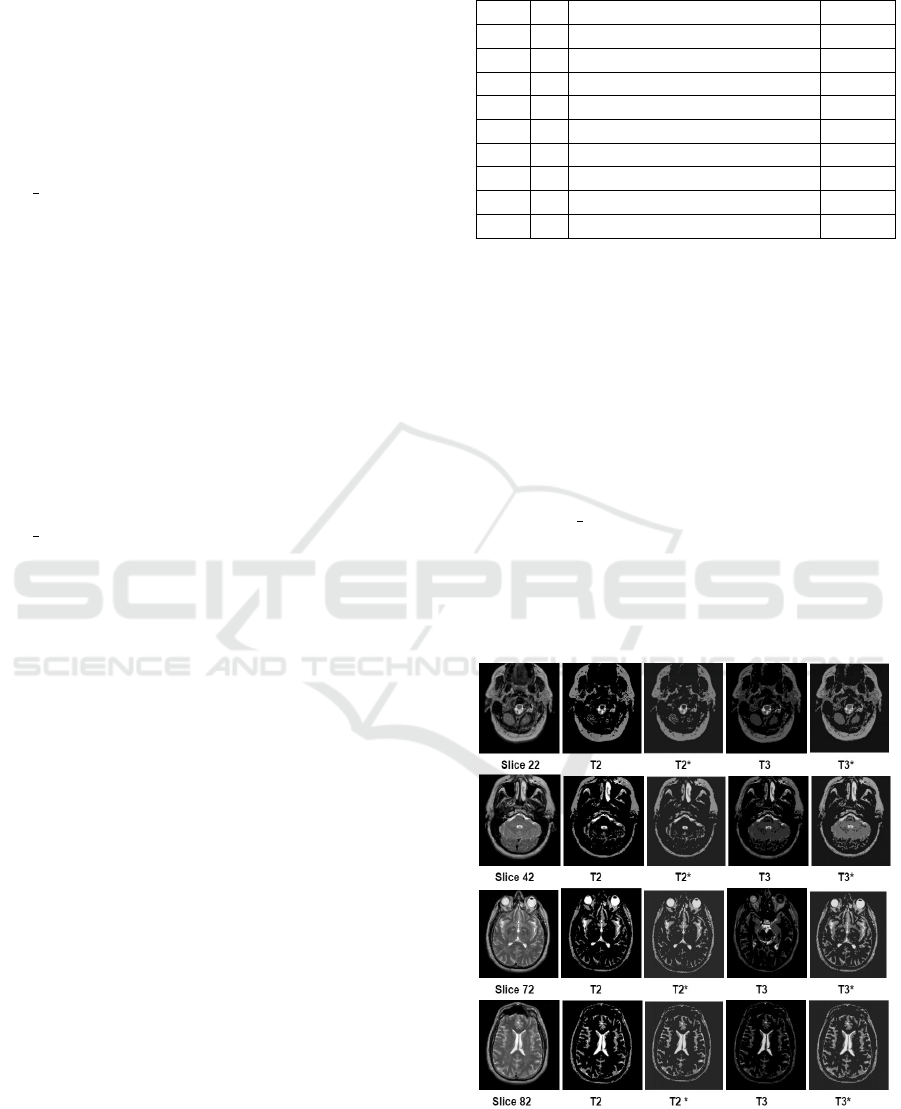
new solutions. Figure 1 shows a visual illustration of

the comparison between thresholded MRI images and

those obtained from (Manikandan et al., 2014). The

ﬁrst row refers to slice 22. T2 is the output of the 2-

level thresholding while T3 is the 3-level thresholding

from the ILS GA. Images labelled T2* and T3* were

extracted from (Manikandan et al., 2014). It can be

seen that there are slight differences between those

obtained from the ILSGA and those obtained from

(Manikandan et al., 2014). This is in line with the

obtained objective function values.

Figure 1: Comparison of Segmented Images.

Automated Design of a Genetic Algorithm for Image Segmentation Using the Iterated Local Search

195

9 CONCLUSION AND FUTURE

WORK

This study proposes an automated genetic algorithm

design using an Iterated Local Search algorithm ap-

proach. The effectiveness of the proposed approach

was evaluated using T2-weighted axial brain MR.

The automated design-evolved GA achieved better re-

sults on the objective function metric than the stan-

dard manually designed GA. The automated design

of metaheuristics has proven to be effective in the ma-

jority of problem domains where metaheuristics have

achieved success. The purpose of this study was to

evaluate the efﬁcacy of an automated design in the do-

main of image segmentation, speciﬁcally multilevel

thresholding. Additionally, the design time of the GA

is less than that of the manual approach, which can

range from one day to several days as the search space

of parameter values is very wide. Future work will in-

volve a comparative analysis between ILS and a more

complex algorithm. The use of an algorithm more

complex than ILS may achieve better results since the

ILS searches in the locality of an initial solution and

can be vulnerable to local optimal. Additionally, con-

sideration of a larger number of specimen images will

be investigated.

REFERENCES

Abbasgholipour, M., Omid, M., Keyhani, A., and Mo-

htasebi, S. S. (2011). Color image segmentation with

genetic algorithm in a raisin sorting system based on

machine vision in variable conditions. Expert Systems

with Applications, 38(4):3671–3678.

Abualigah, L., Almotairi, K. H., and Elaziz, M. A. (2023).

Multilevel thresholding image segmentation using

meta-heuristic optimization algorithms: Comparative

analysis, open challenges and new trends. Applied In-

telligence, 53(10):11654–11704.

Amiriebrahimabadi, M., Rouhi, Z., and Mansouri, N.

(2024). A comprehensive survey of multi-level thresh-

olding segmentation methods for image processing.

Archives of Computational Methods in Engineering,

pages 1–51.

de Oliveira, P. V. and Yamanaka, K. (2018). Image seg-

mentation using multilevel thresholding and genetic

algorithm: An approach. In 2018 2nd international

conference on data science and business analytics

(ICDSBA), pages 380–385. IEEE.

Grefenstette, J. J. (1986). Optimization of control param-

eters for genetic algorithms. IEEE Transactions on

systems, man, and cybernetics, 16(1):122–128.

Hammouche, K., Diaf, M., and Siarry, P. (2008). A mul-

tilevel automatic thresholding method based on a ge-

netic algorithm for a fast image segmentation. Com-

puter Vision and Image Understanding, 109(2):163–

175.

Holland, J. H. (1973). Genetic algorithms and the opti-

mal allocation of trials. SIAM journal on computing,

2(2):88–105.

Hutter, F., Hoos, H. H., and St

utzle, T. (2007). Auto-

matic algorithm conﬁguration based on local search.

In Aaai, volume 7, pages 1152–1157.

Kapur, J. N., Sahoo, P. K., and Wong, A. K. (1985). A new

method for gray-level picture thresholding using the

entropy of the histogram. Computer vision, graphics,

and image processing, 29(3):273–285.

Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-

mization. In Proceedings of ICNN’95-international

conference on neural networks, volume 4, pages

1942–1948. ieee.

Lai, C.-C. and Tseng, D.-C. (2004). A hybrid approach

using gaussian smoothing and genetic algorithm for

multilevel thresholding. International Journal of Hy-

brid Intelligent Systems, 1(3-4):143–152.

opez-Ib

nez, M., Dubois-Lacoste, J., C

aceres, L. P., Bi-

rattari, M., and St

utzle, T. (2016). The irace package:

Iterated racing for automatic algorithm conﬁguration.

Operations Research Perspectives, 3:43–58.

Lourenc¸o, H. R., Martin, O. C., and St

utzle, T. (2003). It-

erated local search. In Handbook of metaheuristics,

pages 320–353. Springer.

Lourenc¸o, H. R., Martin, O. C., and St

utzle, T. (2019). Iter-

ated local search: Framework and applications. Hand-

book of metaheuristics, pages 129–168.

Manikandan, S., Ramar, K., Iruthayarajan, M. W., and

Srinivasagan, K. (2014). Multilevel thresholding

for segmentation of medical brain images using real

coded genetic algorithm. Measurement, 47:558–568.

Mart

ın-Santamar

ıa, R., L

opez-Ib

nez, M., St

utzle, T., and

Colmenar, J. M. (2024). On the automatic genera-

tion of metaheuristic algorithms for combinatorial op-

timization problems. European Journal of Opera-

tional Research.

Ostu, N. (1979). A threshold selection method from gray-

level histograms. IEEE Trans SMC, 9:62.

Rudolph, G. (1997). Local convergence rates of sim-

ple evolutionary algorithms with cauchy mutations.

IEEE Transactions on Evolutionary Computation,

1(4):249–258.

Sun, G., Zhang, A., Yao, Y., and Wang, Z. (2016). A

novel hybrid algorithm of gravitational search algo-

rithm with genetic algorithm for multi-level threshold-

ing. Applied Soft Computing, 46:703–730.

Tsushima, Y., Aoki, J., and Endo, K. (2003). Brain mi-

crohemorrhages detected on t2*-weighted gradient-

echo mr images. American journal of neuroradiology,

24(1):88–96.

Wilcoxon, F. (1992). Individual comparisons by ranking

methods. In Breakthroughs in statistics: Methodology

and distribution, pages 196–202. Springer.

Zhao, Q., Duan, Q., Yan, B., Cheng, S., and Shi, Y. (2023).

Automated design of metaheuristic algorithms: A sur-

vey. Transactions on Machine Learning Research.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

196