A Simple yet Effective Algorithm for the Asteroid Routing Problem

Valentino Santucci

University for Foreigners of Perugia, Perugia, Italy

Keywords:

Expensive Black-Box Permutation Optimization, Asteroid Routing Problem, Randomized Local Search.

Abstract:

In this paper we investigate the application of meta-heuristic algorithms in the context of expensive black-box

permutation optimization. These problems are characterized by solution spaces composed of permutations of

items, where the objective function is not explicitly deﬁned in a closed mathematical form and is costly to

evaluate. The benchmark problem under investigation is the Asteroid Routing Problem (ARP), which aims to

determine the optimal order for a spacecraft to visit asteroids, starting from Earth’s orbit, while minimizing

both energy consumption and visit time. In particular, we examine the effectiveness of a simple algorithm,

namely FAT-RLS, which is mainly based on the randomized local search scheme, equipped with a tabu struc-

ture and a mechanism to regulate the perturbation strength. A series of experiments were performed on ac-

cepted instances of the ARP in order to compare the effectiveness of FAT-RLS with respect to two established

meta-heuristics for the ARP. The results clearly show that FAT-RLS achieves more effective results both con-

sidering a black-box setting and an informed setting, where the meta-heuristics are seeded with a purposely

designed constructive algorithm for the ARP.

1 INTRODUCTION

Expensive black-box optimization is a challenging

task in a variety of domains, from engineering to ﬁ-

nance, and deals with problems where the objective

function lacks a mathematical closed form and re-

quires substantial computational resources, not only

in terms of time but also memory or money. In

such scenarios, algorithms can only gather informa-

tion about the problem through successive objective

function evaluations. However, due to the high cost

of evaluations, these algorithms typically operate un-

der strict computational budget constraints, de facto

limiting the number of evaluations allowed.

When dealing with continuous decision variables,

Bayesian optimization techniques (Frazier, 2018) are

commonly used. These methods iteratively construct

a surrogate model, typically a Gaussian process or

Kriging model, of the objective function at hand.

They then conduct a relatively large number of in-

expensive surrogate evaluations to identify candidate

solutions, which are subsequently evaluated using the

true objective function. This approach reduces the

amount of costly evaluations and allows to apply clas-

sical optimization strategies guided solely by the sur-

rogate model.

https://orcid.org/0000-0003-1483-7998

In this work, we focus on a family of combina-

torial optimization problems, the permutation prob-

lems, where solutions are formed by permutations of

items from a given set. In particular, we investigate

a recently proposed benchmark problem for expen-

sive black-box permutation optimization, the Asteroid

Routing Problem (ARP) introduced in (L

opez-Ib

nez

et al., 2022).

The ARP takes inspiration from the 11–th Global

Trajectory Optimisation Competition

and deals with

a spacecraft that, once launched from Earth, must visit

all the asteroids in a given set by minimizing both

its energy consumption and the total time required to

complete the journey. While our focus is not on the

astrophysical aspects of the problem, it is worth not-

ing that the ARP’s main motivation stems from the

increasing demand for technological devices like mo-

bile phones and computers, which is leading to a rapid

decrease of mineral resources, such as silicon, quartz

or boronite, on Earth. Consequently, one potential so-

lution to this issue is the prospect of mining these ma-

terials from asteroids or other near-Earth objects.

From a computational perspective, the ARP

presents a permutation problem in which the objec-

For complete details about the competition we refer the

interested reader to the following webpage https://sophia.

estec.esa.int/gtoc\ portal/?page\ id=782.

Santucci, V.

A Simple yet Effective Algorithm for the Asteroid Routing Problem.

DOI: 10.5220/0012908900003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 50-59

ISBN: 978-989-758-721-4; ISSN: 2184-3236

tive function requires to run a costly internal com-

putational procedure. As such, it stands as the ﬁrst

benchmark proposed for expensive black-box permu-

tation optimization.

Due to its combinatorial nature, classical

Gaussian-based Bayesian methods cannot be ap-

plied to the ARP. In (L

opez-Ib

nez et al., 2022),

two speciﬁc algorithms were employed: CEGO, a

distance-based Bayesian approach for combinatorial

problems, and UMM, an estimation of distribution

algorithm for permutation problems that has been

redesigned to work in low budget scenarios.

In (Santucci and Baioletti, 2022), it was shown

that both CEGO and UMM were outperformed by a

simple algorithm, called FAT-RLS and based on the

well known randomized local search scheme, when

dealing with classical permutation benchmark prob-

lems such as the Linear Ordering Problem or the Per-

mutation Flowshop Problem. Here we are interested

in studying the effectiveness of FAT-RLS on a proper

expensive black-box permutation problem such as the

ARP.

The rest of the paper is organized as follows. In

Section 2 permutation problems and other prelimi-

nary concepts are presented. Section 3 describes the

computational details of the ARP, while Section 4

presents the FAT-RLS algorithm. Section 5 brieﬂy

recalls the competitor algorithms used in the experi-

mentation, while the experimental settings and results

are presented and discussed in Section 6. Finally, con-

clusions are drawn in Section 7, where future lines of

research are also depicted.

2 PERMUTATION PROBLEMS

Permutations are versatile algebraic objects that ﬁnd

applications in many different ﬁelds because of their

ability to model a variety of concepts, including or-

derings and rankings of items, one-to-one mappings

between two sets, as well as tours and sets of cycles

within a collection of locations.

Permutations, which are usually denoted by

Greek symbols such as π or σ, can be mathemat-

ically deﬁned as bijective functions onto the set

[n] = {1,2,... ,n}. Several notations are available,

though the simplest and most common one is the so-

called single line notation, where a permutation π is

represented as a list of all different items, i.e.,

π = ⟨π(1),π(2),... ,π(n)⟩, (1)

where π(i) ∈ [n] indicates the item in position i ∈ [n]

in the list, ensuring that π(i) ̸= π( j) for any pair i ̸= j.

The set of all the permutations of degree n is de-

noted by S

, which has cardinality n! and is also

known as the symmetric group. In fact, the standard

function composition operation allows to compose

two permutations into a third permutation. Given two

permutations π and σ, their composition is denoted

by πσ and its elements are πσ(i) = π(σ(i)), for all

i ∈ [n]. The composition operation is associative, ad-

mits a unique identity permutation ι = ⟨1,2,... ,n⟩,

and each permutation π has a unique inverse permu-

tation π

−1

such that ππ

−1

= π

−1

π = ι. These three

properties prove that S

is a group, a characteristic

that has been exploited to design both swarm and

evolutionary algorithms based on strong mathemati-

cal foundations (Santucci et al., 2020).

In permutation optimization problems, the goal is

to minimize or maximize a given objective function

of the form f : S

→ R, i.e., a real-valued function

whose domain is the set of permutations S

. Permu-

tation problems are combinatorial in nature, so f is

not differentiable and classical gradient-based algo-

rithms cannot be adopted

. Moreover, if f has no an-

alytical deﬁnition – for example, because it requires

to run an experiment –, the problem is a black-box

problem, so an algorithm can only gather information

about f by testing multiple permutation solutions and

observing the returned objective values. Often, black-

box optimization problems are also characterized by

an objective function that is expensive to evaluate in

terms of time – for example, because it requires to run

a computationally intensive simulation –, but also in

terms of other resources such as memory or money.

Therefore, a suitable algorithm for expensive black-

box permutation optimization problems is required to

navigate the search space of permutations and should

be able to reach a good enough solution within a low

budget of objective function evaluations.

Even in a black-box scenario, it is often possible

to intuitively identify which features of a permutation

are important for a given problem simply by exam-

ining the problem description. Indeed, two distinct

families of permutation problems can be identiﬁed:

• ordering problems, where the objective is to deter-

mine the optimal sequence of items within a given

set A, and

• assignment problems, where the aim is to ﬁnd the

best possible one-to-one correspondence between

two given sets A and B of equal size.

While these classiﬁcations may not be exhaustive,

they cover many permutation problems frequently en-

countered in the scientiﬁc literature. For example, the

Linear Ordering Problem (LOP) (Santucci and Cebe-

rio, 2020) and the Permutation Flowshop Scheduling

Though model-based gradient search algorithms are

possible (Ceberio and Santucci, 2023).

A Simple yet Effective Algorithm for the Asteroid Routing Problem

Problem (PFSP) (Santucci et al., 2016) are two typ-

ical examples of ordering problems, while the poly-

nomially solvable Assignment Problem (Kuhn, 1955)

and its NP-Hard quadratic variant – the Quadratic As-

signment Problem (QAP) (Koopmans and Beckmann,

1955) – are common examples of assignment prob-

lems. Moreover, also the well known Traveling Sales-

man Problem (TSP) (Nagata and Kobayashi, 2013),

though requiring to determine a circular tour among

a given set of cities, can be seen as an ordering prob-

lem by (arbitrarily) designating a start/end city for all

the tours, so that they can be represented as orderings

over the remaining cities.

It is important to note that the distinction be-

tween ordering and assignment problems is not al-

ways clear-cut. In fact, it is known that both TSP and

LOP instances can be seen as special cases of QAP in-

stances (Loiola et al., 2007), thus suggesting that the

boundary between the ordering or assignment nature

of a permutation problem is not yet well understood.

Two of the most commonly used genotypic repre-

sentations for permutation problems are the classical

linear representation and the permutation matrix rep-

resentation. The linear representation is essentially

the transposition in memory of the single line nota-

tion described in Equation (1). In contrast, the permu-

tation matrix representation encodes a permutation as

a binary matrix with exactly one 1-entry in each row

and each column. While the linear representation is

suitable for both ordering and assignment problems,

the matrix representation does not directly encode any

ordering information, but only the pairings between

rows and columns indices. For this reason, in this

work we adopt the linear genotypic representation of

permutation solutions.

In the context of ordering problems, there are two

equivalent linear representations: ordering represen-

tation and ranking representation, as termed in (San-

tucci and Baioletti, 2022). As mentioned earlier, an

ordering problem involves optimally arranging a set

A of n items according to a given objective function.

The ordering representation maps positions to items

of A, while the ranking representation maps items of

A to positions. Since the items of A are denoted by

identiﬁcation numbers in [n], it is apparent how easy

it is to confuse the two. In fact, both linear repre-

sentations convey the same information and can be

converted into each other by a simple permutation in-

version. Anyway, it is crucial to specify which repre-

sentation is being used when deﬁning the objective

function and the algorithms/operators for permuta-

tion problems. In fact, using an incorrect representa-

tion without the necessary conversion, when required

by the objective function or the algorithm/operator at

hand, can lead to errors that are difﬁcult to detect

but detrimental for the effectiveness. In this work we

adopt the ordering representation.

Finally, it is worth noting that in the permuta-

tion space, different movement operators are avail-

able to build local search schemes or genetic opera-

tors such as mutation. The three most commonly used

classes of movement operators are: swaps of two ad-

jacent items (also called adjacent swaps), swaps of

two generic items (also called exchanges), and shifts

of an item to another position (also called insertions).

While exchanges are known to be suitable for as-

signment problems, adjacent swaps and insertions are

appropriate for ordering problems (Baioletti et al.,

2020). Moreover, it is easy to see that insertion moves

include adjacent swaps as special cases, and a single

insertion move is equivalent to a chain of multiple ad-

jacent swaps. Therefore, insertion moves are usually

adopted in the design of algorithms for ordering prob-

lems.

3 THE ASTEROID ROUTING

PROBLEM

The Asteroid Routing Problem (ARP) was introduced

in (L

opez-Ib

nez et al., 2022) as a benchmark for ex-

pensive black-box permutation optimization. It in-

volves planning a route for a spacecraft that, once

launched from Earth, must visit all the asteroids in

a given set of n asteroids A = {a

,. ..,a

} in such

a way that it minimizes both its fuel consumption and

the total time required to complete the journey.

The ARP is a bilevel optimization problem con-

sisting of two nested tasks. The outer task involves

determining an ordering of the asteroids in A, while

the inner task requires calculating the parking and

transit times for reaching each asteroid in the order

given by the outer task.

A solution for the bilevel ARP is a pair (π,t),

where: π ∈ S

encodes the ordering of A, while the

vector t ∈ R

≥0

encodes the parking and transit times

for each asteroid. More speciﬁcally, assuming that a

represents the Earth, for each step i ∈ [n]:

• a

π(i)

is the i-th asteroid visited by the spacecraft,

• t

2i−1

is the parking time spent by the spacecraft in

the orbit of asteroid a

π(i−1)

, and

• t

is the transit time required for the spacecraft to

travel from the orbit of asteroid a

π(i−1)

to the orbit

of asteroid a

π(i)

To formalize the objective function of the ARP, we

also consider the following auxiliary variables:

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

• τ

, for i ∈ {0, 1,..., n − 1}, is the launch epoch

from the orbit of asteroid a

π(i)

;

• ∆v

2i−1

and ∆v

, for i ∈ [n], are the impulses re-

quired for the maneuvers to insert the spacecraft

into the transit orbit between asteroids a

π(i−1)

and

π(i)

, and then into the parking orbit of asteroid

π(i)

, respectively.

The spacecraft is on Earth at start epoch τ

, which

is given by the ARP instance, while the other launch

epochs are computed as follows:

i−1

= τ

2i−1

∑

j=1

. (2)

For each step i ∈ [n], the transit and parking im-

pulses ∆v

2i−1

and ∆v

allow the spacecraft to ren-

dezvous with asteroid a

π(i)

. These velocity impulses

are computed as solutions of the so-called Lambert’s

problem, i.e.,

(∆v

2i−1

,∆v

) = Lambert(a

π(i−1)

π(i)

,τ

i−1

), (3)

for which we refer the interested reader to (L

opez-

nez et al., 2022) and (Izzo, 2015).

Once the upper-level permutation π is available,

Equations (2) and (3) deﬁne the inner task, which con-

sists of n continuous optimization problems that, after

being sequentially solved, yield the vector of times t

and the vector of the velocity impulses ∆v.

In (L

opez-Ib

nez et al., 2022), the inner contin-

uous problems are solved using the Sequential Least

Squares Programming (SLSQP) algorithm (Virtanen

et al., 2020), a deterministic method which allows to

focus on the outer task of the ARP problem by treat-

ing the computations of the values for t and ∆v as

an internal deterministic procedure depending only on

the provided asteroid ordering π. Therefore, the two

levels of the problem are collapsed into one, and the

ARP becomes a black-box permutation problem of

ordering nature, whose goal is to minimize the objec-

tive function deﬁned on the domain of permutations

f (π) =

∑

i=1

|∆v

| +

2 km/s

30 days

∑

i=1

, (4)

where: the ﬁrst summation is proportional to the en-

ergy consumed by the spacecraft to perform all the

maneuvers, the second summation represents the to-

tal time taken by the spacecraft to complete its jour-

ney, while the constant in front of the second sum-

mation has been experimentally derived in (L

opez-

nez et al., 2022).

Since computing Equation (4) is computationally

expensive (because it requires to sequentially solve

n internal continuous optimization tasks), the ARP

stands as an appropriate benchmark for expensive

black-box permutation optimization.

Finally, note that an ARP instance is completely

deﬁned by: the orbital parameters of the Earth and

all asteroids, the starting epoch τ

, and a gravi-

tational parameter. An instance generator is pro-

vided in (L

opez-Ib

nez et al., 2022) which takes

as input a seed parameter and the number of as-

teroids n, i.e., the size of the generated instance.

The implementations of the ARP objective func-

tion and the instance generator are available from

https://doi.org/10.5281/zenodo.5725837.

4 FAT-RLS

The Fast Adaptive Tabu-based Randomized Local

Search (FAT-RLS), introduced in (Santucci and Baio-

letti, 2022), is an iterative optimization heuristic de-

signed for expensive black-box permutation prob-

lems. FAT-RLS is based on the classical random-

ized local search scheme and incorporates two addi-

tional algorithmic components: an adaptive perturba-

tion strength strategy and a tabu-based mechanism to

avoid redundant perturbations.

The randomized local search (RLS) is a trajectory-

based scheme that evolves a single solution by ran-

domly selecting one of its neighbor at each iteration

and, if the neighbor solution is ﬁtter, it replaces the

current solution for the next iteration. Due to its

simplicity, RLS has been extensively studied in theo-

retical evolutionary computation (Neumann and We-

gener, 2007), though it is not commonly used in prac-

tical scenarios. However, we chose RLS as the search

engine for the proposed algorithm because it is very

exploitative and it requires only one objective func-

tion evaluation per iteration. This makes it ideal for

effectively utilizing the limited budget of evaluations

in an expensive black-box scenario. Moreover, every

iteration simply requires applying a movement oper-

ator to the current solution, thus resulting in minimal

computational overhead. This is particularly advanta-

geous, specially if compared to the computationally

intensive model learning and update procedures of

Bayesian approaches such as (Zaefferer et al., 2014b;

Zaefferer et al., 2014a).

Since our focus is on the ARP that, as detailed in

Section 3, can be classiﬁed as a permutation order-

ing problem, we consider insertion moves to perturb

the solutions of FAT-RLS. Given an ARP instance of

size n and a solution π ∈ S

, an insertion (i, j), with

i, j ∈ [n], involves shifting the item π(i) to position

j in π. Therefore, by denoting with σ the permuta-

tion obtained by applying insertion (i, j) to π, we have

A Simple yet Effective Algorithm for the Asteroid Routing Problem

that, in a forward insertion with i < j:

σ(k) =











π(k) if k < i or k > j,

π(k + 1) if i ≤ k < j,

π(i) if k = j,

(5)

while, in a backward insertion with i > j:

σ(k) =











π(k) if k < j or k > i,

π(k − 1) if j < k ≤ i,

π(i) if k = j.

(6)

Equations (5) and (6) show that an insertion (i, j)

rearranges |i − j| + 1 items in a permutation, making

the insertion equivalent to a series of |i − j| adjacent

swaps. Considering forward insertions, as depicted in

Equation (5) (though the case of backward insertions

is analogous), insertion (i, j) corresponds to the fol-

lowing chain of |i − j| adjacent swaps

(i,i + 1), (i + 1,i + 2), ... , ( j − 1, j).

A clear consequence is that the Kendall’s-τ distance

between σ and π is |i − j|. Therefore, we consider

d = |i − j| as the perturbation strength of a generic

insertion (i, j).

In FAT-RLS, rather than randomly selecting one

insertion move as in classical randomized local search

schemes, we control the perturbation strength d at

each iteration. Indeed, FAT-RLS employs an adap-

tive perturbation strength strategy, requiring two hy-

perparameters: the initial perturbation strength d

ini

and the steepness factor β. After initializing the per-

turbation strength d to d

ini

, FAT-RLS perturbs the cur-

rent solution with a randomly selected insertion (i, j)

such that |i − j| = d. Meanwhile, d monotonically de-

creases using a “skewed S-shaped” function regulated

by β. This strategy fosters the transition from explo-

rative to exploitative behaviour over iterations, a well

known best practice in designing meta-heuristic algo-

rithms (Chopard and Tomassini, 2018).

The “skewed S-shaped” function has both domain

and codomain in [0,1] and, given β ≥ 1, is deﬁned as

(p) = 1 −

1 +



1−p



. (7)

Hence, the perturbation strength d at each iteration

is computed by rounding the product of the initial

strength d

ini

and the s function applied to the per-

centage of evolution made (i.e., the ratio of the cur-

rent iteration number to the allowed iteration budget).

A possible deﬁnition for the Kendall’s-τ distance be-

tween two permutations is the number of adjacent swaps to

make one permutation equal to the other.

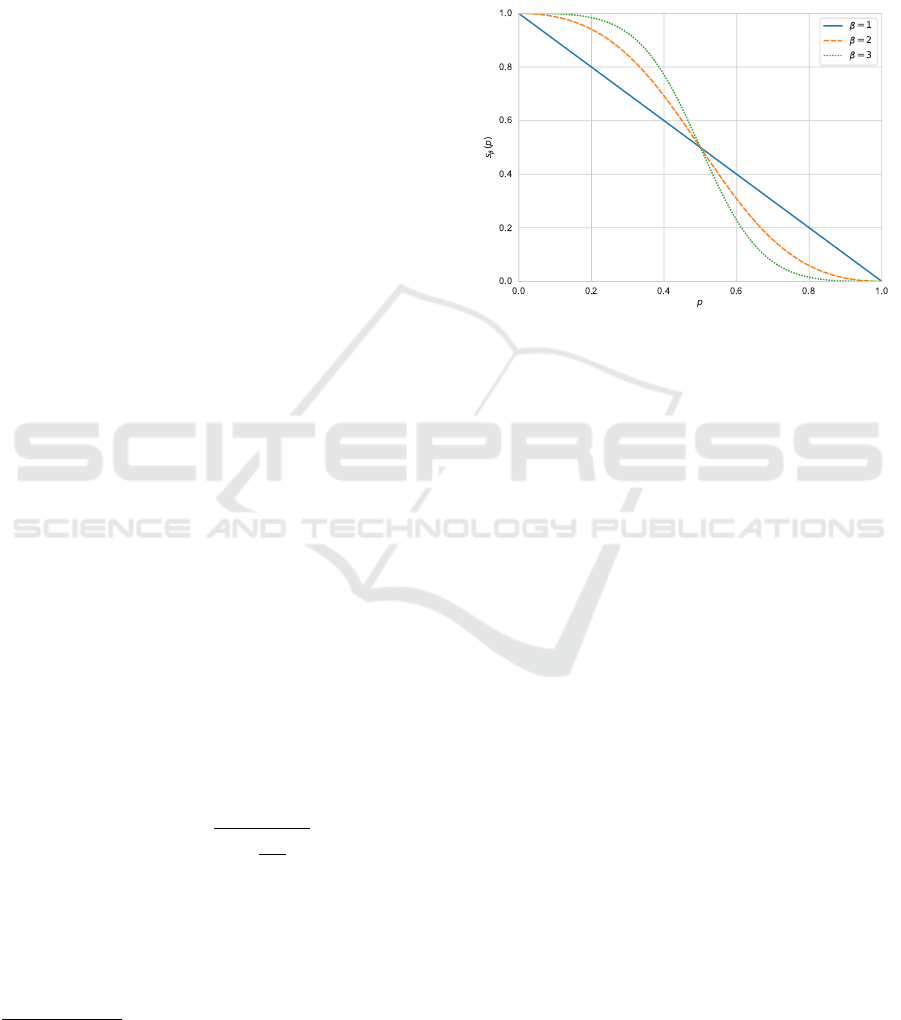
Figure 1 depicts the function s

(p) across various β

values. Speciﬁcally, when β = 1, s

(p) = 1 − p, lead-

ing to a linear decrease of the perturbation strength,

while as β increases the curve steepens in the central

part, thus extending the initial exploration phase and

making more abrupt and quick the transition to the

ﬁnal exploitative phase.

Figure 1: The “skewed S”-shaped function for β = 1, 2,3.

Moreover, as FAT-RLS will be employed in a low-

budget optimization scenario, we introduce a tabu-

based mechanism. Its purpose is not only to avoid

the trajectory followed by a FAT-RLS execution from

revisiting solutions previously explored, but also to

prevent the same items from being shifted too often by

the perturbation operation. FAT-RLS maintains a tabu

queue TQ of maximum size k, an algorithm hyperpa-

rameter. At each iteration, an insertion (i, j ) cannot

be selected if the item σ(i) to be shifted is marked as

tabu, i.e., if σ(i) ∈ TQ. Then, when a valid insertion

(i, j), i.e., such that σ(i) ̸∈ TQ, is selected and applied

to the current permutation, the item σ(i) is pushed

into TQ and, if the queue is full, the oldest inserted

item is removed.

In summary, FAT-RLS adopts a simple random-

ized local search scheme which only performs one

objective function evaluation per iteration and, to im-

prove its effectiveness in the low budget scenario typ-

ical of expensive black-box permutation problems, it

employs both an adaptive perturbation strength strat-

egy and a tabu-based mechanism which restrict the

number of applicable perturbations in each iteration,

aiming to accelerate towards potentially good solu-

tions.

Finally, for the sake of completeness, we present

the pseudocode of FAT-RLS in Algorithm 1. It aims

to minimizes (without loss of generality) an objective

function of the form f : S

→ R, by taking in input the

three hyperparameters d

ini

∈ [1, n), β ≥ 1, and k ≤ n,

as previously discussed.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

Algorithm 1: Pseudocode of FAT-RLS.

1: function FAT-RLS(d

ini

, β, k)

2: /* Initialization */

3: π ← random permutation from S

4: Evaluate f (π)

5: nfev ← 1

6: TQ ←

7: /* Main loop */

8: while nfev < budget do

9: /* Compute perturbation strength */

10: p ← nfev/budget

11: d ← round



1 + s

(p)· (d

ini

− 1)



12: /* Perturbation */

13: σ ← π

14: Sample i, j s.t. |i − j| = d and σ(i) ̸∈ TQ

15: Perform the insertion (i, j) on σ

16: /* Update current solution */

17: Evaluate f (σ)

18: if f (σ) < f (π) then

19: π ← σ

20: nfev ← nfev + 1

21: /* Update tabu queue */

22: Push item σ( j) into TQ

23: if |TQ| = k then

24: Pop oldest item from TQ

25: return π, f (π)

5 OTHER OPTIMIZATION

ALGORITHMS

The goal of this work is to investigate the perfor-

mance of the FAT-RLS algorithm, described in Sec-

tion 4, on the ARP, i.e., the permutation ordering

problem detailed in Section 3. To this end, we ex-

perimentally compare FAT-RLS against four competi-

tor algorithms: a simple Random Search (RS) scheme

used as a baseline competitor, the constructive heuris-

tic called Greedy Nearest Neighbor (GNN) specif-

ically introduced in (L

opez-Ib

nez et al., 2022) for

the ARP, the Bayesian algorithm known as Combina-

torial Efﬁcient Global Optimization (CEGO), intro-

duced in (Zaefferer et al., 2014b), and the estimation

of distribution algorithm termed Unbalanced Mallows

Model (UMM), introduced in (Irurozki and L

opez-

nez, 2021).

In (L

opez-Ib

nez et al., 2022), both UMM and

CEGO were executed under two settings: the unin-

formed setting, where the standalone versions of the

algorithms were run, and the informed setting, where

their initial solutions were created using GNN instead

of being generated randomly.

The four competitor algorithms are brieﬂy de-

scribed in the following subsections.

5.1 Random Search (RS)

The trivial random search procedure, denoted by RS,

is considered as a baseline method in this work. RS

generates a given number of permutation solutions

uniformly at random using the well known Fisher

Yates algorithm (Eberl, 2016), then it evaluates the

objective function on all the generated solutions and

returns the best one. Although trivial, RS is an inter-

esting baseline method because all solutions can be

evaluated in parallel (at least in principle).

5.2 Greedy Nearest Neighbor (GNN)

The Greedy Nearest Neighbor heuristic, from now on

referred to as GNN

, is inspired from the well known

nearest neighbor heuristic for the TSP (Rosenkrantz

et al., 1977).

The main idea behind GNN is that a reasonably

effective permutation of the asteroids can be formed

by repeatedly visiting the asteroid which is closest, in

terms of Euclidean distance, to the last visited one, af-

ter determining the positions of all unvisited asteroids

at the time the spacecraft is arrived in the last visited

one.

The pseudocode of GNN is provided in Algo-

rithm 2, while for further details we refer the inter-

ested reader to (L

opez-Ib

nez et al., 2022).

Algorithm 2: Pseudocode of the GNN heuristic.

1: function GNN

2: s ← a

▷ Earth’s orbit

3: τ ← τ

▷ Epoch of the spacecraft

4: U ← [n] ▷ Unvisited asteroids

5: for i ← 1 to n − 1 do

6: π(i) ← argmin

j∈U

Eucl

(s,a

,τ)

7: (t

2i−1

) ← SLSQP(s,a

π(i)

) ▷ Inner task

8: τ ← τ + t

2i−1

9: U ← U \ {π(i)}

10: s ← a

π(i)

11: return π, f (π)

GNN implementation is available from

https://doi.org/10.5281/zenodo.5725837.

A Simple yet Effective Algorithm for the Asteroid Routing Problem

5.3 Combinatorial Efﬁcient Global

Optimization (CEGO)

The CEGO algorithm (Zaefferer et al., 2014b) builds

upon the well-known EGO method (Jones et al.,

1998) and adapts it for combinatorial optimization

problems. EGO was originally designed for contin-

uous domains and employs a Bayesian approach to it-

eratively learn a surrogate Gaussian process model of

the objective function. In contrast, CEGO addresses

combinatorial spaces by using a distance-based com-

binatorial surrogate model, where the classical Eu-

clidean distance of continuous spaces is replaced with

a discrete distance function which is suitable for the

search space at hand.

In (Zaefferer et al., 2014a), various distance func-

tions for the permutation space are examined. The

available implementation of CEGO

begins by gener-

ating a few initial solutions using a max-min-distance

procedure, which are then used to construct an ini-

tial surrogate model. Subsequently, a genetic algo-

rithm utilizing operators suitable for the permutation

encoding is employed to search for optimal solutions

of the surrogate function. The best solution found is

then evaluated using the true objective function. This

evaluation allows to gain information about the objec-

tive function and to update the surrogate model main-

tained by CEGO. The process is repeated until a spec-

iﬁed termination criterion is met.

Therefore, after the initial warm-up, each round of

CEGO consists of: (i) optimizing the surrogate func-

tion, (ii) one true objective function evaluation, and

(iii) updating the surrogate model. It is important to

note that, as experimentally shown in (Santucci and

Baioletti, 2022), the update of the surrogate model in

the permutation space is a hard problem in itself, re-

quiring a signiﬁcant amount of computational time,

especially when the number of training permutations

(and their size) gets large.

For more details on the settings of the genetic al-

gorithm used in CEGO, we refer interested readers

to (Zaefferer et al., 2014a).

5.4 Unbalanced Mallows Model (UMM)

The UMM algorithm (Irurozki and L

opez-Ib

nez,

2021) belongs to the well known family of estimation

of distribution algorithms. It iteratively alternates be-

tween learning and sampling from a Mallows model,

a well-known probability distribution model for per-

mutations (Ceberio et al., 2013). At the beginning, a

CEGO implementation is available at https://cran.r-

project.org/web/packages/CEGO.

few solutions are randomly generated to construct the

initial Mallows model. Then, in each subsequent iter-

ation, UMM samples a permutation, evaluates it, and

updates the model accordingly.

The Mallows model is characterized by a mode

permutation π

∈ S

and a dispersion parameter θ ∈

R. The mode permutation is determined using the so-

called Unbalanced Borda procedure, which weighs

previously sampled solutions based on their ﬁtness,

ensuring that the top 10% of samples contribute 90%

of the weight. The dispersion parameter θ is corre-

lated to the expected Kendall’s-τ distance E[D] be-

tween a sample and the mode π

. This expected dis-

tance is adjusted by linearly decreasing it from





to 1 over the iterations.

For more detailed information about UMM, inter-

ested readers can refer to (Irurozki and L

opez-Ib

nez,

2021)

6 EXPERIMENTS

6.1 Experimental Settings

Experiments were conducted using the same settings

as described in (L

opez-Ib

nez et al., 2022). Ten ARP

benchmark instances were generated using the in-

stance generator and the seeds provided by the authors

of (L

opez-Ib

nez et al., 2022), allowing us to reuse

the results made available by them for the competitor

and baseline algorithms. Speciﬁcally, two instances

were considered for each size n ∈ {10, 15,20,25,30}

using the seeds 42 and 73. The naming scheme n seed

is used to denote each instance.

Two different experimetnal settings are consid-

ered as follows.

• Black-box setting, where the competing algo-

rithms FAT-RLS, CEGO and UMM are randomly

initialized, while RS is considered as baseline

method.

• Informed setting, where the GNN heuristic is used

both as baseline method and to produce reason-

ably good initial solutions for FAT-RLS, CEGO

and UMM.

In both settings, all the algorithms were run 30

times per instance, with each run having a budget of

100 objective function evaluations.

It is worth noting that in (L

opez-Ib

nez et al.,

2022), two variants of both CEGO and UMM were

UMM implementation is available at

https://zenodo.org/record/4500974.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

run: one that directly considers the evolved permu-

tation for the objective function evaluation, and an-

other that inverts the permutation before evaluating

it. However, according to Section 2, only one of

these variants is actually sound. Therefore, in this

work, we consider just one CEGO and one UMM: the

ones named CEGO-order and UMM-rank in (L

opez-

nez et al., 2022) (that clearly outperformed their

counterparts CEGO-rank and UMM-order).

Finally, the hyperparameters of the competing

algorithms were set according to their original pa-

pers, i.e., (Santucci and Baioletti, 2022) for FAT-RLS

and (L

opez-Ib

nez et al., 2022) for UMM and CEGO.

6.2 Results in the black-box Setting

The results collected in the black-box setting were an-

alyzed from two different perspectives: median per-

formances and peak performances.

For median performances, we calculated the Me-

dian Relative Percentage Deviation (MRPD) for each

algorithm A and instance I as follows

MRPD

A,I

= 100 ·

median

A,I

− best

best

, (8)

where median

A,I

is the median objective value ob-

tained by algorithm A over 30 executions on in-

stance I , while best

is the best objective value ob-

tained by any algorithm in this setting for instance I .

The MRPDs are provided in Table 1. For the

competitor algorithms UMM, CEGO and RS, values

are marked with ▲ if FAT-RLS signiﬁcantly outper-

formed them, and with ▽ if FAT-RLS was signiﬁ-

cantly outperformed. No mark indicates that the per-

formance differences were not signiﬁcant. The statis-

tical analyses were conducted using the well known

Mann Whitney U test (Hollander et al., 2013), with a

signiﬁcance threshold of 0.05.

Table 1 shows that, though FAT-RLS is not com-

petitive enough on the two smallest instance of size

n = 10, it is slightly better than CEGO and signif-

icantly better than the other competitors on the two

instances with n = 15, while, most notably, it signif-

icantly outperforms all the competitors on the larger

instances with n > 15.

For the peak performances, Table 2 presents the

objective values returned by the best execution of

each algorithm for each instance. Values in bold rep-

resent, for each instance, the best objective value ever

achieved by a black-box algorithm.

Table 2 shows that FAT-RLS achieved the best re-

sults in 9 out of 10 instances, while in the remain-

ing instance (10 73) it obtained the second best peak

performance after CEGO. Therefore, as also partially

Table 1: Median Relative Percentage Deviations on Black-

box Experiments. Algorithms whose results are marked

with ▲ are signiﬁcantly outperformed by FAT-RLS, while

those marked with ▽ signiﬁcantly outperform FAT-RLS.

Instance FAT-RLS UMM CEGO RS

10 42 12.36 13.26 9.12 ▽ 21.03 ▲

10 73 16.39 11.30 ▽ 5.07 ▽ 16.19

15 42 13.18 17.48 ▲ 14.01 25.61 ▲

15 73 10.16 15.58 ▲ 12.56 24.62 ▲

20 42 9.56 20.80 ▲ 15.50 ▲ 26.18 ▲

20 73 14.65 30.29 ▲ 23.99 ▲ 33.21 ▲

25 42 14.62 29.32 ▲ 24.57 ▲ 34.42 ▲

25 73 8.62 26.30 ▲ 18.80 ▲ 28.58 ▲

30 42 6.01 27.26 ▲ 18.95 ▲ 28.58 ▲

30 73 7.95 24.46 ▲ 18.96 ▲ 27.31 ▲

Table 2: Best Objective Values on Black-box Experiments.

Bolded results represent the best performance for each in-

stance.

Instance FAT-RLS UMM CEGO RS

10 42 346.7 346.7 346.7 389.6

10 73 329.4 329.9 324.7 343.6

15 42 505.4 516.9 515.7 583.1

15 73 515.1 530.7 523.7 573.0

20 42 698.9 729.1 726.9 777.8

20 73 676.3 810.1 730.8 813.2

25 42 837.4 966.8 945.9 1075.1

73 889.0 1028.7 988.7 1089.6

30 42 1062.3 1260.6 1183.0 1271.0

30 73 1098.2 1232.8 1212.1 1344.2

indicated by Table 1, where the MRPDs of FAT-RLS

improve as n gets larger, it seems that FAT-RLS is ca-

pable of achieving competitive results across the en-

tire spectrum of benchmarks, although it shows a lack

of robustness when the instance size is smaller.

6.3 Results in the Informed Setting

The median and peak performance analyses con-

ducted in Section 6.3 were also carried out in the in-

formed scenario, where algorithms are initialized us-

ing the solution obtained through the GNN heuristic.

Tables 3 and 4 present, respectively, the median

and best results achieved by FAT-RLS, UMM, CEGO,

and GNN in the informed setting.

The results indicate that all three meta-heuristics

improved upon the initial solution provided by GNN.

However, the performance gains over the baseline

algorithm are slightly less pronounced than in the

black-box setting. Probably, this is because the initial

solution is heuristically constructed rather than ran-

domly generated.

In the comparison between informed FAT-RLS

A Simple yet Effective Algorithm for the Asteroid Routing Problem

Table 3: Median Relative Percentage Deviations on In-

formed Experiments. Algorithms whose results are marked

with ▲ are signiﬁcantly outperformed by FAT-RLS, while

those marked with ▽ signiﬁcantly outperform FAT-RLS.

Instance FAT-RLS UMM CEGO GNN

10 42 9.97 10.22 ▲ 8.68 ▽ 12.86 ▲

10 73 20.46 18.69 ▽ 10.73 ▽ 22.67 ▲

15 42 0.96 2.21 ▲ 1.32 ▲ 3.51 ▲

15 73 2.68 6.17 ▲ 2.53 12.50 ▲

20 42 3.36 16.25 ▲ 5.95 22.12 ▲

20 73 1.01 5.06 ▲ 1.73 5.98 ▲

25 42 7.69 14.29 ▲ 8.37 ▲ 17.50 ▲

25 73 0.81 13.64 ▲ 7.56 ▲ 13.72 ▲

30 42 3.59 6.77 ▲ 3.55 8.27 ▲

30 73 2.06 6.85 ▲ 1.18 ▽ 7.63 ▲

Table 4: Best Objective Values on Informed Experiments.

Bolded results represent the best performance for each in-

stance.

Instance FAT-RLS UMM CEGO GNN

10 42 381.3 381.3 346.7 391.3

10 73 385.4 367.6 324.7 398.3

15 42 493.1 490.9 491.4 508.1

15 73 512.3 532.0 519.9 576.4

20 42 689.3 729.7 707.2 841.7

20 73 659.1 672.8 652.5 691.5

25 42 805.3 895.8 865.7 946.3

73 807.5 885.7 863.7 918.3

30 42 1045.3 1093.9 1065.2 1131.7

30 73 959.6 1002.0 952.1 1024.7

and informed UMM, FAT-RLS signiﬁcantly outper-

formed UMM in 9 out of 10 instances, mirroring the

trend observed in the black-box setting. Conversely,

the comparison between informed FAT-RLS and in-

formed CEGO was more balanced. FAT-RLS signif-

icantly outperformed CEGO in 3 instances and was

signiﬁcantly outperformed by CEGO in 3 other in-

stances. Additionally, FAT-RLS achieved the best so-

lution in 5 instances, while CEGO achieved the best

solution in 4 instances.

Finally, by comparing the results of Ta-

bles 2 and 4, it is worth noting that on the two

instances of size n = 10, GNN and informed FAT-

RLS did not match the results of RS and black-box

FAT-RLS, respectively. This likely indicates that

the n = 10 instances have a relatively “shallow

landscape” where random search is sufﬁcient to

provide good results.

7 CONCLUSION AND FUTURE

WORK

In this work we have experimentally studied the effec-

tiveness of FAT-RLS, a simple trajectory-based meta-

heuristic, in dealing with the Asteroid Routing Prob-

lem (ARP). FAT-RLS adopts the well known random-

ized local search scheme, equipped with two addi-

tional algorithmic components such as a tabu data

structure and an adaptive perturbation strength mech-

anism.

We conducted a series of experiments on stan-

dard benchmark instances for the ARP, comparing the

effectiveness of FAT-RLS with two established ap-

proaches for the same problem: CEGO, a Bayesian

method for combinatorial problems, and UMM, an es-

timation of distribution algorithm tailored for permu-

tation problems. The experiments were conducted un-

der two settings: a black-box setting, where initial so-

lution(s) for the competing algorithms were randomly

generated, and an informed setting, where a purposely

deﬁned heuristic method is used to initialize the solu-

tions of the competing meta-heuristics.

The results clearly show that FAT-RLS, despite its

simpler design, outperforms both CEGO and UMM in

the black-box scenario, i.e., when the ARP is blindly

addressed. However, when the heuristic initializa-

tion is adopted, while FAT-RLS clearly outperforms

UMM, there is no deﬁnitive evidence of superiority

over CEGO.

Therefore, these results allow us to reafﬁrm the

take away message previously exposed in (Santucci

and Baioletti, 2022), i.e., simple algorithms such as

FAT-RLS that are mainly based on very strong ex-

ploitation approaches, might be a viable alternative

to more sophisticated techniques when dealing in low

budget expensive black-box combinatorial scenarios.

Furthermore, the analyzed results, particularly

those from the smaller instances, also reveal that FAT-

RLS shows a lack of robustness in some cases, sug-

gesting opportunities for enhancement in this regard.

Therefore, an interesting avenue for future research

involves extending the search engine of the algo-

rithm from the randomized local search scheme to the

(1 + 1)-EA scheme (Doerr et al., 2022). Essentially,

the idea is to maintain to one the expected number

of insertion moves per iteration, while also allowing

the algorithm to perform more than one insertion per

iteration. This should maintain a strong level of ex-

ploitation, while also preventing the algorithm from

easily becoming trapped in a local optimum within

the insertion neighborhood.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

ACKNOWLEDGEMENTS

Valentino Santucci has been partially supported by the

research projects: “Universit

a per Stranieri di Perugia

– Finanziamento Dipartimentale alla Ricerca per Pro-

getti di Ricerca di Ateneo – FDR 2023”, “Universit

per Stranieri di Perugia – Finanziamento Dipartimen-

tale alla Ricerca per Progetti di Ricerca di Ateneo –

FDR 2024”.

REFERENCES

Baioletti, M., Milani, A., and Santucci, V. (2020). Variable

neighborhood algebraic differential evolution: An ap-

plication to the linear ordering problem with cumula-

tive costs. Information Sciences, 507:37–52.

Ceberio, J., Irurozki, E., Mendiburu, A., and Lozano, J. A.

(2013). A distance-based ranking model estimation

of distribution algorithm for the ﬂowshop scheduling

problem. IEEE Transactions on Evolutionary Compu-

tation, 18(2):286–300.

Ceberio, J. and Santucci, V. (2023). Model-based gradient

search for permutation problems. ACM Transactions

on Evolutionary Learning and Optimization, 3(4):1–

35.

Chopard, B. and Tomassini, M. (2018). An introduction to

metaheuristics for optimization. Springer.

Doerr, B., Ghannane, Y., and Brahim, M. I. (2022). Towards

a stronger theory for permutation-based evolutionary

algorithms. In Proceedings of the Genetic and Evolu-

tionary Computation Conference, pages 1390–1398.

Eberl, M. (2016). Fisher-yates shufﬂe. Arch. Formal Proofs,

2016:19.

Frazier, P. I. (2018). A tutorial on bayesian optimization.

arXiv preprint arXiv:1807.02811.

Hollander, M., Wolfe, D. A., and Chicken, E. (2013). Non-

parametric statistical methods, volume 751. John Wi-

ley & Sons.

Irurozki, E. and L

opez-Ib

nez, M. (2021). Unbalanced mal-

lows models for optimizing expensive black-box per-

mutation problems. In Proceedings of the Genetic and

Evolutionary Computation Conference, pages 225–

233.

Izzo, D. (2015). Revisiting lambert’s problem. Celestial

Mechanics and Dynamical Astronomy, 121:1–15.

Jones, D. R., Schonlau, M., and Welch, W. J. (1998).

Efﬁcient global optimization of expensive black-box

functions. Journal of Global optimization, 13(4):455–

492.

Koopmans, T. C. and Beckmann, M. J. (1955). Assign-

ment Problems and the Location of Economic Activi-

ties. Cowles Foundation Discussion Papers 4, Cowles

Foundation for Research in Economics, Yale Univer-

sity.

Kuhn, H. W. (1955). The hungarian method for the as-

signment problem. Naval research logistics quarterly,

2(1-2):83–97.

Loiola, E. M., De Abreu, N. M. M., Boaventura-Netto,

P. O., Hahn, P., and Querido, T. (2007). A survey for

the quadratic assignment problem. European journal

of operational research, 176(2):657–690.

opez-Ib

nez, M., Chicano, F., and Gil-Merino, R. (2022).

The asteroid routing problem: A benchmark for ex-

pensive black-box permutation optimization. In Inter-

national Conference on the Applications of Evolution-

ary Computation (Part of EvoStar), pages 124–140.

Springer.

Nagata, Y. and Kobayashi, S. (2013). A powerful genetic

algorithm using edge assembly crossover for the trav-

eling salesman problem. INFORMS Journal on Com-

puting, 25(2):346–363.

Neumann, F. and Wegener, I. (2007). Randomized lo-

cal search, evolutionary algorithms, and the minimum

spanning tree problem. Theoretical Computer Sci-

ence, 378(1):32–40.

Rosenkrantz, D. J., Stearns, R. E., and Lewis, II, P. M.

(1977). An analysis of several heuristics for the trav-

eling salesman problem. SIAM journal on computing,

6(3):563–581.

Santucci, V. and Baioletti, M. (2022). A fast randomized

local search for low budget optimization in black-box

permutation problems. In 2022 IEEE Congress on

Evolutionary Computation (CEC), pages 1–8. IEEE.

Santucci, V., Baioletti, M., and Milani, A. (2016). Alge-

braic differential evolution algorithm for the permuta-

tion ﬂowshop scheduling problem with total ﬂowtime

criterion. IEEE Transactions on Evolutionary Com-

putation, 20(5):682–694.

Santucci, V., Baioletti, M., and Milani, A. (2020). An

algebraic framework for swarm and evolutionary al-

gorithms in combinatorial optimization. Swarm and

Evolutionary Computation, 55:100673.

Santucci, V. and Ceberio, J. (2020). Using pairwise prece-

dences for solving the linear ordering problem. Ap-

plied Soft Computing, 87.

Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M.,

Reddy, T., Cournapeau, D., Burovski, E., Peterson,

P., Weckesser, W., Bright, J., et al. (2020). Scipy

1.0: fundamental algorithms for scientiﬁc computing

in python. Nature methods, 17(3):261–272.

Zaefferer, M., Stork, J., and Bartz-Beielstein, T. (2014a).

Distance measures for permutations in combinatorial

efﬁcient global optimization. In International Confer-

ence on Parallel Problem Solving from Nature, pages

373–383. Springer.

Zaefferer, M., Stork, J., Friese, M., Fischbach, A., Naujoks,

B., and Bartz-Beielstein, T. (2014b). Efﬁcient global

optimization for combinatorial problems. In Proceed-

ings of the 2014 annual conference on genetic and

evolutionary computation, pages 871–878.

A Simple yet Effective Algorithm for the Asteroid Routing Problem