A Switching Event-Triggered Model Predictive Control for HVAC
Systems
Mojtaba Sharifzadeh
1 a
, Hani Beirami
1
, Federico Bonafini
2
, Matteo Campidelli
2
, Roberto Cavada
1
,
Alessandro Cimatti
1 b
and Stefano Tonetta
1 c
1
Fondazione Bruno Kessler, 38123, Trento, Italy
2
Innova Engineering S.r.l. 38079, Tione di Trento, Italy
fi
Keywords:
Event-Triggered MPC, HVAC, Modeling, System Identification, Switching Control.
Abstract:
Heating, ventilation, and air conditioning (HVAC) systems have great potential for energy savings and inte-
gration with green energy sources. Advanced control of these systems could play a key role in optimizing
consumption while enhancing efficiency and performance. In this paper, a new model-based methodology is
proposed for real-time control of the compressor in HVAC systems, based on switching event-triggered model
predictive control. The approach manages the switch among different operational modes and provides the pos-
sibility to set different constraints to be optimized, enabling a multivariable scheme. It also applies the latest
model-based design standards derived from the AUTOSAR framework to adapt them for an HVAC platform
that offers substantial technical value, while also preserving the model-based design structure for improved
lifecycle management. The models used for the controller in each modality are developed through the sys-
tem identification standards and validated using data acquired from the air-water heat pumps in the test field.
The effectiveness and performance of the control approach are also demonstrated through Model-in-the-Loop
(MIL) testing.
1 INTRODUCTION
In recent years, especially since carbon emissions
have become a serious global issue, substantial re-
search has focused on enhancing the control of heat-
ing, ventilation, and air conditioning (HVAC) sys-
tems. Given that buildings constitute a significant
proportion of global energy consumption, improving
the energy efficiency of building structures is crucial
for reducing energy consumption on a global scale.
The traditionally used controllers in buildings often
rely on feedforward mechanisms or traditional con-
trol strategies, which may not be the most efficient
for energy management (Soyguder et al., 2009).
Several studies on HVAC systems focused on de-
signing various control strategies to enhance system
management and efficiency using PID-based classical
approaches due to their practical feasibility. However,
these strategies often suffer from a lack of real-time
a
https://orcid.org/0000-0002-0552-1951
b
https://orcid.org/0000-0002-1315-6990
c
https://orcid.org/0000-0001-9091-7899
tuning for the controller, as they are not sufficiently
robust, and encounters problems when dealing with
multivariable models (Soyguder et al., 2009; Blasco
et al., 2012).
In recent works (see, e.g., (Taheri et al., 2024a)),
Model Predictive Control (MPC) has emerged as a
standout approach due to its ability to manage multi-
ple variables and provide optimized outcomes within
a set of constraints which makes it a great potential
for use in intelligent buildings, enhancing control, and
achieving greater energy savings.
MPC employs a dynamical model to predict the
anticipated dynamics of the system over a specific
timeframe. These predictions are then used to formu-
late an optimization problem designed to minimize a
defined cost function, which usually measures system
performance.
MPC represents a flexible technique, particularly
effective for multi-input, multi-output (MIMO) con-
trol challenges characterized by notable interactions
between the inputs being manipulated and the outputs
being controlled. A primary benefit of MPC, com-
pared to other model-based control strategies, is its
Sharifzadeh, M., Beirami, H., Bonafini, F., Campidelli, M., Cavada, R., Cimatti, A. and Tonetta, S.
A Switching Event-Triggered Model Predictive Control for HVAC Systems.
DOI: 10.5220/0012912400003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 37-45
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
37

capability to easily incorporate inequality constraints
on variables, including both upper and lower bounds
on inputs or outputs (Darby and Nikolaou, 2012).
There is a considerable volume of literature re-
garding the application of MPC to HVAC systems
(Taheri et al., 2024a; Saletti et al., 2020; Yao and
Shekhar, 2021a). However, none of previous works
yet offered a comprehensive platform in this con-
text, capable of dealing with the different operational
modes typical of HVAC systems (e.g., heating, cool-
ing, and defrost).
In this paper, we aim to develop a switching event-
triggered model predictive control for HVAC systems,
which reacts to external events to switch between dif-
ferent modalities. We implement and evaluate the
approach on an industrial real system, which uses
legacy control software. We begin by processing the
data acquired from HVAC machines during field tests,
which involves standardizing formats, applying filter-
ing methods, resampling, and performing data inter-
polation. We then develop a model of the dynamical
behaviour used to design a multi-variable controller.
We use standard system identification techniques to
create a model from the data in different modalities.
We then design the switching MPC, thus an MPC for
different modalities and a switch logic with a state
machine that activates the various controllers. Finally,
we focus on validating the effectiveness of the model
as well as switching MPC methodology. This step
includes both the validation of the identified models
in the different modalities as well as the evaluation
of the system’s switching behaviour under simulated
conditions.
The organization of the current manuscript is as
follows. In section 2, the related works are given. In
section 3.1 the problem is described in more detail. In
the next sections, the model, data acquisition and sys-
tem identification and successively the switching con-
trol approach implementation, are presented respec-
tively. The results are given in section 6, and eventu-
ally, conclusive remarks are presented in the last sec-
tion.
2 RELATED WORKS
In (Afroz et al., 2018), various modeling techniques
used in HVAC systems are studied, assessing their ap-
plicability, strengths, and weaknesses, together with
their impact on energy efficiency and indoor environ-
mental quality. The existing gaps are highlighted, and
various recommendations to enhance the performance
of building HVAC systems are given. In (Taheri et al.,
2024b), it is demonstrated through simulation that the
Model Predictive Control (MPC) approach provides
a 7% greater reduction in energy consumption com-
pared to the classical PID method when applied to
HVAC systems in commercial buildings. In (Staino
et al., 2016), two different optimization scenarios
(selfish and cooperative) are focused on the analy-
sis of the performance of MPC in the heat pumps of
buildings.
Saletti et al. proposed a novel control methodol-
ogy using MPC for district heating networks, aimed
at optimizing thermal energy distribution to build-
ings using a new optimization algorithm (Saletti et al.,
2020). It is demonstrated that it gives significant re-
ductions in energy consumption and improved indoor
comfort, compared to conventional controllers. How-
ever, it is based on a linearized approximated model
that does not always reflect the real characteristics of
the system.
In (Yao and Shekhar, 2021b), a comprehensive
analysis has been conducted in terms of implemen-
tation, optimization, application, and modeling, as
well as the overall scheme in the context of MPC for
HVAC systems. However, the need for a more real-
istic model that predicts the outlet thermal water dy-
namics has not yet been met. Additional work is re-
quired to achieve optimized output control and to pro-
vide an improved dynamical behavior for the MPC
controller. Specifically, for HVAC systems, the need
to switch in real-time between MPC controllers has
received only limited attention in the literature. It is
concluded that the application of MPC in the HVAC
field remains a wide-open subject, with much work
still to be done.
3 SYSTEM DESCRIPTION
In this section, we give a high-level description of the
problem context and the specific use case under con-
sideration. In the following sub-section, we focus on
the system characterization.
3.1 Problem Description
Our objective is to re-design with a model-based ap-
proach the control of real industrial heat pumps that
are already in operation and that we can test to col-
lect data. In particular, The tested heat pump units
come in a range of power capacity sizes to suit dif-
ferent needs, ranging from 5 kW to 15 kW nominal
capacities. These units offer various installation op-
tions to accommodate different space and aesthetic
requirements. The installation options include tradi-
tional setups, vertical and horizontal outlet configu-
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
38

rations, concealed installations, and more. Further-
more, the heat pump units can be configured with
or without Domestic Hot Water (DHW) systems and
support both heating and cooling applications within
the plant setup. For space heating and cooling, the
units can be paired with fan coil units, radiant sys-
tems, or a combination of both, providing flexibility
to meet specific climate control needs. This versatility
ensures that the heat pump units can be tailored to fit a
wide range of residential or commercial applications.
This justifies even more the need of an advanced con-
trol system that can be adjusted, fine tuned and finally
verified with model based techniques and tools.
The control system operates in seven distinct
modalities: Heating Plant, Heating DHW, Cooling
Plant, Defrost Mode, Off by User Intervention, Off by
Alarm, and Off by Thermal Condition. Depending on
the conditions, it must switch between these modali-
ties in real-time. The Defrost Mode is a crucial op-
erational phase designed to remove accumulated ice
on the Air Exchanger during the Heating Plant under
cold weather conditions. Off by User Intervention is
a modality in which the heat pump/compressor goes
off due to user intervention. If there is an alarm, ac-
cording to predefined logic, the machine or compres-
sor deactivates, and this state is referred to as Off by
Alarm. When all the target temperatures are achieved,
the compressor turns off within the modality of Off by
Thermal Condition. The desired temperature is de-
fined by the water target temperature at the outlet of
the water exchanger.
The model used for the controller is expected to be
obtained and validated with acquired data from one of
our heat pump machines in the testing field (see Fig.
1). The data from these heat pumps, equipped with
different sensors, is collected through Modbus com-
munication interfaces and transmitted to custom dat-
aloggers based on embedded Linux systems, which
send the data securely to a central server in the cloud
for storage in InfluxDB and visualization by Grafana.
3.2 System Characterization
In the context of the HVAC system, thermodynam-
ics could be applied to their various components to
describe how energy behaves within such systems,
which typically take the form of partial differential
equations (PDEs). It generally involves the terms rep-
resenting different energy transfer mechanisms. It is
important to recognize the inherent complexity and
nonlinearity of the derived PDEs that describe the en-
ergy balance in HVAC compressor systems. These
equations capture the detailed physical processes and
interactions within the system, making them difficult
Figure 1: The water-air heat pump under test in the experi-
mental field.
to model and understand, especially for real-time con-
trol applications. The nonlinearity in these equations
arises from the interconnection of various factors in-
cluding the nonlinear behavior of heat transfer and
fluid flow phenomena within the system.
Below, we give a dynamical representation of the
model to introduce the critical variables of the con-
trol system. The simplified nonlinear overall state-
space structure, derived from the dynamic energy bal-
ance equation of the HVAC system, serves as a gray-
box equivalent for thermodynamically derived equa-
tions. It also provides a dynamic representation of the
physical model at the microscale level where could be
given as Equation 1:















x
′
(t) = f


x(t),

Comp
Freq
(t)
S
EEV
(t)

,


W T
W ExIn
(t)
RT
CompDis
(t)
T
air
(t)


, v(t)



W T
W ExOut
(t)
RT
W Ex
(t)

= g


x(t),

Comp
Freq
(t)
S
EEV
(t)

,


W T
W ExIn
(t)
RT
CompDis
(t)
T
air
(t)


, v(t)


(1)
which is presented in a standard nonlinear continu-
ous time-invariant state-space form, which includes
vectors of state variables x(t), control inputs u(t)
shown as Comp
Freq
(t) and S
EEV
(t) , measured distur-
bances w(t), and unmeasured disturbances v(t), re-
spectively, repeated for both the nonlinear functions
f and g. Comp
Freq
(t) denotes the compressor speed,
S
EEV
(t) is the Electronic Expansion Valve (EEV)
step, W T
W ExIn
(t) and W T
W ExOut
(t) stand for the wa-
ter temperature at the water exchanger inlet and outlet
respectively, RT
CompDis
(t) is the refrigerant tempera-
ture at the compressor discharge, and T
air
(t) stands for
the ambient air temperature. The component control
A Switching Event-Triggered Model Predictive Control for HVAC Systems
39

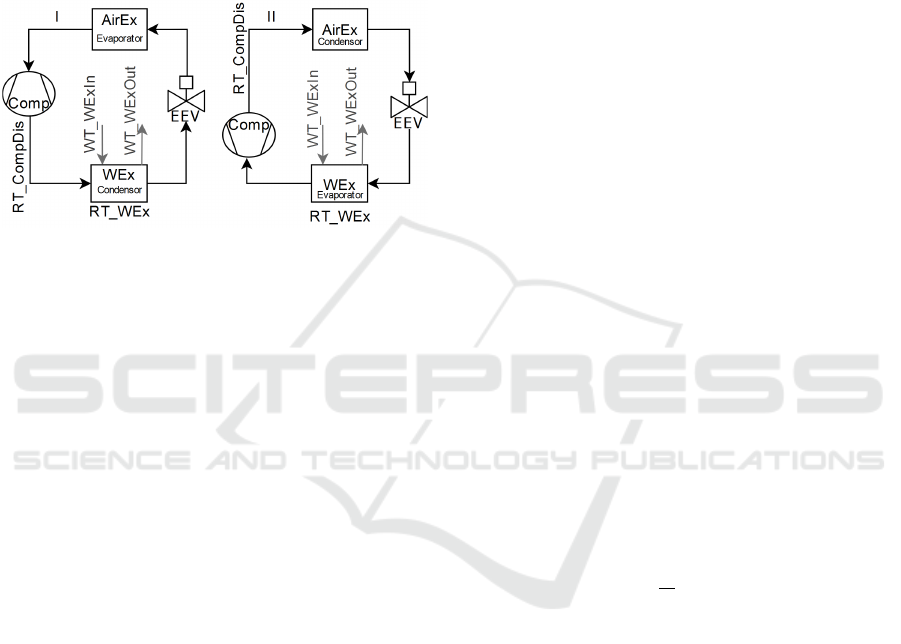
scheme is presented in Fig. 2, which includes both
heating (DHW/plant) and cooling behaviors on the I
and II cases, respectively. The Water Exchanger acts
as a condenser in the first case and as an evaporator in
the second one, while the Air Exchangers act oppo-
sitely. The refrigerant flow direction for the Heating
DHW and Heating Plant modes is as indicated in case
I of Fig. 2. However, the flow direction is reversed for
the Cooling and Defrost modes, as illustrated in case
II.
Figure 2: Component Mechanical Scheme.
4 DATA-DRIVEN
IDENTIFICATION MODEL
To process the functional model, we start from data
acquisition and refinement. This stage forms the
essential foundation for optimally preparing the ac-
quired experimental data from our split air-water 11
kW heat pump with R32 refrigerant and facilitating
subsequent steps. As said earlier, the data is collected
through Modbus communication interfaces and trans-
mitted to several custom dataloggers, which send the
data securely to a central server in the cloud for stor-
age in InfluxDB and visualization by Grafana. Data
preparation involved standardizing formatting, algo-
rithmic filtering, frequency-based filtering, resam-
pling, and data imputation techniques such as inter-
polation, forward filling, and backward filling. A sig-
nificant step following the data preparation phase is
to focus on identifying an appropriate model through
the System Identification approach. Considering the
requirement for a model within the predictive con-
troller to operate efficiently during iterative processes,
and given the planned implementation in an embed-
ded system, we selected a structure that is both highly
effective and simple for this application.







x
1
(t + 1)
x
2
(t + 1)
.
.
.
x
n−1
(t + 1)
x
n
(t + 1)







=







A
11
A
12
··· A
1n−1
A
1n
A
21
A
22
··· A
2n−1
A
2n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A
n−11
A
n−12
··· A
n−1n−1
A
n−1n
A
n1
A
n2
··· A
nn−1
A
nn














x
1
(t)
x
2
(t)
.
.
.
x
n−1
(t)
x
n
(t)







+







B
11
B
21
.
.
.
B
n−11
B
n1







Comp
Freq
(t)
+





F
11
F
1n−1
F
21
F
2n−1
.
.
.
.
.
.
F
n1
F
nn−1






W T
W ExIn
(t)
T
air
(t)

W T
W ExOut
(t) =

C
11
C
12
... C
1n







x
1
(t)
x
2
(t)
...
x
n−1
(t)
x
n
(t)






+ D
11
Comp
Freq
(t) +

E
12
E
13


W T
W ExIn
(t)
T
air
(t)

(2)
The chosen model is discretized and linearized
to enhance computational efficiency. Additionally,
the temperature of the refrigerant is omitted from
the model due to its highly nonlinear characteristics,
which could complicate real-time computations. The
details of the model are presented in Equation 2.
Defining θ as the collection of state-space matri-
ces gives θ = {A; B; F;C; D; E}, where A, B, F, C, D
and E are the system matrices. Hence, the identifica-
tion problem is defined as
ˆ
θ = argmin
θ
1
Ψ
Ψ
∑
k=1
(ε(t
samp
, θ))
2
(3)
The prediction error, denoted as ε(t
samp
, θ), is
defined as the difference between the actual output
y(t
samp
) and the simulated output of the state-space
model ˆy(t
samp
, θ) at the sample time t
samp
given as
Equation 4. While Ψ represents the total number of
data samples. In this work, Prediction Error Method
(PEM) (Ljung, 1998) is addressed through trust re-
gion reflective techniques (Sharifzadeh et al., 2018b;
Senatore et al., 2017; Sharifzadeh et al., 2018a).





ε(k, θ) = y(k) − ˆy(k|θ)
ˆx(k + 1) = θ
A
ˆx(k) + (θ
B
+ θ
F
)u(k)
ˆy(k|θ) = θ
C
ˆx(k) + (θ
D
+ θ
E
)u(k)
(4)
Given the relatively small scale of the HVAC
model, with limited inputs, outputs, and state vari-
ables, the use of the presented method does not lead to
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
40

significant computational challenges. Moreover, the
iterative nature of PEM aligns well with the require-
ments of real-time implementation, ensuring efficient
integration into the control loop.
5 CONTROL DESIGN
5.1 Design of Specific Controllers
Considering the given discrete linear time-invariant
system to be controlled above: x(t + 1) = Ax(t) +
Bu(t) + Fw(t) and y(t) = Cx(t), where A ∈ R
n×n
is
the state matrix, B ∈ R
n×p
is the control input ma-
trix, F ∈ R
n×p
is the measured disturbance matrix,
x(t) ∈ R
n
is the state variable, u(t) ∈ R
p
is the con-
trol input variable, y(t) ∈ R
q
is the output variable,
and C ∈ R
q×n
is the output matrix. where MPC de-
termines the optimal strategy for the current state by
applying the optimization problem for x(k), aiming to
minimize the cost function outlined below:
J
∗
(x(t)) = min
U≜
h
u
T
t
. . . u
T
t+M−1
i
T
F
N
(x(t + N)) +
N−1
∑
k=0
F
k
(x(t + k|t), u(t + k))
subject to
u
min
≤ u(t +k) ≤ u
max
, k = 1, .. ., M − 1
δu
min
≤ δu(t +k) ≤ δu
max
, k = 1, .. ., M − 1
y
min
≤ y(t +k|t) ≤ y
max
, k = 1, .. ., N
x(t + k +1|t) = Ax(t +k|t) + Bu(t +k) +Fw(t + k),
y(t + k) = Cx(t +k|t), k ≥ 0
(5)
where
F
N
(x(t + N)) = ∥x(t + N) − r(t)∥
2
P
F
k
(x(t + k|t), u(t + k)) = ∥x(t + k) − r(t)∥
2
Q
+ ∥u(t + k) − u
r
(t)∥
2
R
having Q = Q
T
≥ 0, R = R
T
> 0, P ≥ 0, x(t + k|t) is
the prediction of x(t + k) at time t hence, x(t|t) = x(t)
and N and M are prediction and control horizons.
When the matrices P and K could be obtained the al-
gebraic Riccati equation, which eventually solves the
constrained problem above, having the weight matri-
ces R and Q.
As given above for the saving energy by opti-
mization of constraints it is possible to set the de-
sired constraints in u
min
≤ u(t +k) ≤ u
max
and δu
min
≤
δu(t + k) ≤ δu
max
.
Regarding the Defrost modality, since the objec-
tive is to achieve pre-specified compressor frequency
targets, a PID controller is selected for this mode. Ad-
vanced control strategies are considered unnecessary
for this modality due to its simple control require-
ments.
5.2 Switching Logic Design
As illustrated in Fig. 3, the model considers four states
Initial Off, HeatCool, Off and Defrost. From which
HeatCool and Off are serving as hierarchical states.
Table 1: High-level logical specifications at Fig. 3.
Guard Definition
Cond Off TrmOff ∨ UsrOff ∨ AL Off ∨ AL StComp
Cond HeatCool
(HPL PlNotPr ∨ HPL PlPr ∨ HDHW1 ∨ HDHW2 ∨
CL PlNotPr ∨ CL PlPr) ∧ (Alarm must off = Al O f f N ∧
Alarm force stop comp = Al St Comp N) ∧ (Defrost need =
De f N ∨ Defrost need =De f tobe Act)
Cond Defrost
Alarm must off = Al O f f N ∧ Alarm force stop comp =
Al St Comp N ∧ Defrost need = De f Act
The transitions between the primary states are
constrained by three specific guards: Cond Off,
Cond HeatCool, and Cond Defrost, whose defini-
tions are provided in Table 1. The hierarchical
state HeatCool decomposes into the sub-states Heat-
ing DHW, Heating Plant, and Cooling Plant, with
their own model and further transitions between these
substates governed by specific guards and accompa-
nied by effects associated with each state. The hierar-
chical state Off is divided into three sub-states Off by
Alarm, Off by Thermal, and Off by User as well. The
effect in these three sub-states is a control action that
turns off the compressor.
In the Off by Alarm sub-state, the compressor is
turned off immediately, whereas in the Off by User
and Thermal Off sub-states, it turns off within a spe-
cific period unique to each sub-state.
Table 2: Identifiers used in the logic and their descriptions.
Identifier Definition Value Description
Defrost
need
Checking the
need for defrost-
ing
Def Act
Defrost is acti-
vated
Def N
Defrost is not ac-
tive
Def tobe
Act
Defrost to be acti-
vated
Alarm force
stop
comp
Checking if the
compressor is
forced to stop due
to an alarm
Al St
Comp N
Compressor is
not forced to stop
due to an alarm
Al St
Comp Act
Compressor is
forced to stop due
to an alarm
Alarm
must off
Checking if it
must be off due
to an alarm
Al Off Act
It must be off due
to an alarm
Al Off N
It must not be off
due to an alarm
A Switching Event-Triggered Model Predictive Control for HVAC Systems
41

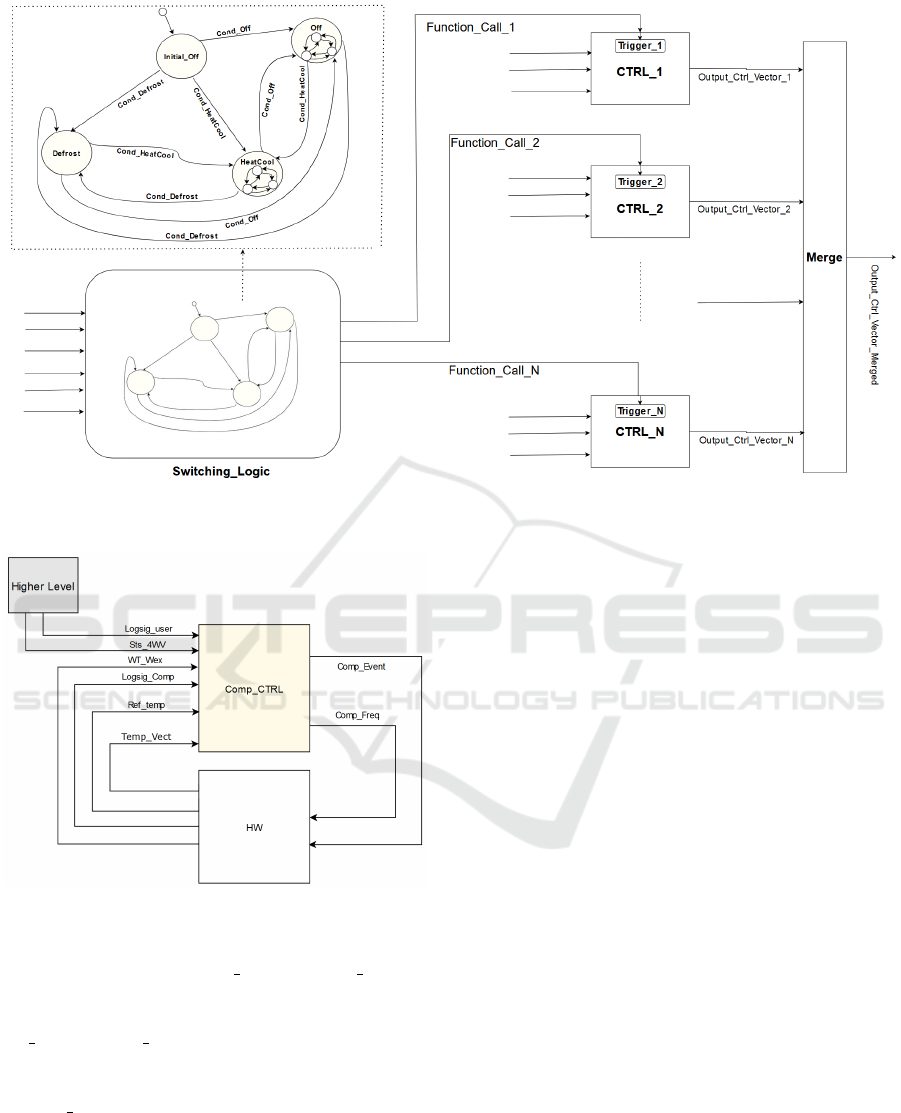
Figure 3: The Scheme of the Switching Event-Triggered MPC.
Figure 4: Component Control Scheme.
MPC is designed for each of these three sub-
states. The conditions HPL PlPr and HPL PlNotPr
represent the heating plant mode, indicating whether
the plant is prioritized or not, respectively. Similarly,
CL PlPr and CL PlNotPr denote the cooling plant
whether the plant is prioritized or not. Two sepa-
rate conditions, HDHW1 and HDHW2, specify when
Heating DHW should be activated. Additionally, Tr-
mOff and UsrOff, which are two of four specified
conditions for the state Off (see Table 2), define the
conditions under which the system should be deac-
tivated due to thermal reasons and user intervention,
respectively. As also shown in Fig. 3, each function
call triggers an event for each modality/functionality.
6 RESULTS
In this section, the previously presented approach will
be illustrated and applied to the use case described
earlier. A test is conducted to check the identified
model and validate the control approach using switch-
ing scenarios. All computations are carried out on an
Intel Core i7-8650U with 4 cores, at 1.90 GHz, with
32 GB RAM, running Matlab R2019b and Python
3.9.13. The Model Predictive Control 6.3.1 and Em-
bedded Coder 7.3 Toolboxes are utilized for the MPC
object and code generation respectively. The refined
version of this generated code gives a standalone code
that is designed in a way that makes it easily expand-
able for future updates and integration.
6.1 Validation of the Identified Model
As for the system identification, using the refined time
series data and dividing it into two sets of training
and validation data, within different periods of the
year for the different modalities, with a sampling fre-
quency of 20 Hz for both datasets and applying the
constraints (e.g., Comp
Freq
< 120 Hz) is considered
for the validation. The cross-validation results pre-
sented in Table 3 illustrate the Mean Absolute Er-
ror (MAE) values for different months of the heating
plant, indicating the accuracy of the identified sys-
tem output compared to the real acquired data points.
The table covers the period from November 2022 to
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
42

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
30
40
Temp [C]
Reference value
Water Temperature at Water Exchanger Outlet
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
0
50
100
Freq [Hz]
Compressor Freq
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
30
40
Temp [C]
Water Temperature at Water Exchanger Inlet
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
0
5
10
15
Temp [C]
Air Temperature
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
0
5
10
Temp [C]
Water Exchanger Temp Difference
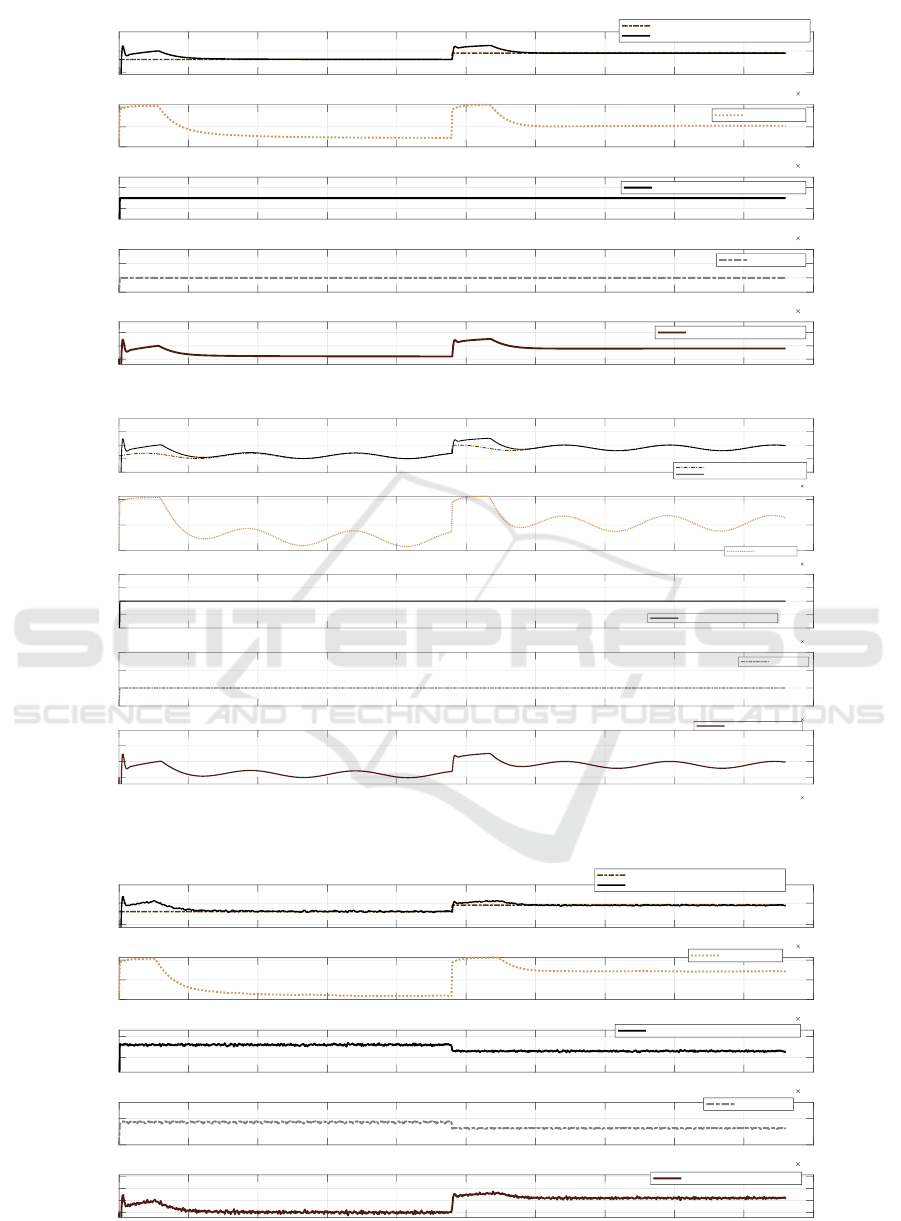
Figure 5: Time history of the measured temperature for the components and the Compressor Frequency.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
30
35
40
45
Temp [C]
Reference value
Water Temperature at Water Exchanger Outlet
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
0
50
100
Freq [Hz]
Compressor Freq
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
25
30
35
40
45
Temp [C]
Water Temperature at Water Exchanger Inlet
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
0
5
10
15
Temp [C]
Air Temperature
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
0
5
10
Temp [C]
Water Exchanger Temp Difference
Figure 6: Time history of the measured temperature for the components and the Compressor Frequency having disturbance.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
30
40
Temp [C]
Reference value
Water Temperature at Water Exchanger Outlet
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
0
50
100
Freq [Hz]
Compressor Freq
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
30
40
Temp [C]
Water Temperature at Water Exchanger Inlet
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
0
10
Temp [C]
Air Temperature
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [S]
10
4
0
5
10
15
Temp [C]
Water Exchanger Temp Difference
Figure 7: Time history of the measured temperature for the components and the Compressor Frequency during uncertainty.
A Switching Event-Triggered Model Predictive Control for HVAC Systems
43

March 2023. Each row represents the MAE for the
output difference explained earlier when trained for
one month and validated against the others. The diag-
onal elements are zero, reflecting the comparison of
the model output against the same month. These re-
sults underscore the model’s robustness and areas for
improvement in predicting specific monthly outputs.
Moreover, it also considered to check observability
and the controllability of the obtained models. The
obtained systems are both controllable and observable
as rank[B, AB, A
2
B] = 4 and rank[C,CA,CA
2
] = 4.
Table 3: Cross-validation results.
Nov 22 Dec 22 Jan 23 Feb 23 Mar 23
Nov 22 0 1.1408 1.0915 1.0636 1.0652
Dec 22 0.6863 0 1.0729 1.0240 0.9041
Jan 23 0.6668 1.1387 0 0.9789 0.8843
Feb 23 0.6587 1.1160 1.0356 0 0.9606
Mar 23 0.8867 1.3945 1.2833 1.2106 0
Table 4 presents given MAE values for three dif-
ferent operational modes—Heating Plant, Heating
DHW, and Cooling—using varying numbers of state
variables (3, 4, and 5). According to the MAE re-
sults for all three modalities, the obtained model ex-
hibits accurate performance. Additionally, the MAE
remains relatively stable across different numbers of
state variables.
Table 4: MAE for various modalities with different numbers
of state variables.
Modality State Variables MAE
Heating Plant
3 1.0132
4 1.0122
5 1.0674
Heating DHW
3 0.9786
4 0.9777
5 0.9785
Cooling
3 0.8499
4 0.8492
5 0.8323
6.2 Performance Analysis of the
Proposed Control Approach
In order to evaluate the performance of the given con-
trol strategy, MIL testing is carried out in various sce-
narios. Fig. 5 is the first test showing the time his-
tory of the measured values in the HVAC system,
which switches from the Heating DHW modality to
the Heating Plant at time 2.4 × 10
4
. The first plot il-
lustrates a precise reference trajectory tracking, where
the water temperature at the Water Exchanger Outlet
follows the reference value. The second sub-figure
shows that the Compressor Frequency performs as ex-
pected over time, especially during the switching pe-
riod. The third sub-figure shows the water tempera-
ture at the Water Exchanger Inlet. The time history of
the air temperature and the water temperature differ-
ence at the Water Exchanger are shown in the last two
sub-figures, respectively. N and M at MPC are set as
600 s and 120 s where Q = 1 and R = .1.
In the second scenario in Fig. 6, the performance
is tested with a harmonic disturbance. As shown, it
provides an acceptable settling time during the test.
In the third scenario at Fig. 7, Gaussian random noise
is introduced for both the water temperature at the
Water Exchanger Outlet and the air temperature. The
test is performed under different conditions involving
a rapid fluctuation in the temperature at the Water Ex-
changer Outlet. It demonstrates an acceptable track-
ing of the reference trajectory, with the overshoot re-
maining within an acceptable range. The control ap-
proach exhibits robust performance in the presence
of harmonic disturbances which demonstrates robust
performance against Gaussian noise. Furthermore, it
is possible to achieve additional reductions in the In-
tegrated Absolute Error (IAE) by optimizing the MPC
(Model Predictive Control) parameters.
7 CONCLUSION
In this paper, we presented a new switching con-
trol methodology based on function calls that trigger
events for each functionality/modality, enhancing the
efficiency and functionality of the HVAC application.
A new model for model-based control was developed
and validated using acquired data from machines in
the test field. This model was also implemented in
the MPC framework and tested through MIL testing
in various machine modalities. As future work, we
intend to deploy and validate the code generated from
the proposed model on the field. We currently have
provided the artefacts in a file available at https://es-
static.fbk.eu/people/ssharifzadeh/ICINCO2024/.
ACKNOWLEDGEMENTS
The work is financed by the Autonomous Province of
Trento in the scope of L.P. No. 6/1999 with determi-
nation. No. 592 of 09/08/2021. – Ref.: 2021-AG12-
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
44

00783. - project NPDCR (Nuova Pompa di Calore
Residenziale - New residential heat pump).
REFERENCES
Afroz, Z., Shafiullah, G., Urmee, T., and Higgins, G.
(2018). Modeling techniques used in building hvac
control systems: A review. Renewable and sustain-
able energy reviews, 83:64–84.
Blasco, C., Monreal, J., Ben
´
ıtez, I., and Lluna, A. (2012).
Modelling and pid control of hvac system according to
energy efficiency and comfort criteria. In Sustainabil-
ity in Energy and Buildings: Proceedings of the 3rd
International Conference in Sustainability in Energy
and Buildings (SEB’11), pages 365–374. Springer.
Darby, M. L. and Nikolaou, M. (2012). Mpc: Current prac-
tice and challenges. Control Engineering Practice,
20(4):328–342.
Ljung, L. (1998). System identification. In Signal analysis
and prediction, pages 163–173. Springer.
Saletti, C., Gambarotta, A., and Morini, M. (2020). Devel-
opment, analysis and application of a predictive con-
troller to a small-scale district heating system. Applied
Thermal Engineering, 165:114558.
Senatore, A., Pisaturo, M., Sharifzadeh, M., et al. (2017).
Real time identification of automotive dry clutch fric-
tional characteristics using trust region methods. In
AIMETA 2017-Proceedings of the XXIII Conference
of the Italian Association of Theoretical and Applied
Mechanics, pages 526–534. AIMETA-Associazione
Italiana di Meccanica Teorica e Applicata.
Sharifzadeh, M., Pisaturo, M., Farnam, A., and Senatore,
A. (2018a). Joint structure for the real-time estima-
tion and control of automotive dry clutch engagement.
IFAC-PapersOnLine, 51(15):1062–1067.
Sharifzadeh, M., Senatore, A., Farnam, A., Akbari, A., and
Timpone, F. (2018b). A real-time approach to robust
identification of tyre–road friction characteristics on
mixed-µ roads. Vehicle system dynamics.
Soyguder, S., Karakose, M., and Alli, H. (2009). Design
and simulation of self-tuning pid-type fuzzy adaptive
control for an expert hvac system. Expert systems with
applications, 36(3):4566–4573.
Staino, A., Nagpal, H., and Basu, B. (2016). Cooperative
optimization of building energy systems in an eco-
nomic model predictive control framework. Energy
and Buildings, 128:713–722.
Taheri, S., Amiri, A. J., and Razban, A. (2024a). Real-
world implementation of a cloud-based mpc for hvac
control in educational buildings. Energy Conversion
and Management, 305:118270.
Taheri, S., Amiri, A. J., and Razban, A. (2024b). Real-
world implementation of a cloud-based mpc for hvac
control in educational buildings. Energy Conversion
and Management, 305:118270.
Yao, Y. and Shekhar, D. K. (2021a). State of the art review
on model predictive control (mpc) in heating ventila-
tion and air-conditioning (hvac) field. Building and
Environment, 200:107952.
Yao, Y. and Shekhar, D. K. (2021b). State of the art review
on model predictive control (mpc) in heating ventila-
tion and air-conditioning (hvac) field. Building and
Environment, 200:107952.
A Switching Event-Triggered Model Predictive Control for HVAC Systems
45