Flow Is Best, Fast and Scalable: The Incremental Parametric Cut for

Maximum Density and Other Ratio Subgraph Problems

Dorit S. Hochbaum

Department of Industrial Engineering and Operations Research, University of California, Berkeley, U.S.A.

Keywords:

Densest Subgraph, Graph Structures, Monotone Integer Programming, Breakpoints Algorithm, Conductance.

Abstract:

The maximum density subgraph, or densest subgraph, problem has numerous applications in analyzing graph

and community structures in social networks, DNA networks and ﬁnancial networks. The densest subgraph

problem has been the subject of study since the early 80s and polynomial time ﬂow-based algorithms are

known, yet research in the last couple of decades has been focused on developing heuristic methods for solv-

ing the problem claiming that ﬂow computations are computationally prohibitive. We introduce here a new

polynomial time algorithm, the incremental parametric cut algorithm (IPC) that solves the maximum density

subgraph problem and many other max or min ratio problems in the complexity of a single minimum-cut.

A characterization of all these efﬁciently solvable ratio problems is given here as problems with monotone

integer programming formulations. IPC is much more efﬁcient than the parametric cut algorithm since instead

of generating all breakpoints it explores only a tiny fraction of those breakpoints. Compared to the heuristic

methods, IPC not only guarantees optimality, but also runs orders of magnitude faster than the heuristic meth-

ods, as shown in an accompanying experimental study.

1 INTRODUCTION

We introduce here a new efﬁcient algorithm for the

maximum density (MD), or densest, subgraph prob-

lem and many other ratio problems. The maximum

density subgraph problem is to identify a subset of

nodes in the graph that maximizes the density, de-

ﬁned as the ratio of the weights of the edges with

both endpoints in the subset, divided by the sum of

weights of the nodes in the subgraph. The densest

subgraph has played a central role in analyzing net-

work structures since the 1970’s. The more recent ap-

plications of the problem are in the context of very

large scale networks, such as identifying emerging

cyber-communities (Kumar et al., 1999), DNA mo-

tif ﬁnding (Fratkin et al., 2006), and real-time story

identiﬁcation (Angel et al., 2014).

The maximum density problem was studied since

the late 70’s. (Picard and Queyranne, 1982) are likely

the ﬁrst to study the problem and recognize its link

to the max-ﬂow min-cut problem. Their method was

based on a general “linearization” approach that ap-

plies for any ratio optimization problem, reducing it

to the λ-question, deﬁned next, which they proposed

https://orcid.org/0000-0002-2498-0512

to solve with a min-cut procedure on a related graph.

A general ratio problem max

x∈F

f (x)

g(x)

can be re-

duced to a sequence of calls to an oracle that provides

a yes/no answer to the λ-question:

Is there a feasible solution x ∈ F such that

f (x)

g(x)

> λ?

Or equivalently “Is there a feasible solution x ∈ F

such that f (x) − λg(x) > 0?”

To answer this λ-question it is sufﬁcient to solve:

(λ-problem) max

x∈F

f (x) − λg(x).

If the maximum value is greater than 0 then there

is a feasible solution of ratio value strictly greater than

λ. Otherwise the answer is no. Speciﬁcally, if the

maximum value is strictly less than 0, then there is no

feasible solution of ratio value great or equal to λ. If

the answer is 0 then the respective optimal solution

for the λ-question has a ratio value of λ which is the

maximum ratio.

Therefore, any ratio problem that has the corre-

sponding λ-problem polynomial time solvable, and

the log of the number of possible values of the ratio

bounded by a polynomial quantity, is solvable in poly-

nomial time by applying binary search on the value of

the parameter λ.

(Picard and Queyranne, 1982) showed that the λ-

Hochbaum, D.

Flow Is Best, Fast and Scalable: The Incremental Parametric Cut for Maximum Density and Other Ratio Subgraph Problems.

DOI: 10.5220/0012917300003838

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 275-282

ISBN: 978-989-758-716-0; ISSN: 2184-3228

275

problem for MD can be solved as a min-cut (mini-

mum s,t-cut) on a related graph, the construction of

which appeared ad-hoc. Their method was essentially

a predecessor of our IPC algorithm, showing that the

λ-problem for MD would be solved up to n times,

where n is the number of nodes in the graph. Here we

show a systematic method that maps any optimization

(and ratio) problem that is a monotone integer pro-

gram to an associated graph and therefore all these

problems are solvable in polynomial time, which as

proved here, is the complexity of one min-cut proce-

dure.

For the maximum density problem, a follow up

paper by (Goldberg, 1984) improved on the algorithm

of Picard and Queyranne, by using binary search on

the λ-problem making multiple call to a min-cut pro-

cedure, up to log n times for the edge-unweighted

node-unweighted problem. A major breakthrough,

the parametric ﬂow procedure, was introduced in

(Gallo et al., 1989), identifying the solutions for all

values of the parameter λ that correspond to all possi-

ble solutions to the λ-problem, and in the complex-

ity of a single min-cut procedure. This parametric

procedure used the push-relabel algorithm of (Gold-

berg and Tarjan, 1988). Later (Hochbaum, 1998;

Hochbaum, 2008) showed a parametric cut proce-

dure using HPF (Hochbaum PseudoFlow) also with

the complexity of a single min-cut. We will refer to

this parametric procedure also as fully parametric, to

differentiate it from “simple” parametric, reviewed in

Section 2.2.

Despite its theoretical efﬁciency, the parametric

ﬂow procedure has never been used to solve the

densest subgraph problem, to the best of our knowl-

edge. One contributing factor for the lack of use

is that there is no implementation available for the

parametric push-relabel version proposed by (Gallo

et al., 1989). (However, for HPF there is a para-

metric ﬂow/cut implementation publicly available,

(Hochbaum, 2020a).) Instead, ﬂow algorithms have

been employed using multiple calls to min-cut in a bi-

nary search process, resulting in high running times.

This perceived inefﬁciency gave rise to current state-

of-the-art algorithms for the maximum density prob-

lem that are based on greedy heuristics that do not

guarantee optimality, (Charikar, 2000), (Boob et al.,

2020), (Harb et al., 2022). A recent justiﬁcation

for not using the polynomial time ﬂow algorithms is

that “ﬂow computations are expensive” (Boob et al.,

2020).

Our main contribution here is a new polynomial

time algorithm, the incremental parametric cut (IPC)

algorithm, that solves optimally and efﬁciently the

densest subgraph problem and many other minimum

or maximum ratio problems. We also provide an easy

characterization of the ratio problems that are solv-

able with this procedure, as those that can be for-

mulated as monotone integer programming problems.

For those problems we describe the respective s,t-

graph construction that follows from the formulation.

In a separate experimental study (Hochbaum

et al., 2024) we show that the number of breakpoints

IPC generates is in the range of 2 − 13 even for

datasets on millions of nodes and hundreds of mil-

lion edges, which is typically less than 1% of the total

number of breakpoints. This results in very fast run-

ning times that are orders of magnitude faster than

those of the parametric ﬂow procedure and recent

state-of-the-art heuristics that do not produce optimal

solutions.

To summarize, the main contributions here are:

1. The incremental parametric cut algorithm IPC that

solves “monotone” ratio optimization problems in the

complexity of a single min-cut.

2. A new, previously unknown, formulation of dens-

est subgraph problem and its generalizations, that

uses half of the number of arcs as compared to the

known formulation.

3. An easy characterization of all ratio problems that

are solved by IPC. Examples are given in Table 1.

1.1 Ratio Problems Solved with IPC

Notation. We consider the graph representation of the

problems, ﬁrstly for undirected graphs corresponding

to symmetric problems. Let G = (V,E) denote an

undirected graph with n denoting the number of nodes

in V, and m denoting the number of edges in E. Every

edge [i, j] ∈ E has an associated weight w

i j

≥ 0. Let

the weighted degree of node i ∈ V be d

∑

[i, j]∈E

i j

For B

⊆ V , let C(B

) =

∑

[i, j]∈E,

i∈B

, j∈B

i j

be the

sum of weights of the edges between nodes in the

set B

and those in set B

. Let q

denote a nonneg-

ative cost value associated with each node, and u

, or

′

denote two types of values associated with each

node, which could be positive or negative. Let the

degree volume of a set of nodes S be d(S) =

∑

i∈S

q(S) =

∑

i∈S

and U(S) =

∑

i∈S

Some ratio problems are deﬁned on directed

graphs, G = (V,A), where each arc (i, j) ∈ A has an

associated weight w

i j

≥ 0. The weighted outdegree

of a node i is d

∑

j|(i, j)∈A

i j

, and the outdegree

volume of a set of nodes S is d

(S) =

∑

i∈S

A sample list of some of the ratio problems solved

here is given in Table 1. The Max density problem

is deﬁned with weighted edges but unit weight on the

nodes. This name refers more often to the special case

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

276

of the unweighted problem where both edges weights

are 1 and node weights are 1.

Many ratio problems appear in contexts where the

size of optimal set is bounded. For example, the ex-

pansion ratio of a graph problem is min

|S|≤

C(S,S)

|S|

This added size restriction turns the problem NP-hard.

The Cheeger constant problem is typically presented

as min

S⊂V

C(S,S)

min{d(S),d(

, which is equivalent to the

size restricted ratio problem min

d(S)≤

d(V)

C(S,S)

d(S)

. The

conductance problem is min

π(S)≤

π(V )

C(S,S)

π(S)

where π

is interpreted as the stationary probability of node i.

We add here the ∗ to the name of the problem to in-

dicate that there is no size restriction, and then the

problem is polynomial time solvable. For the min-

imization problems, the entire set of nodes V is of-

ten the optimal solution of value 0. To avoid that

trivial solution, the problem is typically solved on a

subgraph of nodes V

. For example Metis (Karypis

and Kumar, 1998) has been used to identify a sub-

graph which is likely to contain the optimal solution

for these problems and then the minimization is sub-

ject to

0 ⊂ S ⊆ V

Table 1: A list of some of the ratio problems solved with

the incremental parametric cut. *No size restriction.

Problem name Objective

Max density max

S⊆V

C(S,S)

|S|

Weighted max density max

S⊆V

C(S,S)

q(S)

Ratio quadratic Knapsack max

S⊆V

C(S,S)+U(S)

q(S)

HNC max

0⊂S⊂V

C(S,S)

HNC-equivalent max

0⊂S⊂V

d(S)

C(S,S)

Max HNC-extension max

0⊂S⊂V

U(S)

C(S,S)+U

′

(S)

Expansion ratio* min

0⊂S⊂V

C(S,S)

|S|

Cheeger*/HNC min

0⊂S⊂V

C(S,S)

d(S)

Conductance* min

0⊂S⊂V

C(S,S)

q(S)

The problem HNC (Hochbaum Normalize Cut),

also named NC’ or SNC, was presented in (Sharon

et al., 2006) as an NP-hard problem identical to

the Normalized Cut (Shi and Malik, 2000), but

shown polynomial time solvable in (Hochbaum,

2010). The same mistake was repeated in (Fortunato,

2010), who stated that Cheeger*/HNC, equation (22),

min

0⊂S⊂V

C(S,S)

d(S)

, is the normalized cut problem and

NP-hard.

2 THEORETICAL BACKGROUND

2.1 Characterization of Polynomial

Time Solvability: Monotone Ratio

Problems

If the linearized problem can be formulated as mono-

tone integer programming, IPM

, then it is solvable

with a min-cut procedure on an associated s,t graph,

where the graph construction is uniquely mapped

from the formulation, (Hochbaum, 2002).

IPM problems are classiﬁed as monotone IP2 and

monotone IP3 where IP3 generalizes IP2. An inte-

ger program is a monotone IP2 if each constraint con-

tains at most two of the variables that appear with

opposite sign coefﬁcients. An integer program is a

monotone IP3 if each constraint contains at most two

of the variables that appear with opposite sign coef-

ﬁcients and a third variable that appears in that con-

straint only. (There is an additional requirement that

the “third variables” must have nonnegative coefﬁ-

cients in a minimization objective function, and non-

positive coefﬁcients in a maximization objective func-

tion.) It is thus easy to recognize whether a formula-

tion is monotone.

The formulation of monotone integer program for

a set of n x-variables and a set of constraints involving

a collection of pairs of variables A and a respective set

of z-variables is,

(IPM) max

∑

i=1

−

∑

(i, j)∈A

i j

s.t. a

i j

− b

i j

≤ c

i j

+ z

i j

∀ (i, j) ∈ A

ℓ

≤ x

≤ u

, integer ∀ i ∈ V

i j

≥ 0, integer ∀ (i, j) ∈ A.

Here there is a restriction that the coefﬁcients of

i j

in the objective function are nonnegative for max-

imization and non-positive for minimization.

Any IPM problem is equivalent to the following

binary s-excess problem which is formulated on the

variables x

= 1 iff node i is in the optimal set S:

(s-excess) max

∑

j∈V

−

∑

(i, j)∈A

i j

subject to x

− x

≤ z

i j

for (i, j) ∈ A

binary j = 1, . ..,n

i j

binary (i, j) ∈ A.

The respective graph G

is constructed as follows,

(Hochbaum, 2002): We add nodes s and t to the graph

G, with an arc from s to every positive weight node i,

We use the acronym IPM rather than MIP so as not to

confuse it with Mixed Integer Programming

Flow Is Best, Fast and Scalable: The Incremental Parametric Cut for Maximum Density and Other Ratio Subgraph Problems

277

of capacity u

= w

, and an arc from every negative

weight node j to t of capacity u

= −w

. Let this

added set of arcs, adjacent to s and t (source node and

sink node respectively) be denoted by A

. The arcs

of A each carry the capacity u

i j

which is inﬁnite if

the constraint has only two variables. The graph G

is then (V ∪ {s,t},A ∪ A

). The proof of the follow-

ing lemma is given in (Hochbaum, 2002) and omitted

here.

Lemma 1. S

∗

is a set of maximum s-excess capacity

in the original graph G if and only if S

∗

is the source

set of a minimum s,t-cut in the associated graph G

We say that a ratio problem is a monotone inte-

ger program (IPM), if the corresponding λ-problem

is IPM. For the λ-problem, the corresponding ﬂow

graph G

has arc capacities that are functions of the

parameter λ. An s,t-graph is said to be a parametric

ﬂow graph if it has source-adjacent capacities that are

monotone non-increasing with the parameter λ and

the sink-adjacent capacities that are monotone non-

decreasing with λ (or vice versa). For a λ-problem

represented as a parametric ﬂow graph, G

, the para-

metric cut procedure solves the λ-problem, for all val-

ues of the parameter. This is the case for all the prob-

lems listed in Table 1 and many more.

2.2 Parametric Cut, Nestedness and the

“Continue” Property

Let the minimum cut for graph G

be (S

) with

the “source set” of the minimum cut and

the

“sink set”. A property of the parametric ﬂow graph

is that as the values of λ are increasing, the source

sets of the minimum cuts can only decrease, each a

subset of the previous. Formally, for a monotone in-

creasing sequence of p λ values, λ

< λ

< . . . <

, the corresponding optimal solutions, the source

sets of the minimum cuts in the graph G

, satisfy

⊇ S

⊇ ... ⊇ S

, and the respective sink sets

satisfy

0 =

⊆

⊆ .. . ⊆

. This property

is called nestedness and is proved as a corollary of

the parametric ﬂow algorithms of (Gallo et al., 1989;

Hochbaum, 1998; Hochbaum, 2008). As the value

of the parameter λ increases, the respective cut so-

lutions change when the sink set strictly increases.

The values of the parameter where the change occurs

are called breakpoints. Because of the nestedness the

solution set changes by adding at least one node to

the sink set, and therefore there are at most n break-

points. For ℓ breakpoints, λ

′

< λ

′

< ... < λ

′

ℓ

, the

respective sink sets are strict subsets of each other:

′

⊂

′

⊂ . . . ⊂

′

ℓ

There are two variants of the parametric cut pro-

cedure. The fully parametric variant generates all the

breakpoints (see (Hochbaum, 2020a)). The simple

parametric variant takes as input a sequence of val-

ues of λ, or a sequence of source adjacent capacities

and sink adjacent capacities that are monotone non-

increasing on one side, and monotone non-decreasing

on the other, (Hochbaum, 2020b), and outputs the

minimum cut solution for each of them. A property

required of a min-cut max-ﬂow algorithm in order for

either the fully or simple parametric cut to work in the

complexity of a single min-cut procedure, T (n, m), is

the continue property: Once an optimal solution has

been found for one setting of the capacities, it is used

as the initial solution for the new problem with up-

dated, monotone, capacities. This is done while main-

taining the labels and the invariant structure of the al-

gorithm, which for HPF is called normalized tree. To-

date, only push-relabel and HPF are max-ﬂow min-

cut algorithms that have the continue property. For

HPF the routine HPF-para-continue(λ,S) is the part

that takes a solution, which is the subset S in the re-

lated graph, and updated capacities corresponding to

λ to ﬁnd the optimal solution for the updated problem

which is a subset of S.

The continue operation for HPF using monotonic-

ity is referred to as HPF-para-continue and takes as

input the solution source set for the value of λ pre-

viously used, that is guaranteed to contain the opti-

mal ratio solution (because of nestedness, and the new

value λ).

2.3 The Concave Envelope of the

Breakpoints

For a general maximum ratio problem max

x∈F

f (x)

g(x)

we consider the graph that maps any value of g(x) =

B, so-called “budget”, to the maximum value of

f (x

) = argmax

x∈F

f (x)|g(x) ≤ B, referred to as the

“beneﬁt”. Finding those maximum beneﬁts is in gen-

eral NP-hard.

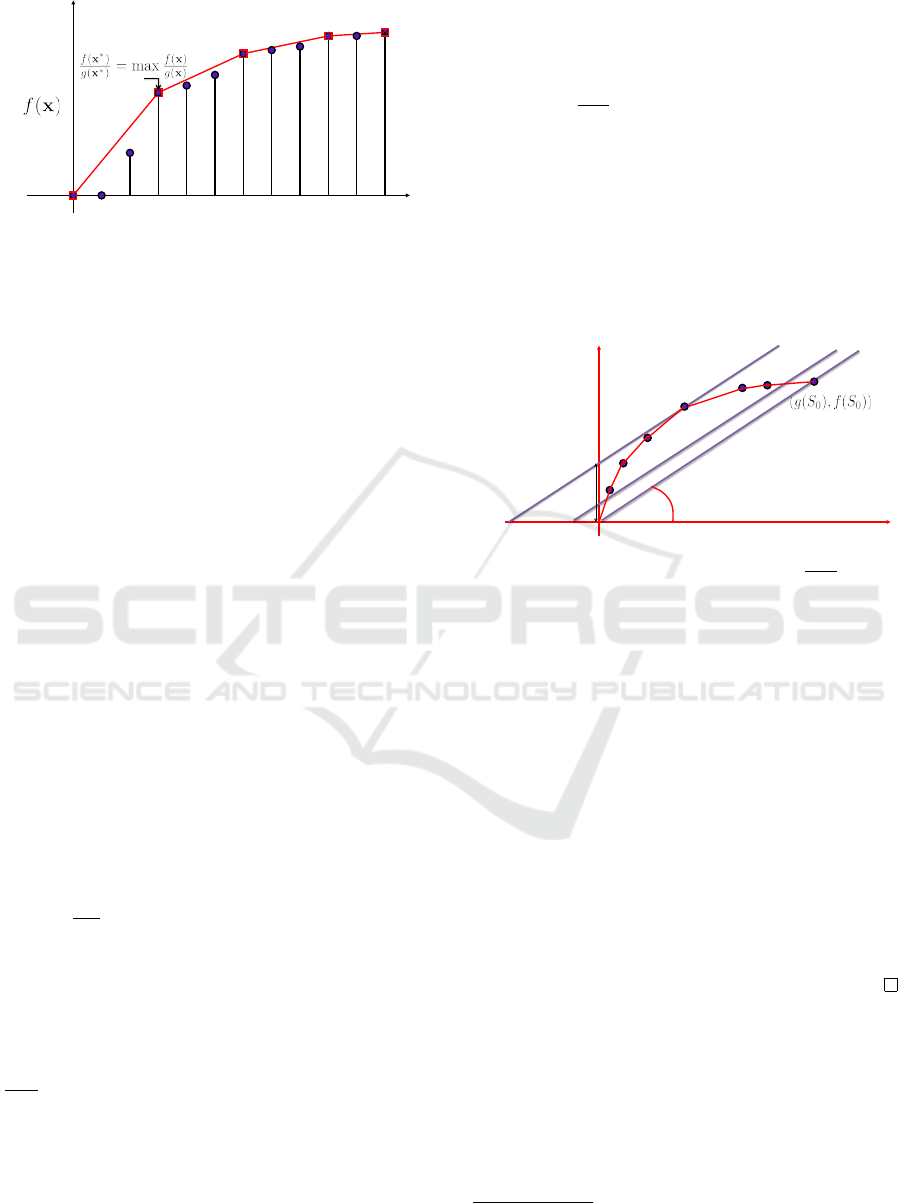
Consider the lower envelope of all the lines that

have the entire collection of optimal solutions below

them. This envelope, shown in red line segments in

Figure 1, is concave piecewise linear and the points

at which the line segment changes, are called break-

points (marked by boxes in Figure 1).

The ratio value corresponding to each optimal

point is the slope of the line connecting it to the ori-

gin. Hence the ﬁrst, leftmost, breakpoint is also the

optimal solution to the maximum ratio problem.

The properties of the concave envelope were stud-

ied, in the context of the dynamic evolution problem,

in (Hochbaum, 2009). These properties include:

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

278

Benefit

Budget

Figure 1: The concave envelope, the breakpoints and the

ratio maximizing solution.

• The concave envelope and breakpoints are found

with fully parametric cut procedure, (Hochbaum,

2020a).

• The breakpoints of the envelope correspond to the

breakpoints of the respective parametric cut solu-

tions, and the left derivative at the ith breakpoint

is equal to the ith parameter breakpoint value λ

′

• At the breakpoints of the envelope the solutions

are optimal.

• The ﬁrst breakpoint – the smallest positive budget

breakpoint – corresponds to the solution which at-

tains the largest ratio of the beneﬁt to the budget.

• The breakpoints correspond to solutions that are

nested and their number is at most n, the number

of variables, or nodes, in the respective graph.

For the respective minimization problems the en-

velope of the breakpoints is convex, and the ﬁrst

breakpoint corresponds to the solution that attains the

smallest ratio of beneﬁt to budget, see e.g. Figure 5.

2.4 Incremental Parametric Cut

Procedure

Consider the general ratio maximization problem

max

x∈F

f (x)

g(x)

where any feasible vector x

′

is associ-

ated with a subset of nodes in the associated graph,

′

= {i ∈ V |x

′

= 1}.

The procedure starts with a set of nodes S

that

is to contain the optimal ratio solution, which for the

maximum density problem can be the entire graph,

= V . The initial value of the parameter is λ

f (S

)

g(S

)

. Solving the λ

-problem either provides a so-

lution with strictly higher ratio value, that is also a

breakpoint solution, or else its value is 0 and there-

fore it is the maximum ratio solution. Because of

the nested property, each subsequent solution set is

strictly contained in the previous iteration’s solution

set. The value of the ratio is then updated and used

as λ in the next iteration. Let S

be an initial feasible

solution.

PROCEDURE INCREMENTAL PARAMETRIC

( f (), g(), S

⊆ F ,k=0).

Step 1: λ

f (S

)

g(S

)

Step 2: HPF-para-continue(λ

) to solve

improve(λ

) = max

S⊆F ∩S

f (S) − λ

g(S).

Let S

k+1

= argmax

S⊆F ∩S

f (S) − λ

g(S).

Step 3: If {improve(λ

) > 0} let k := k + 1. Go to step 1,

else stop. Output S

∗

= S

We now prove the correctness of the procedure in

that it visits a sequence of budget-decreasing break-

points.

λ0

Budget

Benefit

λ0

Figure 2: Identifying a breakpoint with λ

f (S

)

g(S

)

subgra-

dient, skipping over several breakpoints.

Lemma 2. The optimal solution to max

x∈F

f (x) −

g(x), x

, is either a breakpoint on the concave en-

velope at a budget < g(x

) and with strictly larger ra-

tio than that of x

, or x

= x

and it is the maximum

ratio solution.

Proof. Consider the line equation f (x) = λ

g(x) + ∆

where ∆ the intercept of the line, of slope λ

, on the

vertical axis, as in Figure 2. Maximizing ∆ is equiv-

alent to max

x∈F

f (x) − λ

g(x) = ∆

∗

. Therefore the

line f (x) = λ

g(x) + ∆

∗

lies above all feasible solu-

tions and is tangent to the concave envelope at break-

point x

, where x

= argmax

x∈F

f (x) − λ

g(x). x

a breakpoint with a left subgradient equal to λ

ℓ

and

right subgradient equal to λ

, such that λ

ℓ

≥ λ

≥

The complexity of the incremental parametric cut

procedure is that of a single min-cut HPF procedure

on the graph, T (n, m). More precisely, the complexity

is T (n, m) + O(qn) where q is the number of break-

points visited.

As noted in the introduction, this

number is very small in practice.

(Hochbaum, 2023) mistakenly stated that such a pro-

cedure visits adjacent breakpoints.

Flow Is Best, Fast and Scalable: The Incremental Parametric Cut for Maximum Density and Other Ratio Subgraph Problems

279

3 THE METHOD FOR

WEIGHTED MAX DENSITY

Let the weighted maximum density problem, WMD,

be given on a graph G = (V,E) with positive edge

weights u

i j

and node weights q

, max

S⊆V

C(S,S)

q(S)

. The

standard integer programming formulation of the

problem has binary variables for each node i ∈ V :

= 1 if node i is selected in S and 0 otherwise, and

binary variables for each edge [i, j] ∈ E, y

i j

= 1 if both

i and j are in S, and 0 otherwise. With this notation

the formulation of WMD is,

(WMD) max

∑

[i, j]∈E

i j

∑

j∈V

subject to x

≤ y

i j

for [i, j] ∈ E

≤ y

i j

for [i, j] ∈ E

binary j ∈ V

i j

binary [i, j] ∈ E

The graph corresponding to this IP2 formulation

has m + n nodes, one for each variable. We next

present a general procedure for generating an equiv-

alent compact (monotone) formulation for WMD and

other ratio problems. Let d

denote the weighted de-

gree of node i in G: d

∑

j|[i, j]∈E

i j

, and d(S) =

∑

i∈S

. It is easy to see that for any non-empty

subset of nodes S ⊂ V , we have the identity d(S) =

2C(S, S) + C(S,

S). Therefore, C(S, S) =

(d(S) −

C(S,

S)).

Hence, max

S⊆V

C(S,S)

q(S)

max

S⊆V

d(S)−C(S,

q(S)

which is formulated as monotone integer program

as well, with up to 3 variables per inequality using

the same x-variables as in WMD, and “cut” variables

i j

that are equal to 1 if i ∈ S and j ∈

S and zero

otherwise:

(WMD-compact) max

∑

j∈V

−

∑

[i, j]∈E

i j

∑

j∈V

subject to x

− x

≤ z

i j

for [i, j] ∈ E

− x

≤ z

for [i, j] ∈ E

binary j ∈ V

i j

binary [i, j] ∈ E.

The graph associated with the linearized problem,

λ-WMD-compact, has one node for each x

variable

and two arcs for each edge in E resulting in a compact

formulation on n + 2 nodes and 2m + 2n arcs.

Improved Formulation and Smaller Associated

Graph. For WMD as well as for any ratio prob-

lem that includes only C(S, S) along with linear terms,

there is an even more efﬁcient formulation that in-

cludes only one z

i j

variable for every pair that has

positive utility, instead of two. This results in a graph

with n +2 nodes and m + 2n arcs which is about half

of the number of arcs as compared to the formulation

above.

The key is to observe that the problem can be rep-

resented on a directed graph G = (V,A) where for

each pair i and j with positive utility and i < j there

is one arc (i, j) ∈ A from i to j.

max{w

,0} max{−w

,0}

max{w

,0} max{−w

,0}

max{w

,0}

max{−w

,0}

i j

max{w

,0}

max{−w

,0}

max{w

,0} max{−w

,0}

max{d

+ u

j j

− λq

,0} max{λq

− d

− u

j j

,0}

Figure 3: The ﬂow graph G

for λ-WMD-compact1.

Let d

be the weighted out-degree of node i in

G: d

∑

j|(i, j)∈A

i j

. Then, for any subset of nodes

S ⊂ V, d

(S) = C(S, S) +C(S,

S). Therefore (WMD-

compact1) is an IPM formulation of WMD:

(WMD-compact1) max

∑

j∈V

−

∑

(i, j)∈A

i j

∑

j∈V

subject to x

− x

≤ z

i j

for (i, j) ∈ A

binary ∀ j ∈ V

i j

binary ∀(i, j) ∈ A.

The objective function of the linearized ratio

problem for the λ-question of (WMD-compact1)

is, (λ-WMD) max

∑

j∈V

−

∑

(i, j)∈A

i j

−

∑

j∈V

. The associated graph for this λ-WMD

is given in Figure 3 which is obviously a parametric

ﬂow graph.

We conclude with an example of ﬁnding the

densest subgraph with IPC, reported in (Hochbaum

et al., 2024), in the dataset COM-YOUTUBE with n =

1134890 m = 2987624 from (Leskovec and Krevl,

2014). The running time of IPC for this dataset is

1.892 sec. The concave envelope of the breakpoints

is shown in Figure 4.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

280

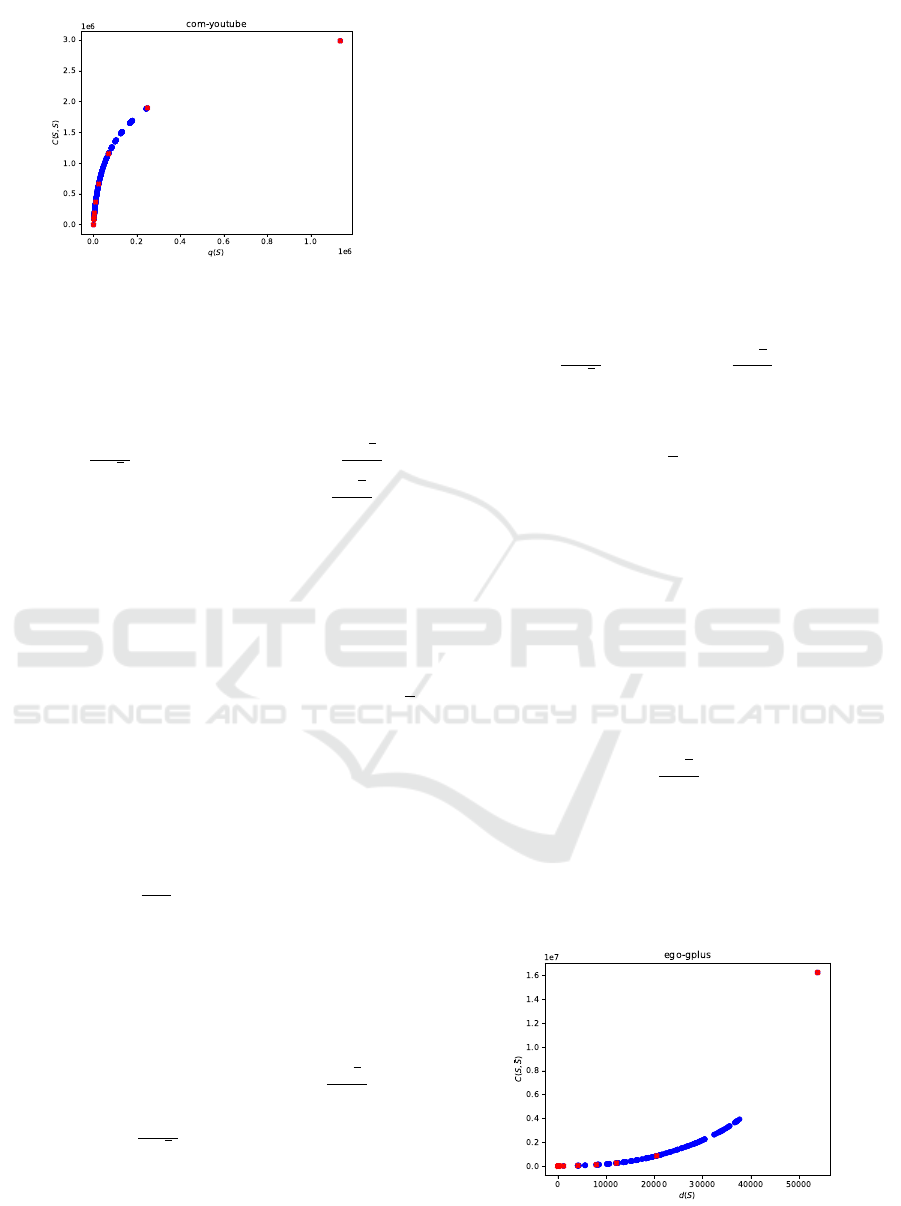
Figure 4: The concave envelope of all 1253 breakpoints, in

blue, versus 9 breakpoints explored by IPC, in red. (Cour-

tesy: A. Irribarra-Cort

es).

4 APPLICATIONS OF IPC

We consider here the three ratio problems: HNC

max

0⊂S⊂V

C(S,S)

, Cheeger’s* min

0⊂S⊂V

C(S,S)

d(S)

and

conductance*/HNC-extension min

0⊂S⊂V

C(S,S)

q(S)

We ﬁrst show, directly from the problem state-

ment, that HNC is an IPM ratio problem. Then pro-

vide a transformation showing that HNC is equivalent

to Cheeger*’s, and obviously conductance is a slight

generalization of both. We then give the formulation

for all three problems that leads to the parametric ﬂow

graph that is solved with IPC.

We ﬁrst comment on the use of the constraint

0 ⊂ S ⊂ V in ratio problems involving the cut C(S,S).

For such problems, unlike WMD, if unrestricted the

solution will be the entire graph with cut value 0. In

general that means that to solve such problems it is

necessary to use seeds which are subsets of nodes so

at least one belongs to the sink set and at least one

belongs to the source set. For these problems, when

they have size constraint, such as for Cheeger’s, of

the form d(S) ≤

d(V)

, the problems are NP-hard. To

address the issue of the seeds and to solve the size re-

stricted ratio problems heuristically one can choose to

ﬁrst identify a subset of the graph where the optimal

subgraph may reside. This was done for example us-

ing the Metis graph partitioning heuristic of (Karypis

and Kumar, 1998) by (Lang and Rao, 2004). Once

the subgraph satisfying the size restriction is found,

say V

′

, the problem becomes min

0⊂S⊂V

′

C(S,S)

d(S)

Consider the integer programming formulation of

HNC max

0⊂S⊂V

C(S,S)

with edge weights w

i j

and bi-

nary variables x

, y

i j

and z

i j

. Let x

= 1 if i ∈ S, y

i j

= 1

if both i and j in S and z

i j

= 1 if i ∈ S j ∈

S. The fol-

lowing is the linearized formulation λ-HNC:

(λ-HNC) max

∑

[i, j]∈E

i j

− λ

∑

j∈V

i j

subject to x

≤ y

i j

for [i, j] ∈ E

≤ y

i j

for [i, j] ∈ E

− x

≤ z

i j

for [i, j] ∈ E

− x

≤ z

for [i, j] ∈ E

binary j ∈ V

i j

binary [i, j] ∈ E

This monotone integer program maps into an as-

sociated graph on m + n + 2 nodes and 2m + 2n

arcs. A compact formulation of HNC, equivalent to

Cheeger’s*, is given in the next lemma (proof omitted

for lack of space):

Lemma 3. The following two problems are

equivalent and have the same optimal solutions:

max

0⊂S⊂V

C(S,S)

, and min

0⊂S⊂V

C(S,S)

d(S)

Therefore solving HNC-extension, or conduc-

tance*, provides solutions to all three problems since

setting q

= d

is HNC or Cheeger’s* problem. The

problem min

0⊂S⊂V

C(S, S) − λq(S) is formulated as

follows.

(λ-HNC-extension)min

∑

[i, j]∈E

i j

− λ

∑

j∈V

subject to x

− x

≤ z

i j

for [i, j] ∈ E

− x

≤ z

for [i, j] ∈ E

binary j ∈ V

i j

binary [i, j] ∈ E.

The graph associated with this monotone integer

program has n + 2 nodes and 2m + 2n arcs which im-

proves on the number of nodes m + n + 2 in the λ-

HNC formulation.

To conclude we provide an example of solving

Cheeger’s* on a subgraph V

′

delivered by the Metis

procedure, min

0⊂S⊂V

′

C(S,S)

d(S)

applied to the dataset

EGO-GPLUS of size n = 107614 m = 12238285, from

(Leskovec and Krevl, 2014) (reported in (Hochbaum

et al., 2024)). The convex envelope shown in Fig-

ure 5 illustrates the difference between the set of all

breakpoints, generated with the fully parametric cut

procedure, versus the set of points explored by IPC.

Figure 5: The convex envelope of all 291 breakpoints, in

blue, versus 11 breakpoints explored by IPC, in red. (Cour-

tesy: A. Irribarra-Cort

es).

Flow Is Best, Fast and Scalable: The Incremental Parametric Cut for Maximum Density and Other Ratio Subgraph Problems

281

ACKNOWLEDGEMENTS

This research was supported in part by the AI4OPT

institute NSF award 2112533.

REFERENCES

Angel, A., Koudas, N., Sarkas, N., Srivastava, D., Svend-

sen, M., and Tirthapura, S. (2014). Dense subgraph

maintenance under streaming edge weight updates for

real-time story identiﬁcation. The VLDB journal,

23:175–199.

Boob, D., Gao, Y., Peng, R., Sawlani, S., Tsourakakis, C.,

Wang, D., and Wang, J. (2020). Flowless: Extract-

ing densest subgraphs without ﬂow computations. In

Proceedings of The Web Conference 2020, pages 573–

583.

Charikar, M. (2000). Greedy approximation algorithms for

ﬁnding dense components in a graph. In International

workshop on approximation algorithms for combina-

torial optimization, pages 84–95. Springer.

Fortunato, S. (2010). Community detection in graphs.

Physics reports, 486(3-5):75–174.

Fratkin, E., Naughton, B. T., Brutlag, D. L., and Bat-

zoglou, S. (2006). Motifcut: regulatory motifs ﬁnd-

ing with maximum density subgraphs. Bioinformat-

ics, 22(14):e150–e157.

Gallo, G., Grigoriadis, M. D., and Tarjan, R. E. (1989). A

fast parametric maximum ﬂow algorithm and applica-

tions. SIAM Journal on Computing, 18(1):30–55.

Goldberg, A. V. (1984). Finding a maximum density sub-

graph. UC Berkeley manuscript.

Goldberg, A. V. and Tarjan, R. E. (1988). A new approach

to the maximum-ﬂow problem. Journal of the ACM

(JACM), 35(4):921–940.

Harb, E., Quanrud, K., and Chekuri, C. (2022). Faster and

scalable algorithms for densest subgraph and decom-

position. Advances in Neural Information Processing

Systems, 35:26966–26979.

Hochbaum, D. S. (1998). The pseudoﬂow algorithm and

the pseudoﬂow-based simplex for the maximum ﬂow

problem. In Integer Programming and Combinato-

rial Optimization: 6th International IPCO Confer-

ence Houston, Texas, June 22–24, 1998 Proceedings

6, pages 325–337. Springer.

Hochbaum, D. S. (2002). Solving integer programs

over monotone inequalities in three variables: A

framework for half integrality and good approxima-

tions. European Journal of Operational Research,

140(2):291–321.

Hochbaum, D. S. (2008). The pseudoﬂow algorithm: A new

algorithm for the maximum-ﬂow problem. Operations

research, 56(4):992–1009.

Hochbaum, D. S. (2009). Dynamic evolution of economi-

cally preferred facilities. European Journal of Opera-

tional Research, 193(3):649–659.

Hochbaum, D. S. (2010). Polynomial time algorithms for

ratio regions and a variant of normalized cut. IEEE

transactions on pattern analysis and machine intelli-

gence, 32(5):889–898.

Hochbaum, D. S. (2020a). Hpf - hochbaum’s

pseudoﬂow. Accessed: May 28, 2022,

https://riot.ieor.berkeley.edu/Applications/full-

para-HPF/pseudoﬂow-parametric-cut.html.

Hochbaum, D. S. (2020b). Pseudoﬂow (simple) parametric

maximum ﬂow solver version 1.0. Accessed: May 28,

2022, https://riot.ieor.berkeley.edu/Applications/

Pseudoﬂow/parametric.html.

Hochbaum, D. S. (2023). Uniﬁed new techniques for np-

hard budgeted problems with applications in team col-

laboration, pattern recognition, document summariza-

tion, community detection and imaging. Proceedings

of the 15th International Joint Conference on Knowl-

edge Discovery, Knowledge Engineering and Knowl-

edge Management, 1:365–372.

Hochbaum, D. S., Irribarra-Cort

es, A., and As

ın-Ach

a, R.

(2024). Fast and optimal incremental parametric pro-

cedure for the densest subgraph problem: An experi-

mental study. UC Berkeley manuscript.

Karypis, G. and Kumar, V. (1998). A fast and high qual-

ity multilevel scheme for partitioning irregular graphs.

SIAM Journal on Scientiﬁc Computing, 20(1):359–

392.

Kumar, R., Raghavan, P., Rajagopalan, S., and Tomkins,

A. (1999). Trawling the web for emerging cyber-

communities. Computer networks, 31(11-16):1481–

1493.

Lang, K. and Rao, S. (2004). A ﬂow-based method for

improving the expansion or conductance of graph

cuts. In Integer Programming and Combinatorial

Optimization: 10th International IPCO Conference,

New York, NY, USA, June 7-11, 2004. Proceedings 10,

pages 325–337. Springer.

Leskovec, J. and Krevl, A. (2014). SNAP Datasets: Stan-

ford large network dataset collection. http://snap.

stanford.edu/data.

Picard, J.-C. and Queyranne, M. (1982). A network ﬂow

solution to some nonlinear 0-1 programming prob-

lems, with applications to graph theory. Networks,

12(2):141–159.

Sharon, E., Galun, M., Sharon, D., Basri, R., and Brandt, A.

(2006). Hierarchy and adaptivity in segmenting visual

scenes. Nature, 442(7104):810–813.

Shi, J. and Malik, J. (2000). Normalized cuts and image

segmentation. IEEE Transactions on pattern analysis

and machine intelligence, 22(8):888–905.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

282