Control of Biohybrid Actuators Using Neuroevolution

Hugo Alcaraz-Herrera

1 a

, Michail-Antisthenis Tsompanas

1 b

, Igor Balaz

2 c

and Andrew Adamatzky

1 d

Unconventional Computing Laboratory, University of the West of England, Bristol, BS16 1QY, U.K.

Laboratory for Meteorology, Physics and Biophysics, Faculty of Agriculture, University of Novi Sad,

Trg Dositeja Obradovica 8, Novi Sad, 21000, Serbia

Keywords:

Neuroevolution, NEAT, HyperNEAT, Genetic Algorithm, Biohybrid Actuator.

Abstract:

In medical-related tasks, soft robots can perform better than conventional robots because of their compliant

building materials and the movements they are able perform. However, designing soft robot controllers is not

an easy task, due to the non-linear properties of their materials. A formal design process is needed since human

expertise to design such controllers is not sufﬁciently effective. The present research proposes neuroevolution-

based algorithms as the core mechanism to automatically generate controllers for biohybrid actuators that

can be used on future medical devices, such as a catheter that will deliver drugs. The controllers generated

by methodologies based on Neuroevolution of Augmenting Topologies (NEAT) and Hypercube-based NEAT

(HyperNEAT) are compared against the ones generated by a standard genetic algorithm (SGA). In speciﬁc, the

metrics considered are the maximum displacement in upward bending movement and the robustness to control

different biohybrid actuator morphologies without redesigning the control strategy. Results indicate that the

neuroevolution-based algorithms produce better-suited controllers than the SGA. In particular, NEAT designed

the best controllers, achieving up to 25% higher displacement when compared with SGA-produced specialised

controllers trained over a single morphology and 23% when compared with general-purpose controllers trained

over a set of morphologies.

1 INTRODUCTION

Soft robotics is a sub-ﬁeld of robotics that studies ma-

chines built with ﬂexible and ductile materials, such

as silicone rubbers (Rus and Tolley, 2015). This

type of robots have demonstrated better performance

in speciﬁc tasks related to healthcare (Hsiao et al.,

2019), due to their morphology and behaviour that are

heavily inspired by living organisms.

Despite their promising applicability, soft robots

face signiﬁcant challenges, i.e., deﬁning an adequate

morphology design. Under a traditional approach of

robot designing, considerable time and material re-

sources are utilised since numerous alternative proto-

types are tested physically (Schulz et al., 2016). On

the other hand, under a soft robots approach, design-

ing process is more complex due to the materials’

ﬂexibility and mechanical properties being non-linear

https://orcid.org/0000-0002-9991-662X

https://orcid.org/0000-0002-6607-7831

https://orcid.org/0000-0002-6831-9232

https://orcid.org/0000-0003-1073-2662

and difﬁcult to characterise (Hiller and Lipson, 2014).

When a suitable design is found, the next step con-

sists of designing an appropriate controller for the soft

robot, a process that can be considered as intricate as

ﬁnding a suitable morphology. The required strate-

gies to control soft robots have two main considera-

tions: (i) the soft materials constituting the robot can

deform at every point, resulting in inﬁnite degrees of

freedom, including bending, extension, contraction,

and torsion, and (ii) soft materials present non-linear

and time-dependent properties. These aspects make

modeling soft robot behaviour and movement a difﬁ-

cult task (Wang and Chortos, 2022).

A methodology that can assist the design of con-

trollers for soft robots which is worth investigat-

ing is Neuroevolution (NE). NE focuses on evolv-

ing the topology and weights of artiﬁcial neural net-

works (ANNs) employing a genetic algorithm (GA)

methodology. Arguably, the most efﬁcient NE al-

gorithm has proved to be Neuroevolution of Aug-

menting Topologies (NEAT) (Stanley and Miikku-

lainen, 2002). Furthermore, under the rationale that

Alcaraz-Herrera, H., Tsompanas, M., Balaz, I. and Adamatzky, A.

Control of Biohybrid Actuators Using Neuroevolution.

DOI: 10.5220/0012919300003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 197-204

ISBN: 978-989-758-721-4; ISSN: 2184-3236

197

natural structures are composed of shape repetition

and patters, an extension of NEAT was developed,

namely Hypercube-based Neuroevolution of Aug-

menting Topologies (HyperNEAT) (Stanley et al.,

2009). HyperNEAT evolves a singular type of ANNs

named Compositional Pattern-Producing Networks

(CPPNs), whose difference to traditional ANNs fo-

cuses around the use of periodic functions (e.g., sine

and square wave), in order to generate patterns, like

symmetry and repetition that help evolve more inter-

esting topologies (Stanley, 2007a).

The fundamental objective of the presented re-

search is assessing the suitability of NEAT and Hyper-

NEAT as design engines for controllers of biohybrid

actuators (BHAs), a particular type of soft robots’

components that are built utilising biological mate-

rial, such as tissues or cells. Speciﬁcally, we anal-

yse the capabilities of the NEAT and HyperNEAT to

design controllers whose objective is to induce an up-

ward bending movement to a given BHA. That BHA

may be embodied into a catheter for targeted drug de-

livery to areas of the human body that are difﬁcult to

reach.

2 BACKGROUND

NEAT has been previously used as a controller design

engine in robotic applications. For instance, NEAT

is implemented to design controllers for a robot in a

crowded environment (Seriani et al., 2021). A ray-

casting model can be implemented in industrial robots

with relative acts as the robot’s perception, which can

perceive objects at the current time and has a memory

of previously perceived objects. Controllers are ﬁrst

assessed in simulated environments and subsequently

in a minimal physical implementation. Results advo-

cate that controllers generated by NEAT converge to

a suitable design in both environments.

In another exemplar research, NEAT is applied

to design locomotive controllers (Tibermacine and

Djedi, 2014). The scope of the study focuses on vir-

tual creatures that are simulated in a physics engine

called Open, Dynamic Engine (ODE). The controllers

generated by NEAT are compared against controllers

evolved in a more standard approach and results indi-

cate that controllers designed by NEAT exhibit better

performance since they consider the locomotive fea-

tures of morphologies and tend to be more robust than

those generated by the traditional approach.

Finally, NEAT has also been utilised to de-

sign controllers for autonomous vehicles. For in-

stance, a reactive navigation hybrid controller for

non-holonomic mobile robots was studied (Caceres

et al., 2017). Experiments were conducted in a sim-

ulation platform developed by the authors and are

based on the kinematic model of a car-like robot. Re-

sults suggest that controllers designed by NEAT ex-

hibited the expected performance of controlling the

kinematics of car-like robots in an unknown envi-

ronment, avoiding obstacles and reaching the target

point.

Moreover, HyperNEAT has also been utilised to

design robot controllers, as well as their shapes.

For instance, a method that aims to ﬁnd suitable

morphologies and controllers has been introduced

(Tanaka and Aranha, 2022). The method was tested

in four scenarios considering the adaptation level ob-

served in the robots used for experimentation. The

results suggested that the approaches can generate

morphologies and that their controllers are capable of

suitably performing on the given tasks.

Furthermore, HyperNEAT has been used to de-

sign locomotion controllers utilised by autonomous

crawler robots with ﬂippers (Sokolov et al., 2017). In

order to evaluate their performance, controllers were

tested in the ROS/Gazebo simulator. The inputs of

CPPNs were Light Detection and Ranging (LIDAR)

data, the robot’s position, orientation, ﬂipper angle,

and track velocities. The outputs were commands to

control the ﬂipper angles and track velocities. The

results indicated that HyperNEAT-based controllers

help crawler robots navigate and overcome obstacles

in three-dimensional environments.

Finally, an implementation of HyperNEAT to de-

sign controllers for quadruped robots has been pro-

posed (Risi and Stanley, 2013). The model had the

morphologies of robots as input. Moreover, the out-

put was neural-network-based controllers capable of

working with different robot morphologies. The per-

formance of controllers was assessed utilising three

morphologies, and they were compared against static

controllers. Results suggested that HyperNEAT iden-

tiﬁed the relationship between morphologies and con-

troller architectures, which help to generate suitable

performance.

Inspired by the aforementioned works of employ-

ing NE for controlling different types of robots (i.e.,

crawlers, runners and even car-like) to achieve higher

displacement, the same methodology is tested here

on robots limited to angular-only movement. To the

best of the authors’ knowledge, this aspect has not

been tested before, and insights gained by this re-

search will assist the design methodology of robotic

controllers for tasks requiring precision movements,

such as medical applications.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

198

3 NEUROEVOLUTION

Two of the most popular NE-based approaches are

utilised in this research. Namely, NEAT (Stanley and

Miikkulainen, 2002), and an extension of NEAT: Hy-

perNEAT (Stanley et al., 2009).

3.1 NEAT

A well-established method to train ANNs is back-

propagation of errors, whereas an alternative method

is utilising evolutionary optimisation methods. The

ﬁtness functions of such methods can be the minimi-

sation of the output errors of ANNs. Namely, NE

iteratively applies selection, crossover and mutation

operators on a population of randomly initialised net-

works to discover the best performing one, after a

given amount of generations. NEAT algorithm was

conceived to alleviate three main “pathologies” ob-

served in previous NE algorithms (Stanley and Mi-

ikkulainen, 2002). Namely, (i) the lack of appro-

priate solution representations that would allow the

recombination of arbitrary network topologies; (ii)

preventing the premature disappearance of novel net-

work topologies discovered during evolution; and (iii)

avoiding the use of ﬁtness functions to punish com-

plex topologies of individuals.

3.2 HyperNEAT

A well-established extension of NEAT is Hyper-

NEAT. This approach employs NEAT to evolve the

topology of a particular type of neural network known

by the term Compositional Pattern-Producing Net-

work (CPPN) (Stanley, 2007b). HyperNEAT evolves

CPPNs and takes advantage of their properties to re-

produce natural patterns observed in nature, such as

symmetry and repetition (Stanley et al., 2009). Two

critical differences exist between NEAT and Hyper-

NEAT: (i) Activation functions and (ii) Substrate.

Commonly, NEAT generates ANNs containing

hidden nodes that uniformly adapt the sigmoid as

their activation function. On the other hand, Hy-

perNEAT can use diverse activation functions in the

nodes within CPPNs. Examples of the possible ac-

tivation functions are trigonometric, periodic, and

Gaussian. Using different activation functions during

evolution allows for exploring a signiﬁcantly more ex-

tensive search space of network topologies.

Due to the pattern reproduction capacity of

CPPNs, HyperNEAT can embody the geometry

within the domain of the problem. Consequently,

those geometrical aspects are considered to determine

the topology of ANNs. The geometric layout where

these ANNs are deﬁned and where HyperNEAT oper-

ates is called substrate.

4 EXPERIMENTAL SETUP

The main objective of this research is to study the suit-

ability of NEAT and HyperNEAT in designing con-

trollers for BHAs. The capacity to induce an upward

bending movement in BHAs is evaluated as the pri-

mary suitability measure of each controller.

4.1 Voxelyze

BHAs are simulated in a physics engine called Voxe-

lyze, which simulates the physical response of BHAs

under speciﬁc conditions, such as gravity and ambient

viscosity (Hiller and Lipson, 2014). The source code

of Voxelyze is freely available and utilised in several

optimisation studies (Kriegman et al., 2020; Tsom-

panas and Balaz, 2024).

In order to evaluate the controllers designed by the

proposed methodologies, for the application of mov-

ing a catheter, one end of the BHA is considered ﬁxed

in place, whereas the other is free to move under the

dictated expansion of the active material in its mor-

phology. Thus, to trace the position of the free end of

BHAs in the x, y, z axes during time t, Voxelyze has

been modiﬁed to represent BHAs with only one de-

gree of freedom in the yz plane (i.e., they only move

vertically). Furthermore, based on the ﬁndings of

previous research (Tsompanas and Balaz, 2024) and

laboratory constraints, BHAs are considered within a

passive enclosure.

The output of Voxelyze (i.e. the position of the

BHA’s free tip) is used to evaluate the performance of

CPPNs. Based on previous research (Alcaraz-Herrera

et al., 2024b), the dimensions of BHA, in terms of

voxels, are twenty units in the x axis and eight units

in the y and z axes. Figure 1 presents an example of

a BHA being simulated by the modiﬁed version of

Voxelyze.

4.2 Conﬁguration Scheme

For NEAT and HyperNEAT, the population is com-

posed of 50 individuals (i.e., ANNs and CPPNs repre-

senting controllers) and each evolutionary trial lasted

200 generations. Moreover, the activation functions

utilised for experimentation are: sine, negative sine,

absolute value, negative absolute value, square, nega-

tive square, squared absolute value, negative squared

absolute value, sigmoid, clamped, cubical, exponen-

tial, Gaussian, hat, identity, inverse, logarithmic,

Control of Biohybrid Actuators Using Neuroevolution

199

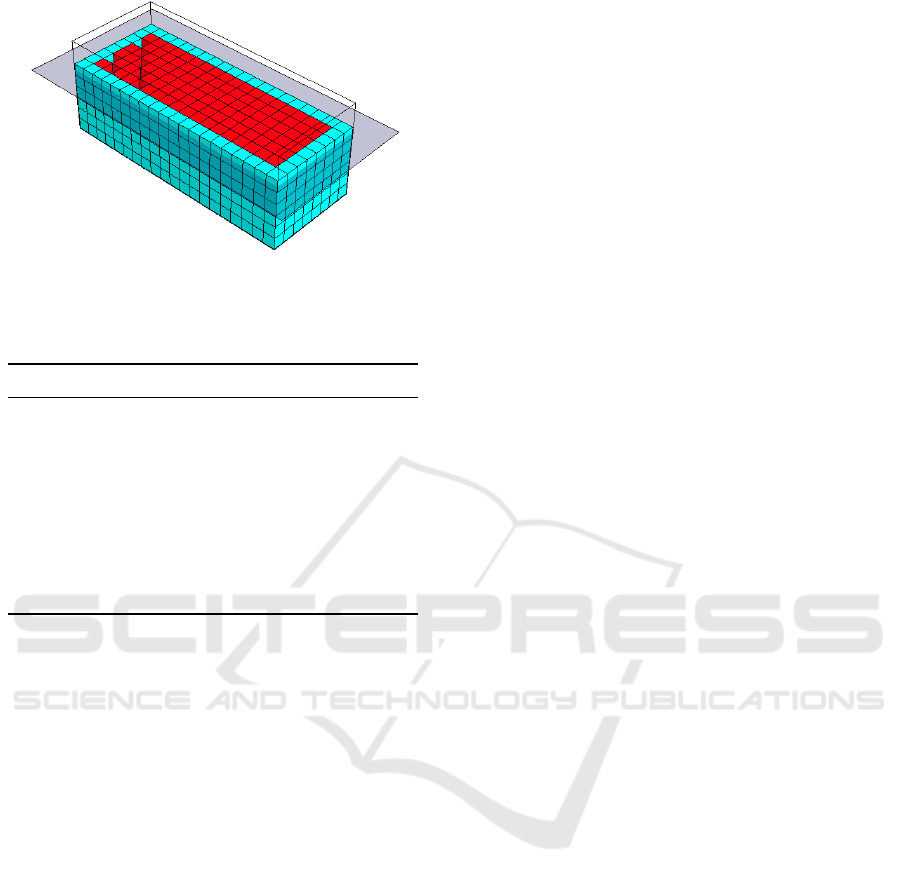
Figure 1: Example of an BHA simulated by Voxelyze.

Table 1: Parameters utilised to evolve CPPNs under NEAT

and HyperNEAT.

Parameter Value

compatibility threshold 3

compatibility disjoint coefﬁcient 1.0

compatibility weight coefﬁcient 0.5

maximum stagnation 25

survival threshold 0.2

activation function mutate rate 0.4

adding/deleting connection rate 0.2/0.1

activating/deactivating connection rate 0.5

adding/deleting node rate 0.2/0.1

ReLU, SeLU, LeLU, eLU, softplus, hyperbolic tan-

gent. The speciﬁc parameters employed for the evo-

lutionary process of CPPNs are presented in Table 1.

Furthermore, individuals are initialised with the

minimal topology possible: no hidden neurons and

input neurons fully connected to output neurons (sim-

ilar to (Tsompanas, 2024)).

4.2.1 NEAT Conﬁguration

Due to BHAs being designed in a discrete three-

dimensional layout with two types of voxels repre-

senting different materials, the input of controllers

considers: (i) the coordinates for each point across

the layout and (ii) the type of material. By the term

voxel, the basic building block in Voxelyze is deﬁned.

Each voxel can be either active (blue color in Fig. 1)

or contractile (red color). Furthermore, the output of

controllers is the phase offset of each voxel across

the layout, dictating the delay in the expansion be-

haviour of active voxels. Thus, under NEAT, CPPNs

are queried as follows:

CPPN(x

, y

, z

, m

) = pho

(1)

where the (x

, y

, z

) tuple represents the coordinates

of the i-th point in the three-dimensional layout and

represents the material of the appropriate voxel lo-

cated in the aforementioned point, which is encoded

as follows: 0, absence of a voxel; 1 passive voxel; 3

contractile voxel. Regarding pho

, it represents the

phase offset of the i-th point of the layout. In or-

der to provide a complete sinusoidal-based contrac-

tion movement, the output of CPPNs (i.e., controllers)

is clamped in the [−2π, 2π] range.

4.2.2 HyperNEAT Conﬁguration

Under HyperNEAT, the ﬁrst deﬁning aspect is the

substrate (i.e., an ANN), which has four input neu-

rons due to the discrete three-dimensional layout

where BHAs are designed and the type of each voxel.

Furthermore, one output neuron is needed to pro-

vide the phase offset of each voxel across the three-

dimensional layout. Equation 2 describes how sub-

strates are queried:

substrate(x

, y

, z

, m

) = pho

(2)

where the (x

, y

, z

) tuple is the coordinates of the i-

th point in the three-dimensional layout. Moreover,

the m

variable is related to the voxel type, encoded as

before. The pho

variable is deﬁned as in the above.

The next step consists of allocating the neurons

composing the substrate. A series of experiments

where the number of hidden layers and the number

of neurons per hidden layer is varied in the range

[3, 10] were conducted to ﬁnd the optimal allocation.

Figure 2 depicts the design of the two-dimensional

substrate employed throughout the experiments de-

scribed in this research. Furthermore, the activation

function implemented for the neurons composing the

substrate is ReLU, since it induces a linear (or close to

linear) behaviour and exhibits representational spar-

sity properties (Glorot et al., 2011).

Due to the evaluation of individuals implying

a simulation procedure, the amount of computation

time is signiﬁcant. Thus, a client-server implemen-

tation was used to take advantage of the distributed

computing capacities of this software architecture

(Alcaraz-Herrera et al., 2024a).

5 NEAT VS HyperNEAT

Three metrics are utilised to assess the suitability

of NEAT and HyperNEAT to design controllers for

BHAs: (i) studying the general performance of con-

trollers in terms of inducing an angular movement on

the yz plane to the BHA during a predeﬁned simulated

time period; (ii) testing the robustness of controllers;

and (iii) analysing the complexity of controllers. Note

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

200

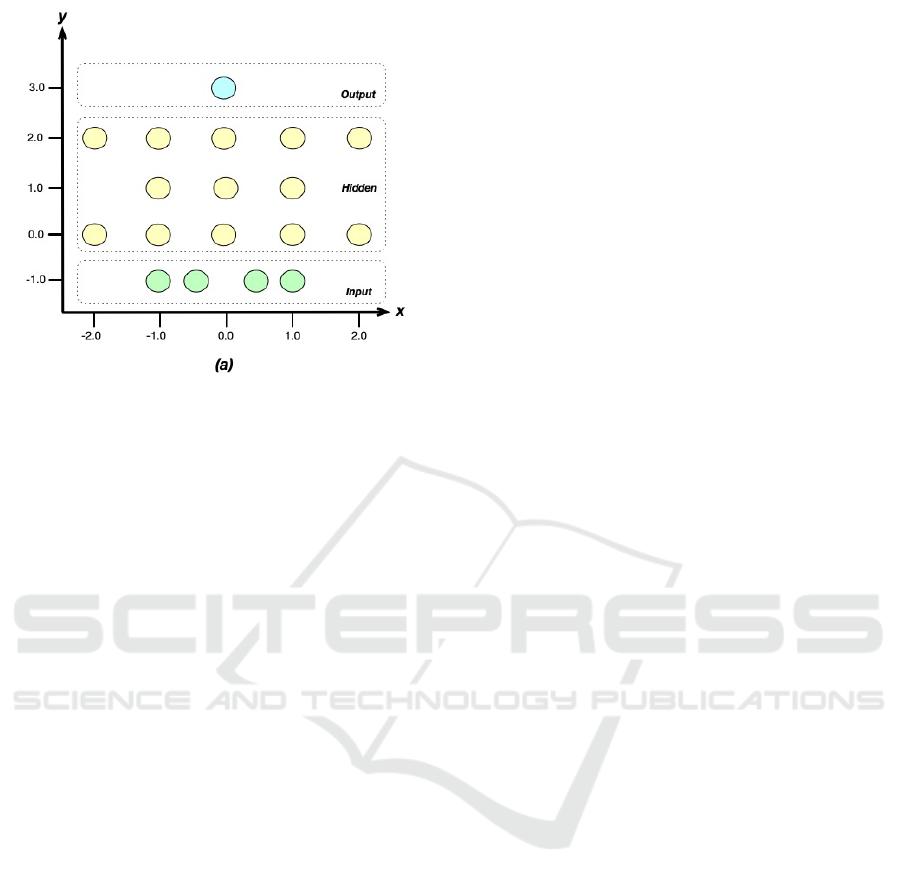
Figure 2: Substrate utilised under HyperNEAT to design

BHA controllers.

here that the displacement of BHAs is measured in

terms of the length of one voxel.

Moreover, a standard genetic algorithm (SGA)

is utilised as a baseline controller design engine.

In order to facilitate the implementation of the el-

ements composing the SGA (i.e., individuals, ﬁt-

ness function, and genetic operators), an object-

oriented framework was employed (Alcaraz-Herrera

and Cartlidge, 2022). Individuals are represented by a

bi-dimensional array (i.e., a matrix) of real numbers in

the [−2π, 2π] range. Regarding the genetic operators,

the crossover implementation is two-point variation

with probability of 0.9. Regarding mutation, one el-

ement of the matrix is randomly chosen and replaced

by a random number within the [−2π, 2π] range. This

takes place with a probability of 0.1.

5.1 General Performance

In this research, the BHAs need to bend in a deter-

mined direction. The case study presented in this re-

search considers upward bending movement as the

target for BHAs controllers. These bending move-

ment is measured utilising the displacement observed

in the yz plane.

Here the general performance of SGA, NEAT,

and HyperNEAT in designing controllers capable of

inducing upward bending movements to BHAs was

analysed. The top three BHA morphologies discov-

ered in previous works (Alcaraz-Herrera et al., 2024b)

are used for experimentation. Figure 3 presents the

mean performance of the ﬁttest controller with 95%

conﬁdence interval depicted by the shaded regions

across 20 evolutionary trials under SGA, NEAT, and

HyperNEAT using three different morphologies: (i)

BHA 1 (Fig. 3-a); (ii) BHA 2 (Fig. 3-b); and (iii) BHA

3 (Fig. 3-c).

NEAT and HyperNEAT signiﬁcantly outperform

SGA regardless of the BHA morphology utilised. The

data collected were tested and proved not to be nor-

mally distributed (Shapiro–Wilk test; p < 0.01). Us-

ing the Wilcoxon test, it is feasible to conﬁrm that sig-

niﬁcant differences in the performance between NE-

based approaches and SGA exist (paired Wilcoxon-

test; p < 0.01). Furthermore, NE-based approaches

found the ﬁttest controller at the early stages of evo-

lution (i.e., at the ﬁrst generations of the evolutionary

process), whereas SGA tends to gradually evolve at

a lower pace. In addition, although the difference in

performance between NEAT and HyperNEAT is not

clearly visible in all BHAs used, NEAT signiﬁcantly

outperforms HyperNEAT (Shapiro–Wilk test, paired

Wilcoxon-test; p < 0.01).

Furthermore, the Kruskal-Wallis test is used to

conﬁrm signiﬁcant differences among the perfor-

mance of all approaches regardless of the BHA (p <

0.01). Consequently, is it possible to rank the perfor-

mance of the three approaches: NEAT > HyperNEAT

> SGA (Dunn’s test; p < 0.01).

Results suggest that NE-based approaches can de-

sign ﬁtter controllers than those designed by SGA

since more elements of the domain problem are con-

sidered, namely, the morphology and material of

BHAs during evolution. Another relevant aspect that

arguably enhances the performance of NEAT and Hy-

perNEAT is the set of properties of CPPNs that help to

design controllers that induce upward bending move-

ments that follow a pattern considering the morphol-

ogy of the BHA.

5.2 Robustness

A controller can perform adequately inducing upward

bending of speciﬁc BHA morphologies. However,

performance may be different if the BHA morphology

changes. This experiment aims to test the robustness

of controllers under a more diverse set of morpholo-

gies (i.e., how suitable the controller’s capacity is to

induce upward bending movements regardless of the

BHA morphology) designed by SGA, NEAT, and Hy-

perNEAT. For each approach, 20 evolutionary trials

were performed.

Controllers are evaluated using the top nine BHAs

discovered in (Alcaraz-Herrera et al., 2024b). There-

fore, nine simulations are run utilising Voxelyze, each

with a different BHA and its phase offsets generated

by the controller. Thus, controllers’ robustness (i.e.,

aptitude) is calculated considering the displacement

observed in the yz plane of each simulation. Equa-

Control of Biohybrid Actuators Using Neuroevolution

201

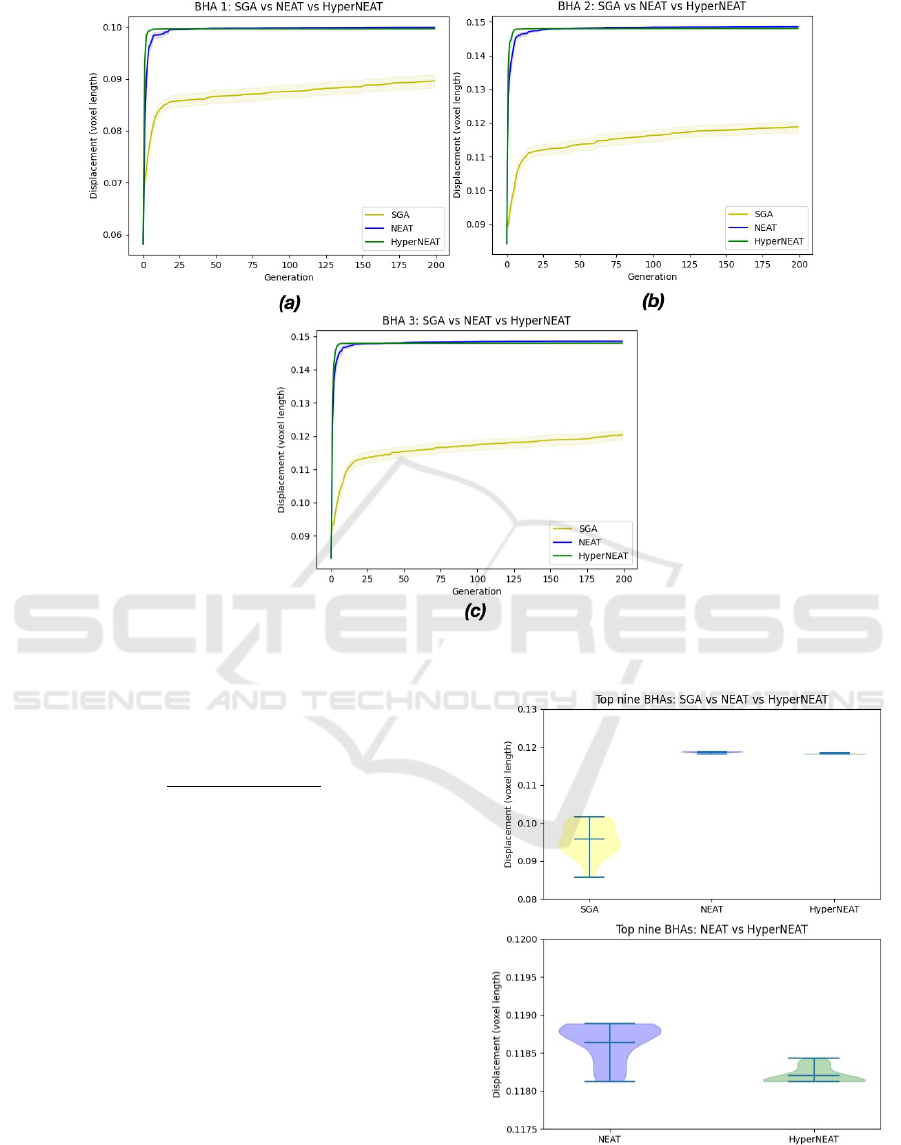
Figure 3: Mean general performance with ±95 conﬁdence interval (shaded region) under SGA, NEAT, and HyperNEAT

using: (a) BHA 1; (b) BHA 2; and (c) BHA 3.

tion 3 deﬁnes how the aptitude of the controller c is

computed:

apt

∑

i=1

displacement

(3)

Figure 4 depicts violin plots comparing the dis-

placement induced by the ﬁttest controller found

by SGA, NEAT and HyperNEAT. Each violin plot

presents median, maximum, minimum and kernel

density estimation of the frequency distribution of

values utilising nine different BHAs.

The displacement induced by all the controllers

exhibit signiﬁcant differences. First, all the data

gathered are not normally distributed (Shapiro-Wilk

test; p < 0.01). Then, through the Kruskal-Wallis

test, it is feasible to conﬁrm signiﬁcant differences

among the displacement induced by the controllers

(p < 0.01). Consequently, a performance ranking can

be deﬁned: NEAT > HyperNEAT > SGA (Dunn’s

test; p < 0.01).

Results indicate that despite the number of BHAs

involved during the evolutionary process, NE-based

approaches are more suitable for designing con-

trollers capable of inducing higher upward bending

Figure 4: Displacement observed in the yz plane of the top

nine BHAs induced by: top - SGA (left), NEAT (centre),

and HyperNEAT (right); bottom (close up) - NEAT (left),

and HyperNEAT (right).

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

202

Table 2: Mean displacement (in voxel lengths) achieved by

the ﬁttest controller designed by SGA, NEAT and Hyper-

NEAT for one morphology and for a set of 9 morphologies.

Scenario SGA NEAT HyperNEAT

BHA 1 0.0896 0.0999 0.0996

BHA 2 0.1188 0.1485 0.1480

BHA 3 0.1202 0.1485 0.1479

Set of 9 0.0957 0.1186 0.1182

Table 3: Mean number of hidden nodes and connections of

the ﬁttest controller designed by NEAT and HyperNEAT.

Approach Hidden Nodes Connections

NEAT 2 3

HyperNEAT 13 36

movements than the standard evolutionary approach.

Again, NEAT and HyperNEAT are more suitable

due to their capacity to consider the morphology and

material of BHAs when designing controllers. Fur-

thermore, CPPNs, the core of both techniques, allow

the production of patterns that have a signiﬁcant con-

tribution to the emergence of more efﬁcient move-

ment. Consequently, the upward bending movements

induced by NEAT and HyperNEAT controllers follow

a pattern based on the morphology of each BHA.

To better compare the results of the two previous

sections, Table 2 is provided.

5.3 Controller Complexity

Since the BHAs utilised for experimentation, rep-

resent soft robotics components that can be imple-

mented in real life (Alcaraz-Herrera et al., 2024b), the

controllers discovered in this study should be feasible

to be built. Thus, the less complex (i.e., fewer nodes

and connections) a network controller is, the simpler

and more efﬁcient the controller device is.

A crucial aspect to consider for this experiment

is that under NEAT, controllers are represented by

CPPNs. In contrast, under HyperNEAT, substrates

(i.e. ANNs) represent the controllers. Furthermore,

SGA is not considered for this experiment due to

the poor performance exhibited previously. Table 3

shows the mean number of hidden nodes and connec-

tions composing the ﬁttest controller across 20 evolu-

tionary trials under NEAT and HyperNEAT.

In general, HyperNEAT produces signiﬁcantly

more complex controllers than NEAT due to the ﬁxed

number of hidden neurons of the substrate where Hy-

perNEAT operates. This restricts the exploration of

the search space since it only ﬁnds the optimal num-

ber of connections, their weights, and the bias of neu-

rons. On the other hand, NEAT explores a broader

search space that includes the activation functions, the

number of neurons (and their bias), and the number of

connections (and their weights), arguably allowing it

to ﬁnd more efﬁcient network structures in terms of

complexity and performance. Due to the capacity of

NEAT to discover simpler controller networks it will

be preferred for implementing real-life controllers.

6 CONCLUSIONS

This work studies the capacity of NEAT and Hy-

perNEAT to produce suitable controllers for BHAs.

Their suitability is compared against a SGA. The per-

formance of the three approaches is analysed under

three metrics: (i) general performance (maximum up-

ward bending movement possible to three BHAs); (ii)

testing the robustness of controllers produced (maxi-

mum upward bending movement on nine BHAs); and

(iii) analysing their complexity. For all metrics, 20

evolutionary trials were conducted under the three ap-

proaches.

Results suggest that NEAT and HyperNEAT are

more suitable for designing controllers for BHAs than

SGA, not only for a single morphology but for numer-

ous alternative morphologies. In general, NE-based

approaches outperform SGA due to: (i) their abil-

ity to consider the morphology and the material of

BHAs when designing the controllers, (ii) their core

mechanisms are based on CPPNs, whose properties

help to produce control patterns that are signiﬁcant in

the emergence of efﬁcient movement (Cheney et al.,

2014).

Although the difference is minimal when the per-

formance of NEAT and HyperNEAT are compared,

NEAT demonstrates a more suitable performance.

Arguably, two factors affected the performance of

HyperNEAT: (a) the substrate design implemented for

experimentation, and (b) the absence of geometrical

aspects of the domain problem that could not be em-

bodied in the design of the substrate. Furthermore,

NEAT was able to design more compact and, hence,

more efﬁcient controllers than HyperNEAT, due to the

fact that the search space included the number of neu-

rons, their connections and their activation functions.

In contrast, the search space, where HyperNEAT op-

erated, is more restricted since it only included the

connections in a ﬁxed number of neurons with the

same activation function.

Future work directions considering the results

gathered from this research can explore the suitability

of the NE-based approaches in more realistic scenar-

ios where elements of the environment (e.g., viscos-

Control of Biohybrid Actuators Using Neuroevolution

203

ity and friction) are included during simulations. Fur-

thermore, adding periodic activation functions, such

as tangent and cosine, could induce other patterns

of more efﬁcient upward bending movements. An-

other avenue of future work may focus on improving

the performance of HyperNEAT with a broader ex-

ploration of hyper-parameters, such as the number of

neurons, hidden layers, and activation functions used

to design the substrate.

ACKNOWLEDGEMENTS

This project has received funding from the European

Union’s Horizon Europe research and innovation pro-

gramme under grant agreement No. 101070328.

UWE researchers were funded by the UK Research

and Innovation grant No. 10044516.

REFERENCES

Alcaraz-Herrera, H. and Cartlidge, J. (2022). Exploration of

ontological representations for evolutionary computa-

tion. In 2022 IEEE Congress on Evolutionary Com-

putation (CEC), pages 1–8.

Alcaraz-Herrera, H., Tsompanas, M.-A., Adamatzky, A.,

and Balaz, I. (2024a). Neuroevolution algorithms ap-

plied in the designing process of biohybrid actuators.

https://arxiv.org/abs/2408.07671.

Alcaraz-Herrera, H., Tsompanas, M.-A., Adamatzky,

A., and Balaz, I. (2024b). Using neuroevo-

lution for designing soft medical devices.

https://arxiv.org/abs/2408.09107.

Caceres, C., Rosario, J. M., and Amaya, D. (2017).

Approach of kinematic control for a nonholonomic

wheeled robot using artiﬁcial neural networks and ge-

netic algorithms. In 2017 International Conference

and Workshop on Bioinspired Intelligence (IWOBI),

pages 1–6.

Cheney, N., MacCurdy, R., Clune, J., and Lipson, H.

(2014). Unshackling evolution: evolving soft robots

with multiple materials and a powerful generative en-

coding. ACM SIGEVOlution, 7(1):11–23.

Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse

rectiﬁer neural networks. In Proceedings of the Four-

teenth International Conference on Artiﬁcial Intelli-

gence and Statistics, Proceedings of Machine Learn-

ing Research, pages 315–323.

Hiller, J. and Lipson, H. (2014). Dynamic simulation of soft

multimaterial 3d-printed objects. Soft robotics, 1(1).

Hsiao, J.-H., Chang, J.-Y., and Cheng, C.-M. (2019). Soft

medical robotics: clinical and biomedical applica-

tions, challenges, and future directions. Advanced

Robotics, 33(21):1099–1111.

Kriegman, S., Blackiston, D., Levin, M., and Bongard,

J. (2020). A scalable pipeline for designing recon-

ﬁgurable organisms. https://github.com/skriegman/

reconﬁgurable

organisms. Accessed: May 29, 2024.

Risi, S. and Stanley, K. O. (2013). Confronting the chal-

lenge of learning a ﬂexible neural controller for a

diversity of morphologies. In Proceedings of the

15th Annual Conference on Genetic and Evolutionary

Computation, GECCO ’13, page 255–262.

Rus, D. and Tolley, M. T. (2015). Design, fabrication and

control of soft robots. Nature, 521(7553):467–475.

Schulz, A., Sung, C., Spielberg, A., Zhao, W., Cheng, R.,

Grinspun, E., Rus, D., and Matusik, W. (2016). In-

teractive robogami: An end-to-end system for design

of robots with ground locomotion. The International

Journal of Robotics Research, 36(10):1131–1147.

Seriani, S., Marcini, L., Caruso, M., Gallina, P., and Med-

vet, E. (2021). Crowded environment navigation with

neat: Impact of perception resolution on controller op-

timization. Journal of Intelligent & Robotic Systems,

101(2).

Sokolov, M., Afanasyev, I., Klimchik, A., and Mavridis,

N. (2017). Hyperneat-based ﬂipper control for a

crawler robot motion in 3d simulation environment.

In 2017 IEEE International Conference on Robotics

and Biomimetics (ROBIO), pages 2652–2656.

Stanley, K. O. (2007a). Compositional pattern pro-

ducing networks: A novel abstraction of develop-

ment. Genetic Programming and Evolvable Ma-

chines, 8(2):131–162.

Stanley, K. O. (2007b). Compositional pattern pro-

ducing networks: A novel abstraction of develop-

ment. Genetic Programming and Evolvable Ma-

chines, 8(2):131–162.

Stanley, K. O., D’Ambrosio, D. B., and Gauci, J. (2009). A

Hypercube-Based Encoding for Evolving Large-Scale

Neural Networks. Artiﬁcial Life, 15(2):185–212.

Stanley, K. O. and Miikkulainen, R. (2002). Evolving neu-

ral networks through augmenting topologies. Evolu-

tionary Computation, 10(2):99–127.

Tanaka, F. and Aranha, C. (2022). Co-evolving morphology

and control of soft robots using a single genome. In

2022 IEEE Symposium Series on Computational In-

telligence (SSCI), pages 1235–1242.

Tibermacine, A. and Djedi, N. (2014). Neat neural net-

works to control and simulate virtual creature’s loco-

motion. In 2014 International Conference on Multi-

media Computing and Systems (ICMCS), pages 9–14.

Tsompanas, M.-A. (2024). Incremental growth on composi-

tional pattern producing networks based optimization

of biohybrid actuators. In International Conference on

the Applications of Evolutionary Computation (Part of

EvoStar), pages 275–289. Springer.

Tsompanas, M.-A. and Balaz, I. (2024). Outline of an evo-

lutionary morphology generator towards the modular

design of a biohybrid catheter. Frontiers in Robotics

and AI, 11.

Wang, J. and Chortos, A. (2022). Control strategies for soft

robot systems. Advanced Intelligent Systems, 4(5):88–

101.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

204