Expanded Applicability: Multi-Agent Reinforcement Learning-Based
Traffic Signal Control in a Variable-Sized Environment
Istv
´
an Gell
´
ert Kn
´
ab
1 a
, B
´
alint Pelenczei
1 b
, B
´
alint K
˝
ov
´
ari
2,3 c
,
Tam
´
as B
´
ecsi
2 d
and L
´
aszl
´
o Palkovics
1,4 e
1
Systems and Control Laboratory, HUN-REN Institute for Computer Science and Control (SZTAKI), Budapest, Hungary
2
Department of Control for Transportation and Vehicle Systems, Faculty of Transportation Engineering and Vehicle
Engineering, Budapest University of Technology and Economics, Budapest, Hungary
3
Asura Technologies Ltd., Budapest, Hungary
4
Sz
´
echenyi Istv
´
an University, Gy
˝
or, Hungary
Keywords:
Machine Learning, Reinforcement Learning, Deep Learning, Traffic Signal Control, Intelligent Transportation
Systems.
Abstract:
During the development of modern cities, there is a strong demand articulated for the sustainability of progress.
Since transportation is one of the main contributors to greenhouse gas emissions, the modernization and effi-
ciency of transportation are key issues in the development of livable cities. Increasing the number of lanes does
not always provide a solution and often is not feasible for various reasons. In such cases, Intelligent Trans-
portation Systems are applied primarily in urban environments, mostly in the form of Traffic Signal Control.
The majority of modern cities already employ adaptive traffic signals, but these largely utilize rule-based algo-
rithms. Due to the stochastic nature of traffic, there arises a demand for cognitive decision-making that enables
event-driven characteristics with the assistance of machine learning algorithms. While there are existing so-
lutions utilizing Reinforcement Learning to address the problem, further advancements can be achieved in
various areas. This paper presents a solution that not only reduces emissions and enhances network through-
put but also ensures universal applicability regardless of network size, owing to individually tailored state
representation and rewards.
1 INTRODUCTION
One of the paramount contemporary challenges per-
tains to air quality, predominantly in densely popu-
lated regions, notably urban centers (Fenger, 1999).
In order to foster the development of livable cities, it
is imperative to implement various measures across
multiple sectors.
As depicted in Figure 1, transportation sig-
nificantly contributes to greenhouse gas emissions
(Ritchie, 2020). From this observation, it is evi-
dent that substantial global progress can be achieved
through the implemented interventions. The efforts
a
https://orcid.org/0009-0007-6906-3308
b
https://orcid.org/0000-0001-9194-8574
c
https://orcid.org/0000-0003-2178-2921
d
https://orcid.org/0000-0002-1487-9672
e
https://orcid.org/0000-0001-5872-7008
touch on numerous technical areas such as vehicle
propulsion and fuel issues where the direction of elec-
tricity is significant (Ritchie, 2024), but in addition,
Figure 1: Emissions by sector (Ritchie, 2020).
Knáb, I., Pelenczei, B., Kõvári, B., Bécsi, T. and Palkovics, L.
Expanded Applicability: Multi-Agent Reinforcement Learning-Based Traffic Signal Control in a Variable-Sized Environment.
DOI: 10.5220/0012920800003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 2, pages 15-25
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
15

Figure 2: Illustration of reaction times in response to traffic signal changes.
infrastructure development can also lead to consider-
able improvements. These advancements allow for a
favorable modulation of emission trends even under
conditions of increasing vehicular traffic. Addition-
ally, they can reduce both the duration of traffic expo-
sure and the incidence of unnecessary delays (Singh
and Gupta, 2015).
Given that the spatial expansion of road networks
is often unfeasible (Zhang et al., 2011) or only jus-
tified during peak periods of congestion, Intelligent
Transportation Systems (ITS) (Dimitrakopoulos and
Demestichas, 2010) are increasingly emphasized. In
urban environments, this approach achieves better uti-
lization of the road network with minimal infrastruc-
ture changes, leading to a reduction in the aforemen-
tioned indicators.
The main guideline in traffic control is to avoid
transients. The reason for this is that the dynamics
of individual vehicles act as constraints on the move-
ment of others as well. The event-driven approach of
this is the ITS, which implements changes and intro-
duces constraints based on the current traffic condi-
tions. The primary objective is to mitigate the nec-
essary alterations occurring within traffic, with two
principal manifestations: human reaction time (Kest-
ing and Treiber, 2008) and losses derived from the
inertia of vehicles. The former presents itself as a cu-
mulative issue, where the reaction time of vehicles in
the queue behind one another can be seen in Figure 2
and delineated as follows:
τ =
n
∑
i=1
τ
i
, (1)
where τ
i
denotes the reaction time of individual vehi-
cles and n denotes the length of the queue.
Alongside reactions, inertia-derived losses sug-
gest that in the event of anomalies, there will in-
evitably be a dissipation of varying degrees, mani-
festing as a moving jam. From this, it follows that
truly efficient traffic management encompasses not
only the handling of existing issues but also their pre-
vention, which is crucial. As a result of this objective
and its cognitive nature, there is a growing empha-
sis on the research domain concerning the application
of Machine Learning (ML) and Deep Learning (DL)
methodologies for the management of diverse traffic
scenarios. Among these, particularly noteworthy due
to their interactivity are multi-agent systems, where
the goal is not merely to optimize the state of a sin-
gle intersection but to seek an optimal solution at the
network level.
The demand for optimal decision-making at the
network level is observable in numerous cases. The
increasing significance of ITS is observable both on
highways and in city environments. In urban areas,
one of the core implementations of ITS is Traffic Sig-
nal Control (TSC) (Qureshi and Abdullah, 2013) (Ro-
take and Karmore, 2012), while for highways, Vari-
able Speed Limit Control (VSLC) (Khondaker and
Kattan, 2015) (K
˝
ov
´
ari et al., 2024) often provides a
versatile solution. The former encompasses demand-
based switching of traffic lights, where predetermined
phases can be overridden based on real-time traffic
data if necessary. With this demand-based approach,
the extent of idle green phases can be reduced while
enhancing throughput capacity.
Behind the method, there is a repository of nu-
merous algorithms. The applied algorithms can be
divided into two main groups. Currently, rule-based
solutions such as SCATS (Sydney Coordinated Adap-
tive Traffic System) (Kustija et al., 2023), Green-
Wave, and RHODES (Real-time Hierarchical Op-
timized Distributed Effective System) (Mirchandani
and Wang, 2005) primarily dominate existing traffic
networks.
The models produced during the tuning of rule-
based systems serve as aids for solving traffic prob-
lems. Among these issues is the problem that the
adaptability of algorithms is limited, which is a
primary consideration in urban traffic management,
given that the distribution of traffic network load is
not uniform over time. Consequently, it is evident in
the case of traffic issues that their resolution requires
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
16

a predictive nature.
Predictive decision-making can be approached
from multiple angles. The two primary methods are
classical control theory solutions with identified sys-
tems, and implementations based on data driven so-
lutions. While Model Predictive Control(Ye et al.,
2019) is a highly popular solution among classical
methods, reinforcement learning is frequently em-
ployed in the field of soft computing for solving such
types of problems. The advantage of the latter is that
it eliminates the need to determine approximate phys-
ical equations, which in many cases are incapable of
adequately approximating reality.
Reinforcement learning (RL) has been employed
in this field for several years, with numerous solu-
tions emerging recently to address the problem (Wei
et al., 2021) (Abdulhai et al., 2003). Several studies
focus on the appropriate selection of different RL ab-
stractions, as alongside the learning parameters, their
proper formulation enables successful training. From
articles (Wei et al., 2018) (Wiering et al., 2000) with
the definition of rewards, it is evident that primarily
macroscopic parameters such as speed and waiting
time are enumerated. The Deep Q Network (DQN)
algorithm used in the research is not unknown in the
world of TSC or in multi-agent systems (Kolat et al.,
2023), but its application still holds new possibili-
ties. Deep learning-based systems offer numerous ad-
vantages over current implementations operating on
networks, as demonstrated by the reviewed literature.
However, in addition to online decision-making, it is
also worth discussing the offline training process.
Decision-making systems founded on machine
learning frequently exhibit superior performance
compared to those reliant on physical models; how-
ever, several critical considerations must be addressed
in this context. Among various factors, the computa-
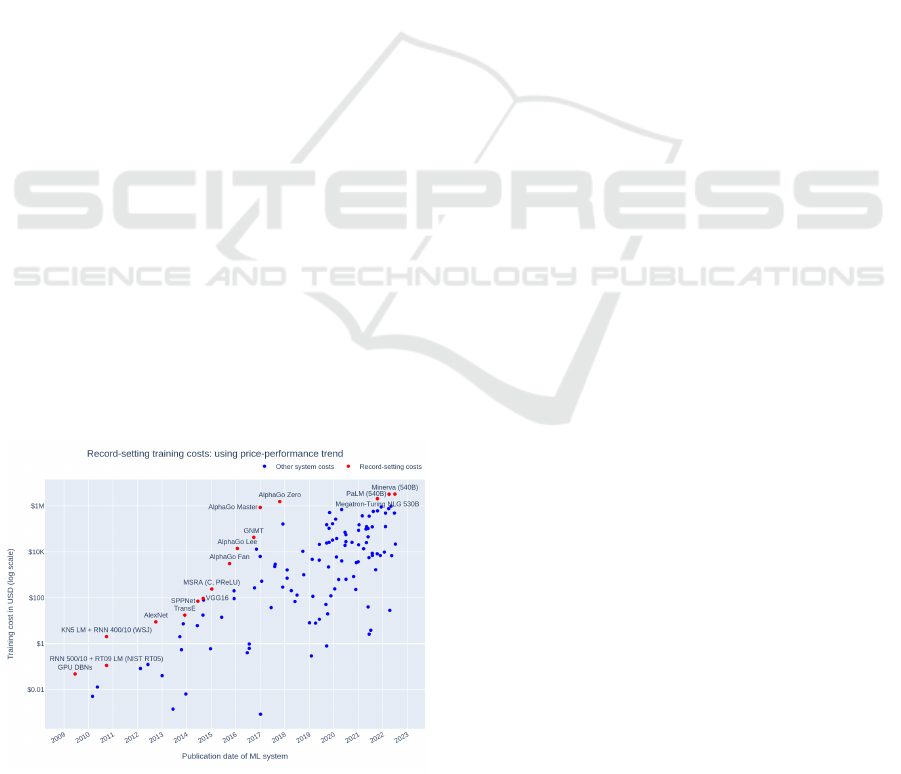
Figure 3: The change in costs over time required to train
ML models (Cottier, 2023).
tional costs associated with the development of con-
temporary models have significantly escalated, as ev-
idenced by the data presented in Figure 3.
To address this issue, several efforts exist, such
as optimizing the reward function using methods like
Monte Carlo Tree Search (K
¨
ov
´
ari et al., 2022). An-
other approach in multi-agent systems involves for-
mulating the state representation and the interven-
tions of individual agents in such a way that they are
reusable.
This research does not focus on the formulation
of individual abstractions as its novelty; instead, the
contribution lies in the use of an agent developed dur-
ing the training process. By appropriately segmenting
the environment, a large task can be divided into many
subtasks, where each entity serves the same objective.
The study aims to demonstrate that although the
performance offered by the algorithm depends on the
number of intervention points, it is capable of show-
ing improved operation in every case, even though
training was conducted in only a single environment
and the model derived from it is applied to networks
of arbitrary size. Limiting the number of training ses-
sions to just one environment can be a step towards
sustainability, as it not only reduces emissions in the
traffic network but also decreases the resources re-
quired for training.
2 METHODOLOGY
With the rising interest in artificial intelligence and
the expansion of its application areas, a new indus-
trial revolution defines the research fields of the 21st
century (Ross and Maynard, 2021). AI is not only
favored in the field of engineering, but its presence
has also become significant in the healthcare (Reddy
et al., 2020), financial (Cao, 2020), and entertain-
ment industries over the past few years. Machine
Learning represents a distinct subgroup within the
domain of artificial intelligence (Nadarajan and Su-
laiman, 2021). It is characterized by its capacity to ex-
ecute a multitude of tasks, surpassing algorithms that
rely on physical models, owing to its inherent cog-
nitive capabilities. Within this domain, three distinct
groups can be identified: supervised, unsupervised,
and reinforcement learning. Although primarily the
first two types are used in the automotive industry,
the suitability of reinforcement learning for sequential
decision-making elevates it to the forefront of modern
research areas. Moreover, an attractive feature of this
approach is that the data collection phase, which often
represents a significant financial resource, is not part
of the workflow here. Instead, the data is generated
Expanded Applicability: Multi-Agent Reinforcement Learning-Based Traffic Signal Control in a Variable-Sized Environment
17

during the learning process based on the agent’s own
experiences.
The real breakthrough in reinforcement learn-
ing was observed when it was combined with Deep
Learning (DL). In 2015, for the first time, a machine
defeated a human in the highly complex game of
Go. The algorithm named AlphaGo, built using neu-
ral networks and Monte Carlo Tree Search (MCTS),
prevailed over the reigning world champion (Wang
et al., 2016). The paper describing DQN (Mnih et al.,
2015), which also appeared in the same year, shows
that the desired cognitive decision-making capabili-
ties were able to surpass human abilities in several
other games as well.
2.1 Reinforcement Learning
The fundamental concept of reinforcement, which
is distinct from the other two branches of machine
learning, is based on the communication between two
classes (Sutton et al., 1999)(Sutton and Barto, 2018).
These two objects are an environment and an agent,
where the agent’s task is to learn a decision-making
strategy that allows it to make optimal decisions over
time. This is implemented through an iterative learn-
ing process that involves storing individual experi-
ences and evaluating the success of specific decisions
based on the resulting state. The numerical represen-
tation of the quality of a given decision is the reward,
which the agent aims to maximize.
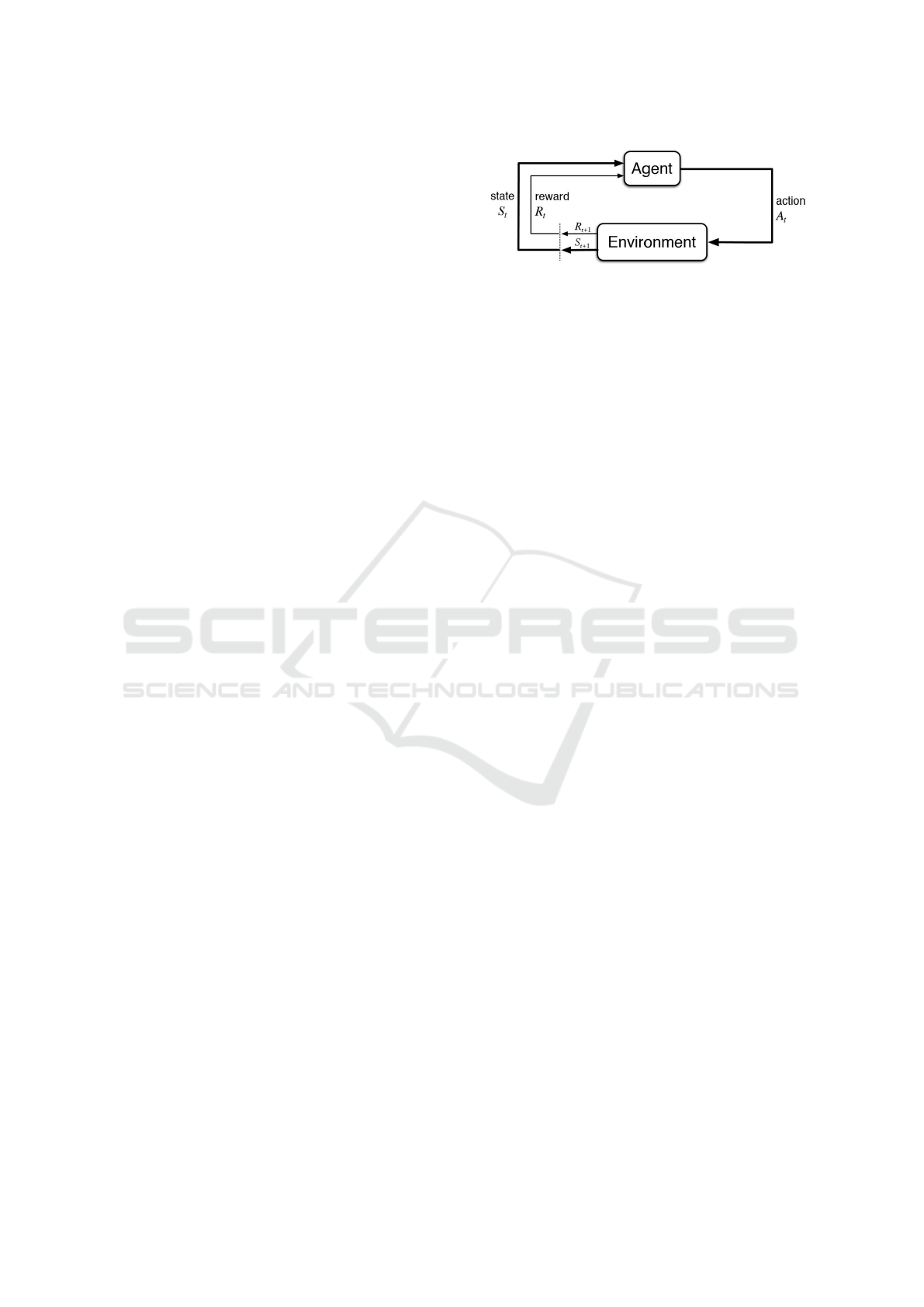
As shown in Figure 4, the agent receives the next
state and the reward from the environment in response
to a decision made in the current state. The encap-
sulation of these in a mathematical framework is the
Markov Decision Process, which describes state tran-
sitions using these abstractions along with the tran-
sition probabilities. For most RL algorithms, during
each step, the resulting data is stored in a buffer of a
predetermined size in the following format:
Transition
t
= (S
t
, A
t
, R
t
, S
t+1
, Done), (2)
from which the individual elements can be seen in
Figure 4, and Done indicates whether a training
episode has ended.
As previously described, the goal of the agent is
not only to make a correct decision at a given point but
also to learn an optimal sequence of decisions. A cu-
mulative reward (Szepesv
´
ari, 2022) is calculated for
this, which includes the rewards attainable by subse-
quent actions. However, it is important to note that
state transitions closer to the given state influence the
cumulative reward value to a greater extent, and there-
fore should have a larger weight. To achieve this, the γ
discount factor was introduced, which allows the for-
malism to be expressed in the following way:
Figure 4: Reinforcement Learning (Sutton and Barto,
2018).
G
t
=
T
∑
t=0
γ
t
· r
t
, (3)
this prioritizes the higher rewards associated with
state transitions that are closer over those that are fur-
ther away. By introducing the cumulative reward, se-
quences can be generated showing the order of ac-
tions and the resulting states, to which various quality
attributes can be assigned. From these, a new qual-
ity attribute can be introduced, the Q value, which is
not just a sum but these values are assigned to specific
state transitions, thus enabling the learning of agents.
The value assigned to these state-action pairs can be
calculated using the Bellman equation, of which most
general form is the following:
q
π
(s, a) = E
π
[G
t
| S
t
= s, A
t
= a] (4)
where q
π
(s, a) is the expected return following pol-
icy π. During training, the more training samples the
system processes, the more information the algorithm
can use to approximate the appropriate Q value. As
a result, during training, the expected behavior is an
increase in Q values in accordance with the reward
trend, converging to the value that defines the bound-
ary of the environment.
However, alongside the observed quality attributes
during training, there arises a need to understand
how decision-making is realized in the initial state
where there is a lack of information. Since this is
about experience-based decision-making, it is neces-
sary to mention one of the main issues in reinforce-
ment learning, the exploration-exploitation dilemma.
An agent can make decisions in two ways: either by
taking a random exploratory step to learn more about
the environment, or by taking the best action accord-
ing to its current knowledge. It is evident from the
task formulation that over time, maximum rewards
are achieved by fully informed decisions. However,
without sufficient experience, even informed deci-
sions will not be optimal. A commonly used method
to resolve this is the ε-greedy method, which initially
allows for complete exploration and gradually transi-
tions to making fully informed decisions over time.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
18

2.2 Deep Q Network
Reinforcement learning uses numerous algorithms.
These algorithms can be categorized into two primary
groups: value-based and policy-based. Additionally,
there exists a hybrid category that integrates both ap-
proaches, known as actor-critic algorithms. Many of
these systems use neural networks in their operation,
sometimes even multiple networks.
The DQN belongs to the first group, where the
model approximates optimal behavior using a value
function. It consists of two value networks: one that
updates at each iteration, and another network that
only copies the weights of the first network after a
certain number of steps. The Equation 4 for the DQN
algorithm can be written as follows:
Q(s, a) = Q(s, a) + α(r + γmax
a
′
Q(s, a
′
) − Q(s, a))
(5)
where the role of the secondary network is to ex-
tract the maximum available Q value, since a con-
stantly changing network is not suitable for making
decisions based on the experiences of previous steps,
as small changes in weights could easily disrupt this
value. The algorithm tunes the networks on a ran-
domly sampled data of a predetermined size. This
tuning is based on gradient descent, using the mean
squared error calculated between predicted-target and
the Q values provided by the network.
Although it is often appropriate to use actor-critic
algorithms such as PPO or TD3 for many tasks, due
to the discrete output requirement in this case, DQN
was chosen, as traffic lights require binary output.
2.3 Multi Agent Reinforcement
Learning
For problems that can be well-separated into sub-
tasks, a favored approach in RL is Multi-Agent Re-
inforcement Learning (MARL). In this case, multiple
agents share an environment (Bus¸oniu et al., 2010), as
shown in Figure 6. Its major advantage is that com-
plex systems composed of many small tasks can be
divided into much more manageable sub-tasks, mak-
ing the overall desired behavior easier to achieve.
The grouping of agents can be done based on two
main principles. In terms of their structure, agents
can be identical, referred to as homogeneous agents,
or different, known as heterogeneous agents (Abed-
Alguni et al., 2014). Additionally, based on their be-
havior, they can be categorized as cooperative, com-
petitive, or independent. While in the first two cases
it is clear that the goal is either to enforce common in-
terests or individual interests, in the case of indepen-
dent learners, they try to optimize their own decision-
making strategies without interacting with each other.
Additionally, they do not attempt to hinder each other
as seen in competitive decision-making.
Among the fundamental abstractions, the reward
strategy is also worth considering in multi-agent sys-
tems. Depending on the nature of the task, it is worth
employing entirely different approaches for each type
of agent. While in cooperative systems the network
often receives a common reward or punishment, mov-
ing towards network-level optimization, which is re-
ferred to as identical payoff (Now
´
e et al., 2012), in
competitive agent scenarios, distributed rewards are a
well-functioning concept.
3 ENVIRONMENT
The environment consists of two important entities.
For simulating traffic networks and assessing their
load, a simulator is necessary to provide the relevant
data for evaluation. In addition, there arises the de-
mand for an environment with which agents can com-
municate to effect changes and alter their own states.
3.1 Simulator
The previously mentioned requirement is fulfilled
by SUMO(Simulation of Urban MObility) (Behrisch
et al., 2011), which is an open-source simulator.
When selecting it, an important consideration was its
good scalability and the ease with which modifica-
tions can be made across a wide range, including traf-
fic generation and network sizingwindow. Addition-
ally, it provides numerous macroscopic characteris-
tics such as speeds, waiting times, or even emission
indicators, which can be retrieved per vehicle or even
per lane. Emissions are not measured using sensors;
instead, SUMO employs models for emission approx-
imation calculations. Specifically, the HBEFA v2.1
Figure 5: A SUMO intersection.
Expanded Applicability: Multi-Agent Reinforcement Learning-Based Traffic Signal Control in a Variable-Sized Environment
19

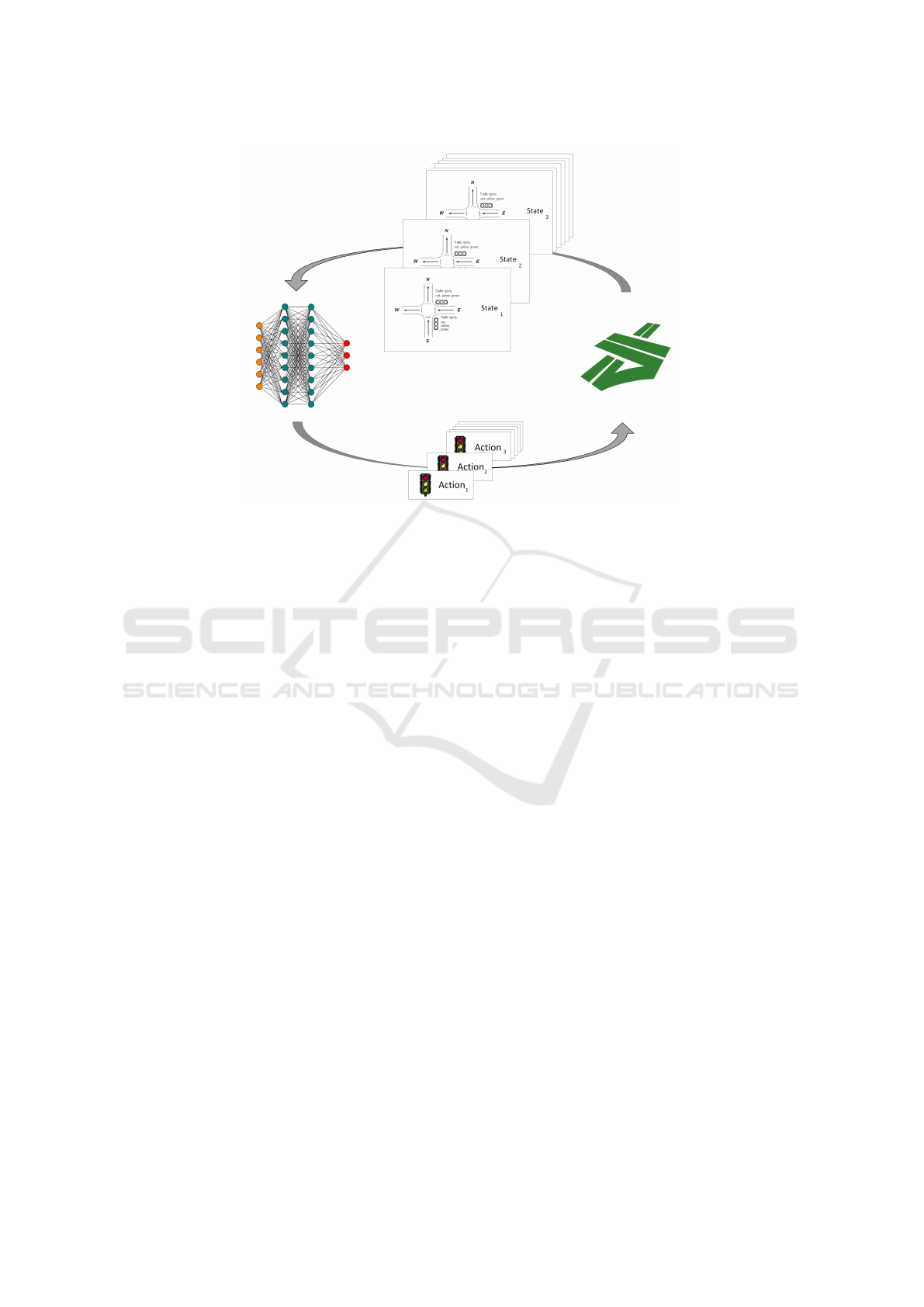
Figure 6: Multi-agent reinforcement learning in multi-intersection environments.
(Krajzewicz et al., 2014) model is utilized, which op-
erates in the following manner:
E = c
0
+ c
1
va + c
2
va
2
+ c
3
v + c
4
v
2
+ c
5
v
3
,
denoting velocity with v, acceleration with a, and the
constant related to the given emissions with c. The
control is carried out with standard three-phase traf-
fic lights, including yellow as a transient, where ei-
ther the north-south direction switches to green, or the
east-west direction. Movement in all directions is al-
lowed from every lane as shown in Figure 5. During
the training, a network consisting of four intersections
was used, while during the evaluation, one, two and
three intersection network was included.
Traffic generation is a crucial aspect of training.
In all four network sizes, the load was simulated in
such a way as to justify the use of TSC. In addition
to the RL implementation, the built-in functions of
SUMO, namely the adaptive mode and delay-based
implementation, are also examined to determine how
effectively they can handle saturation in given net-
works.
3.2 Communication Framework
In the context of RL, the gym architecture is fre-
quently employed for environment simulations. Its
standardized structure offers significant advantages,
as the algorithm can be tested for correct operation
on numerous pre-prepared environments before be-
ing applied to real-world problems. Its fundamental
functions include step, reset, and render. In this case,
the first two are essential, as visual representation is
the responsibility of SUMO, which is enabled during
configuration. The data extracted from the simulator
are processed here for the algorithm, and this is also
where Python communicates the completed interven-
tions back to the simulator.
The environment includes the formulation of in-
dividual RL abstractions. Among these, the state
is most often described by macroscopic characteris-
tics in traffic cases. In this case, the average speeds
defined on the lanes are critical values, as higher
throughput is reflected in their higher values. Since
the algorithm implements the multi-agent nature in
a homogeneous manner, a description is necessary
where each intersection receives an image of the sur-
rounding roads. Based on these, each intersection can
be described with the following state representation:
state
i
=



velocity
1
velocity
2
velocity
3
velocity
4



, (6)
where the individual average speeds are values mea-
sured on the incoming lanes of the intersections. This
description offers a significant advantage in that inter-
sections of identical characteristics can be described
arbitrarily using the same representation, thereby fa-
cilitating the requirement articulated in the contribu-
tion for applicability across any network with just a
single trained agent.
The action space has also been divided, with each
intersection independently controlling either the ver-
tical or horizontal traffic lights to turn green, in the
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
20

following manner:
action =

North − South
East −West

(7)
The formulation of the reward strategy was con-
ceived along analogous lines to that of the state rep-
resentation. Average speeds are also visible within
this level, but waiting time appears alongside it as a
penalized phenomenon. The reward equation can be
described as follows:
R =
v
avg
1 + w
, (8)
where v
avg
represents the average speed defined
across the network, while w denotes the total wait-
ing time accumulated across the network at a given
step. This is necessary because, although the indi-
vidual agents learn based on the independent learner
analogy, the goal is to master a network-level optimal
decision-making strategy.
The formulation of individual abstractions facil-
itates the implementation of multi-agent characteris-
tics with an arbitrary number of agents. As can be
observed, thanks to effective segmentation, the in-
dependent learner concept can be applied to individ-
ual agents, and due to their identical structure, every
agent can be represented by a single neural network.
Despite operating on the analogy of an independent
learner, the agents aim to search for network-level op-
timization. This is achieved in two ways. Firstly, the
states overlap with each other because they are posi-
tioned next to one another. Additionally, the identical
payoff between individual decisions creates a connec-
tion. As seen in Figure 6, each agent makes a decision
and receives a state in return. However, since there is
a common interest in rewards, the training samples at
any given step will always contain the same reward
across all intersections. Thus, within a single time
step, a number of training samples equal to the num-
ber of intersections are introduced into the system. By
studying the convergence curve after the learning pro-
cess, the evaluation phase assesses the results of the
training performed on the four-intersection network.
Figure 7: CO
2
Emission in a 1 intersection network.
4 RESULTS
After a successful training process, the evaluation
takes place in the manner outlined in the introduc-
tion, in terms of sustainability metrics and through-
put. While CO
2
and NO
x
are examined in terms of
emissions, the number of vehicles forced to stop and
the time these vehicles spend waiting will form the
basis for comparison in terms of throughput. As artic-
ulated in the contribution to the research, the training
is conducted only on the largest network, but the eval-
uation contains 1, 2, and 3 intersection networks, thus
examining the size dependency of the multi-agent
system.
Naturally, the thorough assessment encompasses
not merely the uncontrolled environments, but also in-
volves comparative analyses with other event-driven
methodologies implemented within SUMO. This al-
lows the results to be compared with current solu-
tions as well. Among these methods, the ”adaptive”
and ”delay-based” approaches will be examined. The
second method implements efforts similar to those of
the proposed algorithm, with the primary distinction
being that they are not sensitive to vehicle speeds. In-
stead, their primary objective is to minimize delays.
In the course of the evaluation, the load applied to
the transportation system is calibrated to its maximum
capacity, mirroring the conditions during the training
phase. However, the traffic generated on it has a dif-
ferent distribution, thus taking one step further away
from overfitting.
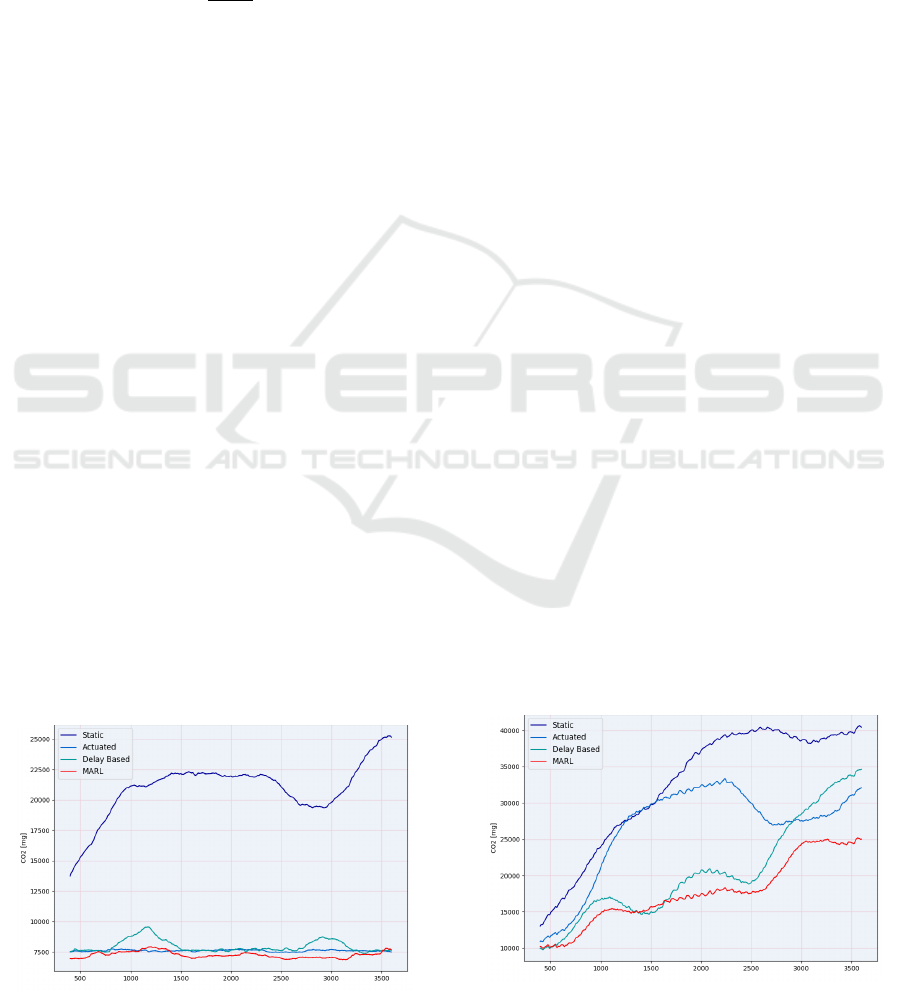
As can be seen in Figure 7-14, the formation of
a shock wave is clearly manifested in both emissions
and waiting times. It is also noticeable from the obser-
vations that as the scale of the network increases, the
phenomenon of persistent congestion within the net-
work becomes more prevalent. Looking at the charac-
teristics of the graphs, it also shows that not only are
the peak values lower for both waiting time and emis-
sion, but the fluctuations also occur to a lesser extent,
hence stabilizing traffic flow. This, as well as the vi-
Figure 8: CO
2
Emission in a 2 intersection network.
Expanded Applicability: Multi-Agent Reinforcement Learning-Based Traffic Signal Control in a Variable-Sized Environment
21

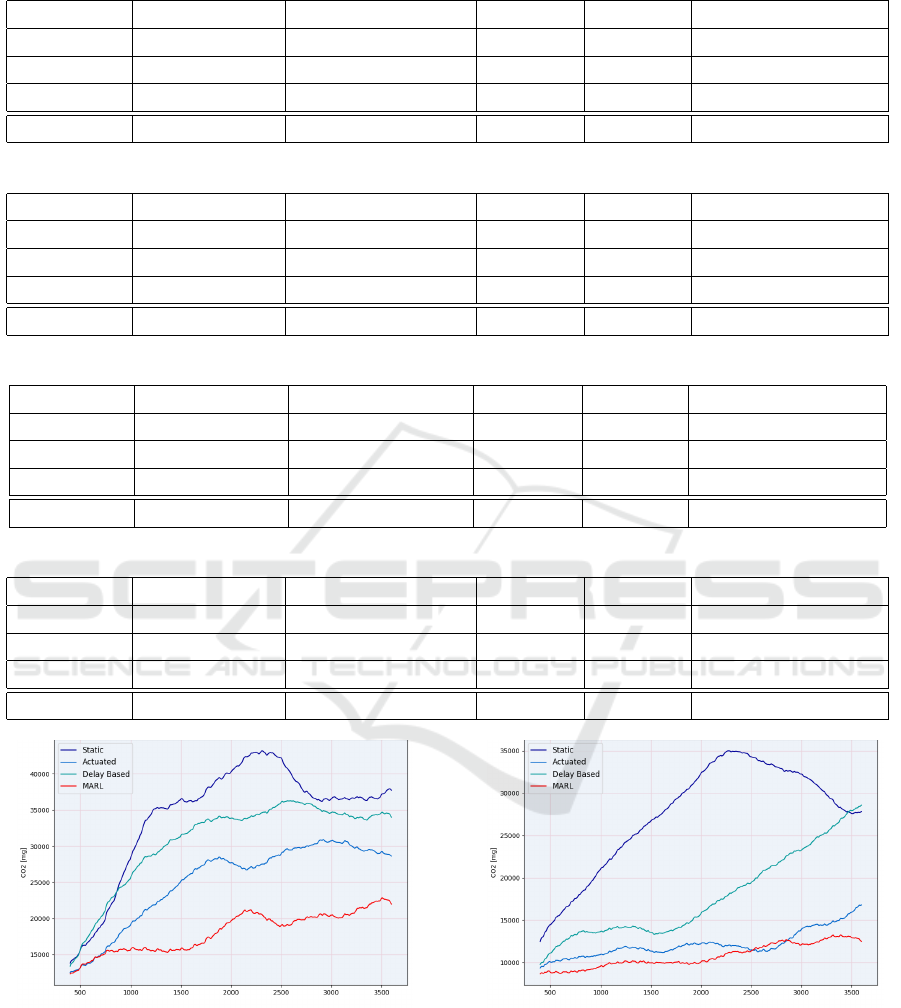
Table 1: A 30-minute time window for testing on a one-intersection network.
Waiting Time[s] Average Speed [m/s] CO2 [mg] NOx [mg] Halting Vehicles [1/s]
Static 67.206 4.1012 19480.115 8.66188 7406.75
Actuated 2.932 7.4978 7596.198 3.20075 1046.0
Delay Based 5.127 6.9916 8013.949 3.39340 1320.0
MARL 1.717 7.2027 7290.073 3.06179 803.25
Table 2: A 60-minute time window for testing on a one-intersection network.
Waiting Time[s] Average Speed [m/s] CO2 [mg] NOx [mg] Halting Vehicles [1/s]
Static 72.856 3.9614 20694.588 9.21786 15991.5
Actuated 2.989 7.5899 7591.442 3.19872 2081.5
Delay Based 4.791 6.9903 7923.337 3.35206 2574.75
MARL 1.828 7.1689 7262.742 3.049596 1626.75
Table 3: A 30-minute time window for testing on a two-intersection network.
Waiting Time[s] Average Speed[m/s] CO2 [mg] NOx [mg] Halting Vehicles [1/s]
Static 86.028 5.1520 24209.949 10.67928 8876.5
Actuated 63.670 5.4120 22015.251 9.66317 7326.125
Delay Based 27.274 6.6790 14743.874 6.31286 3723.75
MARL 10.442 7.2813 13744.383 5.85558 2585.875
Table 4: A 60-minute time window for testing on a two-intersection network.
Waiting Time[s] Average Speed [m/s] CO2 [mg] NOx [mg] Halting Vehicles [1/s]
Static 137.594 4.7504 31886.470 14.21745 25823.75
Actuated 84.979 5.0486 26022.961 11.50417 18866.75
Delay Based 59.250 5.7190 20740.818 9.07874 13926.375
MARL 12.601 6.8569 17664.559 7.65427 6714.75
Figure 9: CO
2
Emission in a 3 intersection network.
sual verification in the simulator, confirms that the al-
gorithm contributes positively to achieving diminish-
ing transients. In addition, the diagrams also show a
decline in the non-controlled environment, which can
be explained by the network becoming so saturated
that, in this case, it cannot accommodate as many ve-
hicles as in the controlled systems.
Figure 10: CO
2
Emission in a 4 intersection network.
The Tables 1-8 also list another argument for the
use of the MARL-based method. Considering the
baseline algorithms, it can be observed that their rel-
ative performance depends on the size of the network
and the duration of the application. The results do not
diverge to such an extent that one can be definitively
identified as more suitable for the entire problem.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
22

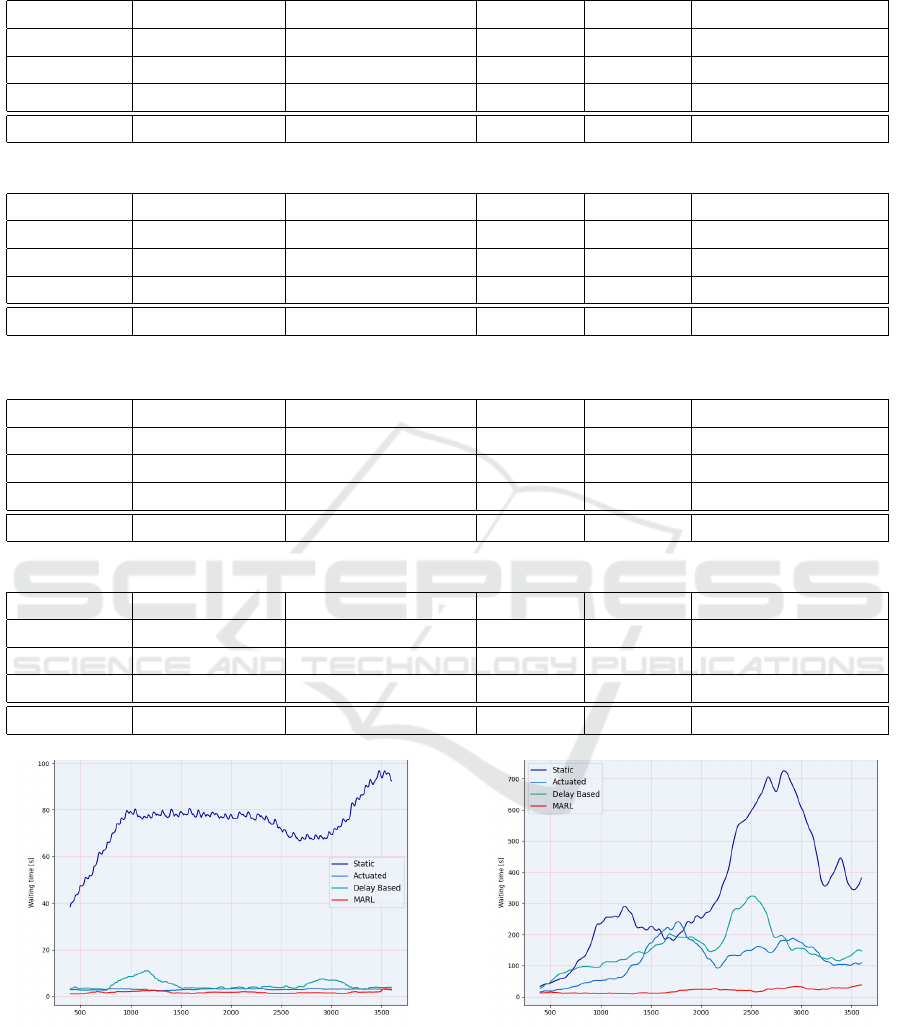
Table 5: A 30-minute time window for testing on a three-intersection network.
Waiting Time[s] Average Speed [m/s] CO2 [mg] NOx [mg] Halting Vehicles [1/s]
Static 163.230 5.3928 27883.710 12.41850 11905.583
Actuated 96.199 6.3263 20162.268 8.84889 7260.666
Delay Based 114.739 5.7035 25289.744 11.21376 10104.166
MARL 14.065 7.5449 15173.915 6.53076 2960.583
Table 6: A 60-minute time window for testing on a three-intersection network.
Waiting Time[s] Average Speed [m/s] CO2 [mg] NOx [mg] Halting Vehicles [1/s]
Static 323.762 4.7415 33404.804 14.96324 30599.5
Actuated 114.715 5.8889 24615.000 10.89000 18852.25
Delay Based 149.480 5.1378 29977.941 13.36289 24615.083
MARL 20.282 7.1369 17934.456 7.79766 7765.5
Table 7: A 30-minute time window for testing on a four-intersection network.
Waiting Time[s] Average Speed [m/s] CO2 [mg] NOx [mg] Halting Vehicles [1/s]
Static 75.367 6.0456 21628.051 9.50294 7924.75
Actuated 16.962 7.7325 10934.342 4.57993 2286.875
Delay Based 32.135 7.2594 12978.820 5.51974 3435.8125
MARL 3.888 8.5647 9487.481 3.90885 1188.8125
Table 8: A 60-minute time window for testing on a four-intersection network.
Waiting Time[s] Average Speed [m/s] CO2 [mg] NOx [mg] Halting Vehicles [1/s]
Static 103.552 5.6438 26662.658 11.81623 21105.1875
Actuated 25.294 7.3910 12265.355 5.187802 5929.75
Delay Based 68.154 6.3610 17919.312 7.78420 12042.75
MARL 5.200 8.1890 10737.716 4.47625 3080.0625
Figure 11: Waiting Time in a 1 intersection network.
This manifests in the sense that, considering waiting
times and average speed, sometimes the application
of one proves to be more advantageous, while at other
times the other does. Of course, this shows a similar
trend to the number of vehicles forced to wait, result-
ing in a decrease in speed for the stationary vehicles.
Figure 12: Waiting Time in a 3 intersection network.
With these values, the trend in emissions also shows a
similar favorability. Compared to these, the MARL-
based solution is able to further reduce emissions in
every case. In addition, it proved to be more success-
ful in every case in reducing both the waiting time and
the number of vehicles forced to wait. The increase in
Expanded Applicability: Multi-Agent Reinforcement Learning-Based Traffic Signal Control in a Variable-Sized Environment
23

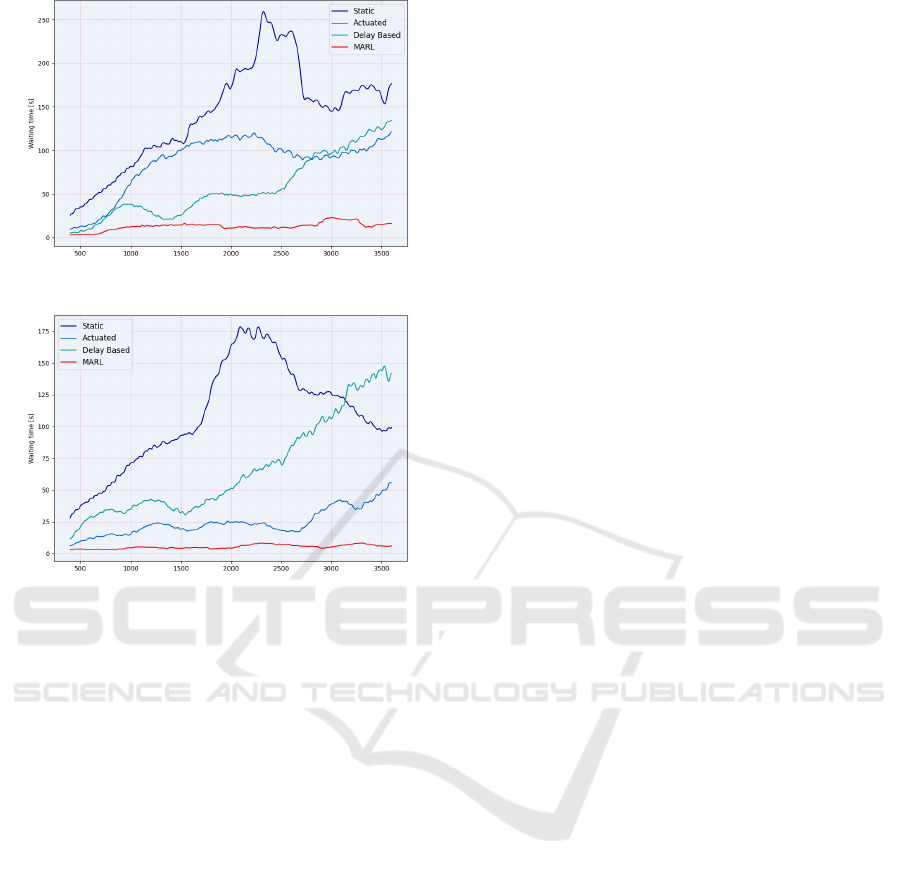
Figure 13: Waiting Time in a 2 intersection network.
Figure 14: Waiting Time in a 4 intersection network.
speed is also almost always noticeable, with only the
adaptive algorithm achieving a marginally higher av-
erage speed in the single-intersection network. How-
ever, this is most expected in this network, since, on
one hand, congestion does not form between traffic
lights here, as the vehicles passing through immedi-
ately flow off the network, and on the other hand, the
advantages of identical payoff hardly apply, consider-
ing that there is only one intersection in the system.
In summary, based on the examination of the de-
sired indicators, the training conducted on the largest
network is suitable for controlling the other networks
as well, since improvements are observed everywhere
in the indicators articulated during the motivation,
compared to the baseline algorithms.
5 CONCLUSION
The results prove, in a new light, that the applica-
tion of MARL is justified in the case of traffic net-
works. The novelty, that not only environments with
a predetermined number of agents can be controlled
in this way, but also that appropriately formulated ab-
stractions can apply a single model across different
sizes, is able to reduce both the speed of training and
the amount of resources allocated for it. With this,
individual models can be deployed more quickly to
real networks, allowing traffic management aimed at
reducing emissions to start sooner, thus accelerating
steps towards sustainability and creating more livable
cities.
Cognitive decision-making still shows numerous
areas for development. Among other things, choos-
ing the size of the training network appears to be
a promising area of research, as faster and thereby
cheaper convergence can be achieved on a smaller
network, but the suitability of the resulting model may
not be sufficient. Researching this and thereby finding
an optimum can provide further important advances.
Additionally, from the perspective of applicability to
a significant part of cities, the problem is that they do
not consist of intersections with identical characteris-
tics. This demonstrates that the deployment of homo-
geneous agents is not feasible in such scenarios. As
a consequence, the application and scalability of het-
erogeneous agents also emerge as important areas of
research, thereby expanding the potential for imple-
mentation in real-world environments.
ACKNOWLEDGEMENTS
This work was supported by the European Union
within the framework of the National Labora-
tory for Autonomous Systems (RRF-2.3.1-21-2022-
00002). T.B. was supported by BO/00233/21/6: the
J
´
anos Bolyai Research Scholarship of the Hungarian
Academy of Sciences.
REFERENCES
Abdulhai, B., Pringle, R., and Karakoulas, G. J. (2003).
Reinforcement learning for true adaptive traffic sig-
nal control. Journal of Transportation Engineering,
129(3):278–285.
Abed-Alguni, B. H. K. et al. (2014). Cooperative reinforce-
ment learning for independent learners. Computer Sci-
ence.
Behrisch, M., Bieker, L., Erdmann, J., and Krajzewicz,
D. (2011). Sumo–simulation of urban mobility: an
overview. In Proceedings of SIMUL 2011, The Third
International Conference on Advances in System Sim-
ulation. ThinkMind.
Bus¸oniu, L., Babu
ˇ
ska, R., and De Schutter, B. (2010).
Multi-agent reinforcement learning: An overview. In-
novations in multi-agent systems and applications-1,
pages 183–221.
Cao, L. (2020). Ai in finance: A review. Available at SSRN
3647625.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
24

Cottier, B. (2023). Trends in the dollar training cost of ma-
chine learning systems. Accessed: 2023-12-18.
Dimitrakopoulos, G. and Demestichas, P. (2010). Intelli-
gent transportation systems. IEEE Vehicular Technol-
ogy Magazine, 5(1):77–84.
Fenger, J. (1999). Urban air quality. Atmospheric environ-
ment, 33(29):4877–4900.
Kesting, A. and Treiber, M. (2008). How reaction time, up-
date time, and adaptation time influence the stability
of traffic flow. Computer-Aided Civil and Infrastruc-
ture Engineering, 23(2):125–137.
Khondaker, B. and Kattan, L. (2015). Variable speed limit:
an overview. Transportation Letters, 7(5):264–278.
Kolat, M., K
˝
ov
´
ari, B., B
´
ecsi, T., and Aradi, S. (2023).
Multi-agent reinforcement learning for traffic signal
control: A cooperative approach. Sustainability,
15(4):3479.
K
˝
ov
´
ari, B., Kn
´
ab, I., and B
´
ecsi, T. (2024). Variable speed
limit control for highway scenarios a multi-agent rein-
forcement learning based appraoch. Technical report,
EasyChair.
K
¨
ov
´
ari, B., Pelenczei, B., and B
´
ecsi, T. (2022). Monte carlo
tree search to compare reward functions for reinforce-
ment learning. In 2022 IEEE 16th International Sym-
posium on Applied Computational Intelligence and
Informatics (SACI), pages 000123–000128. IEEE.
Krajzewicz, D., Hausberger, S., Wagner, P., Behrisch, M.,
and Krumnow, M. (2014). Second generation of pol-
lutant emission models for sumo. In SUMO2014 -
Second SUMO User Conference, Reports of the DLR-
Institute of Transportation Systems.
Kustija, J. et al. (2023). Scats (sydney coordinated adaptive
traffic system) as a solution to overcome traffic con-
gestion in big cities. International Journal of Research
and Applied Technology (INJURATECH), 3(1):1–14.
Mirchandani, P. and Wang, F.-Y. (2005). Rhodes to intelli-
gent transportation systems. IEEE Intelligent Systems,
20(1):10–15.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-
ness, J., Bellemare, M. G., Graves, A., Riedmiller, M.,
Fidjeland, A. K., Ostrovski, G., et al. (2015). Human-
level control through deep reinforcement learning. na-
ture, 518(7540):529–533.
Nadarajan, R. and Sulaiman, N. (2021). Comparative anal-
ysis in execution of machine learning in breast cancer
identification: A review. Journal of Physics: Confer-
ence Series, 1874:012032.
Now
´
e, A., Vrancx, P., and De Hauwere, Y.-M. (2012).
Game theory and multi-agent reinforcement learning.
Reinforcement Learning: State-of-the-Art, pages 441–
470.
Qureshi, K. N. and Abdullah, A. H. (2013). A survey on in-
telligent transportation systems. Middle-East Journal
of Scientific Research, 15(5):629–642.
Reddy, S., Allan, S., Coghlan, S., and Cooper, P. (2020). A
governance model for the application of ai in health
care. Journal of the American Medical Informatics
Association, 27(3):491–497.
Ritchie, H. (2020). Sector by sector: where do global green-
house gas emissions come from? Our World in Data.
https://ourworldindata.org/ghg-emissions-by-sector.
Ritchie, H. (2024). Tracking global data on
electric vehicles. Our World in Data.
https://ourworldindata.org/electric-car-sales.
Ross, P. and Maynard, K. (2021). Towards a 4th industrial
revolution.
Rotake, D. and Karmore, S. (2012). Intelligent traffic signal
control system using embedded system. Innovative
systems design and engineering, 3(5):11–20.
Singh, B. and Gupta, A. (2015). Recent trends in intelligent
transportation systems: a review. Journal of transport
literature, 9:30–34.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-
ing: An introduction. MIT press.
Sutton, R. S., Barto, A. G., et al. (1999). Reinforce-
ment learning. Journal of Cognitive Neuroscience,
11(1):126–134.
Szepesv
´
ari, C. (2022). Algorithms for reinforcement learn-
ing. Springer nature.
Wang, F.-Y., Zhang, J. J., Zheng, X., Wang, X., Yuan, Y.,
Dai, X., Zhang, J., and Yang, L. (2016). Where does
alphago go: From church-turing thesis to alphago the-
sis and beyond. IEEE/CAA Journal of Automatica
Sinica, 3(2):113–120.
Wei, H., Zheng, G., Gayah, V., and Li, Z. (2021). Recent
advances in reinforcement learning for traffic signal
control: A survey of models and evaluation. ACM
SIGKDD Explorations Newsletter, 22(2):12–18.
Wei, H., Zheng, G., Yao, H., and Li, Z. (2018). Intellilight:
A reinforcement learning approach for intelligent traf-
fic light control. In Proceedings of the 24th ACM
SIGKDD international conference on knowledge dis-
covery & data mining, pages 2496–2505.
Wiering, M. A. et al. (2000). Multi-agent reinforcement
learning for traffic light control. In Machine Learning:
Proceedings of the Seventeenth International Confer-
ence (ICML’2000), pages 1151–1158.
Ye, B.-L., Wu, W., Ruan, K., Li, L., Chen, T., Gao, H., and
Chen, Y. (2019). A survey of model predictive control
methods for traffic signal control. IEEE/CAA Journal
of Automatica Sinica, 6(3):623–640.
Zhang, J., Wang, F.-Y., Wang, K., Lin, W.-H., Xu, X., and
Chen, C. (2011). Data-driven intelligent transporta-
tion systems: A survey. IEEE Transactions on Intelli-
gent Transportation Systems, 12(4):1624–1639.
Expanded Applicability: Multi-Agent Reinforcement Learning-Based Traffic Signal Control in a Variable-Sized Environment
25