Memory-Based Learning of Global Control Policies from Local
Controllers
Daniel Nikovski
1 a
, Junmin Zhong
1,2 b
and William Yerazunis
1 c
1
Mitsubishi Electric Research Labs, Massachusetts, U.S.A.
2
Arizona State University, Arizona, U.S.A.
Keywords:
Learning Control, Differential Dynamic Programming, Value Function Approximation, Policy Learning.
Abstract:
The paper proposes a novel method for constructing a global control policy, valid everywhere in the state
space of a dynamical system, from a set of solutions computed for specific initial states in that space by means
of differential dynamic programming. The global controller chooses controls based on elements of the pre-
computed solutions, leveraging the property that these solutions compute not only nominal state and control
trajectories from the initial states, but also a set of linear controllers that can stabilize the system around the
nominal trajectories, as well as a set of localized estimators of the optimal cost-to-go for system states around
the nominal states. An empirical verification of three variants of the algorithm on two benchmark problems
demonstrates that making use of the cost-to-go estimators results in the best performance (lowest average
cost) and often leads to dramatic reduction in the number of pre-computed solutions that have to be stored in
memory, which in its turn speeds up control computation in real time.
1 INTRODUCTION
Optimal sequential control of non-linear dynamical
systems is a difficult problem often present in vari-
ous control applications. An instance of this prob-
lem is when the controller needs to reach a goal state
that is relatively far from its current state and regu-
late the system around that state, in the presence of
disturbances. Common requirements are to reach and
regulate around the goal state in minimum time and
at minimum control cost, while possibly obeying con-
straints on the system’s state and applied controls.
Various control methods have been proposed in
the field of optimal control, addressing specific in-
stances of this problem. When the controlled system
is linear and time-invariant (LTI) and the objective is
to minimize settling time while balancing it with con-
trol effort, the celebrated linear quadratic regulator
(LQR) method can be shown to produce an optimal
controller in the form of a linear mapping from the
system’s state to the optimal control (Stengel, 1994).
The computed control policy is in the form of a full-
state feedback (FSF) controller with fixed gains.
a
https://orcid.org/0000-0003-2919-645X
b
https://orcid.org/0000-0001-7703-0919
c
https://orcid.org/0009-0006-8513-018X
However, when the controlled system is non-
linear and subject to constraints, the LQR solution is
no longer optimal or often not even feasible. An LQR
solution based on the linearization of the system’s dy-
namics around the desired setpoint might work well if
the initial state is in the neighborhood of the setpoint,
but would generally not stabilize the system if started
far from the setpoint, or might fail to even reach the
setpoint at all. In particular, when the control signal
is limited, an FSF controller with constant gains gen-
erally cannot bring the system to a desired state, be-
cause this might require traversing a complicated path
in state space where the feedback error is not neces-
sarily expected to decrease at every control step.
A common solution in such cases is to split the
problem into two parts: the first one is to compute
off-line a suitable trajectory in state space and then
design and apply a feedback controller to track it in
real time. In many applications, knowledge of the an-
alytical form of the dynamics of the system can be
used to compute the optimal trajectory analytically,
for any initial and goal states, and to also design an-
alytically a controller to follow that trajectory (Grass
et al., 2008). This approach, while very effective for
such applications, has two major disadvantages – first,
it presupposes the existence of a detailed and accurate
model of the system’s dynamics in analytical form,
Nikovski, D., Zhong, J. and Yerazunis, W.
Memory-Based Learning of Global Control Policies from Local Controllers.
DOI: 10.5220/0012921900003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 237-244
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
237

and second, it requires significant skill and insight
into designing the controller. As both the derivation
and calibration of the system’s model and the manual
design of the controller require a significant amount
of highly qualified labor, this approach to controller
design is usually very costly and difficult.
In contrast, recent advances in the field of deep
reinforcement learning (DRL) have demonstrated the
remarkable ability of general-purpose DRL algo-
rithms to solve difficult sequential decision and con-
trol problems without access to knowledge of the sys-
tem’s dynamics in analytical form (Lillicrap et al.,
2015). DRL algorithms usually interact directly with
the system and compute an optimal policy by means
of trial and error. A downside of such algorithms is
their often excruciatingly long training times, often
measured in millions of trials (control steps) in the tar-
get environment. For real physical systems, such long
training times on the real hardware are usually com-
pletely infeasible, so training is provided either on a
simulation model of the system, created in a simulator
such as a physics engine, or on a learned parametric
model of the system’s dynamics obtained from a lim-
ited number of interactions with the physical system.
This general approach is known as model-based RL
(MBRL) (Polydoros and Nalpantidis, 2017). Despite
multiple recent successes, the long training times of
DRL algorithms, even in simulation, and the need to
adjust carefully the learning parameters, are still an
impediment to their wider application.
Recognizing the difficulty of obtaining a general
control policy that is valid for every state, another
class of methods aims to find solutions only for a spe-
cific starting state, after it has become known. This
class of methods, generally known as trajectory opti-
mization and stabilization algorithms, effectively au-
tomate the path planning and tracking approach de-
scribed above. Examples of this approach include the
methods of differential dynamic programming (DDP)
(Jacobson and Mayne, 1970), iterative LQR (iLQR)
(Li and Todorov, 2004), as well as direct transcription
and collocation methods for trajectory optimization
(Tedrake, 2023). These methods can be very effec-
tive, as the decision problem they are solving is much
simpler than computing an entire global control pol-
icy – instead of computing a function that maps any
state belonging to the multidimensional state space of
the system to a control, they compute a much simpler
function that maps time, a single-dimensional vari-
able, to control values to be used at that time. How-
ever, a significant disadvantage of such methods is
that trajectory computation must either be done off-
line, introducing a delay before control can start, or
on-line, in a model-predictive control (MPC) fashion
(Tassa et al., 2012). This often necessitates the use
of powerful and expensive micro-controllers and/or
limiting the prediction horizon, which could lead to
failure to reach the goal state for some systems.
One promising approach to avoiding the need
for either long off-line computation or intense on-
line computation associated with trajectory-based lo-
cal control is to combine multiple pre-computed lo-
cal trajectory-centric controllers into a single global
controller by means of a suitable machine learning
method. The highly influential Global Policy Search
(GPS) method trains a deep neural network (DNN) to
emulate the operation of multiple pre-computed con-
trollers by repeatedly sampling the output of these
controllers and gradually adjusting the global policy
encoded by the DNN, thus creating a global con-
troller that can be executed relatively fast at run-time
(Levine et al., 2016). One disadvantage associated
with this method is that policy learning progresses
relatively slowly, as each modification to the control
policy is limited in magnitude in order to avoid di-
vergence of the learning process. Furthermore, the
training method uses only the trajectory computed by
the trajectory optimization solver, but not the entire
controller implied by its solution.
We propose a method that operates on the same
general principle – to combine multiple trajectory-
based local controllers from multiple initial states into
a single global control policy – but using a differ-
ent machine learning method for the combination and
also using more components of the computed local
solutions than just the computed trajectories. As the
chosen machine learning method belongs to the class
of memory-based learning (MBL) methods, its train-
ing time is zero, and consists only of storing the pre-
computed local solutions in memory. The actual pre-
dictive model building takes place at run-time, when
a control for a particular state needs to be computed.
Although computation is shifted to run-time, exper-
imental results indicate that the computation time is
in fact shorter than the time needed to perform a sin-
gle forward pass through a DNN that encodes a pol-
icy computed by a DRL algorithm. Moreover, be-
cause the entire local feedback controllers are used in
the computation, including their gain schedules and
costs-to-go to the goal state, relatively few solutions
in memory are needed, resulting in savings in mem-
ory and computational time.
Several variants of the proposed method are de-
scribed in Section 2. Empirical verification on sev-
eral test problems is described in Section 3. Section
4 proposes several directions for further improvement
of the algorithm and concludes the paper.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
238

2 MEMORY-BASED POLICY
CONSTRUCTION
The proposed algorithm for control policy construc-
tion uses the same two mechanisms employed by
DRL algorithms: dynamic programming and function
approximation, but differently. The algorithm com-
putes several solutions (trajectories) stabilizing the
system from several initial states, and at run-time es-
timates the value function of states never encountered
previously from elements of the pre-computed solu-
tions. The reason for the method’s computational ef-
ficiency is the purposeful manner of computing value
functions by means of dynamic programming in a
backward direction from the goal to the initial state,
which is much more efficient than the random value-
function back-ups applied by DRL algorithms.
2.1 Control Problem Definition
We are considering the stabilization problem for fully
observable nonlinear time-invariant dynamical sys-
tem described by the discrete-time dynamics equation
x
k+1
= f(x
k
,u
k
), where x is a multidimensional state
space, u is a control vector, and f is a nonlinear time-
invariant vector field. We are concerned with control
problems where the goal is to bring the system from
an initial state x
0
to a goal state x
(G)
in an optimal way
and keep the system around the goal state indefinitely.
The optimality of the control method is measured
by means of a cumulative cost J
0
comprising running
(stage) costs l
r
and a final cost l
f
, where the accumu-
lation is computed over a sequence of control steps:
J
0
(x
0
,U) =
H−1
∑
k=0
l
r
(x
k
,u
k
) + l
f
(x
H
), (1)
where the states x
k
, k > 0 obey the dynamics defined
above after x
0
, and U = {u
0
,u
1
,. ..,u
H−1
} is a con-
trol sequence computed over a finite horizon of length
H control steps. A finite horizon is used to avoid infi-
nite cumulative costs, with the assumption that this
horizon is sufficiently long to reach the goal state.
Given appropriate positive running costs l
r
, desired
minimum-time objectives can be achieved.
2.2 Trajectory Optimization Based on
Differential Dynamic Programming
The problem of trajectory optimization is usually
meant to consist of finding an optimal sequence of
controls U
∗
= argmin
U
J
0
(x
0
,U) from a specific start-
ing state x
0
. The DDP and iLQR algorithms solve this
trajectory optimization problem very efficiently when
the dynamics f and stage costs l
r
are differentiable (Li
and Todorov, 2004; Tassa et al., 2012).
An important characteristic of some trajectory op-
timization methods, such as DDP and iLQR, is that
they not only produce nominal state and control tra-
jectories, but also a set of FSF controllers that can
stabilize the system around the nominal state trajec-
tory. These controllers are of the form u
k
= u
∗
k
+
K
k
(x
k
− x
∗
k
), where x
∗
k
and u
∗
k
are the nominal state
and control specifically computed for time step k, x
k
is the actual state the system is in at control step k,
K
k
is a vector of gains, and u
k
is the computed con-
trol. This controller is not global, because it has been
computed with respect to the linearization of the sys-
tem dynamics around the nominal state x
∗
k
and control
u
∗
k
, which is only valid in their neighborhood, but is
still effective there. This property can be leveraged
to compose a global policy by aggregating the FSF
controllers computed for relatively few initial states.
2.3 Memory-Based Trajectory
Aggregation
As noted, trajectory optimization algorithms find an
optimal sequence of controls from a specific starting
state. However, we are looking for a global control
policy u = π(x) that applies to every possible state x.
The proposed algorithm uses multiple iLQR solutions
from a representative number of starting states, and
fuses them into a global policy. Several variants of
this idea can be applied, as described below.
2.3.1 Closest Controller Among the Stored
Solutions
The idea to compute a single global policy from mul-
tiple local solutions has been investigated before. The
algorithm proposed in (Reist et al., 2016) stores a set
of local solutions, each defining implicitly a control-
lable funnel: a part of the state space where the con-
trollers computed for this solution can stabilize the
system. The algorithm finds the closest state from any
solution stored in memory, and follows the sequence
of controllers for this solution until the goal state.
The first variation of the memory-based iLQR
controller (MBiLQR) controller we propose is closely
related to this prior work. The method stores all state-
control-gains tuples of all pre-computed iLQR solu-
tions into a memory set D = {(x
∗
i
,u
∗
i
,K
i
)}
N
i=1
, where
N is the total number of such pairs. If, e.g., I iLQR
solutions have been computed, each of length H time
steps, then the data set will contain N = IH tuples.
At each control step, the index of the closest stored
state i
CC
= argmin
i
d
i
to the current state x is found,
Memory-Based Learning of Global Control Policies from Local Controllers
239

where d
i
= ||x − x
∗
i
||
2
is the Euclidean distance be-
tween pairs of states. Then, the corresponding FSF
controller associated with that state is applied: u
CC
=
u
∗
i
CC
+ K
i
CC
(x − x
∗
i
CC
). (Here, CC stands for ”Closest
Controller”, and we call this variation MBiLQR-CC.)
Unlike the method in (Reist et al., 2016), which
keeps using the same solution until the system reaches
the goal state after it has been identified as the clos-
est to the initial state, the proposed MBiLQR-CC
method can switch between solutions. This could
lead to abrupt changes in the control signal, which is
not desirable. The reason for this is that the state-
control-gains tuples (x
∗
i
,u
∗
i
,K
i
) = (x
∗( j)
k
,u
∗( j)
k
,K
( j)
k
)
have been computed specifically for the k-th control
step of some solution j, and are thus time-dependent.
Fortunately, this time dependency can be rectified
by modifying the iLQR algorithm to compute time-
independent controllers, under the concrete assump-
tion that the controller will reach the goal state x
(G)
and will remain indefinitely in that state under the
control of the last controller in the solution, the one
for time step H. The iLQR algorithm (Li and Todorov,
2004) linearizes the system dynamics around a cur-
rent candidate control trajectory, obtaining effectively
a linear time-variant system with dynamics described
by
¯
x
k+1
= A
k
¯
x
k
+B
k
¯
u
k
, 0 ≤ k < H, defined in terms of
the deviations
¯
x
k
= x
k
−x
∗
k
and
¯
u
k
= u
k
−u
∗
k
from the
nominal trajectory defined by the sequences of states
x
∗
k
and controls u
∗
k
. It then performs a recursive com-
putation of the costs-to-go of states around the current
trajectory, operating backwards from the penultimate
stage k = H −1 and using the assignment
S
k
= Q
k
+ A
T
k
S
k+1
A
k
− A
T
k
S
k+1
B
k
(R
k
+ B
T
k
S
k+1
B
k
)
−1
B
T
k
S
k+1
A
k
,
(2)
where Q
k
and R
k
are quadratic cost matrices (ei-
ther constant or linearized similarly to the dynam-
ics), and S
k
is the matrix that defines the cost-to-
go
¯
V
k
(
¯
x
k
) =
¯
x
T
k
S
k
¯
x
k
for the k-th stage. The original
iLQR algorithm initializes the recursion (2) by setting
S
H
= Q
f
, where Q
f
is the matrix defining the terminal
cost
1
2
(x
H
− x
(G)
)
T
Q
f
(x
H
− x
(G)
). With this initial-
ization, the matrices S
k
, 0 ≤ k < H, will define time-
dependent costs-to-go
¯
V
k
(
¯
x
k
). (This is true even when
the matrices A
k
and B
k
are the same for all stages.)
However, if the recursion (2) is solved instead as
an equation for the last stage by setting S
H−1
= S
H
and using the linearized dynamics around the goal
state A
k
= A
(G)
, B
k
= B
(G)
, it will be equivalent to the
solution of the algebraic Riccati equation for the LTI
system valid in the neighborhood of the goal state,
and the obtained matrix S
H
will represent the cost-
to-go corresponding to regulating the system around
the goal state over an infinite horizon. If we now ini-
tialize the recursion (2) with the computed matrix S
H
(instead of with Q
f
), the recursion will compute a se-
ries of time-independent costs-to-go that correspond
to the infinite-horizon problem of reaching the goal
state and staying in it indefinitely. For more details on
the modification to iLQR, see (Nikovski et al., 2024).
After this modification of the algorithm, the
dataset D = {(x
∗
i
,u
∗
i
,K
i
)}
N
i=1
will consist of param-
eters of time-independent controllers, each defined
around the state component of the tuple x
∗
i
. As
described above, at run time, the closest state x
∗
i
CC
in the data set to the current state x is retrieved
and the corresponding control is computed as u
CC
=
u
∗
i
CC
+ K
i
CC
(x − x
∗
i
CC
). This minimizes the risk of
abrupt changes in the control, expecting that the time-
invariant controllers for the same state obtained in
two different solutions will be largely the same, so
the control will be consistent when switching between
them.
As a computational implementation, if the dimen-
sionality of the state space is not too high, spatial data
structures such as k-d or ball trees can be used for fast
retrieval of the closest tuple in the memory dataset.
2.3.2 Value-Based MBiLQR with the Lowest
Cost-to-Go (MBiLQR-LC)
When considering only the nearest state x
∗
i
CC
in
Euclidean-distance sense and its associated local con-
troller, the policy may end up overlooking a better
solution which is slightly further, but has superior
(lower) cost-to-go. By this logic, we can decide which
controller to use by comparing the expected cost-to-
go of the current state according to the value function
estimates of multiple candidate local controllers. To
this end, we first augment the data set to also include
the matrices S
i
computed by the time-independent
modification of the iLQR algorithm, as well as the
scalars v
i
that represent the costs-to-go along the nom-
inal trajectories: D
V
= {(x
∗
i
,u
∗
i
,K
i
,S
i
,v
i
)}
N
i=1
.
The scalar costs-to-go v
k
are needed because the
matrix S
k
defines only the cost-to-go
¯
V
k
(
¯
x
k
) =
¯
x
T
k
S
k
¯
x
k
of regulating the system from its current state x
k
to
the nominal trajectory, but does not express the to-
tal cost of regulating the system from x
k
to the goal
state x
(G)
, which includes the cost-to-go of the nom-
inal trajectory itself. It is easy to see this if we
start the controller from an actual nominal state x
∗
k
of
some nominal trajectory (x
k
= x
∗
k
), and roll out the
controller in the absence of disturbances for the re-
maining H − k steps. As a result, the system will
traverse exactly the nominal trajectory, and because
the deviations
¯
x
p
= 0 for k ≤ p ≤ H, we will have
¯
V
p
(
¯
x
p
) = 0, too. However, the cost v
k
of getting from
x
k
to x
(G)
will certainly not be zero. Fortunately, this
cost-to-go for each nominal state can easily be com-
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
240

puted in the backward pass of the iLQR algorithm as
v
k
= v
k+1
+ l
r
(x
∗
k
,u
∗
k
), starting with v
H
= 0.
Then, we select a subset D
s
⊆ D
V
of size L, D
s
=
{(x
∗
i
j
,u
∗
i
j
,K
i
j
,S
i
j
,v
i
j
)}
L
j=1
defined by a set of data set
indices {i
1
,i
2
,. ..,i
L
} ⊆ {1,2,...,N}. For the j-th
tuple of the subset, we can compute its value func-
tion estimate V
( j)
(x) of what the cost-to-go for the
current state x might be as V
( j)
(x) =
¯
V
( j)
(x) + v
i
j
=
(x − x
∗
i
j
)
T
S
i
j
(x − x
∗
i
j
) + v
i
j
. The L different estimates
V
( j)
(x) purport to estimate the same variable V(x),
which is the true optimal cost-to-go starting from state
x and following the optimal control policy for the sta-
bilization problem thereafter. However, these L es-
timates are made under different assumption of what
this optimal policy might be. Because the correspond-
ing matrices S
i
j
each came from a specific solution
computed by the modified iLQR algorithm, they as-
sume that the sequence of FSF controllers computed
by that solution will be used as stabilization policy.
Consequently, we can choose which of these solu-
tions will be used according to these estimates: i
LC
=
argmin
j
V
( j)
(x), and u
LC
= u
∗
i
LC
+K
i
LC
(x−x
∗
i
LC
). One
way of looking at this method for control selection is
to think of it as a way to reduce the infinite set of can-
didate control actions u at the current state x to the
much smaller discrete set of L controls prescribed by
the L controllers represented in the data set D
s
, each
of which leads to the goal state via a different path.
Although we can use the estimates V
( j)
(x) of any
number of controllers stored in memory, in practice
only those close to the current state will be accurate.
For this reason, we select the controller only among
those in the neighborhood of the current state. We will
call this variation of the algorithm MBiLQR-LC, for
”Lowest Cost-to-go”. Similarly to the MBiLQR-CC
method, this variant can use k-d trees for fast retrieval
of the subset D
s
, effectively performing a k-nearest
neighbor search. In practice, we found that L = 2 is a
good choice for the test problems we considered.
2.3.3 State Weighted Value Based MBiLQR
(MBiLQR-SWLC)
Finally, another variant of the algorithm addresses
some potential problems with using Euclidean dis-
tances to pre-select the subset D
s
. Weighting equally
all components of the state does not reflect their rel-
ative importance in regulation. However, if the stage
cost is quadratic of the form l
r
(x,u) =
1
2
u
T
Ru+
1
2
(x−
x
(G)
)
T
Q(x − x
(G)
), the Q matrix already expresses
this relative importance of the components of the state
vector. We propose to use Q as a weight matrix
in computing a weighted distance between the cur-
rent state and candidate controllers. Then, we follow
the same second level of data selection as MBiLQR-
LC. We call this variant of the algorithm MBiLQR-
SWLC, for ”State-Weighted Lowest Cost-to-go”.
3 EMPIRICAL EVALUATION ON
TEST SYSTEMS IN
SIMULATION
We evaluated the three variants of the MBiLQR al-
gorithm described above on two well-known bench-
mark control tasks with non-linear unstable dynamics
for two example systems: a torque-limited pendulum
and a rotary (Furuta) pendulum. Both problems are
underactuated and require non-trivial control policies
beyond what classical control methods can produce.
3.1 Torque-Limited Pendulum
The first task consists of swinging up and stabilizing a
torque-limited pendulum (TLP) at its upper unstable
equilibrium position. The dynamics of the pendulum
are described by the equation:
ml
¨
θ = −mgsin θ − b
˙
θ + τ,
where θ represents the angle with respect to the stable
downward vertical position, m is the mass of the bob,
l is the length of the pendulum, g is the acceleration
due to gravity, b is the viscous friction coefficient, and
τ is the applied torque at the pivot point.
The objective is to maneuver the pendulum from
its initial stable equilibrium at θ = 0 (hanging posi-
tion) to the upper unstable equilibrium at θ = π and
to maintain its balance there. Although the task ap-
pears straightforward given sufficient torque, in the
case when the torque is limited and a single swing is
not sufficient to reach the upper equilibrium, a path
through state space must be planned in order to pump
up enough energy to swing up the pendulum. This
presents significant challenges for traditional feed-
back control methods that always ssek to minimize
the feedback error with respect to the goal state, and
makes the task a suitable benchmark for general-
purpose controller-design methods such as the one
proposed in this paper.
We verified the algorithms in simulation, using a
model of TLP implemented in the MuJoCo physics
engine (Todorov et al., 2012), a tool extensively uti-
lized in studies of robotics and control (Zhong et al.,
2023a; Zhong et al., 2023b). The detailed simulation
parameters of the TLP are shown in Table 1. The con-
trol rate was 25 Hz, with the MuJoCo physics engine
integrating the equations of motion over the time step
of the controller (40 ms).
Memory-Based Learning of Global Control Policies from Local Controllers
241

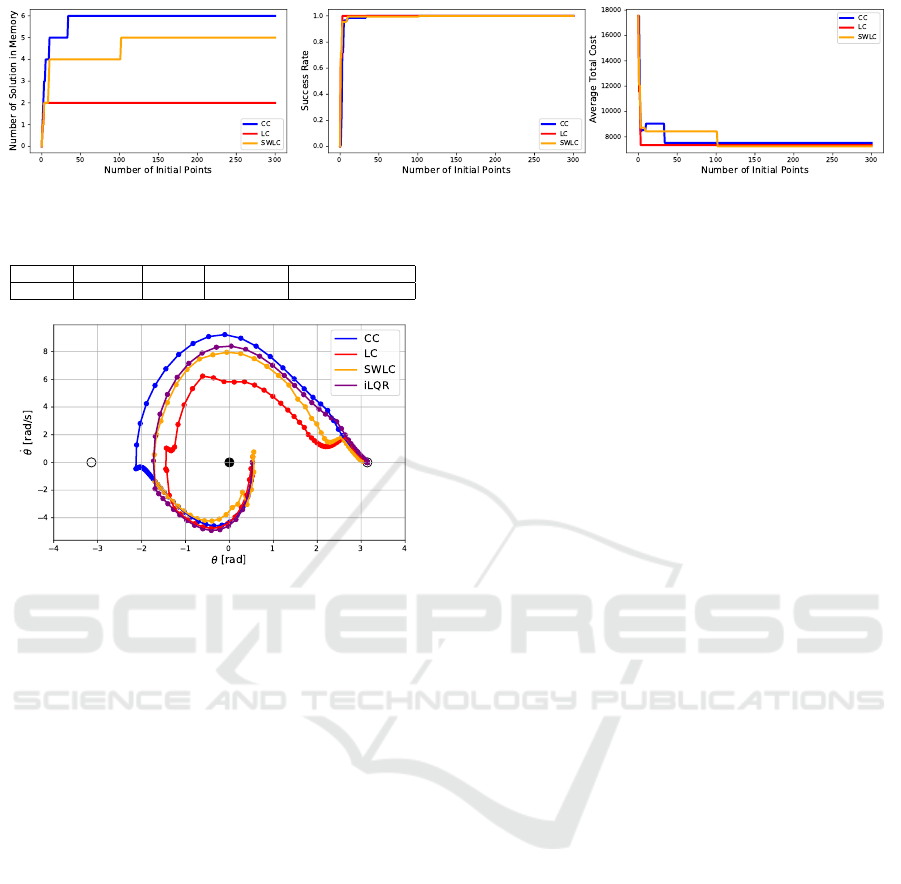
Figure 1: Solution performance of different variants of the MBiLQR algorithm across the same set of initial points.
Table 1: Parameters of the TLP.
Params Length l Mass m Damping b Torque Limit τ
max
Value 0.61 m 0.15 kg 0.05 Ns/m [−0.4,0.4] Nm
Figure 2: Solution trajectory comparison across different
variants of MBiLQR as well as for iLQR.
3.1.1 Computation of MBiLQR Solutions
The initial step in all variations of our proposed al-
gorithm involves computing a set of I nominal iLQR
solutions from multiple (N) starting states. The ef-
fectiveness of our global control method is highly de-
pendent on reliably finding these local solutions. The
initial states are sampled from a subset of the state
space where −π/2 ≤ θ ≤ π/2 (rad) and −3 ≤
˙
θ ≤ 3
(rad/s), with a total of 300 different points. This range
reflects the task’s objective of swinging up the pendu-
lum from a position generally below its suspension
point.
Each execution of the iLQR algorithm comprised
100 iterations, initialized with a completely random
guess for the nominal control trajectory u
k
, where 0 ≤
k ≤ H − 1 and H = 200 time steps. (The effective
time horizon of 8 s is more than sufficient to swing
up the TLP, even if multiple swings are necessary.)
We employed quadratic running and terminal costs,
with a very low control cost (0.001 of the state cost),
effectively instructing the solver that it can saturate
the control in order to minimize stabilization time.
During the solution collection process, we first
evaluate the current MBiLQR policy from the cur-
rent starting point. We determine if the goal state has
been reached successfully by calculating the distance
d = ∥x
H
− x
(G)
∥
2
between the terminal state x
H
and
the desired goal state x
(G)
. An execution of MBiLQR
is considered successful only if this distance is below
a threshold ε: d ≤ ε. We used a threshold of ε = 0.2.
This reflects the fact that an FSF controller without in-
tegral action cannot fully eliminate steady-state error,
where the pendulum is held near the upper unstable
equilibrium by a small amount of torque, so we con-
sidered such runs successful.
If MBiLQR is successful for a starting point, we
proceed with the next starting point until MBiLQR
fails at one of them. When this happens, a full iLQR
solution is computed for that starting point. If the
iLQR solution reaches the goal state, judged by the
same closeness criterion, it is added to the solution
set in memory. If not, the iteration continues with the
next starting point.
After each new solution is added to memory, we
conduct an evaluation session over the same 200 start-
ing points, pre-selected randomly. This session in-
dicates the current performance of the MBiLQR in
terms of the success rate over the 200 random points
and the average total cost from the start to the goal.
3.1.2 Empirical Results
The solution computation results, illustrated in Fig-
ure 1, reveal that among all variants, the CC method
required the most solutions (6 solutions) to achieve a
100% success rate, and even with this larger set of so-
lutions, it resulted in the highest average total cost. In
contrast, the LC variant required only 2 solutions and
had a lower average total cost compared to the CC
method. The SWLC variant required 5 solutions and
achieved the lowest average total cost. This highlights
the clear advantage of using value-based methods, as
they not only can reduce the total number of solutions
needed, but also decrease the average total cost of the
solutions.
Following the MBiLQR solution computation,
we also conducted a comprehensive statistical pol-
icy evaluation over 1,000 test runs across 5 different
random seeds, totaling 5,000 test cases. This evalu-
ation analyzed the performance of the MBiLQR al-
gorithm variants for their respective final number of
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
242

iLQR solutions stored in memory. The evaluation re-
sults, shown in Table 2, indicate that all variant meth-
ods achieved a 100% success rate. Furthermore, as
shown in Table 2, using value-based methods reduces
both the solution collection time and the control com-
putation time compared to the CC method. Notably,
the LC method required only 32% of the collection
time needed by the CC method.
Table 2: Time efficiency of solution collection and compre-
hensive evaluation for TLP compared across all variants.
Methods Solution Collection Time Control Computation Time Evaluation Success Rate
CC 46.05s 0.15 ms 100%
LC 14.97s 0.11 ms 100%
SWLC 39.3s 0.12 ms 100%
For illustration purposes, in Figure 2, we present
the phase space trajectories of the three variants along
with that of the actual iLQR solution starting from the
same initial state [π/6,0]. Even though all MBiLQR
variants reached the goal, notable differences are ob-
served. The CC method exhibits significant cluster-
ing of data points around −2 rad, indicating ineffi-
ciencies that slow down the solution. In contrast, the
LC method mitigates this issue with only minor clus-
tering around −1.3 rad, resulting in a more efficient
trajectory. The SWLC method outperforms all others,
showing smooth trajectories without noticeable clus-
tering, and also finding the most efficient path to the
goal. Additionally, the SWLC method produces a tra-
jectory that is very close to the (locally) optimal iLQR
solution from this initial state. These results under-
score the advantages of value-based methods, partic-
ularly the SWLC variant, which not only reduces the
number of solutions needed but also minimizes the
average total cost and ensures faster convergence.
3.2 Furuta Pendulum
We also investigated empirically the performance of
the proposed method on a more challenging control
benchmark: the task of swinging up and stabilizing
a Furuta pendulum (FP) at its upper unstable equilib-
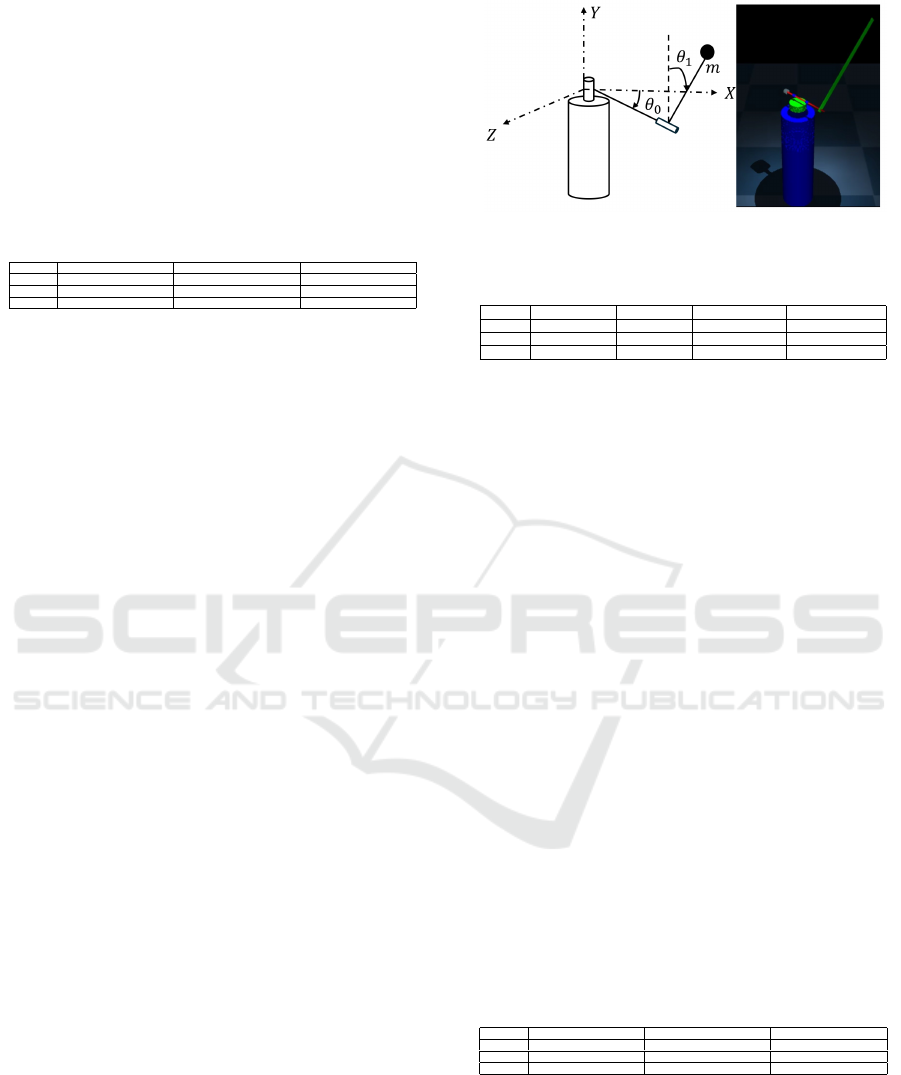
rium position (Xu et al., 2001). This task, depicted
in Figure 3, is a classical difficult control task due to
its nonlinear dynamics and under-actuation, requiring
complex control strategies to manage its inherently
unstable equilibrium. The equations of motion are
described in (Xu et al., 2001). Similarly to the TLP,
we verified the algorithms via simulations which were
conducted using a model of the FP implemented in the
MuJoCo physics engine (Todorov et al., 2012). We
used a shorter horizon of H = 75 time steps.
Figure 3: The Furuta pendulum (left) and its MuJoCo model
(right).
Table 3: Parameters of the FP.
Params Pend Length l
2
Pend Mass m Pend Damping b Torque Limit τ
max
Value 0.305 m 0.15 kg 0.05 Ns/m [−150,150] Nm
Params Arm Length l
1
Arm Mass m Arm Damping b Base Hight m
Value 0.153 m 0.075 kg 0.1 Ns/m 2m
3.2.1 Empirical Results
The comparative analysis of different control strate-
gies for the Furuta Pendulum, depicted in Figure 4
and Table 4, reveals significant differences in perfor-
mance across variants. The CC method, while requir-
ing the most solutions (93 solutions), achieved only
a 78% success rate and incurred the highest average
total cost. Conversely, the LC method demonstrated
greater efficiency, requiring only 45 solutions —- half
the number needed by the CC method —- and achiev-
ing a 91% success rate with a considerably lower av-
erage total cost. The SWLC method stood out by
needing just 5 solutions to attain a 100% success rate
and registering the lowest average total cost, underlin-
ing the substantial benefits of using state-transformed
value-based methods which significantly reduce both
the number of solutions required and the overall cost.
Moreover, Table 4 illustrates that value-based
methods not only enhance performance but also de-
crease both solution collection and control compu-
tation times. Notably, the SWLC method required
merely 14% of the time needed by the CC method for
solution collection, showcasing its efficiency in com-
putational resource utilization.
Table 4: Time efficiency of solution collection and compre-
hensive evaluation for FP compared across all variants.
Methods Solution Collection Time Control Computation Time Evaluation Success Rate
CC 8123.2s 0.28 ms 78.5%
LC 5394.3s 0.22 ms 89.5%
SWLC 1180.1s 0.21 ms 100%
4 CONCLUSION AND FUTURE
WORK
The proposed method constructs a global control pol-
icy valid everywhere in the state space of a dynami-
Memory-Based Learning of Global Control Policies from Local Controllers
243

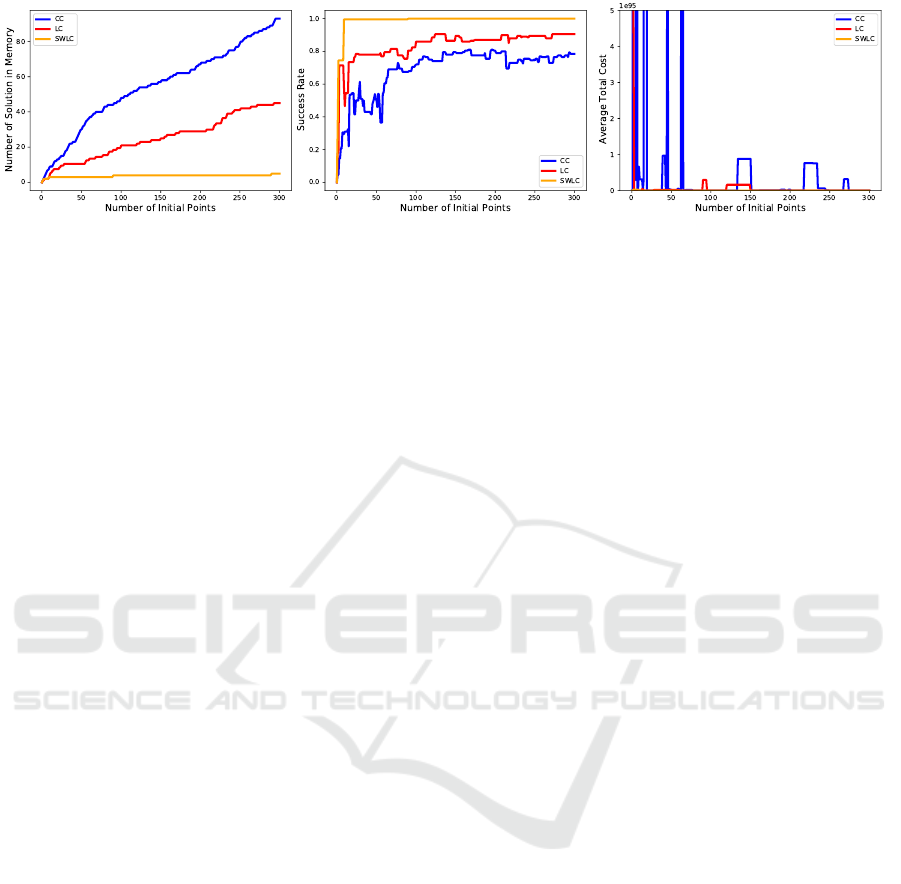
Figure 4: Solution performance of different variants of the MBiLQR algorithm across the same set of initial points.
cal system by aggregating a relatively small number
of solutions computed ahead of time for specific ini-
tial states in that space. These solutions are computed
by means of a modified iLQR method that employs
differential dynamic programming to find not only a
nominal state and control trajectory from a given ini-
tial state, but also a set of linear time-invariant con-
trollers that can stabilize the system around the nom-
inal trajectory, as well as a set of localized estimators
of the optimal cost-to-go for system states around the
states in the nominal trajectory. An empirical ver-
ification of three variants of the proposed memory-
based control algorithm on two benchmark problems
demonstrated that making use of the cost-to-go es-
timators results in the best performance (lowest av-
erage cost). Furthermore, this variant often requires
a lot fewer solutions to be pre-computed and stored
in memory, leading to memory savings and much
faster control computation in real time, thus reduc-
ing the computational requirements for the real-time
controllers deployed to execute the control method.
Although the empirical evaluation suggests that a
relatively small number of solutions stored in mem-
ory is sufficient to achieve 100% success rate on novel
starting points, the proposed algorithm does not have
a formal proof that it will always stabilize the sys-
tem from any starting point. We plan to investigate
whether such a proof can be produced based on the
complementary stability of the computed solutions
that act jointly to stabilize the system in different re-
gions of its state space.
REFERENCES
Grass, D., Caulkins, J. P., Feichtinger, G., Tragler, G., and
Behrens, D. A. (2008). Optimal control of nonlinear
processes. Berlin: Springer.
Jacobson, D. H. and Mayne, D. Q. (1970). Differential dy-
namic programming. Elsevier.
Levine, S., Finn, C., Darrell, T., and Abbeel, P. (2016). End-
to-end training of deep visuomotor policies. Journal
of Machine Learning Research, 17:1–40.
Li, W. and Todorov, E. (2004). Iterative linear quadratic reg-
ulator design for nonlinear biological movement sys-
tems. In First International Conference on Informat-
ics in Control, Automation and Robotics, volume 2,
pages 222–229. SciTePress.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,
Tassa, Y., Silver, D., and Wierstra, D. (2015). Contin-
uous control with deep reinforcement learning. arXiv
preprint arXiv:1509.02971.
Nikovski, D., Zhong, J., and Yerazunis, W. (2024).
Memory-based global iterative linear quadratic con-
trol. In International Conference on Control, Decision
and Information Technologies (CoDIT), Valetta.
Polydoros, A. S. and Nalpantidis, L. (2017). Survey of
model-based reinforcement learning: Applications on
robotics. Journal of Intelligent and Robotic Systems:
Theory and Applications, 86(2):153–173.
Reist, P., Preiswerk, P., and Tedrake, R. (2016). Feedback-
motion-planning with simulation-based LQR-trees.
The International Journal of Robotics Research, pages
1393–1416.
Stengel, R. F. (1994). Optimal control and estimation.
Courier Corporation.
Tassa, Y., Erez, T., and Todorov, E. (2012). Synthesis and
stabilization of complex behaviors through online tra-
jectory optimization. In 2012 IEEE/RSJ International
Conference on Intelligent Robots and Systems, pages
4906–4913. IEEE.
Tedrake, R. (2023). Underactuated Robotics,
https://underactuated.csail.mit.edu. Course Notes for
MIT 6.832.
Todorov, E., Erez, T., and Tassa, Y. (2012). Mu-
joco: A physics engine for model-based control. In
2012 IEEE/RSJ international conference on intelli-
gent robots and systems, pages 5026–5033. IEEE.
Xu, Y., Iwase, M., and Furuta, K. (2001). Time optimal
swing-up control of single pendulum. J. Dyn. Sys.,
Meas., Control, 123(3):518–527.
Zhong, J., Wu, R., and Si, J. (2023a). A long n-step surro-
gate stage reward for deep reinforcement learning. In
Advances in Neural Information Processing Systems,
volume 36, pages 12733–12745. Curran Associates,
Inc.
Zhong, J., Wu, R., and Si, J. (2023b). Mitigating esti-
mation errors by twin td-regularized actor and critic
for deep reinforcement learning. arXiv preprint
arXiv:2311.03711.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
244