Enhancing Intelligent Vehicle Lane-Change Strategies Based on

Deep Reinforcement Learning

Ruihui Li

Jinan University-University of Birmingham Joint Institute, Jinan University, Guangzhou, China

Keywords: Lane-Change Strategies, Deep Reinforcement Learning, Driving Safety.

Abstract: The evolution of intelligent vehicle lane-change strategies, propelled by advancements in automated driving

technology, underscores the significance of efficient road utilization, traffic congestion reduction, and driving

safety. This paper investigates the impact of varying penalty values for unnecessary lane changes at different

speed limits on lane-change decisions, aiming to ascertain effective strategies. Employing deep reinforcement

learning, this study simulates and analyses vehicle lane-change behaviours. Initially, a simulated traffic

environment is constructed, and a reward system is defined to reflect different speed limits and unnecessary

lane-change penalties. Utilizing the deep deterministic policy gradient (DDPG) algorithm, vehicles are trained

to optimize lane-change strategies across diverse scenarios. Evaluation based on average rewards

demonstrates that increasing the penalty for unnecessary lane changes enhances vehicle speed and facilitates

safer time headway maintenance at both low and high-speed limits. Experimental findings indicate that

adjusting the penalty effectively guides vehicles towards cautious lane-change decisions, thereby enhancing

driving efficiency and safety. This discovery presents a novel adjustment mechanism for autonomous driving

system decision algorithms and offers insights for the development of more intelligent traffic management

systems, promoting enhanced road utilization alongside driving safety.

1 INTRODUCTION

Vehicle lane change constitutes an essential vehicular

maneuver involving multiple vehicles in two lanes. It

is performed dynamically, necessitating interaction

with a plurality of proximate vehicles (Winsum,

1999). There is a high degree of randomness and

uncertainty in vehicle lane changes. Recent studies

have revealed that approximately three-quarters of

vehicular accidents are attributable to driver

misjudgments during lane-change processes,

highlighting the critical role of lane-change decisions

in the field of traffic safety. Appropriate decisions

regarding lane changes can markedly diminish

disturbances to adjacent vehicular traffic and enhance

the overall safety of the traffic system. On the

contrary, suboptimal lane-change decisions may

result in significant perturbations to vehicular flow,

precipitate traffic congestion, and potentially initiate

accidents (Ma, 2023). Hence, in-depth research on

lane changes is of vital crucial for promoting the

widespread application of intelligent driving

https://orcid.org/0009-0006-4913-3439

technologies and safeguarding both human lives and

assets. Intelligent driving systems must be capable of

making various decisions when faced with required

lane changes or interactive lane- change behaviors

(Sun, 2021).

Currently, the model of vehicle lane change

problems can be divided into three main categories.

The first category is rule-based models. For instance,

the Gipps model (Gipps P.D. ,1986) is the earliest

proposed lane-change model, serving as the

foundation for various microscopic traffic simulation

software programs. Highly dependent on rules

specified by domain experts, rule-based approaches

offer quick decisions and high interpretability but

lack the ability to adapt to new data and generalize

well. The second category is data-based algorithms.

Data-based models such as machine learning

algorithms and integrated learning algorithms

(Khelfa, 2023) predict lane-change behaviors using

large data sets to train classification algorithms,

offering relatively better performance than rule-based

models. However, financial investments for data are

200

Li, R.

Enhancing Intelligent Vehicle Lane-Change Strategies Based on Deep Reinforcement Learning.

DOI: 10.5220/0012923000004508

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 200-207

ISBN: 978-989-758-713-9

required and legal frameworks need to be considered

in data-based models (Zhang, 2022). As the third

category, Deep Reinforcement Learning (DRL)

models can continuously learn and improve when

interacting with the environment, which is more

generalizable than the rule-based model and can

avoid the need for large datasets effectively.

Combining DRL with vehicle networking technology

for urban road traffic control is a current research

hotspot and frontier field (Sutton, 2018). At present,

there are few studies on the interactions between

multiple autonomous vehicles and cooperative lane

change, while previous studies have rarely considered

the different performances of vehicles at different

speed limits.

The primary aim of this study is to delve into the

cooperative lane-change decisions of multiple

autonomous vehicles. Firstly, employing the deep

deterministic policy gradient (DDPG) framework,

this study tackles the multi-autonomous vehicles’

highway lane-change challenge amidst mixed traffic

scenarios. Here, vehicles collaborate to learn safe and

efficient driving strategies, leveraging averaged

output performance. Secondly, to ensure optimal

vehicle operations, the paper imposes penalties for

unnecessary lane changes while incentivizing

effective lane changes. This addresses the issue of

vehicles excessively or insufficiently changing lanes

to maximize reward values. Thirdly, this study

analyzes and compare the predictive performance of

models under different lane change reward schemes.

Moreover, this study incorporates various speed

limits commonly observed on highways (40, 60, 80

meters per second), adjusting safety distances

between cars accordingly. This resolves the limitation

of employing a uniform speed limit for all vehicles.

Additionally, in crafting the reward function, this

study considers sudden accelerations or decelerations

of vehicles, thereby mitigating the tendency to

prioritize driving efficiency over passenger comfort,

a common oversight in previous studies.

2 METHODOLOGIES

2.1 Dataset Description and

Preprocessing

In order to simulate driving scenarios, the highway-

env platform is used in this study (Leurent, 2018).

Highway-env is an open-source simulation

environment for developing and testing autonomous

driving strategies. Created by Edouard Leurent, the

environment provides a series of customizable, rule-

based traffic scenarios for evaluating the decision-

making and control systems of self-driving vehicles.

In highway-env, there are six specialized driving

scenarios to choose from, which are highway, merge,

roundabout, parking, intersection and racetrack. This

study considers a three-lane, one-way highway, with

a vehicle density of 8 autonomous vehicles and 10

manually driven vehicles kept constant.

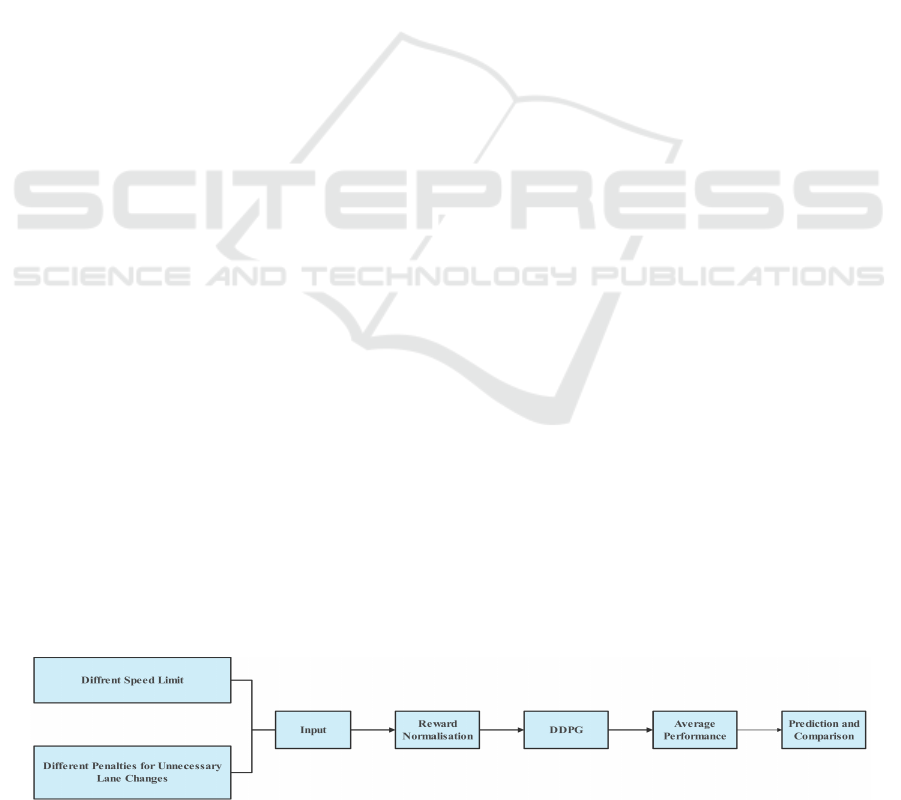
2.2 Proposed Approach

The objective of this research is to investigate the

lane-change performance of autonomous vehicles

when different levels of penalties are imposed for

unnecessary lane changing at different speed limits

respectively, in order to find effective lane- change

strategies. The approach is based on the DDPG, a

DRL algorithm, combined with a highway simulation

environment.

To enhance lane-change effectiveness, a penalty

for unnecessary lane-change distance is introduced.

Meanwhile, the acceleration during lane changes and

the range of the distance between vehicles after lane

changes are limited, which ensures that lane changes

provide a higher level of comfort and has minimal

impact on neighbouring vehicles. This paper

evaluated the average lane-change performance of

multi vehicles in different kind of traffic scenarios by

varying speed limit and penalty for unnecessary lane

change ， controlling the density of vehicles

unchanged. The controlled autonomous vehicles (the

agents) interact with the simulated traffic

environment and utilizes the return from the

environment to develop a lane-change strategy.

Figure 1 below illustrates the structure of the system.

Figure 1: The pipeline of the model (Photo/Picture credit: Original).

Enhancing Intelligent Vehicle Lane-Change Strategies Based on Deep Reinforcement Learning

201

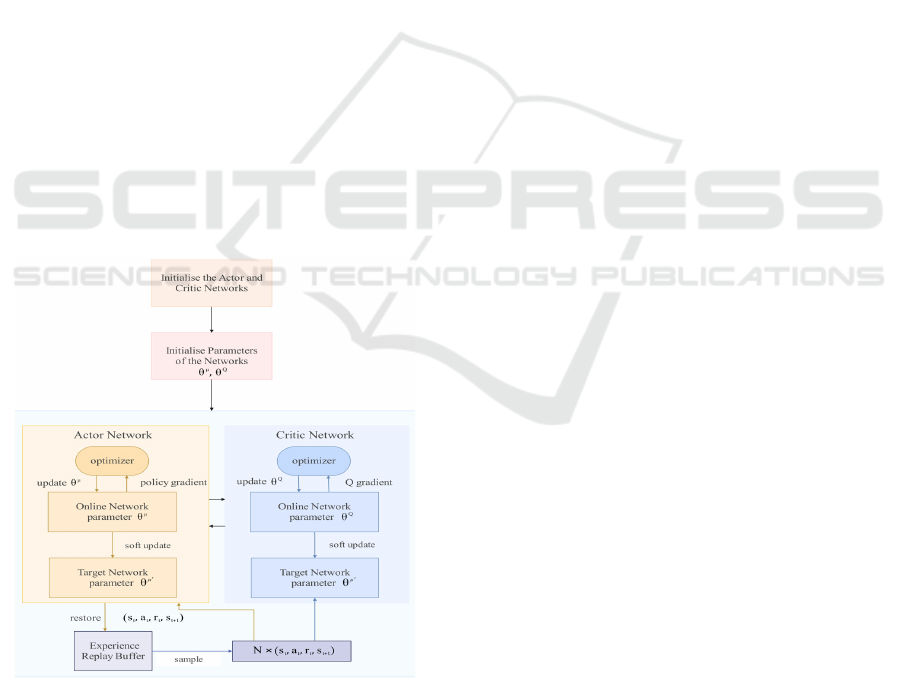
2.2.1 DDPG

The optimal lane change policy for this model is

achieved by the DDPG algorithm, a DRL algorithm

based on the Deterministic Policy Gradient theorem

(DPG). It introduces the Actor-Critic algorithm,

which has two neural networks. The actor network is

used to represent the policy P(a│s) by DPG. The

critic network Q(s, a; w) evaluates the long-term

payoff of taking a particular action (Ye, 2019).

Borrowing the target network in Deep Q-Network

(DQN), the DDPG algorithm uses a dual neural

network architecture (Online network and Target

network) for both the policy function and the value

function, resulting a more stable learning process and

faster convergence. Furthermore, the algorithm

introduces a Replay Buffer borrowed from DQN to

eliminate the correlation and dependence between

samples and facilitates algorithm convergence. Ideal

for continuous action spaces, DDPG outputs specific

actions for a state. The process of DDPG begins with

initializing actor and critic networks, then iteratively

sampling and executing actions, observing results,

storing observations, updating the policy gradient,

amending critic network based on target network and

rewards, and updating target network parameters,

aiding DDPG to gradually learn how to take optimal

actions in the continuous action space. Figure 2 below

shows the process of DDPG.

Figure 2: The process of DDPG (Photo/Picture credit:

Original).

2.2.2 Transformer Encoder

In reinforcement learning, it is crucial to define the

observation space, action space, and reward variables

after specifying the task that the agent need to

accomplish.

1. Observation space: The study sets 8 agents. For

each agent, 6 variables are defined here. It contains

lateral position, longitudinal position, lateral velocity，

longitudinal velocity and the orientation.

2. Action space: For each agent, the study defines

the range of acceleration, steering values, speed and

time headway which are continuous, enabling the

throttle control and cornering control.

3. Reward variables: To ameliorate the training

difficulty and augment the efficacy of the model, the

behavior of each agent is evaluated separately in this

paper. This ensures that rewards are not uniformly

applied to all agents.

Based on the above considerations above, this

paper proposes the reward function R using the linear

combination approach as follows:

1234

Rrr r r=+++

(1)

and calculates the average reward of 8 controlled

autonomous vehicles.

Metrics such as safety, traffic, efficiency, and

passenger comfort are considered in the design of the

reward function.

1) Safety evaluation 𝑟



: The controlled

autonomous vehicles should operate without collision

and without deviating from the road. Thus, this study

establishes penalty for collisions and reward for

vehicles that stay on the road. The safety evaluation

is obtained by linearly summing the two values.

If the vehicle collides with another vehicle, agent

will be penalised by 𝑟



For the vehicle that does not deviate from the

highway, agent will be rewarded by 𝑟



2) Time Headway evaluation 𝑟



: Vehicles should

keep a safe distance from the vehicle ahead to avoid

collision during travelling. This study establishes

reward for time headways promoting the efficient

operation of roads and penalty for unsafe time

headways. The time headway evaluation is obtained

by linearly summing the two values.

For different speed limits, this paper sets different

ranges of time headway to get reward. If the speed

limit is 40, the range of distances awarded is 30 to 35;

if the speed limit is 60, the range of distances awarded

is 60 to 65; and if the speed limit is 80, the range of

distances awarded is 80 to 85. The agent within the

specified time headway range is rewarded with 𝑟



EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

202

According to this paper, distances are deemed

unsafe when they are less than the maximum speed

limit minus 10. It is specified that when the time

headway from the previous vehicle is unsafe, the

agent is penalised with 𝑟



3) Speed evaluates 𝑟



: Vehicles are expected to

travel at a high-speed level while ensuring safety.

This paper stipulates that when a vehicle is

travelling at a speed between the maximum speed

limit minus 5 and the maximum speed limit, the agent

is rewarded with 𝑟



4) Lane change evaluation 𝑟



: In this study, the

initial roads of all 8 controlled autonomous vehicles

are set as the leftmost lane. The effectiveness, safety,

and comfort of lane change are considered, added

linearly as the lane change evaluation.

For the effectiveness of lane change, considering

the limited visibility of the self-driving vehicle (Li,

2022), this study defines that a lane-change action is

not necessary if the time headway of the controlled

autonomous vehicle is greater than 85m. The penalty

of the unnecessary lane change and the reward of the

effective lane change are defined by 𝑟



, i.e.:

0.2

p unecessary lane changes

other lane changes







(2)

where p is the penalty value for unnecessary lane

change. This paper will study the lane change

strategies and compare the performance of controlled

autonomous vehicles when

𝑝 = −0.2, −0.35, −0.5,

respectively.

For the comfort of lane change, it is reflected by

the acceleration of the vehicles at the moment of lane

change in this study, i.e.

0.1 [ 5,5],

0.1

if a

other lane changes

∈−





−



(3)

where 𝑎



denotes the acceleration of controlled

autonomous vehicles during the lane change at time 𝑡.

For the safety of lane change, this paper evaluates

the impact of lane change on the surrounding vehicles

by observing the closest distance between the lane-

change vehicle and the vehicles behind it on this road

at the moment when finishing the lane change, i.e.

1tan,

0.2

if the dis ce is unsafe

other lane changes

−







(4)

In addition, to avoid controlled autonomous

vehicles changing lanes frequently, operating on the

rightmost lane is penalised with 𝑟



4. Reward values. The Table 1 below displays

reward values that are not previously mentioned.

Table 1: Reward values that are not previously mentioned.

Reward Item Reward value

𝑟



-1.5

𝑟



1.8

𝑟



0.4

𝑟



-1.2

𝑟



0.5

𝑟



-0.001

2.2.3 Loss Function

In the DDPG algorithm, there are two loss functions

for training critic and actor networks. Mean Squared

Error (MSE) is adopted for Critic Loss, and the

expression is as follows:

() ( (,| ))

iii

LyQsa

θθ

=−



(5)

where 𝑄



𝑠, 𝑎





is the function evaluation of the

critic network for the output action of the actor

network, θ



denotes a parameter of the critic network,

𝑦



denotes the target value, calculated as 𝑦



= 𝑟



γ𝑄



𝑠



, μ



𝑠



θ





θ





 and 𝑁 denotes the

number of samples. This loss function encourages the

critic network's output to be as close to the true return

value as possible.

The Actor Loss is:

() (,(| )| )

LQss

μμ

θθ

=−



(6)

where μ



𝑠





denotes the action output by the Actor

network, 𝜃



denotes the parameter of the actor

network. This loss function encourages the actor

network to adjust its policy by expanding the

expected return of the selected action. The negative

sign is used to indicate gradient ascent.

In DDPG algorithm, these two loss functions are

interleaved: first the critic network is updated by

critic's loss function, and then the actor network is

updated by the output of the Critic network.

3 RESULTS AND DISCUSSION

3.1 Comparison of Average Rewards

Figures 3(a), (b) and (c) below show the average

rewards of 8 controlled autonomous vehicles when

different penalty values p are set for unnecessary lane

change of the vehicles under the speed limits of 40,

Enhancing Intelligent Vehicle Lane-Change Strategies Based on Deep Reinforcement Learning

203

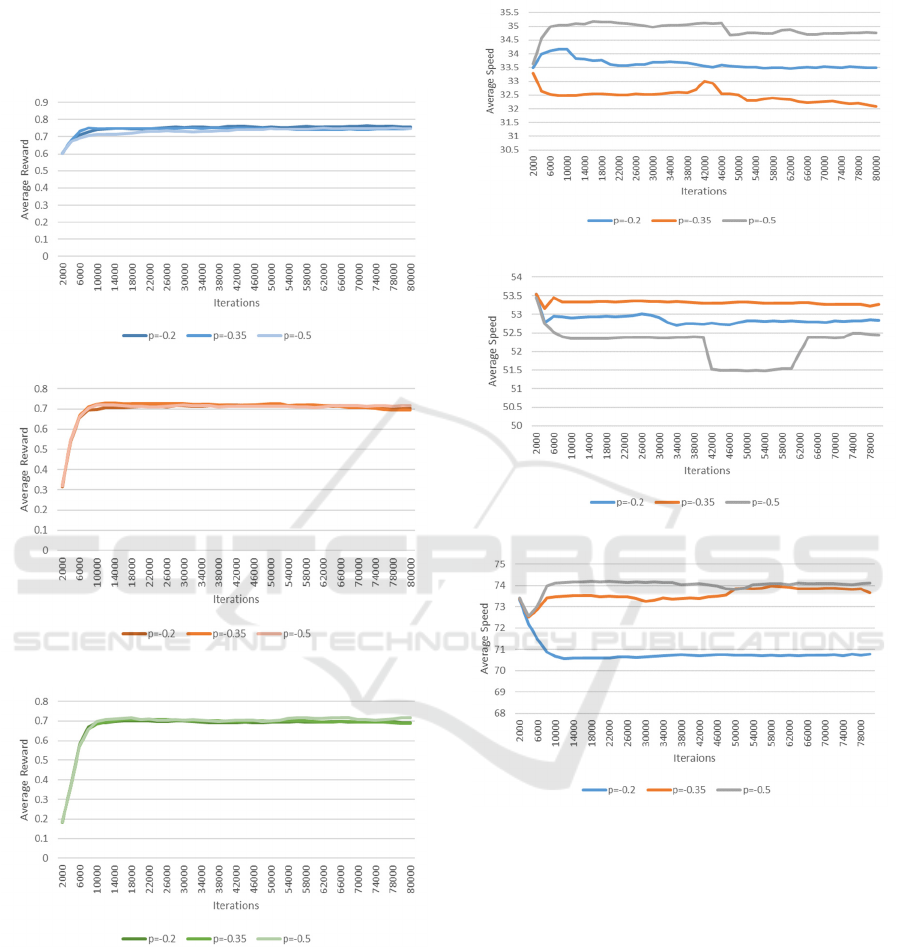
60 and 80, respectively. As can be seen from the

figure, the curves all stabilize after more than about

10,000 iterations, and the average reward value

reaches about 0.7, indicating that the learning process

starts to converge and the algorithm is close to the

optimal strategy.

(a) 40m/s

(b) 60m/s

Figure 3: The average rewards of different

𝑝

(Photo/Picture

credit: Original).

3.2 Comparison of Average Speeds

Figures 4(a), 4(b) and 4(c) below represent the

average speeds of 8 controlled autonomous vehicles

when different penalty values p are set for

unnecessary lane change at speed limits of 40, 60 and

80 respectively.

(a) 40m/s

(b) 60m/s

Figure 4: The average speeds of different

𝑝

(Photo/Picture

credit: Original).

The Figures demonstrate that setting different penalty

values for lane-change behaviors can impact the

behavioral pattern of the vehicles and, consequently,

the overall average speed. Meanwhile, the impact of

varying penalty values on the speed of the vehicles

differs at different speed limits. Figures 4(a) and 4(c)

demonstrate that the group with the highest penalty

values has the highest average speed at speed limits

of 40 and 80. Conversely, Figure 4(b) shows that the

group with the highest penalty values has the lowest

average speed at a speed limit of 60. This suggests

that unnecessary lane changing in low and high-speed

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

204

situations may lead to increased instability in the

traffic flow, making it more chaotic and thus affecting

the speed of vehicles. Simultaneously, if the penalty

for changing lanes is excessively high in medium-

speed scenarios, drivers may become overly cautious

when changing lanes. This over-restriction can result

in over-congestion in some lanes while others remain

relatively free, leading to an irrational allocation of

lane resources.

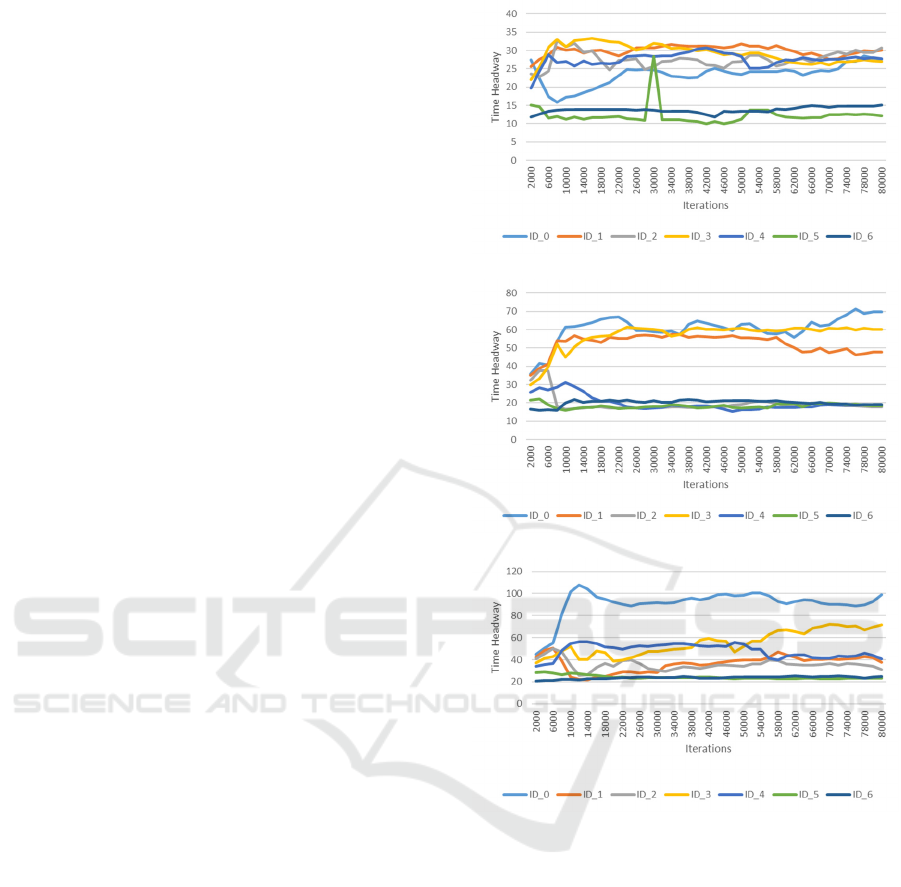
3.3 Analysis of Time Headway

Performance of 8 Autonomous

Vehicles

By calculating the average time headway of 8

autonomous vehicles, this paper concludes that the

maximum numbers of vehicles with safe time

headway are achieved when 𝑝 = −0.35 for a speed

limit of 40 m/s, 𝑝 = −0.35 for a speed limit of 60

m/s, and 𝑝 = −0.5 for a speed limit of 80 m/s.

This suggests that as speed limits increase, higher

penalties for unnecessary lane change are more

effective in maintaining safe distances between

vehicles and preventing vehicles from increasing

their speed by changing lanes without regard for

safety. To ensure safe driving, the data with the

highest number of vehicles with safe time headway

among 8 vehicles at different speed limits is selected

for analysis.

As shown in Figure 5, under three different speed

limits, the vehicle with ID 8 remains at the front of

the road, resulting in no other vehicles overtaking it

and therefore no time headway. The remaining 7

vehicles are shown in the figure, with vehicles ID 0

and 3 maintaining a safe time headway under all three

speed limits, while vehicles ID 5 and 6 do not

maintain a safe time headway. The study finds that 50%

of vehicles travelling under a speed limit of 40 and

50% of cars travelling under a speed limit of 60 can

maintain a safe time headway. However, only 27.5%

of vehicles are able to maintain a safe time headway

at a speed limit of 80. These results suggest that the

model is more suitable for low and medium speed

situations, and that its performance decreases as the

speed limit increases.

To investigate the reasons for the varying

performance of the time headway of the eight

vehicles, this paper considers three factors: average

speed, percentage of no vehicles ahead, and frequent

lane changes of the eight vehicles at different speed

limits. The Table 2 below displays the average speed

and percentage of no vehicles ahead of the eight

(a) 40m/s

(b) 60m/s

Figure 5: The time headways of eight autonomous vehicles

(Photo/Picture credit: Original).

vehicles in the last 10,000 iterations, and Figure 6

illustrates the number of lane-change time points at

different speed limits. The results indicate that

vehicles with IDs 5 and 6 experience a higher

percentage of no vehicles ahead. To avoid penalties

due to small time headway, these two vehicles are

kept at the front of their respective roads by making a

relatively high number of lane changes compared to

all the vehicles at speed limits 40 and 80. Additionally,

these two vehicles are kept at the front of their

respective roads by maintaining a higher speed at

speed limit 60, resulting in a high-speed reward. As

the speed limit increases, the number of vehicles

maintaining an average speed in the high-speed range

increases, and the number of lane changes gradually

Enhancing Intelligent Vehicle Lane-Change Strategies Based on Deep Reinforcement Learning

205

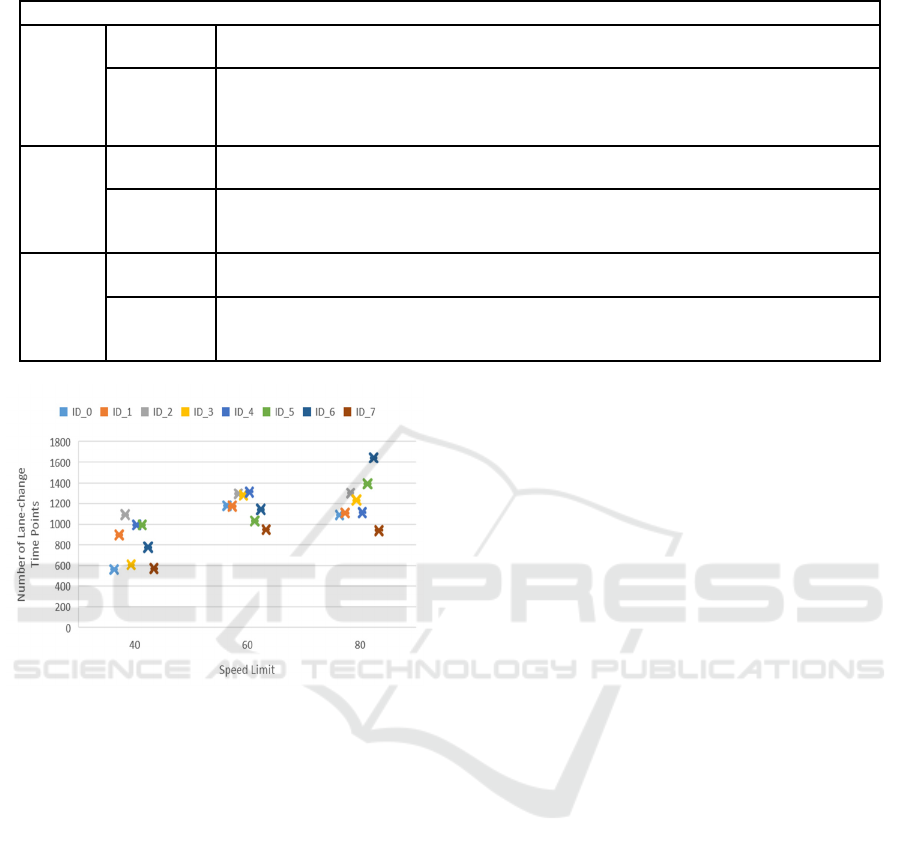
Table 2: Performance of eight autonomous vehicles in the last 10,000 iterations.

ID_0 ID_1 ID_2 ID_3 ID_4 ID_5 ID_6 ID_7

Speed

Limit=40

Average

31.42 37.18 30.83 31.09 31.63 34.61 30.85 29.67

Percentage of

no vehicles

ahead

6.78% 0.30% 2.15% 11.04% 12.67% 15.03% 46.74% 100.00%

Speed

Limit=60

Average

51.19 50.98 50.97 50.97 57.40 57.37 57.27 49.92

Percentage of

no vehicles

ahea

0.37% 1.83% 0.00% 12.58% 27.48% 17.49% 89.68% 100.00%

Speed

Limit=80

Average

77.42 77.61 77.61 70.84 77.36 70.84 70.84 70.09

Percentage of

no vehicles

ahea

0.26% 0.58% 1.29% 1.99% 26.63% 27.24% 85.72% 100.00%

Figure 6: The number of lane-change time points of eight

vehicles (Photo/Picture credit: Original).

rises. Meanwhile, the number of vehicles able to

maintain a safe time headway decreases. This

suggests that the way in which vehicles are rewarded

may gradually shift from a reduction in penalties for

not maintaining a safe time headway to rewards for

high speeds and lane changes as the speed limit

increases.

3.4 Model Improvement Options

To improve the model for the problem where the

vehicle is rewarded by increasing its speed and lane

changing frequency when maintaining small time

headway, the following steps can be taken:

1. Create a safety envelope centred around the

vehicle that represents the minimum safe time

headway that needs to be maintained at any speed. If

a vehicle exceeds this domain, it should be penalised

accordingly (Erlien, 2015).

2. By combining an advanced prediction

algorithm with an adaptive control strategy to help

vehicle intelligently sense changes in the speed of the

vehicle in front of it and promptly adjusts its own

speed and lane-changing manoeuvres, ensuring that

smooth traffic conditions are maintained without

sacrificing safety.

3. The Multi-Agent Deep Deterministic Policy

Gradient algorithm (MADDPG) can be applied to

enhance the synergy between intelligences.

In summary, varying penalty values for lane-

change behaviour impacts the behavioural pattern of

the vehicles. Larger penalties for unnecessary lane-

change result in higher average speeds at both low

and high-speed limits and are more effective in

maintaining safe time headway between vehicles at

high-speed limit. As the speed limit increases,

vehicles may gradually shift from a reduction in

penalties for not maintaining a safe time headway to

rewards for high speeds and lane changes.

4 CONCLUSIONS

This study investigates the cooperative lane change

decisions made by multiple autonomous vehicles.

Utilizing the DDPG algorithm, it examines how

autonomous vehicles perform lane changes under

different speed limits while imposing varied penalties

for unnecessary lane changes. The methodology

involves penalizing such changes, rewarding

effective ones, averaging out rewards among multiple

agents, and analyzing behaviors across diverse speed

limit scenarios. Through extensive experiments, the

proposed method is thoroughly evaluated. Results

indicate that heavier penalties result in higher average

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

206

speeds across varying speed limits, while also

ensuring safe distances between vehicles, especially

at higher speeds. These findings suggest a shift in

behavioral patterns, emphasizing rewards for high

speeds and lane changes rather than penalties for not

maintaining safe distances. Moving forward, the

research will focus on establishing a safety envelope

centered around the vehicle, with attention to

determining suitable values and flexibility for this

safety measure.

REFERENCES

Erlien, S. M., Fujita, S., & Gerdes, J. C. (2015). Shared

steering control using safe envelopes for obstacle

avoidance and vehicle stability. IEEE Transactions on

Intelligent Transportation Systems, vol. 17(2), pp: 441-

451.

Khelfa, B., Ba, I., & Tordeux, A. (2023). Predicting

highway lane-changing maneuvers: A benchmark

analysis of machine and ensemble learning algorithms.

Physica A: Statistical Mechanics and its Applications,

vol. 612, pp: 128471.

Leurent, E. (2018). An Environment for Autonomous

Driving Decision-Making. Computer software.

Li, L. et al., (2022). Three principles to determine the right-

of-way for AVs: Safe interaction with humans. IEEE

Trans. Intell. Transp. Syst., vol. 23(7), pp. 7759– 7774.

Ma, C., & Li, D. (2023). A review of vehicle lane change

research. Physica A: Statistical Mechanics and its

Applications, pp: 129060.

Sun, Q., Wang, C., Fu, R., Guo, Y., Yuan, W., & Li, Z.

(2021). Lane change strategy analysis and recognition

for intelligent driving systems based on random forest.

Expert Systems with Applications, vol. 186, pp: 115781.

Sutton, R. S., and Barto, A. G., (2018). Reinforcement

Learning: An Introduction. Cambridge, MA, USA:

MIT Press.

Winsum, W.V., Waard, D.D., Brookhuis, K.A., (1999).

Lane change manoeuvres and safety margins, Transp.

Res. vol.2(3), pp: 139–149.

Ye, Y., Zhang, X., & Sun, J. (2019). Automated vehicle’s

behavior decision making using deep reinforcement

learning and high-fidelity simulation environment.

Transportation Research Part C: Emerging

Technologies, vol. 107, pp: 155-170.

Zhang, J., Chang, C., Zeng, X., & Li, L. (2022). Multi-agent

DRL-based lane change with right-of-way

collaboration awareness. IEEE Transactions on

Intelligent Transportation Systems, vol. 24(1), pp: 854-

869.

Enhancing Intelligent Vehicle Lane-Change Strategies Based on Deep Reinforcement Learning

207