Fitness Histograms of Expert-Defined Problem Classes in Fitness
Landscape Classification
Vojt
ˇ
ech Uher
a
and Pavel Kr
¨
omer
b
Department of Computer Science, VSB – Technical University of Ostrava, Ostrava-Poruba, Czech Republic
Keywords:
Exploratory Landscape Analysis, Sampling Strategies, Low-Discrepancy Sequences, Fitness Histogram,
Multiclass Classification.
Abstract:
Various metaheuristic algorithms can be employed to find optimal or sub-optimal solutions for different prob-
lems. A fitness landscape (FL) is an abstraction representing a specific optimization task. Exploratory land-
scape analysis (ELA) approximates the FL by estimating its features from a limited number of random solu-
tion samples. Such ELA features help in estimating the properties of the FL and ultimately aid the selection
of suitable optimization algorithms for problems with certain FL characteristics. This paper proposes using
a normalized histogram of fitness values as a simple statistical feature vector for representing FLs. These
histograms are classified using various classifiers to evaluate their effectiveness in representing different prob-
lems. The study focuses on 24 single-objective benchmark problems, grouped into five expert-defined classes.
The performance of several classifiers is compared across different problem dimensions and sample sizes, em-
phasizing the impact of different sampling strategies and the number of histogram bins. The findings highlight
the robustness of histogram representation and reveal promising experimental setups and relationships.
1 INTRODUCTION
Nature-inspired metaheuristic algorithms, such as
swarm, e.g., Particle Swarm Optimization (Eslami
et al., 2012), and evolutionary, e.g., Genetic Algo-
rithm (Katoch et al., 2021; Nowakova and Poko-
rny, 2014), and Differential Evolution (Das and Sug-
anthan, 2010) methods are effective approaches for
solving complex problems through optimization. The
nature of black-box optimization problems that are
most often tackled by bio-inspired metaheuristics is
usually unknown. At the same time, it is well
understood that different metaheuristics perform on
different types of problems differently (Mersmann
et al., 2011) and the selection of an efficient algo-
rithm or algorithm parameters becomes an impor-
tant and challenging issue. An appropriate algo-
rithm well-suited for solving a specific problem can
significantly enhance optimization performance and
conserve valuable resources by reducing the num-
ber of costly fitness function evaluations (Malan,
2021; Lang and Engelbrecht, 2021; Zou et al., 2022).
Landscape analysis is a top-level data-driven pro-
a
https://orcid.org/0000-0002-7475-3625
b
https://orcid.org/0000-0001-8428-3332
cess that can provide at least limited insights into
general optimization problems, estimate their prop-
erties and characteristics, and entangle the relation-
ships between different types of problems and var-
ious optimization algorithms. It can be used for
many downstream tasks including automated algo-
rithm selection (Malan, 2021; Tanabe, 2022), param-
eter tuning (Pikalov and Mironovich, 2021), algo-
rithm performance prediction and explanation (Tra-
janov et al., 2022), problem classification (Uher and
Kr
¨
omer, 2023; Renau et al., 2021), etc.
A fitness landscape (Richter and Engelbrecht,
2014) is an abstraction that represents an opti-
mization problem by a continuous multidimensional
function (hypersurface). However, a complete de-
scription of the problem’s FL would be equivalent
to solving it. Instead, practical landscape analy-
sis methods describe the FLs by carefully selected
features that summarize their important properties,
for example, ruggedness, deceptiveness, and multi-
modality (Mu
˜
noz et al., 2015).
Exploratory landscape analysis (Mersmann et al.,
2011) is a popular problem-agnostic method for char-
acterizing FLs of optimization problems. On the top
level, it consists of a series of steps that enable an
effective and compressed characterization of the hy-
Uher, V. and Krömer, P.
Fitness Histograms of Expert-Defined Problem Classes in Fitness Landscape Classification.
DOI: 10.5220/0012923900003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 205-213
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
205

persurfaces defined by the fitness and other interest-
ing values (e.g., constraint violation score) associ-
ated with problem solutions. Essentially, ELA takes
a finite set of sample problem solutions, computes
for them the characteristic values, and uses them to
compute numerical landscape features (Mersmann
et al., 2011; Zou et al., 2022). The outcomes of ELA
are affected by many parameters, including the em-
ployed sampling strategy, the type of evaluated land-
scape features, etc. The sampling strategies aim to
achieve good coverage of the search space, high regu-
larity, and low discrepancy of samples. Popular sam-
pling strategies include Uniform pseudo-random sam-
pling, quasi-random techniques such as Latin Hyper-
cube Sampling (LHS) (McKay et al., 2000; Kerschke
and Trautmann, 2019), and sampling based on low-
discrepancy sequences such as Sobol (Sobol, 1967)
and Halton sequence (Halton, 1964). A popular set of
landscape features is provided, e.g., in the FLACCO
library (Kerschke and Trautmann, 2019). Several
studies with single (Renau et al., 2021; Lang and
Engelbrecht, 2021) and bi-objective (Kr
¨
omer et al.,
2022; Liefooghe et al., 2023; Kr
¨
omer et al., 2024)
problems demonstrated that the values of landscape
features are significantly affected by the sampling
strategy.
The evaluation of commonly used landscape fea-
tures often involves computationally expensive oper-
ations such as the computation of pairwise distances,
execution of several local searches, and building of lo-
cal optima networks (Kerschke and Trautmann, 2019;
Adair et al., 2019). This makes their use, in par-
ticular for large sets of samples, often inconvenient.
Besides robust and expensive types of landscape fea-
tures, more straightforward and lightweight FL char-
acterization approaches can be considered. Recently,
a simple FL representation based solely on the dis-
tribution of individual fitness values has been investi-
gated (Uher and Kr
¨
omer, 2023). The method repre-
sents the FL by a normalized histogram reflecting the
distribution of fitness values calculated for the sam-
ples generated by a selected sampling strategy. The
study (Uher and Kr
¨
omer, 2023) showed that the fit-
ness histogram is, despite its simplicity, a sufficiently
distinctive landscape representation that enables the
detection of different types of FLs by cluster analy-
sis. It also examined the impact of the sampling strat-
egy and showed that the Uniform and optimized LHS
overcome the performance of the low-discrepancy se-
quences. However, the paper explored the histogram
feature only to a limited extent including fixed set-
ting of 50 histogram bins performing simple clus-
tering analysis leading to relatively weak separabil-
ity (silhouette score ≤ 0.5). These initial results en-
couraged an additional, more detailed investigation of
the effects of different sampling strategies, histogram
parameters, and distance measures in the context of
problem representation by fitness histograms.
This study summarizes the results of an exten-
sive computational investigation into the use of fit-
ness histograms for problem characterization. Clas-
sification based on histograms is a technique known
in image retrieval as color indexing (Swain and Bal-
lard, 1991). In color indexing, each image is rep-
resented by a histogram of the color frequencies of
its pixels. Comparable distributions of colors indicate
similar images (Swain and Ballard, 1991; Barla et al.,
2003). To characterize black-box optimization prob-
lems, the set of fitness values is interpreted as a statis-
tical random variable and its distribution (histogram
with a user-defined number of bins) can be compared
with other random variables (Shirakawa and Nagao,
2016), in this case, the representations of other FLs
corresponding with other problems.
In this work, the ability of fitness histograms to
capture the properties of different types of black-box
optimization problems under a wide variety of exper-
imental configurations is assessed. To do that, we
employ an expert-designed, well-structured, and care-
fully curated set of test problems from the COmparing
Continuous Optimizers (COCO) platform (Hansen
et al., 2021). The experiments are performed on the
24 BBOB single-objective test functions available in
COCO grouped into 5 expert-defined classes. The
functions are first represented by the fitness his-
tograms obtained from solution samples of differ-
ent sizes obtained with the help of different sam-
pling strategies. Then, the Decision tree, Random
forest, and k-Nearest neighbors (kNN) (Renau et al.,
2021) classifiers in combination with standard Eu-
clidean and two statistical (histogram distance, KL-
divergence) distance measures (Uher and Kr
¨
omer,
2023) are applied to learn the expert-defined classes
of the test functions and classify unknown optimiza-
tion problems. The classification process is used as
a verification that the fitness histogram covers suffi-
cient information to distinguish benchmark problems
of different properties. The results show that different
combinations of sampling, distances, and classifiers
yield different abilities to represent problems and sig-
nificantly extend the initial findings on these issues
from (Uher and Kr
¨
omer, 2023).
The following Section 2 describes the ELA
pipeline and the methods used to characterize the test
problems by fitness histograms. Section 3 provides
a detailed description of the experiments and a thor-
ough analysis of their results. Finally, major conclu-
sions are drawn and future work is outlined in 4.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
206

2 FITNESS LANDSCAPE
CLASSIFICATION BY
HISTOGRAMS OF FITNESS
VALUES
Each FL corresponds to one single-objective test
function and is represented by a normalized histogram
of fitness values computed for a set of randomly
selected sample solutions scattered over the search
space. The assumption is that similar functions, i.e.,
from the same class of problems, should be repre-
sented by similar fitness histograms, and functions
from different problem classes should yield dissimi-
lar fitness histograms. We first describe the used test
suite, sampling strategies, the normalized histograms
of fitness values, and summarize the employed classi-
fication methods.
2.1 Test Problems
Numerous benchmark suites are available for evalu-
ation purposes, as highlighted by Engelbrecht et al.
(Lang and Engelbrecht, 2021). We opted to utilize
the single-objective benchmark problems provided by
the COmparing Continuous Optimizers (COCO) plat-
form (Hansen et al., 2021). Specifically, this col-
lection encompasses 24 BBOB noiseless, scalable, and
single-objective test functions, each characterized by
unique fitness landscapes. This selection serves as a
systematic framework for evaluating sampling strate-
gies and their associated histograms. Each function
within this set is accessible in various dimensions
(d ∈ {2,3,5,10,20,40}) and is represented by 15 in-
stances; however, our study focuses exclusively on
the first instance. The COCO test suite provides an
expert-defined classification of the 24 BBOB test func-
tions into 5 groups: 1) Separable functions (f001-
f005), 2) Functions with low or moderate condition-
ing (f006-f009), 3) Functions with high conditioning
and unimodal (f010-f014), 4) Multi-modal functions
with adequate global structure (f015-f019), 5) Multi-
modal functions with weak global structure (f020-
f024). This classification is used as a theoretical back-
ground for our experiments. The COCO platform is
acknowledged as a state-of-the-art publicly available
resource (Renau et al., 2021).
In order to scrutinize the continuous functions as-
sociated with the test problems, a discrete sample set
of size n is generated using a specified sampling strat-
egy, with the stipulation that n be a power of two,
i.e., n = 2
m
. This selection is particularly advanta-
geous for certain low-discrepancy sequences. In the
context of ELA, it is common that n is within the
range of [10
2
· d,...,10
3
· d] (Mu
˜
noz et al., 2015).
The implementation of these methodologies relies on
the Python COCO library, alongside the SciPy and
Scikit-learn Python libraries (publicly available).
2.2 Problem Sampling
In ELA, the goal of problem (solution) sampling is to
select a finite set of problem solutions (sample) that
will represent the entire problem. The fitness values
of the solution sample are computed and used to esti-
mate the characteristics of the fitness landscape and,
consequently, the whole problem (Renau et al., 2020).
A significantly biased set of samples can result in sys-
tematic information loss due to under- or oversam-
pling in specific regions. Various sampling methods
can be utilized to fulfill this overarching goal, aim-
ing to acquire data points and fitness values that en-
able precise characterization of the underlying prob-
lem, emphasizing even coverage of the search space.
As each sampling strategy produces slightly differ-
ent samples and the landscape features computed on
their basis may also vary. In this work, we con-
sidered the effect of several popular sampling strate-
gies. Uniform Random sampling (Uniform) serves
as the baseline sampling method, generating solu-
tions for sampling through a pseudorandom genera-
tor with a uniform probability distribution. Latin
Hypercube Sampling (LHS) generates near-random
samples from multi-dimensional spaces. It divides
the space into a square grid, ensuring that only one
sample is drawn from each column and row (McKay
et al., 2000). The LHS Optimized (LHSO) sampling
used in the experiments is an optimized variant of
LHS that employs random coordinate permutations
to reduce centered discrepancy and enhance space–
filling robustness. Sobol sequence-based sampling
(Sobol) utilizes the Sobol low-discrepancy sequence,
a quasi-random sequence with a base of 2 that binary
represents the position on each dimension and is ef-
ficiently implemented through bit-vector operations
(Sobol, 1967). To enhance the discrepancy of the
sequence, a linear matrix scramble with digital ran-
dom shifting is applied. Halton sequence-based sam-
pling (G-Halton) builds on the Halton low-discrep-
ancy sequence, another quasi-random sequence using
coprime integers as its bases (Halton, 1964). It is a
generalization of the one-dimensional van der Corput
sequence (Chi et al., 2005). While performing well
in low dimensions, a correlation is observed in higher
dimensions that adversely affects the distribution.
Fitness Histograms of Expert-Defined Problem Classes in Fitness Landscape Classification
207

2.3 Normalized Fitness Histogram
A simple global feature aggregated from local fitness
values is defined (Uher and Kr
¨
omer, 2023). Given
a fitness function, f : R
d
→ R, and a set of discrete
samples, S = {s
1
,...,s
n
}, the set of fitness values is
computed as V = {v;∀s ∈ S : v = f (s)}, where d is
the problem dimension and n is the number of sam-
ples. The set, V , is utilized to compute a histogram of
h bins within the range of values [min(V ), max(V )],
subject to
∑
h
j=1
c
j
/n = 1, where c
j
is the number of
fitness values falling to the j-th bin. The normalized
histogram represents a discrete probability distribu-
tion of fitness values c = {c
1
/n,...,c
h
/n}.
The histogram is influenced by landscape prop-
erties such as ruggedness, variance of fitness values,
and multi-modality. The histogram bins, denoted as h,
provide a standardized length to feature vectors, facil-
itating easy comparisons. The value of h also governs
the precision of the captured distribution. A smaller h
results in greater compression of the contained infor-
mation. Normalizing histograms in the existing range
of values is important to obtain comparable represen-
tations of fitness distributions. This feature is invari-
ant to translation, scaling, and rotation and does not
consider any local structure of a fitness function.
2.4 Histogram Classification
A normalized histogram can be interpreted as a real-
valued feature vector of length h, and can be used
with standard classification algorithms, represented
here by Decision tree (DT), Random forest (RF), and
k-Nearest neighbors (kNN) using the Euclidean dis-
tance. These methods are usable for the non-separable
distribution of classes (Renau et al., 2021), but they
do not reflect the statistical meaning of a histogram
that represents a discrete probability distribution of
fitness values. It typically cannot take on arbitrary
values, as the sum of bins equals to 1. Therefore,
two statistical distance measures (histogram distance,
KL-divergence) are provided for usage with kNN for
comparison (Uher and Kr
¨
omer, 2023).
Histogram distance (histDist) is a measure that
can express the degree of similarity of two histograms
as their intersection (Swain and Ballard, 1991; Barla
et al., 2003). Histogram intersection is defined as a
sum of minimum values of corresponding bins of two
histograms, a and b, with the same number of bins,
h, histInt(a,b) =
∑
h
j=1
min(a
j
,b
j
). The histograms
are equal when histInt(a,b) = 1, and the histogram
distance can be therefore defined as histDist(a,b) =
1 − histInt(a, b).
Another way to evaluate the similarity of two
histograms is through Kullback–Leibler-divergence
(KL). For two normalized histograms, i.e. estimates
of probability density functions, a and b, the KL-
divergence (Kullback and Leibler, 1951) evaluates the
relative entropy from the first probability distribution,
a, to the second, b, KL(a ∥ b) =
∑
h
j=1
a
j
log(a
j
/b
j
).
Statistical divergence quantifies the dissimilarity
between two probability distributions. These diver-
gences can be conceptualized as extensions of the
squared Euclidean distance (SED) (Cha and Srihari,
2002). To use it as a distance measure, its sym-
metrized variant is considered (Uher and Kr
¨
omer,
2023): KLDiv(a,b) = (KL(a ∥ b) + KL(b ∥ a))/2.
3 EXPERIMENTS AND RESULTS
An initial cluster analysis of BBOB test functions
demonstrated that they can be well-separated using
the normalized histograms of sampled fitness values
(Uher and Kr
¨
omer, 2023). It also showed that the
sampling strategy can influence the representativeness
of fitness histograms. These results are further ex-
panded here and problem classification accuracy ob-
tained with fitness histograms under different config-
urations is assessed in the context of multi-class clas-
sification. The considered problem classes are the
five expert-defined classes from COCO, introduced in
section 2.1, each of which consists of 4-5 test func-
tions. We examine whether the lightweight fitness
histogram-based representation provides sufficient in-
formation to distinguish the functions belonging to
these 5 classes and investigate the influence of 1) sam-
pling strategies, 2) the number of histogram bins, h,
and 3) the classification algorithms on this ability.
The experimental configuration involves the as-
sessment of 24 BBOB COCO functions, specifically fo-
cusing on the first function instance and search space
bounded by [−5,5]
d
. The study encompasses three
dimensions, d ∈ {5,10,20}, three distinct sample
sizes, n ∈ {2
10
,2
12
,2
14
}, and the use of five sampling
strategies (Uniform, Sobol, G-Halton, LHS, LHSO)
for the generation of solution samples. For each strat-
egy, dimension, and set size, 30 sample sets are ran-
domly generated. Subsequently, each set of samples
undergoes evaluation across the 24 test functions, re-
sulting in sets of corresponding fitness values. To
further analyze the outcomes, normalized histograms
with varying bin counts, h ∈ {3,8,15,25,50}, are
constructed for each function and combination of ex-
perimental parameters. For fitness landscape clas-
sification, three traditional classifiers, Decision tree
(DT), Random forest (RF), and k-Nearest neighbors
(kNN), are used. DT and RF are tested with the de-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
208

fault parameters of Scikit-learn. The kNN is tested
for k = 7 with Euclidean distance and two statistical
dissimilarities (histogram distance, KL-divergence)
for comparison.
3.1 Fitness Landscape Classification
The fitness histograms representing feature vectors of
distinct test functions should differ enough to be dis-
tinguished by classifiers. To create the training and
test sets for more robust performance analysis, the 30
random sample sets are evaluated, so that, each test
function is represented by 30 normalized fitness his-
tograms. The sample sets are split into 15 training and
15 test sets. Therefore, 15 · 24 histograms are used to
build a classification model and the same amount is
used to test it. In this case, 5-class classification is per-
formed based on the expert-defined groups of 24 BBOB
test functions (each group 4-5 functions) and the aver-
age accuracy is computed. This procedure is repeated
for each combination of classifier, sampling strategy,
dimension d, set size n, and number of histogram bins
h. The configurations are never mixed across training
and test sets. Employing the kNN classifier, we set
k = 7, a value approximately equivalent to half of the
training set, which demonstrated good results in con-
ducted experiments.
The results (average accuracies) of 5-class clas-
sification corresponding to the defined test suite
and parameters have been computed to comprehen-
sively study classification performance representing
the background for the following experiments and
conclusions. Obviously, the higher n strongly im-
proves the accuracy as the fitness landscapes are ex-
plored in greater detail. The configurations reaching
the absolute best accuracies for all three dimensions
are summarized here:
d = 5 (acc. 1.000): h ∈ {25,50}, n = 2
14
, kNN
(all) , Uniform & LHS & LHSO
d = 10 (acc. 0.972): h = 8, n = 2
14
, kNN (Histogram
d.), LHSO
d = 20 (acc. 0.992): h = 8, n = 2
14
, kNN (Euclidean
d.), LHS
The basic question is how the histograms repre-
sent the underlying test functions and what is the in-
fluence of the tested parameters. The best results
show accuracies over 97%. First, the impact of num-
ber of histogram bins h is examined. In order to clar-
ify the pattern more comprehensively, we compare
and rank the corresponding accuracies for identical
methods and parameters across resulting tables for
various values of h. Consequently, each value is as-
signed a rank ranging from 1 to 5. Table 1 presents
Table 1: Olympic medal ranking of histogram bins, h.
1st 2nd 3rd 4th 5th
h = 3 56 40 28 37 64
h = 8 102 69 23 25 6
h = 15 44 69 89 16 7
h = 25 34 25 66 93 7
h = 50 13 13 19 53 127
the Olympic medal ranking based on h, indicating the
total count of first, second, and subsequent positions.
The table shows that h ∈ {8, 15} leads to greater av-
erage accuracy, and h = 8 seems to be the best one
in general. The h = 3 leads to unbalanced results
(some outstanding, some substandard), as the repre-
sentation of the fitness values is too compressed. For
h ∈ {25,50}, the representation is overfitted.
One of the main tasks of this paper is to examine
the impact of applied sampling strategies. The cor-
responding Olympic medal ranking is summarized in
table 2. The ranks are assigned to sampling strate-
gies within the same h, n, d, and classifier. The
LHS and LHSO strongly dominate in most cases.
The basic Uniform sampling leads to average results
while the Sobol and G-Halton samplings generally
occupy the last positions. This trend is intensified for
h ∈ {3,8}. A small value of h serves to mitigate over-
fitting, potentially enhancing accuracy in certain sce-
narios. However, it is likely to be sensitive to random
noise, thereby resulting in divergent results. The find-
ings align with the cluster analysis presented in the re-
cently published work (Uher and Kr
¨
omer, 2023), indi-
cating optimal performance with LHSO and Uniform
samplings for histograms with h = 50 (other h is not
given). On the contrary, earlier publications (Renau
et al., 2021; Kr
¨
omer et al., 2022) assert the positive
impact of the Sobol sampling strategy on feature val-
ues resulting in superior classification accuracy, but
the presented differences are not substantial. The his-
togram is a very straightforward representation of FL
sensitive to the used sampling, while the robust fea-
ture sets (e.g. FLACCO) examine the local structure
of FLs overcoming the random noise at higher com-
putational complexity.
Next, the performance of different classification
algorithms is compared for the fixed n, d, and h. The
Olympic medal ranking depending on the h is shown
in table 3. The results indicate that the kNN gener-
ally beats the DT and RF classifiers. This is proba-
bly due to the characteristics of histograms as their
bins cannot be simply interpreted as vector coordi-
nates (ranges of values vary). The measures used with
the kNN algorithm better reflect the discrete probabil-
ity distribution of fitness values. The histogram dis-
tance and KL-divergence perform better for lower h
and the Euclidean distance prevails for higher h.
Fitness Histograms of Expert-Defined Problem Classes in Fitness Landscape Classification
209

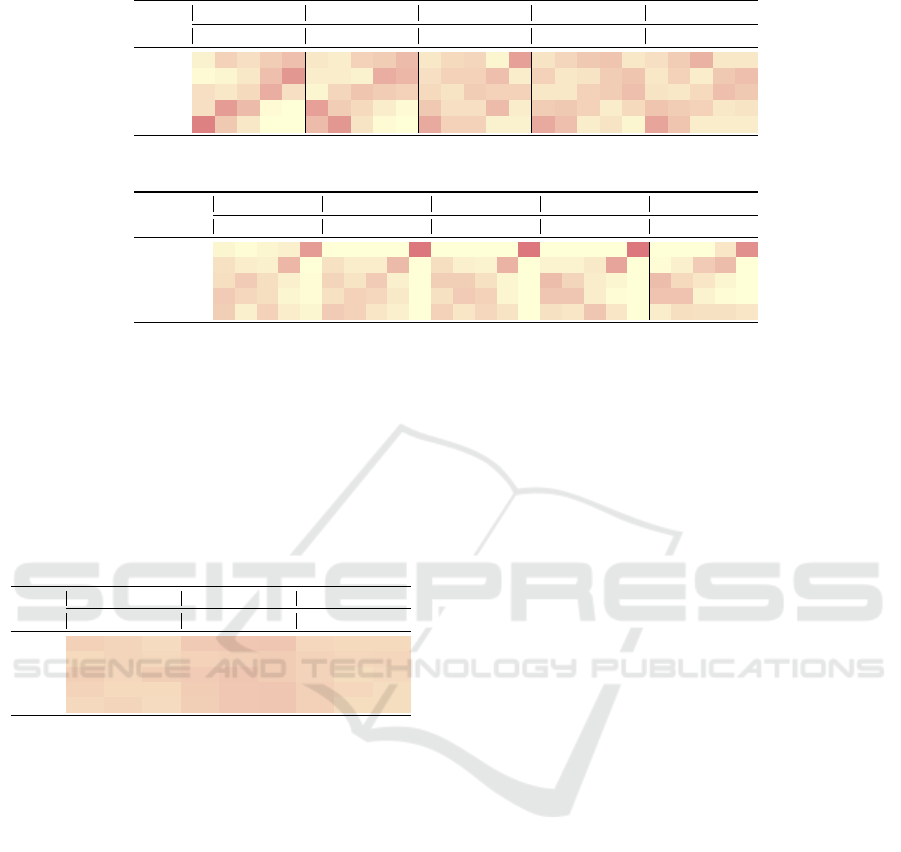
Table 2: Olympic medal ranking of sampling strategies.
h = 3 h = 8 h = 15 h = 25 h = 50
1st 2nd 3rd 4th 5th 1st 2nd 3rd 4th 5th 1st 2nd 3rd 4th 5th 1st 2nd 3rd 4th 5th 1st 2nd 3rd 4th 5th
Uniform 3 10 7 11 14 5 4 10 11 15 5 8 9 2 21 6 9 12 13 5 7 11 17 5 5
Sobol 1 2 5 14 23 4 4 3 18 16 7 10 10 14 4 10 5 6 11 13 5 10 4 12 14
G-Halton 7 5 8 18 7 2 9 13 11 10 8 6 11 10 10 5 5 10 11 14 6 5 8 14 12
LHS 7 22 15 1 0 21 11 8 4 1 12 7 7 15 4 11 12 10 4 8 13 11 10 5 6
LHSO 28 12 5 0 0 15 23 6 1 0 19 10 10 3 3 19 14 4 6 2 20 13 4 4 4
Table 3: Olympic medal ranking of classifiers.
h = 3 h = 8 h = 15 h = 25 h = 50
1st 2nd 3rd 4th 5th 1st 2nd 3rd 4th 5th 1st 2nd 3rd 4th 5th 1st 2nd 3rd 4th 5th 1st 2nd 3rd 4th 5th
DT 3 1 3 5 33 0 0 0 0 45 0 0 0 0 45 0 0 0 0 45 0 0 0 8 37
RF 10 6 5 24 0 10 6 6 23 0 11 5 4 25 0 4 4 7 30 0 1 5 17 22 0
kNN(Eucl.) 11 17 11 5 1 14 9 17 5 0 16 16 10 3 0 22 14 6 3 0 22 12 8 3 0
kNN(Hist.) 17 13 11 3 1 10 15 13 7 0 10 17 15 3 0 19 19 6 1 0 20 20 4 1 0
kNN(KL-div.) 16 5 15 6 3 17 15 8 5 0 15 8 13 9 0 10 8 19 8 0 6 11 10 10 8
Although high accuracies are scattered across all
methods and configurations, several strong trends can
be picked up. Overall, the best average results are ob-
tained for h = 8, n = 2
14
, LHS and LHSO sampling
strategies, and kNN classifier. These trends are also
underlined by the absolute best accuracies and corre-
sponding configurations mentioned before.
Table 4: LOPO: average accuracy of problem classification
for h = 8, and kNN (KL-divergence, k = 7)
d = 5 d = 10 d = 20
n: 2
10
2
12
2
14
2
10
2
12
2
14
2
10
2
12
2
14
Uniform 0.336 0.314 0.256 0.386 0.408 0.417 0.289 0.272 0.275
Sobol 0.275 0.311 0.281 0.331 0.350 0.372 0.322 0.294 0.297
G-Halton 0.353 0.292 0.358 0.383 0.417 0.372 0.325 0.250 0.281
LHS 0.319 0.267 0.267 0.372 0.406 0.417 0.336 0.294 0.250
LHSO 0.281 0.306 0.264 0.358 0.406 0.417 0.339 0.253 0.250
3.2 Leave-One-Problem-Out Scenario
In this section, a deeper investigation of the aver-
age best configurations is conducted in the context
of the expert-defined 5-class classification of 24 BBOB
COCO test functions. Primarily, the compactness of
normalized histograms of functions within the same
class is examined with a special focus on the impact
of various sampling strategies. The previous section
showed that the performance is very high for the sim-
ple scenario when the model includes sample sets of
all test functions. Alternatively, a leave-one-problem-
out (LOPO) cross-validation approach is employed.
Given the division of the 24 functions into 5 groups,
one function is consistently excluded from the train-
ing set and exclusively utilized as the singular func-
tion in the test set. Consequently, the classifier must
learn from the remaining functions, assimilating all
available information to appropriately assign the test
function to its right class. The classification accuracy
is determined as the average across all 24 folds of the
LOPO cross-validation.
The results are shown in table 4 and the experi-
ments were done for h = 8 and kNN (KL-divergence)
which seems to be the best-performing combination.
The table indicates that the accuracies vary between
25% to 41.7%, and thus, they are not as convinc-
ing as in the case of general classification. The best
results are achieved for different samplings and set
sizes. The classifier is best-performing in dimension
d = 10 for n = 2
14
while the results are relatively bet-
ter for n ∈ {2
10
,2
12
} in d ∈ {5, 20}. The best accu-
racy of 41.7% was achieved in d = 10 for all sampling
strategies except to Sobol sampling.
Figure 1 illustrates the similarities between func-
tions, as it displays normalized histograms of all 24
BBOB test functions for LHS sampling, d = 10, h = 8,
and n = 2
14
. The five expert-defined groups are in
order: 1) Separable functions (f001-f005), 2) Func-
tions with low or moderate conditioning (f006-f009),
3) Functions with high conditioning and unimodal
(f010-f014), 4) Multi-modal functions with adequate
global structure (f015-f019), 5) Multi-modal func-
tions with weak global structure (f020-f024). The
comparison of histograms indicates that the distribu-
tions of fitness values can be similar across differ-
ent expert-defined groups. Although the fitness his-
tograms can accurately distinguish single functions,
they cannot represent the properties of the expert-
defined classes very well which explains the low ac-
curacies of LOPO classification.
For the same configuration, the t-SNE clustering
is provided in figure 2 where the fitness histograms of
functions assigned to 5 classes are visualized based on
5 sampling strategies. The points with black edges are
correctly classified using the LOPO scenario. The fig-
ures show that the clusters representing the separate
functions belonging to the same group are generally
spread over the space. Some separate compact clus-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
210

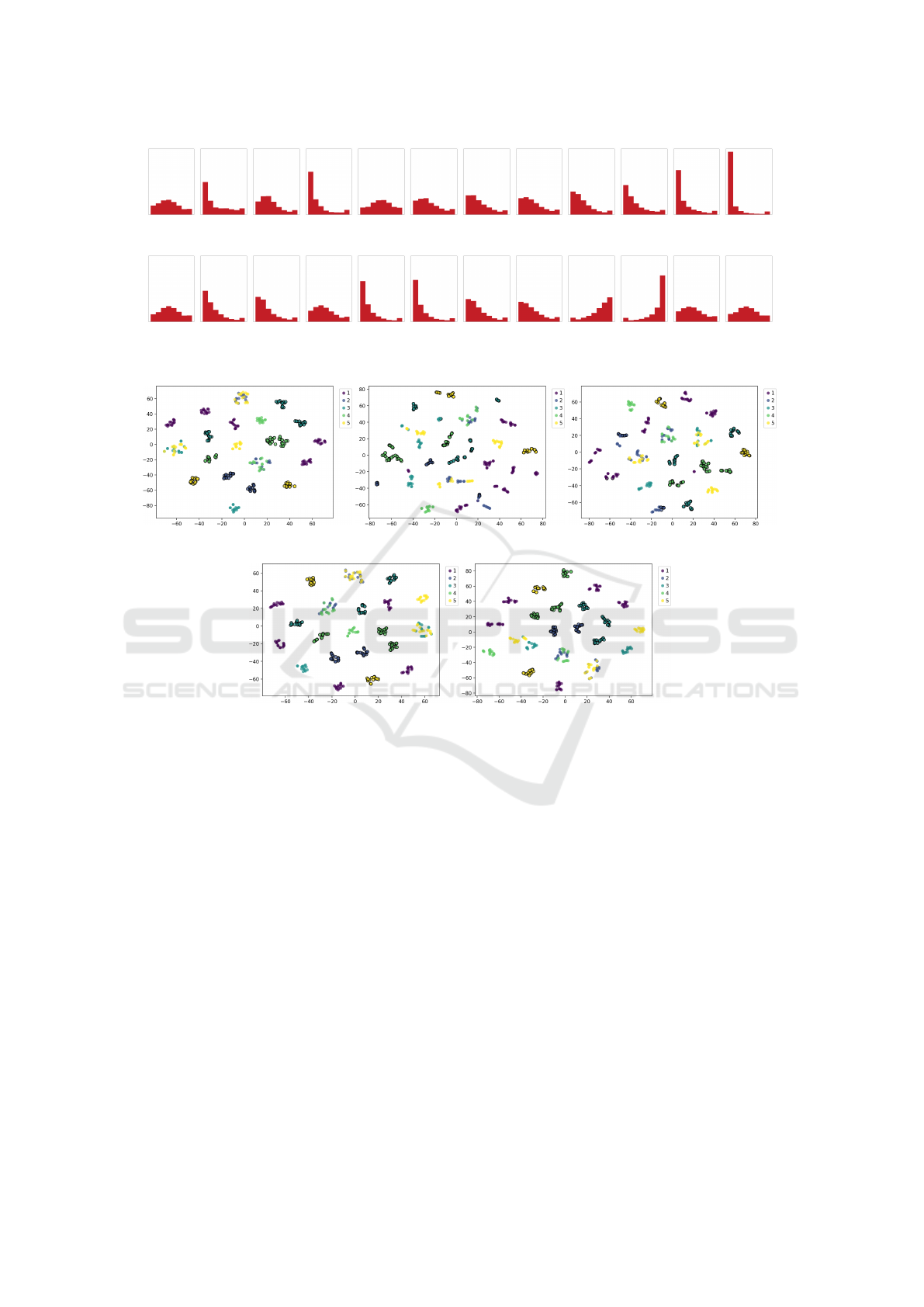
(a) f001 (b) f002 (c) f003 (d) f004 (e) f005 (f) f006 (g) f007 (h) f008 (i) f009 (j) f010 (k) f011 (l) f012
(m) f013 (n) f014 (o) f015 (p) f016 (q) f017 (r) f018 (s) f019 (t) f020 (u) f021 (v) f022 (w) f023 (x) f024
Figure 1: Histograms of fitness values of 24 COCO functions with maximum height set to 0.8 (LHS, d = 10, h = 8, n = 2
14
).
(a) Uniform, acc. 0.417 (b) Sobol, acc. 0.372 (c) G-Halton, acc. 0.372
(d) LHS, acc. 0.417 (e) LHSO, acc. 0.417
Figure 2: t-SNE visualization (perplexity of 3) of normalized fitness histograms computed from samples generated by 5
different samplings using the kNN (KL-div., k = 7) classifier and also KL-divergence as a measure for t-SNE visualization
(d = 10, h = 8, n = 2
14
). The colors represent the 5 COCO classes of test functions. Points with black edges are classified
correctly, the others are misclassified. The accuracies are averaged over all 24 LOPO folds.
ters of functions are well-classified but others are too
far or even overlapping with other classes. This cor-
responds to the figure of normalized histograms that
cannot distinguish the functions properly. The visual-
izations are similar for all 5 samplings.
To even better investigate the 5-class expert-
defined LOPO classification, confusion matrices are
provided in figure 3 for all samplings. The matrices
reveal that there is specifically a problem with the first
class that is almost never classified correctly. Another
issue is the second class, especially for Sobol and G-
Halton sampling strategies. This confirms the find-
ings from the t-SNE visualization in figure 2 where
the first (purple) class is represented by 5 distinct clus-
ters, while the second (blue) class and also the fifth
(yellow) class are sometimes overlapping with others.
4 CONCLUSIONS
In contrast with ELA features including a complex
methodology to estimate the FL properties, we pro-
pose to use a normalized histogram of fitness values
as a simple scale, rotation, and translation invariant
global feature vector.
The main contribution of this paper is a compre-
hensive experimental study of histogram characteris-
tics and its ability to describe the test functions in
the context of the multi-class expert-defined classi-
fication. The initial step in ELA is to generate a
set of random samples properly covering the search
space of the problem (or FL). The selection of random
samples is strongly influenced by different sampling
strategies, and therefore, their impact was thoroughly
Fitness Histograms of Expert-Defined Problem Classes in Fitness Landscape Classification
211

(a) Uniform (b) Sobol (c) G-Halton (d) LHS (e) LHSO
Figure 3: Aggregate confusion matrices using the kNN (KL-div., k = 7) with classification results within all 5 COCO groups
for 5 investigated sampling strategies in one fold of the LOPO cross-validation (d = 10, h = 8, n = 2
10
).
investigated in this paper. The benchmark suite was
based on the 24 BBOB single-objective problems from
the COCO library. The COCO expert-defined groups,
splitting the BBOB problems into 5 classes according
to the properties of the underlying continuous func-
tions. The classification performance measured by
average accuracy reached using the normalized fit-
ness histograms was tested with Decision tree, Ran-
dom forest, and k-Nearest neighbors (k = 7) for Eu-
clidean, histogram distance, and KL-divergence. The
experiments were conducted for 5 sampling strategies
(Uniform, Sobol, G-Halton, LHS, LHSO), 3 sample
sizes n, 3 dimensions d, and 5 numbers of histogram
bins h.
First, the simple classification model was consid-
ered generating 30 sample sets for each test func-
tion, 15 for training, and 15 for test. It means that
all functions were contained in the training set for
the expert-defined 5-class classification. The results
showed very high accuracies. The best ones were over
97%, all achieved for the highest sample size (n =
2
14
). Generally, better classification performance was
achieved for h ∈ {8,15}, suggesting that other config-
urations (h ∈ {3, 25, 50}) possibly resulted in signifi-
cant generalization or overfitting. Clearly, the high-
est performance was reached for LHS and LHSO
sampling strategies followed by average results of
Uniform sampling. In contrast to the recommenda-
tions found in published ELA literature, Sobol and
G-Halton low-discrepancy sequences generally pro-
duced lower accuracies when employed for fitness
histogram computation. This discrepancy may stem
from their emphasis on achieving maximal evenness
in space sampling, potentially leading to discernible
patterns, bias, and heightened sensitivity to noise. In
terms of the used classifier, the kNN clearly beats DT
and RF. When using the kNN, the histogram distance
and KL-divergence perform better for lower h and the
Euclidean distance prevails for higher h. However,
the difference is not substantial.
Next, the best configuration (i.e. h = 8, kNN with
KL-divergence) was selected for further investigation
of classification results. The leave-one-problem-out
scenario was performed excluding one problem from
the training set to keep it as the only test problem. The
average accuracies 25-41.7% indicate that the his-
tograms of functions within the same expert-defined
group differ too much. This trend was thoroughly
examined in the experiments with application of his-
tograms visualization, t-SNE clustering visualization
and confusion matrices. This means that the factors
considered by experts to establish the problem classes
cannot be simply represented by fitness histograms.
Although the simple fitness histograms do not per-
form well in the LOPO classification of one spe-
cific expert-defined grouping, they are outstanding for
standard problem classification. In that context, paper
revealed strong impact of the used sampling strategy,
number of histogram bins, and classifier.
The future work will aim at more benchmarking
of ELA features, and multi-objective problems.
ACKNOWLEDGEMENTS
This work was supported by the Czech Science Foun-
dation in the project “Constrained Multiobjective Op-
timization Based on Problem Landscape Analysis”,
grant no. GF22-34873K, and the Student Grant Sys-
tem, VSB – Technical University of Ostrava, grant no.
SP2024/006.
REFERENCES
Adair, J., Ochoa, G., and Malan, K. M. (2019). Local op-
tima networks for continuous fitness landscapes. In
Proceedings of the Genetic and Evolutionary Com-
putation Conference Companion, GECCO ’19, page
1407–1414, New York, NY, USA. Association for
Computing Machinery.
Barla, A., Odone, F., and Verri, A. (2003). Histogram in-
tersection kernel for image classification. In Proceed-
ings 2003 international conference on image process-
ing (Cat. No. 03CH37429), volume 3, pages III–513.
IEEE.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
212

Cha, S.-H. and Srihari, S. N. (2002). On measuring the
distance between histograms. Pattern Recognition,
35(6):1355–1370.
Chi, H., Mascagni, M., and Warnock, T. (2005). On the op-
timal Halton sequence. Mathematics and Computers
in Simulation, 70(1):9–21.
Das, S. and Suganthan, P. N. (2010). Differential evolution:
A survey of the state-of-the-art. IEEE Transactions on
Evolutionary Computation, 15(1):4–31.
Eslami, M., Shareef, H., Khajehzadeh, M., and Mohamed,
A. (2012). A survey of the state of the art in particle
swarm optimization. Research Journal of Applied Sci-
ences, Engineering and Technology, 4(9):1181–1197.
Halton, J. H. (1964). Algorithm 247: Radical-inverse quasi-
random point sequence. Communications of the ACM,
7(12):701–702.
Hansen, N., Auger, A., Ros, R., Mersmann, O., Tu
ˇ
sar, T.,
and Brockhoff, D. (2021). COCO: A platform for
comparing continuous optimizers in a black-box set-
ting. Optimization Methods and Software, 36(1):114–
144.
Katoch, S., Chauhan, S. S., and Kumar, V. (2021). A review
on genetic algorithm: Past, present, and future. Multi-
media Tools and Applications, 80(5):8091–8126.
Kerschke, P. and Trautmann, H. (2019). Automated al-
gorithm selection on continuous black-box problems
by combining exploratory landscape analysis and ma-
chine learning. Evolutionary Computation, 27(1):99–
127.
Kr
¨
omer, P., Uher, V., Andova, A., Tusar, T., and Filipic,
B. (2022). Sampling strategies for exploratory land-
scape analysis of bi-objective problems. In 2022 Inter-
national Conference on Computational Science and
Computational Intelligence (CSCI), pages 336–342,
Los Alamitos, CA, USA. IEEE Computer Society.
Kr
¨
omer, P., Uher, V., Tu
ˇ
sar, T., and Filipi
ˇ
c, B. (2024). On
the latent structure of the bbob-biobj test suite. In Ap-
plications of Evolutionary Computation, pages 326–
341, Cham. Springer Nature Switzerland.
Kullback, S. and Leibler, R. A. (1951). On Information and
Sufficiency. The Annals of Mathematical Statistics,
22(1):79 – 86.
Lang, R. D. and Engelbrecht, A. P. (2021). An exploratory
landscape analysis-based benchmark suite. Algo-
rithms, 14(3).
Liefooghe, A., Verel, S., Chugh, T., Fieldsend, J., All-
mendinger, R., and Miettinen, K. (2023). Feature-
based benchmarking of distance-based multi/many-
objective optimisation problems: A machine learn-
ing perspective. In Evolutionary Multi-Criterion Op-
timization, pages 260–273, Cham. Springer Nature
Switzerland.
Malan, K. M. (2021). A Survey of Advances in Landscape
Analysis for Optimisation. Algorithms, 14(2):40.
McKay, M. D., Beckman, R. J., and Conover, W. J. (2000).
A comparison of three methods for selecting values of
input variables in the analysis of output from a com-
puter code. Technometrics, 42(1):55–61.
Mersmann, O., Bischl, B., Trautmann, H., Preuss, M.,
Weihs, C., and Rudolph, G. (2011). Exploratory land-
scape analysis. In Proceedings of the 13th Annual
Genetic and Evolutionary Computation Conference
(GECCO), pages 829–836. ACM.
Mu
˜
noz, M. A., Kirley, M., and Halgamuge, S. K. (2015).
Exploratory landscape analysis of continuous space
optimization problems using information content.
IEEE Transactions on Evolutionary Computation,
19(1):74–87.
Nowakova, J. and Pokorny, M. (2014). System identifica-
tion using genetic algorithms. In Proceedings of the
Fifth International Conference on Innovations in Bio-
inspired Computing and Applications (IBICA 2014),
volume 303 of Advances in Intelligent Systems and
Computing, pages 413–418.
Pikalov, M. and Mironovich, V. (2021). Automated pa-
rameter choice with exploratory landscape analysis
and machine learning. In Proceedings of the Genetic
and Evolutionary Computation Conference (GECCO)
Companion, pages 1982–1985. ACM.
Renau, Q., Doerr, C., Dreo, J., and Doerr, B. (2020). Ex-
ploratory landscape analysis is strongly sensitives to
the sampling strategy. In Parallel Problem Solving
from Nature – PPSN XVI, volume 12270, pages 139–
153. Springer.
Renau, Q., Dreo, J., Doerr, C., and Doerr, B. (2021).
Towards explainable exploratory landscape analysis:
Extreme feature selection for classifying BBOB func-
tions. In Applications of Evolutionary Computation,
pages 17–33. Springer.
Richter, H. and Engelbrecht, A. (2014). Recent advances
in the theory and application of fitness landscapes.
Springer.
Shirakawa, S. and Nagao, T. (2016). Bag of local landscape
features for fitness landscape analysis. Soft Comput-
ing, 20(10):3787–3802.
Sobol, I. M. (1967). On the distribution of points in a cube
and the approximate evaluation of integrals. Zhurnal
Vychislitel’noi Matematiki i Matematicheskoi Fiziki,
7(4):784–802.
Swain, M. J. and Ballard, D. H. (1991). Color indexing.
International journal of computer vision, 7(1):11–32.
Tanabe, R. (2022). Benchmarking feature-based algorithm
selection systems for black-box numerical optimiza-
tion. IEEE Transactions on Evolutionary Computa-
tion, pages 1321–1335.
Trajanov, R., Dimeski, S., Popovski, M., Koro
ˇ
sec, P., and
Eftimov, T. (2022). Explainable landscape analysis in
automated algorithm performance prediction. In Ap-
plications of Evolutionary Computation, pages 207–
222. Springer.
Uher, V. and Kr
¨
omer, P. (2023). Impact of different dis-
crete sampling strategies on fitness landscape analy-
sis based on histograms. In Proceedings of the 13th
International Conference on Advances in Information
Technology, pages 1–9.
Zou, F., Chen, D., Liu, H., Cao, S., Ji, X., and Zhang, Y.
(2022). A survey of fitness landscape analysis for op-
timization. Neurocomputing, 503:129–139.
Fitness Histograms of Expert-Defined Problem Classes in Fitness Landscape Classification
213