Exploring the Silver Screen: A Comparative Study of UCB and

EUCBV Algorithms in Movie Genre Recommendation

Yixian Chen

Computer Department, Leeds University, LS2 9JT, Leeds, U.K.

Keywords: Multi-Armed Bandit, Upper Confidence Bound, Efficient-UCBV, Movie-Recommendation.

Abstract: The study explored the comparison of the efficiency between the UCB algorithm and its enhanced version

EUCBV algorithm in the framework of the multi-arm bandit problem. The study first introduced the basic

concept of the two algorithms and explained how the algorithm balances the exploration and the exploitation

when solving the MAB problem. Then I use detailed mathematical formulas to prove the basic concept of

each algorithm while explaining how some important arguments were calculated and their effect on the

process of the algorithm. The study not only discusses the theories of the algorithms, but also involves the

test of the performance and the efficiency of the algorithms that I apply UCB and EUCBV in real-world

situations. The test is about using the algorithm to explore the affection of the movie’s genres to the audience’s

rating, and how to use the algorithm’s result to design a recommendation system to gain higher ratings. I

compare the results and the performance of the two algorithms, which show that by adding a variance term,

the EUCBV’s final reward is much more accurate than the traditional UCB algorithm. Overall, the study fully

explored the algorithms’ concept and the comparison of the performance when applied the algorithm in real-

world situations, which provides me hard evidence of which algorithm is more efficient in some particular

cases.

1 INTRODUCTION

In today’s world of endless choices and online

shopping customers face a plethora of products to

choose from. This presents a challenge, for both

buyers and sellers. Customers have to sift through

options to find what they're looking for while

merchants strive to increase profits and meet

customer needs

(Sundu, 2022)

. Some companies set up

the recommend system to recommend advertisement

to the customers to attract the user’s attention to the

product. But how to decide to recommend what

advertisement that can attract the most attention

becomes the biggest problem. This kind of problem is

called the Multi-Armed Bandits problem, which

comes from the slot machine in the casino

(Chengshuai,

2021)

. The researchers have come up with several

algorithms to solve the MAB problem, such as ETC

algorithm and the Thompson-sampling algorithm.

However, the Upper Confidence Bound (UCB)

algorithm was considered as one of the best

algorithms in some special cases

(Auer, 2002)

https://orcid.org/0009-0008-4074-7420

The key point of the UCB algorithm is to balance

the exploration and exploitation, which explores new

possibilities while exploiting known successes. The

algorithm will calculate the upper confidence bound

for each option in the MAB problem and select the

option which has the largest upper confidence bound

as the present option in this round. At the end of the

round, the algorithm will update the upper confidence

for each arm according to the reward.

Then repeat the same process in the next round.

This kind of model can not only let the algorithm

explore the options which are seldom be selected, but

also use the successful option that has been proved in

order to get the maximization of the rewards

(Jiantao,

n.d)

After finishing the theory part of the study, about

the application part, I search for some related dataset

of the movie’s rating, which is one of the main parts

of the economy. By applying the algorithms to the

dataset and analyzing the result, I searched for which

algorithm is much more effective and accurate to

Chen, Y.

Exploring the Silver Screen: A Comparative Study of UCB and EUCBV Algorithms in Movie Genre Recommendation.

DOI: 10.5220/0012925600004508

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 257-263

ISBN: 978-989-758-713-9

257

decide to recommend which genres of movie can the

merchants get the highest rating.

2 INTRODUCTIONS TO THE

ALGORITHM

2.1 UCB Algorithm

2.1.1 Introduction

In this section, I will examine the UCB algorithm's

operation, clarifying its guiding ideas and examining

the importance of its parameters. I will specifically

look into how each parameter affects the behaviour of

the algorithm and, eventually, the result. I seek to

learn more about the inner workings of the UCB

algorithm and the roles that its parameters play, in

order to enhance my comprehension of its operation

and reveal its effectiveness in resolving the multi-

armed bandit problem. In the study, I will explore

how the UCB algorithm works and how the

arguments in the UCB algorithms are set, and the

arguments’ effect to the final result.

In this section, the number of options is k, each of

the k options has an expected reward when it is

chosen, which called as the value of that action and

denoted as 𝑞

∗



𝑎



.. Let the chosen action at time be 𝐴



and the corresponding payoff be 𝑅



, and I can get that:

𝑞

∗



𝑎



= 𝐸



𝑅



𝐴



= 𝑎







2.1.2 Detailed Algorithm

At the beginning of the algorithm, I need to consider

the Chernoff-Hoeffding Bound. The Chernoff-

Hoeffding bound is a method in probability theory

used to estimate the upper bound of the deviation

between a random variable and its expectation. This

inequality was independently discovered by Chernoff

and Hoeffding and later became known as the

Chernoff-Hoeffding bound

(Sham, n.d).

The Chernoff-Hoeffding bound provides a

probabilistic upper bound estimate of the deviation

between the sample mean and the true mean of a set

of independent and identically distributed random

variables X

,



...X



, whose valuable X



is in the

range [a

,



]. Then let the \bar X



denote the sample

mean of these random variables, defined as 𝑋







𝛴







𝑋



. The Chernoff-Hoeffding bound can be used

to estimate the deviation between the sample mean

and its true mean X



and its true mean E[X



The Chernoff-Hoeffding bound is given by:



x−E



x



≥t



≤e



















⁄





Here, the t > 0 is an arbitrary positive real number

representing the magnitude of the deviation. This

inequality indicates that the probability of the sample

mean x exceeding its true mean E



x



by a certain

amount t is bounded by the exponential function on

the right-hand side, which is used in the Upper

Confidence Bound (UCB) algorithm to derive the

upper confidence bounds for each arm, aiding the

algorithm in making effective arm selections to

maximize cumulative rewards.

Then I need to use the subGaussian to detected the

properties of the reward distribution for each arm. A

1-subGaussian random variable refers to a variable

whose deviations are bounded by a specific upper

limit property

(MIT, n.d). A random variable X is

termed 1-subGaussian if it satisfies the following

inequality:

𝐸𝑒









≤𝑒











Here, μ denotes the expectation of X, and λ is a

non-negative number.

If the reward distributions of each arm satisfy the

1-subGaussian property, one can employ methods

like Chernoff-Hoeffding inequality to derive upper

confidence bounds based on sample means and

variances

(Masrour, 2013). These confidence bounds

provide estimates of the true means of each arm with

a certain level of confidence. In the UCB algorithm,

these upper confidence bounds are used to balance

exploration and exploitation, aiding the algorithm in

effectively selecting the next arm to maximize

cumulative rewards.

After get the result of the 1-subGaussian condition

and Chernoff-Hoeffding bound, I need to use them to

derivate of the principle of UCB algorithm.

With the assumption that 1-subGaussian

condition is true, according to the Chernoff-

Hoeffding Bound:

𝑃



𝜇> 𝜇̅+ 𝜖



≤𝑒





/





Assume that 𝛿= 𝑒





∕

, so the 𝜖=







𝑙𝑛





Substitute it into the formula of Chernoff-

Hoeffding Bound, then have:

𝑃(𝜇≥𝜇̅+



𝑛

𝑙𝑛

𝛿

) ≤𝛿

(

)

𝑃𝜇̅−



𝑛

𝑙𝑛

𝛿

≤𝜇≤𝜇̅+



𝑛

𝑙𝑛

𝛿

≥1 −2𝛿

(

)

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

258

Here, the 1 −2𝛿 is the confidence coefficient,

while the μ+











is Upper confidence bound. Let

the N to be the current total number of rounds and the

δ=





, so the Upper confidence bound is μ+







ln N.

With more and more rounds, the confidence level gets

higher and higher, and as N goes to infinity, the width

of the confidence interval approaches 0, and the

return forecasts become more and more accurate.

For the K-arm-bandit problem, preset the

confidence coefficient, and select the arm whose

Upper confidence bound is the largest as the selected

arm

(Masrour, 2013).

2.2 Efficient-UCBV Algorithm

2.2.1 Introduction

Although the UCB （ Upper Confidence Bound ）

algorithm has achieved some success in addressing

the multi-armed bandit problem, it also has certain

limitations. One of the most significant drawbacks is

its simplistic handling of arm uncertainty, particularly

when the sample size is small or the arms have high

variance

(Emilie, n.d). These kinds of drawback affect

the performance of the algorithm and the final result

to a great extent.

In order to solve the shortcomings of the UCB

algorithm, the researchers have explored a number of

variants of the UCB algorithm, while one of the most

famous variants is the UCB-V with Exploration-

Exploitation Tradeoff utilizing Variance, which

called the Efficient-UCBV (EUCBV) algorithm. It’s

a new kind of UCB variant algorithm which

combined the UCB-V algorithm with the variance of

the dataset to calculate the upper confidence bound

(Subhojyoti, 2018). By introducing the variance, the

variant algorithm performed much better in

compensates for the option’s uncertainty. Thus it

improvement can effectively improve the

performance of the algorithm which can get the upper

confidence bound of each arm more accurately and do

better in balancing exploration and exploitation. In

real-world circumstances, the EUCBV algorithm

performs exceptionally well and is highly adaptive

when managing the diverse uncertainties and

complexities that arise

(Subhojyoti, 2018).

2.2.2 Detailed Algorithm

The main concept of the EUCBV algorithm is quite

similar to the UCB algorithm above. The main

difference between them is that the EUCBV include

the additional variance term, which incorporates

variance information to provide a more accurate

estimate of uncertainty.

The key point of the algorithm is the introduction

of a variance term to better account for arm

uncertainty. The variance term is of the form:



𝑉

,

𝑙𝑜𝑔

(

𝑡

)

𝑁

,

3𝑉

,

𝑙𝑜𝑔

(

𝑡

)

𝑁

,

(

)

And the upper confidence bounds is:

𝑈𝐶𝐵

,

= 𝑋



,



𝑉

,

𝑙𝑜𝑔

(

𝑡

)

𝑁

,

3𝑉

,

𝑙𝑜𝑔

(

𝑡

)

𝑁

,

(

)

Here, the 𝑉

,

denote the estimate of the variance

of the reward obtained from arm i up to time t. While

the X



,

is the sample mean of the reward received

from arm i up to time t, and the N

,

is the number of

times arm i is selected up to time t, which both are

same as in the UCB algorithm.

3 APPLICATIONS EXPERIMENT

The UCB and EUCBV algorithms' underlying

theories were covered in the sections before this one,

giving an overview of how each one tackles the multi-

armed bandit problem. I now turn the attention to a

comparison of the ways in which these algorithms

perform on a particular dataset. The purpose of this

comparison is to assess the performance of UCB and

EUCBV algorithms on real-world data, hence

illuminating their applicability in real-world settings

and offering important insights into algorithm

selection for comparable scenarios.

3.1 Introduction to the Dataset

Within the current dynamic market environment, the

film business is a powerful source of income. The

Motion Picture Association (MPA) has provided

research demonstrating that the film business

stimulates economic growth and creates jobs in local

communities

(MPA, n.d). Consequently, it becomes

critical to develop a system that allows movie

distributors to identify audience preferences for

particular genres of films. Distributors can carefully

adjust their suggestions based on information into

audience proclivities, which attracts a wider audience

and eventually boosts box office revenue and movie

ratings. This calls for the creation of complex

algorithms and analytical frameworks that can

Exploring the Silver Screen: A Comparative Study of UCB and EUCBV Algorithms in Movie Genre Recommendation

259

interpret complex audience preferences, enabling

distributors to choose carefully chosen content

offerings that strongly connect with viewers. These

kinds of projects not only encourage audience

participation but also steady expansion and

competition in the thriving film industry.

The data set that used in the experiment is about

the movie and the user’s rating in the MovieLens. The

dataset contain 1,000,209 anonymous ratings of

approximately 3,900 movies made by 6,040

MovieLens users who joined MovieLens in 2019

(Jesse, 2012)

The dataset includes 3 files: ratings.dat, users.dat,

movies.dat. It comprises ratings, user information,

and movie details. Ratings are recorded in

"ratings.csv" with UserIDs ranging from 1 to 6040,

MovieIDs ranging from 1 to 3952, and ratings given

on a 5-star scale. User information is stored in

"users.csv," including gender (denoted as "M" or "F"),

age (grouped in 10-year intervals), and occupation.

Movie information, found in "movies.csv," uniquely

identifies each movie by movieId, while genres are

listed in a pipe-separated format, drawn from a

selection of 18 main movie genres.

For the dataset, I will use the genres as the arm

of the MAB problem, while the users rating as the

final reward. By using the algorithm about MAB, the

advertisement can have a forecast that by recommend

which kind of genres that can get the highest rating of

the movie.

3.2 UCB Algorithm Experiment

When describing the distributional properties of data,

the sub-Gaussian parameter is typically employed. It

is used to determine whether each arm's reward

distribution satisfies the Sub-Gaussian distribution

assumption in the UCB algorithm. The reward

distribution in the majority of real data sets can be

described by a sub-Gaussian distribution, a family of

probability distributions with restricted variance and

a strong tail concentration feature.

The exploration parameter is an important

parameter in the UCB algorithm to balance the trade-

off between exploration and exploitation. It regulates

how much the algorithm looks into the unidentified

arm while choosing the arm. The algorithm will be

more likely to investigate the unknown arm in order

to learn more about the reward distribution, which

will increase long-term income, if the exploration

parameter is bigger. The algorithm is more likely to

take advantage of the information that is currently

known when the exploration parameter is minimal in

order to produce a more stable payout. On the other

hand, an excessively small exploration parameter

could lead to the algorithm overusing the available

data, which would prevent it from finding a more

ideal arm.

In the UCB algorithm, I put the Sub-Gaussian

sig as 4, and the exploration parameter

𝜌 as 4. In this

condition, I tested separately when the exploration

round of the experiment n (Horizon) equal to 50000,

500000, 5000000. And the final result is as follow:

Figure 1: UCB (sig=4 ρ=4 n=50000).

Figure 2: UCB (sig=4 ρ=4 n=500000).

Figure 3: UCB (sig=4 ρ=4 n=5000000).

Figures 1, 2, and 3 demonstrate how the algorithm's

remorse changes from a continuous ascent to a later

tendency toward stability as the horizon increases. It

displays the algorithm's efficiency and convergence,

demonstrating how well it strikes a balance between

exploitation and exploration before progressively

approaching the almost ideal answer. Put another way,

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

260

as the algorithm gains experience and learns more, it

becomes more adept at predicting which course of

action would yield the most reward. It also avoids

doing unnecessary exploration throughout the

decision-making process, which lowers the pace at

which regret grows.

3.3 E

UCBV Algorithm Experiment

In the EUCBV algorithm experiment, I don’t need to

consider about the Sub-Gaussian due to the variance

term is introduced to account for uncertainty.

The EUCBV algorithm can more precisely

estimate the uncertainty of each arm with the addition

of a variance term. By taking into account the

variance, the algorithm can have a better performance

in decision making and calculating the accuracy

reward of each arm.

What’s more, the variance term increases the

flexibility of the EUCBV exploration strategy. In

contrast to the UCB algorithm's fixed exploration

coefficient, the EUCBV algorithm's exploration

coefficient is modified in proportion to the number of

samples, allowing it to more effectively adapt to

varying settings and data sets.

I need to change the exploration parameter to 0.5,

2.5, 5, 10; and the final result are as follows:

Figure 4: EUCBV cumulative regret (ρ=0.5).

With the exploration parameter rises, Figure 4, 5,

6, and 7 demonstrate that the algorithm will become

more likely to investigate novel activities rather than

take use of well-known, lucrative ones. An

excessively large exploration parameter will cause

the algorithm to over explore and miss opportunities

to take advantage of known actions, which will lower

the overall reward and raise regret.

Figure 5: EUCBV cumulative regret (ρ=2.5).

Figure 6: EUCBV cumulative regret (ρ=5).

Figure 7: EUCBV cumulative regret (ρ=10).

Raising the exploration parameter will force the

algorithm to take reward uncertainty more seriously

and take into account more variance. When there are

some high variance activities, the algorithm might

focus too heavily on them, missing the chance to

benefit from other low variance acts, which would

increase regret.

Exploring the Silver Screen: A Comparative Study of UCB and EUCBV Algorithms in Movie Genre Recommendation

261

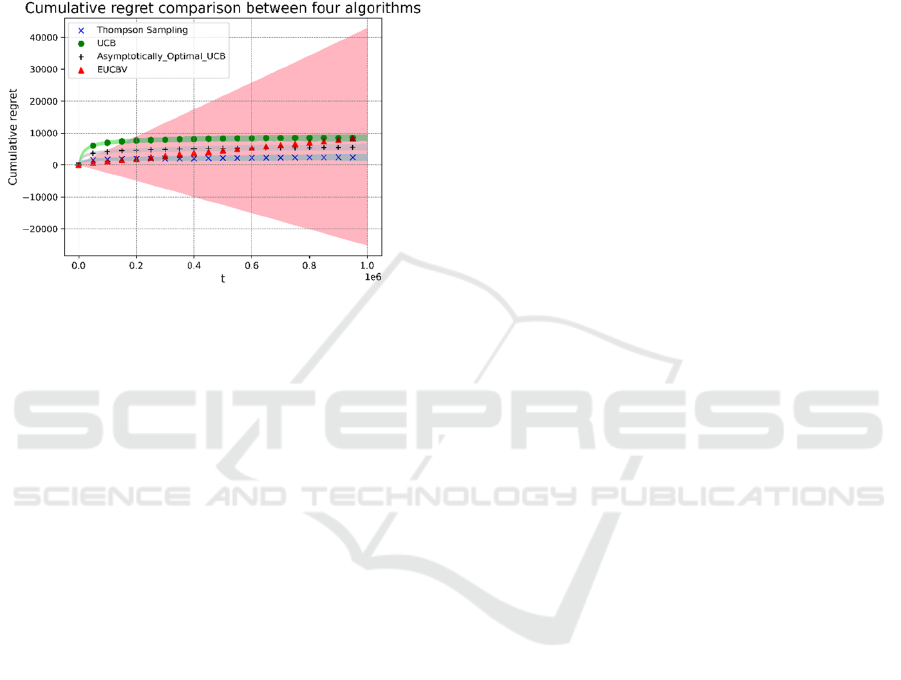
3.4 Comparation of the Two Algorithms

After the apply the algorithm individually, I need to

compare the performance of the EUCBV and UCB

algorithm to have a conclusion. The experiment

explored the cumulative regret between the UCB,

EUCBV, Thompson Sampling algorithms, and get

the result as follow:

Figure 8: Cumulative regret comparison.

As the figure shows that, for one dataset, the four

algorithms performed different result of the regret. By

analysing the figure 8, I can get that the EUCBV

algorithm has the lowest reget. According to the

experimental findings, the EUCBV algorithm

outperforms the UCB algorithm when it comes to

movie suggestion. In particular, the EUCBV

algorithm can converge to the neighbourhood of the

optimal solution faster over long time scales and earn

higher cumulative rewards at the same time scale. The

primary reason for this is that the EUCBV algorithm

takes into account the reward's variance in order to

more precisely assess the action's uncertainty and

prevent the UCB algorithm's potential over-

exploration issue.

The final result shows that both the UCB and

EUCBV algorithm can make contribution to the

movie recommendation system. Although there is a

gap in overall performance between two algorithm,

both of them effectively balanced the exploration and

the exploitation and let the final rating regret tend to

a stable value. The matches can consider to use them

in the movie recommendation system, which can

helps them make better decision to recommend what

kind of movies to the audience to get the higher rating

and income.

4 CONCLUSION

All in all, in this study, I introduce and utilize two

algorithms, UCB and EUCBV, in the context of

Multi-Armed Bandit (MAB) problems. Through

theoretical analysis and application to real-world

scenarios, I have obtained the following key findings:

Start with the dataset’s size, if using the large-

scale problem, the performance of the EUCBV is

much better than the traditional UCB algorithm. In

addition, the EUCBV algorithm has better flexibility

and adaptability, which can make up for the drawback

of the traditional UCB algorithm.

The second is that by applying the algorithm to the

movie rating dataset, I have found the potential of the

UCB and EUCBV algorithm to make contributions to

improving the movie recommendation system. By

applying the algorithm to the recommendation system,

it will improve the effectiveness of decision making

that recommend what genres of movie to the audience.

Not only can it improve the avenge rating of the

movie, but also save the time for the system to decide

which genres of movie do the audience prefer most.

Despite the improved performance of EUCBV

compared to UCB, further research and development

are still needed. What I need to do is to explore and

study the arguments of the EUCBV algorithm, and

apply it in different cases to test its effectiveness.

What’s more, the further study can force on exploring

more efficient algorithm to enhance the efficacy and

efficiency in addressing the challenge of solving the

Multi-Armed Bandit problem.

REFERENCES

Auer, P., Cesa-Bianchi, N., & Fischer, P, 2002. Finite-time

analysis of the multiarmed bandit problem. Machine

Learning, 47(2-3), 235–2561.

Jiantao, J, 2021. UCB-VI Algorithm. Theory of Multi-

armed Bandits and Reinforcement Learning. EE 290.

University of California Berkeley.

Kakade, S., n.d. Hoeffding, Chernoff, Bennet, and

Bernstein Bounds. Statistical Learning Theory. Stat

928. University of Washington.

Kaufmann, E., Cappé, O., & Garivier, A, 2012. On

Bayesian Upper Confidence Bounds for Bandit

Problems. Artificial Intelligence, 22, 592–600.

MIT OpenCourseWare., n.d. Sub-Gaussian Random Variables.

https://ocw.mit.edu/courses/18-s997-high-dimensional-sta

tistics-spring-2015/a69e2f53bb2eeb9464520f3027fc61e

6_MIT18_S997S15_Chapter1.pdf

MPA (Movie Picture Association), n.d. Driving Economic

Growth.

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

262

Mukherjee, S., Naveen, K. P., Sudarsanam, N., &

Ravindran, B., 2018. Efficient-UCBV: An Almost

Optimal Algorithm Using Variance Estimates. In

Proceedings of the AAAI Conference on Artificial

Intelligence, 32 (pp. 6417-6424).

Shi, C., & Shen, C, 2021. Federated Multi-Armed Bandits.

Proceedings of the AAAI, 35(11), 9603–9611.

Sundu, M., Yasar, O, 2022. Data-Driven Innovation:

Digital Tools, Artificial Intelligence, and Big Data.

Organizational Innovation in the Digital Age (pp. 149-

175). Springer Cham.

Vig, J., Sen, S., & Riedl, J. The Tag Genome: Encoding

Community Knowledge to Support Novel Interaction.

ACM Transactions on Interactive Intelligent Systems,

2(3), 13:1–13:44.

Zoghi, M., Whiteson, S., Munos, R., & de Rijke, M, 2013.

Relative Upper Confidence Bound for the K-Armed

Dueling Bandit Problem.

Exploring the Silver Screen: A Comparative Study of UCB and EUCBV Algorithms in Movie Genre Recommendation

263