Optimizing a Multi-Level Logistics Network: Exploring the Location

and Assignment of 3D Printed Orthotic Facilities

Siyu Guo

, Tao Wang

and Thibaud Monteiro

INSA Lyon, Université Lyon 2, Université Claude Bernard Lyon 1, Université Jean Monnet Saint-Etienne, DISP UR4570,

69621 Villeurbanne, France

Université Jean Monnet Saint-Etienne, INSA Lyon, Université Lyon 2, Université Claude Bernard Lyon 1, DISP UR4570,

42300 Roanne, France

Keywords: Optimization, Operational Research, Planning, Logistics, Multi-Level Network Health Care.

Abstract: Proper distribution and location decisions have a direct impact on the accessibility of health care services and

customer satisfaction. The purpose of this study is to explore the Capacitated Location and Routing Problem

(CLRP) in health care, using a real case study from a non-governmental organization (NGO). At the strategic

level, the study focuses on determining the most rational options for facility location and assignment. At the

operational level, the research concentrates on optimizing routes between these facilities and creating

production schedules for the production centers. Currently, a preliminary mixed integer linear programming

model has been developed to address the Capacitated Facility Location Problem (CFLP), laying the

groundwork for more complex systems.

1 INTRODUCTION

Global health spending has more than doubled in real

terms over the past two decades and reached $9.8

trillion in 2021, equivalent to 10.3% of global GDP

(WHO, 2023). Despite the magnitude of this

investment, access to health resources remains

unequal across countries, particularly in low- and

lower-middle-income countries. The WHO estimates

that approximately 100 million people worldwide

need orthotic devices, but only 10 percent have access

to them (WHO, 2021). A study by the International

Society for Prosthetics and Orthotics found that

logistical factors can add up to 20 percent to the cost

of orthotics in developing countries.

In this context, we are collaborating with an NGO

to design a logistics network to supply orthotics made

from recycled material to the disabled. Priority targets

are developing countries. In 2017, the organization

initiated the utilization of 3D printing technology in

its orthotics business. However, this method of

production necessitates the use of filaments crafted

from plastic, which are currently produced in Europe.

https://orcid.org/0009-0000-5770-3928

https://orcid.org/0000-0001-8100-6743

https://orcid.org/0000-0002-6301-7403

This creates logistical challenges, especially at border

crossings, so the fundamental principle is that

resources and production should be local. The

production centers will make filaments from a variety

of locally recycled thermoplastic waste, including

plastic bottles and plastic chairs. This practice will

simultaneously address two key environmental

concerns: the conversion of plastic waste into a

medical resource and the reduction of environmental

pollution. Furthermore, even if these orthotics made

from recycled materials are irreparably damaged or

aging after a period of use, they can still be recycled

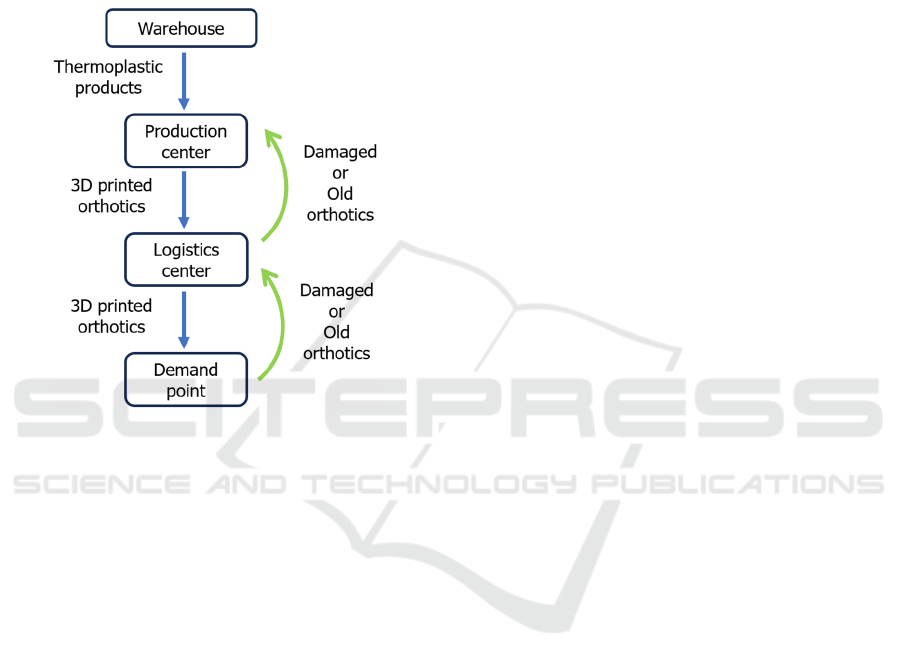
and converted into filament again, as shown in Figure

1. This recycling model contributes significantly to

the sustainable use of resources.

In order to reinforce this concept and enhance the

efficacy of the supply chain, it is essential to devise a

detailed logistics network.

In fact, the efficient distribution of medical

devices requires decisions about the location of

inventory and production facilities, as well as the

means of delivery and distribution. In this problem,

the decision maker will make three types of decisions:

Guo, S., Wang, T. and Monteiro, T.

Optimizing a Multi-Level Logistics Network: Exploring the Location and Assignment of 3D Printed Orthotic Facilities.

DOI: 10.5220/0012926900003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 261-268

ISBN: 978-989-758-717-7; ISSN: 2184-2809

261

1) a decision on the location of the raw material

warehouse (RW), the production center (PC), and the

logistics center (LC); 2) a decision on the assignment

among RW, PC, LC, and demand points (DP); and 3)

a decision on distribution scheduling. In the article,

we refer to the end of the supply chain as the

“Demand point”. In reality, this is not a single

customer, but rather a refugee camp where all those

in need of orthotics are gathered.

Figure 1: The concept of production and recycling.

To achieve this, we consider the facility location

problem (FLP) and the vehicle routing problem

(VRP) together, resulting in a location routing

problem (LRP) to balance customer satisfaction and

cost efficiency.

Although optimization methods for CLRP have

been extensively studied in previous research, few

health care studies have proposed methods for

integrating these decisions. Existing models often do

not sufficiently account for the quality and timeliness

requirements specific to health care services. For

example, by studying a real-world case study, a

dynamic location-inventory-routing (LIR) model was

proposed for the last-mile distribution of emergency

supplies after a disaster. The model considers the

equity of material distribution while minimizing the

weighted sum of distribution cost and equity cost

(Wang and Nie, 2023). The LRP for medical waste

has been studied with the goal of minimizing total

cost and emissions due to random travel time

(Nikzamir and Baradaran, 2020).

The objective of this study is to enhance the CLRP

model to more accurately reflect the influence of

vehicle conditions, road conditions, and inventory

decisions on the overall design of the logistics

network. Given that goods are products with non-

periodic demand, such as orthotics, this study will

investigate the impact of this characteristic on

location decisions. Furthermore, the potential for

assigning DPs to more proximate PCs will be

explored. By integrating these factors, we aim to

construct a more refined and practical model that

considers logistical efficiency while accounting for

the specificity of customer needs, thereby providing a

more reasonable solution.

The current research program is focused on

strategic choice decisions involving the study of the

location of production and logistics facilities, taking

into account capacity constraints, as well as allocation

planning, which is known as the Multi Echelon

Capacitated Facility Location (MECFLP). In order to

address this complex problem, several levels must be

taken into account, (1) the collection of materials, (2)

the production of medical devices, and (3) the

delivery of these devices via logistics centers.

2 LITERATURE REVIEW

The design of an efficient supply chain is a crucial

factor in strategic business decisions. In addition,

decisions regarding the location of facilities must take

into account a number of potential uncertainties.

Firstly, uncertainty in market demand is a key

factor; market demand may fluctuate due to

seasonality or unexpected events. The study of (Lee

et al., 1997) points out that demand fluctuations are

an important cause of supply chain volatility. In

addition, uncertainty in the economic environment

can also affect facility location decisions, especially

exchange rate fluctuations and inflation (Chopra and

Meindl, 2001). Economic recession or rapid growth

can affect market demand and business profitability

thus leading companies to reevaluate their supply

chain strategies.

Uncertainty in the political and regulatory

environment can have a significant impact on facility

siting decisions (Bloom et al., 2007). Changes in

government policies and regulations, such as tax

policies, environmental regulations and trade policies,

can affect a business's operating costs and compliance.

Problems at any link in the supply chain can have

a domino effect throughout the chain (Christopher,

2016). The availability of resources at the front end

of the supply chain is equally important in location

decisions. Supplies of key raw materials can be

disrupted or reduced due to geopolitics, natural

disasters, etc., and uncertainty in energy prices and

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

262

supply can affect production costs and operational

stability. The outbreak of COVID-19 in 2020 caused

massive disruptions in global supply chains, with

many companies facing significant operational

challenges due to raw material shortages (Ivanov and

Das, 2020).

Furthermore, the location or capacity of facilities

cannot be easily altered in the short term due to the

high installation and maintenance costs involved.

This is why the FLP, proposed by (Weber, 1929),

remains one of the most popular investigations among

many research projects.

An extension of the single-echelon FLP problem

(OE-FLP), the two-echelon (2E-FLP) and multi-

echelon FLP problem (ME-FLP) involves several

supply chain stages, each of which must decide which

facilities to open and how to allocate products or

services between them in order to minimize total cost.

Three corresponding mixed linear programming

models have been proposed by (Wu et al., 2017) and

they developed a Lagrangian relaxation method to

solve three two-echelon FLP (2E-FLP) problems with

different foci. The two-echelon FLP (2E-FLP) was

combined with the application of drones to obtain the

worst-case solution with the minimum total cost. This

was achieved using the column constraint generation

method and the Benders decomposition method (Zhu

et al., 2022). An iterative heuristic has been proposed

by (Tancrez et al., 2012) to solve the FLP problem

and inventory management decisions in a three-tier

supply network.

All of the aforementioned studies have a single

objective. However, in the context of actual supply

chain design, it is often necessary to balance various

factors, including delivery time, total cost, and

customer satisfaction. This is an FLP problem with

multiple objectives (MO-FLP). For instance, FLP

with two-step capacity (2E-CFLP) has been

investigated in the context of plasma banks and blood

collection stations. A multi-objective mixed linear

programming model has been developed to consider

the total transport time and total cost of the supply

chain network (Vijaya et al., 2021). The 2E-FLP of

health care facilities was studied by (Zhang et al.,

2022), who determined the location, number, and

coverage of health care facilities in this network,

while taking into account total cost minimization. A

recent study by (Wichapa et al., 2018) examined the

FLP of infectious waste disposal. To address this ME-

FLP problem, a combination of fuzzy hierarchical

analysis and goal-based planning methods was

employed, taking into account environmental, social,

and geological factors.

Other variants of the FLP problem exist, such as

the addition of constraints like maximum distance,

customer incompatibility, and facilities size selection.

Further details can be found in the literature reviews

of (Melo et al., 2010) and (Farahani et al., 2015).

To the best of our knowledge, the ME-CFLP

model, as stated in this paper has never been studied

before. Although 2E-CFLP, which is similar to this

model, has appeared in previous studies (Biajoli et al.,

2019) (Souto et al., 2021), the study of ME-CFLP in

a medical context helps to fill the research gap in this

area. At the same time, the collaboration with NGO

allows us to test the validity of the model using real

data, which is undoubtedly of great interest. The

model presented in this paper can be regarded as a

simplified version of a more complex problem.

However, it provides a solid foundation for the

development of a more comprehensive model. The

outcomes obtained by solving the model using Gurobi

can be utilized to assess the efficacy of algorithms

developed in the future.

3 PROBLEM FORMULATION

The article's model concerns a distribution network

for recyclable plastic orthotics. As previously

mentioned, the model includes different types of

installations. These facilities have a range of potential

site locations within one or more countries in Africa.

We will combine a logistics network through

warehouses, production centers, and distribution

centers located in various locations to distribute

orthotics from the production centers to customers in

the least costly manner. Considering the fact that in

reality the orthotics are 3D printed and made from

plastics that are readily available locally. However, a

single 3D printer requires a minimum of 15 hours to

produce a single orthotic. Therefore, it is assumed

that RW always has sufficient capacity, whereas PC

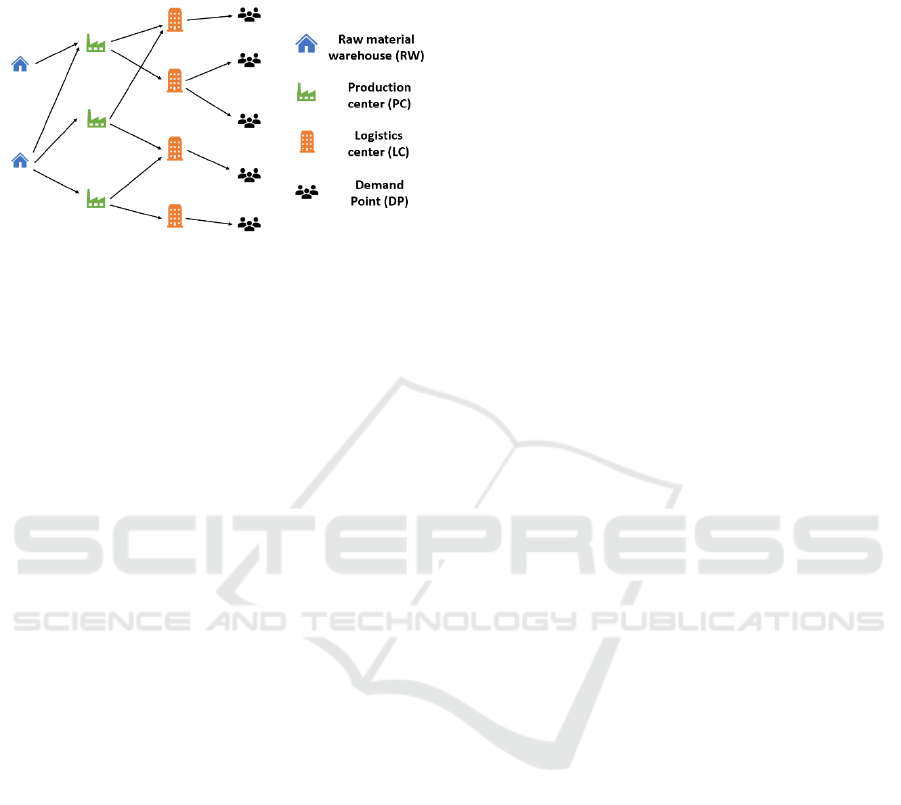
and LC are subject to capacity constraints. All

upstream plants can serve multiple downstream

plants, but a DP can only be served by a single LC, as

illustrated in Figure 2. The number of opened RWs

depends on the cost of transportation per unit distance

and the fixed cost of opening an RW. Since the

capacity of RWs is assumed to be always sufficient,

as mentioned earlier, a large difference between the

values of the cost of transportation per unit distance

and the fixed cost of opening an RW would result in

either all PCs being allocated to only one RW or a

large number of RWs being opened, both of which are

inconsistent with the real situation. Therefore, to be

realistic, we set the value of the cost of transportation

Optimizing a Multi-Level Logistics Network: Exploring the Location and Assignment of 3D Printed Orthotic Facilities

263

per unit distance to be slightly larger than the fixed

cost of opening an RW and limit the opening of up to

4 RWs.

Figure 2: Distribution network for orthotics.

3.1 Notations and Definitions

Set

I : Set of production centers

U : Set of logistics centers

J : Set of demand points

E : Set of raw material warehouse

V : Set of nodes, V =I ∪U ∪J ∪E

Parameters

: Fixed cost of opening a production center i∈

: Fixed cost of opening a logistics center u∈U

: Fixed cost of opening a raw material

warehouse e∈E

: Transport cost per unit distance

: Demand quantity for orthotics from demand

point j∈J

: Maximum storage capacity of the logistics

center u∈U

: Maximum production capacity of the

production center i∈I

: Distance between two points a∈V and b∈V

M : A big number

Variables

: Binary variable indicating whether a

production center i∈I is open (1) or close (0)

: Binary variable indicating whether a logistics

center u∈U is open (1) or close (0)

: Binary variable indicating whether a raw

material warehouse e∈E is open (1) or close (0)

= 1 indicating whether a demand point j

∈

J is

assigned to a logistics center u∈U, 0 otherwise

= 1 indicating whether a logistics center u∈U

is assigned to a production center i∈I, 0 otherwise

= 1 indicating whether a production center i∈

I is assigned to a raw material warehouse e∈E, 0

otherwise

: A real variable indicating the quantity of

products transported from the warehouse e

∈

E to the

production center i

∈

: A real variable indicating the quantity of

products transported from the production center i

∈

to logistics center u

∈

3.2 Modeling

Then, the ME-CFLP can be formulated as follows:

()()

() ( )

()

ii uu

iI uU

ee ujujt

eE uUjJ

iu t

iIuU

ei ei t

eEiI

Min Z y C y C

yC L z C

LzC

∈∈

∈∈∈

∈∈

=⋅+ ⋅

+⋅+ ⋅⋅

+⋅⋅







(1)

Subject to

zjJ

∈

=∀∈



(2)

uj u

zyjJuU≤∀∈∀∈

(3)

, z , ,

iu i iu u

zy yuUiI≤≤∀∈∀∈

(4)

, z , ,

ei e ei i

zy yiIeE≤≤∀∈∀∈

(5)

uj j u u

zD Qy uU

∈

⋅≤⋅ ∀∈



(6)

iu i i

Qy i I

∈

≤⋅ ∀∈



(7)

ei e e

Qy eE

∈

≤⋅ ∀∈



(8)

juj iu

jJ iI

Dz x uU

∈∈

⋅= ∀∈



(9)

iu ei

uU eE

xiI

∈∈

=∀∈



(10)

M , ,

iu iu

ziIuU≤⋅ ∀∈∀∈

(11)

, ,

ei ei

xzMiIeE≤∀∈∀∈⋅

(12)

, ,

juj uj

Dz z M

JuU⋅⋅≤∀∈∀∈

(13)

∈

≤



(14)

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

264

The objective function (1) minimizes the total

costs in a multi-stage supply chain, including the

fixed costs of opening the facility and the distance-

dependent transportation cost.

Constraint (2) represents the assignment of each

DP to only one LC. Constraints (3)-(5) ensure that

services can only be provided by open facilities.

Constraints (6)-(8) are the storage capacity constraint

of the RW, the production volume constraint of the

PC, and the maximum supply constraint of the LC,

respectively. Constraints (9)-(10) are flow

distribution constraints. They state that all raw

materials from the RW are transported to the PC, all

products produced by the PC are transported to the

LC, and all products within the LC are transported to

the DP. Constraints (11)-(13) are linear constraints

representing the relationship between the

transportation quantity x and the assignment relation

z, where 𝑀 is a very large constant. Constraint (14)

represents a limitation on the maximum number of

RW that can be opened.

4 EXPERIMENTAL RESULTS

4.1 Parameter Settings

We solve the model with the commercial solver,

Gurobi, on a server equipped with a CPU model:

AMD EPYC 7702 64-Core processor.

In this experiment, we randomly generate

coordinate points within a 500x500 matrix. The

experiment is divided into three categories, each

containing a different number of PC and LC.

Category 1 is a relatively small dataset covering 20

RWs, 20 PCs, and 20 LCs, Category 2 expands the

scope to a medium size of 20 RWs, 50 PCs, and 50

LCs, and Category 3 explores large-scale problems,

i.e., 20 RWs, 50 PCs, and 100 LCs. In each category,

we tested 10, 15, 20 and 25 DPs, generating a total of

12 datasets. Each dataset contains 10 instances. The

demand for each DP is randomly generated in the

range of 5 to 25.

4.2 Results Analysis

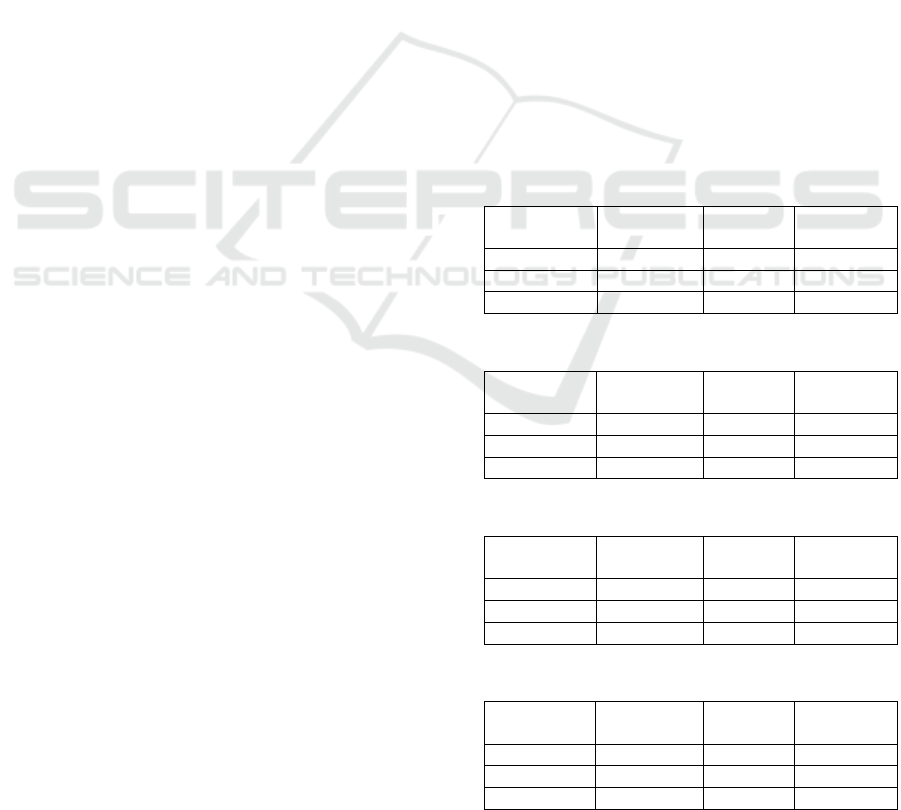
From the data presented in the four tables, it can be

observed that the average computation time for

category 1 is considerably lower than that for

categories 2 and 3. As the number of DPs increases,

the computation time for each category also increases

significantly. In particular, when there are 25 DPs, the

model execution time for categories 1 and 2 grows

rapidly and is approximately four and a half times

longer than the execution time when there are 20 DPs.

For category 2, the solution time begins to increase

significantly at 20 DPs.

While the computation time for category 2 has

been between that of category 1 and category 3, the

gap between the computation time for category 2 and

category 3 continues to widen as the number of DPs

increases. The experimental results indicate that the

computational complexity increases significantly

with the expansion of the search space. Even a modest

increase of five DPs at a time has a significant impact

on the complexity of the problem, as do the other

three dimensions (RW, PC, and LC). The interactions

between variables (e.g. the connection between the

production center and the logistics center) become

more complex as the number of facilities and the

number of demand points increase. This not only

increases the number of combinations that need to be

considered in the solution process, but also increases

the difficulty of finding a globally optimal solution.

Similarly, the expansion of constraints directly

impacts the difficulty of the algorithm's solution,

especially reflected in category 3, where the growth

in the number of constraints requires greater memory

and processing time.

Table 1: Computational results for instances with 10 DP.

Category Av. time

(

)

Variables Constraints

1 4.68 1860 2110

2 24.93 7620 6730

3 61.78 13170 15830

Table 2: Computational results for instances with 15 DP.

Category Av. time

(s)

Variables Constraints

1 11.06 1960 2315

2 82.30 7870 7235

3 280.51 13670 16585

Table 3: Computational results for instances with 20 DP.

Category Av. time

(

)

Variables Constraints

1 24.38 2060 2520

2 209.02 8120 7740

3 965.55 14170 17340

Table 4: Computational results for instances with 25 DP.

Category Av. time

(s)

Variables Constraints

1 112.47 2160 2725

2 721.02 8370 8245

3 1567.31 14670 18095

Optimizing a Multi-Level Logistics Network: Exploring the Location and Assignment of 3D Printed Orthotic Facilities

265

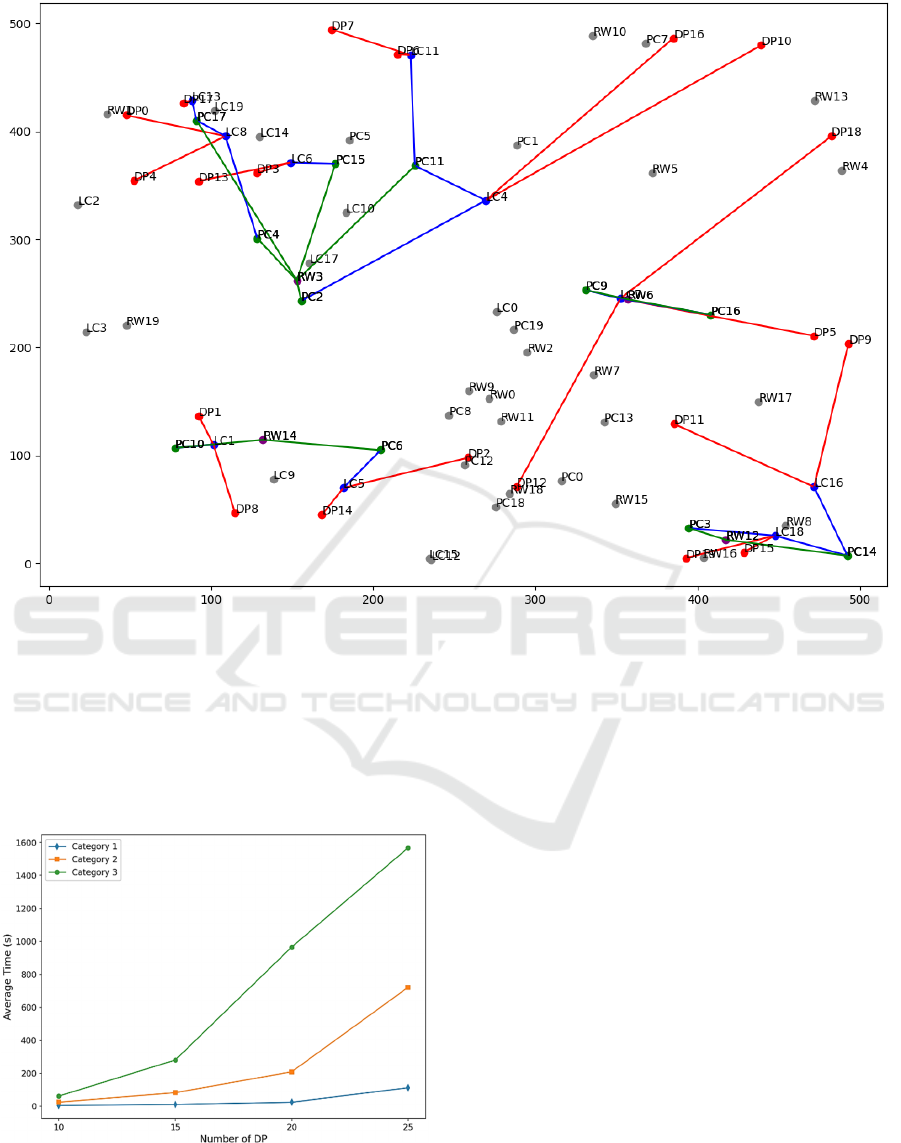
Figure 3: Optimal plan for Category 1 example 20dp_data8.

Figure 3 shows the optimal plan for category 1

example 20dp_data8. We can observe that the red

points DP2, DP14 are assigned to the blue point LC5,

which is assigned to the green point PC6, itself

assigned to the purple point RW14, and so on. The

grey nodes indicate that the facilities concerned are

not activated.

Figure 4: Computational results for different DP.

Figure 4 illustrates that the computational

efficiency of utilizing Gurobi to resolve small-scale

datasets, such as those belonging to category 1, is

relatively high. When horizontally comparing the

solution times of category 2 and category 3, it

becomes evident that the complexity of the medium-

sized problem gradually approaches that of the large-

sized problem as the number of DPs increases. The

computation time of category 3 increases

exponentially with the increase in the number of DPs,

indicating that large-scale datasets are very

demanding in terms of computational resources.

5 CONCLUSION

The primary focus of this research is the investigation

of the Capacitated Location Routing Problem (CLRP)

within the context of health care, with a specific

emphasis on the optimization of the distribution of

orthotics manufactured from recycled plastic. The

model developed in this study will efficiently utilize

local resources and production capacity, thereby

reducing the carbon footprint associated with long-

distance transportation and streamlining the supply

chain.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

266

The study commences with an in-depth analysis

of the Multi-Echelon Capacitated Facility Location

Problem (ME-CFLP), which serves as the foundation

for our exploration. In this initial phase, we develop

an initial approach aimed at efficiently integrating

and coordinating location and assignment decisions

in health care systems. In order to assess the stability

and applicability of our proposed model, we are

conducting tests using randomly generated datasets.

These tests provide a reliable validation of the

accuracy and computation time of our analytical

model under different configurations. For instance,

we modified the demand, adjusted the capacity

constraints of the facilities, and observed how the

model adapted to these changes and how these

adjustments affected the overall cost. The

computational complexity of an optimization

problem is typically proximal to the number of

variables and constraints in the model. The problem

was subsequently demonstrated to be NP-hard

through testing.

The objective of future research is to refine the

capacity parameters of the production center (PC) and

the logistics center (LC). The application of advanced

hyper-parameter tuning techniques will permit the

automatic adjustment of model parameters according

to different data sizes and distributions, thereby

enhancing the robustness and flexibility of the system

in various logistics situations. The next step in the

research will be to apply techniques such as cluster

analysis to optimize the distribution relationship

between demand points (DPs) and logistics centers

(LCs). In order to enhance the realism of the model

and facilitate its adaptation to specific operational

contexts, particularly in less accessible areas, the

incorporation of more precise constraints, such as

maximum travel distance and road conditions, will be

considered. As the complexity of the problem

increases and the exploration space grows, we also

consider proposing a proto-heuristic algorithm to

solve the model. Furthermore, the model is validated

with real-world data to ensure that the developed

solution effectively meets the local needs, while

incorporating user feedback to continuously improve

the model's performance.

ACKNOWLEDGEMENTS

The study of Siyu Guo is supported by the

cooperation program of UT-INSA and the China

Scholarship Council (No.202308070058).

For the purpose of Open Access, a CC-BY public

the present document and will be applied to all

subsequent versions up to the Author Accepted

Manuscript arising from this submission.

REFERENCES

Biajoli, F. L., Chaves, A. A., & Lorena, L. A. N. (2019). A

biased random-key genetic algorithm for the two-stage

capacitated facility location problem. Expert Systems

with Applications, 115, 418-426.

Bloom, N., Bond, S., & Van Reenen, J. (2007). Uncertainty

and investment dynamics. The review of economic

studies, 74(2), 391-415.

Chopra, S., & Meindl, P. (2001). Strategy, planning, and

operation. Supply Chain Management, 15(5), 71-85.

Christopher, M. (2016). Logistics and Supply Chain

Management: Logistics & Supply Chain Management.

Pearson UK.

Farahani, R. Z., Bajgan, H. R., Fahimnia, B. et al (2015).

Location-inventory problem in supply chains: a

modelling review. International Journal of Production

Research. 53(11-12):3769-3788.

Ivanov, D., & Das, A. (2020). Coronavirus (COVID-

19/SARS-CoV-2) and supply chain resilience: A

research note. International Journal of Integrated

Supply Management, 13(1), 90-102.

Lee, H. L., Padmanabhan, V., & Whang, S. (1997). The

Bullwhip Effect in Supply Chains. Sloan Management

Review, 38(3), 93.

Melo, M. T., Nickel, S., Saldanha-De-Gama, F (2010).

Facility location and supply chain management - A

review. Operations Research. 50(1-2): 39-40.

Nikzamir M, et Baradaran V (2020). A healthcare logistic

network considering stochastic emission of

contamination: Bi-objective model and solution

algorithm. Transportation Research Part E: Logistics

and Transportation Review. 142:102060.

Souto, G., Morais, I., Mauri, G. R., Ribeiro, G. M., &

González, P. H. (2021). A hybrid matheuristic for the

two-stage capacitated facility location problem. Expert

Systems with Applications, 185, 115501.

Tancrez, J.S., Lange, J. C., Semal, P. (2012). A location-

inventory model for large three-level supply chains.

Transportation Research Part E: Logistics and

Transportation Review. 48:485-502.

Vijaya, K. M., Tobias, S., Wagner, S. M., Bhanushree, S. et

al. (2021) Convalescent plasma bank facility location-

allocation problem for COVID-19. Transportation

Research. Part E, Logistics and transportation review.

156:102517-102517.

WHO (2023). Global spending on health: Coping with the

pandemic. ISBN: 978-92-4-008674-6.

WHO (2021). WHO standards for prosthetics and orthotics.

Contents: Part 1. Standards; Part 2. Implementation

manual. ISBN: 978-92-4-151248-0.

Wang, Q. Y. et Nie, X. F. (2023). A location-inventory-

routing model for distributing emergency supplies.

Optimizing a Multi-Level Logistics Network: Exploring the Location and Assignment of 3D Printed Orthotic Facilities

267

Transportation Research Part E: Logistics and

Transportation Review. 175:103156.

Weber, A. (1929). Alfred Weber's theory of the location of

industries. The University of Chicago Press. p256.

Wu, T. Y., Chu, F., Yang, Z., Zhou, Z. L. et Zhou. W.

(2017). Lagrangean relaxation and hybrid simulated

annealing tabu search procedure for a two-echelon

capacitated facility location problem with plant size

selection. International Journal of Production Research.

55:2540-2555.

Wichapa, N., Khokhajaikiat, P. (2018). Solving a multi-

objective location routing problem for infectious waste

disposal using hybrid goal programming and hybrid

genetic algorithm. International Journal of Industrial

Engineering Computations. 9(1):75-98.

Zhang, H. Z., Zhang, K., Chen, Y. T., et Ma, L. (2022).

Multi-objective two-level medical facility location

problem and tabu search algorithm. Information

Sciences. 608: 734-756.

Zhu, T. K., Boyles, S. D., Unnikrishnan, A. (2022). Two-

stage robust facility location problem with drones.

Transportation Research Part C: Emerging

Technologies. 137:103563.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

268