Clustering for Explainability: Extracting and Visualising Concepts from
Activation
Alexandre Lambert
1,2,3 a
, Aakash Soni
1 b
, Assia Soukane
1
, Amar Ramdane Cherif
2
and Arnaud Rabat
3
1
LyRIDS, ECE Research Center Paris, France
2
LISV Laboratory, Universit
´
e de Versailles, Paris Saclay, Velizy, France
3
Unit
´
e d’Ergonomie Cognitive des Situations Op
´
erationnelles, IRBA, Br
´
etigny sur Orge, France
Keywords:
Activations Explainability, Concept Extraction and Visualization, Clustering.
Abstract:
Despite significant advances in computer vision with deep learning models (e.g. classification, detection, and
segmentation), these models remain complex, making it challenging to assess their reliability, interpretability,
and consistency under diverse. There is growing interest in methods for extracting human-understandable con-
cepts from these models, but significant challenges persist. These challenges include difficulties in extracting
concepts relevant to both model parameters and inference while ensuring the concepts are meaningful to indi-
viduals with varying expertise levels without requiring a panel of evaluators to validate the extracted concepts.
To tackle these challenges, we propose concept extraction by clustering activations. Activations represent a
model’s internal state based on its training, and can be grouped to represent learned concepts. We propose two
clustering methods for concept extraction, a metric for evaluating their importance, and a concept visualization
technique for concept interpretation. This approach can help identify biases in models and datasets.
1 INTRODUCTION
Deep neural networks (DNNs) and convolutional
neural networks (CNNs) are crucial for artificial
intelligence thanks to their widespread availability
and impressive performance on standardised bench-
marks, particularly in computer vision applications.
However, these models are often considered ”black
boxes”, leaving users uncertain about their decisions-
making process and the knowledge they acquire. This
lack of transparency make them less suitable for ap-
plications where interpretability is critical, such as
medical diagnosis, autonomous driving, and human-
centred models (Lambert et al., 2024). Thus, it is
crucial to develop simple explanation methods to un-
derstand these models. Moreover, the explanation
methods can provide several advantages. Firstly, they
can provide enhanced model comprehension, allow-
ing to interpret the model’s inner workings, under-
stand how it arrives at its predictions, and build trust
in the model’s decision-making process through bet-
ter evaluation and refinement. Secondly, they can of-
a
https://orcid.org/0000-0001-5702-6445
b
https://orcid.org/0000-0002-0882-5280
fer valuable guidance during the training process and
ensure that the model learns the desired information
and avoid potential biases, leading to more robust and
accurate model. Finally, these methods can help bet-
ter understand outliers. In essence, these tools can
offer a powerful perspective allowing non-specialists
to gain deeper insights into the intricate world of
DNNs and CNNs, enabling their use in various ap-
plications (Sivanandan and Jayakumari, 2020; Zhang
et al., 2022; Atakishiyev et al., 2024) The state-of-
the-art explanation methods are divided into two cat-
egories:
Interpretable model are neural network models
designed to be inherently interpretable. They often
incorporate human-interpretable concepts by train-
ing on custom loss functions and adding semantic
knowledge into the networks (Wickramanayake et al.,
2021).
Post hoc explanations methods can be applied to
any model after it has been trained. These methods
analyze the model’s predictions and identify the most
important features for those predictions. It is done by
using feature maps, gradients or input perturbation.
Post-hoc explanations can provide visual insights into
Lambert, A., Soni, A., Soukane, A., Cherif, A. and Rabat, A.
Clustering for Explainability: Extracting and Visualising Concepts from Activation.
DOI: 10.5220/0012927900003838
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 2: KEOD, pages 151-158
ISBN: 978-989-758-716-0; ISSN: 2184-3228
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
151

the model’s decision-making process and identify po-
tential biases in the model (Lapuschkin et al., 2019).
This paper focuses on post-hoc explanations, par-
ticularly through analyzing activations. While the
activation matrix shows the neural network’s inter-
nal state, it may not reveal the conceptual structures
meaningful to humans or that the model is learning.
To address this, we introduce a method to identify and
group informative subsets of activations, referred to as
concepts. Our method aims to make these extracted
concepts interpretable and to assess their importance
in relation to the model’s predictions. This paper pro-
poses: 1) A method to extract concepts that highlight
input image regions prioritized by the model for pre-
dictions. 2) A metric to assess the importance of these
concepts. 3) A technique to visualize these concepts
on the input image. Additionally, our code is publicly
available to support the development of use cases.
The paper is organised as follows: Section 2 re-
views related works. Section 3 presents our method-
ologies and two clustering methods for concept ex-
traction. Section 4 presents the concept extraction
results, followed by a discussion. Finally, the paper
concludes in Section 5.
2 RELATED WORKS
Among post-hoc explainability techniques, attribu-
tion methods are widely used to determine the input
variables contributing to a model’s prediction by gen-
erating importance maps. The Saliency method (Si-
monyan et al., 2014) creates heatmaps based on gra-
dients to highlight influential pixels. GradCAM (Sel-
varaju et al., 2016) method incorporates gradients into
class activation mapping. However, gradient-based
methods can be limited because they capture model
behavior in only a small local area around the in-
put, potentially leading to misleading importance es-
timates (Ghalebikesabi et al., 2021). This is partic-
ularly true for large vision models, where gradients
are often noisy and unreliable (Smilkov et al., 2017).
To address this, perturbation-based methods, like Rise
(Petsiuk et al., 2018), offer a valuable approach to
understanding ”where” a model focuses its attention,
though they may be prone to confirmation bias, po-
tentially leading to misleading explanations. This has
lead to questions about their usefulness.The HIVE
framework (Kim et al., 2022), offers a way to as-
sess explanations in AI-assisted decision-making sce-
narios, enabling falsifiable hypothesis testing, cross-
method comparison, and human-centred evaluation of
visual interpretability methods.
Recent approaches like ACE (Ghorbani et al.,
2019) focus on concept extraction by segmenting im-
ages and analyzing neural network activations, clus-
tering them into ”concepts.” However, ACE can in-
clude irrelevant background segments, necessitating
post-processing to remove outliers. The ICE frame-
work (Zhang et al., 2021) improves upon ACE by
using Non-Negative Matrix Factorization (NMF) for
better interpretability and fidelity, offering both lo-
cal and global concept-level explanations. Simi-
larly, CRAFT (Fel et al., 2023) employs NMF to ex-
tract concepts from model activations, refining them
through recursive decomposition. However, CRAFT
is more suited for groups of images and its methods
for concept localization are complex, potentially chal-
lenging for non-experts.
To enhance interpretability, we propose a method
that avoids the complexity of existing approaches,
which often rely on ”banks of coefficients” and com-
putationally intensive steps that may obscure under-
standing at the single-image level. Our methodol-
ogy to extract concepts uses less complex algorithm,
maintaining efficiency and clarity, and making it more
accessible to a broader audience.
3 METHODOLOGY
3.1 Overview of the Method
In this work, we investigate a supervised learning
scenario, involving a pre-trained black box predictor
M : X → Y with a set of n images X ∈ {x1, ..., xn}
and their corresponding labels Y ∈ {y1, ..., yn}. The
input images are represented as a Ch × H × W ma-
trix, where Ch represents the number of channels (e.g.
RBG, RGBA, LA), and H and W are the image height
and width. For each input image x, the predictor out-
puts M(x). We assume that M is a neural network
with fixed settings that can be divided into two parts:
g transforms the input image into an intermediate rep-
resentation g(x), and h takes this intermediate repre-
sentation to produce the final output M(x) = h(g(x)).
The intermediate representation is in a lower-
dimensional space, determined by the number and
nature of operations in g (e.g. convolution, pool-
ing, down-sampling and scaling). For a given input
x, g(x) produces a set of activations A with a shape
A
N
× A
H
× A
W
, where A
N
is the number of activa-
tions, and A
H
, A
W
are the height and width of each
activation (A
i
).
In most pre-trained models, activations are typi-
cally non-negative due to the ReLU activation. The
activation values within A
i
can be viewed as a spa-
tial distribution feature in a small information matrix.
KEOD 2024 - 16th International Conference on Knowledge Engineering and Ontology Development
152

Combining these values can help identify where spe-
cific information useful for classification is located.
Essentially, when an image is passed through g(x), A
shows what the model has learned during training and
where in the image it focuses during the forward pass,
as these activation values are determinant for classifi-
cation when fed into the classifier h(x).
g
Layer
A
h
p
K
(criterion)
A
0
A
i
...
...
A
k
A
v
...
Convolutional Layer
Pooling Layer
Linear Neural Networks
Output probability
Figure 1: Method overview for concept extraction from a
feature extractor g and a model classifier h. Any CNN ar-
chitecture can replace g and h.
While the activation matrix comprehensively rep-
resents the neural network’s internal state, it may not
directly reveal the underlying conceptual structures
meaningful to humans. This motivates the explo-
ration of methods to identify informative subsets of
activations that can be grouped. We propose that
when a sufficient number of A
i
exhibits similar be-
haviour, they can be considered a set of cohesive units
representing a learned concept C. Identifying these
concepts helps gain insights into the model’s inter-
nal knowledge representation and facilitates a more
nuanced understanding of the phenomena the model
processes.
This work demonstrates that multiple activation
patterns A
i
can be grouped into different concepts C
by satisfying specific criteria regarding a method K,
as summarized in Figure 1. This approach aims to
bridge the gap between raw activations and the high-
level conceptual knowledge encoded by the model.
In the following paragraph, we propose two con-
cept extraction methods: the first focuses on the in-
ternal patterns within each activation, and the second
uses a relatively straightforward approach based on
the position of high activation values.
3.2 Concept Extraction via Clustering
For a given A , we aim to identify different con-
cepts by regrouping different subsets of A that sat-
isfy a given criterion in a clustering method K. As
mentioned earlier, the activation set A is of shape
A
N
× A
H
× A
W
. However, to apply classical cluster-
ing algorithms without losing information, it is con-
venient to reshape A as A
N
×(A
H
×A
W
), without any
need for normalisation.
The classical clustering algorithms re-
quire as input A to produce a set of clusters
γ = {C
1
, C
2
, ...C
N
concept
} that exhibit the same clus-
tering criterion. A concept C
l
in γ obtained using a
clustering algorithm K, is defined in Equation 1:
C
l
= {A
i
⊆ A | f
K
(A
i
, C
l
)} (1)
where f
K
is minimised or maximised with respect to
other clusters, depending on the algorithm K.
This work explores two possible ways of cluster-
ing to extract concepts, as explained in the following
paragraphs.
3.2.1 Clustering Based on General Activations
Patterns (CGAP)
This first approach focuses on obtaining concepts
based on general activation patterns observed in A .
To achieve that, all the non-zero activations in A are
passed to the clustering algorithm K. A non-zero ac-
tivation is A
i
with at least one non-zero value. Since
activations with all zero values do not play any role in
classification, they can be ignored. K aims to regroup
all the A
i
that share similar activation values at similar
indices, such that each C
l
in γ contains unique sets of
A
i
from A.
Given the high dimensionality of A, applying
Clustering directly to A can be computationally in-
tensive and may lead to sub-optimal clustering per-
formance. As a solution, we employ Principal Com-
ponent Analysis (PCA) as a dimensionality reduc-
tion technique before Clustering. PCA transforms the
original high-dimensional activation data (A
H
× A
W
)
into a lower-dimensional space while preserving as
much variance as possible. This transformation helps
highlight the most significant features contributing to
the activation patterns, thus enhancing the effective-
ness of the subsequent clustering process (Ding and
He, 2004). The size of the lower dimension space
depends on the number of desired concepts; in this
study, it equals N
concept
− 1. By reducing the num-
ber of dimensions, PCA helps enhancing computa-
tional efficiency and often improving the performance
of clustering algorithms by emphasising the most dis-
tinctive clusters. After applying PCA, the reduced-
dimensional activation data is fed into the clustering
algorithm K to identify distinct activation patterns,
extracting cohesive and informative concepts from the
model’s learned representations.
It is important to note that the uniqueness of each
cluster in γ can be evaluated and controlled using
some metrics and criteria. However, the size of each
cluster depends on the activation patterns, leading to
Clustering for Explainability: Extracting and Visualising Concepts from Activation
153

some clusters containing more activations than others,
particularly in case of large activation patterns.
Depending on the application, if concepts repre-
senting small patterns in the input image are desired,
the large clusters composing C
l
can be divided into
sub-clusters C
sub
l
by iteratively applying the clustering
algorithm K until the desired number of sub-concepts
is extracted. In this work, the maximum number of
sub-clusters is arbitrarily limited to 3.
3.2.2 Clustering Based on Position of High
Activations (CPHA)
The second approach privileges regrouping activa-
tions A
i
with higher values at similar spatial positions.
Our observations suggest that high activation values
often carry more weight in classification, as they cor-
respond to the parts of the input image most relevant
to the model’s decision. Nevertheless, this may only
sometimes be the case and warrants further investiga-
tion for generalisation. We propose that clustering ac-
tivations with high values reveal concepts of relatively
higher influence in classification and minimise redun-
dancy in concept extraction. For that purpose, first, in
each A
i
the coordinates of max(A
i
), called C oord
i
, are
identified as defined in the Equation 2
Coord
i
= argmaxA
i
(2)
Then, the clustering method K is applied on all the
Coord
i
to obtain γ. By using the set of Coord
i
as
clustering input, the concept extraction focuses on the
spatial position of high activation values. Thus, con-
cepts dispersed along the input image are identified,
and the activations most relevant to the model’s pre-
diction are distinctly regrouped.
3.3 Concept Importance
To assess the importance of each C
l
in classifying a
target class (label), we propose a concept importance
metric I
l
, regardless of the concept extraction method.
For a given image x of target class t, first, we feed
the model classifier h with A . As output, h predicts
the class t with a probability p
t
. Then, to assess the
importance of a concept C
l
in the prediction of t, all
the activation values of A
i
in C
l
are set to 0. The mod-
ified activation set is then fed to h to obtain a new
prediction p
c
l
. Finally, the importance I
l
of concept
C
l
is then calculated from the difference between p
t
and p
c
l
as follows in Equation 3
I
l
=
p
t
− p
c
l
p
t
× 100 (3)
Note that, here, the concept importance is computed
w.r.t a concept of interest C
l
, and the sum of all con-
cept importance is not equal to 100%.
Computing the importance of individual concepts
provides valuable insights into how each concept con-
tributes to the overall prediction score. A positive in-
fluence means that the given concept is responsible
for a higher certainty of the model’s prediction. In
contrast, a negative influence makes the model’s pre-
diction less confident.
3.4 Concept Visualisation
Each concept C
l
is a set of one or more activation A
i
of
shape A
H
× A
W
(usually 8 × 8), which is smaller than
the input image shape (in our work, it is 256 × 256).
So, to project concepts onto the input image, an in-
termediate transformation is needed. It is achieved
by, first, applying an element-wise sum among all the
A
i
in C
l
and, then, interpolating the resulting matrix
(of shape 8 × 8) using bilinear interpolation to the in-
put image size (256 × 256). The resulting matrix (of
shape 256 × 256) is finally min-max normalised. In
the case of sub-clusters C
sub
l
, the normalisation is per-
formed using the minimum and maximum values of
the parent concept C
l
to ensure that the sub-concepts
are visualised proportionally within the context of the
overall concept.
4 RESULTS
A ResNet-50-based classification model pre-trained
on the ImageNet-1k dataset is used to evaluate our
concept extraction methods. The following para-
graphs provide a brief description of the evaluation
environment followed by a discussion on evaluation
metrics and the result.
4.1 Evaluation Environment, Clustering
Algorithms and Metrics
Dataset: ImageNet-1k (Deng et al., 2009) is a
well-known extensive image database containing over
a million images categorised into 1,000 different
classes. We have arbitrarily chosen 11 classes for
this study: rabbit (300 images), tench (387 images),
english springier (395 images), cassette player (357
images), chain saw (386 images), church (409 im-
ages), french horn (394 images), garbage truck (389
images), gas pump (419 images), golf ball (399 im-
ages) and parachute (390 images).
Model: ResNet-50 (He et al., 2016) is a CNN ar-
chitecture designed for image classification. It excels
at identifying objects within images. thanks to its
KEOD 2024 - 16th International Conference on Knowledge Engineering and Ontology Development
154

deep architecture that learns complex patterns from
the image. For the results presented in this paper, we
use a pre-trained ResNet variant, called Norm-Free
ResNet50 (Brock et al., 2021b; Brock et al., 2021a),
that removes all normalization layers. The model has
A
N
= 2048 activations in the last layer, each sized
8×8, and is initialized with ImageNet-1k weight con-
figuration. The input image size is 256 × 256.
Clustering Algorithms and Metrics: We test our
concept extraction method using four well-known
clustering algorithms: k-means, Agglomerative,
Birch and Gaussian Mixture Model (GMM). To eval-
uate the cluster quality representing the extracted con-
cept, three metrics are used:
Silhouette Score (SS) measures the separation be-
tween clusters, with values range from -1 to 1. A
score of 1 indicates well-separated clusters, 0 sug-
gests overlapping clusters, and negative values indi-
cate potential misassignments.
Calinski-Harabasz Index (CHI) (or Variance
Ratio Criterion) evaluates between-cluster and
within-cluster dispersion. Higher values indicate
denser, more distinct clusters.
Davies-Bouldin Index (DBI) measures the aver-
age cluster ’similarity’ by comparing inter-cluster dis-
tance with intra-cluster size. A lower index indicates
better partitioning.
4.2 Evaluating Concepts Quality Based
on the Clustering Metrics
In this section, we compare the performance of the
clustering algorithms using the two methods (CGAP
and CPHA) proposed in Section 3.2 for concept ex-
traction. For comparison, the four clustering algo-
rithms (Agglomerative, Birch, GMM and k-means)
are used to extract N
concept
= 5 concepts from each
input image (belonging to the 11 output labels) inde-
pendently. The uniqueness and clustering consistency
is assessed by comparing the clustering metrics for all
the algorithms.
Table 1 shows the mean value of clustering met-
rics for different clustering algorithms using CGAP
and CPHA methods. We observe that the k-means
algorithm shows the best performance on all the
metrics: 0.64 SS, 441.05 CHI and 0.97 DBI using
CGPA, and 0.43 SS, 984.69 CHI and 0.84 DBI using
CPHA. Both Agglomerative and Birch show similar
or slightly lower performance than k-means. In con-
trast, GMM shows the worst performance. Addition-
ally, the average execution time (in seconds) required
for clustering for each algorithm is also compared in
Table 1, where Agglomerative is observed to be the
fastest and GMM is the slowest.
Table 1: Comparison clustering method (mean over all la-
bels).
Method Cls SS CHI DBI Time
CGAP
A 0.61 398.70 1.00 0.14
B 0.62 398.14 0.97 0.22
G -0.03 111.39 1.84 0.73
k 0.64 441.05 0.97 0.20
CPHA
A 0.41 892.39 0.84 0.14
B 0.37 724.83 0.90 0.22
G 0.32 564.51 1.41 0.73
k 0.43 948.69 0.84 0.20
SS: Silhouette Score, CHI: Calinski-Harabasz Index, DBI:
Davies-Bouldin Index, Cls: Clustering algorithm, A:
Agglomerative, B: Birch, G: GMM, k: k-means
For further comparison, the clustering metrics ob-
tained using CGAP and CPHA for different target la-
bels are shown separately by the boxplots in Figure
2. The clustering metrics for Agglomerative, Birch,
GMM, and k-means are represented by pink, blue,
green, and purple box plots respectively. The y-axis
for each figure in a row is common, where each tick
represents one of the 11 target labels. The x-axis
represents one of the three clustering metrics. The
boxplot edges correspond to the 25th and 75th per-
centiles, the whiskers show the extreme values, and
the dots highlights the outliers. Figure 2 confirms
the same results as Table 1, where Agglomerative and
Birch show similar or slightly lower clustering met-
rics for all the target labels, as compared to k-means.
Meanwhile, the GMM performs worst in all cases.
CGAP and CPHA methods can also be compared
based on the clustering metrics in Figure 2 and Table
1. A common trend is observed where CPHA yields
higher CHI and lower DBI than CGAP, suggest-
ing better cluster compactness and separation with
CPHA. On the contrary, SS is smaller using CPHA
than CGAP, suggesting some loss in overall cluster
distinctness. Nevertheless, in all the cases, k -means
outperforms the other algorithms.
These results suggest that k-means produces more
distinct and consistent clusters. Although Agglom-
erative and Birch produce similar results, the rest of
the evaluation focuses only on k-means for clarity and
space constraints. Full results for all algorithms are
available on our GitHub project page: https://github.c
om/AlexandreLamb/Clustering-for-Explainability.
Table 2 compares the impact of varying the num-
ber of extracted concepts on the clustering metrics.
For CGAP, increasing N
concepts
from 3 to 9 resulted in
a decreased SS and CHI, indicating less distinct and
more overlapping clusters. Conversely, for CPHA, it
Clustering for Explainability: Extracting and Visualising Concepts from Activation
155

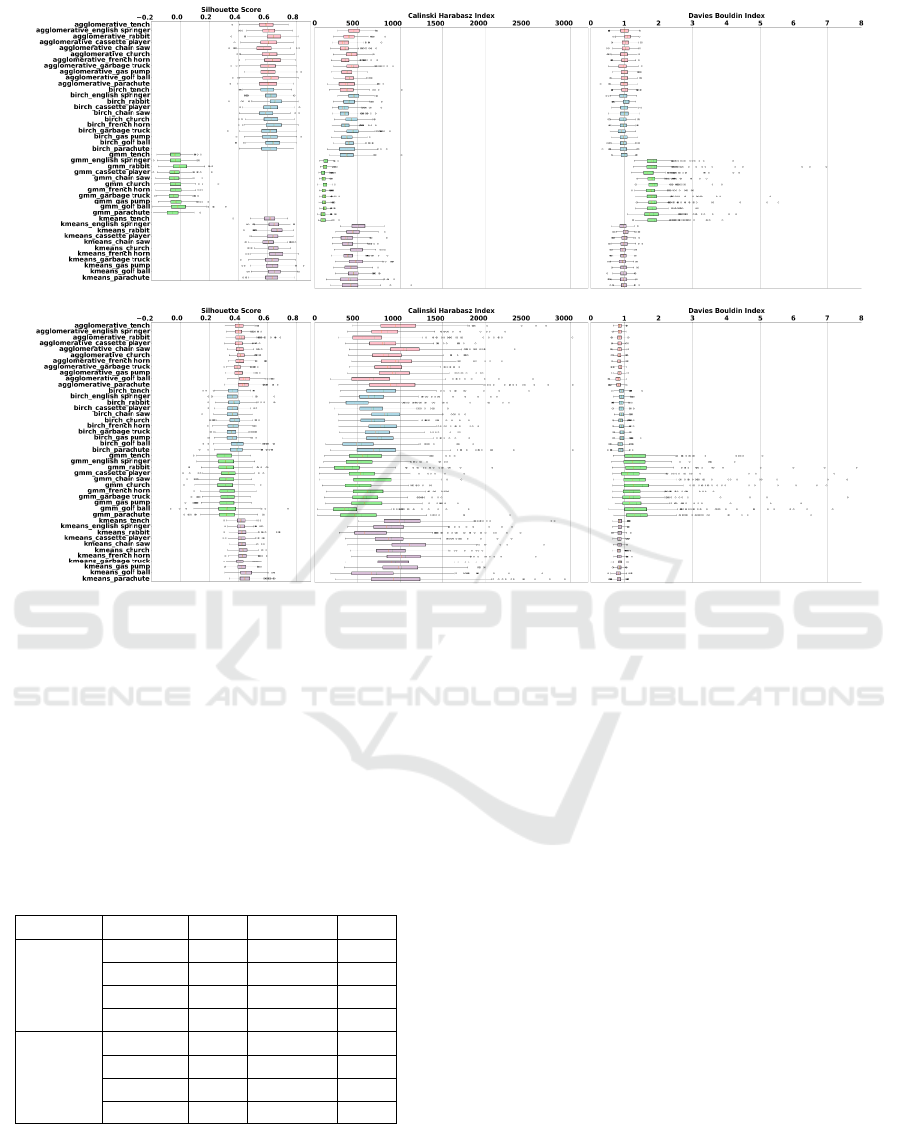
Figure 2: Clustering metrics for Agglomerative (pink), Birch (blue), GMM (green) and k-means (purple) on different labels.
The 4 clustering algorithms are compared using CGAP (top row) and CPHA (bottom row).
led to increased SS and CHI, suggesting more dis-
tinct clusters. On the other hand, DBI does not show
any specific pattern. It varies around the same range
of values, , implying limited usefulness in our study.
Based on these observations, to achieve high-quality
clusters, a smaller number of clusters is desirable for
CGAP, while a large number is preferable for CPHA.
In this study, we arbitrarily chose N
concept
= 5.
Table 2: k-means CGAP with PCA (mean overall label).
Method N
concept
SS CHI DBI
CGAP
3 0.75 966.00 0.72
5 0.64 441.05 0.97
7 0.57 288.34 1.10
9 0.52 218.93 1.17
CPHA
3 0.43 900.18 0.85
5 0.43 948.69 0.84
7 0.44 979.13 0.83
9 0.46 1018.18 0.81
SS: Silhouette Score, CHI: Calinski-Harabasz Index, DBI:
Davies-Bouldin Index
4.3 Concept Visualisation and
Interpretation
In this section, a visual representation of the ex-
tracted concepts is presented using the visualisation
method proposed in Section 3.4. For clear visual-
isation, the input colour images are transformed to
grayscale and the normalised activation values from
concepts are used to weight the original image and
are projected using the ”HOT” colourmap of openCV
(Itseez, 2015). As a result, the concepts are projected
with a colour scale in shades of blue, where bright
blue represents higher activation. For each concept
C
l
, the number of activations (A
N
) within C
l
and the
concept importance I
l
are also presented. The con-
cepts are sorted by decreasing order of I
l
.
4.3.1 Concept Visualisation Based on General
Activation Pattern
Figure 3 visualizes 5 concepts extracted using CGAP
for an image labelled ”Garbage Truck”. These con-
cepts highlight key general activation patterns used
by the model to predict the input image as a garbage
truck. The first three concepts (C
1
, C
3
and C
2
) high-
KEOD 2024 - 16th International Conference on Knowledge Engineering and Ontology Development
156

light the different garbage truck regions, ex. chassis,
driver’s compartment and garbage container, with im-
portances of 46.2, 33.296, and 16.439, respectively.
The remaining activations are clustered into con-
cepts C
0
and C
4
. C
0
contains relatively larger pat-
terns, including the garbage truck and its surround-
ings, with an importance of 13.948. Recall that I
0
represents the average importance of all activations
within C
0
. However, such large activation patterns
can be decomposed into smaller clusters if the im-
portance of the small cluster is of interest, using the
sub-clustering proposed in Section 3.2.1. Figure 4
shows the sub-concepts obtained by decomposing C
0
.
The sub-clusters reveal that the activations represent-
ing the garbage truck (C
01
) have a higher importance
of 12.709, compared to 0.153 and 1.086 for the sur-
roundings (C
00
and C
02
). This sub-clustering confirms
that the model prioritizes relevant concepts for pre-
dicting the garbage truck.
Figure 3: Concept visualisation using the CGAP on an im-
age labelled ”Garbage Truck” with N
concept
= 5.
CONCEPT
SUB CONCEPTS
Figure 4: Sub-clusters of concept C
0
in Figure 3.
The low importance of the surrounding areas, rep-
resented by concepts C
4
, C
00
, and C
02
, is notewor-
thy and may be attributed to potential similar back-
grounds in the training data, which the model asso-
ciated as a relevant concept (Fel et al., 2023). The
impact of these concepts on model predictions varies
by application, but the importance metric helps es-
timate their influence. Figure 5 provides additional
examples of such concepts. For the church, concept
C
0
initially seems to assign high importance (25.329)
to the upper part of the cross. But, decomposing C
0
reveals sub-concepts (C
02
and C
01
) where the activa-
tions highlighting the cross have the importance of
15.698 and 9.97, while the background (C
00
) has neg-
ative importance of -0.339. As stated earlier, a neg-
ative influence means that it makes the model’s pre-
diction less certain. Similarly, in the parachute ex-
ample, the sub-concept (C
00
), including the parachute
and a statue, has an importance of 40.89, whereas the
sub-concepts (C
01
and C
02
) including only the statue
have negative importance. Further decomposition of
C
00
could separate the parachute’s importance, though
this might introduce redundant sub-concepts.
CONCEPT
SUB CONCEPTS
Figure 5: Concepts decomposition into three sub-concepts
for different classes (rabbit, church and parachute).
4.3.2 Comparing CGAP and CPHA
Figure 6 compares chainsaw image concept extraction
in CGAP (top) and CPHA (bottom). The most evi-
dent observation is CPHA’s capacity to extract non-
redundant concepts. For CGAP, the essential concept
is C
2
with I
2
= 38.66 highlighting the wood log and
the chainsaw, which aligns well with this class. The
C
0
with I
0
= 10.022 also highlight the same area but in
a more disparate way. The other three concepts (C
4
,
C
1
and C
3
) redundantly focus on the chain saw en-
gine with a cumulative importance of 65.155. In con-
trast, the CPAH identifies the chainsaw engine as the
most important concept, C
1
, with I
1
= 68.757, similar
to the combined importance of the three CGAP con-
cepts. CPHA also isolates the wood log into separate
concepts (C
3
and C
0
) with importances of 10.32 and
1.002, and highlights the chain and log interaction (C
2
and C
4
) with a cumulative importance of 33.735.
Clustering for Explainability: Extracting and Visualising Concepts from Activation
157

Figure 6: Concept visualisation using the CGAP (top row)
and CPHA (bottom row) on an image labelled ”Chain saw”.
5 CONCLUSION
Analyzing and visualizing concepts is key to under-
standing model predictions. By clustering activa-
tions with similar patterns, we gain insights into the
model’s learned knowledge. We use two methods for
concept extraction: CGAP, which focuses on general
activation patterns, and CPHA, which targets high
activation areas. Decomposing concepts into sub-
concepts helps avoid mixing conflicting elements and
compensates for clustering imperfections.
Our approach is limited by its focus on individual
images, neglecting relationships between activations
across images. Future work could explore clustering
within the same class. While our method highlights
relevant image parts for classification, incorrect clas-
sifications still require human interpretation.
ACKNOWLEDGEMENTS
We appreciate the ECE for funding the Lambda Quad
Max Deep Learning server, which is employed to ob-
tain the results in the present work.
REFERENCES
Atakishiyev, S., Salameh, M., Yao, H., and Goebel, R.
(2024). Explainable Artificial Intelligence for Au-
tonomous Driving: A Comprehensive Overview and
Field Guide for Future Research Directions.
Brock, A., De, S., and Smith, S. L. (2021a). Characteriz-
ing signal propagation to close the performance gap in
unnormalized ResNets.
Brock, A., De, S., Smith, S. L., and Simonyan, K. (2021b).
High-Performance Large-Scale Image Recognition
Without Normalization.
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-
Fei, L. (2009). Imagenet: A large-scale hierarchical
image database. In 2009 IEEE Conference on Com-
puter Vision and Pattern Recognition, pages 248–255.
Ding, C. and He, X. (2004). K-means clustering via prin-
cipal component analysis. In Twenty-First Interna-
tional Conference on Machine Learning - ICML ’04,
page 29, Banff, Alberta, Canada. ACM Press.
Fel, T., Picard, A., Bethune, L., Boissin, T., Vigouroux, D.,
Colin, J., Cad
`
ene, R., and Serre, T. (2023). CRAFT:
Concept Recursive Activation FacTorization for Ex-
plainability.
Ghalebikesabi, S., Ter-Minassian, L., Diaz-Ordaz, K., and
Holmes, C. (2021). On Locality of Local Explanation
Models.
Ghorbani, A., Wexler, J., Zou, J., and Kim, B. (2019). To-
wards Automatic Concept-based Explanations.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep Resid-
ual Learning for Image Recognition. In 2016 IEEE
Conference on Computer Vision and Pattern Recog-
nition (CVPR), pages 770–778, Las Vegas, NV, USA.
IEEE.
Itseez (2015). Open source computer vision library. https:
//github.com/itseez/opencv.
Kim, S. S. Y., Meister, N., Ramaswamy, V. V., Fong, R.,
and Russakovsky, O. (2022). HIVE: Evaluating the
Human Interpretability of Visual Explanations.
Lambert, A., Soni, A., Soukane, A., Cherif, A. R., and Ra-
bat, A. (2024). Artificial intelligence modelling hu-
man mental fatigue: A comprehensive survey. Neuro-
computing, 567:126999.
Lapuschkin, S., W
¨
aldchen, S., Binder, A., Montavon, G.,
Samek, W., and M
¨
uller, K.-R. (2019). Unmasking
Clever Hans predictors and assessing what machines
really learn. Nature Communications, 10(1):1096.
Petsiuk, V., Das, A., and Saenko, K. (2018). RISE: Ran-
domized Input Sampling for Explanation of Black-
box Models.
Selvaraju, R. R., Das, A., Vedantam, R., Cogswell, M.,
Parikh, D., and Batra, D. (2016). Grad-CAM: Why
did you say that? In NIPS. arXiv.
Simonyan, K., Vedaldi, A., and Zisserman, A. (2014). Deep
Inside Convolutional Networks: Visualising Image
Classification Models and Saliency Maps.
Sivanandan, R. and Jayakumari, J. (2020). An Improved Ul-
trasound Tumor Segmentation Using CNN Activation
Map Clustering and Active Contours. In 2020 IEEE
5th International Conference on Computing Commu-
nication and Automation (ICCCA), pages 263–268,
Greater Noida, India. IEEE.
Smilkov, D., Thorat, N., Kim, B., Vi
´
egas, F., and Watten-
berg, M. (2017). SmoothGrad: Removing noise by
adding noise.
Wickramanayake, S., Hsu, W., and Lee, M. L. (2021).
Comprehensible Convolutional Neural Networks via
Guided Concept Learning.
Zhang, R., Madumal, P., Miller, T., Ehinger, K. A., and Ru-
binstein, B. I. P. (2021). Invertible Concept-based Ex-
planations for CNN Models with Non-negative Con-
cept Activation Vectors.
Zhang, Y., Weng, Y., and Lund, J. (2022). Applications
of Explainable Artificial Intelligence in Diagnosis and
Surgery. Diagnostics, 12(2):237.
KEOD 2024 - 16th International Conference on Knowledge Engineering and Ontology Development
158