Impact of Spatial Transformations on Exploratory and Deep-Learning
Based Landscape Features of CEC2022 Benchmark Suite
Haoran Yin
1 a
, Diederick Vermetten
1 b
, Furong Ye
2 c
, Thomas H.W. B
¨
ack
1 d
and Anna V. Kononova
1 e
1
LIACS, Leiden University, Leiden, Netherlands
2
ISCAS, Chinese Academy of Science, Beijing, China
Keywords:
Benchmarking, Exploratory Landscape Analysis, Spatial Transformations, Instance Generation,
Feature Stability.
Abstract:
When benchmarking optimization heuristics, we need to take care to avoid an algorithm exploiting biases in
the construction of the used problems. One way in which this might be done is by providing different versions
of each problem but with transformations applied to ensure the algorithms are equipped with mechanisms
for successfully tackling a range of problems. In this paper, we investigate several of these problem trans-
formations and show how they influence the low-level landscape features of problems from the Congress on
Evolutionary Computation 2022 benchmark suite. Our results highlight that even relatively small transforma-
tions can significantly alter the measured landscape features. This poses a wider question of what properties
we want to preserve when creating problem transformations, and how to measure them fairly.
1 INTRODUCTION
In recent decades, numerous optimization algorithms
have been developed (B
¨
ack et al., 2023; Zhang
et al., 2015). According to the no-free-lunch-theorem
(Wolpert and Macready, 1997), none of these algo-
rithms can be dominant on all optimization problems,
which means that some algorithms will perform bet-
ter than others on specific problems. It is not easy
to determine the conditions under which optimization
algorithms perform well, and rigorous benchmarking
of algorithms is a common way to address this (Bartz-
Beielstein et al., 2020). Benchmarking should encom-
pass a broad spectrum of representative functions,
with an emphasis on generating multiple instances
of each function to reduce bias, improve robustness,
better simulate real-world conditions, and encourage
the development of more versatile and adaptive algo-
rithms (Bartz-Beielstein et al., 2020; Bartz-Beielstein
et al., 2010; Whitley et al., 1996). The mechanism for
generating instances should maintain the fundamental
a
https://orcid.org/0009-0005-7419-7488
b
https://orcid.org/0000-0003-3040-7162
c
https://orcid.org/0000-0002-8707-4189
d
https://orcid.org/0000-0001-6768-1478
e
https://orcid.org/0000-0002-4138-7024
landscape structure and attributes of the original func-
tion while introducing variations, such as shifts in the
optima locations and changes in function value ampli-
tudes. This approach prevents the optimization algo-
rithm design from becoming too specific for a specific
function landscape or from benefiting from a strong
structural bias towards specific regions of the search
space (Vermetten et al., 2022; Kudela, 2022).
Different instances of the same underlying prob-
lem can be created in a variety of ways. For example,
in pseudo-boolean optimization, variables might be
shifted and then fed through the XOR-operator with a
random bitstring (Lehre and Witt, 2010); such trans-
formations have been applied for the pseudo-boolean
optimization suite of the IOHprofiler benchmark en-
vironment (de Nobel et al., 2023). Applying these
transformations to the well-known OneMax problem
efficiently removes the specific bias towards the value
of 1 while keeping the problem structure intact.
In real-valued optimization, problem instances are
generally created by applying a set of transforma-
tions to a base problem. This is the approach taken
by the black-box optimization benchmarking (BBOB)
test suite, which is one of the most well-established
sets of benchmark problems in continuous, noise-
less optimization (Hansen et al., 2009; Hansen et al.,
2021). By generating seeded scaling, rotation, and
60
Yin, H., Vermetten, D., Ye, F., H.W. Bäck, T. and Kononova, A.
Impact of Spatial Transformations on Exploratory and Deep-Learning Based Landscape Features of CEC2022 Benchmark Suite.
DOI: 10.5220/0012933900003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 60-71
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

translation methods, the global landscape properties
of the base functions are preserved, which then allows
the testing for several algorithm invariances (Hansen
et al., 2011).
While the transformation methods used in in-
stance generation are generally designed to preserve
high-level problem properties, their exact impact on
the low-level landscape cannot be ignored. From
the perspective of Exploratory Landscape Analysis
(ELA), the different box-constrained BBOB instances
are statistically different in a variety of ways, and the
corresponding algorithm performance can vary as a
result (Long et al., 2023).
To better understand the relation between problem
transformations and landscape features, we use an-
other popular set of continuous black-box optimiza-
tion problems, known as the Congress on Evolution-
ary Computation (CEC) 2022 problem suite. This
choice is based on the observation of the complex-
ity of CEC benchmark suites and the fresh challenges
they pose each year. Unlike the BBOB suite, the
CEC2022 suite does not natively support instance
generation. As such, it provides an ideal testbed for
the study of various transformation methods, which
might help in determining useful guidelines for future
instance generation within this problem suite.
This research not only explores traditional ELA
features but also extends its exploration to DoE2Vec
features, deep-learning based features for exploratory
landscape analysis, providing a dual perspective on
how spatial transformations affect the landscape of
optimization problems (van Stein et al., 2023).
The remainder of this paper is structured as fol-
lows: Section 2 provides an overview of relevant pre-
vious research, with a focus on landscape features.
This section also describes the CEC2022 problem
suite. In Section 3, we introduce our experimental
setup, which includes the specific ELA features and
the DoE2Vec model used and an instance generation
system for studying the full set of problem transfor-
mations we consider. The results are then discussed
in Section 4, after which Section 5 discusses the key
conclusions and highlights possible future work.
2 RELATED WORK
In this section, we explore existing work, outline sev-
eral key studies within the field, and discuss their rel-
evance to this work.
In the discipline of designing optimization algo-
rithms, several problem test suites are extensively em-
ployed to assess the performance of optimization al-
gorithms. BBOB and CEC are two primary test suites,
each identified by its unique characteristics and ap-
plications. The BBOB test suite is extensively uti-
lized for the evaluation of optimization algorithms
due to its systematic nature and diversity (Hansen
et al., 2009). However, its study on spatial transfor-
mations primarily focuses on employing these trans-
formations as part of the instance generation mecha-
nism, without providing sufficient control and quan-
titative analysis tools. By comparison, the CEC test
suites do not have such an instance generation sys-
tem, which gives us the freedom to fully control the
instance generation process. In addition, the CEC
benchmark suites update the problem set every year,
introducing new challenges and problems (Suganthan
et al., 2005). CEC2022, the problem set used in this
paper, has a higher complexity and is more suitable
for exploring the impact of spatial transformations on
the landscape of optimization problems (Ahrari et al.,
2022).
The methodology of ELA was introduced for
characterizing the properties of the objective func-
tion landscape (Mersmann et al., 2011) to potentially
facilitate the recommendation of well-performing al-
gorithms for unseen problems. One possible way to
achieve this is to understand how problem proper-
ties influence algorithm performance and group test
problems into classes with similar performance of
the optimization algorithms. ELA was proposed to
solve this based on some numerical features (rela-
tively) cheaply computed from limited samples from
the function landscape. With time, ELA has evolved
into an umbrella term for analytical, approximated,
and nonpredictive methods covering a wide range of
characteristics of function landscapes (Mu
˜
noz et al.,
2015). While it has been previously shown that no
single exact or approximate easily computable proxy
of function difficulty is possible for black-box op-
timization (He et al., 2007), typical modern usage
of ELA employs multiple features to characterize
the landscape in aspects such as convexity, function
values distribution, curvature, meta-model and local
search features, dispersion, information content and
principle component features, to name a few (Mers-
mann et al., 2011; Kerschke and Trautmann, 2019).
In addition to classical human-designed ELA
features, deep learning-based approaches such as
DoE2Vec are gaining interest (van Stein et al., 2023).
DoE2Vec uses a Variational Autoencoder (VAE) to
learn and characterize the function landscapes. This
technique starts with a Design of Experiment (DoE)
using Sobol sequences to generate function land-
scapes, which are subsequently fed as input to the
VAE and encoded into the latent space. The core in-
novation of DoE2Vec lies in its vectorized features
Impact of Spatial Transformations on Exploratory and Deep-Learning Based Landscape Features of CEC2022 Benchmark Suite
61

(Vecs), which can be efficiently used in landscape
classification and meta-learning tasks. Unlike tradi-
tional ELA methods, DoE2Vec does not require any
characteristic engineering and can be easily applied to
high-dimensional search spaces.
Pivotal research in the area of analyzing the im-
pact of spatial transformation on ELA features in-
cludes work by Mu
˜
noz et al., who center their study
on the influence of translation of function search areas
and reduction in dimension in feature space on ELA.
They dissect how dimensional changes and transla-
tions perturb the analyzability of landscapes, illumi-
nating that the performance of algorithms may suffer
significant impacts due to subtle alterations in prob-
lems (Mu
˜
noz and Smith-Miles, 2015). They evalu-
ated nine ELA features on the BBOB functions and
on the Sphere, Rastrigin, and Bent Cigar functions
with optima moving evenly along the diagonal in R
2
.
PCA is applied to reduce the ELA feature space from
R
9
to R
2
. They found that some ‘robust’ measures
from ELA cannot capture the fundamental character-
istics when instances are slightly changing, and PCA
alters the results in a potentially deceiving way. Fur-
thermore, recent research by Mu
˜
noz et al. reveals
that certain distributions can lead to an increase in the
sampling size and that some ELA features, including
DISP
q
, H(Y), and R
−2
Q1
, are more reliable than oth-
ers after the problems are transformed (Mu
˜
noz et al.,
2022).
ˇ
Skvorc et al. developed and evaluated a gen-
eralized method for visualizing benchmark prob-
lems (Skvorc et al., 2020). They conducted the ex-
periment with CEC2014, CEC2015 and BBOB. In
relation to our research topic, feature selection meth-
ods were used to identify relevant landscape features
that are invariant to transformations such as scal-
ing and translation, which are commonly applied to
benchmark problems. The research identified that
many landscape features provided by state-of-the-art
libraries are redundant or not invariant to basic trans-
formations, which affects their utility in benchmark-
ing and algorithm selection.
Furthermore, in a recent study, Long et al. (Long
et al., 2023) used ELA to investigate the landscape
characteristics of BBOB problem instances and the
instance generation process by analyzing 500 in-
stances of each BBOB problem. The experiments
reveal a great diversity in the distributions of ELA
features, even for instances of the same BBOB func-
tion. In addition, the authors tested the performance
of eight algorithms on these 500 instances and investi-
gated statistically significant differences between the
performances. The article asserts that although the
transformations applied to the BBOB instances pre-
serve the high-level properties of the functions, in
practice these differences should not be ignored, es-
pecially when the problem is treated as bounded con-
straints rather than unconstrained.
In light of the above research, our work aims to an-
alyze transformations which could potentially be used
in an instance generation system for CEC2022 prob-
lems. Figure 1 shows the landscape of the first five
CEC2022 problems in a 2D search space, and Fig-
ure 2 shows three types of transformation that apply
to the search space. Although there have been many
studies on the CEC2022 problems, its generation
of instances still lacks in-depth exploration (
ˇ
Skvorc
et al., 2022). This is because officially only one in-
stance is provided for each problem in the competition
(Ahrari et al., 2022), and researchers are hardly ex-
ploring the generation of other instances. The above
fact motivates our research on the instance genera-
tion system and on investigating the impact of spa-
tial transformations on landscape characteristics for
the CEC2022 basic benchmark problems.
3 EXPERIMENTAL SETUP
3.1 Considered ELA Features
pflacco is a Python-package that provides an imple-
mentation of the ELA feature calculation (Prager and
Trautmann, 2023b). It provides a number of fea-
ture sets that can compute values based on relatively
small samples of the search space, thus describing the
broader and more specific characteristics of the prob-
lem. From pflacco, we choose a set of 55 features
widely used by researchers (Mu
˜
noz and Smith-Miles,
2015; Skvorc et al., 2020; Long et al., 2023). These
selected features are principal component analysis, y-
distribution, information content, dispersion, levelset,
nearest better clustering, and meta-model, which are
denoted as pca, ela distr, ic, disp, ela level, nbc, and
ela meta in pflacco package.
3.2 DoE2Vec Hyperparameters
DoE2Vec brings us features based on deep learning,
which is different from the features designed by hu-
mans in ELA. Sampling a number of objective val-
ues as the DoE2Vec model requires, it is able to
calculate features then. The pre-trained model la-
beled doe2vec-d10-m8-ls32-VAE-kl0.001 from Hug-
gingface
1
is deployed. This pre-trained model results
1
https://huggingface.co/models?other=doe2vec
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
62

(a) Problem 1, Zakharov Function
(Floudas et al., 2013).
(b) Problem 2, Rosenbrock’s Func-
tion (Rosenbrock, 1960).
(c) Problem 3, Schaffer’s F7 Function
(Schaffer, 2014).
(d) Problem 4, Rastrigin’s Function
(Beyer and Schwefel, 2002).
(e) Problem 5, Levy Function
(Floudas et al., 2013).
Figure 1: Landscapes of CEC2022 first five problems in [−100,100]
2
.
Figure 2: Examples of instance generation via spatial transformations applied to one of the original CEC2022 benchmark
problems, shown here in two dimensions, with optima locations marked by crosses.
in 32 numerical features. The cosine similarity be-
tween the features will be used to quantify the effect
of spatial transformations on landscape.
3.3 Experimented Transformations of
CEC2022
Let D be the dimensionality of the search space, x
be the solution in the search space, and y = f (x) be
its value of the objective function. D = 10 is fixed
in our experiments. In the following, we provide
the definitions of the spatial transformations consid-
ered in our experiments. The settings provided below
are tailored for the CEC functions that are defined in
[−100, 100]
D
.
For each problem in CEC2022, the optima x
∗
is
set by design to be somewhere in [−80, 80]
D
(Ahrari
et al., 2022). In our experiments, we first move x
∗
to the origin o before applying any spatial transfor-
mations. This avoids situations where the optima is
moved outside the search space.
3.3.1 Transformations on the Search Space
• Translation. For every i-th component of x, a
translation offset is independently sampled from
U(−d
x
, d
x
) and added to x
i
, to generate trans-
formed x
′
. To examine the influence of a trans-
lation on the search space, multiple experiments
are carried out with d
x
∈ D
x
=
{
1, 2, 3, . . . , 100
}
,
where for each translation limit.
• Scaling. For the solution x from the search
space, transformed x
′
= k
x
x, where k
x
is a scal-
ing factor. To fully study this transformation,
a number of scaling factors is considered from
K
x
=

2
−3.0
, 2
−2.9
, . . . , 2
−0.1
, 2
0.1
, . . . , 2
2.9
, 2
3.0

,
to record their influence, which allows us to ex-
plore how different levels of scaling in the search
space affect the ELA features. Furthermore, k
x
that are smaller than 2
−3.0
or larger than 2
3.0
make
the search space for CEC2022 basic problems too
small or too large.
• Rotation. The rotation transformation is defined
as x
′
= R · x. The rotation matrix R should be or-
Impact of Spatial Transformations on Exploratory and Deep-Learning Based Landscape Features of CEC2022 Benchmark Suite
63

Figure 3: Distribution of Tr(R) from random sampling. The
result suggests that the distribution of Tr(R) is not uniform
and most of the values are distributed in [−2, 2].
thogonal, which is defined by Equation 1.
R
−1
= R
T
(1)
Following this rule, we first randomly sample 100
matrices R and calculate traces Tr(R) as defined in
Equation 2 because we intend to use it as a mea-
sure of the degree of rotation.
Tr(R) =
n
∑
i=1
R
ii
(2)
However, we found that the distribution of Tr(R)
is not uniform, which is shown in Figure 3.
Thus, rejection sampling is used for sampling
100 R for quantitative analysis of the effects of
rotation. We set 20 bins for Tr(R), which are
[−2.0, −1.8], (−1.8, −1.6], . . . , (1.8, 2.0]. Our re-
jection sampling ensures that only five rotation
matrices are sampled for each bin, giving us
nearly uniformly distributed Tr(R) in [−2, 2].
3.3.2 Transformations on the Objective Value
• Objective Translation. For the objective value
y, a translation offset d
y
is added to y, to gen-
erate y
′
. To investigate the impact of translation
on the objective value, various experiments are
carried out with 20 translation values d
y
∈ D
y
=
{
50, 100, . . . , 1000
}
.
• Objective Scaling. For the objective value y, a
scaling factor k
y
is multiplied by y, to generate y
′
.
To study its influence, a set of scaling factors K
y
=

2
−3.0
, 2
−2.9
, . . . , 2
−0.1
, 2
0.1
, . . . , 2
2.9
, 2
3.0

is ap-
plied based on scaling experiments through k
x
.
3.4 Data Collection
In total, 341 transformations (‘instances’) are consid-
ered for each function: 1 original, 100 with translated
search space, 60 with scaled search space, 100 with
rotated search space, 20 with translated objective val-
ues and 60 with scaled objective values.
In each instance, the ELA features are computed
using pflacco based on m = 100·D points produced by
Latin hypercube sampling (Eglajs and Audze, 1977).
This sample size was chosen to maintain a balance be-
tween computation time and feature stability (Renau
et al., 2019). However, since this sampling-based pro-
cess is, by definition, stochastic, we repeat the sam-
pling 100 times for each generated function instance.
Then these ELA features are Min-Max normalized.
Given that we make use of a total of 55 ELA features,
we end up with a set of 341 · 55 · 100 = 1 875 500 fea-
ture values per problem in CEC2022. Detailed data
from the experiment is publicly available (Anony-
mous, 2024).
3.5 Analytical Methods
3.5.1 Dimensionality Reduction
Uniform Manifold Approximation and Projection
(UMAP) is an algorithm for dimensionality reduction
and visualization of high-dimensional data (McInnes
et al., 2018). It helps understand and visualize com-
plex datasets by mapping the data to the manifold in
a space with lower dimensionality and preserving the
local structure from the high-dimensional space. We
apply this algorithm for mapping results from the 55-
dimensional ELA feature space to a 2D space, to bet-
ter understand how spatial transformations influence
the ELA features of the CEC2022 problems.
3.5.2 Statistical Testing
The Kolmogorov-Smirnov test (KS-test), is a non-
parametric statistical test that determines whether
two samples are statistically the same (Kolmogorov,
1933). As two samples are denoted by symbols P and
Q, if p-value < α, the observed distinction between
P and Q has a statistically significant impact (here,
α = 0.05). Thus, the hypothesis that P and Q conform
to the same distribution is rejected by the results of the
KS-test. The KS-test helps assess whether the spatial
transformation has an impact on the ELA feature and
how this impact changes as the transformation level
changes.
3.5.3 Difference Measure
Earth Mover’s Distance (EMD), also known as
Wasserstein metric, quantifies the difference between
the two distributions (Kantorovich, 1960). It repre-
sents the minimum cost required to move the mass
from one distribution to another. We use this measure
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
64

Figure 4: Visualization of ELA features in 2D space of dif-
ferent problems with different transformations by applying
UMAP. Different problems are marked by different colors,
and different transformations are indicated by different type
of markers.
to have a clearer understanding of how spatial trans-
formation affects different benchmark problems and
to contrast it with the KS-test, helping to draw further
conclusions.
4 RESULTS
4.1 Initial Analysis of CEC2022 Suite
After obtaining the experimental data, we applied
UMAP (see Section 3.5.1) to the data of the ELA
features, represented as 55-dimensional vectors, to
obtain a 2-dimensional projection. The projection
mapping is created on the instances without spatial
transformations and then applied to all constructed in-
stances of all functions.
The upper left sub-figure of Figure 4 shows the
resulting scatter plot of the ELA features of all the
CEC2022 problems. Each point represents a projec-
tion of the full ELA feature vector calculated on a
Latin hypercube sampling, while different colors rep-
resent different problems. Multiple symbols of the
same color represent independent repetitions of the
sampling (see Section 3.4). It appears that most of
the problems form their own clusters, except prob-
lem 2 and problem 10. This seems to indicate that
these two problems share similar landscape charac-
teristics. However, by definition, problem 2 is Rosen-
brock’s function, but problem 10 is a composition
function that composites Schwefel’s function, Rastri-
gin’s function, and HGBat function, which are very
different from problem 2. This may be caused by
the fact that ELA is noisy and that some functions
might indeed resemble other functions without being
evident from their definitions, especially in 10D.
To illustrate the impact of spatial transformations
discussed in Section 3.3, the other sub-figures of Fig-
ures 4 show the projection of the transformed prob-
lems under the same mapping model. From these fig-
ures, we can see that the distributions of the ELA fea-
tures shift from the original distributions. This fact
suggests that the impact of spatial transformations on
the low-level landscape cannot be ignored.
In addition to dimensionality reduction, we also
explore cosine similarities of these features between
different problems. Figure 5 reveals the difference be-
tween non-transformed CEC2022 problems. The data
suggest that, considering the Doe2Vec features, there
are six pairs of problems that are similar, indicated by
yellow values below the diagonal. In comparison, the
ELA features produce lower cosine similarity values
in general. However, the cosine similarity between
problems 3 and 4 remains high for both ELA features
and DoE2Vec features, which indicates that there is
the possibility that these two problems have similar
landscape characteristics.
Throughout the remainder of this section, we will
zoom in on each transformation to identify the rela-
tionship between its parameterization and the change
in the ELA and DoE2Vec representations of the re-
sulting instances.
4.2 Impact of Transformations on the
Search Space
4.2.1 Translation
The first transformation method that we consider is
the translation of the search space. Since we gener-
ate translation vectors with varying bounds, we focus
on the relationship between the chosen bound and the
ELA features. As discussed in Section 3.5, we use
both the KS test and the EMD to quantify the changes
Impact of Spatial Transformations on Exploratory and Deep-Learning Based Landscape Features of CEC2022 Benchmark Suite
65

Figure 5: Cosine similarities between ELA features and
DoE2Vec features of non-transformed CEC2022 problems.
The upper part is the results of ELA features and the
lower part is those of DoE2Vec features. ELA features are
rescaled to [−1, 1] before calculating cosine similarity.
in the ELA features. The percentage of changed ELA
features, as well as normalized EMD, is shown in Fig-
ure 6a, on the corresponding vertical axes. In ad-
dition, DoE2Vec extracts the landscape characteris-
tics of problems into a vector in R
32
, which produces
cosine similarity as the difference between instances.
The difference between the search space translated in-
stances and the origin instances is shown in Figure 7a.
Figure 6a shows that translation factors have a lin-
ear impact on the general distribution of ELA fea-
tures, as indicated by EMD. For most individual fea-
tures, the smallest translations do not yet lead to sta-
tistically significant changes, but this number quickly
increases to almost all features when the translations
become larger. In fact, the only features that are un-
affected by this transformation are those that measure
the properties of the samples themselves without con-
sidering the function values (the PCA class of features
from pflacco).
Compared with the DoE2Vec features, shown in
Figure 7a, it is clear that DoE2Vec is invariant to
translation on x of some problems, including prob-
lems 3, 4, and 7. The changes of other problems’
DoE2Vec features show no greater change than ELA
features.
4.2.2 Scaling
Our scaling-based transformation is parameterized in
a similar way to the translation, where we vary the
scaling factor logarithmically between 2
−3.0
and 2
3.0
.
As such, Figures 6c and 7c follow the same struc-
ture as previously discussed Figures 6a and 7a, show-
ing both the change in the overall distribution accord-
ing to the EMD and the percentage of individual fea-
tures that are statistically significantly impacted by
the corresponding scaling. A scaling factor of 2
0
cor-
responds to the setting of no scaling, for which we by
definition have no change to the base functions.
In Figure 6c, we can see that the impact of the
scaling is rather immediate. Even factors 2
0.1
and
2
−0.1
cause statistically significant changes in some
problems. This is particularly interesting to note on
the side of the negative factors, which correspond to
zooming in on a smaller part of the function, since
this confirms that more local landscape features vary
significantly from the overall function (Jankovi
´
c and
Doerr, 2019), which is an important aspect to consider
when basing algorithmic decisions on ELA features
collected during the course of an optimization run.
Figure 7c shows different changes in the Doe2Vec
features with scaling on x. It can be seen that the
impact of k > 2
0
is obviously greater than k < 2
0
for DoE2Vec features of problems 3, 4, 7 and 12,
while those of problems 1, 2, 8 and 11 are more in-
fluenced by k < 2
0
. Some problems’ DoE2Vec fea-
tures are greatly affected, however, the corresponding
ELA features show invariance in Figure 6c, including
problems 1, 3, and 5. This manifestation of these two
landscape characteristics may indicate that they can
complement each other to some extent.
4.2.3 Rotation
The final set of search space transformations is the
rotations, which we can parameterize by the trace of
the rotation matrix Tr(R), which is closely related to
the rotation angle of the high-dimensional rotation
matrix (Hall and Hall, 2013). Changes in ELA and
DoE2VEc features relative to Tr(R) are illustrated in
Figures 6e and 7e.
From these figures, we do not observe any clear
relation between the parameterization of the rota-
tion and the impact it has on the landscape features.
We do, however, see a separation between problems,
where especially the hybrid and composition-based
ones (5–10) are impacted rather severely when look-
ing at their ELA-features, indicating that these seem
to be more sensitive to the applied rotations. How-
ever, it is worth noting that the DoE2Vec features dis-
play a different level of impact on these functions,
with functions 1, 2 and 8 being the most sensitive,
while e.g. the rotated versions of functions 7 and 10
have a cosine similarity of almost 1 to their respective
untransformed function. These differences in sensi-
tivity highlight a potential complementarity between
ELA and DoE2Vec features.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
66

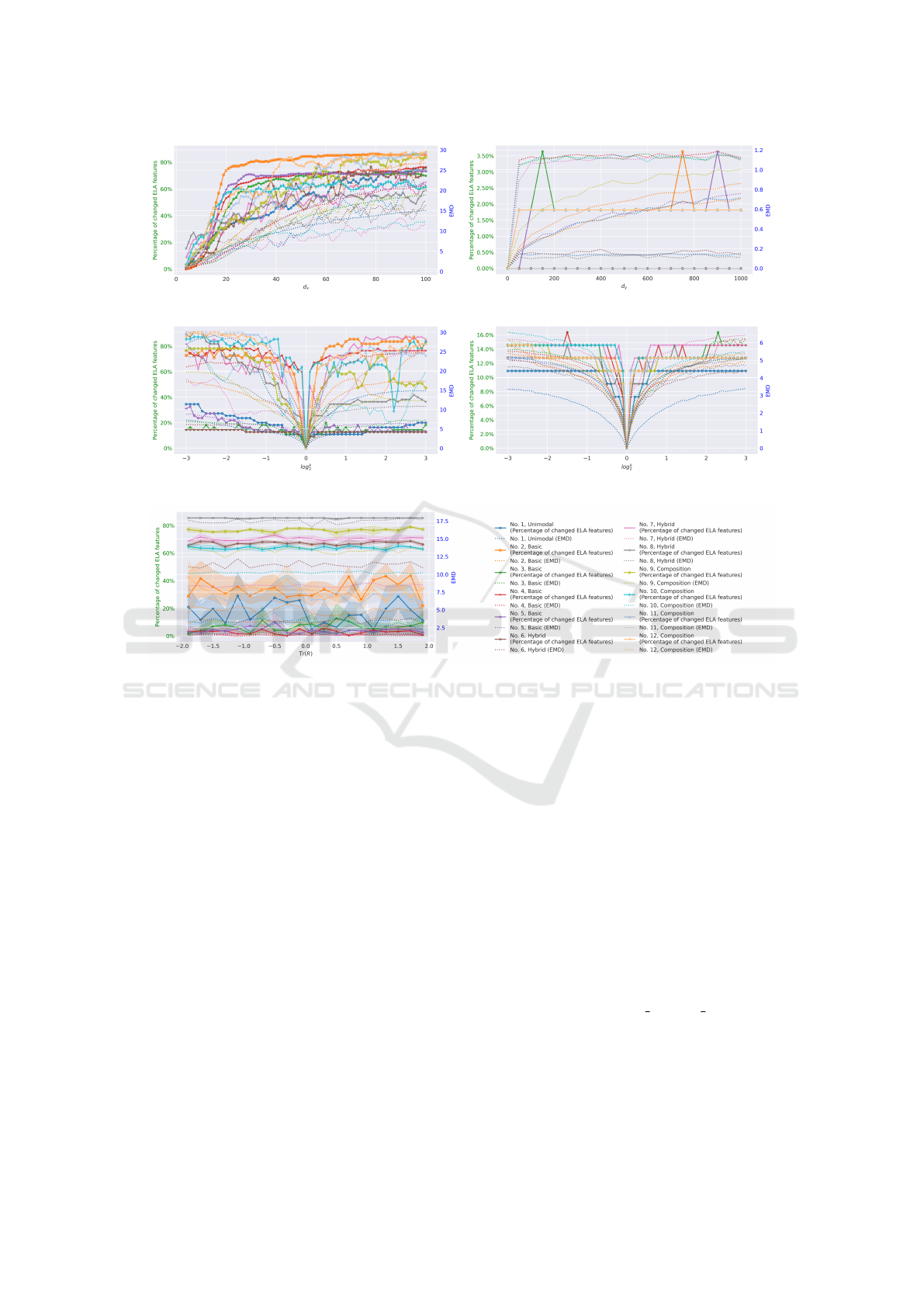
(a) Translation on x. (b) Translation on y.
(c) Scaling on x. (d) Scaling on y.
(e) Rotation on x.
Figure 6: Changes in ELA features after applying five types of transformations on the CEC2022 problems. EMD (dotted
lines, with the blue axis on the right) and the percentage of features (solid lines, with the green axis on the left) rejected by
the KS-test between the original and transformed features via translation (top row) or scaling (second row) applied to x (left
column) or y (right column), the results of applying rotation to x are present in the last figure. Different colors represent
different base problems. The EMD results of different problems are calculated based on the normalized feature values.
4.3 Impact of Transformations on the
Objective Value
The impact of transformations on the objective val-
ues has been the subject of some discussion since
the experimental results suggest that not all fea-
tures are fully invariant to these types of transforma-
tions (
ˇ
Skvorc et al., 2022). However, many of the
algorithms used within evolutionary computation are
comparison-based and thus not influenced by mono-
tone changes in objective value. As such, recent stud-
ies suggest that function values should be normalized
before applying ELA, as this would limit the impact
of objective value scaling (Prager and Trautmann,
2023a).
To better understand what features are affected by
transformations on the objective value, we again con-
sider parameterized translation and scaling methods.
4.3.1 Objective Translation
For translation, we plot the percentage of changed
ELA features for each translation limit, as well as
the overall EMD, in Figure 6b. It should be men-
tioned that KS rejections for problems 4, 7, 9, 10,
11, and 12 coincide exactly, the same can be said
about problems 2 and 5. KS rejections for problem
1, 6, and 8 remain zero all the time, which means that
translation on y has little influence on these problems’
ELA feaures. In this figure, we see that the impact of
this transformation is much smaller than those of x,
with only one feature (ela meta.lin simple.intercept)
being statistically significantly different. For the re-
maining problems, the magnitude of the change was
not large enough to find statistically significant differ-
ences between the translated and original problems,
although the continued increase in EMD suggests that
with larger transformations this might change.
Impact of Spatial Transformations on Exploratory and Deep-Learning Based Landscape Features of CEC2022 Benchmark Suite
67

(a) Translation on x. (b) Translation on y.
(c) Scaling on x. (d) Scaling on y.
(e) Rotation on x.
Figure 7: Changes in DoE2Vec features after applying five types of transformations on the CEC2022 problems. The cosine
similarity between the original and transformed features via translation (top row) or scaling (second row) applied to x (left
column) or y (right column), the results of applying rotation to x are present in the last figure. Different colors represent
different problems.
Figure 7b shows the alterations in DoE2Vec fea-
tures when applying objevtive translation. Although
the differences between transformed and untrans-
formed instances continuously increase, the change of
cosine similarity never exceeds 1%, which is a safe
value for classifying instances according to our re-
sults of cosine similarity at the beginning of Section 4.
Thus, DoE2Vec is invariant to objective translation.
4.3.2 Objective Scaling
Figure 6d shows the impact of the objective scaling
transformation on the CEC2022 problems. Here, we
see a larger difference between the original and trans-
formed problems, with up to eight features statisti-
cally significantly impacted. Similarly to the scaling
on x, the objective scaling also has an obvious influ-
ence on the ELA features, as the number of features
rejected by the KS-test immediately increases regard-
less of whether log
2
k is greater than 0 or smaller than
0. At the same time, the growth of EMD is signifi-
cantly weaker than when scaling is applied on x.
Changes in DoE2Vec are shown in Figure 7d. The
cosine similarity never less than 9.9999e − 1, which
means that the impact of objective scaling is so subtle
for DoE2Vec that the changes are even smaller than
the objective in translation, which is opposite to the
situation of ELA features. Moreover, k < 2
0
have a
more obvious change than k > 2
0
.
4.4 Sensitivity of ELA Features
To obtain a per-feature view of the impact of the
considered transformations, we aggregate the feature
changes across all instances created by each transfor-
mation method into a measure of feature sensitivity.
This is calculated as the fraction of transformed in-
stances in which the distribution of the feature was
statistically different according to the KS-test. The
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
68

Figure 8: Sensitivity of 55 ELA features after applying 5 types of transformation. The brighter the color, the more sensitive
the corresponding ELA feature is after this transformation. The horizontal axis shows the problem id, while the vertical axis is
the ELA feature name. Sensitivity is measured as the fraction of transformed instances in which the distribution of the feature
was statistically different according to the KS-test.
results are illustrated in Figure 8.
We note that very few features are fully invariant
to all transformations, with only the PCA-based fea-
ture set showing no changes when applying domain
transformations. Indeed, the PCA features with no
changes at all are those which depend only on the dis-
tribution of samples within our domain, which is kept
static throughout all instances. On the other hand, the
PCA features which include information on the func-
tion values do seem somewhat sensitive, depending
on which underlying function is considered.
We also observe that, while the intercept of the
linear model is the only feature sensitive to our ap-
plied function-value translation, with more extreme
scaling-based transformations, the other coefficient
values from the linear model are impacted as well.
This is also the case for the information content fea-
tures, which is surprising, given its seemingly ro-
bust ability to contribute to algorithm selection mod-
els even in the quantum domain (P
´
erez-Salinas et al.,
2023).
5 CONCLUSION & FUTURE
WORK
In this paper, we have shown that applying transfor-
mations to a set of benchmark problems can lead to
significant changes in low-level landscape features,
as measured by ELA or DoE2Vec. Although the im-
pact of transformation methods scales with their dis-
ruptiveness, even seemingly small changes to the do-
main, such as minor translation or simple rotation,
have a statistically significant impact on a rather large
subset of ELA features. These findings suggest that
great care should be taken when designing instance
generation mechanisms for the CEC2022 base func-
tions considered here if the aim is to maintain the low-
level features present in the current set of functions.
Another question which remains unanswered is
whether we should consider the full set of ELA fea-
tures going forward. For example, the intercept of a
fitted linear model surely contains some information
about the landscape, but given that it is highly depen-
dent on the specific range of function values, we can
Impact of Spatial Transformations on Exploratory and Deep-Learning Based Landscape Features of CEC2022 Benchmark Suite
69

question its use for more general problem feature de-
tection or future algorithm selection. Previous work
has suggested that a normalization procedure should
be applied to the function values before ELA calcula-
tion (Prager and Trautmann, 2023a), but this merely
shifts the question to, e.g., logarithmic transforma-
tions of the function value.
An overarching question we identify here is how
robust the intuitive link is in practice between low-
level landscape features, such as ELA, and the high-
level properties which they aim to capture. Many
studies using ELA are rather limited in scope, and
while they show great performance within bench-
marking suites, generalizability to other setups seems
rather poor (Vermetten et al., 2023; Kostovska et al.,
2022). More research into the link between high-level
landscape properties, ELA features and algorithm be-
haviour is required to better understand how we can
move towards more generalizable results for our au-
tomated algorithm selection studies.
With the introduction of new alternatives to ELA,
such as DoE2Vec and Deep-ELA (Seiler et al., 2024),
the question of whether low-level features should in-
deed be invariant to search space transformations be-
comes even more relevant. While we observe that
DoE2Vec is still impacted by most transformations,
we note that because these features rely on training
neural networks, their training data could be aug-
mented to e.g. include different transformations of
the used samples, which should result in more stable
features. However, it is not certain that these invari-
ances will be present in the used algorithms, leading
to a loss of information if not accounted for in the fea-
ture space. The goals of landscape features are often
inherently linked to algorithmic behaviour, and this
should not be forgotten when designing or generating
new sets of features.
REFERENCES
Ahrari, A., Elsayed, S., Sarker, R., Essam, D., and Coello,
C. A. C. (2022). Problem definition and evaluation
criteria for the cec’2022 competition on dynamic mul-
timodal optimization. EvOpt Report 2022001.
Anonymous (2024). Impact of spatial transformations on
landscape features of cec 2022 basic benchmark prob-
lems.
B
¨
ack, T. H., Kononova, A. V., van Stein, B., Wang, H.,
Antonov, K. A., Kalkreuth, R. T., de Nobel, J., Ver-
metten, D., de Winter, R., and Ye, F. (2023). Evolu-
tionary algorithms for parameter optimization—thirty
years later. Evolutionary Computation, 31(2):81–122.
Bartz-Beielstein, T., Doerr, C., van den Berg, D., Bossek,
J., Chandrasekaran, S., Eftimov, T., Fischbach, A.,
Kerschke, P., Cava, W. L., Lopez-Ibanez, M., Malan,
K. M., Moore, J. H., Naujoks, B., Orzechowski, P.,
Volz, V., Wagner, M., and Weise, T. (2020). Bench-
marking in optimization: Best practice and open is-
sues.
Bartz-Beielstein, T., Lasarczyk, C., and Preuss, M. (2010).
The sequential parameter optimization toolbox. In Ex-
perimental methods for the analysis of optimization
algorithms, pages 337–362. Springer.
Beyer, H.-G. and Schwefel, H.-P. (2002). Evolution
strategies–a comprehensive introduction. Natural
computing, 1:3–52.
de Nobel, J., Ye, F., Vermetten, D., Wang, H., Doerr, C.,
and B
¨
ack, T. (2023). Iohexperimenter: Benchmarking
platform for iterative optimization heuristics. Evolu-
tionary Computation, pages 1–6.
Eglajs, V. and Audze, P. (1977). New approach to the de-
sign of multifactor experiments. Problems of Dynam-
ics and Strengths, 35(1):104–107.
Floudas, C. A., Pardalos, P. M., Adjiman, C., Esposito,
W. R., G
¨
um
¨
us, Z. H., Harding, S. T., Klepeis, J. L.,
Meyer, C. A., and Schweiger, C. A. (2013). Hand-
book of test problems in local and global optimization,
volume 33. Springer Science & Business Media.
Hall, B. C. and Hall, B. C. (2013). Lie groups, Lie algebras,
and representations. Springer.
Hansen, N., Auger, A., Ros, R., Mersmann, O., Tu
ˇ
sar, T.,
and Brockhoff, D. (2021). Coco: A platform for com-
paring continuous optimizers in a black-box setting.
Optimization Methods and Software, 36(1):114–144.
Hansen, N., Finck, S., Ros, R., and Auger, A. (2009).
Real-parameter black-box optimization benchmark-
ing 2009: Noiseless functions definitions. Technical
Report RR-6829, INRIA.
Hansen, N., Ros, R., Mauny, N., Schoenauer, M.,
and Auger, A. (2011). Impacts of invariance in
search: When cma-es and pso face ill-conditioned
and non-separable problems. Applied Soft Computing,
11(8):5755–5769.
He, J., Reeves, C., Witt, C., and Yao, X. (2007). A
note on problem difficulty measures in black-box opti-
mization: Classification, realizations and predictabil-
ity. Evolutionary Computation, 15(4):435–443.
Jankovi
´
c, A. and Doerr, C. (2019). Adaptive landscape
analysis. In Proceedings of the Genetic and Evolu-
tionary Computation Conference Companion, pages
2032–2035.
Kantorovich, L. V. (1960). Mathematical methods of orga-
nizing and planning production. Management science,
6(4):366–422.
Kerschke, P. and Trautmann, H. (2019). Comprehen-
sive feature-based landscape analysis of continuous
and constrained optimization problems using the r-
package flacco. In Bauer, N., Ickstadt, K., L
¨
ubke,
K., Szepannek, G., Trautmann, H., and Vichi, M., ed-
itors, Applications in Statistical Computing – From
Music Data Analysis to Industrial Quality Improve-
ment, Studies in Classification, Data Analysis, and
Knowledge Organization, pages 93 – 123. Springer.
Kolmogorov, A. N. (1933). Sulla determinazione empirica
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
70

di una legge didistribuzione. Giorn Dell’inst Ital Degli
Att, 4:89–91.
Kostovska, A., Jankovic, A., Vermetten, D., de Nobel,
J., Wang, H., Eftimov, T., and Doerr, C. (2022).
Per-run algorithm selection with warm-starting using
trajectory-based features. In International Conference
on Parallel Problem Solving from Nature, pages 46–
60. Springer.
Kudela, J. (2022). A critical problem in benchmarking and
analysis of evolutionary computation methods. Nature
Machine Intelligence, 4(12):1238–1245.
Lehre, P. K. and Witt, C. (2010). Black-box search by un-
biased variation. In Proceedings of the 12th annual
conference on Genetic and evolutionary computation,
pages 1441–1448.
Long, F. X., Vermetten, D., van Stein, B., and Kononova,
A. V. (2023). BBOB instance analysis: Landscape
properties and algorithm performance across problem
instances. In International Conference on the Applica-
tions of Evolutionary Computation (Part of EvoStar),
pages 380–395. Springer.
McInnes, L., Healy, J., Saul, N., and Grossberger, L. (2018).
Umap: Uniform manifold approximation and projec-
tion. The Journal of Open Source Software, 3(29):861.
Mersmann, O., Bischl, B., Trautmann, H., Preuss, M.,
Weihs, C., and Rudolph, G. (2011). Exploratory land-
scape analysis. In Proceedings of the 13th annual
conference on Genetic and evolutionary computation,
pages 829–836.
Mu
˜
noz, M. A., Kirley, M., and Smith-Miles, K. (2022).
Analyzing randomness effects on the reliability of
exploratory landscape analysis. Natural Computing,
pages 1–24.
Mu
˜
noz, M. A. and Smith-Miles, K. (2015). Effects of func-
tion translation and dimensionality reduction on land-
scape analysis. In 2015 IEEE Congress on Evolution-
ary Computation (CEC), pages 1336–1342. IEEE.
Mu
˜
noz, M. A., Sun, Y., Kirley, M., and Halgamuge, S. K.
(2015). Algorithm selection for black-box continu-
ous optimization problems: A survey on methods and
challenges. Information Sciences, 317:224–245.
P
´
erez-Salinas, A., Wang, H., and Bonet-Monroig, X.
(2023). Analyzing variational quantum land-
scapes with information content. arXiv preprint
arXiv:2303.16893.
Prager, R. P. and Trautmann, H. (2023a). Nullifying the
inherent bias of non-invariant exploratory landscape
analysis features. In International Conference on the
Applications of Evolutionary Computation (Part of
EvoStar), pages 411–425. Springer.
Prager, R. P. and Trautmann, H. (2023b). Pflacco: Feature-
Based Landscape Analysis of Continuous and Con-
strained Optimization Problems in Python. Evolution-
ary Computation, pages 1–25.
Renau, Q., Dreo, J., Doerr, C., and Doerr, B. (2019). Ex-
pressiveness and robustness of landscape features. In
Proceedings of the Genetic and Evolutionary Compu-
tation Conference Companion, pages 2048–2051.
Rosenbrock, H. (1960). An automatic method for finding
the greatest or least value of a function. The computer
journal, 3(3):175–184.
Schaffer, J. D. (2014). Multiple objective optimization with
vector evaluated genetic algorithms. In Proceedings
of the first international conference on genetic algo-
rithms and their applications, pages 93–100. Psychol-
ogy Press.
Seiler, M. V., Kerschke, P., and Trautmann, H. (2024).
Deep-ELA: Deep exploratory landscape analysis with
self-supervised pretrained transformers for single-
and multi-objective continuous optimization prob-
lems. arXiv preprint arXiv:2401.01192.
Skvorc, U., Eftimov, T., and Korosec, P. (2020). Under-
standing the problem space in single-objective numer-
ical optimization using exploratory landscape analy-
sis. Applied Soft Computing, 90:106138.
ˇ
Skvorc, U., Eftimov, T., and Koro
ˇ
sec, P. (2022). A compre-
hensive analysis of the invariance of exploratory land-
scape analysis features to function transformations. In
2022 IEEE Congress on Evolutionary Computation
(CEC), pages 1–8. IEEE.
Suganthan, P. N., Hansen, N., Liang, J. J., Deb, K., Chen,
Y.-P., Auger, A., and Tiwari, S. (2005). Problem defi-
nitions and evaluation criteria for the cec 2005 special
session on real-parameter optimization. KanGAL re-
port, 2005005(2005):2005.
van Stein, B., Long, F. X., Frenzel, M., Krause, P., Gitterle,
M., and B
¨
ack, T. (2023). Doe2vec: Deep-learning
based features for exploratory landscape analysis. In
Proceedings of the Companion Conference on Genetic
and Evolutionary Computation, GECCO ’23 Com-
panion, page 515–518, New York, NY, USA. Asso-
ciation for Computing Machinery.
Vermetten, D., van Stein, B., Caraffini, F., Minku, L. L.,
and Kononova, A. V. (2022). Bias: a toolbox for
benchmarking structural bias in the continuous do-
main. IEEE Transactions on Evolutionary Computa-
tion, 26(6):1380–1393.
Vermetten, D., Ye, F., B
¨
ack, T., and Doerr, C. (2023).
Ma-bbob: A problem generator for black-box opti-
mization using affine combinations and shifts. arXiv
preprint arXiv:2312.11083.
Whitley, D., Rana, S., Dzubera, J., and Mathias, K. E.
(1996). Evaluating evolutionary algorithms. Artificial
intelligence, 85(1-2):245–276.
Wolpert, D. and Macready, W. (1997). No free lunch theo-
rems for optimization. IEEE Transactions on Evolu-
tionary Computation, 1(1):67–82.
Zhang, Y., Wang, S., Ji, G., et al. (2015). A comprehensive
survey on particle swarm optimization algorithm and
its applications. Mathematical problems in engineer-
ing, 2015.
Impact of Spatial Transformations on Exploratory and Deep-Learning Based Landscape Features of CEC2022 Benchmark Suite
71