
On Solving Controlled-Invariance Problems in Dioids Using the
PyMinMaxGD Python Scripts Library
Olivier Boutin
1 a
, Claude Martinez
2 b
and Naly Rakoto
3 c
1
LS2N - UMR6004, 3iL Ingénieurs, Limoges, France
2
LS2N - UMR6004, Nantes Université, École Centrale Nantes, F-44000 Nantes, France
3
LS2N - UMR6004, IMT Atlantique, Nantes, France
Keywords:
Modelling and Control of Discrete-Event Systems, Supervision Systems, Systems Synchronisation,
Controlled Invariance, Manufacturing Process Management, Dioids, Periodic Series, Algebraic Toolbox,
C++, Python, Object-Oriented Programming and Scripting Programming.
Abstract:
MinMaxGD is a C++ library developed and maintained since 2000 at the LARIS laboratory at Angers, France.
It provides ad-hoc primitives for calculations so as to handle periodic series over a dioid (namely M
ax
in
Jγ, δK).
Our aim with PyMinMaxGD is to provide, for this C++ library, a Python interface using SWIG, in order to
allow scripting programming, on top of the already available programming primitives. The use of PyMin-
MaxGD is illustrated here to tackle some general problems of control using the controlled-invariance theory.
The corresponding control problems deal with the meeting of time or marking constraints or even both of
them. First, the set that corresponds to the verification of the constraints is defined, and then the supremal
controlled-invariant set included in this specification set is calculated. In the sequel, a controller that allows
the state of the system to remain in the latter set is given.
1 INTRODUCTION
To the best of our knowledge, the main library to pro-
vide ad-hoc primitives so as to handle periodic series
over a dioid is MinMaxGD (Hardouin, 2024), a C++
library developed and maintained since 2000 (Cot-
tenceau et al., 2000) at the LARIS laboratory at
Angers, France
1
. A JavaScript interface, called Min-
MaxGDJS, has also been developed in 2017 (Fer-
reira Cândido et al., 2017), giving the ability to access
the periodic-series library through any Web browser
on any operating system. This makes it easier to get
insight on calculations with periodic series, without
the hassle of configuring and building the original
C++ library. Another interest is to provide a platform
for giving portable demos. Nevertheless, due to its
locked Web-based interface, it lacks the power to em-
bed the calculations within some other programming
processings. Our aim with PyMinMaxGD is then to
a
https://orcid.org/0009-0000-7292-0672
b
https://orcid.org/0000-0003-1168-3284
c
https://orcid.org/0000-0002-5798-0359
1
See Section 4.1 for detailed information and a compar-
ison between such toolboxes.
provide a different interface for the original library,
meant for Python
2
and using SWIG (SWIG Maintain-
ers, 2024), an open-source software tool used to con-
nect libraries written in C++ with scripting languages,
in order to allow scripting programming. The pro-
duced code keeps the very same computation benefits
as for the original library, extending its portability to
a scripting programming paradigm.
As a first attempt to develop research on the con-
trol of discrete-event systems using the representa-
tion of their behaviour, within the framework of se-
ries in the M
ax
in
Jγ, δK dioid focusing on the state of
a system rather than its transfer function, some as-
pects of the use of series for the controlled-invariance
theory are presented. The concept of controlled in-
variance, or (A, B)-invariance, has been introduced
independently by (Basile and Marro, 1969) and by
(Wonham and Morse, 1970). The whole geometric
approach for control, based on the then new alge-
braic geometry theory (Grothendieck and Dieudonné,
1960), has started from these works. The solution of
many classical control problems, among which the
2
What is actually called an "extension module" in the
Python ecosystem.
Boutin, O., Martinez, C. and Rakoto, N.
On Solving Controlled-Invariance Problems in Dioids Using the PyMinMaxGD Python Scripts Library.
DOI: 10.5220/0012936500003822
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 555-566
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
555

disturbance decoupling problem, the regulator prob-
lem, and various observer design problems, were
given using this controlled-invariance theory – see
for instance (Wonham, 1974) and (Basile and Marro,
1992) for a complete account of these results. The
controlled-invariance theory has been applied also in
the framework of systems over more general algebraic
contexts than fields, such as rings or semirings. For
the sake of extending the classical results in the latter
structures, the concept of controlled-invariant mod-
ule has been introduced; (Hautus, 1982) and (Conte
and Perdon, 1995) are pioneering references for in-
variance control over a ring.
Finally, systems over a semiring, often called
“Max-Plus
3
systems”, have been thoroughly studied
in the founding reference (Baccelli et al., 1992). They
have also received attention from the perspective of
controlled-invariance theory, the first results being
due to (Katz, 2007). It is stated there that there ex-
ists a maximal controlled-invariant module in every
given module in R
max
and many other semirings. It
is pointed out that the computation of this maximal
set is an open problem in general and important par-
ticular cases where the problem is solvable are identi-
fied. Sufficient conditions that allow this computa-
tion are often met in practice. In (Cárdenas et al.,
2015), it was shown that a feedforward control law
is suitable to maintain the state of a system within the
controlled-invariant set. In (Cárdenas et al., 2017), a
procedure to find the greatest controlled-invariant set
included in the admissible set defined by some con-
straints has been presented. There, it has also been
shown that a static non linear state feedback control
law is suitable to maintain the state of a system within
the controlled-invariant set. Some other problems of
control have been tackled in (Martinez et al., 2022)
and (Animobono et al., 2022). All the aforemen-
tioned work on the use of controlled-invariance theory
have been done within the canonical Z
max
and Z
min
dioid frameworks. Based on our information, there
is no research that has tackled the use of controlled-
invariance theory in the context of a dioid of series
such as M
ax
in
Jγ, δK. The purpose of the control prob-
lems given in the present article is to illustrate, for the
first time, that controlled invariance can also be useful
for the class of systems that are modelled with series,
and particularly using the C++ MinMaxGD library.
The remainder of this article is organised as fol-
lows: the following section will briefly define and
describe the theoretical elements based on which our
modelling framework works; then, Section 3 will in-
troduce how control theory can be applied in this
3
Often denoted thanks to Z
max
or R
max
for example,
depending on the exact set of studied values.
mathematical context; afterwards, in Section 4, more
insight will be given on other toolboxes for such work
and why none of them suits our needs, as well as more
details on the features offered by our developments;
subsequently, Section 5 will provide two use cases of
our library, based on a typical problem of a physical
system having to follow a specification, reinterpreted
as a synchronisation problem and a time constraint
meeting, and within the specific M
ax
in
Jγ, δK dioid, in-
cluding detailed Python scripts; finally, a last section
will give some conclusions and openings of this work.
2 BACKGROUND
2.1 Dioids and Systems Representation
A dioid is a set, denoted D, endowed with two bi-
nary operations, a sum (⊕) and a product (⊗). The
complete definition of a dioid (or idempotent semir-
ing) can be found, for example, in (Brunsch et al.,
2013, Section 1.3). The identity element of ⊕, ε, is
also called the zero element of D, while the identity
element of ⊗, e, is also called the unit element of D.
Due to the idempotency property, any dioid can
also be endowed with a natural (partial) order defined
by a ⪯ b ⇔ a ⊕ b = b.
As in a classical field, the binary operations can
be extended to the matrix case in dioids (Cohen et al.,
1989, p.42). For the matrices A, B ∈ D
n×m
and C ∈
D
m×p
one gets
(sum) [A ⊕ B]
i j
= [A]
i j
⊕ [B]
i j
;
(product) [A ⊗C]
i j
=
m
M
k=1
[A]
ik
⊗ [C]
k j
.
Remark 2.1. It is worth noticing that the product of
D
n×m
is not always commutative, i.e. A ⊗ B may be
different from B ⊗ A.
Let us now introduce a 2-dimensional dioid de-
noted B Jγ, δK (Cohen et al., 1989). It is the set of
formal power series in two variables γ and δ with
Boolean coefficients, i.e B = {ε, e} and the exponents
of variables γ and δ are in Z.
The interpretation
4
of a monomial γ
k
δ
t
is that,
considering a previous monomial γ
k
′
δ
t
′
, the epoch be-
ing γ
0
δ
0
, k − k
′
events occur after t −t
′
units of time,
which leads to a compact modelling of information.
Graphically, a series can be seen as a set of dots of a
point cloud in the event-time plane (see Figure 1)
5
.
4
Following the discussion in (Baccelli et al., 1992, Sec-
tion 5.4.4).
5
Bearing in mind that the time part of the modelling is
now an ordinate.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
556
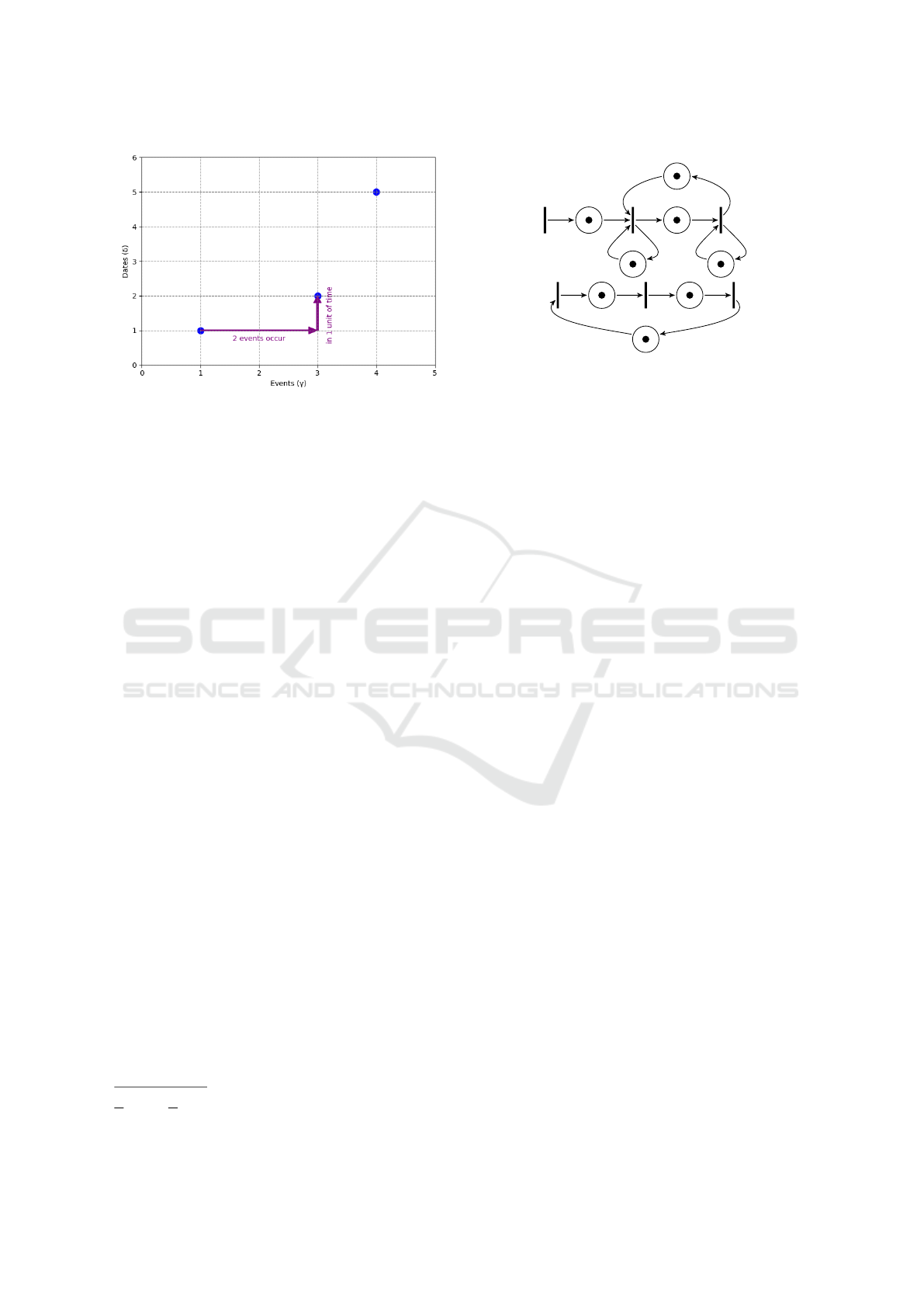
Figure 1: Graphical representation of series s = γ
1
δ
1
⊕
γ
3
δ
2
⊕ γ
4
δ
5
, s ∈ B Jγ, δK.
Actually, the “South-East cone” of each point in
the plane matches a corresponding monomial of a
series. This establishes an equivalence relation and
implies that series may have a “minimal” representa-
tion (Cohen et al., 1989, Comment ii) p.51), based on
the “absorption” of some monomials by others. The
resulting dioid of equivalence classes in B Jγ, δK is de-
noted M
ax
in
Jγ, δK.
Remark 2.2. In order to fully define M
ax
in
Jγ, δK, its
zero and unit elements are defined as ε = γ
+∞
δ
−∞
and
e = γ
0
δ
0
respectively
6
(Cohen et al., 1986, p. 991).
In the next section, complex systems described
by M
ax
in
Jγ, δK series are shown to have their graphi-
cal counterparts in the form of Timed Event Graphs,
which also consists in compact modelling.
2.2 Timed Event Graphs
Timed Event Graphs (TEGs) define a class of timed
Petri nets where there are no conflicts (Ramchandani,
1974, Chapter 4).
Figure 2 shows two examples of TEGs. Please
note that transition t
1
is downstream of t
2
, for reasons
out of the scope of this study.
2.3 Modules in M
ax
in
Jγ, δK
The concept of modules on a semiring is analogous to
the concept of vector spaces on a field. Modules over
a semiring are often called semimodules, and modules
over a dioid are sometimes called moduloid, but the
term module shall rather be used in this article, fol-
lowing the track of (Wagneur, 1996). Here, modules
and submodules of M
ax
in
Jγ, δK, and more specifically
6
+∞ and −∞ being respectively the zero element of
Z
min
and Z
max
. 0 is their common unit element.
u
0
t
2
2
3
t
1
2 2
7
t
3
t
4
1
2
t
5
Figure 2: Two TEGs. The TEG above is meant to be syn-
chronised with a takt time (Haghsheno et al., 2016) given
by the TEG below, thanks to the study to come in Section 5.
finitely generated modules, i.e. those that are gener-
ated with a finite family of vectors of series defined in
M
ax
in
Jγ, δK, are of high interest.
Let us consider a matrix M of size n × m with its
entries in M
ax
in
Jγ, δK, n and m being positive integers.
Let us denote ImM as the submodule of M
ax
in
Jγ, δK
n
that is generated by the columns of M, hence ImM =
{x ∈ M
ax
in
Jγ, δK
n
| ∃v ∈ M
ax
in
Jγ, δK
m
, x = Mv}. By
definition, a submodule M of M
ax
in
Jγ, δK
n
is finitely
generated if there exists a positive integer q and a ma-
trix M ∈ M
ax
in
Jγ, δK
n×q
such that M = ImM. Finitely
generated modules over M
ax
in
Jγ, δK
n
may be repre-
sented in several ways. One can refer to the origi-
nal results of (Butkovi
ˇ
c and Hegedüs, 1984) where
it is established that the family of finitely gener-
ated submodules of R
n
max
coincides with the family
of finitely generated cones that are sets of the form
Cone(R, Q) = {x ∈ R
n
max
| R⊗x = Q⊗x} where R and
Q are matrices of size p×n, p being a positive integer.
This result is applied on submodules of M
ax
in
Jγ, δK
n
.
Theorem 2.1. Given a module M ⊂ M
ax
in
Jγ, δK
n
, the
two following assertions are equivalent.
(i) There exist a positive integer q and a matrix M ∈
M
ax
in
Jγ, δK
n×q
such that M = ImM.
(ii) There exist a positive integer p and matrices
R, Q ∈ M
ax
in
Jγ, δK
p×n
such that M = Cone(R, Q).
Algorithms that permit to switch from a cone rep-
resentation to an image representation have been pre-
sented first in (Butkovi
ˇ
c and Hegedüs, 1984), and
refined by Allamigeon et al. in (Allamigeon et al.,
2010).
For any set S ⊂ M
ax
in
Jγ, δK
m
, its image by M is
denoted by MS. The preimage by M of any set T ⊂
M
ax
in
Jγ, δK
p
is denoted M
−1
T . The difference of two
sets S , S
′
⊂ M
ax
in
Jγ, δK
m
, denoted S ⊖ S
′
is defined as
{x” ∈ M
ax
in
Jγ, δK
m
|∃x ∈ S , x
′
∈ S
′
, x” ⊕ x
′
= x}.
On Solving Controlled-Invariance Problems in Dioids Using the PyMinMaxGD Python Scripts Library
557

3 CONTROL PROBLEMS AND
ALGORITHMS
3.1 Controlled Invariance
Let us consider here a controlled system of the form:
x = Ax ⊕ Bu, (1)
where A ∈ M
ax
in
Jγ, δK
n×n
, B ∈ M
ax
in
Jγ, δK
n×m
, n and
m are positive integers, and x ∈ M
ax
in
Jγ, δK
n
and u ∈
M
ax
in
Jγ, δK
m
. The variable x refers to the state trajec-
tory of the system, and u is its control input.
Note that, in opposition to systems over R
max
,
there is no specific mention of the initial state x
0
be-
cause each entry of the state vector is a series that
represents all the trajectory, including the initial state.
The following definition of controlled invariance is a
transcription of the definition stated for systems over
R
max
, see for instance (Martinez et al., 2022).
Definition 3.1. A set M is said to be controlled-
invariant if, for every vector x ∈ M , there exists a
control u such that the solution of system (1) is en-
tirely in M .
Research about controlled-invariant sets proper-
ties are still in progress. Nevertheless, some proper-
ties are already well known; for instance, the case of
the submodules of R
n
max
, or over various other semir-
ings, has particularly been studied. See (Katz, 2007)
and (Di Loreto et al., 2010), for instance.
Proposition 3.1. A set M ⊂ M
ax
in
Jγ, δK
n
is
controlled-invariant if and only if the following
inclusion is satisfied: AM ⊂ M ⊖ ImB. Equiva-
lently, M is controlled-invariant if and only if the
following inclusion is satisfied:
M ⊂ A
−1
(M ⊖ ImB).
Proof By definition, the set M is controlled-
invariant if each of its elements x satisfies Ax ⊕ Bu ∈
M for some vector u ∈ M
ax
in
Jγ, δK
m
. The result fol-
lows since Bu remains in ImB when u varies, and by
definition of ⊖ (Katz, 2007, Section 2).
Theorem 3.1. The following properties are veri-
fied (Cárdenas et al., 2017).
(i) A module M ⊂ M
ax
in
Jγ, δK
n
is controlled-invariant
if and only if:
AM ⊂ M ⊖ ImB .
(ii) A module M ⊂ M
ax
in
Jγ, δK
n
generated by the
columns of matrix M ∈ M
ax
in
Jγ, δK
n×q
is controlled-
invariant if and only if there exist matrices U ∈
M
ax
in
Jγ, δK
m×q
and V ∈ M
ax
in
Jγ, δK
q×q
such that the
following identity is verified:
AM ⊕BU = MV .
(iii) A module M ⊂ M
ax
in
Jγ, δK
n
such that M =
ImM = Cone(R, Q), for matrices M ∈ M
ax
in
Jγ, δK
n×q
and R, Q ∈ M ∈ M
ax
in
Jγ, δK
p×n
is controlled-invariant
if and only if there exists a matrix U ∈ M
ax
in
Jγ, δK
m×q
such that the following equality is verified:
R(AM ⊕BU) = Q(AM ⊕ BU) .
Not all submodules of M
ax
in
Jγ, δK
n
are controlled-
invariant. But one can show that any module M ⊂
M
ax
in
Jγ, δK
n
contains a maximal controlled-invariant
submodule, denoted V
⋆
M
(A, B). It is shown in
(Di Loreto et al., 2010) that the supremal controlled-
invariant submodule included in a finitely generated
module is the limit of the sequence {V
i
} defined as
follows:
V
0
= M ; V
i+1
= M ∩ A
−1
(V
i
⊖ ImB) , for i ≥ 0 .
(2)
The successive terms of the sequence are finitely gen-
erated modules.
As it is mentioned in (Cárdenas et al., 2017), the
matrices M
i
and (R
i
, Q
i
) can be computed iteratively
such that V
i
= ImM
i
= Cone(R
i
, Q
i
) seeking for a so-
lution of the following equation:
R
i−1
A R
i−1
B
R ε
M
i
U
i
=
Q
i−1
A Q
i−1
B
Q ε
M
i
U
i
. (3)
At each step, one computes M
i
and U
i
and, then,
one computes R
i
et Q
i
using theorem 2.1. The limit
of the sequence is the intersection of modules V
i
.
Finally, if for some integer i, the equality V
i
=
V
i+1
is true, then the sequence stabilises, which leads
to V
k
= V
i
, for every k ≥ i, and therefore V
ω
= V
i
.
Following (2), V
ω
= M ∩A
−1
(V
ω
⊖ ImB) can be de-
duced. Thus, using Proposition 3.1, V
ω
can be con-
sidered as controlled-invariant set, which is included
in M and, therefore, it is included into the maximal
controlled-invariant set V
⋆
M
(A, B).
3.2 Some Control Problems
The first problem tackled here and illustrated in the
example in subsection 5.1 is a problem of synchro-
nisation of two systems, say (Σ
1
) and (Σ
2
), that are
defined as follows:
(Σ
1
)
(
x = A ⊗ x ⊕ B⊗ u
y = C ⊗ x
,
(Σ
2
)
(
w = D ⊗ w
v = E ⊗w
.
Several variants of this problem have been studied
and presented in (Martinez et al., 2022) in the R
n
max
dioid. Systems (Σ
1
) and (Σ
2
) are said to have syn-
chronous outputs if their output solutions coincide,
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
558

i.e. y = v. When no input is applied (say u = ε),
systems are said synchronous if y = v. In practical
situations in industry, the notion of synchronisation
is related to the takt time that somehow defines the
tempo of the factory (Haghsheno et al., 2016). The
problem that is addressed here is that of the forced
synchronisation, which is formulated as follows.
Problem 3.1. (Forced synchronisation)
System (Σ
1
) and (Σ
2
) are synchronised if there ex-
ists a control law u that forces synchronisation be-
tween them, i.e. the outputs of both systems (Σ
1
) and
(Σ
2
) are equal: y = v. Such a control u is said to be
admissible for the synchronisation of (Σ
1
) and (Σ
2
).
In (Martinez et al., 2022), the forced synchroni-
sation problem was slightly different, seeking for a
given k
0
, after which synchronisation would be possi-
ble; then the system was called k
0
-synchronisable. In-
deed, state trajectories that verify the solution of prob-
lem 3.1 can be considered as the target to be reached,
seeking for a set of coreachable x
p
and u
p
.
This extension needs more research work in the
M
ax
in
Jγ, δK dioid.
The second problem tackled here and illustrated
in the second example in subsection 5.2 concerns the
verification of time constraints related to bounded du-
ration for some operations. This problem has been
addressed in (Kim and Lee, 2016) and continued in
(Jacob and Amari, 2017). Then, it has been formu-
lated as a controlled-invariant problem in (Cárdenas
et al., 2017). In this problem, the constraints limit the
maximal duration of certain tasks; that is to say, the
minimal duration is given by the delay τ associated to
a place of a TEG and the constraint to be verified is
that the sojourn time of tokens is lower than a certain
τ
max
, considering the following system (Σ):
(Σ)
(
x = A ⊗ x ⊕ B⊗ u ,
y = C ⊗ x .
Problem 3.2. (Constraints verification) The series x
that models the state behaviour should verify some
additional constraints of the form:
(duration)
γ
0
δ
−τ
max
⊗ x
i
≤ x
j
.
(4)
To take into account several constraints, then, for
each of them, one has to write a single inequality as
in (4). These inequalities are gathered in a matrix in-
equality as follows:
E ⊗ x ≤ x.
The set of solutions of this inequality is Im E
⋆
.
4 TOOLBOXES FOR
CALCULATIONS OVER DIOIDS
4.1 Existing Toolboxes
Almost a dozen of initiatives have been encountered
while looking for a toolbox that could suit our needs.
Table 1 below summarises all these initiatives and
projects, for the ease of comparison
7
.
As a matter of facts, none of them actually in-
clude the four following characteristics together, that
are definitely needed for our research:
1. including both dating and counting dynamics at
the same time;
2. possibility to integrate self-defined routines, like
plug-ins, without having the burden of compiling
the core components every time, for flexibility;
3. possibility to automatise simulations benchmarks,
and re-run parts of them interactively, as with
scripts;
4. interaction with other pieces of software.
For all these reasons, the development of our own
toolbox, described in the following subsection, has
been decided.
4.2 The Proposed Toolbox
The distribution of our piece of software is available
online (Boutin and Martinez, 2024), under GPLv3
license (Free Software Foundation, Inc., 2007). It
mainly consists of a single SWIG interface file of
about 900 lines of code so far, on top of the Min-
MaxGD library, based on roughly 5 000 lines of
code spread over 11 files defining 4 classes and
a few high-level functions and constants. It has
been compiled and installed
8
with the following soft-
ware requirements: 6.1 64-bit (SLTS
9
) Linux®
kernel; g++ 11.3.0; SWIG 4.0.2; Python 3.11.0; the
libpython3.11-dev and python-dev-is-python3
Linux packages and the matplotlib, numpy, pillow
and kiwisolver Python libraries.
Apart from the implementation of the scripts de-
signed to support the algorithms mentioned in Sec-
7
Note that symbol B there stands for the Boolean set
endowed with two binary operations “and” and “or” and
only composed of the elements e and ε.
8
Only once for the inclusion of the core toolbox, as
opposed to the need to compile C++-only code for each
new calculation design or update; then only the user-defined
scripts need to be updated and loaded interactively.
9
Meaning Super Long Time Support (Civil Infrastruc-
ture Platform™, 2023).
On Solving Controlled-Invariance Problems in Dioids Using the PyMinMaxGD Python Scripts Library
559
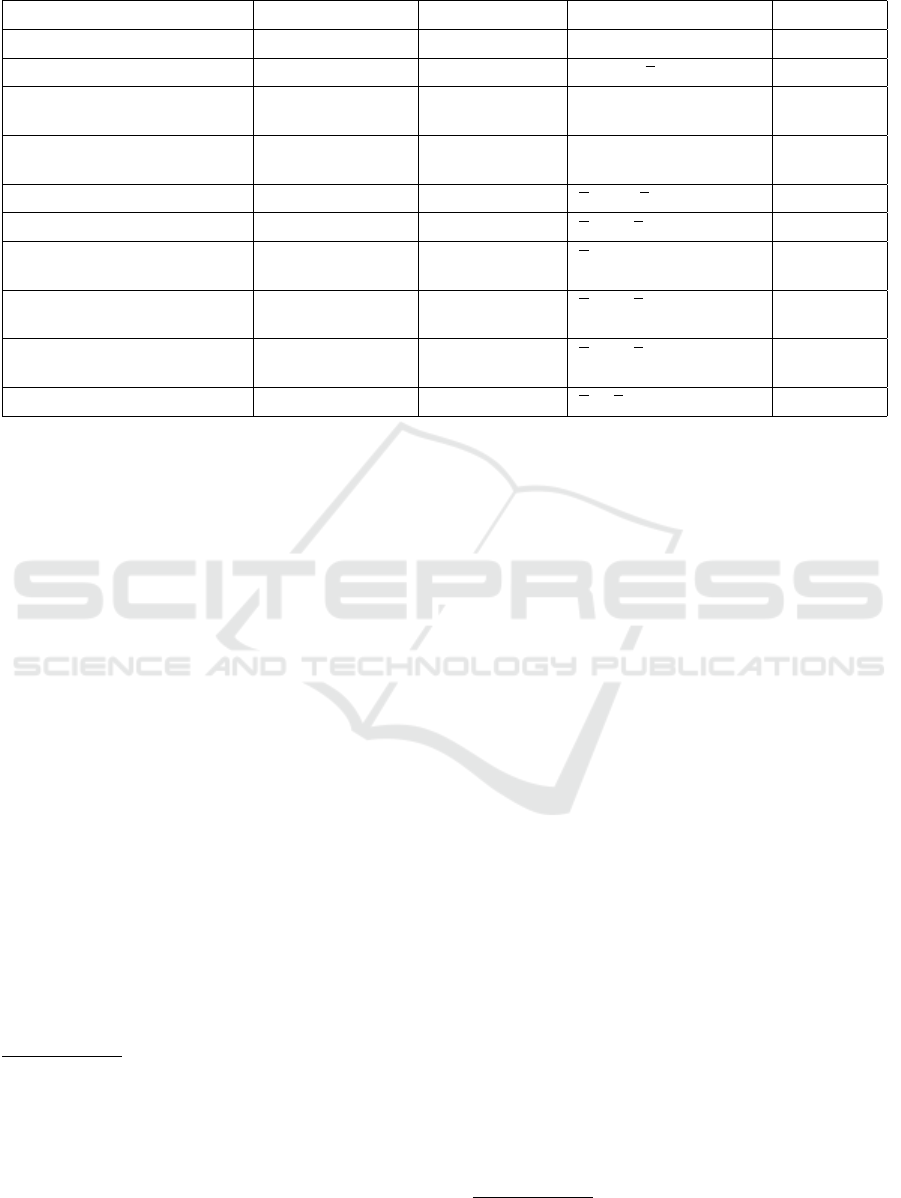
Table 1: Comparison of available dioid toolboxes.
Name Implementation Evolution from Available dioids Last version
10
MinMaxGD (Hardouin, 2024) C++ M
ax
in
J
γ, δ
K
03 Jul. 2024
ContainerMinMaxGD (Corronc, 2013) C++ Fork of MinMaxGD Intervals in Z
min
21 Apr. 2011
MinMaxGDJS (Ferreira Cândido et al.,
2017)
JavaScript wrapping over
C++
Fork of MinMaxGD M
ax
in
J
γ, δ
K
03 May 2019
ETVO (Cottenceau et al., 2022) C++ / WebAssembly
wrapping
Fork of MinMaxGD M
ax
in
J
γ, δ
K
and ET (see (Trunk,
2019, Chap. 5))
20 May 2023
Maxpluspy (Lahaye, 2019) Python Z
max
and “Z
max
-automata” 27 Nov. 2019
PetriTUB (Bednar et al., 2024) Python Z
max
and Z
min
, from Petri nets 14 Mar. 2024
MaxPlus Arithmetic Toolbox (Chance-
lier et al., 2015)
Already included in Sci-
coslab Toolbox
Fork of Scilab 4 Z
max
03 Oct. 2015
MaxPlus.jl (Quadrat, 2024) Julia Port from MaxPlus
Arithmetic Toolbox
Z
max
and Z
min
30 Apr. 2024
Max-Plus Algebra Toolbox (Sta
´
nczyk,
2016)
Matlab/Octave plug-in Z
max
and Z
min
14 Jun. 2016
TropicalNumbers (Liu, 2023) Julia Z
max
, Z
min
, (R
+
, max, ×) and B 26 Sep. 2023
tion 3, our toolbox offers the following new function-
alities compared to the original MinMaxGD toolbox:
• possibility to type user-friendly symbols (+, *, /,
%
11
) for matrix calculations and the + and * sym-
bols for the sum and the product between either
monomials or polynomials, instead of using ver-
bose functions names with parameters;
• comparison via <, <=, > or >= for elements belong-
ing either to series or series matrices;
• series matrices concatenation, if compatible
(when they share the same number of rows);
• matrix import/export from raw text files based on
a dedicated syntax;
• use of actual γ and δ symbols when displaying
monomials, as well as the ε symbol for the zero el-
ement with a precision of the corresponding scope
(monomial, polynomial or series);
• figure generation for the graphical representation
of polynomials in the form of “point clouds” and
series in the form of “step functions” (with the op-
tion of showing several series in the same figure).
All the figures shown in this article were actually
produced thanks to our toolbox;
10
As of 6 September 2024.
11
Used as “left division”, for commutativity issues
exposed in Remark 2.1. The \ character cannot not be
overloaded, as it is reserved in Python for line joining
or escape sequence specifications. See docs.python.org/
3/reference/lexical_analysis.html#explicit-line-joining
and docs.python.org/3/reference/lexical_analysis.html#
escape-sequences
• user-friendly deep copy of matrices instead of
standard Python shallow copies
12
, when needed.
All these features are embedded in current version
1.2 of our toolbox, together with a SWIG typemap
between the internal C++ 2-element array, for the
cells of series matrices, and a Python 2-tuple to en-
able user-friendly assignment syntax (of the kind
M[row,col] = given_series), as in the original
C++ code. For instance, the point cloud of Figure 1
can be obtained thanks to the following simple script:
# Toolbox functionalities loading first
from pyminmaxgd import *
# Then a call to the high-level routine
point_cloud(mono(1,1) + mono(3,2) + mono(4,5))
Two examples of use cases of our toolbox are pre-
sented in the following section.
5 EXAMPLES
5.1 Synchronising Production with a
Takt Time Clock
Some problems of synchronisation have been pre-
sented in (Martinez et al., 2022) and (Animobono
et al., 2022). An example of synchronisation of a
simple production plant that has to produce items at
a given pace is presented here. The “physical” sys-
tem Σ
1
and the takt time clock Σ
2
(its specification)
are modelled by TEGs, represented in Figure 2. The
following systems of equation in dioid M
ax
in
Jγ, δK is
used to describe their behaviour:
12
See docs.python.org/3/library/copy.html.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
560

(Σ
1
)
n
x = A ⊗ x ⊕ B⊗ u ,
(Σ
2
)
n
w = A
r
⊗ w,
with
A =
γ
1
δ
2
γ
1
δ
2
γ
1
δ
3
γ
1
δ
2
!
, B =
ε
e
!
,
and
A
r
=
ε ε γ
1
δ
1
γ
1
δ
7
ε ε
ε γ
1
δ
2
ε
.
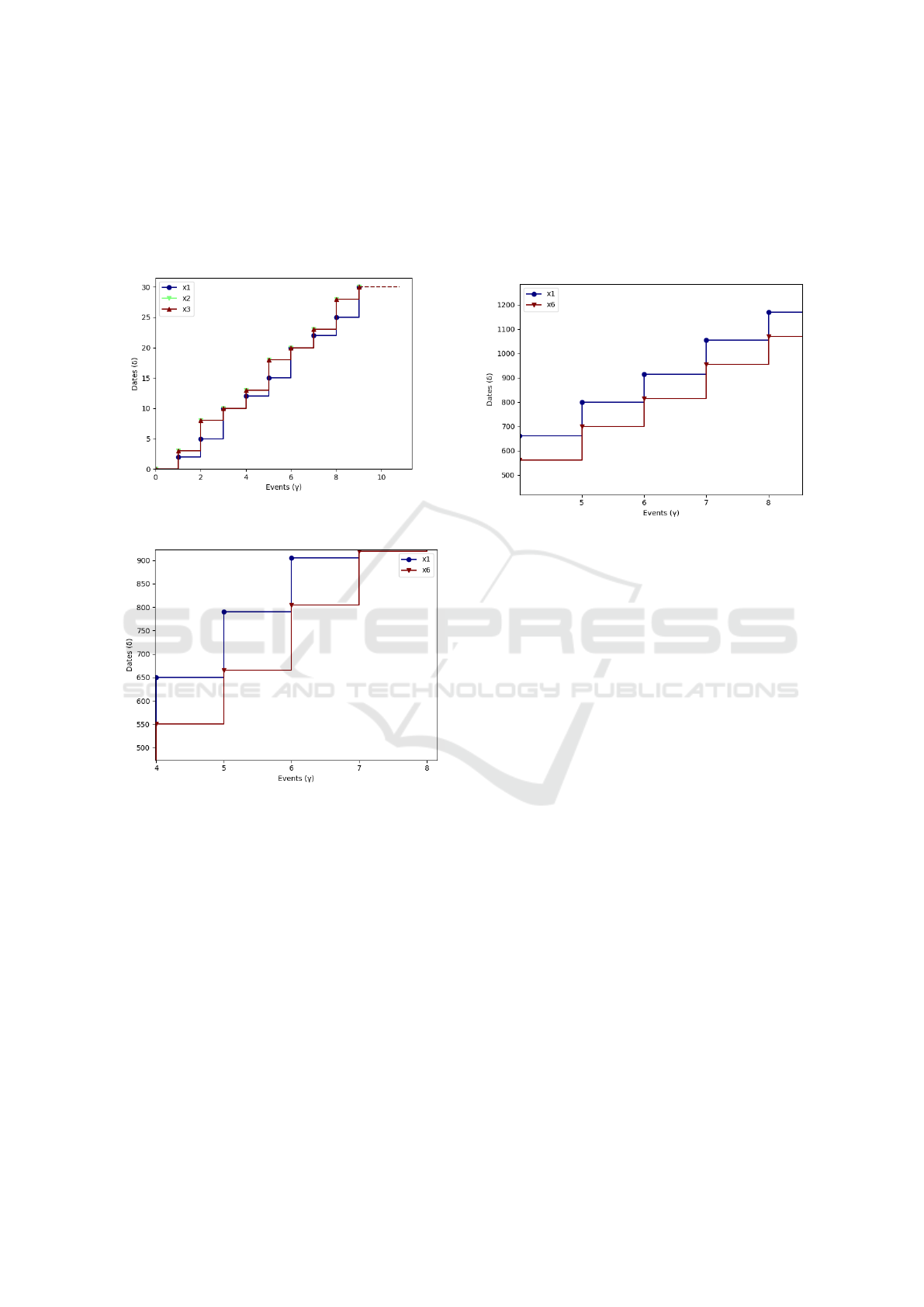
The behaviour of some internal transitions of the
TEGs of Figure 2 are represented in Figure 3 (x
i
is the
state representation of transition t
i
).
Figure 3: State behaviour of systems internal transitions.
In order to solve the problem of synchronisation,
let us first build an extended system Σ with matrices
A
b
and B
b
as follows:
A
b
=
γ
1
δ
2
γ
1
δ
2
ε ε ε
γ
1
δ
3
γ
1
δ
2
ε ε ε
ε ε ε ε γ
1
δ
1
ε ε γ
1
δ
7
ε ε
ε ε ε γ
1
δ
2
ε
,
B
b
=
ε
e
ε
ε
ε
.
The state X of Σ has to remain in a module K =
ImK that verifies the following constraint:
S ⊗ X ≤ T ⊗ X,
with S and T as follows:
S =
ε ε e ε ε
e e ε ε ε
!
,
T =
e e ε ε ε
ε ε e ε ε
!
.
Therefore K can be obtained:
K =
ε ε e ε
ε ε ε e
ε ε e e
e ε ε ε
ε e ε ε
,
of which module K is not controlled-invariant.
Hence, the sequence described in equation (3) is ap-
plied and the supremal controlled-invariant module
included in the module K is M
4
= ImM
4
, with M
4
described below.
M
4
=
ε e ε e ε e e
e ε e ε e ε ε
e e e e e e e
γ
0
δ
2
γ
0
δ
5
γ
0
δ
4
γ
0
δ
2
γ
0
δ
5
γ
0
δ
5
γ
0
δ
4
γ
0
δ
1
γ
0
δ
2
γ
0
δ
4
γ
0
δ
2
γ
0
δ
2
γ
0
δ
2
γ
0
δ
4
.
It also permits to find matrix U
4
:
U
4
=
γ
1
δ
2
γ
1
δ
3
γ
1
δ
5
γ
1
δ
3
γ
1
δ
3
γ
1
δ
5
γ
5
δ
5
.
And finally, a control law u = FX can be found.
The corresponding feedback is obtained with U
4
=
F ⊗ M
4
:
F =
γ
1
δ
3
γ
1
δ
2
γ
1
δ
2
ε γ
1
δ
1
. (5)
See in Figure 4 the controller that has been added to
the original TEG of Figure 2.
After applying the controller, the new behaviour
of the internal transitions of the system are repre-
sented in Figure 5. One can easily see that the dy-
namics of the transitions of the upper TEG of Figure 2
match as closely as possible
13
the cyclic behaviour of
the lower TEG.
5.2 Verifying Time Constraints
Problems of duration control are relatively frequent
in industry, one of them concerns the control of semi-
conductor wafer fabrication with cluster tools (Kim
13
Dynamics of t
2
and t
3
actually coincide.
On Solving Controlled-Invariance Problems in Dioids Using the PyMinMaxGD Python Scripts Library
561
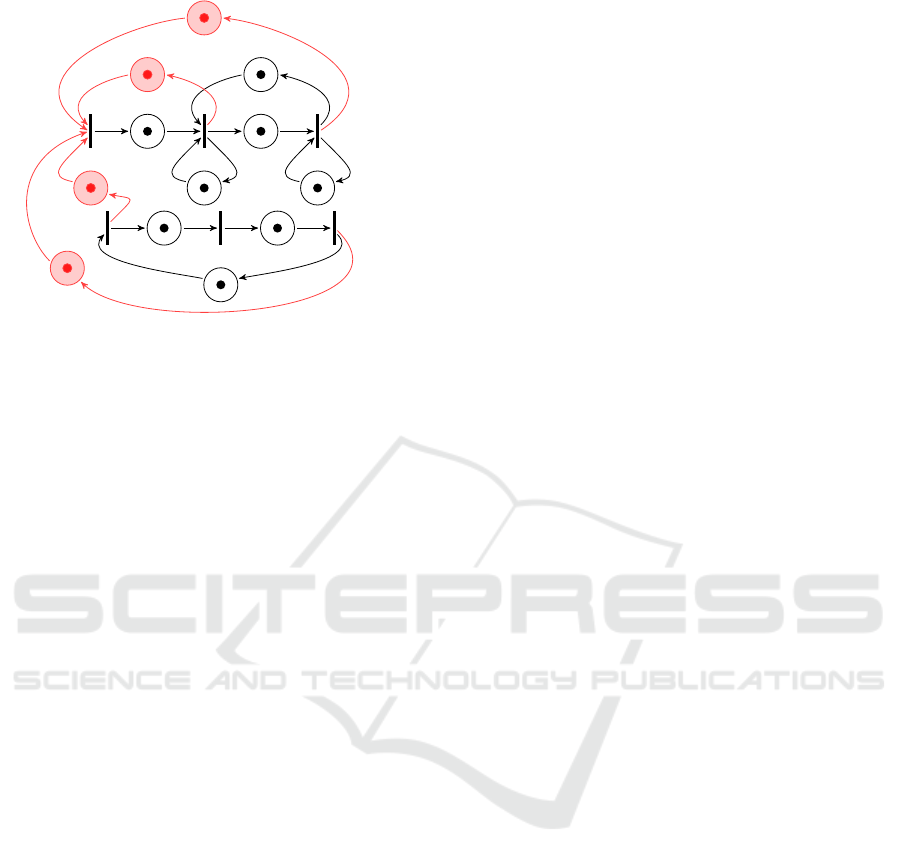
u
0
t
2
2
3
t
1
2
2 2
7
t
3
t
4
1
2
t
5
3
2
2
Figure 4: The upper TEG of Figure 2 is synchronised with
a takt time thanks to a feedback (in red).
and Lee, 2016; Jacob and Amari, 2017; Cárdenas
et al., 2017). Some operations that occur in process
modules, or chambers, have a limitation in terms of
duration variation or a maximal duration that should
not be exceeded. This kind of problems has al-
ready been tackled as a controlled-invariant problem
in (Cárdenas et al., 2017) in dioid R
max
. The exam-
ple presented here have also been solved in (Kim and
Lee, 2016; Jacob and Amari, 2017). The example
given in (Cárdenas et al., 2017) is transposed here
into the M
ax
in
Jγ, δK dioid and solved with scripts writ-
ten thanks to our toolbox. The system given hereafter
has to verify time constraints given as an inequality.
The goal is to seek the supremal controlled-invariant
set included in the set of solution of that constraint
inequality. The systems behaviour follows (1) with:
A =
ε γ
1
δ
100
ε ε ε γ
1
δ
280
ε ε
ε γ
1
δ
115
ε ε ε γ
1
δ
295
ε ε
ε γ
1
δ
5
ε ε ε γ
1
δ
240
ε ε
ε γ
1
δ
20
ε ε ε γ
1
δ
255
ε ε
ε ε ε ε e ε ε ε
ε e ε ε ε ε ε ε
ε ε ε e ε ε ε ε
ε ε ε ε ε ε e ε
, B =
ε
e
ε
ε
ε
ε
ε
ε
.
The state trajectories have to verify the constraints
expressed by the following inequality:
E ⊗ x ≤ x,
with matrix E:
E =
ε ε ε ε ε ε ε ε
ε ε ε ε ε ε ε ε
ε ε ε ε ε ε ε ε
ε ε ε ε ε ε ε ε
ε ε ε ε ε ε ε ε
γ
0
δ
−110
ε ε ε ε ε ε ε
ε ε ε ε ε ε ε ε
ε ε γ
0
δ
−250
ε ε ε ε ε
,
the set of solution is ImE
⋆
with
E
⋆
=
e ε ε ε ε ε ε ε
ε e ε ε ε ε ε ε
ε ε e ε ε ε ε ε
ε ε ε e ε ε ε ε
ε ε ε ε e ε ε ε
γ
0
δ
−110
ε ε ε ε e ε ε
ε ε ε ε ε ε e ε
ε ε γ
0
δ
−250
ε ε ε ε e
.
By calculation, the supremal controlled-invariant
module is M
3
= ImM
3
, M
3
being described in (6).
M
3
is also feedback controlled-invariant, so U
3
=
F ⊗ M
3
:
F =
ε γ
1
δ
115
ε γ
1
δ
180
γ
1
δ
295
ε ε ε
.
(7)
Two simulations are presented in Figure 6. The
initial state do not belong to M
3
and there is no feed-
back applied. Let us observe that there is a variation
of the sojourn time between x
6
and x
1
and its duration
may exceed 110 time units. In Figure 7, the initial
state belongs to M
3
and feedback F is applied. Ob-
serve the regularity of the sojourn time between x
6
and x
1
and its duration never exceeds 110 time units.
5.3 Scripting with PyMinMaxGD
All the calculations and figures presented in this sec-
tion have been realised using Python scripts within
our toolbox and are available in our distribution.
For instance, the high-level script that gives the
results shown in Section 5.1 is the following one:
from pyminmaxgd import *
# CIlib: controlled-invariance library
from CIlib import eye, mpsolve
from CIlib import computeModule, normalize
from CIlib import computeVM, fb_calcul
# Model of the production system
A = smatrix(2, 2)
# File definition of the matrix cells
load(A, "A.sm")
# Only entry for the production system
B = smatrix(2, 1)
B[1, 0] = mono(0, 0)
# Model of the specifications to follow
Ar = smatrix(3, 3)
load(Ar, "Ar.sm")
# Extended matrices,
# including both systems
Ab = smatrix(A, smatrix(2, 3))
Arr = smatrix(smatrix(3, 2), Ar)
Abt = smatrix(transpose(Ab), transpose(Arr))
Ab = transpose(Abt)
Bbt = smatrix(transpose(B), smatrix(1, 3))
Bb = transpose(Bbt)
# x has to remain in the module
# defined by S x <= T x
S = smatrix(2, 5)
load(S, "S.sm")
T = smatrix(2, 5)
load(T, "T.sm")
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
562
M
3
=
ε ε ε ε ε ε ε ε ε ε ε e ε
ε ε ε e e e e e e e γ
0
δ
−35
ε ε
ε ε ε ε ε ε ε ε ε ε ε ε e
ε ε ε γ
0
δ
−130
γ
0
δ
−120
γ
0
δ
−95
γ
0
δ
−30
γ
0
δ
−55
γ
0
δ
−30
γ
0
δ
−20
e ε ε
ε ε ε ε γ
0
δ
−170
ε γ
0
δ
−170
ε ε γ
0
δ
−225
γ
0
δ
−205
ε ε
e ε ε ε ε ε ε ε ε ε ε γ
0
δ
−110
ε
ε e ε γ
0
δ
−245
γ
0
δ
−180
γ
0
δ
−245
γ
0
δ
−245
γ
0
δ
−235
γ
0
δ
−215
ε ε
ε ε e ε ε ε ε ε ε ε ε ε γ
0
δ
−250
(6)
Figure 5: State behaviour of systems internal transitions,
after synchronisation.
Figure 6: State behaviour of systems internal transitions x
1
and x
6
.
# Computation of the admissible domain,
# i.e. where x should remain in ImS0,
# solution of S x <= T x,
S0 = mpsolve(S, T, eye(5, 5))
# Computation of the Module,
# thanks to Theorem 3.1
module = computeModule(S0, Ab, Bb)
# Normalization of the module
# in order to reduce its size
normalModule = normalize(module)
# Computation of V_M^
*
(A,B)
# This function is not detailed here.
# See the reference [Cárdenas et al.
# '17] for more details
# alpha is a kind of starting point
Figure 7: State behaviour of systems internal transitions x
1
and x
6
. Controller F is applied to the system, initial state
starts in M
3
.
alpha = mono(0, 29)
M, V = computeVM(normalModule, Ab, Bb, alpha)
# The corresponding static feedback
F = fb_calcul(M, V, Ab, Bb)
print("F=\n", F, sep="")
save(F, "F.sm")
The possibility to load matrices from external files
has been used in the previous script, in order to sim-
plify it. In the end, we store the feedback result in a
new file, for the sake of the persistence of the data.
The file contents of the four previously loaded
series-matrix are displayed below.
Series matrix A :
2 x 2
| 0 | 1 |
0 | (1,2)[e]* | (1,2)[e]* |
1 | (1,3)[e]* | (1,2)[e]* |
Series matrix Ar :
3 x 3
| 0 | 1 | 2 |
0 | eps | eps | (1,1)[e]* |
1 | (1,7)[e]* | eps | eps |
2 | eps | (1,2)[e]* | eps |
Series matrix S :
2 x 5
| 0 | 1 | 2 | 3 | 4 |
0 | eps | eps | (e)[e]* | eps | eps |
1 | (e)[e]* | (e)[e]* | eps | eps | eps |
Series matrix T :
On Solving Controlled-Invariance Problems in Dioids Using the PyMinMaxGD Python Scripts Library
563

2 x 5
| 0 | 1 | 2 | 3 | 4 |
0 | (e)[e]* | (e)[e]* | eps | eps | eps |
1 | eps | eps | (e)[e]* | eps | eps |
The last export of the first script indeed yields the
same result as the one shown in (5):
1 x 5
| 0 | 1 | 2 | 3 | 4 |
0 | (1,3)[e]* | (1,2)[e]* | (1,2)[e]* | eps | (1,1)[e]* |
As for the high-level script that gives the results
shown in Section 5.2, its content is as follows:
# In this file we tackle the control
# of DESs that has to meet time
# constraints: example of Jae Kim and
# Tae-Eog Lee, published in 2003
from pyminmaxgd import *
# CIlib: controlled-invariance library
from CIlib import computeModule, normalize
from CIlib import computeVM, fb_calcul
from CIlib import ones, Includespan
from CIlib import getfullcol
A = smatrix(8, 8)
load(A, "A2.sm")
B = smatrix(8, 1)
B[1, 0] = mono(0, 0)
E = smatrix(8, 8)
load(E, "E2.sm")
print("E=", E)
Es = star(E)
print("E*=", Es)
# Computation of the Module
module = computeModule(Es, A, B)
normalModule = normalize(module)
alpha = mono(-30, 300)
M, V = computeVM(module, A, B, alpha,
memorySafe=True)
F = fb_calcul(M, V, A, B)
print("F=\n", F, sep="")
save(F, "F2.sm")
# Now some simulations using F
answer = Includespan(M, A * M + B * F * M)
print("Is M (A+B*F) invariant ?", answer)
x0 = ones(A.getcol(), 1)
print("with x0=\n", x0)
print("Is x0 in ImM ?", Includespan(M, x0))
xk1 = A * x0
xk2 = A * xk1
xk3 = A * xk2
xk4 = A * xk3
xk5 = A * xk4
xk6 = A * xk5
xk7 = A * xk6
xk8 = A * xk7
xk9 = A * xk8
s = x0 + xk1 + xk2 + xk3 + xk4 + xk5
s = s + xk6 + xk7 + xk8 + xk9
print("Sequence s from x0 out of ImM:", s)
answer = Includespan(M, s)
print("x remains in ImM w/o fb?", answer)
ColA = A.getcol()
x1 = getfullcol(M, 0)
x2 = getfullcol(M, 1)
V4 = smatrix(ColA, 1)
V4[1, 0] = mono(0, 180)
V4[3, 0] = mono(0, 60)
V4[4, 0] = mono(0, 10)
V4[6, 0] = mono(0, 0)
V5 = smatrix(ColA, 1)
V5[0, 0] = mono(0, 110)
V5[5, 0] = mono(0, 0)
V6 = smatrix(ColA, 1)
V6[2, 0] = mono(0, 250)
V6[7, 0] = mono(0, 0)
x0 = x1 + x2 + V4 + V5 + V6
print("with x0=\n", x0)
print("Is x0 in ImM ?", Includespan(M, x0))
Abf = A + B * F
xl1 = Abf * x0
xl2 = Abf * xl1
xl3 = Abf * xl2
xl4 = Abf * xl3
xl5 = Abf * xl4
xl6 = Abf * xl5
xl7 = Abf * xl6
xl8 = Abf * xl7
xl9 = Abf * xl8
l = x0 + xl1 + xl2 + xl3 + xl4 + xl5
l = l + xl6 + xl7 + xl8 + xl9
print("Sequence l starting from x0 in ImM", l)
answer = Includespan(M, l)
print("x remains in ImM w/ fb ?", answer)
# Should yield True
blist = [s[0, 0], s[5, 0]]
glist = [l[0, 0], l[5, 0]]
legend = ["x1", "x6"]
title1 = "Without controller"
title2 = "With controller F"
multidraw(blist, legend, mono(5, 1000), title1)
multidraw(glist, legend, mono(5, 1000), title2)
A special Boolean parameter memorySafe has
been used in order to call a memory-safe internal al-
gorithm for the RAM size. Please note the use of the
multidraw() function, in order to draw several series
trajectories at the same time in the very same figure.
The last export of the second main script indeed
yields the same result as the one shown in (7):
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
564

1 x 8
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
0 | eps | (1,115)[e]* | eps | (1,180)[e]* | (1,295)[e]* | eps | eps | eps |
The file contents of the two previously loaded
series-matrix are displayed below.
Series matrix A :
8 x 8
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
0 | eps | (1,100)[e]* | eps | eps | (1,280)[e]* | eps | eps | eps |
1 | eps | (1,115)[e]* | eps | eps | (1,295)[e]* | eps | eps | eps |
2 | eps | (1,5)[e]* | eps | eps | (1,240)[e]* | eps | eps | eps |
3 | eps | (1,20)[e]* | eps | eps | (1,255)[e]* | eps | eps | eps |
4 | eps | eps | eps | (1,0)[e]* | eps | eps | eps | eps |
5 | eps | (1,0)[e]* | eps | eps | eps | eps | eps | eps |
6 | eps | eps | eps | (1,0)[e]* | eps | eps | eps | eps |
7 | eps | eps | eps | eps | eps | eps | (1,0)[e]* | eps |
Series matrix E :
8 x 8
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
0 | eps | eps | eps | eps | eps | eps | eps | eps |
1 | eps | eps | eps | eps | eps | eps | eps | eps |
2 | eps | eps | eps | eps | eps | eps | eps | eps |
3 | eps | eps | eps | eps | eps | eps | eps | eps |
4 | eps | eps | eps | eps | eps | eps | eps | eps |
5 | (0,-110)[e]* | eps | eps | eps | eps | eps | eps | eps |
6 | eps | eps | eps | eps | eps | eps | eps | eps |
7 | eps | eps | (0,-250)[e]* | eps | eps | eps | eps | eps |
6 CONCLUSION
To the best of our knowledge, nobody had applied the
controlled-invariance theory on systems described in
M
ax
in
Jγ, δK ever before.
Thanks to PyMinMaxGD, the Python toolbox de-
veloped on top of the C++ MinMaxGD library, it is
now possible to easily compute a control law that en-
forces a takt time for a given production system. With
the same library a solution of a problem of time con-
straints control expressed in the M
ax
in
Jγ, δK dioid has
been given. More examples and problems will be in-
vestigated using the same framework. Some other fu-
ture work will also deal with the compatibility and
compilation of our toolbox on main other operating
systems (OS’s), namely macOS® and Windows®. In
the meantime, a first workaround for users of these
OS’s could be to install a Linux virtual machine on
their computers, which should work fine with nowa-
days technology.
ACKNOWLEDGEMENTS
Linux is the registered trademark of Linus Torvalds in
the U.S. and other countries.
For the purpose of Open Access, a CC-
BY public copyright licence (available at https://
creativecommons.org/licenses/by/4.0/) has been ap-
plied by the authors to the present document and will
be applied to all subsequent versions up to the Author
Accepted Manuscript arising from this submission.
REFERENCES
Allamigeon, X., Gaubert, S., and Goubault, E. (2010). The
Tropical Double Description Method. In Marion, J.-
Y. and Schwentick, T., editors, Proceedings of the
27
th
International Symposium on Theoretical Aspects
of Computer Science (STACS 2010), page 47 – 58,
Nancy, France. Springer.
Animobono, D., Scaradozzi, D., Zattoni, E., Perdon, A.,
and Conte, G. (2022). The Model Matching Problem
for Switching Max-Plus Systems: a Geometric Ap-
proach. IFAC-PapersOnLine, 55(40):7 – 12. 1
st
IFAC
Workshop on Control of Complex Systems COSY
2022.
Baccelli, F., Cohen, G., Olsder, G. J., and Quadrat, J.-P.
(1992). Synchronization and Linearity, An Algebra
for Discrete Event Systems. Wiley. www.rocq.inria.fr/
metalau/cohen/documents/BCOQ-book.pdf.
Basile, G. and Marro, G. (1969). Controlled and con-
ditioned invariant subspaces in linear system theory.
Journal of Optimization Theory and Applications,
3(5):306 – 315.
Basile, G. and Marro, G. (1992). Controlled and condi-
tioned invariants in linear system theory. Prentice
Hall, Englewood Cliffs.
Bednar, J., Clevorn, J., Dvorak, J., Tirpak, D., and
Zorzenon, D. (2024). PetriTUB – Python toolbox to
manipulate untimed Petri nets and timed event graphs
in the max-plus and min-plus algebra. git.tu-berlin.de/
control/discrete-event-systems/petritub. Retrieved on
6 September 2024.
Boutin, O. and Martinez, C. (2024). PyMinMaxGD. gitlab.
univ-nantes.fr/dioids/python-toolbox. Retrieved on 6
September 2024.
Brunsch, T., Raisch, J., Hardouin, L., and Boutin, O.
(2013). Discrete-Event Systems in a Dioid Frame-
work: Modeling and Analysis, pages 431 – 450.
Springer London, London.
Butkovi
ˇ
c, P. and Hegedüs, G. (1984). An elimination
method for finding all solutions of the system of lin-
ear equations over an extremal algebra. Ekonomicko-
matematicky Obzor, 20:203 – 214.
Cárdenas, C., Loiseau, J. J., and Martinez, C. (2015). Con-
trolled Invariance and Dynamic Feedback for Systems
over Semirings. pages 1 – 8.
Cárdenas, C., Loiseau, J. J., and Martinez, C. (2017). Invari-
ance par retour d’état sur le demi-anneau max-plus. In
MSR 2017, Modélisation des Systèmes Réactifs, pages
1 – 8, Marseille.
Chancelier, J.-P., Delebecque, F., Pinçon, B., and Quadrat,
J.-P. (2015). ScicosLab. www.scicoslab.org. Retrieved
on 6 September 2024.
Civil Infrastructure Platform™ (2023). Ker-
nel Maintenance. wiki.linuxfoundation.org/
civilinfrastructureplatform/cipkernelmaintenance#
cip_kernel_-_slts_kernel. Retrieved on 25 April
2024.
Cohen, G., Moller, P., Quadrat, J.-P., and Viot, M. (1986).
Dating and Counting events in Discrete-Event Sys-
tems. In Proceedings of the 25
th
IEEE Conference
On Solving Controlled-Invariance Problems in Dioids Using the PyMinMaxGD Python Scripts Library
565

on Decision and Control, pages 988 – 993, Athens,
Greece.
Cohen, G., Moller, P., Quadrat, J.-P., and Viot, M. (1989).
Algebraic Tools for the Performance Evaluation of
Discrete Event Systems. Proceedings of the IEEE,
77(1):39 – 58. Special issue on Discrete Event Sys-
tems.
Conte, G. and Perdon, A. M. (1995). The disturbance de-
coupling problem for systems over ring. SIAM J. Con-
trol & Optimization, 33:750 – 764.
Corronc, E. L. (2013). Activités de recherche – Librairies
de calcul. homepages.laas.fr/elecorro/Recherche/
softwares.php. Retrieved on 6 September 2024.
Cottenceau, B., Hardouin, L., and Trunk, J. (2022).
(Event|Time)-Variant Operators – A C++ toolbox to
handle series for event-variant/time-variant (max,+)
systems. perso-laris.univ-angers.fr/~cottenceau/
ETVOintroduction.pdf. Retrieved on 6 September
2024.
Cottenceau, B., Lhommeau, M., Hardouin, L., and Boi-
mond, J.-L. (2000). Data Processing Tool for Calcula-
tion in Dioid, pages 469 – 470. Springer US, Boston,
MA.
Di Loreto, M., Gaubert, S., Katz, R. D., and Loiseau, J. J.
(2010). Duality between invariant spaces for max-plus
linear discrete event systems. SIAM J. Control & Op-
timization, 48(8):5606 – 5628.
Ferreira Cândido, R. M., Lhommeau, M., Hardouin, L.,
and Santos-Mendes, R. (2017). MinMaxGDJS : A
web toolbox to handle pseudo-periodic series in Min-
Max[[gamma,delta]] semiring. In IFAC 2017 World
Congress, Toulouse, France.
Free Software Foundation, Inc. (2007). GNU General Pub-
lic License. www.gnu.org/licenses/gpl-3.0.en.html.
Retrieved on 6 September 2024.
Grothendieck, A. and Dieudonné, J. (1960). Éléments de
géométrie algébrique. Publications Mathématiques de
L’Institut des Hautes Études Scientifiques, pages 5 –
214.
Haghsheno, S., Binninger, M., Dlouhy, J., and Sterlike, S.
(2016). History and Theoretical Foundations of Takt
Planning and Takt Control. In Proc. 24th Ann. Conf.
of the Int’l. Group for Lean Construction, pages 53 –
62, Boston, MA, USA. www.iglc.net/Papers/Details/
1297/pdf.
Hardouin, L. (2024). Data processing tools to handle
periodic series in dioid. perso-laris.univ-angers.fr/
~hardouin/outils.html. Retrieved on 6 September
2024.
Hautus, M. L. J. (1982). Controlled invariance in systems
over ring. Feedback Control of Linear and Nonlinear
Systems. Proceeding of the Joint Workshop on Feed-
back and Synthesis of Linear and Nonlinear Systems,
pages 107 – 122.
Jacob, R. and Amari, S. (2017). Output feedback control of
discrete processes under time constraint: application
to cluster tools. International Journal of Computer
Integrated Manufacturing, 30:880 – –894.
Katz, R. D. (2007). Max-plus (A, B)-invariant spaces and
control of timed discrete-event systems. IEEE Trans-
actions on Automatic Control, 52(2):229 – 249.
Kim, C. and Lee, T.-E. (2016). Feedback control of clus-
ter tools for regulating wafer delays. IEEE Transac-
tions on Automation Science and Engineering, 13:189
– 1199.
Lahaye, S. (2019). Maxpluspy: a Python library for compu-
tations in max-plus algebra and manipulations of max-
plus automata. perso-laris.univ-angers.fr/~lahaye/
maxpluspy.html. Retrieved on 6 September 2024.
Liu, J. (2023). TropicalNumbers. github.com/TensorBFS/
TropicalNumbers.jl. Retrieved on 6 September 2024.
Martinez, C., Kara, R., Abdesselam, A. N., and Loiseau,
J. J. (2022). Systems synchronisation in Max-Plus al-
gebra: a controlled invariance perspective In memo-
riam Édouard Wagneur. In 1
st
IFAC Workshop on
Control of Complex Systems, Bologna, Italy.
Quadrat, Q. (2024). MaxPlus.jl – Julia’s (max,+) and
(min,+) Algebra Toolbox. github.com/Lecrapouille/
MaxPlus.jl. Retrieved on 6 September 2024.
Ramchandani, C. (1974). Analysis of Asynchronous Con-
current Systems by Petri Nets. PhD thesis, Mas-
sachusetts Institue of Technology.
Sta
´
nczyk, J. (2016). Max-Plus Algebra Toolbox for Mat-
lab®. www.stanczyk.pro/mpa/max-plus-1.7.pdf. Re-
trieved on 6 September 2024.
SWIG Maintainers (2024). SWIG. www.swig.org. Re-
trieved on 25 April 2024.
Trunk, J. (2019). On the modeling and control of ex-
tended Timed Event Graphs in dioids. PhD thesis,
Université d’Angers ; Production technology Cen-
ter PTC(Technische Universität Berlin) (Berlin (Alle-
magne)).
Wagneur, E. (1996). Torsion matrices in the max-algebra.
In Proceedings of the Workshop on Discrete Event
Systems (WODES’96), pages 165 – 168, Edimburgh,
United Kingdom.
Wonham, W. (1974). Linear multivariable control. Optimal
control theory and its applications, pages 392 – 424.
Wonham, W. and Morse, A. (1970). Decoupling and pole
assignment in linear multivariable systems: a geomet-
ric approach. SIAM Journal on Control, pages 1 – 18.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
566
