A Study on Multi-Arm Bandit Problem with UCB and Thompson
Sampling Algorithm
Haowen Yang
a
Department of Electrical and Computer Engineering, University of Florida, Gainesville, Florida, U.S.A.
Keywords: Reinforced Learning, Bandit Algorithm, Probability, Regret Analysis, Algorithm, Machine Learning,
Decision-Making, Applied Mathematics.
Abstract: Multi-Armed Bandit (MAB) problem is a sequential decision-making process with wide influence in many
fields across medical, and commercial application. In MAB problem, the initial reward distribution was
unknown, and observed during the process. In MAB application, Upper Confidence Bound algorithm and
Thompson Sampling algorithm are widely used for great performance. This work briefly review the basic
concept of MAB problem. Also, this work reviews the formulation of Upper Confidence Bound (UCB) and
Thompson Sampling (TS) algorithm. This work shows that UCB algorithm demonstrate a logarithmic
relationship. This work also review that TS is a Bayesian method solution of MAB problem. This work carried
out a brief test on the cumulative regret on UCB and Thompson sampling algorithm. The testing result shows
that TS algorithm was able to generate a lower cumulative regret compared to UCB algorithm under the same
scenario. The testing result also show that under a small probability difference and large number of arms TS
has similar performance compared to UCB algorithms.
1 INTRODUCTION
The Multi-Armed Bandit problem (MAB) is a
decision-making process with a series of constrained
actions. The MAB problem is a sequential process
where each action was taken and selected with the
result of that action being observed. The term bandit
derives from the slot machine as each time the arm on
the machine there could be a payoff or loss to the
investment to that event. In the MAB scenario, the
player is facing instead of one, but many arms, each
has individual reward distribution. The MAB aims to
seek the answer of the maximum reward from set of
arms (Bubeck & Cesa-Bianchi, 2012) (Mahajan &
Teneketzis, 2008).
MAB problem is presented with a limited dataset,
and even little prior knowledge of the data. The MAB
algorithm balances the exploration and exploitation
phase of the experiment to achieve two goals:
minimize the loss, maximize the gain (Lattimore &
Szepesv´ari, 2020).
MAB problem was applied in many different
commercial fields with great usability. For example,
website optimization is a great example of MAB
a
https://orcid.org/0009-0006-9076-8508
application. Website elements, such as picture, font,
layout, could be sequentially decided for the best
reward. The clickthrough or the number of deals and
revenues generated from the website serves as a great
benchmark to analyse the resulting reward from the
reward distribution.
Similarly, MAB problem is also practical in the
advertisement placement. Different advertising
suggestions to the customer exhibits different
performance in customer interactions indicator, such
as click rate, preference score, or purchase rate. There
has been previous work on gaining using A/B testing
in the study of customer behaviour and successfully
gain data from one of the largest e-commerce
companies in Japan (Yuta, Shunsuke, Megumi, &
Yusuke, 2021).
In the MAB problem, the learner was unaware of
the environment of the dataset. So, the true
distribution lies in the environment class. The
measurement of MAB problem performance is regret.
Regret is a measurement of the numerical difference
between the reward at round n, the sub-optimal arm,
and the overall maximum reward or the most optimal
reward over n rounds of playing (Lai & Robbins,
Yang, H.
A Study on Multi-Arm Bandit Problem with UCB and Thompson Sampling Algorithm.
DOI: 10.5220/0012938400004508
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 375-379
ISBN: 978-989-758-713-9
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
375

1985). In the stochastic bandit, the 𝑋

is the reward
for round 𝑛. 𝑎 is in the set of the environment class
𝐴. 𝜇

is denoted as the reward for action 𝑎. So, the
regret formula is expressed as follows: (Lattimore &
Szepesv´ari, 2020)
𝑅

= 𝑛 max
∈
𝜇

− 𝐸𝑋





1

The first term expresses the maximum reward
under the certain environment class. The second term
expresses the reward observed after the action, also
known as the suboptimal reward. So, if the action was
the optimal reward, the regret should be zero.
Therefore, as discussed earlier that MAB balances
exploration and exploitation, the goal is always to
develop the algorithm to reduce the regret across the
exploration and exploitation phase to best utilize the
dataset available to us.
Another important factor to be noted in this paper
is that this work only discusses the setting of
stochastic bandits (also known as stationary bandits)
where the action is independent from each and will
not be affected by the previous action taken
throughout the process. So, the dataset remains
untouched during the operation.
2 UPPER CONFIDENCE BOUND
ALGORITHM
The upper confidence bound algorithm (UCB) was
first proposed in 1985 (Lai & Robbins, 1985). The
UCB algorithm chooses an upper confidence bound
of each arm and its reward distribution. Over a
sequential decision-making process, each arm was
played and generated a confidence interval. The
algorithm always picks the arm with the largest upper
confidence bound value across all the armed had been
played. However, there is a possibility for
overestimate the optimal arm, and therefore causes
inaccuracy. However, as more data was added to an
arm, there could be a scenario where the arm will
never be chosen since the confidence interval shrinks
and upper confidence bound falls under the assumed
optimal confidence upper bound (Lattimore &
Szepesv´ari, 2020).
The UCB1 is initialized by playing each arm one
to obtain the initial reward distribution. Then, at every
time step 𝑡, each arm 𝑖 was selected to gain the
maximum result:
𝜇̂+

2log

1
𝛿

𝑛

2

, where 𝜇̂ is the mean reward of the all the arms
played. 𝑢 are the rounds played so far. (Auer, Cesa-
Bianchi, & Fischer, 2002) The regret formulation was
analysed to be logarithmic order as
𝑂(log 𝑛) (Agrawal, 1995).
To average the overestimation, the previous work
therefore defines the upper confidence bound as the
following:







is define as the confidence interval of
the sample. (Lai & Robbins, 1985) 𝛿 is defined as the
error probability. Considering in the bandit problem
scenario, the term 𝑇

(
𝑡−1
)
is defined as the samples,
and the reward as 𝑈𝐶𝐵

(
𝑡−1, 𝛿
)
. 𝛿 is denote as the
error probability. Therefore, the UCB algorithm is
defined as follows:
Table 1: Upper Confidence Bound Algorithm.
input k and 𝛿
for t = 1 to n
choose action
𝐴

=argmax𝑈𝐶𝐵

(𝑡−1, 𝛿)
observe reward 𝑋

and update the upper
confidence bounds.
end for
where the UCB index is defined as
𝑈𝐶𝐵

(
𝑡−1, 𝛿
)
= 𝜇
̂

(
𝑡−1
)
+

2log

1
𝛿

𝑇

(
𝑡−1
)
(
3
)
3 THOMPSON SAMPLING
Thompson proposed one of the first method for bandit
problem in 1933. His method was later called
Thompson Sampling (TS). (Thompson, 1933) In a
general setting of Thompson Sampling, for a series of
action (𝑥

, 𝑥

, 𝑥

,….𝑥

) ∈𝑋 in an environment
class, one action is selected as 𝑥

for 𝑖

round action.
After each action, and reward 𝑦 is observed. With the
observation of reward, there generation a random
distribution based on the prior distribution of the set
𝑋 (Russo, Van Roy, Kazerouni, Osband, & Wen,
2018).
In a Bayesian scenario, for each round 𝑖, this work
chooses an arm 𝑎 in a set of all action and obtain a
reward 𝑟

. Each arm is related to the probability
density 𝑃(𝑟|𝑎) with an expected average reward
EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence
376

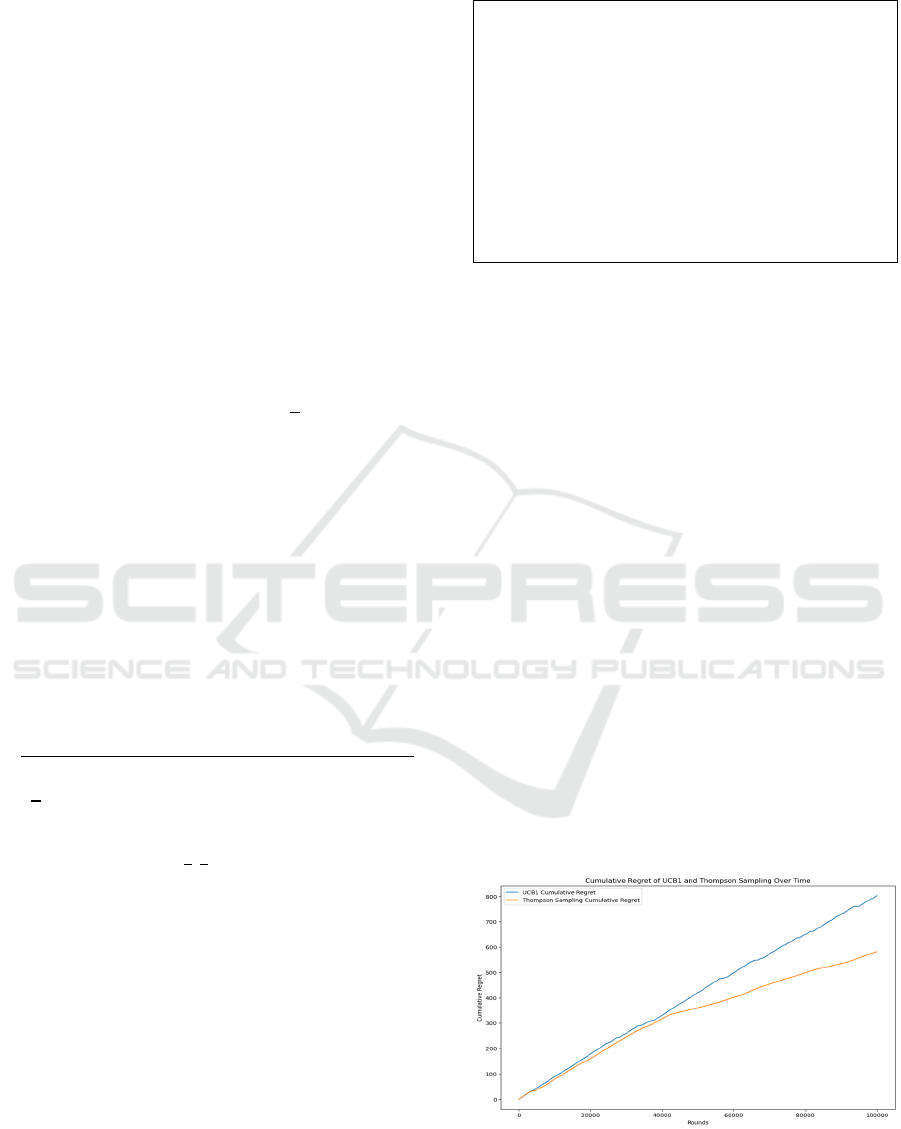
𝜇

= 𝐸

(
𝑟
|
𝑎
)
𝑟|𝑎. In a Bayesian setting, the reality
distribution, denoted as 𝑃
(
𝑟
|
𝑎
)
is unknown.
Therefore, this work introduces a separate parameter
𝜃 to represent the present 𝑃(𝑟|𝑎) as per observed.
The reward distribution was updated after each action
and reward being observed. Therefore, the updated
distribution became the prior distribution for the next
action. And the real distribution was obtained after a
sequence of action and observation. So, the term
𝑃
(
𝜃
|
𝑎

𝑡

, 𝑟

)
is redefined as 𝑃

(𝜃) (Viappiani,
2013).
Here, this work presents a quick example to show
the process of Bayesian distribution being update
after an action was taken from the unknown
distribution of an environment class. Here is an
untransparent bag with two white balls (WW) and a
white ball and black ball (WB). Before any
observation was made, it is assumed that:
𝑃
(
𝑊𝑊
)
= 𝑃
(
𝑊𝐵
)
=
1
2
Such conclusions can only be made before any
observation. To update the prior distribution based on
the observations after one action so that the
distribution is closer to the real distribution of the
balls in the bag, when one black ball is picked
(𝑏𝑙𝑎𝑐𝑘) , the action obtains the following:
𝑃
(
𝑊𝑊
|
𝑏𝑙𝑎𝑐𝑘)=0 & 𝑃
(
𝑊𝐵
|
𝑏𝑙𝑎𝑐𝑘)=1
Therefore, the posterior distribution of the balls in the
bag is 0 1.
If one white ball was picked
(
𝑤ℎ𝑖𝑡𝑒
)
, the action
obtains the following:
𝑃
(
𝑊𝑊
|
𝑤ℎ𝑖𝑡𝑒)
= 𝑃
(
𝑤ℎ𝑖𝑡𝑒
|
𝑊𝑊)
∗
𝑃
(
𝑊𝑊
)
𝑃
(
𝑤ℎ𝑖𝑡𝑒
|
𝑊𝑊∗𝑃
(
𝑊𝑊
)
+ 𝑃
(
𝑤ℎ𝑖𝑡𝑒
|
𝑊𝐵) ∗𝑃(𝑊𝐵)
)
=
2
3
Therefore, the updated posterior distribution of
the balls in the bag is 




.
In the context of Thompson Sampling, to perform
a Bayesian distribution calculation, it is introduced a
randomized generated number that represents each
arm. Therefore, setting an individual set of numbers
as a flag for each arm, the system is able to update the
posterior distribution based on the observation
(Lattimore & Szepesv´ari, 2020) (Scott, 2010) (Li,
& Olivier, 2011).
The Thompson Sampling Algorithm in the
Bayesian setting are defined as follows:
Table 2: Thompson Sampling Algorithm.
Input: Cumulative Density Function of the
mean rewards of arms
For 𝑡=1 to 𝑛
Random assign distribution 𝜃: 𝜃

(
𝑡
)
~𝐹

(𝑡) for
each arm 𝑖
Choose 𝐴

=argmax𝜃

(𝑡)
Observe 𝑋

and update:
𝐹


(
𝑡+1
)
= 𝑈𝑃𝐷𝐴𝑇𝐸 𝐹


(
𝑡
)(
4
)
End fo
r
4 PERFORMANCES OF
ALGORITHM
As described in the previous section, when choosing
a sub-optimal arm, a difference called regret was
generated. The MAB problem is balancing the
exploration and exploitation phase. The primary
objective of the MAB algorithm is to finalize the best
policy from exploration phase and apply the policy in
the exploitation phase. Therefore, cumulative regret
is the benchmark of the performance of the algorithm.
To accurately compare the UCB Algorithm and
Thompson Sampling, the following test was set up to
simulate the performance of two algorithms under the
same environment class.
There are four different settings of environment
class. This work is presenting the setting of 10 arms,
𝑘=10, and 100 arms, 𝑘= 100 to test the algorithm.
The best reward probability was set as 0.4 and reward
probability difference as 𝛿. For all arms except the
best arm, the reward probability is 0.4 −𝛿. The sub-
optimal arm is set 𝛿 as 0.1 and 0.01. The experiment
was set to be performed 100000 time.
Figure 1: Test
Result of 𝑘=10,𝛿=0.01.
A Study on Multi-Arm Bandit Problem with UCB and Thompson Sampling Algorithm
377

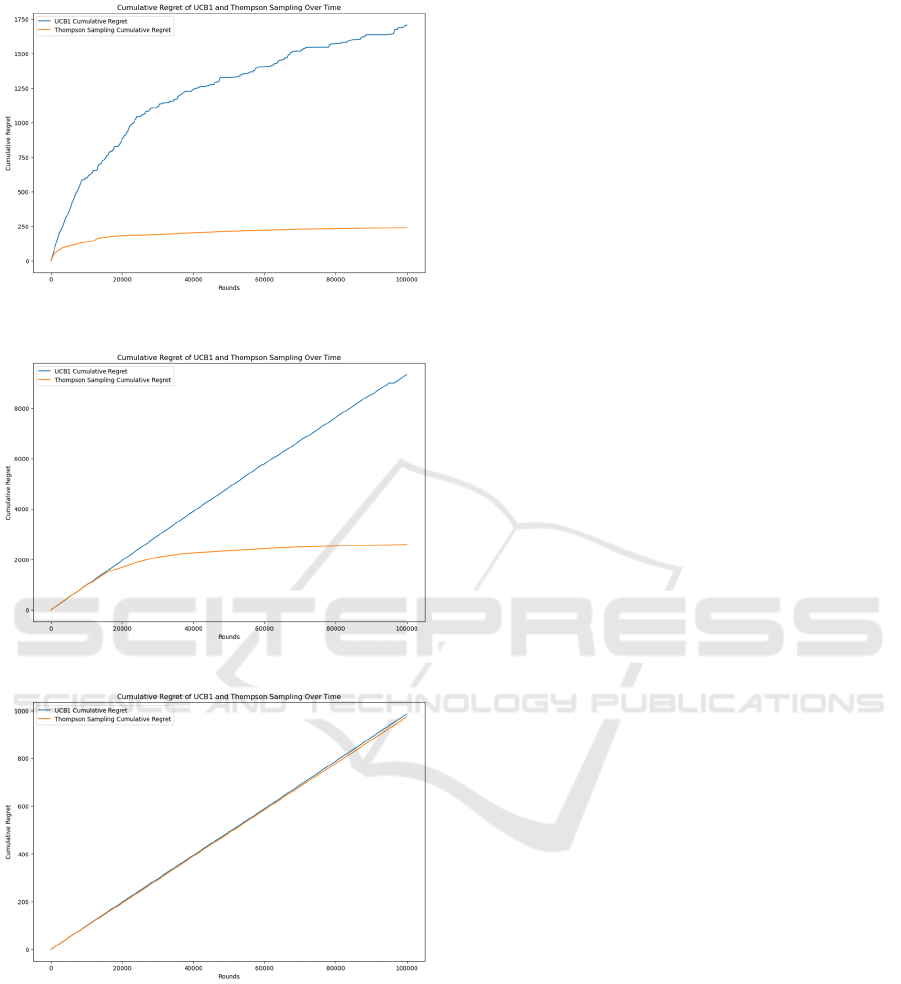
Figure 2: Test Result of 𝑘= 10, 𝛿=0.1.
Figure 3: Test Result of 𝑘= 100, 𝛿=0.1.
Figure 4: Test Result of 𝑘= 100, 𝛿=0.01.
Based on the testing result, under the following
setting: 𝑘= 100 𝛿=0.1, 𝑘=10 𝛿=0.01, and
𝑘=10 𝛿=0.01 , the Thompson Sampling is
showing an exceptionally better performance
compared to UCB algorithm. Under the UCB
Algorithm, Agrawal proved that regret displays
logarithmic scale. (Agrawal, 1995) Figure 2 shows
that regret is trending on a logarithmic scale. Also, it
is worth noting that, under 𝑘= 100, 𝛿=0.01
environment class setting, the Thompson Sampling is
demonstrating similar performance compared to
Upper Confidence Bound algorithm.
5 CONCLUSIONS
The Thompson Sampling is demonstrating an
exceptional performance compared to UCB
algorithm under all the setting except for 𝑘=
100, 𝛿=0.01. In the Thompson sampling, part of the
reason for a small regret deduction is due to the
posterior update. After each action, the posterior
distribution ensures that the distribution is closer to
the real distribution so that each action is induced
with less regret.
It is worth noting that although Thompson
Sampling generally displaying an exceptional, there
is an exception under the 𝑘= 100, 𝛿=0.01, where
both algorithms are demonstrating a very similar
performance in terms of cumulative regret. In fact,
Thompson Sampling demonstrated slightly worse
performance compared to UCB algorithm. It is worth
discussing in the future that under high number of
arms, and small reward probabilities difference, the
potential reason that led to the similar performance of
both algorithms.
REFERENCES
Agrawal, R. (1995). Sample mean based index policies by
o (log n) regret for the multi-armed bandit problem.
Advances in applied probability, 27(4), 1054-1078.
Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-
time analysis of the multiarmed bandit problem.
Machine learning, 47, 235-256.
Bubeck, S., & Cesa-Bianchi, N. (2012). Regret Analysis of
Stochastic and Nonstochastic Multi-armed Bandit
Problems. Foundations and Trends in Machine
Learning, 1-122.
Bubeck, S., & Cesa-Bianchi, N. (2012). Regret analysis of
stochastic and nonstochastic multi-armed bandit
problems. Foundations and Trends® in Machine
Learning, 5(1), 1-122.
Lattimore, T., & Szepesvári, C. (2020). Bandit algorithms.
Cambridge University Press.
Chapelle, O., & Li, L. (2011). An empirical evaluation of
thompson sampling. Advances in neural information
processing systems, 24.
Mahajan, A., & Teneketzis, D. (2008). Multi-armed bandit
problems. In Foundations and applications of sensor
management (pp. 121-151). Boston, MA: Springer US.
Russo, D. J., Van Roy, B., Kazerouni, A., Osband, I., &
Wen, Z. (2018). A tutorial on thompson sampling.
EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence
378

Foundations and Trends® in Machine Learning, 11(1),
1-96.
Scott, S. L. (2010). A modern Bayesian look at the multi‐
armed bandit. Applied Stochastic Models in Business
and Industry, 26(6), 639-658.
Slivkins, A. (2019). Introduction to multi-armed bandits.
Foundations and Trends® in Machine Learning, 12(1-
2), 1-286.
Thompson, W. R. (1933). On the likelihood that one
unknown probability exceeds another in view of the
evidence of two samples. Biometrika, 25(3-4), 285-294.
Viappiani, P. (2013). Thompson sampling for Bayesian
bandits with resets. In Algorithmic Decision Theory:
Third International Conference, ADT 2013, Bruxelles,
Belgium, November 12-14, 2013, Proceedings 3 (pp.
399-410). Springer Berlin Heidelberg.
A Study on Multi-Arm Bandit Problem with UCB and Thompson Sampling Algorithm
379